Тепловая проводимость контакта — Энциклопедия по машиностроению XXL
ТЕПЛОВАЯ ПРОВОДИМОСТЬ КОНТАКТА [c.66]Тепловая проводимость контакта пропорциональна плотности контакта, фактической площади, обратно пропорциональна высоте третьего тела под нагрузкой и зависит от теплопроводности контактирующих тел с учетом микрорельефа [c.66]
К — тепловая проводимость контакта [c.66]
Ск — тепловая проводимость контакта, вт/ м град) [c.5]
В результате экспериментов было выявлено, что тепловая проводимость контакта прямо пропорциональна нагрузке и квадрату абсолютной температуры при одном и том же значении нагрузки. [c.13]
| Рис. 1-22. Влияние направления теплового потока на тепловую проводимость контакта пары. |

Из большого числа формул по контактному теплообмену, приведенных в рассматриваемых работах, для приближенного расчета термического сопротивления или тепловой проводимости контакта могут быть рекомендованы для плоских поверхностей с чистотой обработки 4—9-го класса выражение (1-3), для поверхностен выше 7-го класса чистоты прн наличии неплоскостности (11-8), для контакта в вакууме поверхностей с макроотклонениями (1-14), для всех поверхностей в вакууме (1-35) и в га. зовых средах (1-36). [c.43]
Подставив (3-6) и (3-22) в (1-1), получим выражение для определения тепловой проводимости контакта при первоначальном нагружении поверхностей с чистотой обработки до 5-го класса из высокопластичных материалов при /7[c.87]
Выражение для тепловой проводимости контакта при повторных приложениях нагруз ки для всех классов чистоты обработки поверхностей, а также при первоначальных нагружениях для поверхностей с чистотой обработки выше 11-го класса получим путем подстановки (3-9) и (3-236) в (1-1)
[c. 87]
87]
В этом случае вторая составляющая общей тепловой проводимости контакта при начальном нагружении имеет вид
Рассмотренное выше влияние продолжительности контакта на формирование величины площади фактического контакта и сближение показывает, что в каждом частном случае в той или ной мере имеет место рост тепловой проводимости контакта. [c.97]
Наибольшей способностью к росту тепловой проводимости контакта обладают материалы с малым пределом текучести и, наоборот, наименьший рост проводимости тепла в зоне контакта будет наблюдаться при высоком модуле упругости материала. [c.98]
Вернемся к порядку проведения экспериментов. По установлении стационарного теплового режима, когда тепловая защита и компенсационные обогреватели позволяют добиться линейного закона изменения температуры вдоль образцов, тепловая проводимость контакта определяется следующим выражением
 108]
108]
При нестационарном тепловом режиме в зоне контакта в данный момент времени t тепловая проводимость контакта Ок.нст или обратное ей термическое сопротивление 7 к.пст определяется следующим выражением [c.109]
Б гл. 2 отмечено, что при значительной по времени выдержке поверхностей под нагрузкой увеличивается площадь контакта и растет сближение. Все это несомненно ведет к увеличению тепловой проводимости контакта с ростом времени т приложения нагрузки. Это подтверждается результатами опытов, проведенных по программе, включающей пять серий опытов (табл. 5-7). [c.127]
Конечное значение тепловой проводимости контакта соединения нагреватель — образец по формуле (3-25)
Конечное значение тепловой проводимости контакта соединения образец — холодильник определяется по формуле (3-25) [c.176]
Конечное значение тепловой проводимости контакта нагреватель—образец определяется из выражения (3-30)
[c. 177]
177]
Конечное значение тепловой проводимости контакта образец — холодильник [c.178]
Полную тепловую проводимость контакта определяем по выражению (1-2) без учета влияния окисной пленки [c.185]
Полная тепловая проводимость контакта согласно формуле (1-2) равна [c.186]
Полная тепловая проводимость контакта согласно (1-2) равна
Подставив полученные значения величин в выражение (3-30), получим величину тепловой проводимости контакта плоской и волнистой поверхностей [c.190]
Полная тепловая проводимость контакта труба — оребрение нз формулы (. -26). [c.191]
Общая тепловая проводимость контакта шероховатых поверхностей определится формулой [c.324]
В реальных конструкциях тепловой контакт между соприкасающимися деталями обычно нельзя считать идеальным. Контактирующие поверхности являются шероховатыми и имеют отклонения от правильной геометрической формы.
Для расчета эффективной тепловой проводимости на границах контакта блока с основанием основания с наружным колпаком и осно- [c.41]
Рис, 1-17. Зависимость тепловой проводимости соединений от температуры для различных материалов в зоне контакта [Л. 55].
Р.СЛИ в процессе туннелирования электрон передаёт часть энергии локальному примесному состоянию, то открывается ДОПОЛНИТ- канал для туннелирования. Включение туннелирования через примесное состояние увеличивает проводимость контакта при eV=hij)o, где ш — энергия возбуждения примесного центра. На кривой d 1 jdV это отражают дополнит, пики. Форма линии при этом зависит от естеств. ширины линии, энергии возбуждения и температурного уширения из-за теплового размазывания энергетич. распределения электронов (рис. 3).
На кривой d 1 jdV это отражают дополнит, пики. Форма линии при этом зависит от естеств. ширины линии, энергии возбуждения и температурного уширения из-за теплового размазывания энергетич. распределения электронов (рис. 3).
Роджерс [ Л- 33] обратил внимание на уменьшение теплового сопротивления контакта с ростом температуры, отмеченное в [Л. 2]. Им была создана специальная экспериментальная установка, позволяющая изменять направление теплового потока при сохранении контакта неизменным. Автор обнаружил, что тепловое сопротивление контакта стали с алюминием зависит от направления теплового потека теплопроводность от алюминия к стали выше, чем от стали к алюминию. Этот эффект исчезал при установке слюдяной прокладки между образцами. На основании этого автор связывает полученное явление с механизмом проводимости в точках металлического контакта. Когда металлы, имеющие различную величину работы выхода, находятся в контакте, создается потенциальный барьер, который уменьшает дрейф свободных электронов в одном направлении и увеличивает в другом
 11]
11]
Ом — тепловая проводимость фактического контакта, йг/(л град) [c.5]
Не — тепловая проводимость среды в зоне контакта, вт/(м град) [c.5]
Тепловая проводимость через зону контакта образцов вычислялась по формуле а = Ш /ЛГ5, где - [c.12]
Тепло па границе раздела может передаваться теплопроводностью через контактные пятна, теплопроводностью, конвекцией и излучением в промежутках между пятнами. Если пренебречь лучистым теплообменом между поверхностями, разделенными газовой прослойкой, которым передается около 1—2% тепла, то в порядке приближения можно считать, что тепловая проводимость контакта jR равна сумме тепловых проводимостей контактных пятен Rk и газовой прослойки ilRr.
Шероховатость первой пары из стали ЭИ69 была Н р = 4,1 мк (кривая 1), второй пары Н р = 2,8 мк (кривая 2). Из графиков видно, что с увеличением давления р контактное сопротивление падает, т. е. тепловая проводимость контактов однозначно не определяется теплофизическими характеристиками материалов она зависит также от механических свойств контактирующих тел и нагрузки.
Из графиков видно, что с увеличением давления р контактное сопротивление падает, т. е. тепловая проводимость контактов однозначно не определяется теплофизическими характеристиками материалов она зависит также от механических свойств контактирующих тел и нагрузки.
В работе [Л. 15] считается что тепловая проводимость контакта определяется в осно аном передачей тепла через места непосредственного контакта при давлении в камере порядка 10 — мм рг. ст. В то же время отмечается, что и01выщение давления гелия до 10 мм рт. ст. повышает тепловую проводимость контакта при нагрузке р = 30-10 н1м в 3 раза. Это объясняется тем, что при давлении в камере 10 мм рт. ст. значительно увеличивается передача тепла через газовую прослойку. К сожалению, отсутствие данных по чистоте контактирующих поверхностей не дает возможности провести какие-либо сопоставления. [c.13]
Несколько в другом плане выглядит рассмотрение характера теплообмена в зоне контакта при соприкосновении поверхностей с отклонениями от плоскости в интерпретации Клаузинга и Чао [Л. 30]. Авторами этой работы предпринимается попытка проанализировать природу тепловой проводимости контакта в вакууме на примере собственной модели. Авторы считают далекими от действительности предложенные ранее модели, в которых были сделаны допущения о равномерном расположении микроскопических контактных пятен по номинальной поверхности соприкооновения. В действительности же в реальных контактных соединениях вследствие неплоскостности сопрягаемых поверхностей возникают крупномасштабные области расположения контактных пятен в так называемых контурных областях контакта, которые оказывают существенное -влияние на распределение линий теплового потока при подходе к концентрациям этих пятен.
[c.24]
30]. Авторами этой работы предпринимается попытка проанализировать природу тепловой проводимости контакта в вакууме на примере собственной модели. Авторы считают далекими от действительности предложенные ранее модели, в которых были сделаны допущения о равномерном расположении микроскопических контактных пятен по номинальной поверхности соприкооновения. В действительности же в реальных контактных соединениях вследствие неплоскостности сопрягаемых поверхностей возникают крупномасштабные области расположения контактных пятен в так называемых контурных областях контакта, которые оказывают существенное -влияние на распределение линий теплового потока при подходе к концентрациям этих пятен.
[c.24]
Определение тепловой проводимости контакта по выран ению (1-26) сводится в основном к получению значения относительной фактической площади контакта. Операции по определению относительной площади фактического контакта теоретическим путем из-за сложности получения функциональной связи между площадью фактического касания, давлением, механическими свойствами материалов и геометрией поверхностей чрезвычайно трудоемки, поэтому автор считает целесообразным обобщить большой экспериментальный материал по контактному теплообмену. [c.41]
[c.41]
Исходя из выражений, определяющих тепловую проводимость контакта плоскостно-шероховатых поверхностей, зависимости для теплового контакта волнистых поверхностей имеют следующий вид при начальном нагружении [c.95]
Из уравнения (3-34) видно, что в начальный лериод тепловая проводимость контакта растет достаточно интенсивно, затем рост ее постепенно снижается и стремится постоянной величине. [c.98]
Рис, 5-14. Зависимость тепловой проводимости контакта от времени приложения нагрузки при различных термических условиях для пары с неметаллическим материалом (а) и продольные и поперечные профилограммы ее поверхностей (б). Материалы пары ФК16Л — сталь 45 нагрузка 19,6-10 н м . [c.129]
Рассмотрим процесс теплообмена в зоне комбинированной клее-метал-лической прослойки (рис. 4-26,а), схема включения термического сопротивления которой для плоскошероховатых поверхностей субстрата показана на рис. 4-26,6, где Ян.с.ш, Ясг.т, Ro — термические сопротивления соответственно клеевого слоя, стягивания к пятнам контакта, окисных пленок (см. гл. 1). Общая тепловая проводимость клее-метал-лической прослойки представляется соотношением 1 1,1
[c.149]
4-26,6, где Ян.с.ш, Ясг.т, Ro — термические сопротивления соответственно клеевого слоя, стягивания к пятнам контакта, окисных пленок (см. гл. 1). Общая тепловая проводимость клее-метал-лической прослойки представляется соотношением 1 1,1
[c.149]
Для более высокотеплопроводных и пластичных металлов (дюралюмин Д16 и Д1) характерна более выря женная зависимость термического сопротивления от нагрузки. Это объясняется превалирующим значением ст.ш по сравнению с Як.с.ш в общем сопротивлении (см. расчетные кривые ст.ш и Як.с.ш на рис. 4-31). Повышение чистоты обработки поверхностей субстратов приводит к значительному снижению термического сопротивления клее-металлической прослойки, причем кривые в этом случае имеют более пологий характер. Такой характер расположения опытных кривых обусловливается снижением влияния, оказываемого ст.ш на с увеличением нагрузки. Действительно, при уменьшении высоты выступов микронеровностей повышается проводимость клеевого слоя, т. е. возрастает первый член правой части выражения (4-62), практически мало зависящий от нагрузки. В этом случае второй член правой части данного выражения, т. е. проводимость фактического контакта, зависящая от нагрузки, снижает свое влияние на тепловую проводимость клее-металлической прослойки, отчего зависимость Яш=1(р) ослабевает.
[c.158]
возрастает первый член правой части выражения (4-62), практически мало зависящий от нагрузки. В этом случае второй член правой части данного выражения, т. е. проводимость фактического контакта, зависящая от нагрузки, снижает свое влияние на тепловую проводимость клее-металлической прослойки, отчего зависимость Яш=1(р) ослабевает.
[c.158]
Первое слагаемое в этом уравнении — тепловая проводимость межконтактной среды, второе — тепловая проводимость через места теплового контакта металлов Яс — коэффициент теплопроводности межконтактной среды кк — приведенная теплопроводность контактирующих металлов Ям=2Ям1 м2/(Ям1-1-Ям2)] N — номинальная нагрузка Ов — временное сопротивление разрыву — номинальная (геометрическая) площадь контакта. [c.247]
Тепловые свойства меди
Характерной особенностью меди является ее высокая теплопроводность, в 6 раз большая, чем у железа, и более высокая, чем у железа, механическая стойкость при низких температурах.
Коэффициент теплопроводности меди при температуре 20–100 °С составляет 394 Вт/(м*К) – выше только у серебра. Стальной прокат уступает меди по этому показателю почти в 9 раз, а железо – в 6. Различные примеси по-разному влияют на физические свойства металлов. У меди скорость передачи тепла снижается при добавлении в материал или попадании в результате технологического процесса алюминия, железа, кислорода, мышьяка, сурьмы, серы, селеа, фосфора.
Высокая теплопроводность характеризуется быстрым распространением энергии нагрева по всему объему предмета. Эта способность обеспечила меди широкое применение в любых системах теплообмена, особенно труб, листовой меди и медной проволоки. Ее используют при изготовлении трубок и радиаторов холодильников, кондиционеров, вакуумных установок, автомашин для отвода избыточного тепла охлаждающей жидкости. В отопительных приборах подобные изделия из меди служат для обогрева.
Способность меди проводить тепло снижается при нагреве. Значения коэффициента теплопроводности меди в воздухе зависит от температуры последнего, которая влияет на теплоотдачу (охлаждение). Чем выше температура окружающей среды, тем медленнее остывает металл и ниже его теплопроводность. Поэтому во всех теплообменниках используют принудительный обдув вентилятором – это повышает эффективность работы устройств и одновременно поддерживает тепловую проводимость на оптимальном уровне.
Значения коэффициента теплопроводности меди в воздухе зависит от температуры последнего, которая влияет на теплоотдачу (охлаждение). Чем выше температура окружающей среды, тем медленнее остывает металл и ниже его теплопроводность. Поэтому во всех теплообменниках используют принудительный обдув вентилятором – это повышает эффективность работы устройств и одновременно поддерживает тепловую проводимость на оптимальном уровне.
Тепловое расширение меди (при 20 — 100 град. C) — 0,0168 мм / м / ºC.
Чистая медь и ее сплавы не являются жаростойкими материалами, однако, в некоторых случаях они применяются при повышенных температурах, когда от конструкции требуется повышенная электропроводность или теплопроводность. Используется медь с низким содержанием кислорода (<<0,04 %). Когда требуется прочность изделия, то вводится мышьяк (0,4 %). Добавки Сё (1,0 %), Сг (0,3 %) и Ag (0,1 %) также улучшают механические свойства меди при повышенных температурах, причем электропроводность при этом остается практически без изменения.
У меди высокая теплопроводность, что обуславливает достаточно сложный процесс монтажных и других работ, имеющих свою специфику. Сварка, пайка, резка меди требует более концентрированного нагрева, чем для стали, и зачастую предварительного и сопутствующего подогрева металла.
Медь, помимо широкого применения в технике по причине ее высокой электропроводности, используется в химическом машиностроении в качестве конструкционного материала для изготовления разнообразной химической аппаратуры и, в особенности, теплообменной аппаратуры (выпарные аппараты, теплообменники, конденсаторы, испарители, змеевики). Объясняется это высокой теплопроводностью меди и ее сплавов, их благоприятными физико-механическими свойствами при достаточно высокой.
Существует несколько марок меди, теплопроводность которых при низких температурах может быть весьма различной в зависимости от количества и характера примесей.
Температура плавления меди 1083,85 C (1357.77 ± 0.20·K).
Принятые значения термодинамических величин для меди и ее соединений в кристаллической и жидкой фазах.
|
Вещество |
Состояние |
H°(298.15K)-H°(0) |
S°(298.15K) |
Cp°(298.15K) |
Коэффициенты в уравнении для Cp°(T)а |
Интервал температур |
Ttr или Tm |
DtrHили DmH |
|||
|
кДж×моль‑1 |
Дж×K‑1×моль‑1 |
a |
b×103 |
c×10‑5 |
K |
кДж×моль‑1 |
|||||
|
Cu |
к, куб. |
5.004 |
33.15 |
24.44 |
22.287 |
12.923 |
0.587б |
298.15-1357.77 |
1357.77 |
13.14 |
|
|
ж |
— |
— |
— |
32.8 |
— |
— |
1357.77-4500 |
— |
— |
||
|
CuO |
к,монокл. |
7.11 |
42.74 |
42.30 |
48. |
7.201 |
7.499 |
298.15-1500 |
1500 |
49 |
|
|
ж |
— |
— |
— |
67 |
— |
— |
1500-4000 |
— |
— |
||
|
Cu2O |
к, куб. |
12.6 |
92.55 |
62.60 |
64.553 |
17.578 |
6.395 |
298.15-1517 |
1517 |
65. |
|
|
ж |
— |
— |
— |
100 |
— |
— |
1517-4000 |
— |
— |
||
|
Cu(OH)2 |
к, ромб. |
12.45 |
80.50 |
78,0 |
95.784 |
11.521 |
18.862 |
298.15-322 |
322 |
0.456 |
|
|
к, ромб. |
— |
— |
— |
95. |
11.521 |
18.862 |
322-1000 |
— |
— |
||
|
CuF |
к, куб. |
9.5 |
65 |
52.0 |
55.024 |
9.137 |
5.110 |
298.15-1300 |
— |
— |
|
|
к, куб. |
— |
— |
— |
66.6 |
— |
— |
1300-2000 |
— |
— |
||
|
CuF2 |
кII,монокл. |
12.15 |
77.8 |
65.815 |
73.100 |
21.277 |
12.115 |
298.15-1065 |
1065 |
3 |
|
|
кI, куб. |
— |
— |
— |
90 |
— |
— |
1065-1109 |
1109 |
55 |
||
|
ж |
— |
— |
— |
100 |
— |
— |
1109-3000 |
— |
— |
||
|
CuCl |
кII, куб. |
11.4 |
87.74 |
52.55 |
38.206 |
38.315 |
-2.596 |
298.15-685 |
685 |
6.5 |
|
|
кI, гекс. |
— |
— |
— |
79 |
— |
— |
685-696 |
696 |
7.08 |
||
|
ж |
— |
— |
— |
29.319 |
14. |
-116.637 |
696-1200 |
— |
— |
||
|
ж |
— |
— |
— |
49.200 |
5.000 |
— |
1200-3000 |
— |
— |
||
|
CuCl2 |
кII,монокл. |
14.983 |
108.07 |
71.88 |
78.888 |
5.732 |
7.749 |
298.15-675 |
675 |
0.7 |
|
|
кI, куб. |
— |
— |
— |
82.4 |
— |
— |
675-871 |
871 |
15 |
||
|
ж |
— |
— |
— |
100 |
— |
— |
871-2000 |
— |
— |
||
|
CuBr |
кIII, куб. |
12.104 |
96.1 |
54.90 |
-324.417 |
2241.940 |
-38.227б |
298.15-657 |
657 |
4.6 |
|
|
кII, гекс. |
— |
— |
— |
93.175 |
-27.924 |
— |
657-741 |
741 |
2.15 |
||
|
кI, куб. |
— |
— |
— |
83 |
— |
— |
741-759 |
759 |
5.1 |
||
|
ж |
— |
— |
— |
38.365 |
7.807 |
-115.447 |
759-1200 |
— |
— |
||
|
ж |
— |
— |
— |
49.750 |
5.000 |
— |
1200-2000 |
— |
— |
||
|
CuBr2 |
к,монокл. |
15.5 |
135 |
75.0 |
81.117 |
4.547 |
6.643 |
298.15-2000 |
— |
— |
|
|
CuI |
кIII, куб. |
12.1 |
96.1 |
54.0 |
381.138 |
-1139.67 |
77.215б |
298.15-643 |
643 |
3.1 |
|
|
кII, гекс. |
— |
— |
— |
-85.852 |
339.060 |
— |
643-679 |
679 |
2.7 |
||
|
кI, куб. |
— |
— |
— |
116.854 |
-62.123 |
— |
679-868 |
868 |
7.93 |
||
|
ж |
— |
— |
— |
55.205 |
-2.435 |
-105.925 |
868-1400 |
— |
— |
||
|
ж |
— |
— |
— |
50.20 |
5.0 |
— |
1400-2000 |
— |
— |
||
|
CuI2 |
к |
16 |
153 |
76 |
70.053 |
19.947 |
— |
298.15-1000 |
— |
— |
|
|
CuS |
к, гекс. |
9.44 |
67.27 |
47.31 |
43.675 |
20.127 |
2.103 |
298.15-2000 |
— |
— |
|
|
Cu2S |
кIII,монокл. |
15.8 |
116.22 |
76.86 |
17.070 |
163.596 |
-9.791 |
298.15-376 |
376 |
3.79 |
|
|
кII, гекс. |
— |
— |
— |
-1831.18 |
7221.15 |
-537.89б |
376-710 |
710 |
1.19 |
||
|
кI, куб. |
— |
— |
— |
53.634 |
20.768 |
-81.748 |
710-1400 |
1400 |
12.8 |
||
|
ж |
— |
— |
— |
90 |
— |
— |
1400-3000 |
— |
— |
||
|
CuSO4 |
к, ромб. |
16.86 |
109.2 |
98.87 |
89.674 |
106.341 |
17.016б |
298.15-1100 |
— |
— |
|
|
ж |
— |
— |
— |
159.4 |
— |
— |
1100-2000 |
— |
— |
||
|
aCp°(T)=a + bT — cT-2 + dT2 + eT3 (вДж×K‑1×моль‑1) Cu: бd=-13.927×10-6, e=7.476. 10-9 CuBr: б d=-4815.530×10-6, e=3620.190. 10-9 CuI: б d=1119.510.10-6 Cu2S: б d=-10044.20×10-6, e=4895.09.10-9 CuSO4: б d=-37.887.10-6 |
|||||||||||
Способ определения тепловой проводимости контактов твердых тел
Изобретение относится к способу определения теплофизических характеристик твердых тел, а именно тепловой проводимости контактов твердых тел.
Способ позволяет определять тепловую проводимость контактов твердых тел в диапазоне от 400 до 200000 Вт/(м2 К) и наиболее подходит для контактов, созданных с использованием дополнительных материалов, улучшающих теплопередачу между телами, таких как теплопроводная паста, теплопроводный клей, эпоксидная смола, а также оптических контактов и контактов типа термодиффузионной сварки. Способ позволяет исследовать тепловой контакт между двумя прозрачными образцами твердых тел или между прозрачным образцом и образцом из высокотеплопроводного материала. В частности это широко востребовано в области разработки твердотельных лазеров и их компонентов, где в качестве прозрачного образца выступает прозрачный элемент лазерной системы, находящийся под тепловой нагрузкой, а в качестве высокотеплопроводного образца выступает радиатор. Тепловой контакт между двумя прозрачными образцами возникает при создании композитных оптических элементов с использованием методов сращивания, например термодиффузионной сварки, или метода оптического контакта.
Существует способ измерения тепловой проводимости контакта между прозрачным образцом и высокотеплопроводным материалом [S. Chernais, F. Druon, S. Forget, F. Balembois, P. Georges «On thermal sffect in solid-state lasers: the case of ytterbium-doped materials», Progress in Quantum Electronics, 30, р.89-153 (2006)], основанный на измерении распределения температуры на поверхности образца с помощью инфракрасной камеры, когда образец нагревают лазерным излучением и охлаждают через тепловые контакты с высокотеплопроводным материалом. Тепловую проводимость контактов вычисляют из измеренного распределения температуры, рассчитанного тепловыделения в образце, теплопроводности образца и геометрии системы.
Недостатки данного способа в том, что из-за использования лазерного нагрева в качестве образца может выступать только активный элемент лазера, для каждого образца необходимо применять греющее излучение на нужной длине волны, математический расчет сложен и требует точного знания тепловыделения в образце.
Наиболее близким к предлагаемому изобретению по технической сущности является взятый за прототип способ измерения коэффициента теплопередачи теплопроводных электроизоляционных материалов [Американский стандарт ASTM D5470, http://www.astm.org/5470.htm]. Способ включает создание стационарного одномерного теплового потока через систему, представляющую собой два металлических образца известной теплопроводности, выполненных в форме одинаковых прямых круговых цилиндров, приведенных в контакт основаниями, между которыми сжимают исследуемый материал. Тепловой поток направляют перпендикулярно плоскости контакта. Вдоль образцов закрепляют термопары для определения градиента температуры в образцах и скачка температуры между контактирующими гранями образцов. Коэффициент теплопередачи через контакт или тепловая проводимость контакта вычисляются из измеренного градиента температуры, скачка температуры и теплопроводности образцов. Система также обладает возможностью изменения давления на контакт и измерения толщины зазора между образцами.
Данный способ позволяет тестировать различные материалы. Однако коэффициент теплопередачи через контакт сильно зависит также и от материалов контактирующих поверхностей, которые на практике могут быть самыми разнообразными. Используемые в способе-прототипе образцы изготовлены из металла и не могут быть заменены прозрачными образцами из-за громоздкости системы, которая не может быть уменьшена из-за использования термопар для измерения температуры.
Задачей, на которую направлено изобретение, является создание способа, позволяющего определять тепловую проводимость контактов между прозрачными образцами или между прозрачным и высокотеплопроводным образцами.
Технический эффект достигается тем, что создают стационарный одномерный тепловой поток через систему из не менее чем двух образцов твердых тел с известной теплопроводностью, где образцы выполнены в форме прямых цилиндров с одинаковыми основаниями, которыми они приведены в контакт, при этом образцы в системе, расположенные по краям, изготавливают из одного материала, а тепловой поток в системе направляют перпендикулярно плоскости контакта.
Новым является то, что в системе используют два либо три образца, прямые цилиндры выполняют в виде прямоугольных параллелепипедов, образцы, расположенные по краям, изготавливают с длинами сторон не менее 1 мм из прозрачного материала, в случае системы из трех образцов твердых тел средний образец изготавливают из высокотеплопроводного материала, систему помещают в интерферометр, при этом световой пучок интерферометра направляют перпендикулярно одной из боковых граней каждого прозрачного образца, при создании в системе стационарного одномерного теплового потока интерференционным методом измеряют изменение профиля фазы светового пучка интерферометра, проходящего через прозрачные образцы, а тепловую проводимость любого из контактов вычисляют из измеренного изменения профиля фазы светового пучка интерферометра, известной теплопроводности и геометрических размеров образцов.
Способ поясняется Фиг. 1, на которой изображена система из приведенных в контакт образцов твердых тел, а также нагреватель и радиатор, которые создают через систему стационарный одномерный тепловой поток.
Способ осуществляют следующим образом. Используют систему, представленную на Фиг. 1. Система из двух образцов представляет собой два скрепленных прозрачных образца 4 одинаковой формы, выполненных из одного материала. В системе из трех образцов между прозрачными образцами закреплен высокотеплопроводный образец 3. Теплопроводность всех образцов известна. Все образцы выполнены в виде прямоугольных параллелепипедов с одинаковыми основаниями, которыми они и приведены в контакт. Прозрачные образцы 4 имеют высоту от 2 до 5 мм. Высокотеплопроводный образец — высоту 1 мм. Определяют тепловую проводимость контактов 5. С одной стороны к системе прикрепляют нагреватель 1, с другой — радиатор с проточным охлаждением 2, которые в момент измерений создают в системе стационарный одномерный тепловой поток, направленный перпендикулярно плоскости контакта. Систему помещают в интерферометр и интерференционным методом измеряют изменение профиля фазы светового пучка интерферометра, проходящего через прозрачные образцы 4, которое появляется при включении в системе стационарного теплового потока. При этом световой пучок интерферометра перпендикулярен одной из боковых граней каждого из прозрачных образцов 4.
Из измеренного изменения профиля фазы светового пучка интерферометра (L) вычисляют градиент изменения профиля фазы пучка в прозрачных образцах 4 (dL1/dx и dL2/dx) и скачок изменения профиля фазы пучка между обращенными друг к другу основаниями прозрачных образцов 4 (ΔL).
В случае системы из двух прозрачных образцов 4 тепловую проводимость контакта вычисляют по формуле:
,
где dL/dx — среднее арифметическое от dL1/dx и dL2/dx, κ0 — теплопроводность прозрачных образцов 4. Данная формула получается из формулы, используемой для расчета в способе-прототипе:
,
где Т — изменение температуры при включении в системе стационарного теплового потока, ΔT — скачок изменения температуры между обращенными друг к другу основаниями прозрачных образцов 4, dT/dx — среднее арифметическое градиентов изменения температуры в прозрачных образцах 4. При этом используется линейная связь изменения профиля фазы светового пучка интерферометра, проходящего через прозрачные образцы 4, с изменением распределения температуры в них:
,
где L0 — толщина одного из прозрачных образцов 4 в том направлении, в котором направлен световой пучок интерферометра, dn/dT — температурное изменение показателя преломления одного из прозрачных образцов 4, α — коэффициент теплового расширения одного из прозрачных образцов 4.
В случае системы из трех образцов величина ΔL связана со скачком температуры на двух контактах 5 и скачком температуры на высокотеплопроводном образце 3. В этом случае тепловую проводимость любого из контактов вычисляют по формуле:
,
где h — высота высокотеплопроводного образца 3, κ — теплопроводность высокотеплопроводного образца 3.
Мощность тепла, уходящего в атмосферу, оценивают из разности градиентов изменения профиля фазы пучка в прозрачных образцах 4. Она должна быть много меньше мощности тепла, протекающей через систему. Если это условие не выполняется, систему покрывают теплоизолирующей оболочкой или помещают в вакуумную камеру.
Способ может быть применен для измерения при температурах от 10 К до 400 К помещением системы в вакуумную камеру и использованием системы охлаждения с возможностью стабилизации температуры на любом уровне из заданного диапазона.
При этом в качестве хладагентов используют воду (от 280 К), жидкий азот (от 80 К) или жидкий гелий (от 10 К).
Таким образом, предлагаемый способ позволяет определять тепловую проводимость контактов между прозрачными образцами или между прозрачным и высокотеплопроводным образцами.
Результаты измерений могут быть использованы при расчетах распределения температуры и для оптимизации тепловых контактов в конструкциях, состоящих из контактирующих прозрачных и высокотеплопроводных элементов, в частности при разработке твердотельных лазеров и их компонентов.
Способ определения тепловой проводимости контактов твердых тел, в котором создают стационарный одномерный тепловой поток через систему из не менее чем двух образцов твердых тел с известной теплопроводностью, где образцы выполнены в форме прямых цилиндров с одинаковыми основаниями, которыми они приведены в контакт, при этом образцы в системе, расположенные по краям, изготавливают из одного материала, а тепловой поток в системе направляют перпендикулярно плоскости контакта, отличающийся тем, что в системе используют два либо три образца, прямые цилиндры выполняют в виде прямоугольных параллелепипедов, образцы, расположенные по краям, изготавливают с длинами сторон не менее 1 мм из прозрачного материала, в случае системы из трех образцов твердых тел средний образец изготавливают из высокотеплопроводного материала, систему помещают в интерферометр, при этом световой пучок интерферометра направляют перпендикулярно одной из боковых граней каждого прозрачного образца, при создании в системе стационарного одномерного теплового потока интерференционным методом измеряют изменение профиля фазы светового пучка интерферометра, проходящего через прозрачные образцы, а тепловую проводимость любого из контактов вычисляют из измеренного изменения профиля фазы светового пучка интерферометра, известной теплопроводности и геометрических размеров образцов.Сопротивление термического контакта — 2018
Полезность того, что имеется аналогия между течением электрического тока и потоком тепла, становится очевидной, если требуется удовлетворительное описание процесса переноса тепла на поверхности взаимодействия двух проводящих тепло сред. Ввиду ограничений машинной обработки, никакие две поверхности никогда не смогут образовать абсолютный контакт при сжатии их вместе. Крошечные зазоры воздуха всегда будут существовать между двумя контактирующими поверхностями ввиду определенной грубости из обработки.Существует два режима переноса тепла через пространство взаимодействия двух контактирующих граней. Первый режим представляет собой проведение тепла через точки контакта твердого тела с твердым телом (Qпроводимости), являющееся весьма эффективным. Второй способ – это проведение тепла через заполненные газом промежутки (Qпромежутка), которое, ввиду низкой способности проведения тепла, может быть весьма слабым. Для рассмотрения понятия сопротивления термического контакта по обеим сторонам контакта последовательно с проводящими средами вставляется граничная проводимость или hc, как показано на следующем рисунке.
Проводимость hc подобна коэффициенту конвективной теплопередачи и имеет те же единицы измерения (Вт/м2 ºK). Если ΔT – разница температур по граничной области взаимодействия сред площадью A, то скорость переноса тепла Q задается равенством Q = A hc ΔT. Используя аналогию между теплом и электричеством, можно записать Q = ΔT/Rt, где Rt означает сопротивление термического контакта, задаваемое как Rt = 1/(A hc).
Проводимость в пограничной области или hc зависит от следующих факторов:- Качество обработки поверхностей контактирующих граней.
- Материал каждой грани.
- Давление, с которым грани прижаты друг к другу.
- Вещество, находящееся в зазорах между двумя контактирующими гранями.
Следующая таблица показывает некоторые типовые значения межграничной проводимости тепла для обычной обработки поверхностей и умеренных давлений на область контакта (от 1 до 10 атм.). Воздушные зазоры не разреженные, если это не оговорено специально:
| Контактные грани | Проводимость (hc) (Вт/м2 ºK) |
|---|---|
| Железо/алюминий | 45,000 |
| Медь/медь | 10,000 — 25,000 |
| Алюминий/алюминий | 2200 — 12000 |
| Нержавеющая сталь/нержавеющая сталь | 2000 — 3700 |
| Нержавеющая сталь/нержавеющая сталь (разреженные зазоры) | 200 — 1100 |
| Керамика/керамика | 500 — 3000 |
В следующей таблице перечислены сопротивления термического контакта для металлических поверхностей в условиях вакуума:
| Термическое сопротивление, RтермическоеX10-4 (м2.K/Вт) | ||
|---|---|---|
| Контактное давление | 100 кН/м2 | 10000 кН/м2 |
| Нержавеющая сталь | 6-25 | 0.7-4.0 |
| Медь | 1-10 | 0.1-0.5 |
| Магний | 1.5-3.5 | 0.2-0.4 |
| Алюминий | 1.5-5.0 | 0.2-0.4 |
тепловая проводимость — это… Что такое тепловая проводимость?
- тепловая проводимость
теплопроводность
Cловарь химических синонимов I . Под редакцией С. Собецкой, В. Хоинского и П. Майорек. 2013.
- тепловая обработка
- тепловая функция
Смотреть что такое «тепловая проводимость» в других словарях:
Проводимость — звуковая, тепловая, электрическая, или звукопроводность, теплопроводность, электропроводность. Противоположное электропроводности (или реже гальванопроводности) есть сопротивление (электрическое, гальваническое): тело, обладающее малой… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
теплопроводность — тепловая проводимость … Cловарь химических синонимов I
ПЭРРОТ Джон — ПЭРРОТ (Parrott) Джон (1926 95), английский физик. Основные труды в области физики твердого тела. Изучал транспортные явления в твердых телах, термоэлектрические свойства, фотоэлектрические явления. Работы в области теории солнечных элементов.… … Энциклопедический словарь
Полупроводники — широкий класс веществ, характеризующихся значениями электропроводности σ, промежуточными между электропроводностью металлов (См. Металлы) (σ Полупроводники 106 104 ом 1 см 1) и хороших диэлектриков (См. Диэлектрики) (σ ≤ 10 10 10 12 ом… … Большая советская энциклопедия
ГОСТ 25529-82: Диоды полупроводниковые. Термины, определения и буквенные обозначения параметров — Терминология ГОСТ 25529 82: Диоды полупроводниковые. Термины, определения и буквенные обозначения параметров оригинал документа: 87. Временная нестабильность напряжения стабилизации стабилитрона D. Zeitliche Instabilitat der Z Spannung der Z… … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р МЭК 60974-1-2004: Источники питания для дуговой сварки. Требования безопасности — Терминология ГОСТ Р МЭК 60974 1 2004: Источники питания для дуговой сварки. Требования безопасности оригинал документа: 3.7 внешний осмотр: Внешний осмотр на наличие явных отклонений от технической документации с учетом требований… … Словарь-справочник терминов нормативно-технической документации
ГОСТ 21515-76: Материалы диэлектрические. Термины и определения — Терминология ГОСТ 21515 76: Материалы диэлектрические. Термины и определения оригинал документа: 32. Абсолютная диэлектрическая проницаемость По ГОСТ 19880 74 Определения термина из разных документов: Абсолютная диэлектрическая проницаемость … Словарь-справочник терминов нормативно-технической документации
ПОЛУПРОВОДНИКИ — широкий класс в в, характеризующийся значениями уд. электропроводности s, промежуточными между уд. электропроводностью металлов s=106 104 Ом 1 см 1 и хороших диэлектриков s=10 10 10 12 Ом 1см 1 (электропроводность указана при комнатной темп ре).… … Физическая энциклопедия
полупроводники — ов; мн. (ед. полупроводник, а; м.). Физ. Вещества, которые по электропроводности занимают промежуточное место между проводниками и изоляторами. Свойства полупроводников. Производство полупроводников. // Электрические приборы и устройства,… … Энциклопедический словарь
Полупроводник — (Semiconductor) Определение полупроводника, строение полупроводников и принцип действия Информация об определении полупроводника, строение полупроводников и принцип действия Содержание Содержание 1. Исторические 2. Свойства 3. Строение… … Энциклопедия инвестора
Шарик коррозионной устойчивости алюминиевый, твердая тепловая проводимость элементов запечатывания шариков подшипника
| Название продукта: | Алюминиевые шарики подшипника | цвет: | Анодированные цвета |
|---|---|---|---|
| Функция: | Хорошее электрическое | твердость: | 20ХВ0.5 — 180ХВ |
| Применение: | Элементы запечатывания (задавленные шарики) | Плотность: | ³ 2,7 г/км |
| Высокий свет: | aluminum ball,aluminium ball | ||
Шарик коррозионной устойчивости алюминиевый, твердая тепловая проводимость элементов запечатывания шариков подшипника
шарики алюминия шариков подшипника 2.2мм 1.2мм 1.1мм 2.8мм миниатюрные твердые алюминиевые
Характерный
(а) низкий вес, хорошее электрическое и тепловая проводимость
(б) высокая коррозионная устойчивость но низкая механическая прочность
(к) выстучанные Эаслилы, который подвергли механической обработке, просверленные и
Алюминиевые шарики охарактеризованы хорошими свойствами коррозионной устойчивости и трудно-носить,
и также приведенный с ровными поверхностными финишами.
Основной класс (1кскскс) просто имеет хорошие носку и коррозионную устойчивость, и приведенный с минимальным алюминиевым содержанием 99%.
Однако, они также алюминиевые сплавы, поэтому трассировки утюга, магния, кремния, и меди будут.
Светлые шарики отличаемые хорошим сопротивлением корозии и носки, очень хорошей поверхностной отделкой.
сплавы серии 1кскскс нет обработанной жары -. Шарики можно обеспечить в запассивированных условиях.
Особенные подшипники и клапаны, элементы запечатывания (задавленные шарики), они использованы в автомобильной промышленности (предохранительных устройствах), авиации и авиационно-космической промышленности, электронной промышленности, процессах заварки. |
Физические/механические/термальные/электрические/магнитные свойства
Специфическая жара | |||||
Коэффициент линейного теплового расширения | |||||
Термальная проводимость | |||||
Электрическая резистивность | Электрический | ||||
Относительная магнитная проницаемость | Парамагнитный |
Технические данные
Окончательная прочность на растяжение | |||||
Обслуживайте температуру |
Содержание выпуска №2/2016
М.М. Чайковский, В.М. Никифоров, А.П. Курдюков, А.А. Гусев, К.А. Андреев
Синтез двухканального анизотропийного регулятора для управления одноосной гиростабилизированной платформой
ФГУП «НПЦАП имени академика Н.А. Пилюгина», г. Москва
Институт проблем управления им. В.А. Трапезникова РАН, г. Москва
E-mail: [email protected]
Данная статья является продолжением ряда работ, посвященных синтезу робастных законов управления для одноосного гиростабилизатора на основе линейных матричных неравенств. Система стабилизации углового положения платформы выполнена в виде обратной связи по измеряемому угловому положению оси прецессии чувствительного элемента гироблока, включающей цифровой линейный динамический регулятор, спроектированный с учетом коррелированного шума с неизвестными параметрами распределения (с неопределенной ковариационной матрицей) в канале измерений. Применяемый закон анизотропийного стохастического робастного управления стабилизирует систему, подверженную влиянию неизвестного возмущающего момента, в условиях неточных измерений. Приводятся результаты математического моделирования управления гиростабилизированной платформой в режиме стабилизации. С помощью моделирования выполнено сравнение синтезированного управляющего устройства со стабилизирующими регуляторами, построенными другими методами.
Ключевые слова. Одноосный гиростабилизатор, дискретная линейная модель, неопределенные внешние возмущения, стохастическое робастное управление, линейные матричные неравенства.
А.А. Гусев, К.А. Андреев, В.М. Никифоров
Макетирование следящего рулевого электропривода с нечетким регулятором
ФГУП «НПЦАП имени академика Н.А. Пилюгина»
E-mail: [email protected]
E-mail: [email protected]
Рассматривается задача практической реализации нечеткого регулятора для следящего рулевого электропривода. Описана структура макета следящего рулевого электропривода с нечетким регулятором. Сравнивается качество отработки углового положения математической моделью следящего рулевого электропривода и макетом.
Ключевые слова. Следящий рулевой электропривод, нечеткий регулятор, макетирование.
Г.Н. Румянцев, М.В. Мурашов
Методика расчета теплового состояния комплекса приборов
ФГУП «НПЦАП имени академика Н.А. Пилюгина»
E-mail: [email protected]
В статье предложен нуль-мерный подход к задаче определения нестационарного температурного состояния сложного комплекса приборов, например, комплекса командных приборов ракеты-носителя. Для решения системы нелинейных уравнений использован метод Рунге-Кутты. Разработанные методика и компьютерная программа могут быть использованы для быстрых оценок на этапе эскизного проектирования новых конструкций.
Ключевые слова. Температурное состояние, сборка деталей, контактная тепловая проводимость, метод Рунге-Кутта, излучение.
А.С. Анохин, К.С. Кузьмин, Е.С. Смирнов
Оценка вибрационной погрешности «сухого» акселерометра
ФГУП «НПЦАП имени академика Н.А. Пилюгина»
E-mail: [email protected]
Предложена методика оценки вибрационной погрешности «сухого» акселерометра на основе структурной схемы, построенной с учетом нелинейностей. Приведен вид зависимости вибрационной погрешности от частоты, полученный как по результатам моделирования, так и экспериментально.
Ключевые слова. Маятниковый компенсационный акселерометр, вибрационная погрешность, нелинейность.
Г.Ф. Утробин, Ю.И. Мышляев, В.И. Краснощеченко, С.В. Мышляева
Фильтрация дискретных сигналов методом структурного погружения
ФГУП «НПЦАП имени академика Н.А. Пилюгина»
E-mail: [email protected]
Рассматривается метод решения задачи фильтрации полезного сигнала на ограниченной выборке на фоне неизвестной помехи. Метод позволяет идентифицировать минимальную структуру модели процесса и её параметры.
Ключевые слова. Фильтрация дискретных сигналов, метод структурного погружения.
А.М. Бурдин, В.Н. Васин
Автоматизированная система многокритериальной оптимизации блочно-модульного испытательного комплекса устройств обмена
ФГУП «НПЦАП имени академика Н.А. Пилюгина»
E-mail: [email protected]
В статье представлен метод многокритериальной параметрической оптимизации блочно-модульных испытательных систем на основе ранжирования критериев качества модулей и генетического алгоритма. Проведена экспериментальная оценка стабильности работы выбранного алгоритма. На основе предложенного метода разработано программное обеспечение для оптимизации модульных испытательных систем.
Ключевые слова. Параметрическая оптими-зация, блочно-модульная архитектура, ранжи-рование критериев, генетический алгоритм.
Ю.Г. Егоров, Е.А. Попов
Выбор измерительных положений в программах калибровки триады акселерометров БИНС
МГТУ имени Н.Э. Баумана, г. Москва
ОАО «ЦНИИАГ», г. Москва
E-mail: [email protected], [email protected]
В статье предлагается рациональный способ выбора измерительных положений при инвариантной к ошибкам выставки и инструментальным погрешностям испытательного стенда калибровке триады акселерометров. Вводятся критерии точности и проводится их анализ.
Ключевые слова. Калибровка, измерительное положение, программа калибровки, точность, триада акселерометров, акселерометр.
С.А. Черников
Развязка взаимосвязанных широкополосных каналов трехосного гиростабилизатора
МГТУ имени Н.Э. Баумана, г. Москва
[email protected]
Рассматривается возможность автономизации каналов стабилизации широкополосного трехосного гиростабилизатора путем введения в цепи стабилизации связей, компенсирующих дестабилизирующую взаимосвязь, обусловленною зависимостью управляющих сигналов гироскопов от углового движения стабилизированной платформы относительно осей, параллельных осям прецессии гироскопов.
Существенным является простота физической реализации алгоритма декомпозиции, особенно если оси прецессии гироскопов лежат в одной плоскости, например, в плоскости максимальных перегрузок. Тогда взаимосвязанными оказываются только два канала. Реализация алгоритма декомпозиции в этом случае может быть осуществлена, например, с помощью установленных на осях прецессии гироскопов тахогенераторов, сигналы с которых подаются в перекрестные каналы стабилизации. При этом в качестве тахогенераторов могут быть использованы датчики моментов.
Ключевые слова. Трехосный гиростабилизатор, взаимосвязь каналов стабилизации, развязка каналов.
Л.И. Малыхин
Исследование структуры и обоснование метода последовательных предпочтений на основе комбинаторной топологии и геометрии
МГТУ имени Н.Э. Баумана
E-mail: [email protected]
В работе рассматривается двухэтапный метод анализа сетей и его сравнение с методом последовательных предпочтений. Приведены вычислительные результаты проверки эффективности двухэтапного метода, которые показали его превосходство над методом последовательных предпочтений.
Ключевые слова. Метод анализа сетей, метод последовательных предпочтений, метод анализа иерархий.
Л.И. Малыхин
Матроиды в анализе сетей
МГТУ имени Н.Э. Баумана
E-mail: [email protected]
В работе рассматривается двухэтапный метод анализа сетей и его сравнение с методом последовательных предпочтений. Приведены вычислительные результаты проверки эффективности двухэтапного метода, которые показали его превосходство над методом последовательных предпочтений.
Ключевые слова. Метод анализа сетей, метод последовательных предпочтений, метод анализа иерархий.
Прямое измерение теплопроводности твердого железа в условиях ядра планеты
Лабросс, С. Тепловая и магнитная эволюция ядра Земли. Phys. Планета Земля. Интер. 140 , 127–143 (2003)
ADS Статья Google ученый
Стейси, Ф. Д. и Лопер, Д. Э. Пересмотренная оценка проводимости железного сплава при высоком давлении и ее значение для баланса энергии ядра. Phys. Планета Земля. Интер. 161 , 13–18 (2007)
ADS CAS Статья Google ученый
Ниммо, Ф. в Трактат по геофизике 2-е изд. (Изд. Шуберт Г.) 27–55 , 201–219 (Elsevier, 2015)
Статья Google ученый
Ша, X. и Коэн, Р. Исследования из первых принципов удельного электрического сопротивления железа под давлением. J. Phys. Конденс. Дело 23 , 075401 (2011)
ADS PubMed Статья CAS Google ученый
Gomi, H. et al. Высокая проводимость железа и тепловая эволюция ядра Земли. Phys. Планета Земля. Интер. 224 , 88–103 (2013)
ADS CAS Статья Google ученый
Поццо, М., Дэвис, К., Габбинс, Д. и Алф, Д. Тепловая и электрическая проводимость железа в условиях ядра Земли. Природа 485 , 355–358 (2012)
ADS CAS PubMed PubMed Central Статья Google ученый
де Кокер, Н., Стейнле-Нойман, Г. и Влчек, В. Удельное электрическое сопротивление и теплопроводность жидких сплавов Fe при высоких значениях P и T, а также тепловой поток в ядре Земли. Proc.Natl Acad. Sci. США 109 , 4070–4073 (2012)
ADS CAS PubMed Статья Google ученый
Олсон П. Новый основной парадокс. Наука 342 , 431–432 (2013)
ADS CAS PubMed Статья PubMed Central Google ученый
Ниммо, Ф. в Трактат по геофизике (изд.Шуберт, Г.) 31–65 , 217–241 (Elsevier, 2007)
Google ученый
Тардуно, Дж. А., Коттрелл, Р. Д., Дэвис, В. Дж., Ниммо, Ф. и Боно, Р. К. Геодинамо от Хаде до Палеоархея, зарегистрированное с помощью одиночных кристаллов циркона. Наука 349 , 521–524 (2015)
ADS CAS PubMed Статья Google ученый
McWilliams, R.С., Конопкова, З. и Гончаров, А. Ф. Метод мгновенного нагрева для измерения теплопроводности при высоком давлении и температуре: применение к Pt. Phys. Планета Земля. Интер. 247 , 17–26 (2015)
ADS CAS Статья Google ученый
Мак-Вильямс, Р. С., Дальтон, Д. А., Конопкова, З., Махмуд, М. Ф. и Гончаров, А. Ф. Измерения непрозрачности и проводимости благородных газов в условиях планетных и звездных недр. Proc. Natl Acad. Sci. США 112 , 7925–7930 (2015)
ADS CAS PubMed Статья PubMed Central Google ученый
Стейси, Ф. Д. и Андерсон, О. Л. Электрическая и теплопроводность сплава Fe-Ni-Si в условиях сердечника. Phys. Планета Земля. Интер. 124 , 153–162 (2001)
ADS CAS Статья Google ученый
Сигл, К.Т., Коттрелл, Э., Фей, Ю. В., Хаммер, Д. Р., Пракапенка, В. Б. Электрические и теплопередающие свойства железа и сплава железо-кремний при высоком давлении. Geophys. Res. Lett. 40 , 5377–5381 (2013)
ADS CAS Статья Google ученый
Bi, Y., Tan, H. & Jing, F. Электропроводность железа при ударном сжатии до 200 ГПа. J. Phys. Конденс. Дело 14 , 10849 (2002)
ADS CAS Статья Google ученый
Киллер Р.Н. и Ройс, Э. Б. в Физика высоких плотностей энергии Vol. 48 (ред. Caldirola, P. & Knoepfel, H.) 106–125 (Academic Press, 1971)
Google ученый
Franz, R. & Wiedemann, G. Ueber die Wärme-Leitungsfähigkeit der Metalle. Ann. Phys. 165 , 497–531 (1853)
Артикул Google ученый
Анзеллини, С., Деваэле, А., Мезуар, М., Лубейр, П. и Морард, Г. Плавление железа на внутренней границе ядра Земли на основе быстрой дифракции рентгеновских лучей. Наука 340 , 464–466 (2013)
ADS CAS PubMed Статья Google ученый
Бёлер Р. Температуры в ядре Земли по результатам измерений температуры плавления железа при высоких статических давлениях. Природа 363 , 534–536 (1993)
ADS CAS Статья Google ученый
Комабаяши Т., Фей, Ю., Менг, Ю. и Пракапенка, В. Измерения дифракции рентгеновских лучей на месте перехода γ-ε границы железа в ячейке с алмазной наковальней с внутренним нагревом. Планета Земля. Sci. Lett. 282 , 252–257 (2009)
ADS CAS Статья Google ученый
Дэн Л., Сигл К., Фей Ю. и Шахар А. Удельное электрическое сопротивление железа при высоком давлении и температуре и последствия для ядер планет. Geophys. Res. Lett. 40 , 33–37 (2013)
ADS CAS Статья Google ученый
Джексон, Дж. М. и др. Плавление сжатого железа путем мониторинга атомной динамики. Планета Земля. Sci. Lett. 362 , 143–150 (2013)
ADS CAS Статья Google ученый
Ривольдини А., Ван Хоолст Т.И Верхувен, О. Внутренняя структура Меркурия и содержание серы в его ядре. Икарус 201 , 12–30 (2009)
ADS CAS Статья Google ученый
Хо, К. Ю., Пауэлл, Р. У. и Лили, П. Э. Теплопроводность элементов. J. Phys. Chem. Ref. Данные 1 , 279–422 (1972)
ADS CAS Статья Google ученый
Хаук, С.А., Домбард А. Дж., Филлипс Р. Дж. И Соломон С. С. Внутренняя и тектоническая эволюция Меркурия. Планета Земля. Sci. Lett. 222 , 713–728 (2004)
ADS CAS Статья Google ученый
Конопкова З., Лазор П., Гончаров А. Ф., Стружкин В. В. Теплопроводность ГПУ-железа при высоком давлении и температуре. Высокий пресс. Res. 31 , 228–236 (2011)
ADS Статья CAS Google ученый
Дубровинский, Л.С., Саксена, С. К., Тутти, Ф., Рехи, С. и ЛеБехан, Т. Рентгеновское исследование теплового расширения и фазового перехода железа при многомегабарном давлении на месте. Phys. Rev. Lett. 84 , 1720–1723 (2000)
ADS CAS PubMed Статья PubMed Central Google ученый
Секко Р. А. и Шлессин Х. Х. Удельное электрическое сопротивление твердого и жидкого Fe при давлениях до 7 ГПа. Дж.Geophys. Res. Твердая Земля 94 , 5887–5894 (1989)
Артикул Google ученый
Ниммо Ф. и Стивенсон Д. Дж. Влияние ранней тектоники плит на тепловую эволюцию и магнитное поле Марса. J. Geophys. Res. Планеты 105 , 11969–11979 (2000)
ADS Статья Google ученый
Монтойя, Дж.А., Гончаров, А.Ф. Расчет с помощью метода конечных элементов зависящих от времени тепловых потоков в ячейке с алмазной наковальней, нагретой лазером. J. Appl. Phys. 111 , 112617 (2012)
ADS Статья CAS Google ученый
Johannsen, P. G. Показатель преломления галогенидов щелочных металлов. 1. Модель постоянной совместной плотности состояний. Phys. Ред. B 55 , 6856–6864 (1997)
ADS CAS Статья Google ученый
Гримсдич, М., Letoullec, R., Polian, A. & Gauthier, M. Определение показателя преломления в ячейках с алмазной наковальней: результаты для аргона. J. Appl. Phys. 60 , 3479–3481 (1986)
ADS CAS Статья Google ученый
Chen, B. et al. Упругость, прочность и показатель преломления аргона при высоких давлениях. Phys. Ред. B 81 , 144110 (2010)
ADS Статья CAS Google ученый
Деваэле, А.и другие. Квазигидростатическое уравнение состояния железа выше 2 Мбар. Phys. Rev. Lett. 97 , 215504 (2006)
ADS PubMed Статья CAS PubMed Central Google ученый
Sommerfeld, A. Zur Elektronentheorie der Metalle auf Grund der Fermischen Statistik. Z. Phys. 47 , 1–32 (1928)
ADS CAS МАТЕМАТИКА Статья Google ученый
Parker, W.Дж., Дженкинс, Р. Дж., Эбботт, Г. Л. и Батлер, К. П. Флэш-метод определения температуропроводности, теплоемкости и теплопроводности. J. Appl. Phys. 32 , 1679 (1961)
ADS CAS Статья Google ученый
Татено С., Хиросе К., Охиси Ю. и Тацуми Ю. Структура железа во внутреннем ядре Земли. Наука 330 , 359–361 (2010)
ADS CAS Статья Google ученый
Шен, Г., Пракапенка, В. Б., Риверс, М. Л., Саттон, С. Р. Структура жидкого железа при давлениях до 58 ГПа. Phys. Rev. Lett. 92 , 185701 (2004)
ADS PubMed Статья CAS PubMed Central Google ученый
Гончаров А.Ф. и др. Дифракция рентгеновских лучей в ячейке с алмазной наковальней, нагреваемой импульсным лазером. Rev. Sci. Instrum. 81 , 113902 (2010)
ADS PubMed Статья CAS PubMed Central Google ученый
Росс, Р.Г., Андерссон, П., Сундквист, Б., Бэкстрем, Г. Теплопроводность твердых тел и жидкостей под давлением. Rep. Prog. Phys. 47 , 1347 (1984)
ADS CAS Статья Google ученый
Болин Л. Теплопроводность металлов при высоком давлении. Solid State Commun. 19 , 389–390 (1976)
ADS CAS Статья Google ученый
Шарма, С.К. Температура Дебая ГПУ-железа при экстремальном сжатии. Solid State Commun. 149 , 2207–2209 (2009)
ADS CAS Статья Google ученый
Дубровинский, Л. С., Саксена, С. К., Дубровинская, Н. А., Рехи, С. и Ле Бихан, Т. Грюнайзен Параметр ε-железа до 300 ГПа по данным рентгеновского исследования на месте. г. Минеральная. 85 , 386–389 (2000)
ADS CAS Статья Google ученый
Van Zytveld, J.Удельное электрическое сопротивление жидких переходных металлов. J. Phys. Coll. 41 , C8-503-C8-506 (1980)
Google ученый
Френч, М. и Маттссон, Т. Р. Термоэлектрические транспортные свойства молибдена на основе моделирования ab-initio. Phys. Ред. B 90 , 165113 (2014)
ADS Статья CAS Google ученый
Киттель, К. Введение в физику твердого тела 8-е изд. (John Wiley & Sons, 2005)
Панеро В. Р. и Жанло Р. Градиенты температуры в нагреваемой лазером ячейке с алмазной наковальней. J. Geophys. Res. Твердая Земля 106 , 6493–6498 (2001)
Артикул Google ученый
Кифер Б. и Даффи Т. С. Моделирование методом конечных элементов нагреваемой лазером ячейки с алмазной наковальней. Дж.Прил. Phys. 97 , 114902 (2005)
ADS Статья CAS Google ученый
Гончаров А.Ф. и др. Теплопроводность аргона при высоких давлениях и высоких температурах. J. Appl. Phys. 111 , 112609 (2012)
ADS Статья CAS Google ученый
Beck, P. et al. Измерение температуропроводности при высоком давлении с использованием метода нестационарного нагрева. заявл. Phys. Lett. 91 , 181914 (2007)
ADS Статья CAS Google ученый
Yamazaki, D. et al. Уравнение состояния P-V-T для ε-железа до 80 ГПа и 1900 К с использованием аппарата высокого давления типа Kawai, оснащенного спеченными алмазными наковальнями. Geophys. Res. Lett. 39 , L20308 (2012)
ADS Google ученый
Хиросе, К., Labrosse, S. & Hernlund, J. Состав и состояние ядра. Annu. Преподобный «Планета Земля». Sci. 41 , 657–691 (2013)
ADS CAS Статья Google ученый
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом.Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Теплопроводность металлов и сплавов
В этой статье представлены данные теплопроводности для ряда металлов и сплавов. Теплопроводность измеряет способность материала пропускать тепло через проводимость.
Теплопроводность измеряет способность материала пропускать тепло через проводимость. Теплопроводность материала сильно зависит от состава и структуры. Вообще говоря, плотные материалы, такие как металлы и камень, являются хорошими проводниками тепла, в то время как вещества с низкой плотностью, такие как газ и пористая изоляция, плохо проводят тепло.
Теплопроводность материалов требуется для анализа сетей теплового сопротивления при изучении теплопередачи в системе.
Дополнительную информацию см. В статье «Значения теплопроводности для других распространенных материалов».
В следующих таблицах показана теплопроводность некоторых металлов и сплавов при различных температурах.
| Материал | Температура | Теплопроводность | Температура | Теплопроводность | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Адмиралтейство Латунь | 20 | 96.1 | 68 | 55,5 | ||||||
| 100 | 103,55 | 212 | 59,8 | |||||||
| 238 | 116,44 | 460 | 116,44 | 460 | 6782 | 460 | 6782 905 | 130 | ||
| 100 | 218 | 212 | 126 | |||||||
| 371 | 192 | 700 | 111 | |||||||
| Сурьма | 3 | 68 | 10,6 | |||||||
| 100 | 16,8 | 212 | 9,69 | |||||||
| Бериллий | 20 | 139 | 806 132 9082 905 905 | 76,2 | ||||||
| 371 | 109 | 700 | 63,0 | |||||||
| Латунь | -165 | 106 | -265 | 61,0 | 2082 905 9050 | |||||
| 182 | 177 | 360 | 102 | |||||||
| Бронза | 20 | 189 | 68 | 109 | ||||||
| 100 | 90,3 | 212 | 52,2 | |||||||
| Медь | 20 | 401 | 68 | 232 | ||||||
| 100 | 905 905 905 905 | 367 | 700 | 212 | ||||||
| Золото | 20 | 317 | 68 | 183 | ||||||
| Германий | 20 | 58.8 | 68 | 34,0 | ||||||
| Инконель X | -3 | 13,2 | 27 | 7,62 | ||||||
| 20 | 13,7 | 686 | 905 905 905 90587 | 905 107014,7 | ||||||
| Железо | 20 | 71,9 | 68 | 41,6 | ||||||
| 100 | 65,7 | 212 | 38,0 | 38,0 | 38,0 | 700 | 25,8 | |||
| Чугун (кованый) | 20 | 60,4 | 68 | 34,9 | ||||||
| 100 | 59,9 | 212 | 212 3482 | 212 3458 | литой53 | 48,0 | 127 | 27,7 | ||
| Свинец | 0 | 35,1 | 32 | 20,3 | ||||||
| 20 | 3482 2058 901 | 1|||||||||
| 260 | 30,3 | 500 | 17,5 | |||||||
| Магний | 20 | 170 | 68 | 98,5 | ||||||
| 10082 | ||||||||||
| 10082 905 188 | 163 | 370 | 93,9 | |||||||
| Молибден | 0 | 137 | 32 | 79,0 | ||||||
| 20 | 13682 9058 9058.4 | |||||||||
| 427 | 115 | 800 | 66,7 | |||||||
| Монель | -250 | 20,73 | -418 | 11,98 | 11,98 | 2|||||
| 800 | 46,9 | 1472 | 27,1 | |||||||
| Никель | 20 | 62,4 | 68 | 36,0 | ||||||
| 100 | 58.0 | 212 | 33,5 | |||||||
| 293 | 47,5 | 560 | 27,4 | |||||||
| Палладий | 20 | 67,5 | 2 68 | 90568 | 41,0 | |||||
| 100 | 70,6 | 212 | 40,8 | |||||||
| 427 | 69,2 | 800 | 40,0 | 65 | 68 | 5,00 | ||||
| Родий | 20 | 152 | 68 | 88.0 | ||||||
| Серебро | 20 | 419 | 905 | 212 | 234 | |||||
| 316 | 366 | 600 | 211 | |||||||
| Сталь, 1% углерод | 20 | 45,3 | 68 | 26.2 | ||||||
| 100 | 44,8 | 212 | 25,9 | |||||||
| SS ANSI 301, 302, 303, 304 | 35 | 14,0 | 882 905 905 905 905 212 | 8,69 | ||||||
| 900 | 28,0 | 1652 | 16,2 | |||||||
| нерж.3 | 68 | 7,11 | ||||||||
| 900 | 32,0 | 1652 | 18,5 | |||||||
| нерж. 212 | 10,2 | |||||||||
| 300 | 18,4 | 572 | 10,6 | |||||||
| 900 | 22,6 | 1652 | 13,1 | 9057 SS61 | 13,1 | 9057 SS610 | -58 | 7,51 | ||
| 20 | 13,9 | 68 | 8,04 | |||||||
| 950 | 26,1 | 1742 | 15,1 | 9057 905 7014,3 | -94 | 8,25 | ||||
| 20 | 15,7 | 68 | 9,06 | |||||||
| 900 | 29,4 | 1652 | 905 905 ANSI, SS 1652 905 905 , 420-70 | 26.0 | -94 | 15,0 | ||||
| 20 | 26,0 | 68 | 15,0 | |||||||
| 1000 | 26,0 | 1832 | SS58 | SS58 | 122 | 12,6 | ||||
| 900 | 25,0 | 1652 | 14,4 | |||||||
| SS ANSI 440 | 100 | 22,1 | 212 | 12.8 | ||||||
| 500 | 27,5 | 932 | 15,9 | |||||||
| SS ANSI 446 | 0 | 22,4 | 32 | 13,0 | 9058 22582 905 905 905 905 905 905||||||
| 1000 | 38,0 | 1832 | 22,0 | |||||||
| SS ANSI 501, 502 | 30 | 37,0 | 86 | 21,4 | ||||||
| 100 90.2 | 212 | 20,9 | ||||||||
| 830 | 27,8 | 1526 | 16,0 | |||||||
| Тантал | 20 | 55,0 | 6882 | 55,0 | 6882 | 32 | 29,0 | |||
| Торий | 20 | 29,4 | 68 | 17,0 | ||||||
| 100 | 30,5 | 212 | 17.6 | |||||||
| 299 | 33,3 | 570 | 19,3 | |||||||
| Олово | 20 | 62,1 | 68 | 35,9 | 905 905 905 905 905 905 Титан | 20 | 15,6 | 68 | 9,00 | |
| 100 | 15,3 | 212 | 8,86 | |||||||
| 299 | 14.7 | 570 | 8,50 | |||||||
| Вольфрам | 20 | 159 | 68 | 92,0 | ||||||
| 100 | 154 | 212 8982 | 154 | 212 8982 905 905 905 9058 | 212 8982 905 905 | 82,0 | ||||
| Уран | 20 | 24,2 | 68 | 14,0 | ||||||
| 100 | 26,0 | 212 | 15,0 | 905 9056 | 1418 | 23,4 | ||||
| Ванадий | 20 | 34,6 | 68 | 20,0 | ||||||
| Цинк | 20 | 111 112 | 112 | 212 | 63,9 | |||||
| Цирконий | 0 | 19,0 | 32 | 11,0 |
Теги статьи
Недавно обнаруженный 91 неорганический материал с низкой теплопроводностью
Мы все знаем, что мир отчаянно нуждается в переходе на возобновляемые источники энергии, но многие из нас забывают, что нам также необходимо сделать наши энергетические системы более эффективными.
В настоящее время примерно 70 процентов всей энергии, которую мы производим в мире, теряется в виде тепла — часто на самих электростанциях. Это серьезная проблема, которую можно хотя бы частично решить за счет улучшения термоэлектрических материалов, которые могут уменьшить потери тепла, а также улавливать потерянную тепловую энергию.
Теперь исследователи под руководством Ливерпульского университета в Великобритании сделали важный шаг к этой цели, открыв новый неорганический материал с самой низкой теплопроводностью, о которой когда-либо сообщалось.
Фактически, при комнатной температуре материал замедляет передачу тепла почти так же, как и воздух.
Новый материал имеет формулу Bi 4 O 4 SeCl 2 (название не броское, мы знаем), и его создание является «прорывом в управлении тепловым потоком в атомном масштабе», пресс релиз объясняет.
«Обнаруженный нами материал имеет самую низкую теплопроводность среди всех неорганических твердых тел и почти так же плохо проводит тепло, как и сам воздух», — говорит химик и руководитель группы Мэтт Россейнски из Ливерпульского университета.
«Значение этого открытия имеет большое значение как для фундаментального научного понимания, так и для практического применения в термоэлектрических устройствах, которые собирают отходящее тепло, и в качестве тепловых барьерных покрытий для более эффективных газовых турбин».
Если принять теплопроводность стали за 1, то вода и строительный кирпич будут иметь теплопроводность 0,01. Воздух будет около 0,0005, а новый материал — всего 0,001.
Что особенно интересно, так это то, что этот материал был создан с помощью хитроумного расположения слоев атомов, и команда говорит, что они могут использовать ту же технику для добавления дополнительных свойств.
В будущем это может означать создание материалов, которые не только невероятно устойчивы к нагреву, но также являются сверхпроводниками электричества — два свойства, которые будут чрезвычайно полезны для энергосистемы.
«Помимо переноса тепла, эта стратегия может быть применена к другим важным фундаментальным физическим свойствам, таким как магнетизм и сверхпроводимость, что приведет к снижению энергопотребления и более эффективной транспортировке электричества», — поясняет физик Джон Алария.
Неорганические материалы — это материалы, которые не содержат углерода, а этот был сделан из BiOCl и Bi 2 O 2 Se.Как следует из названия, это соединение висмута, кислорода, селена и хлора.
Чтобы создать новый проводящий материал, команда обнаружила два разных расположения атомов в этих материалах, что привело к плохой теплопроводности.
Затем они изучили механизмы, ответственные за замедление нагрева в каждой из этих схем, и нашли способ объединить их таким образом, чтобы они могли комбинировать эффекты замедления нагрева вместо простого усреднения разницы.
На изображении ниже вы можете увидеть визуальное представление двух различных атомных расположений, представленных желтым и синим цветом, которые в сочетании наиболее эффективно замедляют движение тепла через материал.
Два атомных расположения (желтый и синий) объединились, чтобы создать материал. (Ливерпульский университет)
В результате Bi 4 O 4 SeCl 2 является гораздо более слабым проводником тепла, чем любое из двух устройств по отдельности, обеспечивая теплопроводность при комнатной температуре всего 0.1 Вт K −1 м −1 . Другими словами, материал — это сумма больше, чем его части.
Важно отметить, что это исследование рассматривало только теплопроводность нового материала и не рассматривало другие эффекты, такие как электропроводность или магнетизм. Поэтому пока не ясно, можно ли использовать этот материал в реальных приложениях, таких как вычисления или в электрических сетях.
Но теперь, когда мы знаем, как наслоить атомы таким сложным способом, это открывает большой потенциал для новых материалов, которые берут эти свойства теплопроводности и сочетают их с другими желательными характеристиками для улучшения термоэлектрических характеристик или открытия сверхпроводимости.
«Этот потенциал для оптимизации множества свойств иллюстрирует, как синергия между модульными блоками с совместимым соединением может обеспечить химическое генерирование и управление функцией», — пишут исследователи.
Исследование опубликовано в Science. ].Теплопроводность — k — это тепло, передаваемое за счет единичного температурного градиента в установившихся условиях через единицу площади слоя материала единичной толщины. Следующее свойство — термическая эффузия — требуется при анализе условий, зависящих от времени. Он отражает способность материала обмениваться теплом с окружающей средой, то есть накапливать или рассеивать тепло. Значения теплопроводности и эффузии позволяют рассчитать коэффициент температуропроводности — свойство, которое описывает, насколько быстро материал реагирует на изменение температуры.Это мера изменения температуры в единице объема материала, вызванного теплом, которое течет в единицу времени через тело единичной площади и единичной толщины при единичной разнице температур между его поверхностями. Исследование этих параметров горных пород проводится с целью определения местоположения геотермальных систем [3, 4, 5], геотермического моделирования [6] и материалов для строительства горных пород с точки зрения экономии тепловой энергии [7]. Термические свойства связаны с минеральным составом, уплотнением (и, как следствие, пористостью) и анизотропией породы.Другими важными факторами в формировании породы являются объемные отношения между твердой, жидкой и газовой фазами и содержание влаги. Принято считать, что теплопроводность горных пород уменьшается с увеличением температуры и увеличивается с увеличением давления, а влияние температуры и давления противодействует друг другу [2]. Следовательно, в некоторых исследованиях этими эффектами можно пренебречь; Однако следует отметить, что необходимо учитывать водонасыщение для корректировки теплопроводности на месте. Теплопроводность горных пород обычно находится в диапазоне 0,40–7,00 Вт · м −1 K −1 [8]. Низкие значения характерны для сухих, неуплотненных осадочных пород, таких как гравий и песок. Более высокие значения теплопроводности характерны для большинства осадочных и метаморфических пород, а очень высокие — для кислых магматических пород. Породы с высоким содержанием кварца (например, кварцит, песчаник), а также водонасыщенные породы являются лучшими проводниками тепла [9]. Balckwell и Steele [10] приводят значения теплопроводности песчаников в диапазоне 2.50–4,20 Вт · м −1 K −1 , для сланца: 1,05–1,45 Вт · м −1 K −1 , а для аргиллита и алевролита: 0,80–1,25 Вт · м −1 K −1 . Хотя было выполнено много измерений теплопроводности магматических и метаморфических пород, осадочным породам и тепловым потокам в осадочных бассейнах уделялось мало внимания [9, 11]. Геотермические исследования осадочных пород связаны с поиском углеводородов, связывая теплопроводность и глубину залегания или стратиграфический возраст [12].Термическая эволюция материнских пород и, как следствие, термическая зрелость зависят от литологии осадочного бассейна и начальной теплопроводности горных пород [1]. В случае осадочных пород, особенно сланцев, которые имеют тенденцию быть сильно анизотропными, важной информацией является направление измерения теплопроводности. Для оценки земного теплового потока релевантной теплопроводностью является теплопроводность, перпендикулярная слоистости [11]. При анализе содержания минералов в горных породах содержание кварца рассматривается как фактор первого порядка, поскольку кварц является идеальным теплопроводным материалом с высокой теплопроводностью: 6.5–11,3 Вт м −1 K −1 (параллельно оптической оси c кристалла) [13]. В случае осадочных пород важным фактором является пористость. Когда поры заполнены воздухом с низкой теплопроводностью (0,026 Вт · м −1 K −1 ), высокая пористость, очевидно, снижает теплопроводность породы. Когда воздух заменяется водой (или рассолом) в условиях водонасыщения, теплопроводность породы выше. Помимо пористости, происхождение конкретного осадка также рассматривается как фактор, контролирующий теплопроводность осадочных пород [2]. Целью нашего исследования было определение теплопроводности в породах, представляющих Карпатский флишевой пояс, Люблинский бассейн и Балтийский бассейн, которые являются перспективными для добычи традиционных и нетрадиционных углеводородов соответственно. Измеренные значения могут быть полезны для разработки соответствующих моделей коллектора, а также для расчета состава жидкостей гидроразрыва, особенно жидкостей под напряжением и пен. Для сравнения были исследованы сланцевые породы из других мест (Судетские горы и Святой Крест), которые могут иметь важное значение в качестве строительного материала. В данном исследовании мы проанализировали некоторые образцы мелкозернистых осадочных пород, в основном сланцев; Следовательно, важным вопросом было сравнение значений теплопроводности в параллельном и перпендикулярном направлениях слоистости в горных породах. В случае сланцев, поступающих из скважин, размер пробы невелик; Поэтому использовался анализатор теплопроводности TCi от C-Therm Technologies (Канада), так как он позволяет быстро измерять небольшой образец. Thermal Interface Materials (TIM) полезны для управления температурой в электронных компонентах, поскольку они улучшают передачу тепла от компонента, выделяющего тепло, к рассеивателю тепла или радиатору.Одним из важных аспектов при выборе TIM для вашего приложения является знание способности материала передавать тепло, которое часто определяется теплопроводностью и / или тепловым сопротивлением. По всей отрасли производители часто публикуют данные о теплопроводности в единицах Вт / метр-Кельвин, а также о тепловом сопротивлении в градусах Цельсия — дюймах. 2 / Ватт в своих таблицах. Итак, в чем разница между этими двумя и как их следует учитывать при выборе TIM? Теплопроводность — это свойство материала, которое описывает способность данного материала проводить тепло.Следовательно, когда теплопроводность материала высока, материал является лучшим проводником тепла. Это свойство не зависит от размера, формы или ориентации материала в однородном материале, и поэтому теплопроводность является идеализированной величиной. Чтобы понять термическое сопротивление , мы должны сначала понять термическое сопротивление и сопротивление теплового контакта. Следовательно, термическое сопротивление материала представляет собой сумму его теплового сопротивления и всех контактных сопротивлений. Когда термический импеданс материала ниже, материал является лучшим проводником тепла в этом приложении. Исходя из этого, становится понятно, что такие факторы, как шероховатость поверхности, плоскостность поверхности, давление зажима, наличие клея, неоднородность и толщина материала, имеют большое влияние на термическое сопротивление материала. Таким образом, термический импеданс является лучшим тепловым свойством «реального мира», поскольку он учитывает больше переменных, специфичных для приложения. Таким образом, при сравнении различных TIM для конкретного приложения вы можете начать с теплопроводности для общих сравнений, но данные о зависимости теплового импеданса от давления будут гораздо более точными для ваших «реальных» условий. Поскольку точное определение теплопроводности является сложной задачей (часто не признаваемой ни разработчиками, ни поставщиками), методы, основанные на измерении другого физического свойства, однозначно связанного с теплопроводностью, очень сложные. Один из таких методов основан на так называемом законе Видемана-Франца, который связывает теплопроводность с электропроводностью в соответствии с: к / = LТ , где k — теплопроводность в Вт / мК, T — абсолютная температура в K, — электрическая проводимость в -1 м -1 , а L — число Лоренца, равное 2,45 10 -8 Б / К 2 . Очевидно, что существует огромная разница между измерением электропроводности и измерением теплопроводности.Это соотношение справедливо только для материалов с более или менее свободно движущимися электронами; другими словами, металлы (по крайней мере, при комнатной температуре). Закон Видемана-Франца основан на аргументах кинетической теории газов, применяемых в физике твердого тела, и был сформулирован около 150 лет назад. Свободные электроны в металлической решетке взаимодействуют с колебаниями решетки (называемыми «фононами»), тем самым набирая энергию. При приложении электрического поля электроны переносят эту энергию и, следовательно, переносят как электрический заряд, так и тепло.Очевидно прямая связь должна существовать. Однако фононы также переносят тепло (это единственный механизм переноса в изоляторах). Только в тех случаях, когда вклад электронов намного выше, чем вклад фононов, закон Видемана-Франца выполняется достаточно хорошо. Это справедливо для всех чистых металлов, но для полупроводников (и, возможно, также для некоторых сплавов) Закон не действует. В этом столетии теория была улучшена с помощью квантовой механики, и интересно отметить, что обе теории генерируют примерно одинаковое значение числа Лоренца.Однако это чисто случайное совпадение. Два члена в формулировке кинетического газа оказались далекими от правильного значения, но, как оказалось, они компенсируют друг друга. Источник: Данные о физических свойствах для инженера-проектировщика, под ред. Битон и Хьюитт, Полушарие, 1989 В приведенной выше таблице представлены экспериментальные значения L для ряда чистых металлов. Разница между теплопроводностью и тепловым сопротивлением
Материалы Как теплопроводность соотносится с электропроводностью

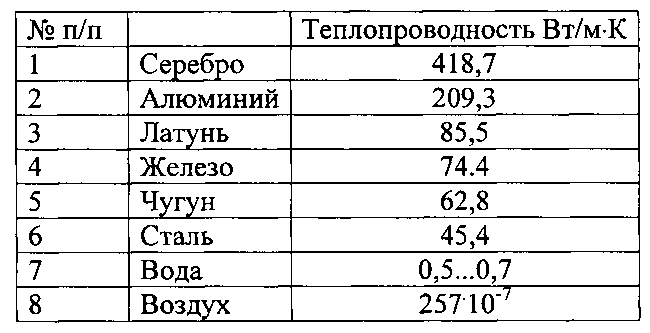
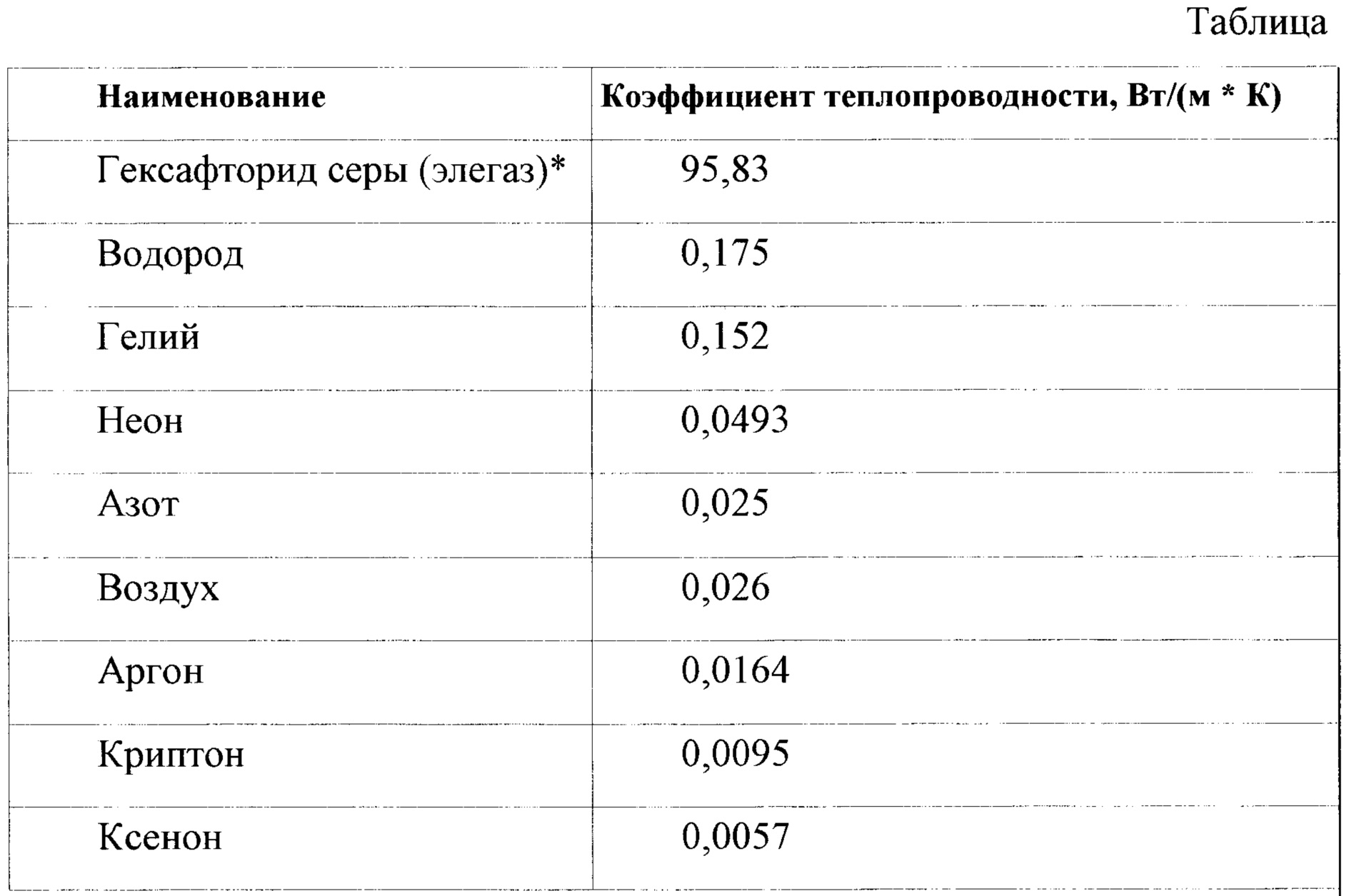 589
589 6
6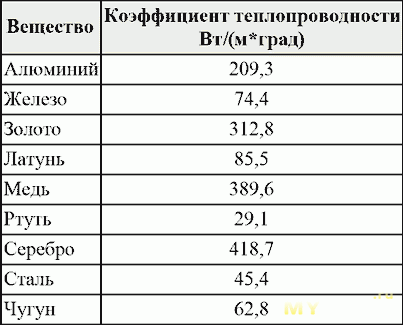 784
784

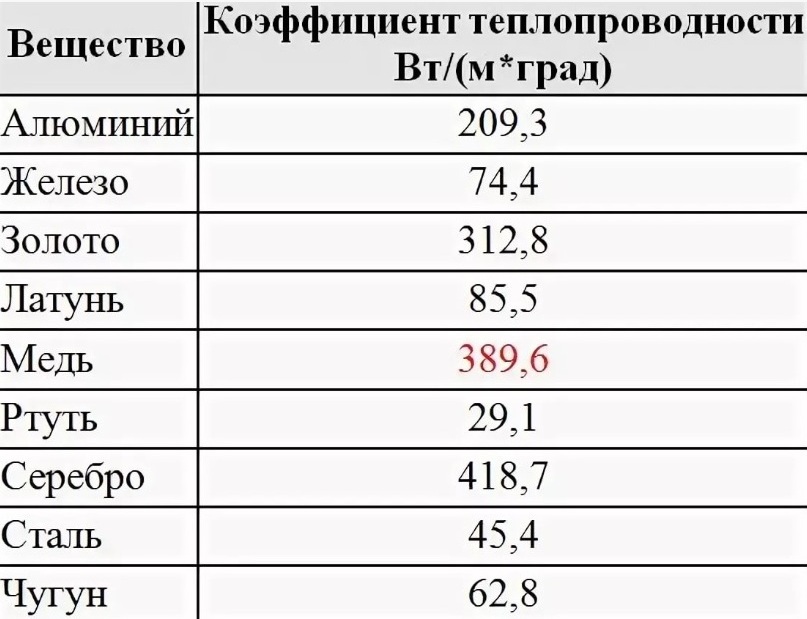 818
818