и НИИБ_Т: Таблица удельной теплоемкости жидкостей
| Жидкости | Cp, Дж/(кг·К) |
| Азотная кислота (100%-ная) Nh4 | 1720 |
| Анилин C6H5Nh3 | 2641 |
| Антифриз (тосол) | 2990 |
| Ацетон C3H6O | 2160 |
| Бензин | 2090 |
| Бензин авиационный Б-70 | 2050 |
| Бензол C6H6 | 1050 |
| Вода h3O | 4182 |
| Вода морская | 3936 |
| Вода тяжелая D2O | 4208 |
Водка (40% об.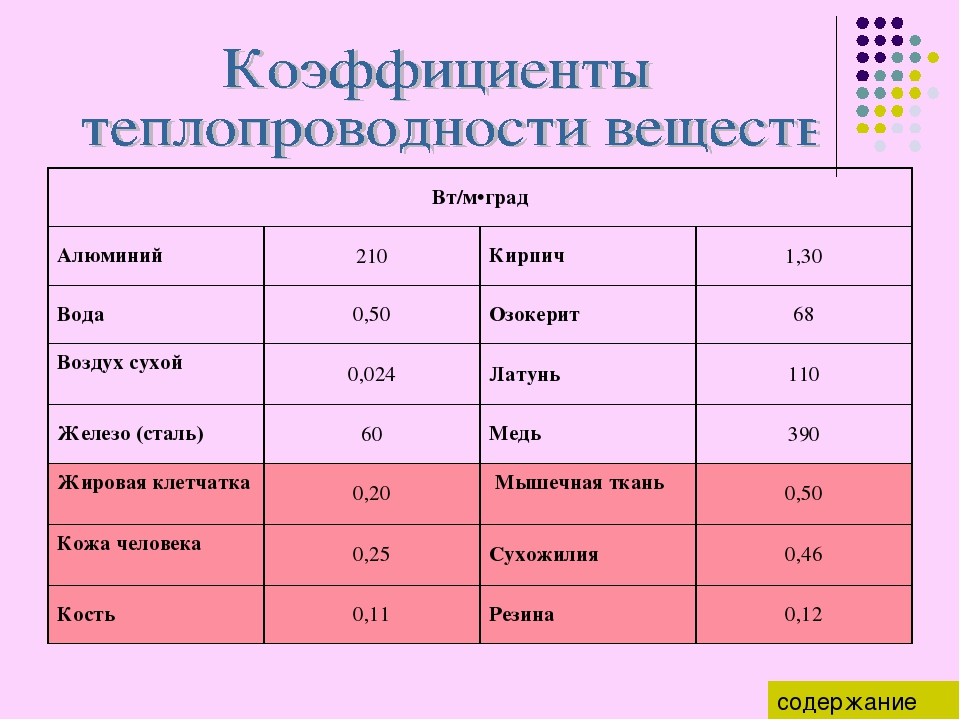 ) ) | 3965 |
| Водный раствор хлорида натрия (25%-ный) | 3300 |
| Газойль | 1900 |
| Гидроксид аммония | 4610 |
| Глицерин C3H5(OH)3 | 2430 |
| Даутерм | 1590 |
| Карборан C2h22B10 | 1720 |
| Керосин | 2085…2220 |
| Кефир | 3770 |
| Мазут | 2180 |
| Масло АМГ-10 | 1840 |
| Масло ВМ-4 | 1480 |
| Масло касторовое | 2219 |
| Масло кукурузное | 1733 |
| Масло МС-20 | 2030 |
| Масло подсолнечное рафинированное | 1775 |
| Масло ТМ-1 | 1640 |
| Масло трансформаторное | |
| Масло хлопковое рафинированное | 1737 |
| Масло ХФ-22 | 1640 |
| Молоко сгущенное с сахаром | 3936 |
| Молоко цельное | 3906 |
| Нефть | 2100 |
| Парафин жидкий (при 50С) | 3000 |
| 3940 | |
| Серная кислота (100%-ная) h3SO4 | 1380 |
| Сероуглерод CS2 | 1000 |
| Силикон | 2060 |
| Скипидар | 1800 |
| Сливки (35% жирности) | 3517 |
| Сок виноградный | 2800…3690 |
| Спирт метиловый (метанол) Ch4OH | 2470 |
| Спирт этиловый (этанол) C2H5OH | 2470 |
| Сыворотка молочная | 4082 |
| Толуол C7H8 | 1130 |
| Топливо дизельное (солярка) | 2010 |
| Топливо реактивное | 2005 |
| Уротропин C6h22N4 | 1470 |
| Фреон-12 CCl2F2 | 840 |
| Эфир этиловый C4h20O | 2340 |
взято — thermalinfo. ru/eto-interesno/tablitsy-udelnoj-teploemkosti-veshhestv
ru/eto-interesno/tablitsy-udelnoj-teploemkosti-veshhestv
Результаты измерений теплопроводности жидкостей.
Содержание:
Результаты измерений теплопроводности жидкостей.
Результаты измерений теплопроводности жидкостей. Теплопроводность обусловлена движением энергии в результате движения молекул, и в отличие от явления конвекции, энергия перемещается от одного слоя к другому, не изменяя порядка расположения слоев молекул. Согласно теории ламинарного пограничного слоя, основное сопротивление теплопередаче от жидкости к стенке (или в обратном направлении) оказывает неподвижный слой жидкости вблизи стенки. Через этот слой тепло передается не через конвекцию, а через теплопроводность. Теплопроводность жидкости намного выше, чем теплопроводность газа. Внутри таблицы. Х -!Показано значение коэффициента теплопроводности X ряда органических жидкостей при различных температурах. Таблица Х-1 Теплопроводность жидкости| 1, 2, 3] Продолжение табл. Х-1.
Температурная зависимость теплопроводности некоторых жидкостей показана на рисунке. Х-1 указывает на незначительное изменение теплопроводности жидкости по мере повышения температуры(наклон кривой невелик) Людмила Фирмаль
- .Поэтому изменение температуры существенно влияет на теплопроводность жидкости больше, чем на ее вязкость. Обычно при повышении температуры до 10°С теплопроводность жидкости снижается на 0,5-2% (в среднем на 1%). Значение X также зависит от области, в которой изменяется температура. В узком диапазоне изменения температуры от Г0 до Г зависимость можно считать простой.

- Абас-Заде предложил следующую формулу для насыщенных органических жидкостей: X-число= arya(X-2) Где Х° теплопроводность жидкости при атмосферном давлении, при той же температуре, что и Х°. P-плотность жидкости. а и Р-постоянные величины, характерные для конкретного вещества. Когда система жидкость-пар нагревается вблизи критической точки, наблюдается, что теплопроводность пара увеличивается с теплопроводностью жидкости.

Обычно теплопроводность жидкости измеряют в диапазоне температур, не превышающем нормальную температуру кипения. Людмила Фирмаль
- Шеффи и Джонсон [11]измерили теплопроводность некоторых жидкостей между температурой кипения жидкости Tkap и критической температурой Г,; p, и систематизировали результаты.
 На рисунке х-3 показана зависимость теплопроводности метанола, этанола и бензола от понижающей температуры. тт. пл. Т р т ПЛ ми= Здесь Tal это точка плавления. Кривые исследуемых жидкостей схожи по форме. В нормально обследованной области (0> 0, 5) зависимость в основном простая; при 6 > 0.7 наблюдается выраженная кривизна (Уменьшения Х).Теплопроводность жидкой ЛПЛ в точке плавления примерно в 3 раза превышает теплопроводность в критической точке. cr. (Х-3) значение L зависит от давления. Показывает теплопроводность при давлении от A0 до 0 и давлении от p до 0 Диэтиленгликоль рафинированный керосин Сернокислотное шпиндельное масло Парафиновое масло Трихлорэтилен хлористый Масляный эфир. Ацетат метилового эфира Propyl ацетат Эстера Теплопроводность некоторых жидкостей[9, 10] XPU Bridgman [12, 13] получил отношение (ChrDo)> 1, то есть увеличение теплопроводности жидкостей под высоким давлением(таблица X-4). Влияние давления на теплопроводность больше, когда степень сжатия жидкости больше, то есть чем выше temperature.
На рисунке х-3 показана зависимость теплопроводности метанола, этанола и бензола от понижающей температуры. тт. пл. Т р т ПЛ ми= Здесь Tal это точка плавления. Кривые исследуемых жидкостей схожи по форме. В нормально обследованной области (0> 0, 5) зависимость в основном простая; при 6 > 0.7 наблюдается выраженная кривизна (Уменьшения Х).Теплопроводность жидкой ЛПЛ в точке плавления примерно в 3 раза превышает теплопроводность в критической точке. cr. (Х-3) значение L зависит от давления. Показывает теплопроводность при давлении от A0 до 0 и давлении от p до 0 Диэтиленгликоль рафинированный керосин Сернокислотное шпиндельное масло Парафиновое масло Трихлорэтилен хлористый Масляный эфир. Ацетат метилового эфира Propyl ацетат Эстера Теплопроводность некоторых жидкостей[9, 10] XPU Bridgman [12, 13] получил отношение (ChrDo)> 1, то есть увеличение теплопроводности жидкостей под высоким давлением(таблица X-4). Влияние давления на теплопроводность больше, когда степень сжатия жидкости больше, то есть чем выше temperature. As ориентир, в среднем.
As ориентир, в среднем.
Смотрите также:
Методические указания по гидравлике
Возможно эти страницы вам будут полезны:
Смотрите также:
Методические указания по гидравлике
Возможно эти страницы вам будут полезны:
- Выбор метода расчета теплопроводности газовой смеси.
- Примеры расчета теплопроводности газовой смеси.
- Основы теории теплопроводности жидкостей.
- Эмпирические зависимости.
Справочник по теплопроводности жидкостей и газов (1990)
ОГЛАВЛЕНИЕ
Предисловие………………………………….. 4
Глава первая- Подготовка справочных таблиц……………….. 5
Глава вторая- О роли радиационного переноса теплоты………….. 6
Глава третья. Теплопроводность одноатомных веществ………….. 8
Глава четвертая. Теплопроводность двухатомных простых веществ …… 27
Глава пятая. Теплопроводность воздуха. ………………….. 40
………………….. 40
Глава шестая. Теплопроводность неорганических веществ …………. 43
Глава седьмая. Теплопроводность обычной и тяжелой воды……….. 59
Глава восьмая. Теплопроводность щелочных металлов ………….. 68
Глава девятая. Обобщение данных о теплопроводности паров нормальных
углеводородов метанового ряда при р = 0,1 МПа…………….. 75
Глава десятая. Теплопроводность органических веществ Ci……….. 76
Глава одиннадцатая. Теплопроводность органических веществ Сг…….. 104
Глава двенадцатая. Теплопроводность органических вешеств Сз …….. 128
Глава тринадцатая. Теплопроводность органических веществ С* …….. 144
Глава четырнадцатая. Теплопроводность органических веществ Cs……. 162
Глава пятнадцатая. Теплопроводность органических веществ Сб …….. 173
Глава шестнадцатая. Теплопроводность органических веществ С7…….. 200
Глава семнадцатая. Теплопроводность органических веществ Cg. ……. 222
……. 222
Глава восемнадцатая. Теплопроводность органических веществ С9……. 250
Глава девятнадцатая. Теплопроводность органических веществ Сю …… 263
Глава двадцатая. Теплопроводность органических веществ Сц……… 277
Глава двадцать первая. Теплопроводность органических веществ С12….. 284
Глава двадцать вторая. Теплопроводность органических веществ Cj 3….. 291
Глава двадцать третья. Теплопроводность органических веществ Cj4 ….. 294
Глава двадцать четвертая. Теплопроводность органических веществ С15 300
Глава двадцать пятая. Теплопроводность органических веществ Cjg….. 302
Глава двадцать шестая. Теплопроводность органических веществ Ci 7….. 307
Глава двадцать седьмая. Теплопроводность органических веществ Cig 308
Глава двадцать восьмая. Теплопроводность органических веществ С; 9 312
Глава двадцать девятая. Теплопроводность органических веществ Сго 313
Глава тридцатая. Теплопроводность органических веществ С21. …….. 316
…….. 316
Глава тридцать первая. Теплопроводность органических веществ С22….. 316
Глава тридцать вторая. Теплопроводность органических веществ Сгз • • — ¦ 320
Глава тридцать третья. Теплопроводность органических веществ Сг4 ….. 321
Глава тридцать четвертая. Теплопроводность органических веществ С25 323 Глава тридцать пятая. Теплопроводность изотопно замещенных соединений ………………………………………. 323
Список литературы……………………………… 328
Предметный указатель…………………………. 341
ПРЕДИСЛОВИЕ
За прошедшие 10 лет после издания книги «Теплопроводность жидкостей и газов» [1] в системе Госстандарта СССР аттестованы таблицы справочных данных для ряда технически важных веществ, включающие данные о теплопроводности.
Согласно ГОСТ 8.310-78 «Государственная служба стандартных справочных данных. Основные положения» стандартные справочные данные (ССД) обязательны к применению во всех отраслях народного хозяйства. В этой связи данные таблиц ССД для тех веществ, для которых они имеются, включены в настоящий справочник. Данные таблиц рекомендуемых справочных данных (РСД) приведены в справочнике в том случае, когда они более предпочтительны по сравнению с другими справочными данными. Во всех случаях в справочнике сделаны ссылки на используемые данные категорий ССД или РСД.
В этой связи данные таблиц ССД для тех веществ, для которых они имеются, включены в настоящий справочник. Данные таблиц рекомендуемых справочных данных (РСД) приведены в справочнике в том случае, когда они более предпочтительны по сравнению с другими справочными данными. Во всех случаях в справочнике сделаны ссылки на используемые данные категорий ССД или РСД.
Однако для подавляющего большинства веществ, рассматриваемых в справочнике, данные категорий ССД или РСД отсутствуют, и для этих веществ предлагаемый читателям справочник содержит сведения о теплопроводности, полученные только на основе экспериментальных данных.
Новым является включение в справочник таблиц теплопроводности щелочных металлов в жидком и паровом состояниях и новых веществ, прежде недостаточно либо совершенно не изученных, в основном это органические высокомолекулярные соединения.
Готовя настоящее издание, авторы сочли правильным построить его по форме, близкой к справочному изданию, исключив из него детали принципа отбора и анализа работ по тому или иному веществу, за исключением наиболее важных технических веществ, в отличие от того, как это было сделано в [l], Это, на наш взгляд, позволило сделать справочник более практичным и удобным для использования его в технических расчетах.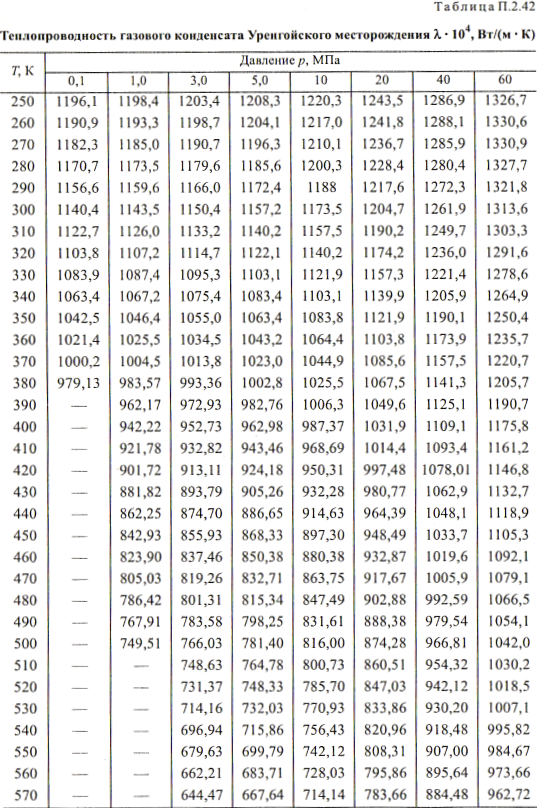
Предлагаемое читателю издание включает в себя практически все известные сведения о теплопроводности чистых жидкостей или газов. В этом смысле оно остается единственным изданием такого рода в СССР и за рубежом.
…Теплопроводность изопропилового спирта | Мир сварки
Вы здесь
Сообщение об ошибке
Warning: count(): Parameter must be an array or an object that implements Countable в функции antispam_user_load() (строка 1545 в файле /home/nikolai3/6.nikolai3.z8.ru/docs/sites/all/modules/antispam/antispam.module).Теплопроводность изопропилового спирта
| T, K | λ·103, Вт/(м·К), при p, МПа | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0,1 | 1 | 2 | 3 | 4 | 5 | 10 | 20 | 40 | |
| 300 | 138 | 138 | 138 | 139 | 140 | 140 | 142 | 146 | 154 |
| 320 | 134 | 134 | 135 | 135 | 136 | 136 | 138 | 142 | 151 |
| 340 | 131 | 131 | 132 | 132 | 133 | 133 | 135 | 140 | 148 |
| 350 | 129 | 129 | 130 | 130 | 131 | 131 | 134 | 138 | 146 |
| 360 | — | 128 | 129 | 129 | 130 | 130 | 133 | 137 | 145 |
| 380 | — | 125 | 126 | 126 | 127 | 127 | 130 | 135 | 144 |
| 400 | 25,4 | 122 | 123 | 123 | 124 | 124 | 126 | 132 | 141 |
| 420 | 27,7 | 119 | 120 | 120 | 121 | 122 | 125 | 130 | 139 |
| 440 | 29,9 | — | 116 | 117 | 118 | 119 | 122 | 128 | 137 |
| 460 | 32,3 | — | — | 113 | 115 | 116 | 119 | 126 | 135 |
| 480 | 34,7 | 37,3 | 42,1 | — | — | 113 | 117 | 124 | 134 |
| 500 | 37,3 | 39,4 | 42,7 | — | — | 108 | 114 | 122 | 133 |
| 520 | 40,0 | 41,5 | 43,8 | 47,3 | 53,2 | 64,8 | 110 | 119 | 131 |
| 540 | 42,6 | 43,8 | 45,5 | 47,7 | 51,7 | 57,8 | 105 | 116 | 129 |
| 560 | 45,4 | 46,2 | 47,4 | 49,0 | 51,0 | 54,0 | 97,0 | 113 | 127 |
Литература
- Справочник по теплопроводности жидкостей и газов / Н.
 Б. Варгафтик, Л.П. Филиппов, А.А. Тарзиманов, Е.Е. Тоцкий. – М.: Энергоатомиздат, 1990. – 352 с.
Б. Варгафтик, Л.П. Филиппов, А.А. Тарзиманов, Е.Е. Тоцкий. – М.: Энергоатомиздат, 1990. – 352 с.
Страница не найдена | Кафедра физики твердого тела ПетрГУ
http://secretary.rid.go.th/
http://rtlabs.nitk.ac.in/
http://www.ei.ksue.edu.ua/
http://www.unajma.edu.pe/
http://www.drbrambedkarcollege.ac.in/
https://esperanza.eastern.edu/
https://www.hsri.or.th/
https://www.agrft.uni-lj.si/
http://www4.fe.usp.br/
https://www.cnba.uba.ar/
https://www.osgoode.yorku.ca bak hocam 2yildir kullandigim siteye gelip kod ekliyorsun not yazip kodlarini siliyorum (insan olan utanir kusura bakma hocam diyip giderdi) kendine dusmanmi ariyorsun? belliki sen disli birine denk gelmemissin hayatin boyunca ama ben cok ugrastim cokta denk geldim bu sekilde tanimadigin birini tehtit etmen ya deli oldugunu gosterir yada tecrubesizligini sen bana isimi ogretecegine once baskalarina ait olan sitelere girmemeyi ogren ondan sonra bana isimi ogretirsin ben cok takintili bir adamim beni kotu bir insan olmaya zorlama rica ediyorum bak lutfen birbirimizi uzmeyelim emin ol bu site felan umrumdami saniyorsun? olay tamamen prensip meselesi sen benim yatakodama gelip beraber yatacagiz diyorsun oyle bir olay yok isine bak oldu 10 kisi daha cagir 500 kod eklesin herkes yorumbacklink isimi yapiyorsun? sacmalamissin daha fazla beni muatap etme kendinle yaptigin terbiyesizligin farkina var illa darbe yiyincemi aklin basina gelecek anlamiyorum ki o kadar yaziyorum ki birbirimize kotuluk yapmayalim kalp kirmayalim birbirimizi uzmeyelim sana daha once boyle notlar yazan bir linkci gordun mu Allah askina ben bazen goruyorum ana baci duymadigim kufurler yaziyor adamlar birbirine sen benim gibi bir insani uzuyorsun ama lutfen. . 8yildir ben kimseyle ortak site kullanmadim babam gelse onunlada kullanmam en hassas oldugum konudur bu bir daha kod eklememeni siddetle tavsiye ediyorum yoksa farkli seyler olur ve kendine nur topu gibi manyak bir dusman edinirsin bos yere bu polemigi uzatiyorsun haksiz olan sensin kod disinde birsey yazmak istersen yazabilirsin ama rica ediyorum isi inada bindirme senden ERDEMLİ DÜRÜST VE OLGUN bir davranis bekliyorum beni anladigini umuyorum ve tekrar inşAllah kod eklemeyecegini umuyorum olumlu olumsuz notunu buraya yazablirsin bende bir daha bu siteyi kullanmiyacagim sanada kullandirmam tabiki is site isi degil prensip isi.. ihtiyacin olabilir site sayin azdir bunlar dogal seyler ben gerekirse kendim eklerim senin kodlarini oyle bir durumda kendi kodlarimida silerim sadece senin olur ama o son not garip bir insan oldugunu dusunduruyor bana ve inan ugrasacak vaktim de kafamda yok kendine sardirma hepimiz ekmek davasindayiz senle isim yok benden sana kotulukte gelmez ama beni zorlama lutfen.
. 8yildir ben kimseyle ortak site kullanmadim babam gelse onunlada kullanmam en hassas oldugum konudur bu bir daha kod eklememeni siddetle tavsiye ediyorum yoksa farkli seyler olur ve kendine nur topu gibi manyak bir dusman edinirsin bos yere bu polemigi uzatiyorsun haksiz olan sensin kod disinde birsey yazmak istersen yazabilirsin ama rica ediyorum isi inada bindirme senden ERDEMLİ DÜRÜST VE OLGUN bir davranis bekliyorum beni anladigini umuyorum ve tekrar inşAllah kod eklemeyecegini umuyorum olumlu olumsuz notunu buraya yazablirsin bende bir daha bu siteyi kullanmiyacagim sanada kullandirmam tabiki is site isi degil prensip isi.. ihtiyacin olabilir site sayin azdir bunlar dogal seyler ben gerekirse kendim eklerim senin kodlarini oyle bir durumda kendi kodlarimida silerim sadece senin olur ama o son not garip bir insan oldugunu dusunduruyor bana ve inan ugrasacak vaktim de kafamda yok kendine sardirma hepimiz ekmek davasindayiz senle isim yok benden sana kotulukte gelmez ama beni zorlama lutfen. . zaten kafamda bir dunya sorun var hayat acimasiz hayat zor benim derdim bana yetiyor butun ictenligim ve iyi niyetim ile sana bu notu yaziyorum bu kadar sozden sonra kod ekleyecegini sanmiyorum birde seninle ugrasmayayim guzel kardesim arkadasim lutfen rica ediyorum LUTFEN barış her zaman erdemli insanlarin isidir lutfen ayni olgunluk ile senden olumlu donusunu bekliyorum eger yazdiklarimda kalp kirici yada incitici birsey varsa lutfen kusura bakma 1-2defa kontrol ettim ama belki gozumden kacmis olabilir hakkini helal et ve en iyisi ikimiz icinde helallesip bu isi noktalamaktir inan kotu biri degilim selam ve sevgiyle..
. zaten kafamda bir dunya sorun var hayat acimasiz hayat zor benim derdim bana yetiyor butun ictenligim ve iyi niyetim ile sana bu notu yaziyorum bu kadar sozden sonra kod ekleyecegini sanmiyorum birde seninle ugrasmayayim guzel kardesim arkadasim lutfen rica ediyorum LUTFEN barış her zaman erdemli insanlarin isidir lutfen ayni olgunluk ile senden olumlu donusunu bekliyorum eger yazdiklarimda kalp kirici yada incitici birsey varsa lutfen kusura bakma 1-2defa kontrol ettim ama belki gozumden kacmis olabilir hakkini helal et ve en iyisi ikimiz icinde helallesip bu isi noktalamaktir inan kotu biri degilim selam ve sevgiyle..
Теплопроводность жидкостей
Около 10-15 лет назад жидкости либо напрямую (в основном фторуглероды), либо косвенно (холодные пластины, омываемые водой) охлаждали большинство мейнфреймов. В настоящее время ожидаемое увеличение плотности теплового потока вызывает возобновление интереса как к пассивному, так и к активному жидкостному охлаждению, поскольку пределы воздушного охлаждения становятся вполне досягаемыми. Другие практические приложения, в которых жидкости играют роль, включают материалы с фазовым переходом и тепловые трубы.
Другие практические приложения, в которых жидкости играют роль, включают материалы с фазовым переходом и тепловые трубы.
Если мы сосредоточимся на максимизации коэффициента теплопередачи, становится ясно, что теплопроводность жидкости является доминирующим параметром.В целом теплопроводность твердых тел падает на 15-40% при температуре плавления, что связано с увеличением беспорядка. Однако для воды разница гораздо больше. Лед при «нормальных» температурах имеет теплопроводность более чем в три раза выше. Что еще более важно для целей охлаждения, теплопроводность воды намного выше, чем у всех других (неметаллических) жидкостей, представляющих практический интерес для охлаждения электроники.
Что касается зависимости от температуры, то у большинства жидкостей теплопроводность снижается на 10 % в диапазоне температур от 0 до 100 °C.Однако, как обычно, вода является исключением, показывая увеличение на 10%.
В приведенной ниже таблице представлены данные некоторого порядка для различных классов жидкостей. Многие другие данные, в том числе в зависимости от температуры, можно найти в VDI Warmeatlas, Springer Verlag Heidelberg, Германия.
Многие другие данные, в том числе в зависимости от температуры, можно найти в VDI Warmeatlas, Springer Verlag Heidelberg, Германия.
| Жидкость | Теплопроводность (Вт/мК) |
| Вода | 0,6 |
| Прочие полярные жидкости | 0,2-0,6 |
| Флуоринерты | 0.06-0,07 |
| Масла низкой вязкости | 0,11-0,15 |
| Прочие органические жидкости | 0,12-0,20 |
| Расплавленные соли | 1-4 |
| Расплавленные металлы | 10-100 |
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.

- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Уравнение теплопроводности жидкостей и искусственная нейронная сеть
[1] Кардос А., «Theorie der Wärmeleitung von Flussigkeiten», Forschung auf dem Gebiete des Ingenieurwesens , Vol. 5, № 1, 1934, стр. 14–24. doi: https://doi.org/10.1007/BF02578814
[2] Бриджмен П. В., «Теплопроводность жидкостей под давлением», Proceedings of American Academy of Arts and Sciences , Vol. 59, 1923, стр. 141–169. doi: https://doi.org/10.2307/20026073
[3] Weber H. F., «Untersuchungen über die Wärmeleitung in Flussigkeiten», Annalen der Physik und Chemie , Vol.10, № 3, 1880 г., стр. 103–130.
[4] Сесил О.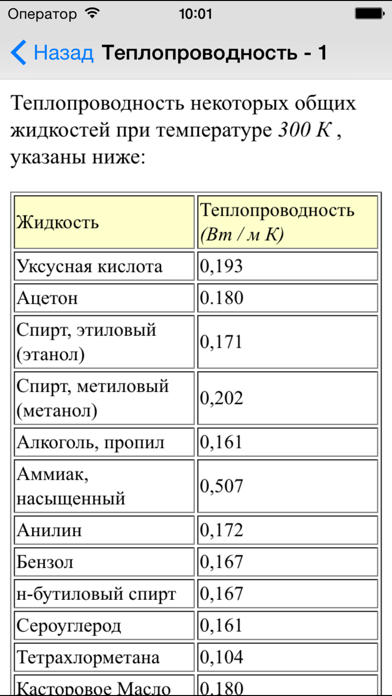 Б. и Мунк Р. Х., «Теплопроводность некоторых органических жидкостей», Industrial & Engineering Chemistry , Vol. 48, № 3, 1956, стр. 437–440.
Б. и Мунк Р. Х., «Теплопроводность некоторых органических жидкостей», Industrial & Engineering Chemistry , Vol. 48, № 3, 1956, стр. 437–440.
[5] Бриджмен П. В., «Теплопроводность жидкостей под давлением», Proceedings of the American Academy of Arts and Sciences , Vol. 59, № 7, 1923, с. 141. doi:https://doi.org/10.2307/20026073 PAAAAV 0065-6836
[6] Варгафтик Н.Б., Всесоюзного Теплотехнического Института , Вып. 8, 1949, с. 6.
[7] Poling BE, Prausnitz JM and O’Connell JP, The Properties of Gases and Liquids , 5th ed., McGraw-Hill, New York, 2001.
[8] Reid RC, Prausnitz JM and Sherwood TK, The Properties of Gases and Liquids , 3-е изд., McGraw-Hill, Нью-Йорк, 1799, стр. 518–525.
[9] Гарагейзи Ф., Илани-Кашкули П., Саттари М., Мохаммади А. Х., Рамьюгернатх Д. и Ришон Д., «Развитие количественной зависимости между структурой и теплопроводностью жидкости для чистых химических соединений», Равновесия жидкой фазы , Vol. 355, октябрь 2013 г., стр. 52–80. doi: https://doi.org/10.1016/j.fluid.2013.06.043 FPEQDT 0378-3812
355, октябрь 2013 г., стр. 52–80. doi: https://doi.org/10.1016/j.fluid.2013.06.043 FPEQDT 0378-3812
[10] Шеффи В.Ю. и Джонсон Э.Ф., «Теплопроводность жидкостей при высоких температурах» Журнал химических и Технические данные , Том. 6, № 2, 1961, с.245–249. doi: https://doi.org/10.1021/je60010a019
[11] Барончини С., Ди Филиппо П., Латини Г. и Пачетти М., «Теплопроводность жидкостей: сравнение расчетных значений с экспериментальными результатами при различных температурах», High Temperature—High Pressure , Vol. 11, 1978, стр. 581–586.
[12] Барончини К., Ди Филиппо П., Латини Г. и Пачетти М., «Улучшенные корреляции для расчета теплопроводности жидкости», Международный журнал теплофизики , Vol.1, № 2, 1980, стр. 159–175. doi: https://doi.org/10.1007/BF00504518 IJTHDY 0195-928X
[13] Барончини С., Ди Филиппо П., Латини Г. и Пачетти М., «Теплопроводность органических жидкостей: метод прогнозирования в диапазоне пониженных температур от 0,3 до 0,8», International Journal of Thermophysics , Vol. 35, № 1, 1981, стр. 21–38. doi: https://doi.org/10.1007/BF00503572 IJTHDY 0195-928X
35, № 1, 1981, стр. 21–38. doi: https://doi.org/10.1007/BF00503572 IJTHDY 0195-928X
[14] Baroncini C., Di Filippo P. и Latini G., «Оценка теплопроводности органических и неорганических хладагентов в насыщенных Liquid State», International Journal of Refrigeration , Vol.6, № 1, 1983, стр. 60–62. doi: https://doi.org/10.1016/0140-7007(83)
[15] Латини Г. и Барончини С., «Влияние температуры и давления на теплопроводность Органические жидкости», High Temperature—High Pressure , Vol. 15, № 4, 1982, стр. 407–411.
[16] Латини Г., Барончини К. и Пьерпаоли П., «Жидкости под давлением: анализ методов прогнозирования теплопроводности и общая корреляция», High Temperature—High Pressure , Vol.19, № 1, 1987, стр. 43–50.
[17] Гарагейзи Ф., Илани-Кашкули П., Саттари М., Мохаммади А.Х., Рамьюгернатх Д. и Ришон Д., «Разработка общей модели для определения теплопроводности жидких химических соединений при атмосферном давлении». », AIChE Journal , Vol. 59, № 5, 2013. С. 1702–1708. doi: https://doi.org/10.1002/aic.13938 ACTJB3 0569-3845
», AIChE Journal , Vol. 59, № 5, 2013. С. 1702–1708. doi: https://doi.org/10.1002/aic.13938 ACTJB3 0569-3845
[18] Наджафи А., Хамзехи М. Э., Наджиби Х., Сулеймани М., Ван Гервен Т., Ван дер Брюгген Б. и Мазинани С., «Прогнозирование теплопроводности чистых жидкостей с использованием многослойной нейронной сети персептрона», Журнал теплофизики и теплопередачи , Vol. 29, № 1, 2015. С. 197–202. doi: https://doi.org/10.2514/1.T4405 JTHTEO 0887-8722
[19] Варгафтик Н.Б., Филиппов Л.П., Тарзиманов А.А., Тоцкий Е.Е., Справочник по теплопроводности жидкостей и газов , CRC Press, Бока-Ратон, Флорида, 1994, стр. 84–329.
[20] Ди Никола Г., Ciarrocchi E., Pierantozzi M. и Stryjek R., «Новое уравнение для теплопроводности органических соединений», Journal of Thermal Analysis and Calorimetry , Vol. 116, № 1, 2014. С. 135–140. doi: https://doi.org/10.1007/s10973-013-3422-7 JTACF7 1418-2874
[21] Ритвельд Т. и Ван Хаут Р., Статистические методы изучения языка и языкового поведения , Mouton de Gruyter, New York, 1993, стр. 251–293.
и Ван Хаут Р., Статистические методы изучения языка и языкового поведения , Mouton de Gruyter, New York, 1993, стр. 251–293.
[22] Феррейра К., «Программирование экспрессии генов: новый адаптивный алгоритм решения проблем», Complex Systems , Vol. 13, № 2, 2001. С. 87–129. CPSYEN 0891-2513
[23] Хамзехи М.Е., Фаттахи М., Наджиби Х., Ван дер Брюгген Б. и Мазинани С., «Применение искусственных нейронных сетей для оценки растворимости кислых газов (h3S и CO2) в 32 обычно ионных жидкостях и растворах аминов», Journal of Natural Gas Science and Engineering , Vol. 24 мая 2015 г., стр.106–114. doi:https://doi.org/10.1016/j.jngse.2015.03.014
[24] Марквардт Д. В., «Алгоритм оценки методом наименьших квадратов нелинейных параметров», Журнал Общества промышленных и Прикладная математика , Том. 11, № 2, 1963, стр. 431–441. doi: https://doi.org/10.1137/0111030 JSMCAL
[25] Хайкин С. , Neural Networks: A Comprehensive Foundation , 2-е изд., Prentice-Hall, New York, 1999, стр. 22. –334.
, Neural Networks: A Comprehensive Foundation , 2-е изд., Prentice-Hall, New York, 1999, стр. 22. –334.
[26] Цыбенко С.V., «Приближение суперпозицией сигмоидальной функции», Математика управляющих сигналов и систем , Vol. 2, № 4, 1989, стр. 303–314. doi: https://doi.org/10.1007/BF02551274
[27] Ариана М.А., Вафери Б. и Карими Г., «Прогнозирование теплопроводности наножидкостей на водной основе оксида алюминия с помощью искусственных нейронных сетей», Порошок Технология , Вып. 278, июль 2015 г., стр. 1–10. doi: https://doi.org/10.1016/j.powtec.2015.03.005 POTEBX 0032-5910
[28] Эсфе М.Х., Афранд М., Ян В.-М. и Акбари М., «Применимость искусственной нейронной сети и нелинейной регрессии для прогнозирования моделирования теплопроводности наножидкостей Al2O3 – вода с использованием экспериментальных данных», International Communications in Heat and Mass Transfer , Vol.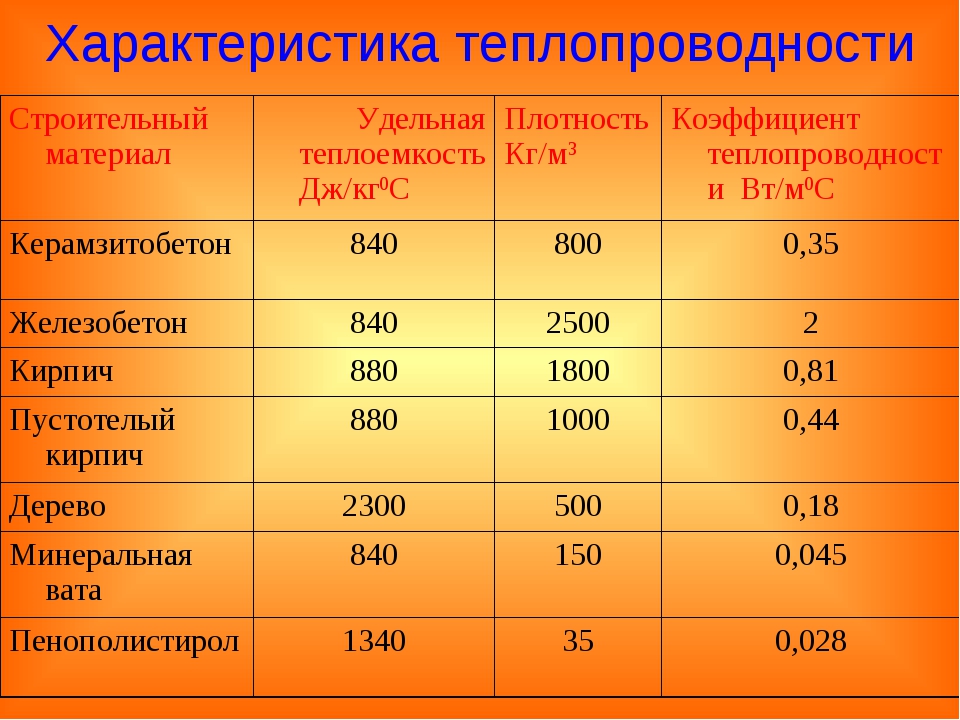 66, август 2015 г., стр. 246–249. doi: https://doi.org/10.1016/j.icheatmasstransfer.2015.06.002 IHMTDL 0735-1933
66, август 2015 г., стр. 246–249. doi: https://doi.org/10.1016/j.icheatmasstransfer.2015.06.002 IHMTDL 0735-1933
[29] Лонго Г.А., Зилио К., Чезерачу Э. и Реджиани М., «Применение искусственных нейронов». Сеть (ANN) для прогнозирования теплопроводности оксидно-водных наножидкостей», Nano Energy , Vol.1, № 2, март 2012 г., стр. 290–296. doi:https://doi.org/10.1016/j.nanoen.2011.11.007
[30] Курт Х. и Кайфечи М., «Прогнозирование теплопроводности растворов этиленгликоль-вода с помощью искусственных нейронных сетей », Applied Energy , Vol. 86, № 10, октябрь 2009 г., стр. 2244–2248. doi: https://doi.org/10.1016/j.apenergy.2008.12.020 ПРИЛОЖЕНИЕ 0306-2619
[31] Хезаве А.З., Раиси С. и Лашкарболооки М., «Оценка теплопроводности ионных жидкостей с использованием нейронная сеть персептрона», Industrial and Engineering Chemistry Research , Vol.51, № 29, 2012. С. 9886–9893. doi: https://doi. org/10.1021/ie202681b IECRED 0888-5885
org/10.1021/ie202681b IECRED 0888-5885
[32] Хорник К., Стинчкомб М. и Уайт Х., «Многослойные сети с прямой связью — универсальные аппроксиматоры», Neural Networks , Том. 2, № 5, 1989, стр. 359–366. doi: https://doi.org/10.1016/0893-6080(89)-8 NNETEB 0893-6080
[33] Hecht-Nielsen R., «Theory of the Back Propagation Neural Network», Neural Сети , Том. 1, 1989, с.593–606. doi: https://doi.org/10.1109/IJCNN.1989.118638
| ||||
(10 -10 N -1 м 2 )
 9
9Данные Фрэнкса, Феликса, «Вода, матрица жизни», 2-е изд., Королевское химическое общество, 2000.
Жидкий натрий используется в качестве теплоносителя в реакторах на быстрых нейтронах.
Tables
Water Concepts
Reference
Franks
Экспериментальные измерения теплопроводности наножидкостей на основе глицерина с различными температурными контрастами
вязкостные наножидкости на основе глицерина. Были приготовлены три наножидкости с разным тепловым контрастом путем суспендирования чешуек графена, оксидов меди или наночастиц кремнезема в чистом глицерине. Наножидкости были термически охарактеризованы при комнатной температуре по методике 3 ω с малыми амплитудами колебаний температуры. Значительное повышение теплопроводности обнаружено как в наножидкостях глицерин/оксид меди, так и в наножидкостях глицерин/чешуйчатый графен. Наши результаты ставят под сомнение роль броуновского движения в микроскопических механизмах теплопроводности высоковязких наножидкостей на основе глицерина.Аналогичное поведение теплопроводности в зависимости от объемной доли наночастиц было обнаружено для всех трех исследованных в настоящее время наножидкостей на основе глицерина. Эти результаты можно объяснить на основе фрактальной агрегации в наножидкостях.
Были приготовлены три наножидкости с разным тепловым контрастом путем суспендирования чешуек графена, оксидов меди или наночастиц кремнезема в чистом глицерине. Наножидкости были термически охарактеризованы при комнатной температуре по методике 3 ω с малыми амплитудами колебаний температуры. Значительное повышение теплопроводности обнаружено как в наножидкостях глицерин/оксид меди, так и в наножидкостях глицерин/чешуйчатый графен. Наши результаты ставят под сомнение роль броуновского движения в микроскопических механизмах теплопроводности высоковязких наножидкостей на основе глицерина.Аналогичное поведение теплопроводности в зависимости от объемной доли наночастиц было обнаружено для всех трех исследованных в настоящее время наножидкостей на основе глицерина. Эти результаты можно объяснить на основе фрактальной агрегации в наножидкостях.
1. Введение
За последние несколько лет улучшение теплопередачи стало обязательным требованием для оптимизации использования энергии в различных промышленных и технологических областях, в основном из-за дефицита ископаемого топлива, побуждающего к использованию текущих ресурсов. более эффективно.Среди различных направлений, исследованных за последние два десятилетия для улучшения передачи тепла, использование наножидкостей стало привлекательной альтернативой, которая интенсивно изучается международным научным сообществом. Согласно терминологии, введенной Чоем в 1995 г. [1], наножидкость состоит из стабильной дисперсии наночастиц (НЧ) в базовой жидкости. Этот вид дисперсии вызвал значительный интерес в последние несколько лет, так как с несколькими наножидкостями было достигнуто значительное улучшение эффективной теплопроводности.Было продемонстрировано, что диспергирование высокопроводящих наночастиц в жидкостях даже в очень малых количествах (менее 1% по объему) способно увеличить эффективную теплопроводность базовой жидкости почти на 200% с углеродными нанотрубками (УНТ). например [2] и примерно на 40% в случае НЧ оксида меди [3]. Для сохранения конфигурации и объема системы теплоотвода (например, системы охлаждения аккумуляторов в ограниченном багажнике электромобиля) и повышения теплоотводящей способности можно использовать наножидкости, поскольку они эффективно передают тепло [4].
более эффективно.Среди различных направлений, исследованных за последние два десятилетия для улучшения передачи тепла, использование наножидкостей стало привлекательной альтернативой, которая интенсивно изучается международным научным сообществом. Согласно терминологии, введенной Чоем в 1995 г. [1], наножидкость состоит из стабильной дисперсии наночастиц (НЧ) в базовой жидкости. Этот вид дисперсии вызвал значительный интерес в последние несколько лет, так как с несколькими наножидкостями было достигнуто значительное улучшение эффективной теплопроводности.Было продемонстрировано, что диспергирование высокопроводящих наночастиц в жидкостях даже в очень малых количествах (менее 1% по объему) способно увеличить эффективную теплопроводность базовой жидкости почти на 200% с углеродными нанотрубками (УНТ). например [2] и примерно на 40% в случае НЧ оксида меди [3]. Для сохранения конфигурации и объема системы теплоотвода (например, системы охлаждения аккумуляторов в ограниченном багажнике электромобиля) и повышения теплоотводящей способности можно использовать наножидкости, поскольку они эффективно передают тепло [4]. Например, что касается использования УНТ для отвода тепла, были измерены характеристики теплопередачи наножидкостей УНТ/вода (CNWNF) [5]; измерения показали, что использование УНТ в концентрации 0,5% по массе в горизонтальной трубе увеличивает теплопередачу на 350%.
Например, что касается использования УНТ для отвода тепла, были измерены характеристики теплопередачи наножидкостей УНТ/вода (CNWNF) [5]; измерения показали, что использование УНТ в концентрации 0,5% по массе в горизонтальной трубе увеличивает теплопередачу на 350%.
Несмотря на эти обнадеживающие результаты, остаются вопросы относительно интереса этих жидкостей к теплопередаче. Эти сомнения возникают из-за высокой изменчивости экспериментальных результатов, опубликованных на сегодняшний день в литературе, т.е.g., обзоры Wang и Mujumdar [6] и Aybar et al. [7]. Как отмечает Corcione [8], расхождения между данными, доступными в литературе, иногда составляют порядка 50% и более. Для данного типа НЧ причины этих расхождений различны и могут быть связаны с различиями в пробоподготовке (способы синтеза НЧ, размер, форма, окисление, режимы диспергирования, используемые химические добавки и агломерация, используемые базовые жидкости) или в методы измерения (переходная горячая проволока, переходный плоский источник, метод 3 ω и горячий диск). Среди всех этих причин ключевую роль, несомненно, играет состояние дисперсности и агломерации НЧ.
Среди всех этих причин ключевую роль, несомненно, играет состояние дисперсности и агломерации НЧ.
Несколько исследований [9, 10] показали, что теплопроводность наножидкостей на основе воды и этиленгликоля со временем резко снижается, возвращаясь к значению базовой жидкости примерно через десять минут после диспергирования. Это зависящее от времени поведение теплопроводности обусловлено агломерацией частиц и, следовательно, осаждением.
Чтобы избежать этого вредного влияния образования кластеров, обычно используются некоторые химические добавки, обеспечивающие более длительную стабильность раствора.Контроль значения pH, использование поверхностно-активных веществ и полимерная прививка на поверхности НЧ являются распространенными методами стабилизации против оседания. К сожалению, такая обработка поверхности может изменить способ передачи тепла внутри суспензии и, таким образом, скрыть реальное влияние НЧ на эффективную теплопроводность наножидкости [11]. Следовательно, использование различных способов стабилизации и химических добавок, отличающихся от одного экспериментального исследования к другому, может способствовать изменению результатов эксперимента. Кроме того, использование базовых жидкостей с низкой вязкостью, таких как вода ( мПа·с при комнатной температуре), неизбежно ставит под сомнение влияние конвекции на измерение теплопроводности как на микроскопическом, так и на макроскопическом уровне.
Кроме того, использование базовых жидкостей с низкой вязкостью, таких как вода ( мПа·с при комнатной температуре), неизбежно ставит под сомнение влияние конвекции на измерение теплопроводности как на микроскопическом, так и на макроскопическом уровне.
Эта путаница также отражается в большом количестве моделей, предложенных для объяснения различных экспериментальных результатов [6, 7]. Некоторые авторы [10] даже показали, что при низких концентрациях (менее 1%) не наблюдается значительного улучшения проводимости в случае хорошо диспергированных наножидкостей, для которых результаты теории эффективной среды, такие как теория Максвелла- Законы Гарнетта и Гамильтона-Кроссера все еще применяются.Используя наножидкости, содержащие наночастицы магнетита [12–14], Philip et al. показали, что изначально хорошо диспергированные наночастицы не вызывают значительного повышения теплопроводности (TC) их суспензий. Напротив, при воздействии магнитного поля на их суспензии они добились значительного повышения TC за счет индуцирования линейных агломератов наночастиц магнетита в базовых жидкостях. Они показали, что наблюдаемые усиления TC были связаны с эффективным переносом тепла через индуцированные цепочечные агрегаты наночастиц, а не с броуновской микроконвекцией.
Они показали, что наблюдаемые усиления TC были связаны с эффективным переносом тепла через индуцированные цепочечные агрегаты наночастиц, а не с броуновской микроконвекцией.
Чтобы ограничить влияние как химической обработки, так и конвекции, наши суспензии были приготовлены с использованием высоковязкой базовой жидкости. Такой выбор может помочь максимально четко определить реальные теплодиффузионные свойства наножидкости.
В качестве базовой жидкости был выбран глицерин, с одной стороны, из-за его высокой вязкости при комнатной температуре и отсутствия специфической реакционной способности с используемыми здесь НЧ. По сравнению с водой глицерин в рамках нашего исследования имеет ряд преимуществ.Его высокая вязкость позволяет получать стабильные суспензии без какой-либо специфической функционализации и без использования химических добавок для ускорения диспергирования. Как упоминалось ранее, эта химическая нейтральность очень важна. Это позволяет нам макроскопически охарактеризовать эффективную теплопроводность наножидкости без микроскопического влияния химической обработки, обычно неизбежной для менее вязких жидкостей.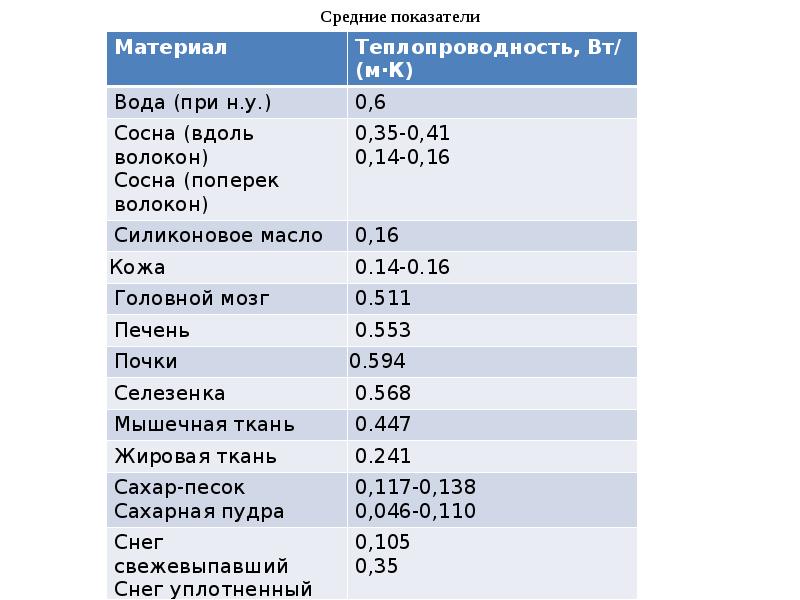 Кроме того, как упоминалось Moghaddam et al. [15], глицерин имеет правильную растворимость дисперсии, необходимую для приготовления устойчивых суспензий графена.
Кроме того, как упоминалось Moghaddam et al. [15], глицерин имеет правильную растворимость дисперсии, необходимую для приготовления устойчивых суспензий графена.
Многие исследователи заметили, что повышение теплопроводности наряду с повышением температуры, независимо от выбора наноматериалов, происходит из-за броуновского движения, при котором поглощение кинетической энергии приводит к большему количеству столкновений частиц. Тем не менее, тепловые характеристики наножидкости, как правило, будут зависеть от соответствующего количества концентраций массовых/объемных процентов, что поставит под угрозу другие [16]. Одной из основных задач данной работы является анализ влияния броуновской микроконвекции и агрегации на повышение теплопроводности высоковязких жидкостей в зависимости от объемной доли твердого вещества.
2. Экспериментальные методы
2.1. Подготовка образцов
В настоящем исследовании использовались НЧ, обладающие различной теплопроводностью, независимо от их размера и формы.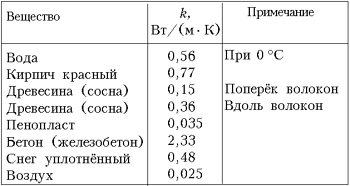 Сферические частицы кремнезема (рис. 1(а)) со средним диаметром 50 нм были синтезированы в лаборатории с использованием процесса Штёбера [17]. Они соответствуют наименьшей из изученных здесь теплопроводностей. НЧ оксида меди со средним диаметром 7 нм (рис. 1(б)) были синтезированы в лаборатории термическим разложением ацетилацетоната меди (II) олеиламином [18].Процесс был улучшен добавлением небольшого количества триоктиламина во время разложения [19]. Из-за очень высокой реакционной способности этих малых НЧ полученный порошок состоит из смеси частиц CuO и Cu 2 O, как показал анализ РФЭС, выполненный на этих НЧ оксида меди непосредственно перед введением в глицерин.
Сферические частицы кремнезема (рис. 1(а)) со средним диаметром 50 нм были синтезированы в лаборатории с использованием процесса Штёбера [17]. Они соответствуют наименьшей из изученных здесь теплопроводностей. НЧ оксида меди со средним диаметром 7 нм (рис. 1(б)) были синтезированы в лаборатории термическим разложением ацетилацетоната меди (II) олеиламином [18].Процесс был улучшен добавлением небольшого количества триоктиламина во время разложения [19]. Из-за очень высокой реакционной способности этих малых НЧ полученный порошок состоит из смеси частиц CuO и Cu 2 O, как показал анализ РФЭС, выполненный на этих НЧ оксида меди непосредственно перед введением в глицерин.
Наконец, мы также использовали нанопорошок графена, состоящий из чешуек толщиной 8 нм, средним поперечным размером 550 нм, удельной поверхностью 100 м 2 /г и .Он был куплен у компании Graphene Supermarket Company и диспергирован в глицерине без какой-либо другой химической обработки. На рис. 2 показаны изображения листов ВНП, полученные с помощью сканирующего электронного микроскопа (СЭМ). Предполагается, что НЧ графена обладают самой высокой теплопроводностью, протестированной в настоящем исследовании.
2 показаны изображения листов ВНП, полученные с помощью сканирующего электронного микроскопа (СЭМ). Предполагается, что НЧ графена обладают самой высокой теплопроводностью, протестированной в настоящем исследовании.
Наночастицы были выбраны с различной теплопроводностью: (i) Графен обладает выдающейся теплопроводностью. Таким образом, ожидается, что использование наножидкостей на основе графена может значительно улучшить тепловые характеристики жидкостей-теплоносителей (II) Наножидкости на основе графена оказывают меньшее воздействие на окружающую среду (iii) Наночастицы CuO и SiO 2 демонстрируют разные контрасты теплопроводности
Из-за высокой гигроскопичности глицерина для приготовления суспензий использовалась только свежая жидкость (Sigma-Aldrich, глицерин для ).Герметичные меры предосторожности, касающиеся хранения образцов и работы измерительной ячейки, были реализованы, чтобы избежать растворения атмосферного водяного пара в наножидкости. Для обеспечения хорошей гомогенизации суспензии в макроскопическом масштабе НЧ постепенно вводят в нагретый глицерин (при температуре 50°С), чтобы уменьшить его вязкость и облегчить процесс гомогенизации. Затем 20 мл этой умеренно нагретой суспензии перемешивают и, наконец, обрабатывают ультразвуком при малой мощности (160 Вт–35 кГц) в течение 48 часов, чтобы разрушить агрегаты.Сначала готовили более концентрированные суспензии с использованием аналитических весов (0,0001 г) для точного измерения массы НЧ. Суспензии меньшей объемной фракции готовили разбавлением более концентрированной путем добавления необходимого количества чистого глицерина.
Для обеспечения хорошей гомогенизации суспензии в макроскопическом масштабе НЧ постепенно вводят в нагретый глицерин (при температуре 50°С), чтобы уменьшить его вязкость и облегчить процесс гомогенизации. Затем 20 мл этой умеренно нагретой суспензии перемешивают и, наконец, обрабатывают ультразвуком при малой мощности (160 Вт–35 кГц) в течение 48 часов, чтобы разрушить агрегаты.Сначала готовили более концентрированные суспензии с использованием аналитических весов (0,0001 г) для точного измерения массы НЧ. Суспензии меньшей объемной фракции готовили разбавлением более концентрированной путем добавления необходимого количества чистого глицерина.
Значения различной теплопроводности материалов, использованных в этом исследовании, приведены в таблице 1 (комнатная температура).
| 8 | ||||
| 8 | глицерин | Silica NPS | Оксид меди NPS | 8 |
| 8 | ||||
0. 28 28 | 1.4 | 50 | ||
2.2. Suspension Characterization
Для изучения состояния дисперсии наночастиц в базовой жидкости и для оценки наличия и размера графеновых агрегатов образцы каждой суспензии после высушивания анализировали с помощью СЭМ. На рис. 3 показан пример наножидкости на основе глицерина с объемной долей графена 0,25%. Собирали по одной капле каждого образца, помещали на сетку СЭМ и затем медленно сушили в печи.На рисунке 3 показано, что нанолисты графена равномерно распределены и что морфология этих нанолистов не изменяется после этапов перемешивания и обработки ультразвуком.
2.3. Экспериментальная установка для определения тепловых характеристик
2.3.1. Режим работы
Чтобы измерить эффективную теплопроводность наших суспензий, мы адаптировали метод 3 ω , разработанный Кэхиллом для тепловых характеристик твердых диэлектриков [20], к случаю электропроводящих жидкостей [21]. , 22].Здесь предпочтение отдается этому методу, а не обычному методу нестационарной горячей проволоки (THW), поскольку использование очень эффективного двухфазного синхронного детектора (DPSD) позволяет использовать очень низкие амплитуды температуры измерительной проволоки (порядка 1 K), что снижает влияние естественной конвекции на измерение температуропроводности.
, 22].Здесь предпочтение отдается этому методу, а не обычному методу нестационарной горячей проволоки (THW), поскольку использование очень эффективного двухфазного синхронного детектора (DPSD) позволяет использовать очень низкие амплитуды температуры измерительной проволоки (порядка 1 K), что снижает влияние естественной конвекции на измерение температуропроводности.
Температуру измерения наножидкости стабилизировали с помощью термостатической бани (0,1 K). Низкоамплитудный ток возбуждения использовался для возбуждения тепловых сигналов (2 ω гармоник температуры и электрического сопротивления) по всей проволоке и жидкости.Процедура измерения в основном состоит в сканировании частоты тока возбуждения при низких значениях (обычно десять значений между 0,1 и 1 Гц) и измерении соответствующих гармонических изменений температуры провода (синфазная и квадратурная составляющие), которые содержат все необходима информация о теплопроводности окружающей жидкости [21]. Для каждой из этих частот два значения температурных компонентов, измеренные DPSD, были записаны, когда они были стабилизированы до менее чем 1% флуктуаций. Для этой процедуры стабилизации обычно требуется не менее пятидесяти периодов накопления измерений на частоту с помощью DPSD; это означает время измерения между () и () на частоту. Таким образом, весь процесс измерения одного значения теплопроводности занимает в среднем около тридцати минут. Мы повторяли по крайней мере несколько раз каждое измерение теплопроводности и сообщали в настоящем исследовании (см. Таблицы 2 и 3) их средние арифметические значения. Максимальная относительная неопределенность 5% была получена в результате статистической обработки наших измерений ТС.
Для этой процедуры стабилизации обычно требуется не менее пятидесяти периодов накопления измерений на частоту с помощью DPSD; это означает время измерения между () и () на частоту. Таким образом, весь процесс измерения одного значения теплопроводности занимает в среднем около тридцати минут. Мы повторяли по крайней мере несколько раз каждое измерение теплопроводности и сообщали в настоящем исследовании (см. Таблицы 2 и 3) их средние арифметические значения. Максимальная относительная неопределенность 5% была получена в результате статистической обработки наших измерений ТС.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,25 | 0,5 | 1,0 | ||
| Глицерин / SiO 2 | 0,285 | 0,285 | 0,285 | 0,286 |
| Глицерин / графен | 0,400 | 0,513 | 0,667 | 0,926 |
| 8 0.078 | 0,16 | 0,32 | 0.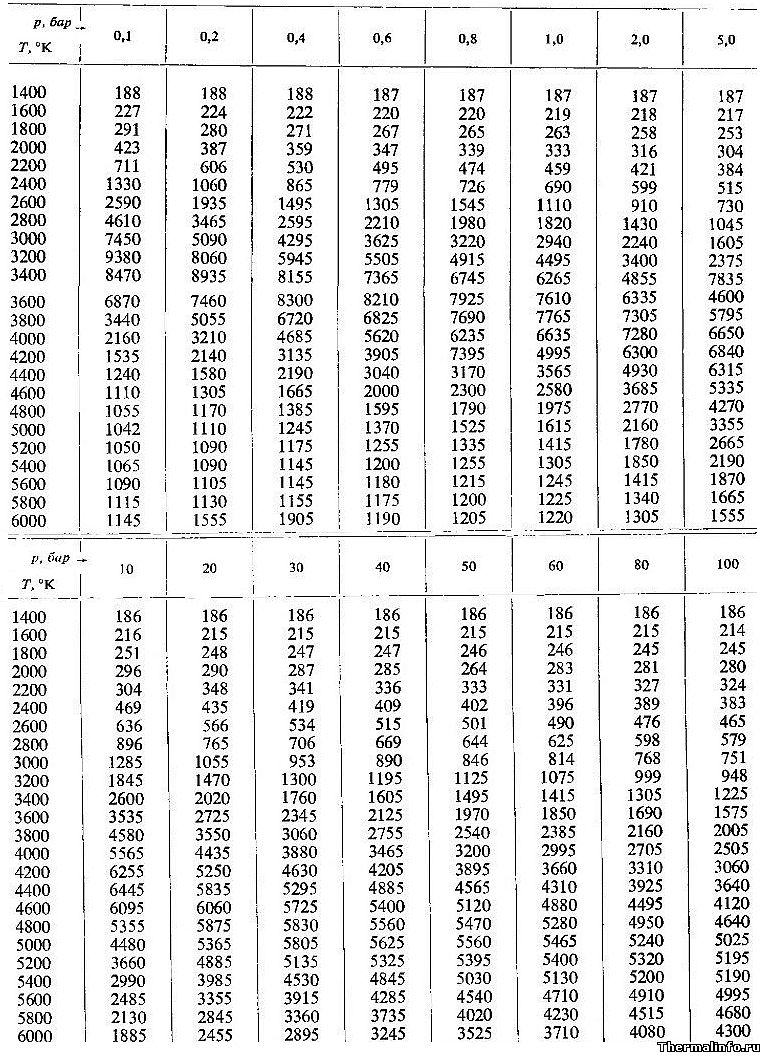 32 32 | |
| глицерин / Cuo-Cu 2 O | 0.382 | 0.447 | 0.479 | 0,627 |
2.3.2. Проверка устройства
Чтобы проверить работу нашего устройства, мы сначала измерили теплопроводность обычных жидкостей, таких как вода и этанол, при комнатной температуре. Полученные нами результаты соответствовали обычным значениям теплопроводности этих жидкостей в пределах упомянутой ранее максимальной относительной погрешности 5%.Однако, поскольку наше исследование было сосредоточено на тепловых свойствах наножидкостей на основе глицерина, мы усовершенствовали калибровку нашего устройства, измерив теплопроводность чистого глицерина в зависимости от температуры. Результаты показаны в таблице 2 и на рисунке 4. Мы также построили линейные модели, полученные по значениям CINDAS [23] (пунктирная линия) и по нашим измерениям (сплошная линия). Сравнивая наши результаты с результатами, полученными в CINDAS, мы можем сделать вывод, что наше устройство дает правильные значения в случае глицерина с точностью около 5% (резкая оценка, худшее из наших измерений (для) составляет менее 5% соответствующего значения CINDAS.).
Сравнивая наши результаты с результатами, полученными в CINDAS, мы можем сделать вывод, что наше устройство дает правильные значения в случае глицерина с точностью около 5% (резкая оценка, худшее из наших измерений (для) составляет менее 5% соответствующего значения CINDAS.).
3. Результаты
3.1. Термическая характеристика наножидкостей на основе глицерина
Были изучены изменения теплопроводности трех различных наножидкостей на основе глицерина в зависимости от объемной доли твердого вещества: глицерин/SiO 2 , глицерин/CuOCu 2 O и глицерин/графеновые наножидкости. Все образцы были приготовлены по одному и тому же протоколу без какой-либо химической обработки. Все измерения проводились при одной и той же температуре с использованием устройства, описанного ранее в разделе 2.3. Значения теплопроводности, измеренные для каждой из этих наножидкостей, как функция объемной доли твердого вещества, собраны в таблице 3.
Изменения теплопроводности наножидкостей на основе глицерина представлены в виде объемная доля на рисунках 5, 6 и 7. Как видно из рисунка 5, не было обнаружено особого повышения теплопроводности в случае наножидкости глицерин/диоксид кремния, при этом объемные доли наночастиц столь же малы, как и использованные здесь.Это было ожидаемо из-за низкой теплопроводности кремнезема. Эти результаты согласуются с результатами, найденными в литературе. Например, Сулейман и др. пришел к выводу, что наночастицы SiO 2 имели повышение теплопроводности примерно на 6,1% выше при суспендировании в этиленгликоле по сравнению с 3,1% в глицерине при 30°C [24].
Как видно из рисунка 5, не было обнаружено особого повышения теплопроводности в случае наножидкости глицерин/диоксид кремния, при этом объемные доли наночастиц столь же малы, как и использованные здесь.Это было ожидаемо из-за низкой теплопроводности кремнезема. Эти результаты согласуются с результатами, найденными в литературе. Например, Сулейман и др. пришел к выводу, что наночастицы SiO 2 имели повышение теплопроводности примерно на 6,1% выше при суспендировании в этиленгликоле по сравнению с 3,1% в глицерине при 30°C [24].
Однако в случае наножидкостей, содержащих наночастицы оксида меди или графен, результаты совершенно другие.Наилучшие результаты получаются в случае наножидкостей на основе графена, для которых наблюдается очень большой прирост теплопроводности даже при малых фракциях. Это улучшение достигает, например, 224 % в случае объемной доли графена, равной 1 %. Эти очень впечатляющие результаты обусловлены высокой теплопроводностью графена и вполне сравнимы с результатами, полученными с некоторыми наножидкостями, приготовленными из углеродных нанотрубок ([2], увеличение на 200% для объемной доли всего лишь 0.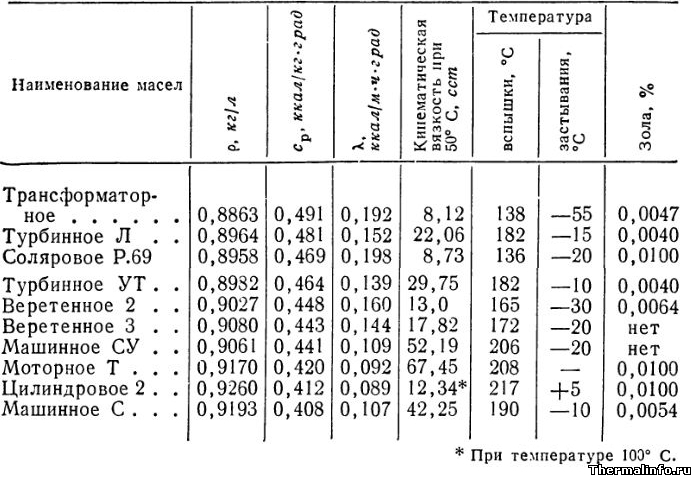 35%) и для силиконовой термопасты на основе графена ([25], усиление на 120% для 1% графена). Теплопроводность наножидкостей графен-вода с объемными концентрациями 0,05, 0,1 и 0,15% и температурами от 10 до 50°C экспериментально исследована Ahammed et al. Усиления на 19,1% и 37,2% были обнаружены при 10°С и 50°С соответственно для максимальной объемной концентрации 0,15% [26].
35%) и для силиконовой термопасты на основе графена ([25], усиление на 120% для 1% графена). Теплопроводность наножидкостей графен-вода с объемными концентрациями 0,05, 0,1 и 0,15% и температурами от 10 до 50°C экспериментально исследована Ahammed et al. Усиления на 19,1% и 37,2% были обнаружены при 10°С и 50°С соответственно для максимальной объемной концентрации 0,15% [26].
Повышение теплопроводности, наблюдаемое в случае промежуточной ситуации наножидкостей на основе оксида меди, также очень интересно и может достигать в данном случае значения до 121%, что оправдывает интерес к таким композитным системам.
Наножидкости на основе глицерина продемонстрировали хорошее улучшение теплопроводности, что подтверждается несколькими литературными исследованиями, например, наножидкости, содержащие наночастицы трех разных размеров (31 нм, 55 нм и 134 нм), приготовленные двухстадийным методом, при объемных долях от 0,5% до 4%. Экспериментальные результаты показали, что наножидкости имеют значительно более высокую теплопроводность, чем базовая жидкость, максимальное увеличение относительной теплопроводности составляет 19. 5% для случая 31 нм при объемной доле 4% [27]. Нтумба и др. показали, что коэффициент теплопроводности увеличивается линейно с объемной долей наночастиц MgO при постоянной температуре и показывает максимальное увеличение ≈19% при 4% объемной доле MgO-глицерина [28].
5% для случая 31 нм при объемной доле 4% [27]. Нтумба и др. показали, что коэффициент теплопроводности увеличивается линейно с объемной долей наночастиц MgO при постоянной температуре и показывает максимальное увеличение ≈19% при 4% объемной доле MgO-глицерина [28].
3.2. Анализ и обсуждение
Существуют различные элементарные модели для описания эволюции теплопроводности суспензий в зависимости от объемной доли , среди которых мы рассматриваем правило смешивания Максвелла-Гарнетта (МГ) для случая сферических НЧ; он выражает отношение теплопроводности наножидкости к базовой жидкости как
В данном случае тепловой контраст очень высок, ; таким образом, можно аппроксимировать (1) как , с .В случае наночастиц оксида меди, взвешенных в глицерине, мы нашли, что для , в то время как соответствующее значение, обеспечиваемое MG, т. е. в 45 раз больше. Эти результаты ясно показывают, что традиционные модели эффективной среды не подходят для описания улучшений теплопроводности, наблюдаемых с двумя изученными здесь высококонтрастными глицериновыми наножидкостями.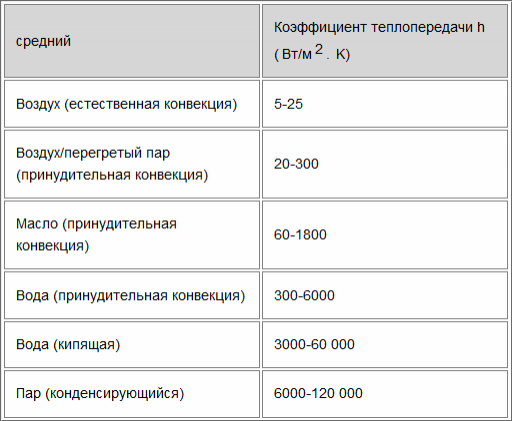
Другой популярной моделью, используемой для определения теплопроводности наножидкостей, является модель Брюггемана (2).Он справедлив для сферических частиц и учитывает взаимодействие между частицами [29].
Как видно из рисунков 6 и 7, закон Брюггемана не может описать значительное увеличение теплопроводности, наблюдаемое с наножидкостями глицерин/CuO-Cu 2 O и глицерин/графен, даже при малых объемных долях.
Среди новых моделей, предложенных для объяснения значительного повышения эффективной теплопроводности наножидкостей, многочисленные подходы подчеркивают ключевую роль, которую играет броуновское движение наночастиц в микроскопических механизмах повышения теплопроводности [30].Большинство этих моделей были введены в случае базовых жидкостей с низкой вязкостью, таких как вода, и в основном касаются сферических наночастиц. Они были обобщены Chon et al. [31] через следующий эмпирический закон:
где , , , , , и – безразмерные числа, определяемые для каждого типа наножидкости; и – соответственно молекулярный диаметр базовой жидкости (здесь глицерина) и средний диаметр наночастиц; — число Прандтля глицерина при . Число Рейнольдса, основанное на броуновском движении наночастиц, определяется выражением
где – постоянная Больцмана; , Па·с и нм, соответственно, плотность, динамическая вязкость и длина свободного пробега глицерина при T = 298 K. Chon et al. определили следующий набор величин в случае наножидкостей вода/Al 2 O 3 : , , , , , и [31].
Число Рейнольдса, основанное на броуновском движении наночастиц, определяется выражением
где – постоянная Больцмана; , Па·с и нм, соответственно, плотность, динамическая вязкость и длина свободного пробега глицерина при T = 298 K. Chon et al. определили следующий набор величин в случае наножидкостей вода/Al 2 O 3 : , , , , , и [31].
Та же модель была использована Corcione et al. [8, 32], но с другими коэффициентами.
Ни одна из многочисленных моделей, предложенных в обзорах [6, 7], не позволила нам описать результаты, полученные нами с нашими наножидкостями.В некотором смысле это относительно логично, поскольку ни одна из базовых жидкостей, представленных в этих обзорах, не обладает такой высокой вязкостью, как глицерин.
В случае глицериновых наножидкостей, изучаемых здесь, мы использовали модифицированную форму соотношения Чона, записанную как
где зависит от жидкости, а также является функцией межфазных сопротивлений. Это модифицированное соотношение было впервые применено к наножидкости глицерин/CuO-Cu 2 O, для которой частицы имеют сферическую форму и нанометровый размер, со средними значениями теплопроводности и диаметра наночастиц . Мы обнаружили хорошее соответствие между экспериментальными результатами и моделью (6), как показано в таблице 4 и на рисунке 6. Тот же анализ применим к моделированию теплопроводности наножидкости глицерин/графен. Как видно на рис. 7, соответствие между измерениями и законом (6) очень хорошее в случае взвешенных в глицерине чешуек графена. Соответствующее значение показателя степени, указанное в таблице 4, идентично найденному Чоном в случае наножидкостей на водной основе.
Мы обнаружили хорошее соответствие между экспериментальными результатами и моделью (6), как показано в таблице 4 и на рисунке 6. Тот же анализ применим к моделированию теплопроводности наножидкости глицерин/графен. Как видно на рис. 7, соответствие между измерениями и законом (6) очень хорошее в случае взвешенных в глицерине чешуек графена. Соответствующее значение показателя степени, указанное в таблице 4, идентично найденному Чоном в случае наножидкостей на водной основе.
+
| |||||||||||||||||||||||||||||||
Использование высоковязкой базовой жидкости также позволяет нам наножидкости на основе глицерина. Согласно соотношению (5) отношение чисел Рейнольдса, связанное с броуновским движением сферических НЧ, взвешенных соответственно в глицерине и воде, может быть выражено как
Вспомнив, что плотности глицерина и воды очень близки, и применив ту же гипотезу для длины свободного пробега, можно записать в очень хорошем приближении, что .Даже если число Рейнольдса значительно больше для наножидкостей на водной основе, чем для наножидкостей на основе глицерина, в последнем случае наблюдается значительное увеличение теплопроводности. Поэтому, учитывая очень большие различия в вязкости между глицерином и водой, в случае наножидкостей на основе глицерина представляется затруднительным приписать основную роль броуновскому движению в повышении теплопроводности. Эванс и др. показали, что объединение наночастиц в кластеры может привести к значительному увеличению теплопроводности, величина которой определяется морфологией кластера [33].Мы применили соотношение (6) к результатам их моделирования методом Монте-Карло в случае, когда химическая размерность кластеров равна фрактальной размерности , с тепловым контрастом и нулевым межфазным термическим сопротивлением. Мы обнаружили хорошее совпадение их результатов с нашей моделью со значением показателя степени, близким к найденным в наших экспериментах (табл. 4). Напомним, что значения коэффициента зависят, среди прочего, от природы базовой жидкости и от химических обработок и поэтому не могут сравниваться здесь.
Эванс и др. показали, что объединение наночастиц в кластеры может привести к значительному увеличению теплопроводности, величина которой определяется морфологией кластера [33].Мы применили соотношение (6) к результатам их моделирования методом Монте-Карло в случае, когда химическая размерность кластеров равна фрактальной размерности , с тепловым контрастом и нулевым межфазным термическим сопротивлением. Мы обнаружили хорошее совпадение их результатов с нашей моделью со значением показателя степени, близким к найденным в наших экспериментах (табл. 4). Напомним, что значения коэффициента зависят, среди прочего, от природы базовой жидкости и от химических обработок и поэтому не могут сравниваться здесь.
4. Заключение
В этом исследовании три наножидкости на основе глицерина были термически охарактеризованы при комнатной температуре. Использование НЧ кремнезема не приводит к заметному повышению теплопроводности, как можно было бы ожидать, исходя из низкой теплопроводности кремнезема. Напротив, для НЧ оксида меди и тем более для чешуек графена, взвешенных в глицерине, наблюдается значительное увеличение теплопроводности, сравнимое с полученным с углеродными нанотрубками в некоторых наножидкостях.Последнее объясняется высокой теплопроводностью графена.
Напротив, для НЧ оксида меди и тем более для чешуек графена, взвешенных в глицерине, наблюдается значительное увеличение теплопроводности, сравнимое с полученным с углеродными нанотрубками в некоторых наножидкостях.Последнее объясняется высокой теплопроводностью графена.
Теории эффективной среды, такие как законы Брюггемана и Максвелла-Гарнетта, совершенно неадекватны для описания этих результатов. Однако зависимость коэффициента усиления от объемной доли НЧ можно аппроксимировать с помощью модифицированной версии эмпирического степенного закона [31], применяемого к НЧ, взвешенным в маловязких жидкостях, таких как вода: , со значениями, очень близкими для трех наножидкости.
В моделях, рассматриваемых для описания коэффициента усиления в маловязких жидкостях, броуновское движение играет ключевую роль.Однако числа Рейнольдса, связанные с броуновским движением, для наножидкостей на основе глицерина на 6-7 порядков ниже, чем для наножидкостей на водной основе, поэтому броуновское движение не может играть существенной роли в исследуемых наножидкостях. С другой стороны, было показано, что объединение НЧ в кластеры приводит к значительному повышению теплопроводности [33]. Моделирование Монте-Карло, основанное на этом подходе, хорошо согласуется с эмпирическим степенным законом, соответствующим нашим результатам для наножидкостей на основе глицерина.
С другой стороны, было показано, что объединение НЧ в кластеры приводит к значительному повышению теплопроводности [33]. Моделирование Монте-Карло, основанное на этом подходе, хорошо согласуется с эмпирическим степенным законом, соответствующим нашим результатам для наножидкостей на основе глицерина.
Ведутся работы по изучению влияния температуры и размера НЧ на тепловые и механические транспортные свойства наножидкостей на основе глицерина.
Доступность данных
Заявляю, что все экспериментальные данные можно найти в статье. Библиографические данные, использованные в этой рукописи, можно скачать по следующим ссылкам. В случае запроса данных, пожалуйста, отправьте мне письмо по электронной почте: [email protected]. — Библиографические справочные ссылки: [1] https://www.juadinggate.net/publication/236353373_enhance_THERMAL_CONDUCTIVE_OF_FLUIDS_WITH_NANOPARTICLES, [2] 10.1063 / 1.2193161, [3] / 196074 / 1.1341218, [4], [5] 10.1016 / J.IJHEATMATSSTRANSSERSFER. 2005.07.009, [6] 10.1016 / J .ijthermalsci.2006.06.010, [7] 10.1080/01457632.2015.987586, [8] 10.1016/j.enconman.2010.06.072, [9] 10.1016/j.ijheatmasstransfer.2006.02.012, [10] 10.1016/jmatchemphys .2007.10.029, [11] 10.1115/1.1571080, [12] 10.1063/1.2812699, [13] 10.1063/1.2838304, [14] 10.1088/0957-4484/19/30/305706 [15]1016/j.cej.2013.07.006, [16] 10.1155/2020/2061343, [17] 10.1016/0021-9797(68)
2005.07.009, [6] 10.1016 / J .ijthermalsci.2006.06.010, [7] 10.1080/01457632.2015.987586, [8] 10.1016/j.enconman.2010.06.072, [9] 10.1016/j.ijheatmasstransfer.2006.02.012, [10] 10.1016/jmatchemphys .2007.10.029, [11] 10.1115/1.1571080, [12] 10.1063/1.2812699, [13] 10.1063/1.2838304, [14] 10.1088/0957-4484/19/30/305706 [15]1016/j.cej.2013.07.006, [16] 10.1155/2020/2061343, [17] 10.1016/0021-9797(68)
-5, [18] 10.1016/j.apsusc.2006.05.023, [19] http://www.theses.fr/2010ORLE2086, [20] 10.1063/1.1141498, [21] https://www.intechopen.com/books/two-phase-flow-phase-change-and-numerical-modeling/ наножидкости для теплопередачи, [22] 10.1016/J.SNA.2011.11.002, [23] https://www.worldcat.org/title/properties-of-inorganic-and-organic-fluids/oclc/ 17107861, [24] https://dx.doi.org/10.1016/j.icheatmasstransfer.2017.08.001, [25] 10.1016/j.physleta.2013.10.017, [26] https://dx.doi.org/10.1016/j.icheatmasstransfer.2015.11.002, [27] https://dx.doi.org/10.1016/j. icheatmasstransfer.2017.04.001, [28] https://dx. doi.org/10.1080/01457632.2016.1151297, [29] 10.1002/andp.19354160705, [30] 10.1063/1.1756684, [31] 10.2063, [31] 10.2063 ] 10.1155/2016/3693249 и [33] 10.1016/j.ijheatmasstransfer.2007.10.017.
doi.org/10.1080/01457632.2016.1151297, [29] 10.1002/andp.19354160705, [30] 10.1063/1.1756684, [31] 10.2063, [31] 10.2063 ] 10.1155/2016/3693249 и [33] 10.1016/j.ijheatmasstransfer.2007.10.017.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Жидкости | Бесплатный полнотекстовый | Теплопроводность ионных жидкостей и ионаножидкостей.Может ли молекулярная теория помочь?
1. Введение
Ионные жидкости появились в последние два десятилетия как одна из наиболее перспективных категорий жидкостей для применения в химии, химической технологии и медицине. Состоящие как минимум из одного катиона и одного аниона, они представляют собой низкотемпературные расплавленные соли, способные кристаллизоваться при температурах ниже комнатной и сохранять термическую и кинетическую стабильность до 550 К, что для большинства из них ограничено содержанием органического углерода. С молекулярной точки зрения это очень интересные жидкости, поскольку в них присутствует большинство хорошо известных внутри- и межмолекулярных сил, которые, следовательно, играют фундаментальную роль в структуре и свойствах этих низкотемпературных ионных расплавов.
Для операций химической обработки, таких как экстракция, разделение, движение жидкости, тепло- и массоперенос и разработка реакций, свойства ионных жидкостей и их смесей с молекулярными и ассоциированными растворителями необходимы для проектирования и эксплуатации химических заводов. Кроме того, их производство по разумной цене требует оптимизации и расширения текущего лабораторного типа синтеза.
Благодаря большому количеству существующих катионов и анионов количество их комбинаций в ионных жидкостях огромно.Для получения значений теплофизических свойств, необходимых для оптимального проектирования процесса, таких как плотность, теплоемкость, вязкость и теплопроводность, существуют три альтернативы: экспериментальные измерения, методы прогнозирования/оценки и молекулярное моделирование [1,2,3,4]. ,5]. Будучи «целевыми» или «ориентированными на выполнение задач» материалами, оценка их свойств требует не только экспериментальных измерений (весьма ограниченных и трудоемких), но и теоретических разработок и компьютерного моделирования, чтобы разработать устойчивые и полезные инструменты для проектирования, которые мы провели для молекулярных жидкостей. Эти аргументы прокладывают путь к методам прогнозирования/оценки, фундаментальному инструменту, который необходимо разработать и включить в симуляторы проектирования процессов. Благодаря современным знаниям о методах молекулярного моделирования понимание структуры ионных жидкостей и свойств ионных жидкостей и их смесей в настоящее время прогрессирует, что делает ионные жидкости основным классом жидкостей для изучения и использования в ближайшие десятилетия. Концепция использования дисперсных наноматериалов (НМ), особенно те, которые основаны на углероде, в ионных жидкостях [6], называемых иононаножидкостями, десять лет назад открыли потенциал использования этих наножидкостей в нескольких операциях переноса и хранения тепла благодаря улучшению, обнаруженному в их тепловых свойствах. свойства, особенно их эффективная теплопроводность.В дополнение к молекулярно-ионным взаимодействиям в ионных жидкостях стало интересно изучить новый аспект, межфазную область IL-NM, и ее вклад в повышение теплопроводности.
Эти аргументы прокладывают путь к методам прогнозирования/оценки, фундаментальному инструменту, который необходимо разработать и включить в симуляторы проектирования процессов. Благодаря современным знаниям о методах молекулярного моделирования понимание структуры ионных жидкостей и свойств ионных жидкостей и их смесей в настоящее время прогрессирует, что делает ионные жидкости основным классом жидкостей для изучения и использования в ближайшие десятилетия. Концепция использования дисперсных наноматериалов (НМ), особенно те, которые основаны на углероде, в ионных жидкостях [6], называемых иононаножидкостями, десять лет назад открыли потенциал использования этих наножидкостей в нескольких операциях переноса и хранения тепла благодаря улучшению, обнаруженному в их тепловых свойствах. свойства, особенно их эффективная теплопроводность.В дополнение к молекулярно-ионным взаимодействиям в ионных жидкостях стало интересно изучить новый аспект, межфазную область IL-NM, и ее вклад в повышение теплопроводности.
Целью данной статьи является анализ методов прогнозирования и оценки теплопроводности ионных жидкостей и ионных наножидкостей в зависимости от температуры. Сделана попытка прояснить употребление и неправильное употребление терминов в литературе. Термин «прогнозирование» широко использовался в прошлом для обозначения методологий, которые имеют совершенно разные уровни теоретической или эмпирической поддержки, в то время как оценка также используется без разбора для чисто основанных на эмпирических схемах и для методов с некоторым теоретическим пониманием.
2. Концепции прогнозирования и оценки
Самый последний доступный инструмент для проектирования химического технологического оборудования и моделирования его управления и эксплуатации использует очень многие функции проектирования технологических систем, реализованные в обширных программных кодах, закрытых для пользователя. экспертиза. Оценка теплофизических свойств материалов, участвующих в процессе, встроена в это программное обеспечение и также недоступна. Поэтому инженерам, использующим эти инструменты, необходимо знать об ограничениях теплофизических данных, генерируемых таким образом.В равной степени на ученых, которые предоставляют эту информацию, ложится повышенная ответственность за четкое определение ее происхождения и ее вероятной достоверности. Как правило, такие пакеты программного обеспечения предлагают выбор между уровнями сложности и предполагаемой точностью для различных средств получения требуемых данных о теплофизических свойствах, которые могут включать таблицы или корреляции экспериментальных данных, расчеты на основе молекулярной теории и полностью эмпирические процедуры оценки без теоретического обоснования. служба поддержки.Для пользователя четкая иерархия номенклатуры всех этих процессов является бесценным ориентиром в отношении их вероятной надежности [7]. Некоторое время назад мы представили такую четкую иерархию схем формирования значений транспортных свойств жидкостей [8]. Однако с тех пор новые жидкости, такие как ионные жидкости, стали гораздо более распространенными в дискурсе вокруг химической промышленности, и к этому добавились наножидкости в целом и иононаножидкости в частности.
Поэтому инженерам, использующим эти инструменты, необходимо знать об ограничениях теплофизических данных, генерируемых таким образом.В равной степени на ученых, которые предоставляют эту информацию, ложится повышенная ответственность за четкое определение ее происхождения и ее вероятной достоверности. Как правило, такие пакеты программного обеспечения предлагают выбор между уровнями сложности и предполагаемой точностью для различных средств получения требуемых данных о теплофизических свойствах, которые могут включать таблицы или корреляции экспериментальных данных, расчеты на основе молекулярной теории и полностью эмпирические процедуры оценки без теоретического обоснования. служба поддержки.Для пользователя четкая иерархия номенклатуры всех этих процессов является бесценным ориентиром в отношении их вероятной надежности [7]. Некоторое время назад мы представили такую четкую иерархию схем формирования значений транспортных свойств жидкостей [8]. Однако с тех пор новые жидкости, такие как ионные жидкости, стали гораздо более распространенными в дискурсе вокруг химической промышленности, и к этому добавились наножидкости в целом и иононаножидкости в частности. Ученые и инженеры, занимающиеся этими новыми материалами, гораздо меньше знакомы с предпосылками и реализацией такой иерархии, и поэтому существует опасность значительной путаницы как в литературе, так и в качестве схем для получения данных о теплофизических свойствах таких систем.Поэтому мы хотели бы повторить наши предложения по иерархии в этом новом контексте.
Ученые и инженеры, занимающиеся этими новыми материалами, гораздо меньше знакомы с предпосылками и реализацией такой иерархии, и поэтому существует опасность значительной путаницы как в литературе, так и в качестве схем для получения данных о теплофизических свойствах таких систем.Поэтому мы хотели бы повторить наши предложения по иерархии в этом новом контексте. Во-первых, отметим, что полагаться только на точные экспериментальные данные невозможно из-за огромного количества материалов и их смесей, которые необходимо изучить. Во-вторых, хотя, возможно, желательно применение строгой молекулярной теории с известными межмолекулярными потенциалами для расчета свойств из первых принципов, оно возможно только для систем не более сложных, чем газообразный метан в разбавленном газообразном состоянии.Если оба эти утверждения были верны для простых жидкостей, они еще более верны для таких сложных систем, как ионные жидкости и иононаножидкости. Конечно, в последнем случае, например, имеющийся в настоящее время огромный разброс экспериментальных измерений теплопроводности таких жидкостей означает, что и этот путь опасен. Как следствие, все альтернативные подходы, которые мы рассмотрели в нашей предыдущей работе в рамках иерархии, более заметны.
Как следствие, все альтернативные подходы, которые мы рассмотрели в нашей предыдущей работе в рамках иерархии, более заметны.
 Эта идея была развита Миллатом и соавт. [9], в главе 3 этого справочника. Как следствие, было продемонстрировано, что неопределенность полученных данных о теплофизических свойствах возрастает по мере того, как процедура все больше отходит от надежной теоретической основы. Схема полностью полагается на правильную интерпретацию предсказания, оценки и корреляции, которые часто используются взаимозаменяемо и неправильно в литературе. Это особенно актуально сейчас в области ионных жидкостей независимо от того, содержат они наночастицы или нет, и оправдывает повторение правильного описания этих терминов, установленного более 30 лет назад [8]. Предсказание определяется как схема, имеющая строгую теоретическую основу и требующая в качестве входной информации только физически значимых величин, полученных из минимального набора точных экспериментов или рассчитанных из других фундаментальных источников. Как упоминалось выше, наиболее эффективной заменой прямого измерения транспортных свойств жидкостей была бы полная, строгая статистико-механическая теория, которая позволяла бы вычислять свойства макроскопического ансамбля молекул на основе знания молекулярных свойств и сил.
Эта идея была развита Миллатом и соавт. [9], в главе 3 этого справочника. Как следствие, было продемонстрировано, что неопределенность полученных данных о теплофизических свойствах возрастает по мере того, как процедура все больше отходит от надежной теоретической основы. Схема полностью полагается на правильную интерпретацию предсказания, оценки и корреляции, которые часто используются взаимозаменяемо и неправильно в литературе. Это особенно актуально сейчас в области ионных жидкостей независимо от того, содержат они наночастицы или нет, и оправдывает повторение правильного описания этих терминов, установленного более 30 лет назад [8]. Предсказание определяется как схема, имеющая строгую теоретическую основу и требующая в качестве входной информации только физически значимых величин, полученных из минимального набора точных экспериментов или рассчитанных из других фундаментальных источников. Как упоминалось выше, наиболее эффективной заменой прямого измерения транспортных свойств жидкостей была бы полная, строгая статистико-механическая теория, которая позволяла бы вычислять свойства макроскопического ансамбля молекул на основе знания молекулярных свойств и сил.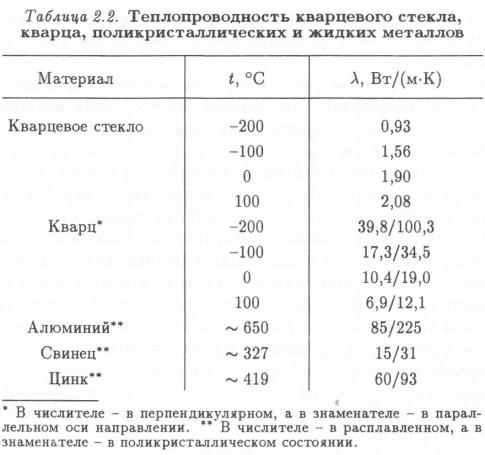 между молекулами (или ионами).Однако этот подход пока ограничивается расчетом транспортных свойств разбавленных газов простых молекул и их смесей с использованием кинетической теории газов, начатой Больцманом в 1872 г. и развитой Чепменом-Энскогом, с ее распространением на многоатомные частицы [9]. ,10]. Важно отметить, что одна и та же теория позволяет проверять согласованность между несколькими характеристиками переноса и, таким образом, сертифицировать современные измерительные инструменты. Мы обозначаем как полутеоретические прогнозы подмножество прогностических схем, где существует строгая теория, которая лишена аппроксимаций или содержит аппроксимации, которые хорошо охарактеризованы.Такая теория может привести к отношениям между свойствами, которые отличают одно свойство, которое трудно измерить, от другого, которое легче измерить. Например, коэффициент Эйкена для свойств разбавленного газа [4]. В качестве альтернативы тот же подход позволяет приблизиться к теории на молекулярном уровне, чтобы сделать расчеты свойств более удобными.
между молекулами (или ионами).Однако этот подход пока ограничивается расчетом транспортных свойств разбавленных газов простых молекул и их смесей с использованием кинетической теории газов, начатой Больцманом в 1872 г. и развитой Чепменом-Энскогом, с ее распространением на многоатомные частицы [9]. ,10]. Важно отметить, что одна и та же теория позволяет проверять согласованность между несколькими характеристиками переноса и, таким образом, сертифицировать современные измерительные инструменты. Мы обозначаем как полутеоретические прогнозы подмножество прогностических схем, где существует строгая теория, которая лишена аппроксимаций или содержит аппроксимации, которые хорошо охарактеризованы.Такая теория может привести к отношениям между свойствами, которые отличают одно свойство, которое трудно измерить, от другого, которое легче измерить. Например, коэффициент Эйкена для свойств разбавленного газа [4]. В качестве альтернативы тот же подход позволяет приблизиться к теории на молекулярном уровне, чтобы сделать расчеты свойств более удобными. Первым примером такого подхода является теория теплопроводности многоатомных газов Мейсона и Мончика [11,12]. Еще два примера дает использование предполагаемых моделей межмолекулярного парного потенциала для оценки данных о вязкости разбавленного газа для полярных газов [13] или первого коэффициента плотности вязкости и теплопроводности умеренно плотных неполярных газов [14,15, 16].При сохранении строгости теории можно разработать менее точные прогностические схемы, которые весьма полезны даже для фаз с низкой плотностью. Эти методы прогнозирования обычно используют физическую модель взаимодействий между молекулами в системе (гомо- и гетероядерными) и обозначаются методами и моделями прогнозирования. Наиболее известной из этих схем, наименее отступающей от абсолютной строгости, является Расширенный закон соответствующих состояний — ELCS, основанный на размерном анализе теории Чепмена-Энскога и ее интегралах столкновений, который считает, что сферические межмолекулярные парные потенциалы для среди вещества можно сделать конформными за счет подходящего выбора параметров масштабирования для энергии ε и расстояния σ, разработанных Кестином и его сотрудниками в 60-х годах [17], позже распространенных на вязкость и бинарную диффузию газовых смесей [18].
Первым примером такого подхода является теория теплопроводности многоатомных газов Мейсона и Мончика [11,12]. Еще два примера дает использование предполагаемых моделей межмолекулярного парного потенциала для оценки данных о вязкости разбавленного газа для полярных газов [13] или первого коэффициента плотности вязкости и теплопроводности умеренно плотных неполярных газов [14,15, 16].При сохранении строгости теории можно разработать менее точные прогностические схемы, которые весьма полезны даже для фаз с низкой плотностью. Эти методы прогнозирования обычно используют физическую модель взаимодействий между молекулами в системе (гомо- и гетероядерными) и обозначаются методами и моделями прогнозирования. Наиболее известной из этих схем, наименее отступающей от абсолютной строгости, является Расширенный закон соответствующих состояний — ELCS, основанный на размерном анализе теории Чепмена-Энскога и ее интегралах столкновений, который считает, что сферические межмолекулярные парные потенциалы для среди вещества можно сделать конформными за счет подходящего выбора параметров масштабирования для энергии ε и расстояния σ, разработанных Кестином и его сотрудниками в 60-х годах [17], позже распространенных на вязкость и бинарную диффузию газовых смесей [18]. Подробный анализ, включая расширения теплопроводности и вязкости многоатомных газов, был проведен Урибе и Мейсоном [19]. Схема может быть применена к смесям, прогнозируя коэффициенты бинарной диффузии по данным о вязкости, к вязкости многокомпонентных газовых смесей, теплопроводности многокомпонентных одноатомных газовых смесей, к бинарной диффузии многокомпонентных газовых смесей и другим расширениям для более сложных многоатомных молекул.
Подробный анализ, включая расширения теплопроводности и вязкости многоатомных газов, был проведен Урибе и Мейсоном [19]. Схема может быть применена к смесям, прогнозируя коэффициенты бинарной диффузии по данным о вязкости, к вязкости многокомпонентных газовых смесей, теплопроводности многокомпонентных одноатомных газовых смесей, к бинарной диффузии многокомпонентных газовых смесей и другим расширениям для более сложных многоатомных молекул.Процедуры оценки часто считают менее точными, чем описанные выше методы.Однако мы хотели бы определить оценку с точки зрения степени отклонения от прочной теоретической основы, чтобы затем можно было выделить иерархию уровней процедуры и, следовательно, определить нашу степень уверенности в схеме с прямым отражение в неопределенности оценки. В этом случае у нас может быть четыре уровня достоверности, а именно: полутеоретическая оценка, приближенные теоретические модели, полуэмпирическая оценка и эмпирическая оценка.
При полутеоретической оценке теория сохраняется, но некоторые параметры в ней должны оцениваться без использования точных измерений.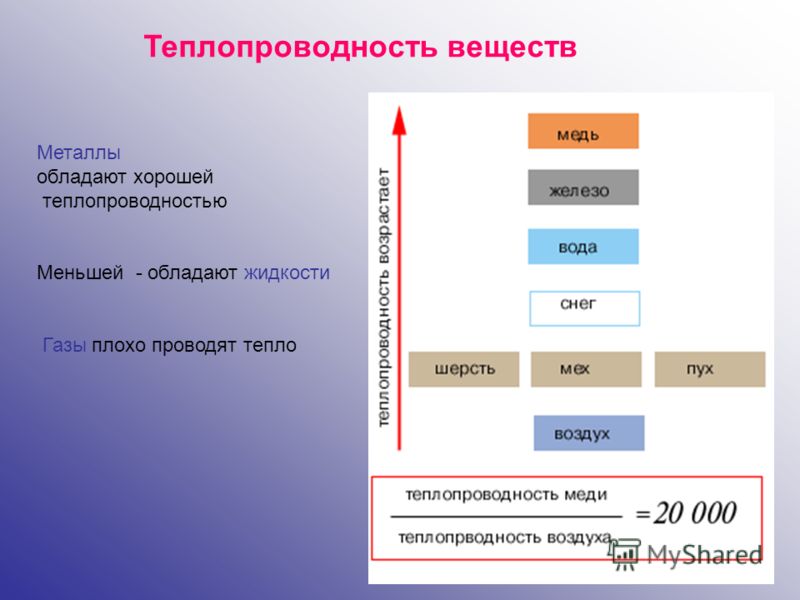 Очевидно, что полученные таким образом данные о свойствах менее точны, чем если бы для оценки этих параметров использовались экспериментальные данные. С другой стороны, использование правильной теории гарантирует, что полученные результаты сохранят по существу правильную структуру. В качестве примера можно привести использование законов смешения для расчета параметров взаимодействия разнородных пар из одинаковых параметров взаимодействия при применении ELCS к смесям [4,13]. Второй класс теоретически вдохновленных методов оценки возникает, когда существует формальная теория, но ее применение для интерпретации экспериментальных данных или оценки свойств невозможно из-за сочетания математических трудностей и недостаточного знания других необходимых физических величин.Это случай транспортных свойств простых жидкостей. Статистическая механическая теория, разработанная Бирманом и Кирквудом (1958) [20], среди прочего, выражает их коэффициенты переноса через многие функции распределения частиц и межмолекулярные потенциалы.
Очевидно, что полученные таким образом данные о свойствах менее точны, чем если бы для оценки этих параметров использовались экспериментальные данные. С другой стороны, использование правильной теории гарантирует, что полученные результаты сохранят по существу правильную структуру. В качестве примера можно привести использование законов смешения для расчета параметров взаимодействия разнородных пар из одинаковых параметров взаимодействия при применении ELCS к смесям [4,13]. Второй класс теоретически вдохновленных методов оценки возникает, когда существует формальная теория, но ее применение для интерпретации экспериментальных данных или оценки свойств невозможно из-за сочетания математических трудностей и недостаточного знания других необходимых физических величин.Это случай транспортных свойств простых жидкостей. Статистическая механическая теория, разработанная Бирманом и Кирквудом (1958) [20], среди прочего, выражает их коэффициенты переноса через многие функции распределения частиц и межмолекулярные потенциалы. Поскольку ни одна из этих величин не известна, теория не может быть применена в настоящее время (иначе она была бы классифицирована как предсказание). Приближенными теоретическими моделями называются модели, в которых процедуры основаны на неточной теории.Теория может быть неточной, потому что при ее разработке были сделаны упрощения или потому, что она основана на определенной модели. Классическим примером такой ситуационной процедуры в термодинамике является уравнение состояния Ван-дер-Ваальса и все вдохновленные им, такие как уравнения состояния Редлиха-Квонга, Пенга и Робинсона, Соаве [7] и др. В области транспортных свойств жидкостей аналогичным типом процедуры является модель Ван-дер-Ваальса [21], основанная на теории плотных твердых сфер Энскога [22,23].Другой могла бы быть модель Бриджмена для теплопроводности жидкостей, на которую мы обратимся позже [24], которая предполагала, что молекулы жидкости расположены в кубической решетке и что энергия передается от одной плоскости решетки к другой со скоростью какой звук распространяется через интересующую жидкость (параллельно с исходной элементарной кинетической теорией газов Максвелла).
Поскольку ни одна из этих величин не известна, теория не может быть применена в настоящее время (иначе она была бы классифицирована как предсказание). Приближенными теоретическими моделями называются модели, в которых процедуры основаны на неточной теории.Теория может быть неточной, потому что при ее разработке были сделаны упрощения или потому, что она основана на определенной модели. Классическим примером такой ситуационной процедуры в термодинамике является уравнение состояния Ван-дер-Ваальса и все вдохновленные им, такие как уравнения состояния Редлиха-Квонга, Пенга и Робинсона, Соаве [7] и др. В области транспортных свойств жидкостей аналогичным типом процедуры является модель Ван-дер-Ваальса [21], основанная на теории плотных твердых сфер Энскога [22,23].Другой могла бы быть модель Бриджмена для теплопроводности жидкостей, на которую мы обратимся позже [24], которая предполагала, что молекулы жидкости расположены в кубической решетке и что энергия передается от одной плоскости решетки к другой со скоростью какой звук распространяется через интересующую жидкость (параллельно с исходной элементарной кинетической теорией газов Максвелла). Модель проста и для расчета теплопроводности жидкости необходимы данные о плотности, скорости звука и адиабатической сжимаемости (или изотермической сжимаемости).Биддл и др. [25] применили эту модель для предсказания теплопроводности переохлажденной воды с относительным успехом. Эта модель была недавно применена к [C 2 mim][CH 3 SO 3 ] [26], расчетное значение для многоатомной жидкости оказалось примерно на 30% ниже экспериментального значения. Когда приближенная теория связана с поведением, определяемым только из эксперимента, развиваются другие схемы, обозначаемые здесь полуэмпирической оценкой. Одной из таких схем является метод расширенных соответствующих состояний, предложенный Hanley, Ely et al.[27,28,29,30,31,32,33] для неполярных жидкостей, хладагентов и расплавленных солей, которые сходятся в одном из самых мощных программных пакетов для термодинамических и транспортных свойств жидкостей, REFPROP, теперь в версии 10.0 [34]. Упрощенная, но приблизительная версия точной теории в сочетании с анализом размерностей приводит к процедуре соответствующих состояний в терминах редуцированных макроскопических переменных, ее реализация требует знания свойств эталонной жидкости.
Модель проста и для расчета теплопроводности жидкости необходимы данные о плотности, скорости звука и адиабатической сжимаемости (или изотермической сжимаемости).Биддл и др. [25] применили эту модель для предсказания теплопроводности переохлажденной воды с относительным успехом. Эта модель была недавно применена к [C 2 mim][CH 3 SO 3 ] [26], расчетное значение для многоатомной жидкости оказалось примерно на 30% ниже экспериментального значения. Когда приближенная теория связана с поведением, определяемым только из эксперимента, развиваются другие схемы, обозначаемые здесь полуэмпирической оценкой. Одной из таких схем является метод расширенных соответствующих состояний, предложенный Hanley, Ely et al.[27,28,29,30,31,32,33] для неполярных жидкостей, хладагентов и расплавленных солей, которые сходятся в одном из самых мощных программных пакетов для термодинамических и транспортных свойств жидкостей, REFPROP, теперь в версии 10.0 [34]. Упрощенная, но приблизительная версия точной теории в сочетании с анализом размерностей приводит к процедуре соответствующих состояний в терминах редуцированных макроскопических переменных, ее реализация требует знания свойств эталонной жидкости. Эмпирическое определение поведения эталонного вещества дает средства для определения регулируемых параметров (факторов формы) для большого количества других жидкостей из ограниченного набора информации.Преимущества такого рода методик заключаются в их общности и возможности проводить оценки в широком диапазоне состояний и классов чистых веществ и смесей. Расширение таких процедур с помощью дополнительных эмпирических шагов, связывающих необходимые параметры веществ с параметрами критической точки и/или молекулярной структурой, затем позволяет проводить оценки транспортных свойств веществ, для которых не существует прямых измерений. Последний подмножество методов оценки определяется как те, для которых в настоящее время нет теоретического обоснования, но которые основаны на эмпирических наблюдениях взаимосвязей между экспериментальными термодинамическими и транспортными свойствами жидкостей и другими макроскопическими величинами для тех же жидкостей.Этот тип оценки обозначается термином эмпирическая оценка.
Эмпирическое определение поведения эталонного вещества дает средства для определения регулируемых параметров (факторов формы) для большого количества других жидкостей из ограниченного набора информации.Преимущества такого рода методик заключаются в их общности и возможности проводить оценки в широком диапазоне состояний и классов чистых веществ и смесей. Расширение таких процедур с помощью дополнительных эмпирических шагов, связывающих необходимые параметры веществ с параметрами критической точки и/или молекулярной структурой, затем позволяет проводить оценки транспортных свойств веществ, для которых не существует прямых измерений. Последний подмножество методов оценки определяется как те, для которых в настоящее время нет теоретического обоснования, но которые основаны на эмпирических наблюдениях взаимосвязей между экспериментальными термодинамическими и транспортными свойствами жидкостей и другими макроскопическими величинами для тех же жидкостей.Этот тип оценки обозначается термином эмпирическая оценка. Это, безусловно, самые многочисленные, но и самые ненадежные из существующих методов. Большинство методов, разработанных для расчета теплофизических свойств газов при высоких плотностях и жидкостей, относятся к этому подмножеству методов [7,35]. Примером может служить представление обратной величины вязкости жидкости, текучести, как функции ее молярного объема, предложенное Хильдебрандом (1971) [36], проверенное для нескольких жидкостей и распространенное на отношения с другими свойствами, такими как коэффициенты диффузии и электролитическая проводимость.Все методы, основанные на групповых вкладах, посредством которых выбираются свойства групп атомов или молекулярных фрагментов, вносящие вклад в значение свойства молекулы, попадают в эту категорию схем. В случае теплопроводности метод Koller et al. Еще одним примером является работа [37], основанная на эмпирическом соотношении между теплопроводностью и плотностью, также примененном в нашей недавней публикации [26]. Никакой параметр не связан с молекулярной структурой соединения, а параметры получены только путем n-функциональной подгонки к экспериментальным данным.
Это, безусловно, самые многочисленные, но и самые ненадежные из существующих методов. Большинство методов, разработанных для расчета теплофизических свойств газов при высоких плотностях и жидкостей, относятся к этому подмножеству методов [7,35]. Примером может служить представление обратной величины вязкости жидкости, текучести, как функции ее молярного объема, предложенное Хильдебрандом (1971) [36], проверенное для нескольких жидкостей и распространенное на отношения с другими свойствами, такими как коэффициенты диффузии и электролитическая проводимость.Все методы, основанные на групповых вкладах, посредством которых выбираются свойства групп атомов или молекулярных фрагментов, вносящие вклад в значение свойства молекулы, попадают в эту категорию схем. В случае теплопроводности метод Koller et al. Еще одним примером является работа [37], основанная на эмпирическом соотношении между теплопроводностью и плотностью, также примененном в нашей недавней публикации [26]. Никакой параметр не связан с молекулярной структурой соединения, а параметры получены только путем n-функциональной подгонки к экспериментальным данным. Такие корреляции формулируются на основе значительного объема данных в умеренном диапазоне температур, а затем применяются повсеместно ко всем жидкостям. Их успех обычно не объясняется теоретически, но расчетные значения иногда разумны. Однако процедуры этого типа имеют очевидные недостатки с точки зрения точности их оценок, обычно применимы для определенного набора соединений и, кроме того, обычно не указывается возможность распространения на любое количество компонентов без дополнительных эвристических приближений. .Они также, очевидно, зависят от качества экспериментальных данных, которые используются в качестве входных данных. Для некоторых систем, которые мы здесь исследуем, это, очевидно, важный факт. Единственное преимущество таких схем заключается в том, что их можно применять к любому химическому соединению, независимо от молекулярной сложности изучаемой системы, хотя риск использования этих значений может быть очень высок. К сожалению, слова предсказание и оценка , два термина, используемые в современной литературе взаимозаменяемо, без каких-либо ссылок на их происхождение и достоверность.
Такие корреляции формулируются на основе значительного объема данных в умеренном диапазоне температур, а затем применяются повсеместно ко всем жидкостям. Их успех обычно не объясняется теоретически, но расчетные значения иногда разумны. Однако процедуры этого типа имеют очевидные недостатки с точки зрения точности их оценок, обычно применимы для определенного набора соединений и, кроме того, обычно не указывается возможность распространения на любое количество компонентов без дополнительных эвристических приближений. .Они также, очевидно, зависят от качества экспериментальных данных, которые используются в качестве входных данных. Для некоторых систем, которые мы здесь исследуем, это, очевидно, важный факт. Единственное преимущество таких схем заключается в том, что их можно применять к любому химическому соединению, независимо от молекулярной сложности изучаемой системы, хотя риск использования этих значений может быть очень высок. К сожалению, слова предсказание и оценка , два термина, используемые в современной литературе взаимозаменяемо, без каких-либо ссылок на их происхождение и достоверность.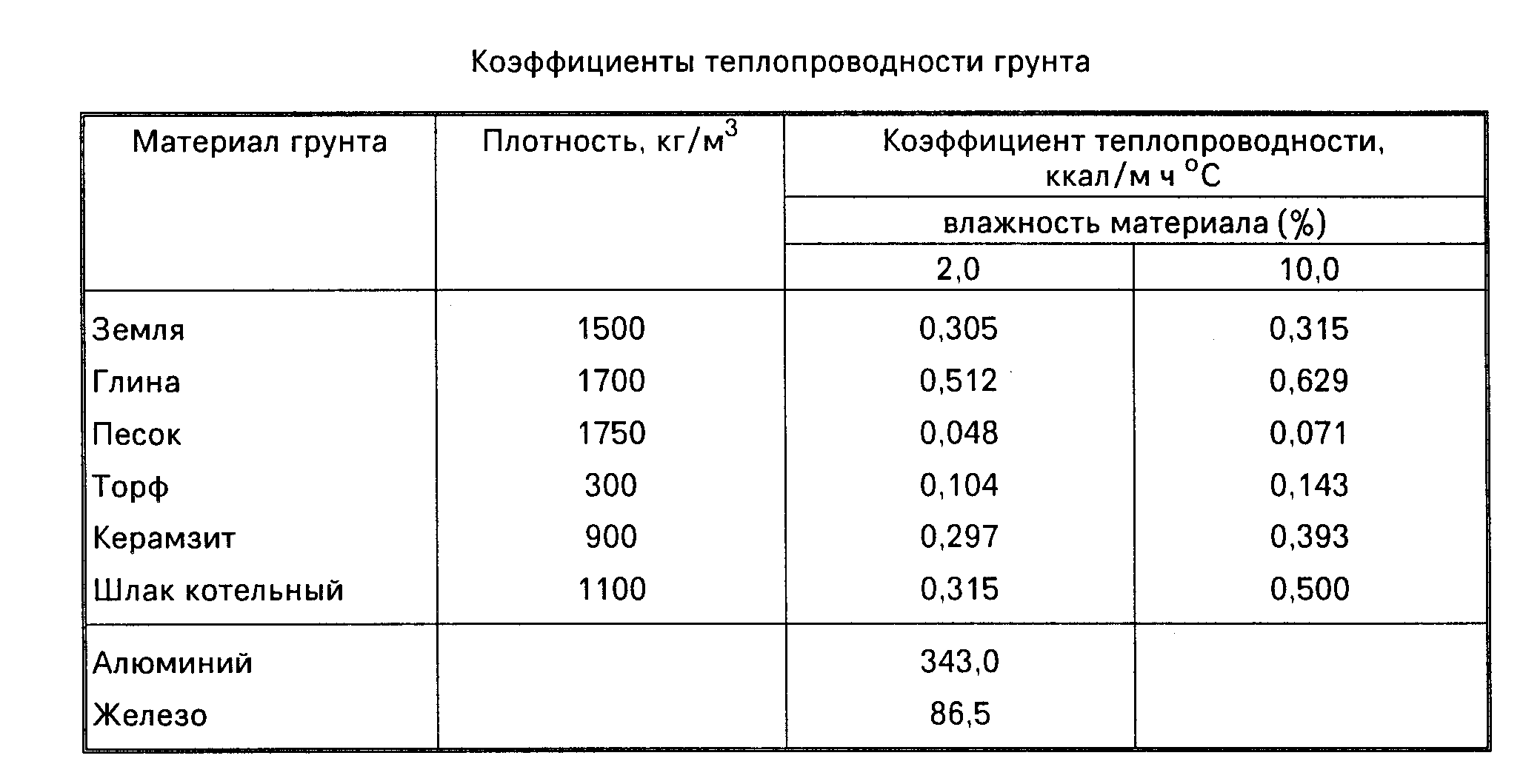 В частности, оценка слов редко включается в названия статей, поскольку авторы (и рецензенты) предпочитают, казалось бы, более эрудированное предсказание слов. Мы резюмируем на рисунке 2 соотношение между предсказанием, оценкой и неопределенностью схем расчета свойств. Стрелки также определяют направление каждого вклада (теория, эксперимент, достоверность, универсальность, предположение и специфичность) для величины ожидаемой неопределенности схемы расчета свойств. Значения неопределенностей для молекулярных жидкостей приведены только в качестве примера.Для ионных жидкостей их можно, как мы покажем ниже, легко умножить на три. Они также будут меняться от свойства к свойству. Последний комментарий связан со словом корреляция. Корреляция различных свойств как функция независимой переменной, такой как температура или давление, может быть просто эмпирической или разработанной с некоторым теоретическим пониманием. К счастью, этот последний подход использовался в течение последних двадцати лет для изучения теплофизических свойств избранных часто встречающихся жидкостей в широком диапазоне температур и давлений.
В частности, оценка слов редко включается в названия статей, поскольку авторы (и рецензенты) предпочитают, казалось бы, более эрудированное предсказание слов. Мы резюмируем на рисунке 2 соотношение между предсказанием, оценкой и неопределенностью схем расчета свойств. Стрелки также определяют направление каждого вклада (теория, эксперимент, достоверность, универсальность, предположение и специфичность) для величины ожидаемой неопределенности схемы расчета свойств. Значения неопределенностей для молекулярных жидкостей приведены только в качестве примера.Для ионных жидкостей их можно, как мы покажем ниже, легко умножить на три. Они также будут меняться от свойства к свойству. Последний комментарий связан со словом корреляция. Корреляция различных свойств как функция независимой переменной, такой как температура или давление, может быть просто эмпирической или разработанной с некоторым теоретическим пониманием. К счастью, этот последний подход использовался в течение последних двадцати лет для изучения теплофизических свойств избранных часто встречающихся жидкостей в широком диапазоне температур и давлений. Эти корреляции нуждаются в надежном EOS, и многие примеры можно увидеть в Journal of Physical and Chemical Reference Data. Однако в литературе использование корреляции очень часто ограничивается узким диапазоном температур (а иногда и давлений) и одними свойствами, полученными экспериментально. Такие корреляции, как правило, нельзя использовать за пределами диапазона условий, для которых имеются данные, и поэтому они имеют ограниченную полезность [9].
Эти корреляции нуждаются в надежном EOS, и многие примеры можно увидеть в Journal of Physical and Chemical Reference Data. Однако в литературе использование корреляции очень часто ограничивается узким диапазоном температур (а иногда и давлений) и одними свойствами, полученными экспериментально. Такие корреляции, как правило, нельзя использовать за пределами диапазона условий, для которых имеются данные, и поэтому они имеют ограниченную полезность [9].3. Случай ионных жидкостей — инструменты для прогнозирования и оценки теплофизических свойств
Природа низкотемпературных солей определяется сложной комбинацией кулоновских, водородных связей и ван-дер-ваальсовых взаимодействий их ионов.В простых солях взаимодействия контролируются дальнодействующими кулоновскими силами между суммарными зарядами ионов. Кроме того, с ионами, состоящими в основном из органических фрагментов, их громоздкий размер и асимметричное распределение заряда смягчают кулоновские силы и вызывают высоконаправленные взаимодействия более короткого действия (см.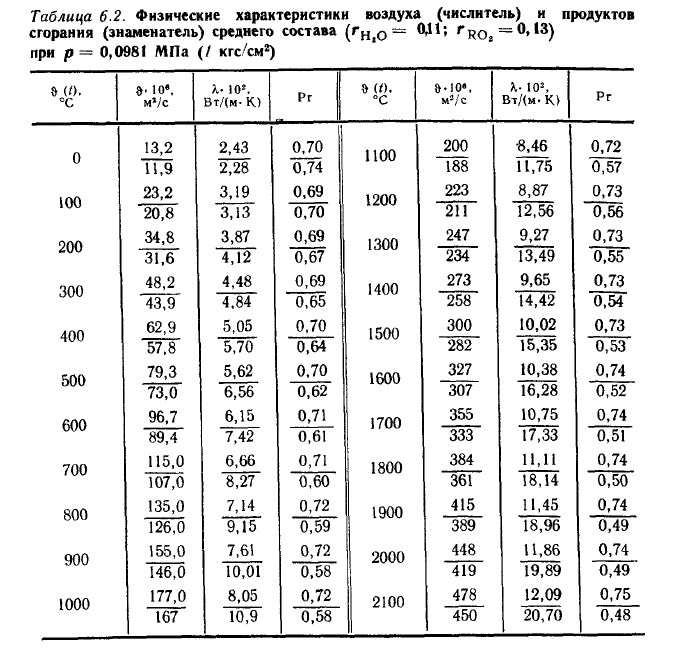 Таблицу 1 для краткого списка одновалентных катионов и анионов, присутствующих в ионных жидкостях). Следовательно, потенциал взаимодействия зависит не только от расстояния r ионов, но и от набора углов Ω их взаимной ориентации, что обуславливает несферические взаимодействия, причем в худшем случае при наличии водородной связи.Эти силы вызывают ряд явлений, таких как конформационные равновесия в катионах, образование ионных пар и крупных ионных кластеров в жидкой фазе, которые влияют на динамику движения молекул, особенно важных для транспортных свойств, таких как вязкость, теплопроводность, электрическая проводимость и ионная диффузия. Число комбинаций катионов и анионов огромно, ~10 18 , а структура катионов (обычно несимметричная) и анионов очень варьирует.Поэтому распределения зарядов рассчитать непросто, и все эти факты усложняют моделирование или разработку теории. Упаковка молекул в ионных жидкостях подобна кристаллической в первых 2-3 координационных сферах, с хорошо выраженным пиком катион-анион (четко выраженные пики при r ~ 0,4 и 0,8 нм — расстояние имидазолиевого кольца до хлора).
Таблицу 1 для краткого списка одновалентных катионов и анионов, присутствующих в ионных жидкостях). Следовательно, потенциал взаимодействия зависит не только от расстояния r ионов, но и от набора углов Ω их взаимной ориентации, что обуславливает несферические взаимодействия, причем в худшем случае при наличии водородной связи.Эти силы вызывают ряд явлений, таких как конформационные равновесия в катионах, образование ионных пар и крупных ионных кластеров в жидкой фазе, которые влияют на динамику движения молекул, особенно важных для транспортных свойств, таких как вязкость, теплопроводность, электрическая проводимость и ионная диффузия. Число комбинаций катионов и анионов огромно, ~10 18 , а структура катионов (обычно несимметричная) и анионов очень варьирует.Поэтому распределения зарядов рассчитать непросто, и все эти факты усложняют моделирование или разработку теории. Упаковка молекул в ионных жидкостях подобна кристаллической в первых 2-3 координационных сферах, с хорошо выраженным пиком катион-анион (четко выраженные пики при r ~ 0,4 и 0,8 нм — расстояние имидазолиевого кольца до хлора).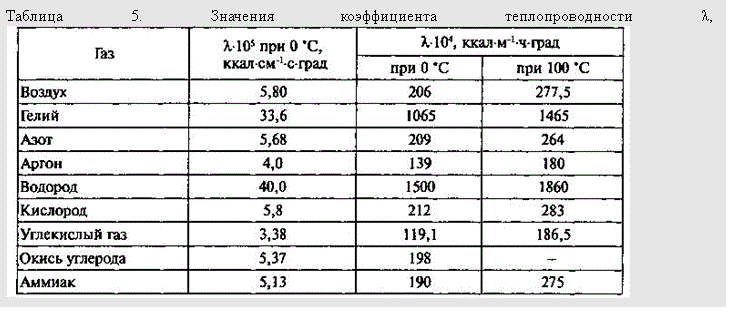 ион) и нечеткий пик катион-катион при r ~ 0,92 нм, как наблюдали Hardacre et al. [38] нейтронными и рентгеноструктурными исследованиями [dmim][Cl], который плавится при 401 К и дает относительно простую структуру ионной жидкости (рис. 3а).Canongia Lopes и Padua в 2006 г. [39] с помощью компьютерного моделирования показали, что всеатомное силовое поле предсказывает, что чистые ионные жидкости семейства 1-алкил-3-метилимидазолия [C n mim][PF6] (n = 2–12), имеют структуру своих жидких фаз, аналогичную микрофазовому разделению между полярными и неполярными доменами, как показано на рис. 3b для n = 2 и 6. Было замечено, что полярный домен имеет структуру трехмерная сеть ионных каналов, тогда как неполярный домен организован как дисперсная микрофаза для 1-этил-3-метилимидазолиевых ИЖ и как непрерывная для более длинных боковых цепей, таких как гексил, октил или додецил; бутильная боковая цепь отмечает начало перехода от одного типа структуры к другому.Можем ли мы использовать методологию, описанную в разделе 2 для ионных жидкостей? Обобщения невозможны из-за нашего ограниченного текущего понимания существующих межмолекулярных сил и поддерживающих теорий на наноуровне, чрезвычайно сложно разработать теоретически обоснованные прогностические схемы.
ион) и нечеткий пик катион-катион при r ~ 0,92 нм, как наблюдали Hardacre et al. [38] нейтронными и рентгеноструктурными исследованиями [dmim][Cl], который плавится при 401 К и дает относительно простую структуру ионной жидкости (рис. 3а).Canongia Lopes и Padua в 2006 г. [39] с помощью компьютерного моделирования показали, что всеатомное силовое поле предсказывает, что чистые ионные жидкости семейства 1-алкил-3-метилимидазолия [C n mim][PF6] (n = 2–12), имеют структуру своих жидких фаз, аналогичную микрофазовому разделению между полярными и неполярными доменами, как показано на рис. 3b для n = 2 и 6. Было замечено, что полярный домен имеет структуру трехмерная сеть ионных каналов, тогда как неполярный домен организован как дисперсная микрофаза для 1-этил-3-метилимидазолиевых ИЖ и как непрерывная для более длинных боковых цепей, таких как гексил, октил или додецил; бутильная боковая цепь отмечает начало перехода от одного типа структуры к другому.Можем ли мы использовать методологию, описанную в разделе 2 для ионных жидкостей? Обобщения невозможны из-за нашего ограниченного текущего понимания существующих межмолекулярных сил и поддерживающих теорий на наноуровне, чрезвычайно сложно разработать теоретически обоснованные прогностические схемы. Даже если мы теперь понимаем структуру ИЖ в жидком состоянии (в основном с имидазолиевыми кольцами), мы еще не можем рассчитать свойства, кроме как путем моделирования взаимодействий и проведения экспериментов по молекулярной динамике.
Даже если мы теперь понимаем структуру ИЖ в жидком состоянии (в основном с имидазолиевыми кольцами), мы еще не можем рассчитать свойства, кроме как путем моделирования взаимодействий и проведения экспериментов по молекулярной динамике.Поэтому необходимо разработать ряд методов оценки, позволяющих рассчитать транспортные свойства, на основе:
- (a)
приблизительных теоретических моделей (например, модели Бриджмена),
- (b)
эвристические расширения теории (например, модель Ван-дер-Ваальса, теория свободного объема);например, методы группового вклада) или эмпирические зависимости между теплофизическими свойствами (например, метод Коллера).
Ниже приводится краткое описание каждого подхода с особым упором на методы Бриджмена, Ван-дер-Ваальса и Коллера.
3.1. Модель Бриджмена
Как объяснялось выше, Бриджмен [24] предположил, что молекулы жидкости расположены в кубической решетке и что энергия передается от одной плоскости решетки к другой со скоростью, с которой звук распространяется через интересующую жидкость.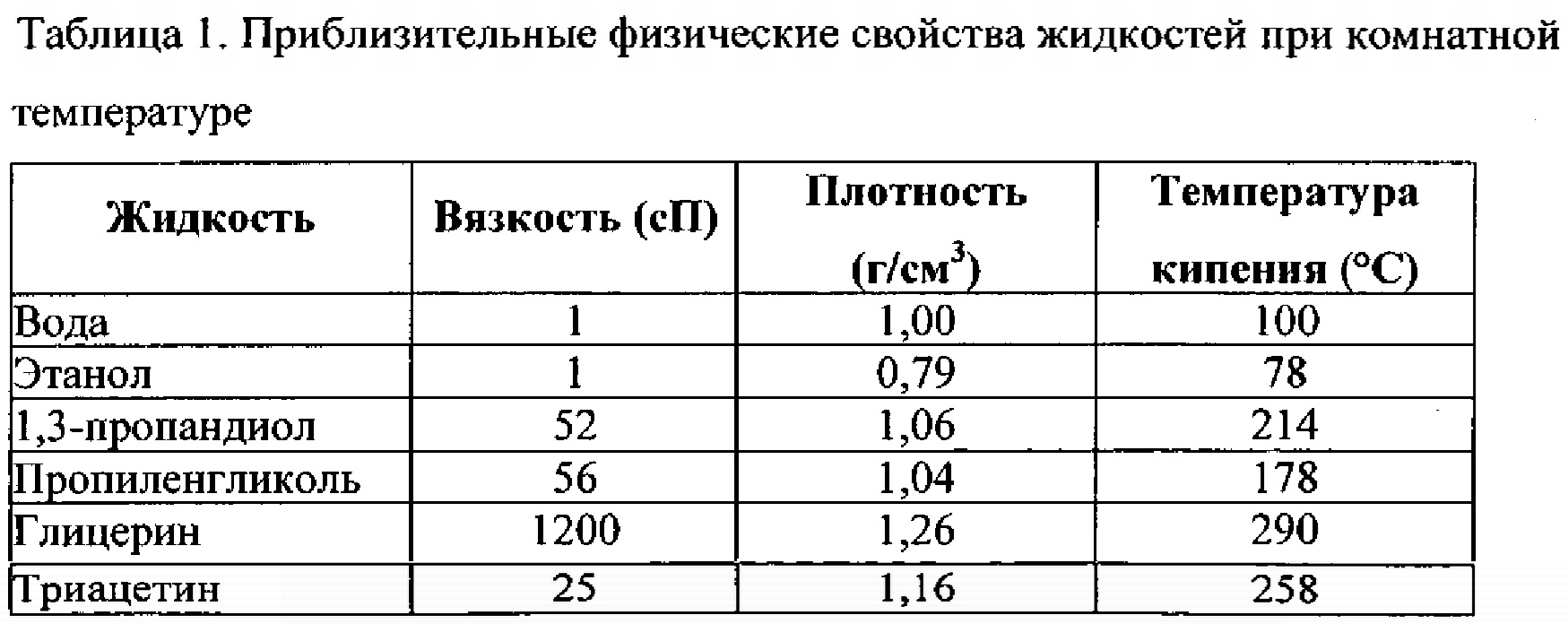 Кубическая решетка была выбрана так, чтобы расстояние между центрами определялось как (v*) 1/3 , где v* представляет собой объем на молекулу (молекулярный объем). Расстояние, пройденное между двумя последовательными столкновениями, и, следовательно, расстояние между соседними плоскостями, равно расстоянию между центрами. Развитие основано на новой интерпретации кинетической теории газов (твердых сфер) и может быть найдено на книга Хиршфельдера, Кертисса и Берда [40], ведущая к:
Кубическая решетка была выбрана так, чтобы расстояние между центрами определялось как (v*) 1/3 , где v* представляет собой объем на молекулу (молекулярный объем). Расстояние, пройденное между двумя последовательными столкновениями, и, следовательно, расстояние между соседними плоскостями, равно расстоянию между центрами. Развитие основано на новой интерпретации кинетической теории газов (твердых сфер) и может быть найдено на книга Хиршфельдера, Кертисса и Берда [40], ведущая к:λ=2,8 кБ(v*)−2/3u
(1)
где λ — теплопроводность жидкости; k B – постоянная Больцмана; u скорость звука в пределе нулевой частоты.Первоначально числовой коэффициент был равен 3, но был эмпирически изменен до 2,8 для обеспечения лучшего совпадения с экспериментальными данными. Используя термодинамическое соотношение: при отсутствии данных о скорости звука, где ρ — плотность, а κ S — адиабатическая сжимаемость, получаем:λ=2,8 кБ(v*)−2/3(1ρκS)1/2
(3)
Поскольку получить адиабатическую сжимаемость очень сложно, в методе используется модификация Айринга [34], описанная Biddle et al. [25]:
[25]:λ=2.8 кБ(v*)−2/3(1ρκT)1/2
(4)
где κ T изотермическая сжимаемость, величина, которую получить гораздо проще. Это уравнение ограничено плотностью, значительно превышающей критическую плотность, поскольку оно предполагает, что каждая молекула колеблется в «клетке», образованной ее ближайшими соседями. Он получен для одноатомных жидкостей, для которых С V = 3 к В /m, где m — масса молекулы, которая меньше теплоемкости многоатомных жидкостей. Следовательно, уравнение (4) занижает расчетное значение теплопроводности, и мы обсудим этот момент в разделе 5.1. Эта модель совершенно нереалистична для простых жидкостей, где компьютерное моделирование не поддерживает идею клетки молекул со случайными прыжками на большие расстояния, но структура внутри ИЖ означает, что она может быть более подходящей для них. Эта модель была впервые применена Lozano-Martín et al. (2020) [26] для ионной жидкости [C 2 mim][CH 3 SO 3 ] и будет продолжено в этой статье для других ионных жидкостей.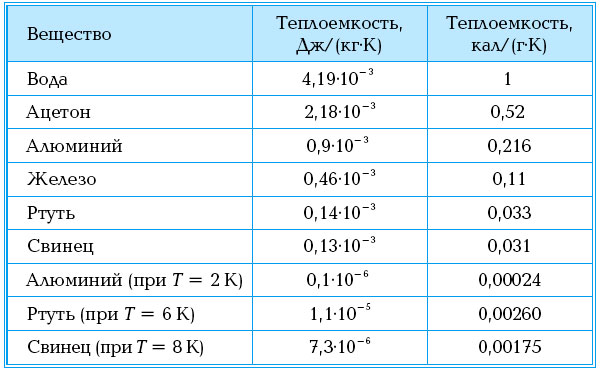
3.2. Модель Ван-дер-Ваальса
О применении схемы твердых сфер для оценки вязкости и теплопроводности ионных жидкостей сообщили Gaciño et al.в 2014 г. [41] с успехом. Использовалась база данных 461 измерения вязкости и 170 измерений теплопроводности для 19 ионных жидкостей. Расширенная неопределенность при доверительном уровне 95% составила 4,6% и 6,3%. В соответствии с моделью приведенная теплопроводность λ* определяется уравнением (5) как:λ*=1,936 × 107(МРТ)1/2λV2/3Rλ
(5)
Эта приведенная теплопроводность является функцией приведенного молярного объема V r = V/V 0 , где V — молярный объем, а V 0 — характерный молярный объем жидкости, слабо зависящий от температуры (первоначально рассматривается как плотно упакованный объем).M представляет собой молекулярную массу, а R — универсальную газовую постоянную. Параметр R λ , введенный для многоатомных молекул, объясняет отклонения от поведения гладких твердых сфер [23].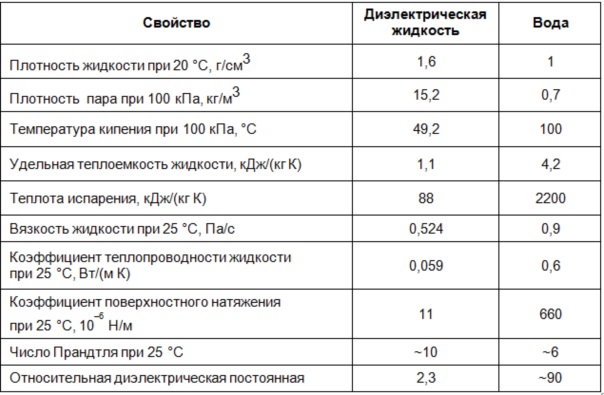 Поскольку вязкость более чувствительна к характеристическому молярному объему, V 0 была получена из данных по вязкости. В методе используется корреляция экспериментальных данных, имеющихся для рассматриваемых ионных жидкостей, с коэффициентами, приведенными в табл. 1 и 7 ссылки [41].Метод ограничен системами, для которых существуют данные о плотности ионных жидкостей, но это не очень серьезное ограничение, поскольку это наиболее общедоступное теплофизическое свойство [42]. Кроме того, если коэффициент шероховатости теплопроводности R λ зависит от температуры, то среднее абсолютное отклонение всех данных теплопроводности ионной жидкости может быть уменьшено до 0,91% для теплопроводности, а расширенная неопределенность при уровень достоверности 95% к 1.82%, что является очень хорошим результатом. На рис. 4 показано отклонение экспериментальных данных от предложенной корреляционной схемы в зависимости от приведенного молярного объема. При использовании этой схемы для оценки теплопроводности 19 ионных жидкостей, использованных в разработке, получается максимальная погрешность ±4%.
Поскольку вязкость более чувствительна к характеристическому молярному объему, V 0 была получена из данных по вязкости. В методе используется корреляция экспериментальных данных, имеющихся для рассматриваемых ионных жидкостей, с коэффициентами, приведенными в табл. 1 и 7 ссылки [41].Метод ограничен системами, для которых существуют данные о плотности ионных жидкостей, но это не очень серьезное ограничение, поскольку это наиболее общедоступное теплофизическое свойство [42]. Кроме того, если коэффициент шероховатости теплопроводности R λ зависит от температуры, то среднее абсолютное отклонение всех данных теплопроводности ионной жидкости может быть уменьшено до 0,91% для теплопроводности, а расширенная неопределенность при уровень достоверности 95% к 1.82%, что является очень хорошим результатом. На рис. 4 показано отклонение экспериментальных данных от предложенной корреляционной схемы в зависимости от приведенного молярного объема. При использовании этой схемы для оценки теплопроводности 19 ионных жидкостей, использованных в разработке, получается максимальная погрешность ±4%.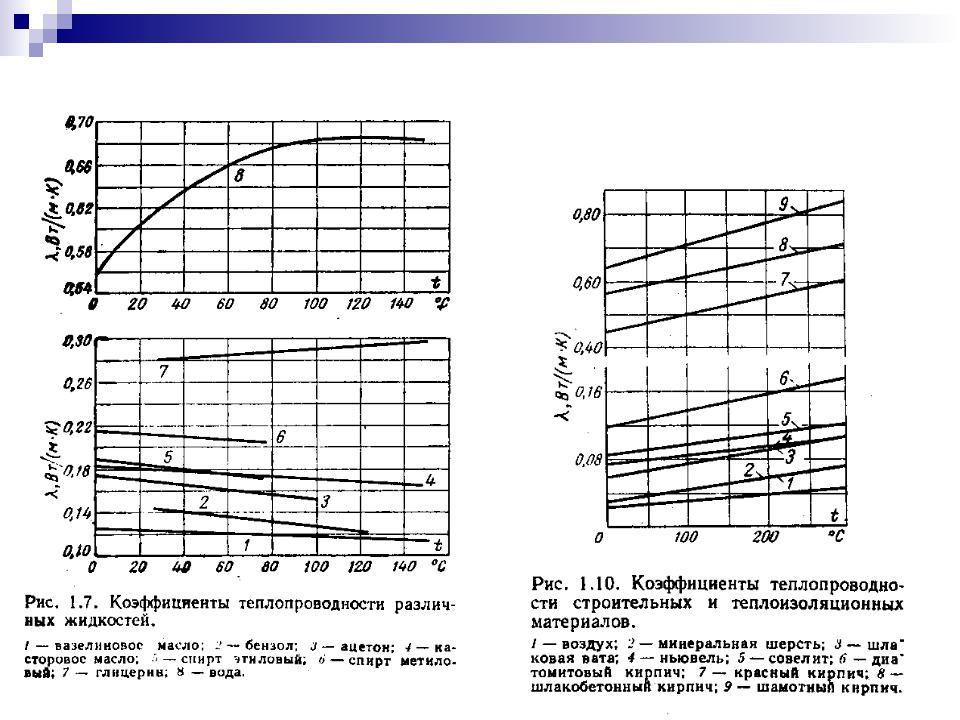 Стоит отметить, что отклонения такого размера меньше, чем вероятная экспериментальная неопределенность в измерениях транспортных свойств, особенно теплопроводности, а также вязкости.
Стоит отметить, что отклонения такого размера меньше, чем вероятная экспериментальная неопределенность в измерениях транспортных свойств, особенно теплопроводности, а также вязкости.3.3. Метод Коллера
Из чисто эмпирических методов, основанных на связях между другими теплофизическими свойствами и теплопроводностью, можно выделить зависимость Моханти, основанную на теории Андраде для вязкости жидкости [43] и описанной выше теории Бриджмена для молекулярных столкновений. Моханти [44] предложил очень простую зависимость между теплопроводностью и вязкостью, Mλ/η = Const, при которой константа имеет среднее значение 10,8 для органических жидкостей при комнатной температуре.Эта взаимосвязь была исследована Tomida et al. [45]. 335 К при давлении до 20 МПа. Они пришли к выводу, что постоянная Моханти на практике является функцией молекулярной массы ионных жидкостей, и получили уравнение (6):log(Mλη)=1,9596−0,004499 M
(6)
Однако, чтобы сохранить согласие с данными для н-алканов, гораздо менее вязких, пришлось умножить на 2 значение молекулярной массы ионных жидкостей, т. е.е., М’ = 2 М, что крайне неудовлетворительно с принципиальной точки зрения.
е.е., М’ = 2 М, что крайне неудовлетворительно с принципиальной точки зрения.
 Для этого случая коэффициенты в уравнении (7) равны A = 1,244 и B = 18,84, когда все величины выражены в единицах СИ. Стандартное процентное отклонение составило 7,8% (15,6% при доверительном уровне 95%).Это уравнение также было адаптировано Ferreira et al. [47] для катионов фосфония и аммония, используя значения A = 1,36 и B = 8,533, со стандартным процентным отклонением 4% (8% при доверительном уровне 95%). На рис. 5 показаны отклонения теплопроводности ионных жидкостей [P 66614 ] + с различными анионами, Ferreira et al. [47], Ge et al. [48] и França et al. [49]. Видно, что кроме бис(2,4,4-триметилпентил)фосфината, уже отмеченного Ferreira et al.[47], для остальных ионных жидкостей отклонения колеблются от -5% до +15%. Однако эти результаты показывают определенную зависимость от температуры, вероятно, потому, что методы, такие как метод Fröba et al. [46], не учитывают различное температурное изменение плотности и теплопроводности. Эрлангенская группа попыталась разрешить эту ситуацию, введя поправку, учитывающую температурное изменение, о которой сообщают Коллер и др.
Для этого случая коэффициенты в уравнении (7) равны A = 1,244 и B = 18,84, когда все величины выражены в единицах СИ. Стандартное процентное отклонение составило 7,8% (15,6% при доверительном уровне 95%).Это уравнение также было адаптировано Ferreira et al. [47] для катионов фосфония и аммония, используя значения A = 1,36 и B = 8,533, со стандартным процентным отклонением 4% (8% при доверительном уровне 95%). На рис. 5 показаны отклонения теплопроводности ионных жидкостей [P 66614 ] + с различными анионами, Ferreira et al. [47], Ge et al. [48] и França et al. [49]. Видно, что кроме бис(2,4,4-триметилпентил)фосфината, уже отмеченного Ferreira et al.[47], для остальных ионных жидкостей отклонения колеблются от -5% до +15%. Однако эти результаты показывают определенную зависимость от температуры, вероятно, потому, что методы, такие как метод Fröba et al. [46], не учитывают различное температурное изменение плотности и теплопроводности. Эрлангенская группа попыталась разрешить эту ситуацию, введя поправку, учитывающую температурное изменение, о которой сообщают Коллер и др. [37]. Их соотношение, основанное на существующих данных по теплопроводности для 53 ИЖ, выражается уравнением (8):
[37]. Их соотношение, основанное на существующих данных по теплопроводности для 53 ИЖ, выражается уравнением (8):λ(T)=(A+BMρ(Tref))(ρ(T)ρ(Tref))C
(8)
где λ — расчетная теплопроводность, ρ — плотность, а M — молярная масса, все они выражены в единицах СИ.Они сообщают следующие параметры: A = 0,0960, B = 21,43, C = 0,826 и T ref = 293,15 K, с величинами, выраженными в единицах СИ. Это уравнение имеет заявленное AARD (среднее абсолютное относительное отклонение) 6,3% (12,6% при доверительном уровне 95%), а также включает многие жидкости аммония и фосфония, объект анализа Ferreira et al. [47]. Эти результаты очень хорошие, так как большинство экспериментальных данных, использованных при разработке, имеют погрешности такого порядка. Отклонения для соединений, не использованных в разработке, таких как [C 2 mim][CH 3 SO 3 ] [26], занижают теплопроводность на 8% при 293 К и 14% при 343 К, интересный результат .3.
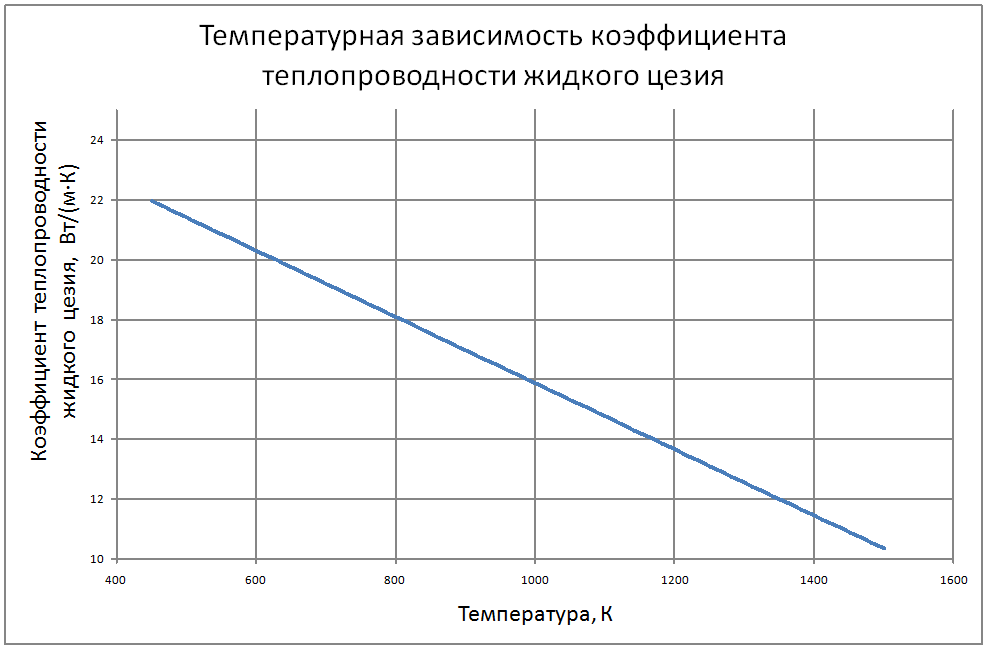 4. Методы группового вклада
4. Методы группового вкладаОбсуждение методов группового вклада будет кратким, поскольку они не будут применяться в данной статье. Многие из них связаны с другими теплофизическими свойствами, такими как изобарная теплоемкость C P .
Гардас и Коутиньо разработали методы группового вклада для оценки теплофизических и транспортных свойств ИЖ по вязкости, электропроводности, теплопроводности, показателю преломления, изобарическому расширению и изотермической сжимаемости [50].Определены параметры методов группового вклада для имидазолиевых, пиридиниевых, пирролидиниевых, пиперидиновых, фосфониевых и аммониевых ионных жидкостей. Для теплопроводности 16 IL среднее абсолютное относительное отклонение AARD оказалось равным 1,06 %, с отклонениями ±2–4 %, для более низких и более высоких теплопроводностей очень хороший результат. Вклады групп рассчитывались для ограниченного числа катионов, анионов, метиленовых и метильных групп из-за нехватки данных по теплопроводности на момент публикации. Несмотря на свою простоту, метод не позволяет оценить свойства жидкостей с катионами и анионами, не входящими в базовый набор, как, например, для ионов DCA или P 66614 . Wu et al. [51] приняли новое уравнение, похожее по форме на уравнение Рейделя [52], для корреляции теплопроводности ионных жидкостей, основанной на пониженной температуре, с температурами кипения и критическими температурами, оцененными по Valderama et al. формулы [53]. Однако эти параметры получаются с большой неопределенностью из-за малого давления паров ионных жидкостей, которые разлагаются до достижения критической точки пар-жидкость.Было покрыто 36 ионных жидкостей. Групповые вклады были оптимизированы для групп с кольцами и без колец, и читатель может обратиться к таблице 1 ссылки [51]. Для исследованных ионных жидкостей общий AARD составил 1,66% (3,3% при доверительном уровне 95%) с максимальным отклонением менее 11 (22%). Опять же, это приложение ограничено ИЖ, в которых группы, составляющие анион и катион, были оценены авторами.
Несмотря на свою простоту, метод не позволяет оценить свойства жидкостей с катионами и анионами, не входящими в базовый набор, как, например, для ионов DCA или P 66614 . Wu et al. [51] приняли новое уравнение, похожее по форме на уравнение Рейделя [52], для корреляции теплопроводности ионных жидкостей, основанной на пониженной температуре, с температурами кипения и критическими температурами, оцененными по Valderama et al. формулы [53]. Однако эти параметры получаются с большой неопределенностью из-за малого давления паров ионных жидкостей, которые разлагаются до достижения критической точки пар-жидкость.Было покрыто 36 ионных жидкостей. Групповые вклады были оптимизированы для групп с кольцами и без колец, и читатель может обратиться к таблице 1 ссылки [51]. Для исследованных ионных жидкостей общий AARD составил 1,66% (3,3% при доверительном уровне 95%) с максимальным отклонением менее 11 (22%). Опять же, это приложение ограничено ИЖ, в которых группы, составляющие анион и катион, были оценены авторами. Метод Wu et al. [51] был оптимизирован Oster et al. [54], используя расчеты DFT для оптимизации распределения заряда и структурных вкладов, а также используя последние данные для новых ионных жидкостей, всего 55.В разработанной модели использовался новый подход, учитывающий влияние атома ядра катиона на структуру и физические свойства ионных жидкостей. Общий AARD для всех используемых наборов данных составляет 1,66% (3,3% при доверительном уровне 95%), что намного лучше, чем средняя неопределенность используемых экспериментальных данных, с максимальным AARD 7,16% для 1,3-дибутилимидазолия бис[(трифторметил )сульфонил]имид, [C 4 C 4 im][(CF 3 SO 2 ) 2 N]. В таблицах 2 и 3 ссылки [54] показаны рассмотренные ионные жидкости и новые параметры уравнения модели Ву.В заключение можно сказать, что методы группового вклада могут быть очень удобными и простыми, но они ограничены ионными жидкостями с фрагментами, охватываемыми их разработкой.
Метод Wu et al. [51] был оптимизирован Oster et al. [54], используя расчеты DFT для оптимизации распределения заряда и структурных вкладов, а также используя последние данные для новых ионных жидкостей, всего 55.В разработанной модели использовался новый подход, учитывающий влияние атома ядра катиона на структуру и физические свойства ионных жидкостей. Общий AARD для всех используемых наборов данных составляет 1,66% (3,3% при доверительном уровне 95%), что намного лучше, чем средняя неопределенность используемых экспериментальных данных, с максимальным AARD 7,16% для 1,3-дибутилимидазолия бис[(трифторметил )сульфонил]имид, [C 4 C 4 im][(CF 3 SO 2 ) 2 N]. В таблицах 2 и 3 ссылки [54] показаны рассмотренные ионные жидкости и новые параметры уравнения модели Ву.В заключение можно сказать, что методы группового вклада могут быть очень удобными и простыми, но они ограничены ионными жидкостями с фрагментами, охватываемыми их разработкой.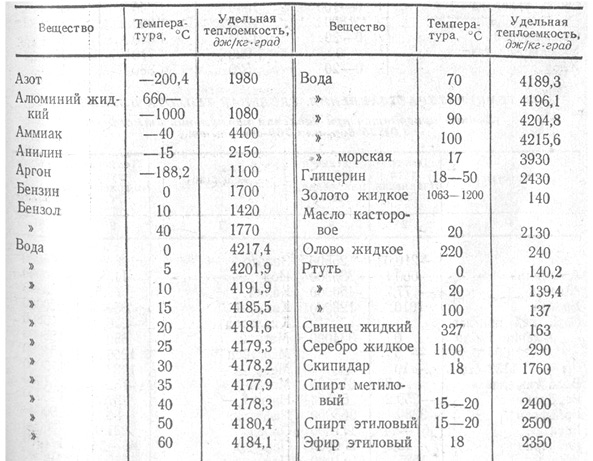 Наиболее общий из них принадлежит Oster et al. [54], которые расширили и модифицировали работу Wu et al. [51].
Наиболее общий из них принадлежит Oster et al. [54], которые расширили и модифицировали работу Wu et al. [51].4. Случай ионаножидкостей — инструменты для расчета повышения теплопроводности
Дисперсии наночастиц в нескольких жидкостях впервые были изучены Янгом и Маа [55] в 1984 г. в их исследовании теплопередачи при кипении, а Масуда и др.[56] при изучении вязкости и эффективной теплопроводности ультрадисперсных частиц Al 2 O 3 , SiO 2 и TiO 2 (анатаз) (13, 12 и 27 нм соответственно), диспергированных в вода. Эта эффективная теплопроводность не является истинной теплопроводностью, поскольку исследуемые системы являются по крайней мере двухфазными, и некоторые авторы обозначают ее как кажущуюся теплопроводность. Однако эти авторы выявили то, что казалось одним из наиболее чувствительных явлений теплопередачи в прошлом веке, повышение теплопроводности среды по отношению к исходной базовой жидкости.Влияние наножидкостей на современную науку и технологии было катализировано работой Choi et al. с использованием классических теплоносителей, таких как вода, этиленгликоль и моторное масло [57], чьи результаты (теперь показано, что они являются очень существенными завышенными оценками), тем не менее, способствовали революции в исследованиях теплоносителей. Об использовании композитов углеродных наноматериалов в ионных жидкостях, а именно многостенных углеродных нанотрубок (МУНТ), впервые сообщили Aida et al. [58], которые смешивали ионные жидкости с углеродными нанотрубками (УНТ), образуя высоковязкие гели, называемые гелями Баки, в честь архитектора Ричарда Бакминстера Фуллера (Баки), известного своими геодезическими куполами.Эти наносистемы теперь называются IoNanofluids [6] — стабильной дисперсией наноматериалов в ионных жидкостях. Эти и связанные с ними системы имеют ряд применений, в том числе в новых материалах, процессах и электронных или электрохимических устройствах. Ионные жидкости, содержащиеся в гелях, применимы в качестве мембран для разделения [59], могут быть разработаны в качестве растворителей для отшелушивания [60, 61] углеродных наноматериалов, что приводит к созданию стабильных суспензий и новых способов функционализации или манипулирования этими наноматериалами или новых композитных фаз.
с использованием классических теплоносителей, таких как вода, этиленгликоль и моторное масло [57], чьи результаты (теперь показано, что они являются очень существенными завышенными оценками), тем не менее, способствовали революции в исследованиях теплоносителей. Об использовании композитов углеродных наноматериалов в ионных жидкостях, а именно многостенных углеродных нанотрубок (МУНТ), впервые сообщили Aida et al. [58], которые смешивали ионные жидкости с углеродными нанотрубками (УНТ), образуя высоковязкие гели, называемые гелями Баки, в честь архитектора Ричарда Бакминстера Фуллера (Баки), известного своими геодезическими куполами.Эти наносистемы теперь называются IoNanofluids [6] — стабильной дисперсией наноматериалов в ионных жидкостях. Эти и связанные с ними системы имеют ряд применений, в том числе в новых материалах, процессах и электронных или электрохимических устройствах. Ионные жидкости, содержащиеся в гелях, применимы в качестве мембран для разделения [59], могут быть разработаны в качестве растворителей для отшелушивания [60, 61] углеродных наноматериалов, что приводит к созданию стабильных суспензий и новых способов функционализации или манипулирования этими наноматериалами или новых композитных фаз.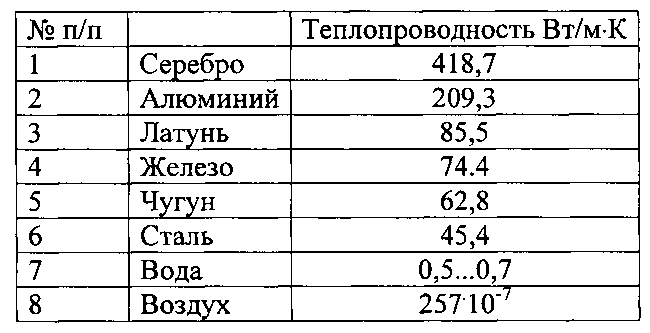 Сегодня широко рассматриваются области применения иононаножидкостей с более низкой вязкостью. Интерфейс между ионными жидкостями и углеродными наноматериалами актуален во многих контекстах, например, при разработке улучшенных электролитических суперконденсаторов [62], при разработке органического электролита или электродного нанопористого углеродного материала [63], при использовании углеродных нановолокон в Каталитические слои на основе ИЖ для улучшения удельной площади поверхности [64] или повышения производительности сенсибилизированных красителем солнечных элементов с электролитами ИЖ с использованием углеродных точек [65].Дисперсии наноматериалов в ионных жидкостях уже изучались нашей группой в различных системах [6, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77], как с экспериментальной, так и с теоретической точки зрения. зрения; системы включали МУНТ, меланин (природный наноматериал [66]) и графен. Были измерены теплофизические свойства иононаножидкостей и объяснена интерпретация неожиданного повышения теплопроводности с учетом влияния химии поверхности частиц и межфазной структуры частица/жидкость.
Сегодня широко рассматриваются области применения иононаножидкостей с более низкой вязкостью. Интерфейс между ионными жидкостями и углеродными наноматериалами актуален во многих контекстах, например, при разработке улучшенных электролитических суперконденсаторов [62], при разработке органического электролита или электродного нанопористого углеродного материала [63], при использовании углеродных нановолокон в Каталитические слои на основе ИЖ для улучшения удельной площади поверхности [64] или повышения производительности сенсибилизированных красителем солнечных элементов с электролитами ИЖ с использованием углеродных точек [65].Дисперсии наноматериалов в ионных жидкостях уже изучались нашей группой в различных системах [6, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77], как с экспериментальной, так и с теоретической точки зрения. зрения; системы включали МУНТ, меланин (природный наноматериал [66]) и графен. Были измерены теплофизические свойства иононаножидкостей и объяснена интерпретация неожиданного повышения теплопроводности с учетом влияния химии поверхности частиц и межфазной структуры частица/жидкость.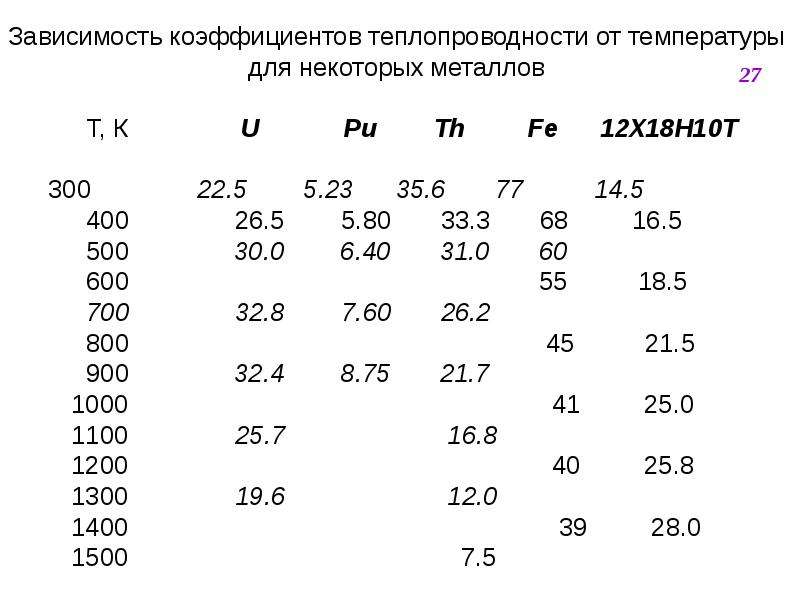 В данной работе мы ограничимся анализом систем на основе дисперсий МУНТ в ионных жидкостях. В нашей первой статье [6] модель Максвелла [77] и модель Леонга и др. [78,79] модели для сферических наночастиц использовались для объяснения повышения теплопроводности в нескольких иононаножидкостях. Однако во второй из этих моделей на расчеты сильно влияют принятые значения теплопроводности межфазного слоя и его толщины [49,69,70,71]. Например, для межфазной толщины 2 нм модель Леонга и др.может применяться только к системам с усилением выше 20%, что обычно происходит только для больших объемных фракций наночастиц (> 3%). В нашей системе с [C 4 mim][(C 2 F 5 ) 3 PF 3 ][76] было обнаружено очень небольшое усиление (6,2%). На рисунке 6 обобщены средние улучшения теплопроводности, обнаруженные для всех иононаножидкостей, исследованных в нашей лаборатории, между 293 и 353 К при концентрации МУНТ 1% (масс./масс.).Значения варьируются от 2 до 12%, что является довольно скромным эффектом; и не может быть идентифицирована зависимость от молекулярной структуры катионов или анионов.
В данной работе мы ограничимся анализом систем на основе дисперсий МУНТ в ионных жидкостях. В нашей первой статье [6] модель Максвелла [77] и модель Леонга и др. [78,79] модели для сферических наночастиц использовались для объяснения повышения теплопроводности в нескольких иононаножидкостях. Однако во второй из этих моделей на расчеты сильно влияют принятые значения теплопроводности межфазного слоя и его толщины [49,69,70,71]. Например, для межфазной толщины 2 нм модель Леонга и др.может применяться только к системам с усилением выше 20%, что обычно происходит только для больших объемных фракций наночастиц (> 3%). В нашей системе с [C 4 mim][(C 2 F 5 ) 3 PF 3 ][76] было обнаружено очень небольшое усиление (6,2%). На рисунке 6 обобщены средние улучшения теплопроводности, обнаруженные для всех иононаножидкостей, исследованных в нашей лаборатории, между 293 и 353 К при концентрации МУНТ 1% (масс./масс.).Значения варьируются от 2 до 12%, что является довольно скромным эффектом; и не может быть идентифицирована зависимость от молекулярной структуры катионов или анионов. Например, если мы выберем только эффективную теплопроводность жидкостей с одним и тем же катионом [C 4 mim] + и сравним их со значениями теплопроводности базовой жидкости, результат отобразится на рис. 7. Порядок усиления уменьшается, как показано на рисунке 7а, в то время как теплопроводность соответствующей ионной жидкости изменяется случайным образом (7б).На рисунке 8 показано изменение повышения теплопроводности с тем же катионом [C 2 mim] + (а) и с тем же анионом [(CF 3 SO 2 ) 2 N] − , (б). Размер иона, по-видимому, не оказывает специфического влияния, как это обсуждалось для зависимости теплопроводности тех же жидкостей [77]. Для теплопроводности получена следующая последовательность: [(CN) 2 N] − > [C(CN) 3 ] − ≈ [SCN] − > [BF 4 ] − > [PF 6 ] — > [CF 3 SO 3 ] — > [(CF 3 SO 2 ) 2 N] — > [(C 2 Ф 5 ) 3 ПФ 3 ] − .
Например, если мы выберем только эффективную теплопроводность жидкостей с одним и тем же катионом [C 4 mim] + и сравним их со значениями теплопроводности базовой жидкости, результат отобразится на рис. 7. Порядок усиления уменьшается, как показано на рисунке 7а, в то время как теплопроводность соответствующей ионной жидкости изменяется случайным образом (7б).На рисунке 8 показано изменение повышения теплопроводности с тем же катионом [C 2 mim] + (а) и с тем же анионом [(CF 3 SO 2 ) 2 N] − , (б). Размер иона, по-видимому, не оказывает специфического влияния, как это обсуждалось для зависимости теплопроводности тех же жидкостей [77]. Для теплопроводности получена следующая последовательность: [(CN) 2 N] − > [C(CN) 3 ] − ≈ [SCN] − > [BF 4 ] − > [PF 6 ] — > [CF 3 SO 3 ] — > [(CF 3 SO 2 ) 2 N] — > [(C 2 Ф 5 ) 3 ПФ 3 ] − .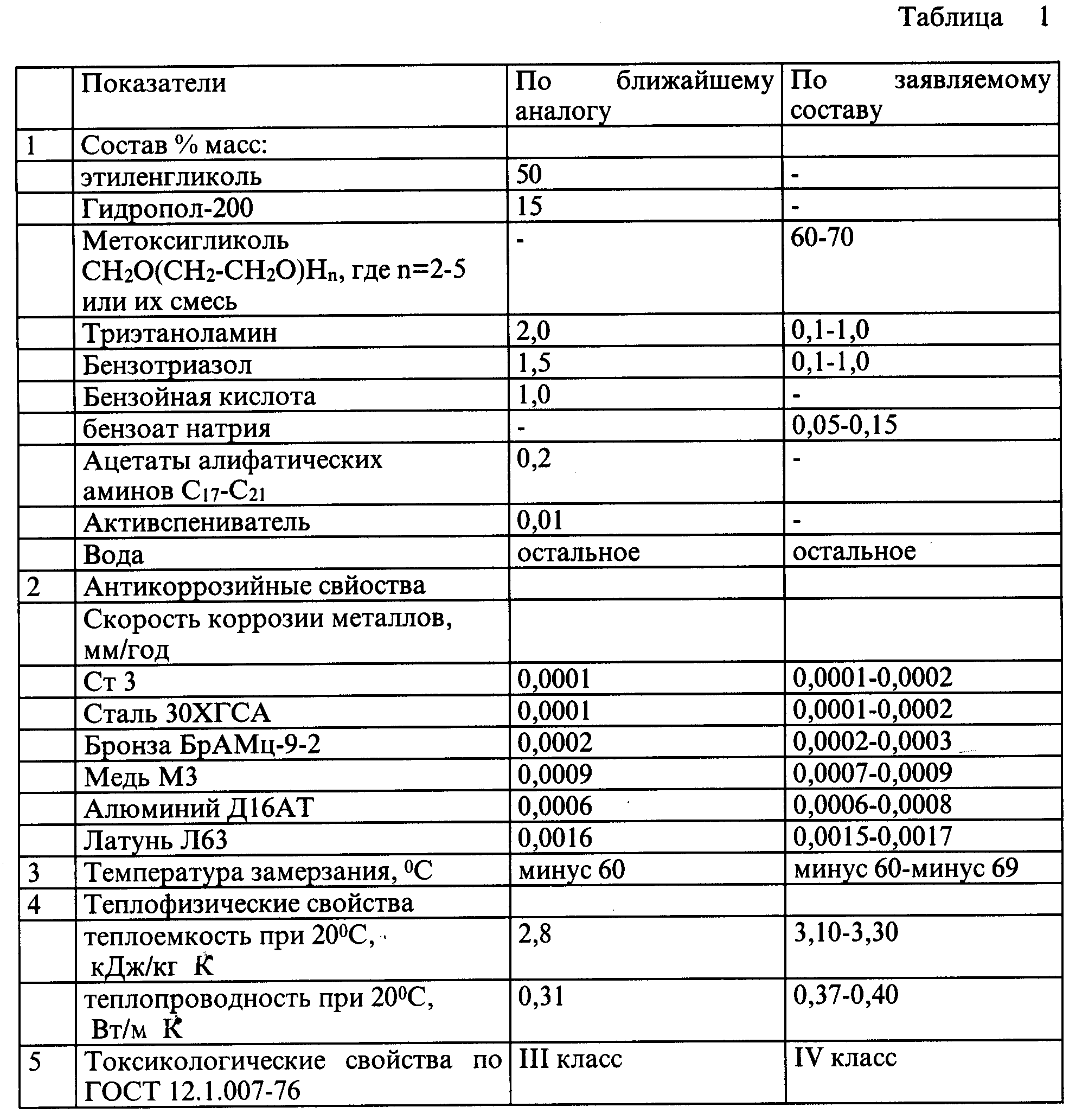 Объемный ион, такой как [(C 2 F 5 ) 3 PF 3 ] — , который гораздо менее подвижен, по-видимому, способствует очень низкой теплопроводности. Цианионы привносят гораздо более высокое значение теплопроводности и более сильную зависимость от температуры. Теплопроводность [C 4 mim][BF 4 ] с наименьшим анионом высока, но ниже, чем у цианосоединений, особенно при более низких температурах. Для остальных ИЖ значение теплопроводности увеличивается с уменьшением размера аниона.Меньшие анионы, в принципе, обладают большей подвижностью, усиливая ионные взаимодействия и, следовательно, способствуя большему количеству тепловых путей. Кажется, что механизм передачи тепловой энергии в ионаножидкости, макроскопически отражающийся в теплопроводности, не очень зависит от свойств основная ионная жидкость. Однако утверждалось, что это может зависеть от взаимодействия между частями ионной жидкости и поверхностью наноматериала (граница раздела частица / жидкость) и от вовлеченной химии поверхности.
Объемный ион, такой как [(C 2 F 5 ) 3 PF 3 ] — , который гораздо менее подвижен, по-видимому, способствует очень низкой теплопроводности. Цианионы привносят гораздо более высокое значение теплопроводности и более сильную зависимость от температуры. Теплопроводность [C 4 mim][BF 4 ] с наименьшим анионом высока, но ниже, чем у цианосоединений, особенно при более низких температурах. Для остальных ИЖ значение теплопроводности увеличивается с уменьшением размера аниона.Меньшие анионы, в принципе, обладают большей подвижностью, усиливая ионные взаимодействия и, следовательно, способствуя большему количеству тепловых путей. Кажется, что механизм передачи тепловой энергии в ионаножидкости, макроскопически отражающийся в теплопроводности, не очень зависит от свойств основная ионная жидкость. Однако утверждалось, что это может зависеть от взаимодействия между частями ионной жидкости и поверхностью наноматериала (граница раздела частица / жидкость) и от вовлеченной химии поверхности. Этот результат был выводом нашей публикации [49], а также группы Белфаста/Манчестера [80] и группы Катовице [81]. Другие возможные вклады в повышение теплопроводности ионаножидкостей, содержащих МУНТ, не рассматривались. França et al. В работе [75] показано, что для атомов ионных жидкостей и углеродных наноматериалов, взаимодействующих между собой, притяжение сильнее для катионов (чем для анионов) выше и ниже π-системы наноматериалов, тогда как анионы сильнее притягиваются к гидрированным краям.Упорядочивание ионов вокруг и внутри (7, 7) и (10, 10) одностенных нанотрубок, а также вблизи стопки листов графена анализировалось с точки зрения функций распределения плотности. Анионы, как и катионы, были обнаружены в первом межфазном слое, взаимодействующем с углеродными наноматериалами, что удивительно, учитывая используемые поверхности потенциала взаимодействия. Методом неравновесной молекулярной динамики рассчитана теплопроводность ионных жидкостей и композитных систем, содержащих во взвешенном состоянии одну нанотрубку или один графеновый пакет.
Этот результат был выводом нашей публикации [49], а также группы Белфаста/Манчестера [80] и группы Катовице [81]. Другие возможные вклады в повышение теплопроводности ионаножидкостей, содержащих МУНТ, не рассматривались. França et al. В работе [75] показано, что для атомов ионных жидкостей и углеродных наноматериалов, взаимодействующих между собой, притяжение сильнее для катионов (чем для анионов) выше и ниже π-системы наноматериалов, тогда как анионы сильнее притягиваются к гидрированным краям.Упорядочивание ионов вокруг и внутри (7, 7) и (10, 10) одностенных нанотрубок, а также вблизи стопки листов графена анализировалось с точки зрения функций распределения плотности. Анионы, как и катионы, были обнаружены в первом межфазном слое, взаимодействующем с углеродными наноматериалами, что удивительно, учитывая используемые поверхности потенциала взаимодействия. Методом неравновесной молекулярной динамики рассчитана теплопроводность ионных жидкостей и композитных систем, содержащих во взвешенном состоянии одну нанотрубку или один графеновый пакет. В композитных системах, содержащих нанотрубки, наблюдается повышение общей теплопроводности, причем расчетные значения хорошо согласуются с экспериментами по суспензиям нанотрубок, а именно с точки зрения порядка различных ионных жидкостей. Очень подробный обзор существующих моделей для расчета эффективную теплопроводность суспензий твердых частиц (λ eff ), таких как наножидкости, особенно с УНТ, можно увидеть в ссылках [82,83,84,85,86], и здесь подробное обсуждение проводиться не будет.Большинство из них имеют механистическую основу, касающуюся диспергирования хорошо диспергированных твердых частиц в сплошной среде, восходящую к аналогичной электрической задаче пионерской работы Максвелла [77]. Эта трактовка справедлива только для сферических частиц. Гамильтон и Кроссер [86] модифицировали его для несферических частиц и ввели коэффициенты формы для частиц, таких как цилиндры. Последняя модель показывает, что увеличение теплопроводности для несферических частиц выше, чем для сферических частиц.
В композитных системах, содержащих нанотрубки, наблюдается повышение общей теплопроводности, причем расчетные значения хорошо согласуются с экспериментами по суспензиям нанотрубок, а именно с точки зрения порядка различных ионных жидкостей. Очень подробный обзор существующих моделей для расчета эффективную теплопроводность суспензий твердых частиц (λ eff ), таких как наножидкости, особенно с УНТ, можно увидеть в ссылках [82,83,84,85,86], и здесь подробное обсуждение проводиться не будет.Большинство из них имеют механистическую основу, касающуюся диспергирования хорошо диспергированных твердых частиц в сплошной среде, восходящую к аналогичной электрической задаче пионерской работы Максвелла [77]. Эта трактовка справедлива только для сферических частиц. Гамильтон и Кроссер [86] модифицировали его для несферических частиц и ввели коэффициенты формы для частиц, таких как цилиндры. Последняя модель показывает, что увеличение теплопроводности для несферических частиц выше, чем для сферических частиц. Было обнаружено, что эти классические модели не могут предсказать и объяснить экспериментальную теплопроводность наножидкостей, а именно зависимость от температуры и объемной доли частиц [81,84,87]. Несмотря на большие исследовательские усилия, направленные в последнее десятилетие на выявление механизмов и разработку теоретических моделей теплопередачи в наножидкостях, текущие знания о реальных механизмах теплопередачи скудны и противоречивы [49,84]. Как правило, были предложены дополнительные механизмы для объяснения, по крайней мере качественно, наблюдаемого увеличения эффективной теплопроводности наножидкостей сверх того, что предсказывается этими классическими моделями.Эти дополнительные механизмы включают броуновское движение наночастиц (для сферической формы), межфазный нанослой на поверхности раздела наночастиц/основной жидкости и кластеризацию или агрегацию наночастиц. Эти механизмы хорошо обсуждаются в литературе [83, 84, 88] и не будут подробно рассматриваться здесь. Среди этих механизмов межфазный нанослой был предложен в качестве основного фактора увеличения эффективной теплопроводности наножидкостей [79].
Было обнаружено, что эти классические модели не могут предсказать и объяснить экспериментальную теплопроводность наножидкостей, а именно зависимость от температуры и объемной доли частиц [81,84,87]. Несмотря на большие исследовательские усилия, направленные в последнее десятилетие на выявление механизмов и разработку теоретических моделей теплопередачи в наножидкостях, текущие знания о реальных механизмах теплопередачи скудны и противоречивы [49,84]. Как правило, были предложены дополнительные механизмы для объяснения, по крайней мере качественно, наблюдаемого увеличения эффективной теплопроводности наножидкостей сверх того, что предсказывается этими классическими моделями.Эти дополнительные механизмы включают броуновское движение наночастиц (для сферической формы), межфазный нанослой на поверхности раздела наночастиц/основной жидкости и кластеризацию или агрегацию наночастиц. Эти механизмы хорошо обсуждаются в литературе [83, 84, 88] и не будут подробно рассматриваться здесь. Среди этих механизмов межфазный нанослой был предложен в качестве основного фактора увеличения эффективной теплопроводности наножидкостей [79]. Молекулы жидкости вблизи поверхности частицы взаимодействуют и/или поглощаются поверхностью наночастицы, создавая слоистую структуру, которая демонстрирует характеристики организованной «твердоподобной» системы [80,81,82,83,84,85,88,89]. .На рисунке 9 показан схематический рисунок этой концепции и ее реализация с использованием молекулярной динамики João França et al. (2017) [75,90], для моделирования с SWCNT + [C 4 mim][C(CN) 3 ], при 363 K. Это наблюдение подтвердило наше предыдущее понимание осуществимости модели Леонг и др. [73,79] и подобных моделей, что в системе УНТ-ИЖ существует граница раздела со скачком температуры на поверхности трубы, влияющим на механизм теплопередачи. Существование слоя было подтверждено его применением в ионных жидкостях не только для ОУНТ, но и для графена.В моделях Леонга и соавт. затем можно использовать эту теоретическую разработку для расчета теплопроводности IoNanofluid с углеродными трубками, как только мы узнаем, экспериментально или с использованием эмпирических методов оценки, теплопроводность базовой ионной жидкости, а также свойства межфазный слой, а именно его толщина и теплопроводность.
Молекулы жидкости вблизи поверхности частицы взаимодействуют и/или поглощаются поверхностью наночастицы, создавая слоистую структуру, которая демонстрирует характеристики организованной «твердоподобной» системы [80,81,82,83,84,85,88,89]. .На рисунке 9 показан схематический рисунок этой концепции и ее реализация с использованием молекулярной динамики João França et al. (2017) [75,90], для моделирования с SWCNT + [C 4 mim][C(CN) 3 ], при 363 K. Это наблюдение подтвердило наше предыдущее понимание осуществимости модели Леонг и др. [73,79] и подобных моделей, что в системе УНТ-ИЖ существует граница раздела со скачком температуры на поверхности трубы, влияющим на механизм теплопередачи. Существование слоя было подтверждено его применением в ионных жидкостях не только для ОУНТ, но и для графена.В моделях Леонга и соавт. затем можно использовать эту теоретическую разработку для расчета теплопроводности IoNanofluid с углеродными трубками, как только мы узнаем, экспериментально или с использованием эмпирических методов оценки, теплопроводность базовой ионной жидкости, а также свойства межфазный слой, а именно его толщина и теплопроводность. Конечно, весь процесс ограничен неопределенностью используемых экспериментальных значений теплопроводности.Необходимо краткое описание основных уравнений моделей, используемых в данном исследовании. Модель Максвелла [78] предсказывает эффективную теплопроводность жидких и твердых суспензий для сферических частиц и приводит к уравнению (9):
Конечно, весь процесс ограничен неопределенностью используемых экспериментальных значений теплопроводности.Необходимо краткое описание основных уравнений моделей, используемых в данном исследовании. Модель Максвелла [78] предсказывает эффективную теплопроводность жидких и твердых суспензий для сферических частиц и приводит к уравнению (9):λINF=λILλp+2λIL−2ϕp(λIL−λp)λp+2λIL+ϕp(λIL−λp)
(9)
где λ p и λ IL — теплопроводность наночастиц и базовой ионной жидкости соответственно, λ INF — эффективная теплопроводность IoNanofluid, а ϕ p — объемная доля наночастицы в IoNanofluid.Гамильтон и Кроссер [86] модифицировали модель Максвелла как для сферических, так и для несферических частиц, применив коэффициент формы n, учитывающий форму дисперсных частиц. Этот коэффициент формы является функцией сферичности, которая ранее использовалась для характеристики формы частиц, падающих в жидкости [91]. Сферичность ψ определяется как отношение площади поверхности сферы с объемом, равным объему наночастицы, к площади поверхности наночастицы. Модель Гамильтона и Кроссера приводит к уравнению (10):
Модель Гамильтона и Кроссера приводит к уравнению (10):λINF=λILλp+(n−1)λIL−2(n−1)ϕp(λIL−λp)λp+(n−1)λIL+ϕp(λIL−λp)n=3ψ
(10)
Как упоминалось выше, эта модель показывает увеличение теплопроводности для несферических частиц (с той же объемной долей) больше, чем для сферических частиц.Это выражение сводится к модели Максвелла для сферических частиц (n = 1).
Леонг и др. [78,79] разработали две модели с учетом влияния размера частиц, их концентрации и добавления межфазного нанослоя для наножидкостей, содержащих сферические и цилиндрические наночастицы. Их модель (MLY) [92] для наножидкостей, содержащих цилиндрические/трубчатые наночастицы, для расчета эффективной теплопроводности нашей IoNanofluid, λ INF , имеет вид:λINF=λILϕpω(λp−ωλIL)[γ12−γ2+1]+(λp+ωλIL)γ12[ϕpγ2(ω−1)+1]γ12(λp+ωλIL)−(λp−ωλIL)ϕp[γ12+γ2− 1]
(11)
И определяя F как:F=ϕpω(λp−ωλIL)[γ12−γ2+1]+(λp+ωλIL)γ12[ϕpγ2(ω−1)+1]γ12(λp+ωλIL)−(λp−ωλIL)ϕp[γ12+γ2− 1]
(12)
получаем для повышения теплопроводности, Δλ/λIL,ΔλλIL=λINFλIL−1=F−1
(13)
где λ p и λ IL – теплопроводность наночастиц и базовой ионной жидкости, ϕ p – объемная доля наночастиц в ионаножидкости, ω = λ lr /λ IL , ? p — радиус наночастицы.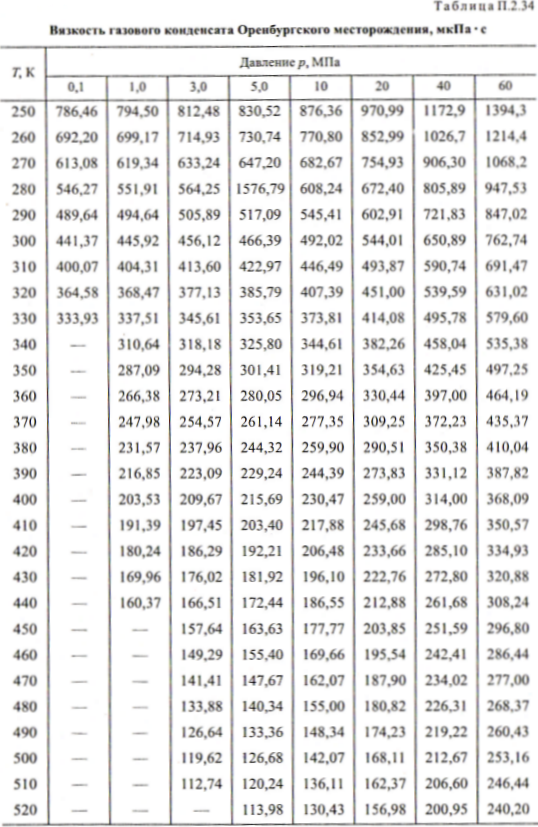 Значения λ p и λ IL можно получить из литературы (или оценить, если необходимо), если используемые наночастицы хорошо охарактеризованы. Однако значения h и λ lr существенно влияют на вычисленное значение теплопроводности IoNanofluid. Порядок и ориентация молекул жидкости, абсорбированных на поверхности наночастиц, по-видимому, приводят к значению теплопроводности нанослоя, которое является промежуточным между теплопроводностью твердого тела и базовой жидкости; я.е., λ IL λ lr λ p . Для УНТ их теплопроводность составляет порядка 3000 Вт·м -1 · К -1 , измеренная с помощью микроизготовленного подвесного устройства [93], что в 20 000 раз больше, чем средняя теплопроводность ионная жидкость. Однако эта величина является спорной, так как многие авторы разными методами пришли к значениям теплопроводности одиночных или пучковых одностенных и МУНТ в диапазоне от 20 до 6000 Вт·м −1 ·K −1 [94,95,96,97].
Значения λ p и λ IL можно получить из литературы (или оценить, если необходимо), если используемые наночастицы хорошо охарактеризованы. Однако значения h и λ lr существенно влияют на вычисленное значение теплопроводности IoNanofluid. Порядок и ориентация молекул жидкости, абсорбированных на поверхности наночастиц, по-видимому, приводят к значению теплопроводности нанослоя, которое является промежуточным между теплопроводностью твердого тела и базовой жидкости; я.е., λ IL λ lr λ p . Для УНТ их теплопроводность составляет порядка 3000 Вт·м -1 · К -1 , измеренная с помощью микроизготовленного подвесного устройства [93], что в 20 000 раз больше, чем средняя теплопроводность ионная жидкость. Однако эта величина является спорной, так как многие авторы разными методами пришли к значениям теплопроводности одиночных или пучковых одностенных и МУНТ в диапазоне от 20 до 6000 Вт·м −1 ·K −1 [94,95,96,97].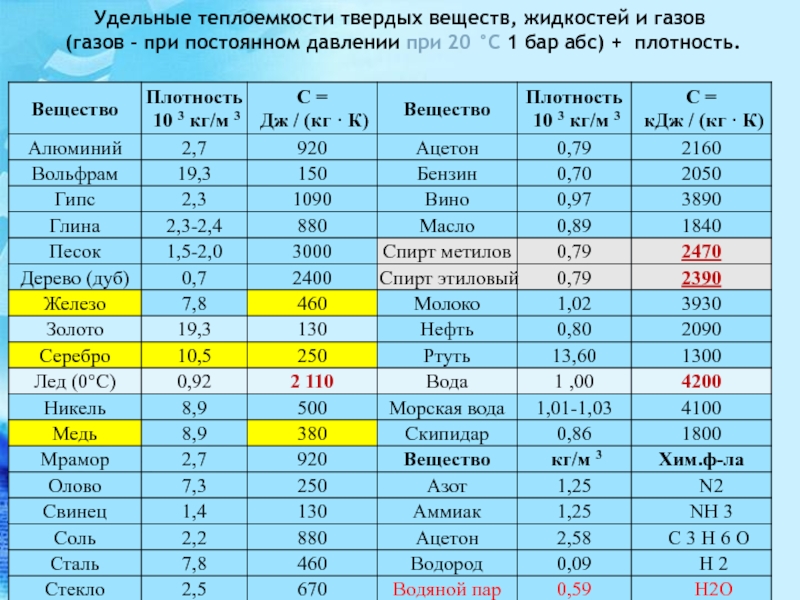 Наши МУНТ были предоставлены компанией Bayer бесплатно (Baytubes ® C150HP, номер CAS 308068-56-6), с длиной от 1 до 10 мкм, со средним внешним диаметром 13–16 нм, объемной плотностью 140–230 кг·м −3 и чистотой ≥ 99%. Трубки запутаны и похожи на цепочки в полимерах [98], как показано на рис. 10. В отсутствие экспериментальных измерений мы оценили значение между 2000–3000 Вт·м −1 ·K −1 для этого типа MWCNT в наших предыдущих публикациях, что согласуется с тем, что использовалось другими [80,81].
Наши МУНТ были предоставлены компанией Bayer бесплатно (Baytubes ® C150HP, номер CAS 308068-56-6), с длиной от 1 до 10 мкм, со средним внешним диаметром 13–16 нм, объемной плотностью 140–230 кг·м −3 и чистотой ≥ 99%. Трубки запутаны и похожи на цепочки в полимерах [98], как показано на рис. 10. В отсутствие экспериментальных измерений мы оценили значение между 2000–3000 Вт·м −1 ·K −1 для этого типа MWCNT в наших предыдущих публикациях, что согласуется с тем, что использовалось другими [80,81].6. Выводы и рекомендации
Прогнозирование, оценка и корреляция теплофизических свойств жидкостей является очень важной задачей для научных и технических приложений. Однако уверенность, которую в настоящее время можно придать любому расчету этих свойств, сильно зависит от используемых методов. Как объясняется здесь, молекулярная основа должна быть основой точности и достоверности прогноза. Представлен обзор современного состояния методов прогнозирования и оценки теплопроводности ионных жидкостей и многостенных углеродных нанотрубок.
В настоящее время невозможно использовать полные молекулярные модели и теорию для предсказания теплопроводности ионных жидкостей. Таким образом, слово предсказание не должно использоваться в соответствующей литературе. Можно использовать ряд методов оценки, позволяющих рассчитать теплопроводность, которые обсуждались в этой статье на основе приближенных теоретических моделей (например, модель Бриджмена с недооценкой до 50%), эвристических расширений теории (например, , модель Ван-дер-Ваальса, теория свободного объема, применимая только к некоторым ионным жидкостям, положенным в основу схемы) или полностью эмпирическая информация, такая как методы группового вклада, или эмпирические соотношения между теплофизическими свойствами (например,г., Коллер и др. методом, с отклонениями порядка ±20%). Среди этих моделей оценки модель Ван-дер-Ваальса кажется наиболее успешной, и рекомендуется ее расширение для большего количества ионных жидкостей.
В случае ионаножидкостей из многослойных углеродных нанотрубок, особенно тех, которые охвачены данным исследованием, не удалось различить четкой зависимости от молекулярной структуры катионов и анионов базовой жидкости. Следовательно, механизм усиленного переноса тепловой энергии, макроскопически отражаемый теплопроводностью ионаножидкости, мало зависит от базовой ионной жидкости (в отличие от зависимости базовой жидкости от нее), но в рамках модели MLY сильно зависит от взаимодействия между фрагментами ионной жидкости и границей раздела наночастиц (стенками трубки), что также подтверждается молекулярным моделированием.Использование модели MLY показало, что она не чувствительна к наблюдаемому изменению увеличения теплопроводности с температурой и очень зависит от межфазных свойств наносистемы, а именно толщины интерфейса и теплопроводности, ее регулируемых параметров.
Следовательно, механизм усиленного переноса тепловой энергии, макроскопически отражаемый теплопроводностью ионаножидкости, мало зависит от базовой ионной жидкости (в отличие от зависимости базовой жидкости от нее), но в рамках модели MLY сильно зависит от взаимодействия между фрагментами ионной жидкости и границей раздела наночастиц (стенками трубки), что также подтверждается молекулярным моделированием.Использование модели MLY показало, что она не чувствительна к наблюдаемому изменению увеличения теплопроводности с температурой и очень зависит от межфазных свойств наносистемы, а именно толщины интерфейса и теплопроводности, ее регулируемых параметров.
Модель MLY не может использоваться без настраиваемых параметров. Однако его можно использовать для оценки теплопроводности ионаножидкостей, если некоторую информацию можно получить экспериментально или с помощью молекулярного моделирования, которое редко доступно.В этом случае модель попадает в категорию оценивания с использованием приближенных теоретических методов.

Риски, связанные с использованием всех имеющихся данных без оценки их качества, могут ограничивать полезность и достоверность разработанных корреляций и процедур оценки и вызывать ряд проблем при проектировании промышленного оборудования и процессов.
Свойства воды при атмосферном давлении
Свойства воды приведены ниже в таблице в метрических единицах СИ для температур от 0°C до 100°C при атмосферном давлении 101,325 кПа. часто называют свойствами насыщенной воды, насыщенной жидкости или теплофизическими свойствами.В таблице указаны плотность, динамическая вязкость, кинематическая вязкость, удельная теплоемкость, теплопроводность и число Прандтля. Под таблицей находится версия файла изображения для просмотра в автономном режиме
. Свойства указаны для чуть выше точки замерзания и чуть ниже точки кипения.
Примечание: Обратите внимание на единицы измерения вязкости. Пример: 1,7292×10 -6 м 2 /с = 0,0000017292 м 2 /с
| Температура (Т) | Плотность (ρ) | Динамическая вязкость (мк) | Кинематическая вязкость (v) | Удельная теплоемкость (cp) | Теплопроводность (k) | Число Прандтля (Pr) |
|---|---|---|---|---|---|---|
| ◦с | кг/м 3 | x 10 -3 Па. с с | x 10 -6 м 2 /с | кДж/кг.К | Вт/м.К | – |
| 0 | 999,84 | 1,792 | 1,792 | 4.219 | 0,561 | 13,47 |
| 5 | 999,97 | 1,518 | 1,518 | 4.205 | 0,571 | 11.19 |
| 10 | 999,70 | 1.306 | 1.306 | 4,195 | 0,580 | 9,45 |
| 15 | 999.10 | 1,138 | 1,139 | 4.189 | 0,589 | 8.09 |
| 20 | 998.21 | 1,002 | 1,003 | 4,185 | 0,598 | 7,00 |
| 25 | 997.05 | 0,890 | 0,893 | 4.182 | 0,607 | 6.13 |
| 30 | 995,65 | 0,797 | 0,801 | 4. 180 180 | 0,616 | 5,41 |
| 35 | 994.04 | 0,719 | 0,724 | 4.179 | 0,623 | 4,82 |
| 40 | 992.22 | 0,653 | 0,658 | 4.179 | 0,631 | 4,33 |
| 45 | 990.22 | 0,596 | 0,602 | 4.179 | 0,637 | 3,91 |
| 50 | 988.05 | 0,547 | 0,553 | 4.180 | 0,644 | 3,55 |
| 55 | 985,71 | 0,504 | 0,511 | 4.181 | 0,649 | 3,25 |
| 60 | 983.21 | 0,466 | 0,474 | 4.183 | 0,654 | 2,98 |
| 65 | 980,57 | 0,433 | 0,442 | 4,185 | 0,659 | 2,75 |
| 70 | 977,78 | 0,404 | 0,413 | 4,188 | 0,663 | 2,55 |
| 75 | 974,86 | 0,378 | 0,387 | 4.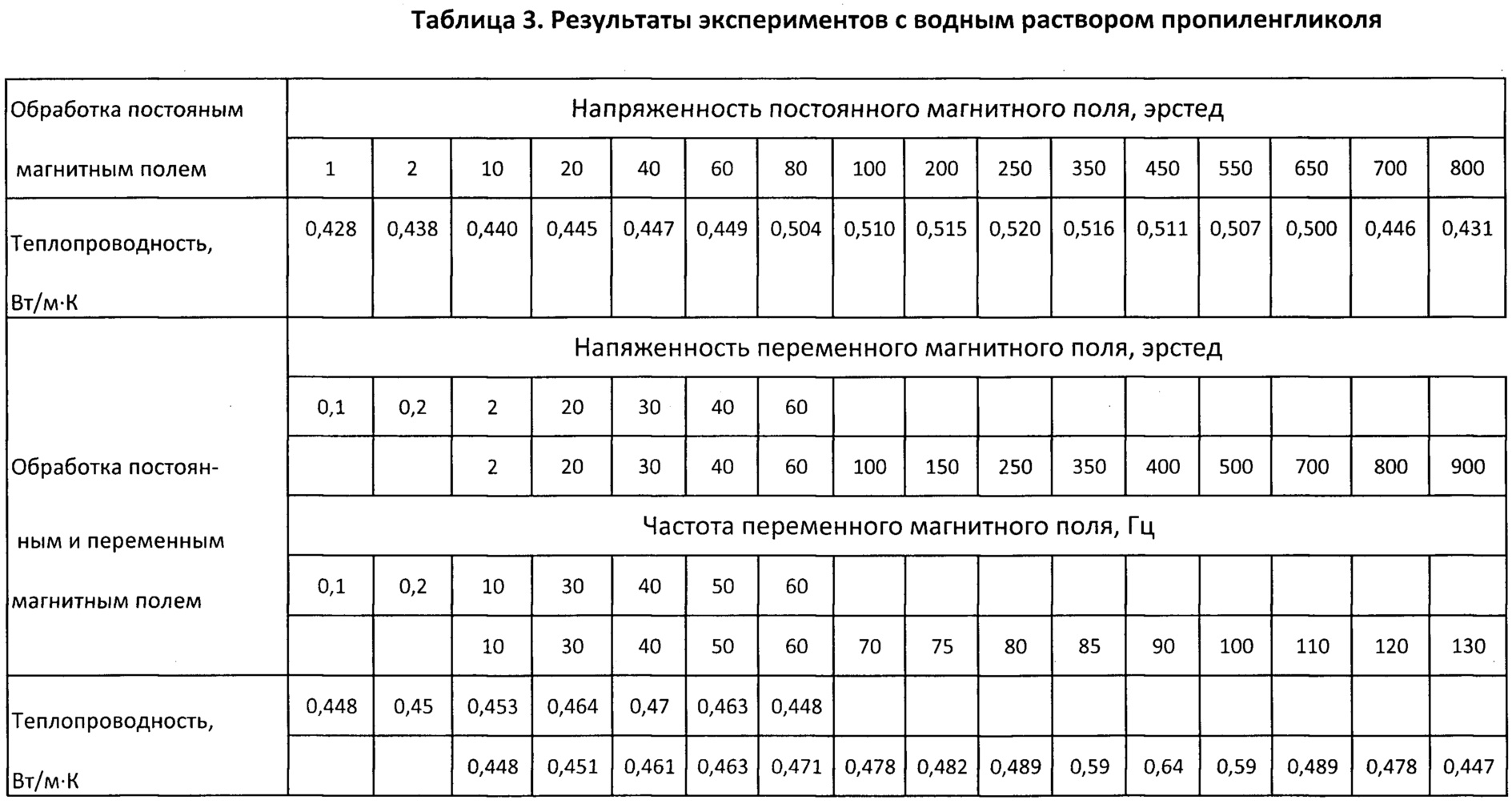 akson-quick.ru © 2019
|



 На рисунке х-3 показана зависимость теплопроводности метанола, этанола и бензола от понижающей температуры. тт. пл. Т р т ПЛ ми= Здесь Tal это точка плавления. Кривые исследуемых жидкостей схожи по форме. В нормально обследованной области (0> 0, 5) зависимость в основном простая; при 6 > 0.7 наблюдается выраженная кривизна (Уменьшения Х).Теплопроводность жидкой ЛПЛ в точке плавления примерно в 3 раза превышает теплопроводность в критической точке. cr. (Х-3) значение L зависит от давления. Показывает теплопроводность при давлении от A0 до 0 и давлении от p до 0 Диэтиленгликоль рафинированный керосин Сернокислотное шпиндельное масло Парафиновое масло Трихлорэтилен хлористый Масляный эфир. Ацетат метилового эфира Propyl ацетат Эстера Теплопроводность некоторых жидкостей[9, 10] XPU Bridgman [12, 13] получил отношение (ChrDo)> 1, то есть увеличение теплопроводности жидкостей под высоким давлением(таблица X-4). Влияние давления на теплопроводность больше, когда степень сжатия жидкости больше, то есть чем выше temperature.
На рисунке х-3 показана зависимость теплопроводности метанола, этанола и бензола от понижающей температуры. тт. пл. Т р т ПЛ ми= Здесь Tal это точка плавления. Кривые исследуемых жидкостей схожи по форме. В нормально обследованной области (0> 0, 5) зависимость в основном простая; при 6 > 0.7 наблюдается выраженная кривизна (Уменьшения Х).Теплопроводность жидкой ЛПЛ в точке плавления примерно в 3 раза превышает теплопроводность в критической точке. cr. (Х-3) значение L зависит от давления. Показывает теплопроводность при давлении от A0 до 0 и давлении от p до 0 Диэтиленгликоль рафинированный керосин Сернокислотное шпиндельное масло Парафиновое масло Трихлорэтилен хлористый Масляный эфир. Ацетат метилового эфира Propyl ацетат Эстера Теплопроводность некоторых жидкостей[9, 10] XPU Bridgman [12, 13] получил отношение (ChrDo)> 1, то есть увеличение теплопроводности жидкостей под высоким давлением(таблица X-4). Влияние давления на теплопроводность больше, когда степень сжатия жидкости больше, то есть чем выше temperature.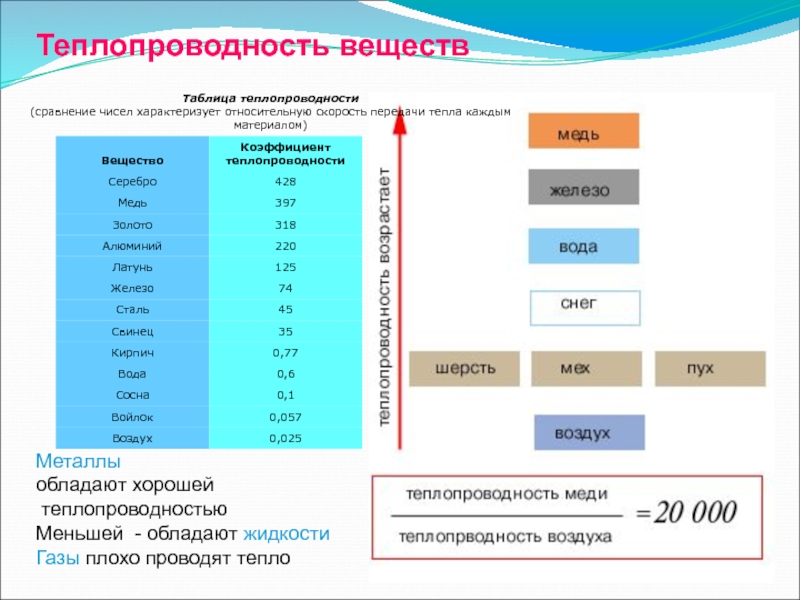 As ориентир, в среднем.
As ориентир, в среднем.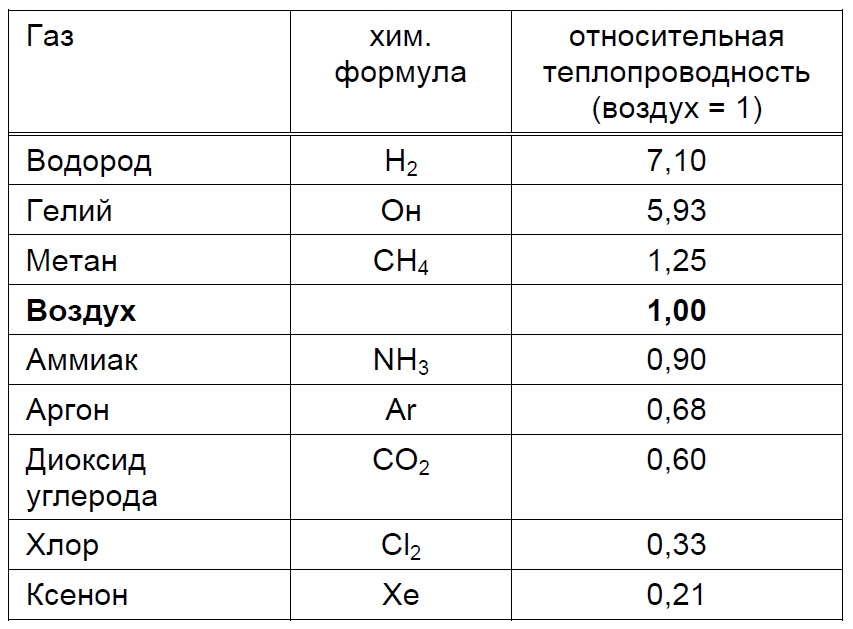 Б. Варгафтик, Л.П. Филиппов, А.А. Тарзиманов, Е.Е. Тоцкий. – М.: Энергоатомиздат, 1990. – 352 с.
Б. Варгафтик, Л.П. Филиппов, А.А. Тарзиманов, Е.Е. Тоцкий. – М.: Энергоатомиздат, 1990. – 352 с.
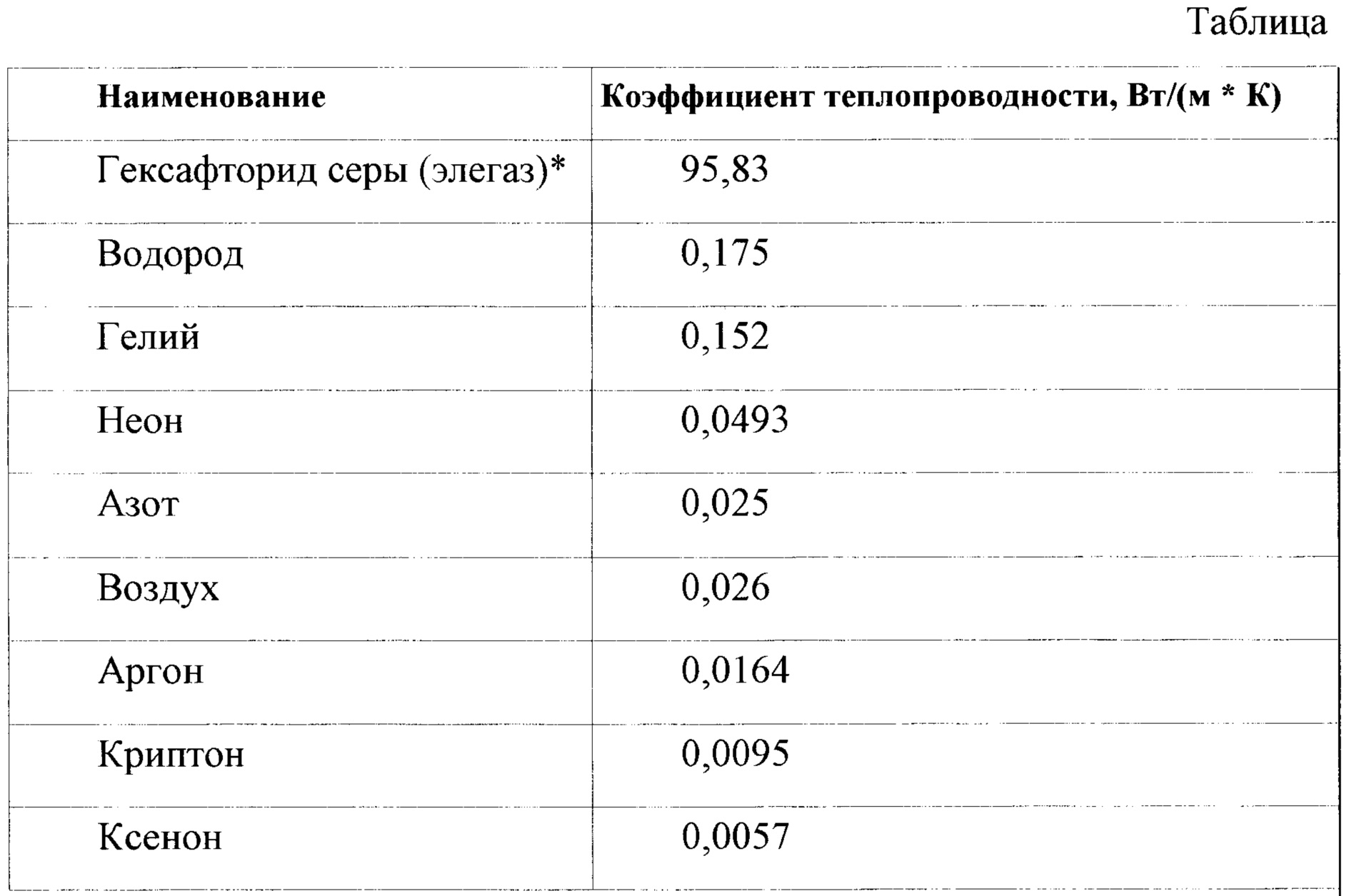 7
7 3
3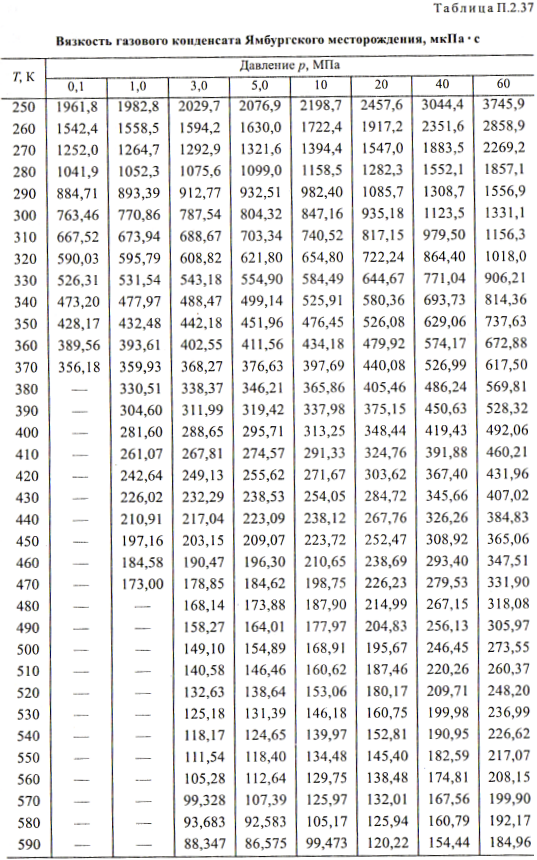 0000
0000 746
746