Измеритель теплопроводности мёрзлых грунтов ИТП-МГ4 Грунт
Измеритель теплопроводности ИТП-МГ4 «Грунт» предназначен для определения теплопроводности мерзлых грунтов в лабораторных условиях по ГОСТ 26263. Прибор состоит из блока управления с дисплеем и термоконтейнера, помещаемого в морозильную камеру (в комплект не входит) для промораживания образца грунта и поддержания стационарного теплового режима. Термоконтейнер состоит из нижней и верхней термоплит, нагрузочного устройства и датчиков для измерения температур, теплового потока и силы.
Измеритель ИТП-МГ4 «Грунт» позволяет задавать необходимое давление на образец мерзлого грунта и определять его теплопроводность в автоматическом режиме при средней температуре от 20 до +2°С, обеспечивая поддержание заданной разницы температур нижней и верхней термоплит в диапазоне от 0 до 5°С. Прибор имеет режим непрерывной регистрации процесса испытаний образца грунта, энергонезависимую память на 500 результатов испытаний, промаркированных датой и временем измерения, часы реального времени и режим передачи данных на ПК по USB интерфейсу.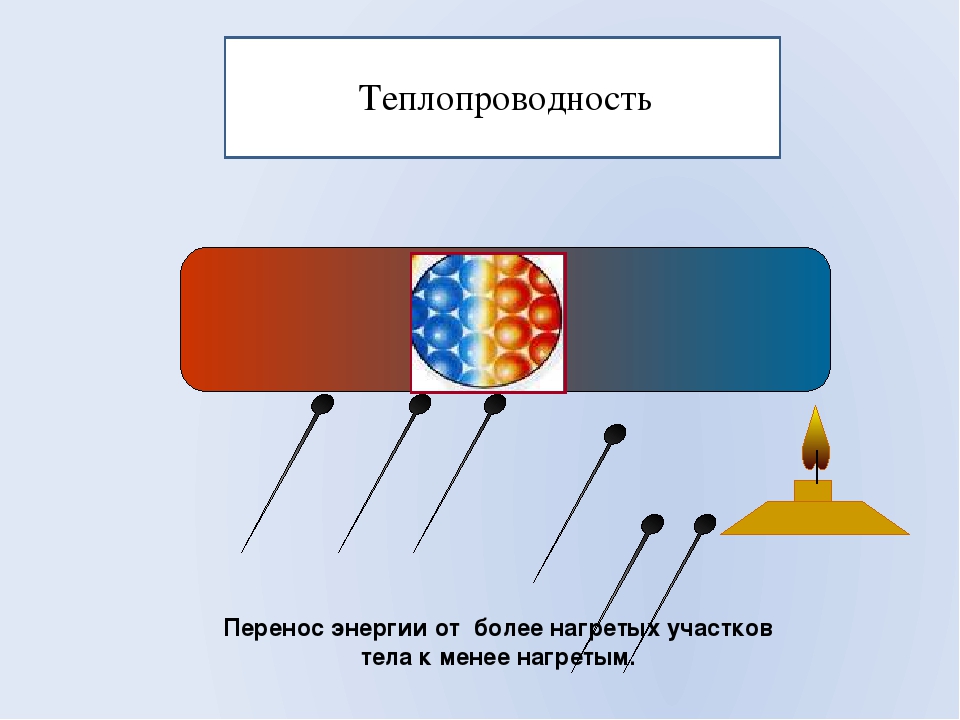
Технические характеристики измерителя теплопроводности ИТП-МГ4 Грунт приведены в следующей таблице
| Характеристика | Значение |
| Диапазон определения коэффициента теплопроводности, Вт/м•К | 0,15 … 3,0 |
| Диапазон нагружения, Н | 0 … 500 |
| Диапазон регулирования температуры, °С | -21,5 … +4 |
| Погрешность измерения коэффициента теплопроводности, % | ±6 |
| Размеры испытуемого образца, мм | Ø100×30 |
| Время одного измерения, ч, не более | 20 |
| Потребляемая мощность, кВт, не более | 0,6 |
| Электрическое питание | 220 В (50 Гц) |
| Габаритные размеры, мм, не более: − блока управления − теплометрической установки |
280×230×100 230×230×350 |
| Масса, кг, не более: − блока управления − теплометрической установки |
1,5 6,6 |
Комплект поставки: блок управления, термоконтейнер, блок вентиляторов, морозильная камера (по спецзаказу), регулятор холодильной камеры, обойма для образца грунта, обойма с металлическим дном для сыпучих образцов, калибровочный образец, кабель связи с ПК, CD с программным обеспечением, руководство по эксплуатации, упаковочная тара.
Гарантийный срок эксплуатации 18 месяцев. Обеспечивается сервисное и метрологическое обслуживание в течение всего срока эксплуатации.
Купить прибор для измерения теплопроводности мёрзлых грунтов ИТП-МГ4 Грунт можно с доставкой до двери или до терминалов транспортной компании в следующих городах: Москва, Санкт-Петербург, Екатеринбург, Саратов. Амурск, Ангарск, Архангельск, Астрахань, Барнаул, Белгород, Бийск, Брянск, Воронеж, Великий Новгород, Владивосток, Владикавказ, Владимир, Волгоград, Волгодонск, Вологда, Иваново, Ижевск, Йошкар-Ола, Казань, Калининград, Калуга, Кемерово, Киров, Кострома, Краснодар, Красноярск, Курск, Липецк, Магадан, Магнитогорск, Мурманск, Муром, Набережные Челны, Нальчик, Новокузнецк, Нарьян-Мар, Новороссийск, Новосибирск, Нефтекамск, Нефтеюганск, Новочеркасск, Нижнекамск, Норильск, Нижний Новгород, Обнинск, Омск, Орёл, Оренбург, Оха, Пенза, Пермь, Петрозаводск, Петропавловск-Камчатский, Псков, Ржев, Ростов, Рязань, Самара, Саранск, Смоленск, Сочи, Сыктывкар, Таганрог, Тамбов, Тверь, Тобольск, Тольятти, Томск, Тула, Тюмень, Ульяновск, Уфа, Ханты-Мансийск, Чебоксары, Челябинск, Череповец, Элиста, Ярославль и другие города, кроме того, в Республике Крым.
Высокая теплопроводность — Китай Высокая теплопроводность, тяжелая медь
Основная Информация.
Тип
Твёрдая Монтажная Плата
FR-4
Материал
Эпоксидная Смола Стекловолокна
Применение
Motor Coil
Огнезащитным Свойства
V0
Механическая Жесткая
Жесткая
Технология обработки
Основное вещество
Fr4
Изоляционные материалы
Эпоксидная смола
China
Описание Продукции
1.Окончательнаятолщинамеди5/5/5/5/5/5/5/5/5/5 =50 унций;3.Толщинамедистенкиотверстия≥45um
Рабочие эталоны теплопроводности
Данное оборудование указано в следующих разделах каталога:
Предназначены для
- аттестации,
- поверки
- и градуировки
рабочих средств измерения теплопроводности.
Выполняют функции рабочих эталонов 0-го или 1-го разряда в соответствии с Государственной поверочной схемой для средств измерений теплопроводности твёрдых тел по ГОСТ 8.140-2009.
Значения теплоёмкости, воспроизводимые рабочими эталонами 0-го разряда, устанавливаются на аппаратуре Государственного первичного эталона единицы теплопроводности твёрдых тел (ГЭТ 59-81).
Границы относительной погрешности (при P=0,95) рабочих эталонов:
- 0-го разряда: ±(0,005…0,015)
- 1-го разряда: ±(0,03…0,05)
Изготавливаются в форме таблеток (цилиндров) диаметром 15 мм, пластин 100…350 мм.
| Регистрационный номер | Материал | Диапазон температур | Диапазон теплопроводности, Вт/(м×К) | Межповерочный интервал |
| 01.01.001 | Органическое стекло | 90. ..350 ..350 |
0,143…0,200 | 3 года |
| 01.01.002 | Оптическое стекло марки ТФ1 | 90…500 | 0,354…0,899 | |
| 01.01.003 | Оптическое стекло марки КВ | 90…500 | 0,651…1,663 | |
| 01.01.004 | Оптическое стекло марки ЛК5 | 90…500 | 0,563…1,474 | |
| 01.01.005 | Нержавеющая сталь 12X18h20T | 290…600 | 14,65…19,88 | |
| 01.01.006 | Пеноплэкс | 283..350 | 0,024…0,035 | 1 год |
| 01.01.007 | Изотерм | 283..300 | 0,030…0,040 | |
| 01.01.008 | КВГ-210 | 283..300 | 0,048…0,060 |
Поставляются в упаковочной таре.
Тип 8222 — Conductivity meter, ELEMENT design
Изображения изделий могут отличаться от конкретной фактической конструкции.
Обращайте внимание на информацию, указанную в технических характеристиках и технических описаниях!
Описание типа
The Bürkert conductivity meter Type 8222 is designed for measuring the conductivity of fluids. The sensor element comprises a two-electrode cell and a Pt1000 temperature probe. The sensor itself is available with three different cell constants C. These with C= 0.01 or 0.1 cm-1 are fitted with stainless steel electrodes and those with C= 1.0 cm-1 are fitted with graphite electrodes.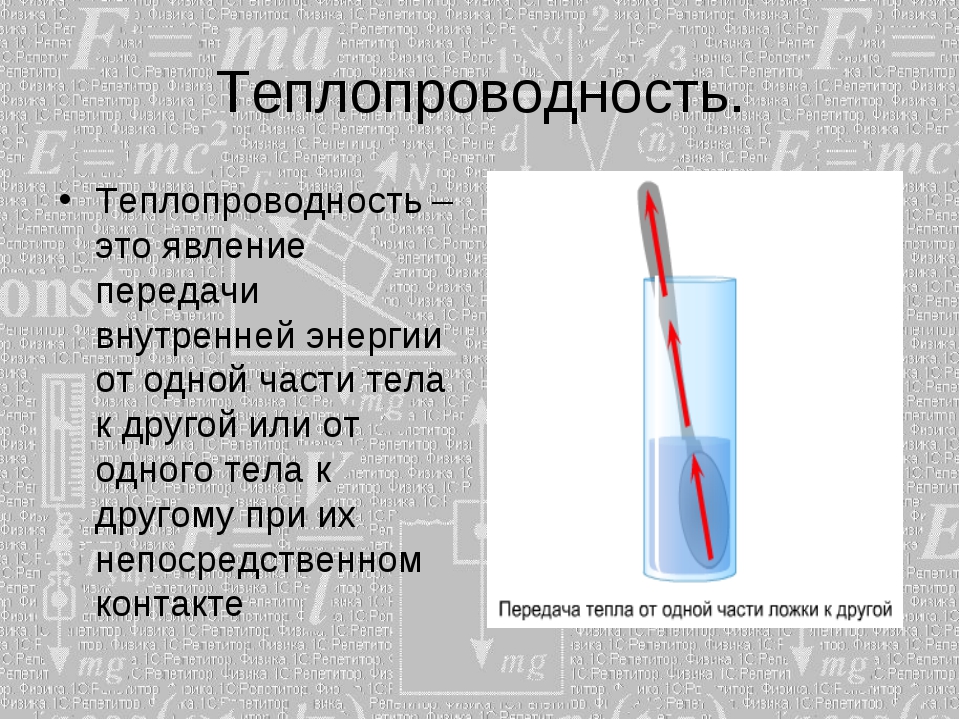 Thus, due to the measurement device’s design, Bürkert has simplified installation and maintenance work. Device type 8222 is available in two variants: The first one, the so-called ELEMENT standard is proposed either with three adjustable outputs (two digital outputs and one analogue output) or with four adjustable outputs (two digital and two analogue) and can be equipped with a display. The display is only necessary for start-up, configuration (e.g. selection pH/ORP measurement, measurement range, units, calibration, thresholds, etc) or as a display of process values. The second, the so-called ELEMENT neutrino is a 2-conductor device, without a display, with a 4…20 mA current output and is available with two variants of pipe connections, either with a G 1½» union nut for installation with an adapter with a G 1½» external thread sensor connection or with a G ¾» external thread for screwing into an adapter with a G ¾» internal thread sensor connection. The device type 8222 converts the measuring signal, shows different values in different measuring units in the ELEMENT standard device (if display is installed) and calculates the output signals, which are transferred in the ELEMENT standard device via one or two M12 plug connections or in the ELEMENT neutrino version via an M12 plug connection or on a terminal strip via a cable gland.
Thus, due to the measurement device’s design, Bürkert has simplified installation and maintenance work. Device type 8222 is available in two variants: The first one, the so-called ELEMENT standard is proposed either with three adjustable outputs (two digital outputs and one analogue output) or with four adjustable outputs (two digital and two analogue) and can be equipped with a display. The display is only necessary for start-up, configuration (e.g. selection pH/ORP measurement, measurement range, units, calibration, thresholds, etc) or as a display of process values. The second, the so-called ELEMENT neutrino is a 2-conductor device, without a display, with a 4…20 mA current output and is available with two variants of pipe connections, either with a G 1½» union nut for installation with an adapter with a G 1½» external thread sensor connection or with a G ¾» external thread for screwing into an adapter with a G ¾» internal thread sensor connection. The device type 8222 converts the measuring signal, shows different values in different measuring units in the ELEMENT standard device (if display is installed) and calculates the output signals, which are transferred in the ELEMENT standard device via one or two M12 plug connections or in the ELEMENT neutrino version via an M12 plug connection or on a terminal strip via a cable gland.
- Perfect for clean water and slightly concentrated liquids
- Compact measurement device for direct connection to PLC
- Parameterisation, calibration and transfer of parameterisation data all possible thanks to a removable display/configuration module
- Simulation of process values for diagnostics
- Universal process connection, three different cell constants to cover a wide range of applications such as reverse osmosis
Для корректного подбора продукта ознакомьтесь с техническими параметрами, графическими изображениями, схемами и инструкциями по применению, указанными в техническом описании.
Теплопроводность
Содержание:
Теплопроводность
- Теплопроводность В следующей главе 4 описываются физические явления, физические законы, физические свойства и их математические формулировки.
 Эти знания необходимы при изучении процесса теплопроводности. Тепловой поток твердого тела определяется только его теплопроводностью, но в жидкостях и газах процессы теплопроводности, конвекции и теплового излучения действуют одновременно.
Эти знания необходимы при изучении процесса теплопроводности. Тепловой поток твердого тела определяется только его теплопроводностью, но в жидкостях и газах процессы теплопроводности, конвекции и теплового излучения действуют одновременно.
Наибольшее внимание уделяется рассмотрению всех твердых тел («предыдущие рассуждения и результаты задач, рассмотренных в предыдущей главе о теплопроводности, относятся ко всем твердым телам. Теплопроводность (также относится к жидкостям и газам. Исследование теплопроводности твердых тел следует разделить на 4 отдельных раздела.1) Теория теплопроводности и уравнение теплопроводности, 2)теплопроводность в стационарных условиях, 3)теплопроводность в нестационарных условиях, 4) теплопроводность при движении границы.
Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости. Людмила Фирмаль
Эти единицы выбираются произвольно и помогают систематизировать представленный материал. Теплопроводность с макроскопической, феноменологической точки зрения легко понять без микроскопического представления явлений тепловыделения в твердых телах. Тем не менее, не следует считать, что физика твердого тела не играет никакой роли, поскольку эта наука также имеет future. To глубоко понимая науку о тепломассообмене, необходимо обладать всесторонними знаниями как микроскопических, так и макроскопических перспектив.
Теплопроводность с макроскопической, феноменологической точки зрения легко понять без микроскопического представления явлений тепловыделения в твердых телах. Тем не менее, не следует считать, что физика твердого тела не играет никакой роли, поскольку эта наука также имеет future. To глубоко понимая науку о тепломассообмене, необходимо обладать всесторонними знаниями как микроскопических, так и макроскопических перспектив.
- Его следует рассматривать на основе макроскопических . При таком подходе к решению задачи физические понятия легко распознаются, но математическое представление таких понятий, как температурное поле, интенсивность теплового потока и температурно-временная зависимость, обычно очень сложное. Вы столкнетесь с чисто математическими трудностями, но это не значит, что материал, представленный в книге, переполнен ими. Читатель Carslow and Jaeger (L. 5) в отличной книге вы найдете более сложные задачи и задачи о граничных условиях.
За исключением 1 или 2 случаев, теплопроводность считается независимой от температуры. Такие допущения не только упрощают математическое описание, но и являются приемлемой аппроксимацией 3 решений различных физических задач в случае малых флуктуаций температуры. При решении задач, связанных с химическими реакциями или фазовыми переходами, нельзя игнорировать температурную зависимость.
Такие допущения не только упрощают математическое описание, но и являются приемлемой аппроксимацией 3 решений различных физических задач в случае малых флуктуаций температуры. При решении задач, связанных с химическими реакциями или фазовыми переходами, нельзя игнорировать температурную зависимость.
В газах коэффициент теплопроводности может быть найден по приближённой формуле. Людмила Фирмаль
Поэтому при выборе физической константы необходимо досконально разобраться в каждой поставленной задаче с точки зрения физики. Обычно задача теплопроводности влияет на конвекцию или лучистый теплообмен, если установлены соответствующие граничные условия. Коэффициент теплопередачи считается известным, если учитывать конвективный теплообмен. Сущность коэффициента теплопередачи и методика его определения установлены в главе о конвективном теплопередаче.
Смотрите также:
Теплопроводность рекламы / Хабр
Хочу представить вашему вниманию небольшой набросок.
Здесь будет показано, как, используя уравнения физики, можно описать некоторые социальные механизмы.
В качестве первого примера — рассмотрим распространение информации о продукте после рекламной кампании.
В общем случае, формат рекламного носителя не важен, но для простоты будем считать, что это видеоролик.
Пусть Cx — множество всех возможных потребителей товаров, а x — некоторый потребитель.
На Cx задана функция L(x1, x2) — разность количества социальных связей между x1 и x2.
Чем больше у человека связей, тем больше информации передается от него, к его знакомым.
Пусть L(x1, x2) — непрерывна, т.е. одинокий интроверт не дружит с известным рок-музыкантом.
На Cx также задана функция u(x) — время, через которое x купит товар с вероятностью 0.5
(мы считаем, что в этом мире, человек рано или поздно купит всё что угодно).
Функция задана в виде u(x) = max(f(x), Ax), где Ax — уникальный параметр потребителя,
на который реклама воздействовать не в силах. Брутальный спортсмен будет откладывать
Брутальный спортсмен будет откладывать
покупку мулине максимально долго.
Тогда реклама — это процесс охлаждения, т.е. снижение значения u(x) на некотором подмножестве Cx (таргетинг).
Через некоторое время после прекращения рекламы, u(x) сглаживается.
Действие рекламной кампании снижается после её завершения, от неё остаётся только след.
Воспользуемся уравнением теплопроводности (заглавная картинка).
Интересное свойство уравнения заключается в том, что для некоторой окрестности x,
значение u(x) либо имело минимум в прошлом, либо минимум находится на границе окрестности
в настоящий момент (следует из закона сохранения энергии).
Рекламная кампания может быть сориентирована на необходимый эффект.
Если проводить общее охлаждение системы, то u(x) снизится в у всех потребителей одновременно.
Силы воздействия (рекламных ресурсов) может не хватить на долгий захват внимания.
Это значит, что многие люди получат сильный импульс совершить покупку, но вскоре это желание
пройдет и мысли переключатся на что-то новое, если кампания не будет продолжена.
В случае более локальной заморозки u(x), так скажем, дожимая вероятных клиентов.
Эффект будет держаться намного сильнее, и реклама будет действовать как бы из прошлого.
Если считать что отсчет времени покупки начинается от первого просмотра рекламы,
то более длительное воздействие выглядит привлекательнее чем больший охват.
Борьба за время клиента выглядит разумной в мире огромной конкуренции товаров конкурентов
и заменителей. Чем дольше потребитель думает о товаре, тем больше продажи компании производителя.
Уравнение теплопроводности
Температурная зависимость электрической и теплопроводности моноволокна серебра — научные доклады
Предметы
- Механическая инженерия
- Nanowires
Аннотация
В этой работе термический и электрический транспорт в отдельной серебряной нанопроволоке охарактеризован до 35 К для глубокого понимания рассеяния электронов, вызванного сильным структурным дефектом. Результаты показывают, что при комнатной температуре удельное электрическое сопротивление увеличивается примерно в 4 раза по сравнению с объемным серебром. Температура Дебая (151 K) серебряной нанопроволоки на 36% ниже, чем у (235 K) объемного серебра, что подтверждает сильное размягчение фононов. При комнатной температуре теплопроводность снижается на 55% по сравнению с объемным серебром. Это снижение становится больше, когда температура понижается. Для объяснения противоположных тенденций теплопроводности ( κ ) ~ температуры ( Т ) нанопроволоки серебра и объемного серебра, единое тепловое сопротивление (
Результаты показывают, что при комнатной температуре удельное электрическое сопротивление увеличивается примерно в 4 раза по сравнению с объемным серебром. Температура Дебая (151 K) серебряной нанопроволоки на 36% ниже, чем у (235 K) объемного серебра, что подтверждает сильное размягчение фононов. При комнатной температуре теплопроводность снижается на 55% по сравнению с объемным серебром. Это снижение становится больше, когда температура понижается. Для объяснения противоположных тенденций теплопроводности ( κ ) ~ температуры ( Т ) нанопроволоки серебра и объемного серебра, единое тепловое сопротивление (
) используется для выяснения механизма рассеяния электронов. Большой остаточный Θ наблюдается для серебряной нанопроволоки, в то время как остаточный объем серебра почти равен нулю. Такой же
Тенденция ~ T предполагает, что серебряная нанопроволока и объемное серебро имеют одинаковый механизм фонон-электронного рассеяния для теплового транспорта. Благодаря фононному переносу энергии электронов через границы зерен число Лоренца в нанопроволоке серебра оказывается намного больше, чем у объемного серебра, и уменьшается с понижением температуры.
Вступление
В последнее время серебряная нанопроволока привлекла значительное внимание благодаря ее огромным возможностям для таких применений, как гибкий сенсорный экран, солнечные элементы и прозрачные электроды 1, 2, 3, 4, 5 . Для проектирования и оптимизации этих применений тепловые и электрические свойства отдельной нанопроволоки серебра являются критическими и фундаментальными, но о них редко сообщается. До настоящего времени электрические свойства нанопроволоки, особенно инертных металлических нанопроволок и жгутов нанопроволоки, не сложно измерить 6, 7, = 15 нм: Применимость теоремы Блоха-Грюнайзена.Phys.Rev. B 74, 035426 (2006). «Href = / article / srep10718 # ref8 aria-label =» Reference 8 «data-track = щелкните data-track-label = link> 8, 9 Но только для характеристики тепловых свойств было сообщено о нескольких экспериментальных исследованиях из-за трудностей с подвешиванием одной нанопроволоки, снижением контактного сопротивления и точными измерениями температуры. Оу и др. исследовали теплопроводность и электрическую проводимость одиночной нанопроволоки никеля от 15 до 300 К. Его число Лоренца больше значения Зоммерфельда с температурой выше 75 К и быстро снижается, когда температура опускается ниже 75 К 10. Экспериментальные результаты Фелькляйна и др. показали теплопроводность и электрическую проводимость одиночной нанопроволоки Pt от 260 К до 360 К. Лоренц число было меньше, чем значение Зоммерфельда, в то время как причины их работы неясны 11. Стоянович и др. измерили теплопроводность решеток из нанопроволок из алюминия вместо одной нанопроволоки при комнатной температуре. f Эти массивы нанопроволок были измерены как 105–145 Вт / К · м, когда ширина нанопроволоки составляла от 75 до 150 нм. Фононный вклад в общую теплопроводность составил около 21 Вт / К · м 12 .
Оу и др. исследовали теплопроводность и электрическую проводимость одиночной нанопроволоки никеля от 15 до 300 К. Его число Лоренца больше значения Зоммерфельда с температурой выше 75 К и быстро снижается, когда температура опускается ниже 75 К 10. Экспериментальные результаты Фелькляйна и др. показали теплопроводность и электрическую проводимость одиночной нанопроволоки Pt от 260 К до 360 К. Лоренц число было меньше, чем значение Зоммерфельда, в то время как причины их работы неясны 11. Стоянович и др. измерили теплопроводность решеток из нанопроволок из алюминия вместо одной нанопроволоки при комнатной температуре. f Эти массивы нанопроволок были измерены как 105–145 Вт / К · м, когда ширина нанопроволоки составляла от 75 до 150 нм. Фононный вклад в общую теплопроводность составил около 21 Вт / К · м 12 .
Для металлических наноструктур, когда размер системы приближается или меньше, чем длина свободного пробега объемного электрона, граница и поверхность зерна становятся важными источниками рассеяния, которые ограничивают длину свободного пробега электрона и впоследствии уменьшают тепловую и электрическую проводимость. Рассеянные электроны не могут проходить через границу зерна, но могут обмениваться энергией с локальными фононами посредством электрон-фононного рассеяния. Фононы могут переноситься через границу зерна легче, чем электроны. Следовательно, часть энергии рассеянных электронов передается через границу зерна через фононы, а заряд рассеянных электронов отражается обратно. Это приводит к значительному снижению электропроводности и снижению теплопроводности. Результирующие числа Лоренца металлических наноструктур больше, чем значение Зоммерфельда. Большие числа Лоренца наблюдаются в большинстве экспериментальных исследований 10, 13, 14, 15, 16, 17, 18 . Но объемные числа Лоренца также наблюдаются экспериментально для металлических нанопленок, нанесенных на биоматериалы, такие как волокна молочая и шелкопряда. Это объясняется туннелированием и прыжком электронов через насыщенные молекулы или / и сопряженные молекулы в этих субстратах биоматериала 19, 20, 21 . Работа Бид и соавт.
Рассеянные электроны не могут проходить через границу зерна, но могут обмениваться энергией с локальными фононами посредством электрон-фононного рассеяния. Фононы могут переноситься через границу зерна легче, чем электроны. Следовательно, часть энергии рассеянных электронов передается через границу зерна через фононы, а заряд рассеянных электронов отражается обратно. Это приводит к значительному снижению электропроводности и снижению теплопроводности. Результирующие числа Лоренца металлических наноструктур больше, чем значение Зоммерфельда. Большие числа Лоренца наблюдаются в большинстве экспериментальных исследований 10, 13, 14, 15, 16, 17, 18 . Но объемные числа Лоренца также наблюдаются экспериментально для металлических нанопленок, нанесенных на биоматериалы, такие как волокна молочая и шелкопряда. Это объясняется туннелированием и прыжком электронов через насыщенные молекулы или / и сопряженные молекулы в этих субстратах биоматериала 19, 20, 21 . Работа Бид и соавт. = 15 нм: применимость теоремы Блоха-Грунейзена.Phys.Редакция B 74, 035426 (2006). «Href = / Articles / srep10718 # ref8 aria-label =» Ссылка 8 «data-track = click data-track-label = link> 8 посвящена электрическим свойствам массивов нанопроволок серебра вместо одной нанопроволоки. Они измерили электрическое сопротивление массива нанопроволоки, не зная площади поперечного сечения. Удельное электрическое сопротивление получено, если предположить, что нанопровод имеет одинаковый наклон электрического сопротивления по отношению к температуре с объемным серебром (тот же электрон-фононный связь). В работе Койды и др. 22, опубликованной совсем недавно, основное внимание уделяется термоэлектрическим свойствам монокристаллических нанопроводов серебра. В этой статье наша работа фокусируется на механизме рассеяния электронов в отдельных поликристаллических нанопроводах Ag и его влиянии на тепловые и электрические Основным структурным рассеянием в их работе является поверхностное рассеяние, в то время как в нашей работе рассеяние на границах зерен.
= 15 нм: применимость теоремы Блоха-Грунейзена.Phys.Редакция B 74, 035426 (2006). «Href = / Articles / srep10718 # ref8 aria-label =» Ссылка 8 «data-track = click data-track-label = link> 8 посвящена электрическим свойствам массивов нанопроволок серебра вместо одной нанопроволоки. Они измерили электрическое сопротивление массива нанопроволоки, не зная площади поперечного сечения. Удельное электрическое сопротивление получено, если предположить, что нанопровод имеет одинаковый наклон электрического сопротивления по отношению к температуре с объемным серебром (тот же электрон-фононный связь). В работе Койды и др. 22, опубликованной совсем недавно, основное внимание уделяется термоэлектрическим свойствам монокристаллических нанопроводов серебра. В этой статье наша работа фокусируется на механизме рассеяния электронов в отдельных поликристаллических нанопроводах Ag и его влиянии на тепловые и электрические Основным структурным рассеянием в их работе является поверхностное рассеяние, в то время как в нашей работе рассеяние на границах зерен. В нашей работе введено единое тепловое сопротивление, чтобы объяснить Различные тренды температурно-зависимой теплопроводности нанопроволоки и объемного серебра. Теплопроводность в нашей работе близка к теплопроводности Kojda et al. 22 Но наше удельное электрическое сопротивление намного больше, чем в работе Kojda et al. Это приводит к большому числу Лоренца в нашей выборке, что можно объяснить фонон-опосредованным переносом электронов через границу зерна. В нашей работе также наблюдается смягчение фононов и усиление электрон-фононного взаимодействия.
В нашей работе введено единое тепловое сопротивление, чтобы объяснить Различные тренды температурно-зависимой теплопроводности нанопроволоки и объемного серебра. Теплопроводность в нашей работе близка к теплопроводности Kojda et al. 22 Но наше удельное электрическое сопротивление намного больше, чем в работе Kojda et al. Это приводит к большому числу Лоренца в нашей выборке, что можно объяснить фонон-опосредованным переносом электронов через границу зерна. В нашей работе также наблюдается смягчение фононов и усиление электрон-фононного взаимодействия.
В этой работе одна серебряная нанопроволока подвешена на двух электродах, и электронно-лучевое осаждение (EBID) используется для нанесения Pt-подушек на концах нанопроволоки для подавления электрических и термических контактных сопротивлений. Вид сверху и вид сбоку взвешенных нанопроволок серебра и атомно-силового микроскопа (АСМ) фигуры поверхности нанопроволоки показаны на рис. 1. Рентгеновская дифракция (XRD) используется для характеристики структуры нанонитей серебра и XRD. Рисунок показан на рис. 2. Более подробную информацию о пробоподготовке и структуре можно найти в разделе «Методы». Тепловые и электрические свойства одиночной суспендированной нанопроволоки серебра характеризуются электротермическим методом в стационарном состоянии от комнатной температуры до 35 К. Также определяется зависящее от температуры число Лоренца. Теплопроводность и электропроводность нанопроволоки сравниваются с их объемным аналогом, и для выявления механизма рассеяния используется единое тепловое сопротивление.
Рисунок показан на рис. 2. Более подробную информацию о пробоподготовке и структуре можно найти в разделе «Методы». Тепловые и электрические свойства одиночной суспендированной нанопроволоки серебра характеризуются электротермическим методом в стационарном состоянии от комнатной температуры до 35 К. Также определяется зависящее от температуры число Лоренца. Теплопроводность и электропроводность нанопроволоки сравниваются с их объемным аналогом, и для выявления механизма рассеяния используется единое тепловое сопротивление.
( а ) Принципиальная схема электродов и суспендированной серебряной нанопроволоки (вид сверху). ( б ) СЭМ-изображение электродов и взвешенной серебряной нанопроволоки (вид сверху). ( в ) Принципиальная схема электродов и суспендированной серебряной нанопроволоки (вид сбоку). ( d ) СЭМ-изображение электродов и взвешенной серебряной нанопроволоки (вид сбоку). ( e ) АСМ-изображение серебряных нанонитей, диспергированных на стеклянной подложке для измерения шероховатости. ( f ) Точно отсканированное AFM-изображение выбранной области 160 × 160 нм 2, обозначенной в ( e ) красным квадратом. Профили поперечного сечения в направлениях x (синий) и y (красный) показаны на верхней и правой сторонах контурного графика соответственно.
( f ) Точно отсканированное AFM-изображение выбранной области 160 × 160 нм 2, обозначенной в ( e ) красным квадратом. Профили поперечного сечения в направлениях x (синий) и y (красный) показаны на верхней и правой сторонах контурного графика соответственно.
Изображение в полном размере
Согласно результатам XRD, интервал плоскости решетки для пиков (111), (220) и (311) составляет 2, 3616, 1, 4518 и 1, 2287, соответственно. Соответствующая постоянная решетки может быть рассчитана как 4, 09 Å, 4, 11 Å и 4, 08 Å для нанопроволоки в нашей работе. Константа решетки объемного серебра составляет 4, 09 Å. Это подтверждает структуру FCC кристалла серебра.
Изображение в полном размере
Результаты
Электропроводность
Набор небольших электрических токов ( I ) в диапазоне от 0, 1 мА до 0, 5 мА был приложен к образцу. Благодаря джоулевому нагреву температура и сопротивление образца увеличиваются. Электрическое сопротивление без джоулевого нагрева может быть получено путем линейной подгонки измеренного сопротивления к I 2 и его экстраполяции к пределу нулевого тока. Более подробную информацию можно найти в разделе «Методы». Зная геометрические размеры пленок, можно рассчитать удельное электрическое сопротивление. Зависимое от температуры удельное электрическое сопротивление показано на рис. 3 и соответствует формуле Блоха-Грюнайзена. Для сравнения, зависящее от температуры удельное электрическое сопротивление объемного серебра также показано на рис. 3 и соответствует формуле Блоха-Грюнайзена 23 . Кроме того, электрическое сопротивление серебряной нанопроволоки также показано на рис. 3. Согласно правилу Маттиссена и теории Блоха-Грюнайзена 24, удельное электрическое сопротивление может быть выражено как
Более подробную информацию можно найти в разделе «Методы». Зная геометрические размеры пленок, можно рассчитать удельное электрическое сопротивление. Зависимое от температуры удельное электрическое сопротивление показано на рис. 3 и соответствует формуле Блоха-Грюнайзена. Для сравнения, зависящее от температуры удельное электрическое сопротивление объемного серебра также показано на рис. 3 и соответствует формуле Блоха-Грюнайзена 23 . Кроме того, электрическое сопротивление серебряной нанопроволоки также показано на рис. 3. Согласно правилу Маттиссена и теории Блоха-Грюнайзена 24, удельное электрическое сопротивление может быть выражено как
,
является остаточным удельным сопротивлением, которое возникает в результате структурного рассеяния, такого как рассеяние на границах зерен, рассеивание примесей и поверхностное рассеяние Он практически не зависит от температуры, и его значение представляет собой удельное электрическое сопротивление, когда температура приближается к нулю. зависит от температуры удельное электрическое сопротивление, вызванное рассеянием фононов, и может быть выражено как
зависит от температуры удельное электрическое сопротивление, вызванное рассеянием фононов, и может быть выражено как
Они оснащены формулой Блоха-Грюнайзена. Зависимое от температуры электрическое сопротивление серебряной нанопроволоки также показано с координатой справа.
Изображение в полном размере
где
параметр электрон-фононной связи.
температура Дебая и
обычно принимает значение 5 для немагнитных металлов = 15 нм: применимость теоремы Блоха-Грюнайзена.Phys.Rev. B 74, 035426 (2006). «Href = / article / srep10718 # ref8 aria-label =» Reference 8 «data-track = щелкнуть data-track-label = ссылка> 8. Посредством подбора экспериментальных данных Дебай температура и константа электрон-фононной связи могут быть получены соответственно. Температура Дебая нанопроволоки серебра и объемного серебра составляет 151 К и 235 К, а константа электрон-фононной связи нанопроволоки серебра и объемного серебра составляет 9, 90 × 10 — 8 Ом · м и 5, 24 × 10 −8 Ом · м. Превосходные аппроксимирующие кривые показывают, что фонон-электронное рассеяние доминирует над температурно-зависимой частью удельного электрического сопротивления. Большая константа электрон-фононного взаимодействия серебряной нанопроволоки указывает на усиленный электрон -фононное взаимодействие, которое также наблюдается в ультратонких пленках меди из-за шероховатости поверхности 25. В данной работе поверхность нанопроволоки сканируется с помощью атомно-силового микроскопа. Результаты показывают, что шероховатость поверхности составляет ± 2 нм. Подробная информация о сканировании АСМ можно найти я В разделе Методы. Эта шероховатость поверхности в сочетании с внутренними поверхностями, такими как границы зерен, ответственна за усиленное электрон-фононное взаимодействие.
Превосходные аппроксимирующие кривые показывают, что фонон-электронное рассеяние доминирует над температурно-зависимой частью удельного электрического сопротивления. Большая константа электрон-фононного взаимодействия серебряной нанопроволоки указывает на усиленный электрон -фононное взаимодействие, которое также наблюдается в ультратонких пленках меди из-за шероховатости поверхности 25. В данной работе поверхность нанопроволоки сканируется с помощью атомно-силового микроскопа. Результаты показывают, что шероховатость поверхности составляет ± 2 нм. Подробная информация о сканировании АСМ можно найти я В разделе Методы. Эта шероховатость поверхности в сочетании с внутренними поверхностями, такими как границы зерен, ответственна за усиленное электрон-фононное взаимодействие.
Из рисунка 3 видно, что остаточное электрическое сопротивление объемного серебра почти равно нулю (1 × 10 -11 Ом · м), тогда как удельное сопротивление серебряной нанопроволоки намного больше (3, 25 × 10 -8 Ом · м). Удельное электрическое сопротивление нанопроволоки серебра при низких температурах более чем на три порядка больше, чем у объемного серебра. Это связано с интенсивным структурным рассеянием электронов, таким как зернограничное рассеяние и поверхностное рассеяние. Поскольку при низких температурах фононное рассеяние уменьшается, только структурное рассеяние способствует препятствующему переносу электронов. Удельное электрическое сопротивление серебряной нанопроволоки при комнатной температуре в пять раз больше аналога объемного серебра. Это связано с совместным эффектом различного структурного и фононного рассеяния. Для объемного серебра при комнатной температуре доминирует фонон-электронное рассеяние. Но для серебряной нанопроволоки как фононное рассеяние, так и структурное рассеяние вносят вклад в большое электрическое удельное сопротивление.
Удельное электрическое сопротивление нанопроволоки серебра при низких температурах более чем на три порядка больше, чем у объемного серебра. Это связано с интенсивным структурным рассеянием электронов, таким как зернограничное рассеяние и поверхностное рассеяние. Поскольку при низких температурах фононное рассеяние уменьшается, только структурное рассеяние способствует препятствующему переносу электронов. Удельное электрическое сопротивление серебряной нанопроволоки при комнатной температуре в пять раз больше аналога объемного серебра. Это связано с совместным эффектом различного структурного и фононного рассеяния. Для объемного серебра при комнатной температуре доминирует фонон-электронное рассеяние. Но для серебряной нанопроволоки как фононное рассеяние, так и структурное рассеяние вносят вклад в большое электрическое удельное сопротивление.
Из рисунка 3 видно, что удельное электрическое сопротивление изменяется линейно с температурой, когда температура не очень низкая. Наклон удельного электросопротивления серебряной нанопроволоки к температуре (1, 68 × 10 -10 Ом м / К) намного больше, чем у объемного серебра (6, 11 × 10 -11 Ом м / К). Подобное явление также наблюдается в сверхрешетках Co / Ni 26 . Кроме того, удельное электрическое сопротивление серебряной нанопроволоки и объемного серебра хорошо согласуется с теорией Блоха-Грюнайзена. Результаты подгонки показывают, что температура Дебая нанопроволоки серебра (151 К) намного меньше, чем у объемного серебра (235 К). Пониженная температура Дебая обусловлена размягчением поверхностных фононов. Недостающие связи атомов на поверхностях, включая внутренние поверхности, такие как границы зерен, приводят к изменению фононных мод и частоты колебаний. Эти изменения приводят к снижению температуры Дебая 6, 7, 26, 27, 28 . В заключение следует отметить, что усиленное электрон-фононное взаимодействие и пониженная температура Дебая приводят к большому наклону электросопротивления к температуре.
Подобное явление также наблюдается в сверхрешетках Co / Ni 26 . Кроме того, удельное электрическое сопротивление серебряной нанопроволоки и объемного серебра хорошо согласуется с теорией Блоха-Грюнайзена. Результаты подгонки показывают, что температура Дебая нанопроволоки серебра (151 К) намного меньше, чем у объемного серебра (235 К). Пониженная температура Дебая обусловлена размягчением поверхностных фононов. Недостающие связи атомов на поверхностях, включая внутренние поверхности, такие как границы зерен, приводят к изменению фононных мод и частоты колебаний. Эти изменения приводят к снижению температуры Дебая 6, 7, 26, 27, 28 . В заключение следует отметить, что усиленное электрон-фононное взаимодействие и пониженная температура Дебая приводят к большому наклону электросопротивления к температуре.
Электропроводность серебра
, Здесь m и e — масса и заряд электрона;
время релаксации, а n плотность электронов. Когда температура приближается к нулю, эффект рассеяния фононов будет уменьшаться, а структурные рассеяния доминируют при переносе электронов. Остаточное удельное сопротивление может быть записано как
, Электронная плотность серебра составляет 5, 85 × 10 28 м −329 . Время релаксации
1, 87 × 10 −14 с. Скорость Ферми для серебра составляет 1, 39 × 10 6 м / с 29 . Таким образом, длина свободного пробега электрона, вызванная структурным рассеянием на основе остаточного электрического сопротивления, составляет 26 нм. Эта длина характеристики близка к размеру кристалла (21 нм) в направлении (311). Направление переноса электронов в нашей работе — вдоль осевого направления серебряной нанопроволоки, мы можем заключить, что осевое направление — вдоль (311).
Остаточное удельное сопротивление может быть записано как
, Электронная плотность серебра составляет 5, 85 × 10 28 м −329 . Время релаксации
1, 87 × 10 −14 с. Скорость Ферми для серебра составляет 1, 39 × 10 6 м / с 29 . Таким образом, длина свободного пробега электрона, вызванная структурным рассеянием на основе остаточного электрического сопротивления, составляет 26 нм. Эта длина характеристики близка к размеру кристалла (21 нм) в направлении (311). Направление переноса электронов в нашей работе — вдоль осевого направления серебряной нанопроволоки, мы можем заключить, что осевое направление — вдоль (311).
Теплопроводность серебряной нанопроволоки
При подаче различных электрических токов температура нанопроволоки будет изменяться из-за джоулевого нагрева. Изменение температуры приведет к изменению электрического сопротивления. После построения модели теплопередачи теплопроводность может быть выведена на основании отношения между приложенными токами и сопротивлениями. Более подробную информацию можно найти в разделе методов. Измеренная зависящая от температуры теплопроводность нанопроволоки серебра показана и сравнена с объемными значениями на рис. 4 30 . Как видно из рис. 4, теплопроводность серебряной нанопроволоки при 290 К уменьшается на 55% по сравнению с соответствующим объемным значением. Помимо фонон-электронного рассеяния, подобного рассеянию в объемном серебре, экстенсивное структурное рассеяние, такое как межзеренная граница и поверхностное рассеяние, также способствует этому уменьшению. Эти рассеяния ограничивают длину свободного пробега электронов и, как следствие, приводят к снижению теплопроводности. Измеренная теплопроводность одиночной нанопроволоки серебра близка к значению в [1]. 22 При понижении температуры теплопроводность серебряной нанопроволоки ведет себя совершенно иначе, чем у объемного аналога. Теплопроводность нанопроволоки серебра уменьшается с понижением температуры, а теплопроводность объемного серебра увеличивается с понижением температуры.
Более подробную информацию можно найти в разделе методов. Измеренная зависящая от температуры теплопроводность нанопроволоки серебра показана и сравнена с объемными значениями на рис. 4 30 . Как видно из рис. 4, теплопроводность серебряной нанопроволоки при 290 К уменьшается на 55% по сравнению с соответствующим объемным значением. Помимо фонон-электронного рассеяния, подобного рассеянию в объемном серебре, экстенсивное структурное рассеяние, такое как межзеренная граница и поверхностное рассеяние, также способствует этому уменьшению. Эти рассеяния ограничивают длину свободного пробега электронов и, как следствие, приводят к снижению теплопроводности. Измеренная теплопроводность одиночной нанопроволоки серебра близка к значению в [1]. 22 При понижении температуры теплопроводность серебряной нанопроволоки ведет себя совершенно иначе, чем у объемного аналога. Теплопроводность нанопроволоки серебра уменьшается с понижением температуры, а теплопроводность объемного серебра увеличивается с понижением температуры. В частности, для объемного серебра теплопроводность увеличивается более чем в десять раз, когда температура снижается до 20 К. Но для нанопроволоки серебра теплопроводность уменьшается на 79% при снижении температуры до 35 К. Примечательно, что при низких температуры, почти на два порядка уменьшение теплопроводности наблюдается для нанопроволоки серебра по сравнению с объемным серебром.
В частности, для объемного серебра теплопроводность увеличивается более чем в десять раз, когда температура снижается до 20 К. Но для нанопроволоки серебра теплопроводность уменьшается на 79% при снижении температуры до 35 К. Примечательно, что при низких температуры, почти на два порядка уменьшение теплопроводности наблюдается для нанопроволоки серебра по сравнению с объемным серебром.
Линии, соединяющие экспериментальные данные, используются только для наведения глаз. На вставке показана линейная зависимость между электрическим сопротивлением и квадратом электрического тока при 290 К во время измерения теплопроводности нанопроволоки серебра. Линия подгонки R = 53, 15 + 1, 833 × I 2 .
Изображение в полном размере
Для объемного серебра структурные рассеяния редки, и фононное рассеяние доминирует над электронным транспортом. Когда температура понижается, фононы коротких волн замерзают. Количество возбужденных фононов, которые связаны с рассеянием фононов на электронах, уменьшается с понижением температуры. Вот почему теплопроводность объемного серебра увеличивается с понижением температуры. Но для серебряной нанопроволоки как структурное рассеяние, так и фононное рассеяние играют важную роль в переносе электронов. Когда температура понижается, фононное рассеяние уменьшается, но структурные рассеяния все еще существуют и доминируют в электронном транспорте. Кроме того, теплоемкость электронов уменьшается линейно с температурой, когда температура не слишком высока. Вот почему теплопроводность серебряной нанопроволоки уменьшается с понижением температуры. Это явление также наблюдалось в никелевой нанопроволоке 10, золотых и платиновых нанопленках 13, 31, 32 и сплавах 33 .
Вот почему теплопроводность объемного серебра увеличивается с понижением температуры. Но для серебряной нанопроволоки как структурное рассеяние, так и фононное рассеяние играют важную роль в переносе электронов. Когда температура понижается, фононное рассеяние уменьшается, но структурные рассеяния все еще существуют и доминируют в электронном транспорте. Кроме того, теплоемкость электронов уменьшается линейно с температурой, когда температура не слишком высока. Вот почему теплопроводность серебряной нанопроволоки уменьшается с понижением температуры. Это явление также наблюдалось в никелевой нанопроволоке 10, золотых и платиновых нанопленках 13, 31, 32 и сплавах 33 .
Здесь дается объяснение аномальной зависящей от температуры теплопроводности этих наноструктур. Теплопроводность может быть записана как
, Здесь C v — объемная теплоемкость электрона;
скорость Ферми и
это время релаксации. Объемная теплоемкость электронов изменяется линейно с температурой, когда температура не слишком высокая (
). Вот
является константой (0, 646 мДж / (K 2 · моль) для серебра). Скорость Ферми серебра составляет 1, 39 × 10 6 м / с, а его электронная плотность составляет 5, 85 × 10 28 м −329 . Температура в теплоемкости электронов затмевает физику механизма рассеяния за изменением теплопроводности в зависимости от температуры. Вместо того, чтобы использовать традиционное тепловое сопротивление, здесь мы используем унифицированное тепловое сопротивление
объяснить теплопроводность наноструктур. Унифицированное тепловое сопротивление связано исключительно со временем релаксации электронов, как показано ниже:
Вот
является константой (0, 646 мДж / (K 2 · моль) для серебра). Скорость Ферми серебра составляет 1, 39 × 10 6 м / с, а его электронная плотность составляет 5, 85 × 10 28 м −329 . Температура в теплоемкости электронов затмевает физику механизма рассеяния за изменением теплопроводности в зависимости от температуры. Вместо того, чтобы использовать традиционное тепловое сопротивление, здесь мы используем унифицированное тепловое сопротивление
объяснить теплопроводность наноструктур. Унифицированное тепловое сопротивление связано исключительно со временем релаксации электронов, как показано ниже:
Согласно правилу Маттиссена, единую температуропроводность можно разделить на две части: часть рассеяния фононов и часть рассеяния структуры, как показано ниже:
Избавляясь от влияния температуры на удельное тепловое сопротивление из-за теплоемкости электронов, единое тепловое удельное сопротивление извлекает влияние температуры на механизм рассеяния электронов. Зависимое от температуры единое термическое удельное сопротивление нанопроволоки серебра и объемного серебра изображено на рис. 5. Как видим, единое термическое удельное сопротивление нанопроволоки серебра (
) и основная масса серебра (
) разделяет ту же тенденцию при изменении температуры. Две линии параллельны, когда температура не слишком низкая. Когда температура превышает 60 K, наклон единого изменения удельного теплового сопротивления нанопроволоки серебра по отношению к температуре составляет 2, 57 × 10 -3 м · К / Вт, а у объемного серебра — 2, 41 × 10 -3 м · К / Вт. Склоны почти одинаковые. Это связано с тем, что число возбужденных фононов изменяется линейно с температурой, когда температура не слишком низкая. Это подтверждает, что серебряная нанопроволока и объемное серебро имеют сходный механизм фонон-электронного рассеяния (
) но имеют разные структурные рассеяния (
). Различное структурное рассеяние приводит к различным остаточным значениям (
) единого термического удельного сопротивления.
Зависимое от температуры единое термическое удельное сопротивление нанопроволоки серебра и объемного серебра изображено на рис. 5. Как видим, единое термическое удельное сопротивление нанопроволоки серебра (
) и основная масса серебра (
) разделяет ту же тенденцию при изменении температуры. Две линии параллельны, когда температура не слишком низкая. Когда температура превышает 60 K, наклон единого изменения удельного теплового сопротивления нанопроволоки серебра по отношению к температуре составляет 2, 57 × 10 -3 м · К / Вт, а у объемного серебра — 2, 41 × 10 -3 м · К / Вт. Склоны почти одинаковые. Это связано с тем, что число возбужденных фононов изменяется линейно с температурой, когда температура не слишком низкая. Это подтверждает, что серебряная нанопроволока и объемное серебро имеют сходный механизм фонон-электронного рассеяния (
) но имеют разные структурные рассеяния (
). Различное структурное рассеяние приводит к различным остаточным значениям (
) единого термического удельного сопротивления. Для объемного серебра остаточное единое термическое удельное сопротивление почти равно нулю, поскольку структурное несовершенство в объемном серебре практически равно нулю. Для серебряной нанопроволоки остаточное унифицированное тепловое сопротивление велико из-за границ зерен и поверхностного рассеяния, которые не зависят от температуры. Это остаточное удельное тепловое сопротивление можно использовать для характеристики структуры нанопроволоки серебра, поскольку фононы замерзают, когда температура приближается к нулю. При низких температурах доминирующее структурное рассеяние не зависит от температуры. Таким образом, аналогично удельному электрическому сопротивлению, остаточное удельное тепловое сопротивление слабо зависит от температуры при низких температурах. Эта тенденция подтверждается значениями теплового удельного сопротивления серебра. Таким образом, мы можем оценить остаточное удельное тепловое сопротивление, используя значение при 30 К. В соответствии с остаточным удельным тепловым сопротивлением (0, 9 м · К 2 / Вт), время релаксации
составляет около 2, 77 × 10 -14 с и длина характеристики (
) составляет 38, 5 нм.
Для объемного серебра остаточное единое термическое удельное сопротивление почти равно нулю, поскольку структурное несовершенство в объемном серебре практически равно нулю. Для серебряной нанопроволоки остаточное унифицированное тепловое сопротивление велико из-за границ зерен и поверхностного рассеяния, которые не зависят от температуры. Это остаточное удельное тепловое сопротивление можно использовать для характеристики структуры нанопроволоки серебра, поскольку фононы замерзают, когда температура приближается к нулю. При низких температурах доминирующее структурное рассеяние не зависит от температуры. Таким образом, аналогично удельному электрическому сопротивлению, остаточное удельное тепловое сопротивление слабо зависит от температуры при низких температурах. Эта тенденция подтверждается значениями теплового удельного сопротивления серебра. Таким образом, мы можем оценить остаточное удельное тепловое сопротивление, используя значение при 30 К. В соответствии с остаточным удельным тепловым сопротивлением (0, 9 м · К 2 / Вт), время релаксации
составляет около 2, 77 × 10 -14 с и длина характеристики (
) составляет 38, 5 нм. Эта длина характеристики (длина свободного пробега электрона, ограниченная структурным несовершенством) включает эффект фонон-опосредованной передачи энергии электронов через границы зерен. Это больше, чем реальный структурный размер кристаллов в серебряной нанопроволоке.
Эта длина характеристики (длина свободного пробега электрона, ограниченная структурным несовершенством) включает эффект фонон-опосредованной передачи энергии электронов через границы зерен. Это больше, чем реальный структурный размер кристаллов в серебряной нанопроволоке.
Когда температура превышает 60 K, наклон единого изменения удельного теплового сопротивления нанопроволоки серебра по отношению к температуре составляет 2, 57 × 10 -3 м · К / Вт, а для объемного серебра — 2, 41 × 10 -3 м · К / Вт.
Изображение в полном размере
Следует отметить, что для нанопроволоки серебра наклон изменения электросопротивления к температуре сильно отличается от его объемного аналога. Но наклон Θ к температуре почти такой же, как у объемного серебра. Один и тот же механизм рассеяния фононов приводит к различным воздействиям на электрические и термические транспортные свойства. Для пленок Ir, нанесенных на нить молочая, мы наблюдали, что ∂Θ / ∂ T и ∂ ρ e / ∂ T для пленки Ir показывают очень похожее отклонение от объемного Ir 19, 34 . Возможными причинами очень большой разницы в теплопроводности и электропроводности серебряных нанонитей являются изменение силы электрон-фононной связи, вызванное структурным беспорядком и эффектом квантового размера, а также изменение заселенности фононов и электронной структуры, что связано с рассеянием на малые и большие углы. 35, 36 . Из-за малого размера нанокристаллов в серебряной нанопроволоке отношение поверхности к объему является большим, и эффект квантового размера становится важным. Низкая координация и неудовлетворенные связи поверхностных атомов приводят к размягчению фононов и изменению электронной структуры. Фононные моды металлических нанокристаллов дискретизируются, что приводит к изменению каналов связи электрон-фононных взаимодействий 35 . Из-за ограничения электронной волновой функции электронные состояния являются дискретными. Плотность состояний и электронная плотность вблизи уровня Ферми уменьшаются. Дискретность уровней энергии электронов также приведет к изменению силы электрон-фононного взаимодействия 36 .
Возможными причинами очень большой разницы в теплопроводности и электропроводности серебряных нанонитей являются изменение силы электрон-фононной связи, вызванное структурным беспорядком и эффектом квантового размера, а также изменение заселенности фононов и электронной структуры, что связано с рассеянием на малые и большие углы. 35, 36 . Из-за малого размера нанокристаллов в серебряной нанопроволоке отношение поверхности к объему является большим, и эффект квантового размера становится важным. Низкая координация и неудовлетворенные связи поверхностных атомов приводят к размягчению фононов и изменению электронной структуры. Фононные моды металлических нанокристаллов дискретизируются, что приводит к изменению каналов связи электрон-фононных взаимодействий 35 . Из-за ограничения электронной волновой функции электронные состояния являются дискретными. Плотность состояний и электронная плотность вблизи уровня Ферми уменьшаются. Дискретность уровней энергии электронов также приведет к изменению силы электрон-фононного взаимодействия 36 . Это подтверждается большой константой электрон-фононного взаимодействия, полученной методом Блоха-Грюнайзена для определения удельного электрического сопротивления серебряной нанопроволоки. Эти изменения приводят к различным реакциям электрического и теплового транспорта на рассеяние фононов.
Это подтверждается большой константой электрон-фононного взаимодействия, полученной методом Блоха-Грюнайзена для определения удельного электрического сопротивления серебряной нанопроволоки. Эти изменения приводят к различным реакциям электрического и теплового транспорта на рассеяние фононов.
Для чистых металлов хорошо задокументировано, что вклад решетки в общую теплопроводность пренебрежимо мал 37 . Но для серебряной нанопроволоки в этой работе общая теплопроводность при низких температурах очень мала. Фононный вклад будет значительным. Здесь в качестве примера мы берем случай при 36 К для оценки верхнего предела решеточной теплопроводности. Удельная теплота серебра при 36 К составляет 64, 65 Дж / (кг К), а плотность составляет 10, 49 × 10 3 кг / м 338 . Скорость звука (2600 м / с) используется для оценки скорости фононов серебра 39 . При низких температурах длина свободного пробега фонон-фононного рассеяния становится очень большой из-за уменьшения плотности фононов. Кроме того, в фонон-фононном рассеянии преобладает N-процесс, который не препятствует тепловому потоку напрямую и вносит небольшой вклад в тепловое сопротивление. Поэтому при низких температурах длина свободного пробега фононов ограничена границами зерен (21 нм). Так что верхний предел теплопроводности ( $config[ads_text16] not found ) рассчитывается как 12, 3 Вт / К · м при 36 К. Средняя длина свободного пробега фононов должна быть меньше 21 нм, поскольку другие рассеяния, такие как электрон-фононное рассеяние и фононное рассеяние на точечных дефектах, также ограничивают длину свободного пробега фононов. Реальная фононная теплопроводность должна быть меньше 12, 3 Вт / К · м при 36 К. Наша измеренная теплопроводность составляет 40, 46 Вт / К · м, поэтому вклад фонона в общую теплопроводность значителен, но электронная теплопроводность все еще доминирует при низких температурах.
Кроме того, в фонон-фононном рассеянии преобладает N-процесс, который не препятствует тепловому потоку напрямую и вносит небольшой вклад в тепловое сопротивление. Поэтому при низких температурах длина свободного пробега фононов ограничена границами зерен (21 нм). Так что верхний предел теплопроводности ( $config[ads_text16] not found ) рассчитывается как 12, 3 Вт / К · м при 36 К. Средняя длина свободного пробега фононов должна быть меньше 21 нм, поскольку другие рассеяния, такие как электрон-фононное рассеяние и фононное рассеяние на точечных дефектах, также ограничивают длину свободного пробега фононов. Реальная фононная теплопроводность должна быть меньше 12, 3 Вт / К · м при 36 К. Наша измеренная теплопроводность составляет 40, 46 Вт / К · м, поэтому вклад фонона в общую теплопроводность значителен, но электронная теплопроводность все еще доминирует при низких температурах.
Изменение числа Лоренца с температурой
После того, как удельное электрическое сопротивление и теплопроводность были получены, можно рассчитать число Лоренца. Но измеренное удельное электрическое сопротивление находится при T 0 (температура без джоулевого нагрева), а измеренная теплопроводность — при T ave (средняя температура во время джоулевого нагрева T ave = ( T 0 + T 1 ) / 2, T 1 является самой высокой температура с джоулевым подогревом). Несмотря на то, что повышение температуры в процессе измерения, а именно разность между T 0 и T 1, очень мало (менее 5 К), мы не можем непосредственно рассчитать число Лоренца. Следовательно, линейная интерполяция использовалась для получения удельного электрического сопротивления на T ave . Тогда число Лоренца в T ave было определено как
Но измеренное удельное электрическое сопротивление находится при T 0 (температура без джоулевого нагрева), а измеренная теплопроводность — при T ave (средняя температура во время джоулевого нагрева T ave = ( T 0 + T 1 ) / 2, T 1 является самой высокой температура с джоулевым подогревом). Несмотря на то, что повышение температуры в процессе измерения, а именно разность между T 0 и T 1, очень мало (менее 5 К), мы не можем непосредственно рассчитать число Лоренца. Следовательно, линейная интерполяция использовалась для получения удельного электрического сопротивления на T ave . Тогда число Лоренца в T ave было определено как
, Аналогично, число Лоренца в каждом T ave может быть определено, и зависящие от температуры числа Лоренца показаны на рис. 6.
На вставке показаны зависимые от температуры термические и электрические длины пробега электронов.
Изображение в полном размере
Как видно из рис. 6, число Лоренца при 292 К (5, 2 × 10 -8 Ом · Вт / К 2 ) намного больше значения Зоммерфельда (2, 44 × 10 -8 Ом · Вт / К 2 ). Большие числа Лоренца также наблюдаются для нанопроволок никеля, золота, платины и иридия 10, 13, 14, 15, 16, 17, 18 . Это связано с передачей энергии электронов с помощью фононов через границы зерен. Эти наноструктуры состоят из нанокристаллов, и среди них имеется большое количество границ зерен и поверхностей. Часть электронов будет отражаться обратно при рассеянии на границах зерен. Отраженные электроны могут обмениваться энергией с локальными фононами. Фононы могут переходить через границы зерна легче, чем электроны. После переноса фононов через границы зерен они могут обмениваться энергией с электронами и фононами по другую сторону границ зерен. Поэтому, когда электроны отражаются назад, заряды не переносятся через границы зерен, а часть энергии электронов переносится через границы зерен. Это приводит к значительному снижению электропроводности и меньшей теплопроводности.
6, число Лоренца при 292 К (5, 2 × 10 -8 Ом · Вт / К 2 ) намного больше значения Зоммерфельда (2, 44 × 10 -8 Ом · Вт / К 2 ). Большие числа Лоренца также наблюдаются для нанопроволок никеля, золота, платины и иридия 10, 13, 14, 15, 16, 17, 18 . Это связано с передачей энергии электронов с помощью фононов через границы зерен. Эти наноструктуры состоят из нанокристаллов, и среди них имеется большое количество границ зерен и поверхностей. Часть электронов будет отражаться обратно при рассеянии на границах зерен. Отраженные электроны могут обмениваться энергией с локальными фононами. Фононы могут переходить через границы зерна легче, чем электроны. После переноса фононов через границы зерен они могут обмениваться энергией с электронами и фононами по другую сторону границ зерен. Поэтому, когда электроны отражаются назад, заряды не переносятся через границы зерен, а часть энергии электронов переносится через границы зерен. Это приводит к значительному снижению электропроводности и меньшей теплопроводности.
Согласно рис. 6, число Лоренца нанопроволоки серебра уменьшается с понижением температуры, особенно при низких температурах. Это связано с уменьшением числа возбужденных фононов и малым углом рассеяния. С одной стороны, при понижении температуры количество возбужденных фононов падает. Это приводит к уменьшению числа фононов, которые используются для передачи энергии электронов. Следовательно, число Лоренца при пониженной температуре станет меньше, чем число при комнатной температуре. С другой стороны, при понижении температуры возбуждаются только фононы с малым волновым вектором. Волновой вектор заселенности фононов постепенно поворачивается к нижнему пределу. Электрон-фононное рассеяние изменилось бы из-за изменения фононного волнового вектора. Рассеяние электронов на фононах с большими волновыми векторами называется рассеянием на большие углы, а рассеяние электронов на фононах с малыми волновыми векторами — рассеянием на малые углы. Рассеяние на большие углы в равной степени препятствует переносу тепла и заряда, тогда как рассеяние на малые углы значительно тормозит перенос тепла и оставляет перенос заряда относительно неизменным 10, 40, 41 . При низких температурах число Лоренца нанопроволоки серебра также уменьшалось бы из-за обширного рассеяния на малые углы.
При низких температурах число Лоренца нанопроволоки серебра также уменьшалось бы из-за обширного рассеяния на малые углы.
Электрические и тепловые длины свободного пробега электронов, показанные на вставке к рис. 6, можно использовать для интерпретации числа Лоренца нанопроволоки серебра. Поскольку модель свободных электронов применима к серебру, средняя длина свободного пробега электрического электрона рассчитывается по удельному электрическому сопротивлению (
,
скорость Ферми серебра, m масса электрона, n плотность электронов серебра и ρ удельное электрическое сопротивление). Кроме того, средняя длина свободного пробега теплового электрона вычисляется из теплопроводности [
или же
]. Как видно из вставки на рис. 6, длина свободного пробега электрического и теплового электронов увеличивается с понижением температуры. Это связано с уменьшением числа возбужденных фононов и последующим уменьшением электрон-фононного рассеяния. Источники уменьшенного рассеяния увеличивают длину свободного пробега электрона. Когда температура приближается к абсолютному нулю, все фононы замерзают. Фононы не будут рассеивать электроны. Единственным источником рассеяния являются структурные рассеяния, такие как межзеренная граница, поверхностные и точечные дефекты, и эти структурные рассеяния не зависят от температуры. Таким образом, длина свободного пробега электрона при экстремально низких температурах может отражать структурную информацию о кристаллической структуре нанопроволоки серебра. Здесь длина свободного пробега электрического электрона при экстремально низких температурах составляет около 26 нм. Это значение соответствует размеру кристалла (21 нм) в направлении (311) согласно рентгенограмме. Для длины свободного пробега теплового электрона его значение больше среднего свободного пробега. Это связано с тем, что в эту величину входит вклад фононной передачи энергии электронов через границы зерен. Разница между длиной электрического пробега электрического и теплового электронов приводит к большому числу Лоренца.
Когда температура приближается к абсолютному нулю, все фононы замерзают. Фононы не будут рассеивать электроны. Единственным источником рассеяния являются структурные рассеяния, такие как межзеренная граница, поверхностные и точечные дефекты, и эти структурные рассеяния не зависят от температуры. Таким образом, длина свободного пробега электрона при экстремально низких температурах может отражать структурную информацию о кристаллической структуре нанопроволоки серебра. Здесь длина свободного пробега электрического электрона при экстремально низких температурах составляет около 26 нм. Это значение соответствует размеру кристалла (21 нм) в направлении (311) согласно рентгенограмме. Для длины свободного пробега теплового электрона его значение больше среднего свободного пробега. Это связано с тем, что в эту величину входит вклад фононной передачи энергии электронов через границы зерен. Разница между длиной электрического пробега электрического и теплового электронов приводит к большому числу Лоренца. Несмотря на то, что в этой работе мы не измеряем теплопроводность до нуля, предсказуемо, что тепловая и электрическая длина свободного пробега станут одинаковыми, когда температура приблизится к абсолютному нулю. Число Лоренца станет значением Зоммерфельда при абсолютном нуле. Анализ неопределенности этой работы можно найти дополнительную информацию. В этой работе мы исследовали только одну одиночную нанопроволоку и ее структурное влияние на рассеяние электронов. Предполагается, что нанопроволоки с разными диаметрами могут обеспечивать разное тепловое / электрическое сопротивление. Нанопроволоки с разными диаметрами потенциально имеют разные размеры зерен и поверхностное рассеяние. Структурные дефекты будут рассеивать электроны по-разному.
Несмотря на то, что в этой работе мы не измеряем теплопроводность до нуля, предсказуемо, что тепловая и электрическая длина свободного пробега станут одинаковыми, когда температура приблизится к абсолютному нулю. Число Лоренца станет значением Зоммерфельда при абсолютном нуле. Анализ неопределенности этой работы можно найти дополнительную информацию. В этой работе мы исследовали только одну одиночную нанопроволоку и ее структурное влияние на рассеяние электронов. Предполагается, что нанопроволоки с разными диаметрами могут обеспечивать разное тепловое / электрическое сопротивление. Нанопроволоки с разными диаметрами потенциально имеют разные размеры зерен и поверхностное рассеяние. Структурные дефекты будут рассеивать электроны по-разному.
Выводы
В этой работе термические и электрические транспортные свойства отдельной нанопроволоки серебра были охарактеризованы до 35 К. Результаты показали, что тепловая и электрическая проводимость были значительно снижены по сравнению с их объемными аналогами. Температура Дебая серебряной нанопроволоки (151 К) на 36% ниже, чем у объемного серебра из-за размягчения фононов. Теплопроводность серебряной нанопроволоки уменьшалась с понижением температуры, в то время как теплопроводность объемного серебра увеличивалась. Для объяснения этих различных тенденций было использовано единое термическое удельное сопротивление для различения электрон-фононного рассеяния и дефектного рассеяния электронов. Большое остаточное единое термическое удельное сопротивление (0, 9 м · К 2 / Вт) наблюдалось для серебряной нанопроволоки. Он количественно определяет эффект рассеяния дефектов электронами. For bulk silver, the residual unified thermal resistivity is almost zero, reflecting the relatively low defect level inside. The unified thermal resistivity changed linearly with temperature when the temperature was not too low. This is because the number of the excited phonons decreased linearly with temperature in this temperature range. The unified thermal resistivity of the silver nanowire and the bulk silver shared the same trend, proposing that the silver nanowire and the bulk silver shared the similar phonon-electron scattering.
Температура Дебая серебряной нанопроволоки (151 К) на 36% ниже, чем у объемного серебра из-за размягчения фононов. Теплопроводность серебряной нанопроволоки уменьшалась с понижением температуры, в то время как теплопроводность объемного серебра увеличивалась. Для объяснения этих различных тенденций было использовано единое термическое удельное сопротивление для различения электрон-фононного рассеяния и дефектного рассеяния электронов. Большое остаточное единое термическое удельное сопротивление (0, 9 м · К 2 / Вт) наблюдалось для серебряной нанопроволоки. Он количественно определяет эффект рассеяния дефектов электронами. For bulk silver, the residual unified thermal resistivity is almost zero, reflecting the relatively low defect level inside. The unified thermal resistivity changed linearly with temperature when the temperature was not too low. This is because the number of the excited phonons decreased linearly with temperature in this temperature range. The unified thermal resistivity of the silver nanowire and the bulk silver shared the same trend, proposing that the silver nanowire and the bulk silver shared the similar phonon-electron scattering. Additionally, due to phonon-assisted electron energy transfer across the grain boundaries, the Lorenz number of the silver nanowire (5.20 × 10 −8 Ω·W/K 2 ) was found much larger than the bulk counterpart (2.32 × 10 −8 Ω·W/K 2 ). Its value decreased with decreasing temperature due to the reduced number of the excited phonons and small angle scattering.
Additionally, due to phonon-assisted electron energy transfer across the grain boundaries, the Lorenz number of the silver nanowire (5.20 × 10 −8 Ω·W/K 2 ) was found much larger than the bulk counterpart (2.32 × 10 −8 Ω·W/K 2 ). Its value decreased with decreasing temperature due to the reduced number of the excited phonons and small angle scattering.
методы
Sample preparation and structure
Silver nanowires used in this work were purchased from Sigma-aldrich and they were supplied as suspensions in isopropyl alcohol (IPA) with a concentration of 0.5%. The purchased dispersion was further diluted with IPA and dropped on a piece of gel film. The silver nanowires remained on the gel film after IPA evaporated. In this process, the purchased dispersion should be diluted to a degree that single silver nanowires stayed on the gel film without contact with the surrounding ones. Then we used a very simple but effective way to make electrodes for suspending a single nanowire. First of all, a 180 nm thick Au film was deposited on a thermal oxide silicon wafer with a 1 μm thick SiO 2 layer. The wafer (Au/SiO 2 /Si) was cut into pieces and assembled into two electrodes on a glass slide. The trench width is adjustable and the minimum trench width by this method is 5 μm. If the width is smaller than 5 μm, the two electrodes would be prone to connect with each other electrically. The width used in this work was about 25 μm. The two ends of the trench were fixed to the glass slide by epoxy glue.
First of all, a 180 nm thick Au film was deposited on a thermal oxide silicon wafer with a 1 μm thick SiO 2 layer. The wafer (Au/SiO 2 /Si) was cut into pieces and assembled into two electrodes on a glass slide. The trench width is adjustable and the minimum trench width by this method is 5 μm. If the width is smaller than 5 μm, the two electrodes would be prone to connect with each other electrically. The width used in this work was about 25 μm. The two ends of the trench were fixed to the glass slide by epoxy glue.
Before bridging the nanowire, the two electrodes were checked to make sure that they did not connect with each other electrically. After that, a probe station was used to manipulate a single silver nanowire and bridge it across the electrodes. Finally, to suppress thermal and electrical contact resistance, EBID was used to deposit Pt on the two ends of the silver nanowire. To guarantee the good thermal and electrical contact between the silver nanowire and the electrodes, the Pt pads are large and thick enough to cover the entire silver nanowire ends. For the thermal and electrical characterization of the single silver nanowire at low temperatures, a cryogenic system [CCS-450, JANIS] was used to provide cryogenic experiment environment as low as 10 K. The sample was put in a vacuum chamber to suppress the convection heat transfer. The pressure of the chamber is below 0.5 mTorr. The schematic diagram and SEM picture of the two electrodes and the silver nanowire sample (top view) are shown in Fig. 1(a). The side views are shown in Fig. 1(c). According to the top view and side view of the silver nanowire, the three dimension coordinates of the nanowire can be extracted and the length of the suspended silver nanowire is calculated as 27.23 μm. Unlike the length, the average nanowire diameter is easy to measure using SEM and its value is determined as 227 nm.
For the thermal and electrical characterization of the single silver nanowire at low temperatures, a cryogenic system [CCS-450, JANIS] was used to provide cryogenic experiment environment as low as 10 K. The sample was put in a vacuum chamber to suppress the convection heat transfer. The pressure of the chamber is below 0.5 mTorr. The schematic diagram and SEM picture of the two electrodes and the silver nanowire sample (top view) are shown in Fig. 1(a). The side views are shown in Fig. 1(c). According to the top view and side view of the silver nanowire, the three dimension coordinates of the nanowire can be extracted and the length of the suspended silver nanowire is calculated as 27.23 μm. Unlike the length, the average nanowire diameter is easy to measure using SEM and its value is determined as 227 nm.
To characterize the structure of the silver nanowire, XRD was used to scan the sample. The XRD system (Siemens D 500 diffractometer) is equipped with a copper tube that was operated at 40 kV and 30 mA. Because a single silver nanowire is too small compared with the XRD spot size and cannot provide enough signals, five drops of purchased dispersion which contained plenty of silver nanowires were dropped on the XRD sample holder. The XRD pattern is shown in Fig. 2. The XRD pattern shows that the silver nanowire is composed of crystals. According to the pattern, the crystal size can be estimated based on the peaks. The crystal size calculated from Peak (111) is 126 nm and those sizes calculated from Peak (220) and Peak (311) are 8 nm and 21 nm respectively. All of the crystal sizes in these directions are much smaller than the diameter of the silver nanowire. This proves that the silver nanowire is polycrystalline. The grain boundaries among these nanocrystals in the silver nanowires are abundant. Also the different crystallite size determined by the peaks indicates that the crystallite in the nanowire is not cube-like or sphere-like. Instead, the crystallite is expected to be ellipsoid-like.
Because a single silver nanowire is too small compared with the XRD spot size and cannot provide enough signals, five drops of purchased dispersion which contained plenty of silver nanowires were dropped on the XRD sample holder. The XRD pattern is shown in Fig. 2. The XRD pattern shows that the silver nanowire is composed of crystals. According to the pattern, the crystal size can be estimated based on the peaks. The crystal size calculated from Peak (111) is 126 nm and those sizes calculated from Peak (220) and Peak (311) are 8 nm and 21 nm respectively. All of the crystal sizes in these directions are much smaller than the diameter of the silver nanowire. This proves that the silver nanowire is polycrystalline. The grain boundaries among these nanocrystals in the silver nanowires are abundant. Also the different crystallite size determined by the peaks indicates that the crystallite in the nanowire is not cube-like or sphere-like. Instead, the crystallite is expected to be ellipsoid-like.
An AFM (MicroNano D 3000) was employed to study the surface roughness of silver nanowires. To prepare a sample for the AFM scanning, a small amount of aqueous solution containing silver nanowires was dropped on a glass substrate. After water evaporated, the silver nanowires were dispersed on the substrate and ready for scanning. Figure 1(e) shows the AFM image of the silver nanowires on the substrate. Then a carefully selected 160 × 160 nm 2 area was finely scanned and the surface image is shown in Fig. 1(f). The cross-section profiles show a fluctuation of ±2 nm in surface roughness.
Электрическая характеристика
For the electrical characterization of the silver nanowire, a set of small electrical currents ranging from 0.1 mA to 0.5 mA were applied. The current source is Keithley 6221 DC and AC Current Source. Due to the electrical heating effect, the electrical resistance would rise when the electrical current increases. The measured electrical resistance should change proportionally with the electrical current’s square. A linear fitting was used to extrapolate the electrical resistance without heating effect, namely the resistance when the electrical current is zero.
A linear fitting was used to extrapolate the electrical resistance without heating effect, namely the resistance when the electrical current is zero.
Thermal characterization
The thermal conductivity of the nanowire was characterized by the steady-state electro-thermal technique. The silver nanowire was suspended across the two electrodes in the characterization. We can consider the two electrodes as two heat sinks. Its temperature is the same as the environment temperature T 0 . The sample was placed in a high vacuum chamber to suppress the convection effect. Moreover, the radiation effect would be small because the nanowire is very short. Also, it is well known that silver has a very small emissivity (about 0.03). Therefore, the effect of convection and radiation is negligible in this work. When a constant electrical current is applied through the nanowire, the joule self-heating in the nanowire would induce a temperature rise. The steady-state heat transfer governing equation is as below:
Вот,
is the thermal conductivity and
is the heat generation rate per unit volume. It can be described as
, I is the applied electrical current; R 1 is the electrical resistance of the nanowire; A c is the cross section area of the nanowire (
) and L is the length of the nanowire. The expression of T ( x ) is
, The average temperature along the sample is
It can be described as
, I is the applied electrical current; R 1 is the electrical resistance of the nanowire; A c is the cross section area of the nanowire (
) and L is the length of the nanowire. The expression of T ( x ) is
, The average temperature along the sample is
The temperature rise is , As we can see, the temperature rise is proportional to electrical current’s square. When the temperature is higher than 35 K, the electrical resistance of the silver nanowire is proportional to its temperature. The temperature change can be monitored by the electrical resistance variation :
It can be seen from equation (6) that is proportional to and the slope is Then the thermal conductivity of the nanowire can be determined as below:
Now we take the thermal conductivity characterization of the silver nanowire at 290 K as an example to demonstrate the measurement process. At first, a series of electrical currents ranging from 0.1 mA to 0.5 mA were applied through the sample and the corresponding voltages were measured by a digit multimeter (Agilent 34401A). Then we plot the relation between the electrical resistance and the current’s square as shown in the inset of Fig. 4. After fitting the data linearly, the slope (1.83 Ω/mA 2 ) and intercept (53.15 Ω) can be obtained. The intercept is the electrical resistance ( R 0 ) at 290 K. After we measured the electrical resistances at different temperatures, the value of
(0.1165 Ω/K) can be determined. The diameter and length of the silver nanowire were measured by a scanning electron microscopy (SEM) after the experiment was finished. Finally, the thermal conductivity of the silver nanowire was determined as 191.5 W/K·m. In order to improve the measurement accuracy, the electrical resistance rise induced in all the experiments was carefully selected as about 1%. The temperature rises were all controlled within 5 K.
Then we plot the relation between the electrical resistance and the current’s square as shown in the inset of Fig. 4. After fitting the data linearly, the slope (1.83 Ω/mA 2 ) and intercept (53.15 Ω) can be obtained. The intercept is the electrical resistance ( R 0 ) at 290 K. After we measured the electrical resistances at different temperatures, the value of
(0.1165 Ω/K) can be determined. The diameter and length of the silver nanowire were measured by a scanning electron microscopy (SEM) after the experiment was finished. Finally, the thermal conductivity of the silver nanowire was determined as 191.5 W/K·m. In order to improve the measurement accuracy, the electrical resistance rise induced in all the experiments was carefully selected as about 1%. The temperature rises were all controlled within 5 K.
Дополнительная информация
How to cite this article : Cheng, Z. et al. Temperature Dependence of Electrical and Thermal Conduction in Single Silver Nanowire. Sci. Rep. 5, 10718; doi: 10.1038/srep10718 (2015).
Sci. Rep. 5, 10718; doi: 10.1038/srep10718 (2015).
Дополнительная информация
PDF файлы
- 1.
Дополнительная информация
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Принципы сообщества. Если вы обнаружили что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неуместное.
серебро теплопроводность изображения, фото и картинки
изображение теплопроводности
теплопроводность воды картинка
теплопроводность воздуха картинки
теплопроводность металлов фото
Предыдущий Следующий 1 / 50 Фото товары: Связанные ключевые слова: термопаста термомастика анизотропная проводящая пленка нормы поведения измеритель проводимости датчик проводимостиПрорывы в сверхвысокой теплопроводности кристаллов арсенида бора
Ph. D. Студент трижды выступал в качестве соавтора в науке, увеличивая участие в TcSUH
D. Студент трижды выступал в качестве соавтора в науке, увеличивая участие в TcSUH
За время работы в Хьюстонском университете доктор философии по физике. студентка Гитал Амила Гэмидж написала двенадцать статей в академических журналах, в том числе три статьи первого автора.
кандидат физико-математических наук. студентка Гиталь Амила Гамидж работает над определением характеристик монокристалла арсенида бора.Благодаря своим достижениям в прошлом году он получил стипендию CW Chu Техасского центра сверхпроводимости при UH (TcSUH) за выдающиеся академические и исследовательские достижения.
Все свободное время, которое у него есть, большую часть времени он посвящает работе в Техасском центре сверхпроводимости Хьюстонского университета (TcSUH) в качестве председателя Комитета студенческих семинаров, в обязанности которого входит выбор докладчиков для семинаров и проведение презентаций.
В прошлом году он был сопредседателем организации и благодарит комитет за помощь в его коммуникативных навыках.
«Люди говорят, что научные исследования — это сложно, но я бы сказал, что если вы сделаете исследования своим хобби, вам будет намного легче работать», — сказал Гэмидж.«Нужно иметь хорошие коммуникативные навыки. Если вы пытаетесь работать в одиночку, это очень сложно, но если вы общаетесь со своими сверстниками, вам будет легче работать».
Выращивание монокристаллов арсенида бора
Гамаж начал свою аспирантуру в университете в 2016 году. Его исследования проводились под руководством профессора кафедры доктора медицинских наук Андерсона Жифэн Рена, директора ТГГУ и физика Колледжа естественных наук и математики УГ. Вместе с Реном он вырастил и охарактеризовал кристаллы арсенида бора и изучил их сверхвысокую теплопроводность.
Гэмидж прикрепляет монокристалл арсенида бора к держателю образца для измерения электропроводности и подвижности носителей. Когда Гэмидж впервые прибыл, он нашел работу над арсенидом бора особенно интересной. Однако он не думал, что сможет добиться крупного прорыва в области кристаллов арсенида бора всего за несколько лет.
— Но я принял вызов, — сказал он. «Доктор. Рен много меня направлял. Он хорошо известен за этот вид материала. Когда у меня есть вопрос, я всегда обращаюсь к доктору.У Рена всегда есть предложения».
В 2018 году Гэмидж, Рен и восемь исследователей UH опубликовали свои выводы о кристаллах арсенида бора в журнале Science. Они обнаружили, что кристаллы демонстрируют гораздо более высокую теплопроводность, чем любые другие полупроводники и металлы, используемые в настоящее время.
Рен сказал: «Geethal добился огромного прогресса не только в размере кристаллов, но и в их качестве, что помогло нам лучше понять рост кристаллов и механизм их высокой теплопроводности.
Найдите время для хобби
Вне лаборатории Геймидж увлекается фотографией. «Я люблю фотографировать людей, — сказал он. «Мои друзья просят меня сфотографироваться, когда у них мероприятие или вечеринка»
Он также фотографирует природу – так началась его любовь к фотографии. После переезда в США из Шри-Ланки со своей женой он побывал в 15 штатах.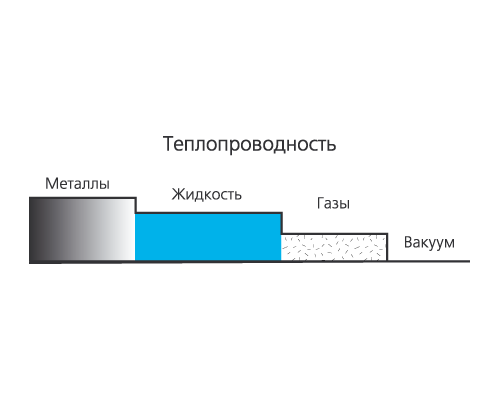
Тем не менее, Гэмидж проводит большую часть своего времени в университете, особенно потому, что его жена является доктором наук.Д. студентка химического факультета.
Он благодарен UH, NSM, TcSUH, своим коллегам по группе и особенно Рену за широкие возможности для проведения исследований. Гэмидж сказал, что Рен был основной причиной, по которой он пришел в UH, и отклонил предложения трех других университетов.
«Гетал проделал выдающуюся работу», — сказал Рен о работе Гэмиджа. «Я очень доволен его прогрессом. Я уверен, что он продолжит делать гораздо больше и гораздо больше достижений в науке».
В планыGamage на будущее входит получение отраслевого опыта за счет работы с полупроводниками.Работа в США является его главным приоритетом, но в какой-то момент своей карьеры он хотел бы преподавать.
Он планирует окончить Хьюстонский университет в 2021 году.
— Ребека Трехо, Колледж естественных наук и математики
Управление фазовым разделением в термоэлектрическом Pb1-xGexTe для минимизации теплопроводности
rsc.org/schema/rscart38″> За последнее десятилетие были проведены интенсивные исследования по выявлению наноструктурированных термоэлектрических материалов, позволяющих эффективно преобразовывать отработанное тепло в электрическую энергию.Однако стабильности таких материалов при рабочих температурах, обычно 400 °C или выше, уделяется меньше внимания. Керамика с традиционной наноструктурой имеет тенденцию к росту зерен при высокой температуре, снижая плотность поверхностей раздела и повышая теплопроводность, что отрицательно сказывается на работе устройства. Поэтому предпочтительнее идентифицировать материалы со стабильными наноструктурами, например, системы, которые претерпевают спонтанное фазовое разделение. Здесь мы исследуем сплавы PbTe–GeTe, в которых спинодальный распад происходит при начальном охлаждении выше 580 °C с образованием сложных наноструктур, состоящих из обогащенных Ge и Pb доменов разного размера.Возникающее в результате плотное расположение интерфейсов в сочетании с флуктуациями массы, связанными со смешением Pb-Ge, усиливает рассеяние фононов и сильно снижает теплопроводность. Здесь мы сосредоточимся на номинальном составе Pb 0,49 Ge 0,51 Te и покажем, что, настраивая процедуру синтеза, мы можем контролировать структуру композиционных доменов и плотность интерфейсов между ними. Это позволяет поддерживать низкую теплопроводность решетки даже после термоциклирования в диапазоне рабочих температур.
Здесь мы сосредоточимся на номинальном составе Pb 0,49 Ge 0,51 Te и покажем, что, настраивая процедуру синтеза, мы можем контролировать структуру композиционных доменов и плотность интерфейсов между ними. Это позволяет поддерживать низкую теплопроводность решетки даже после термоциклирования в диапазоне рабочих температур.Эта статья находится в открытом доступе
Подождите, пока мы загрузим ваш контент… Что-то пошло не так. Попробуй снова?
Попробуй снова?Теплопроводность жидкостей на JSTOR
Перейти к основному содержанию Есть доступ к библиотеке? Войдите через свою библиотекуВесь контент Картинки
Поиск JSTOR Регистрация Вход- Поиск
- Расширенный поиск
- Поиск изображений
- Просматривать
- от Субъекта
- по названию
- по коллекциям
- от издателя
- Инструменты
- Рабочее пространство
- Анализатор текста
- Серия JSTOR Understanding
- Данные для исследований
Минимум теплопроводности градуированных сверхрешеток из-за локализации фононов: APL Материалы: Том 9, № 9
B. Зависимое от длины отношение участия и пропускание 90 015 Чтобы проиллюстрировать локализацию фононов, мы показываем зависящее от длины PR, взвешенное PR и передачу градуированных SL с шестью единицами SL на рис. 5. PR, взвешенное PR и пропускание уменьшаются. с увеличением длины и сходятся после L ∼ 84 uc (Np ∼ 4). По сравнению с эталонными периодическими СЛ с p = 1 uc ЧМ среднечастотных (3–7 ТГц) и высокочастотных (>~10 ТГц) фононов в градуированных СЛ значительно снижены, что свидетельствует о локализации .Уменьшение PR очень низкочастотных фононов (. Длина конвергенции Np ∼ 4 представляет собой количество периодов, которое требуется в каждой единице SL, чтобы хорошо сформировать соответствующие свернутые собственные моды. Как только свернутые моды в каждой единице SL хорошо сформированы и интерферируют деструктивно, степень локализации будет сходиться при Np > 4–5.В блоках СР градуированных СР имеются ограниченные (локализованные) высокочастотные оптические моды из-за рассогласования спектров 60 60.
Зависимое от длины отношение участия и пропускание 90 015 Чтобы проиллюстрировать локализацию фононов, мы показываем зависящее от длины PR, взвешенное PR и передачу градуированных SL с шестью единицами SL на рис. 5. PR, взвешенное PR и пропускание уменьшаются. с увеличением длины и сходятся после L ∼ 84 uc (Np ∼ 4). По сравнению с эталонными периодическими СЛ с p = 1 uc ЧМ среднечастотных (3–7 ТГц) и высокочастотных (>~10 ТГц) фононов в градуированных СЛ значительно снижены, что свидетельствует о локализации .Уменьшение PR очень низкочастотных фононов (. Длина конвергенции Np ∼ 4 представляет собой количество периодов, которое требуется в каждой единице SL, чтобы хорошо сформировать соответствующие свернутые собственные моды. Как только свернутые моды в каждой единице SL хорошо сформированы и интерферируют деструктивно, степень локализации будет сходиться при Np > 4–5.В блоках СР градуированных СР имеются ограниченные (локализованные) высокочастотные оптические моды из-за рассогласования спектров 60 60.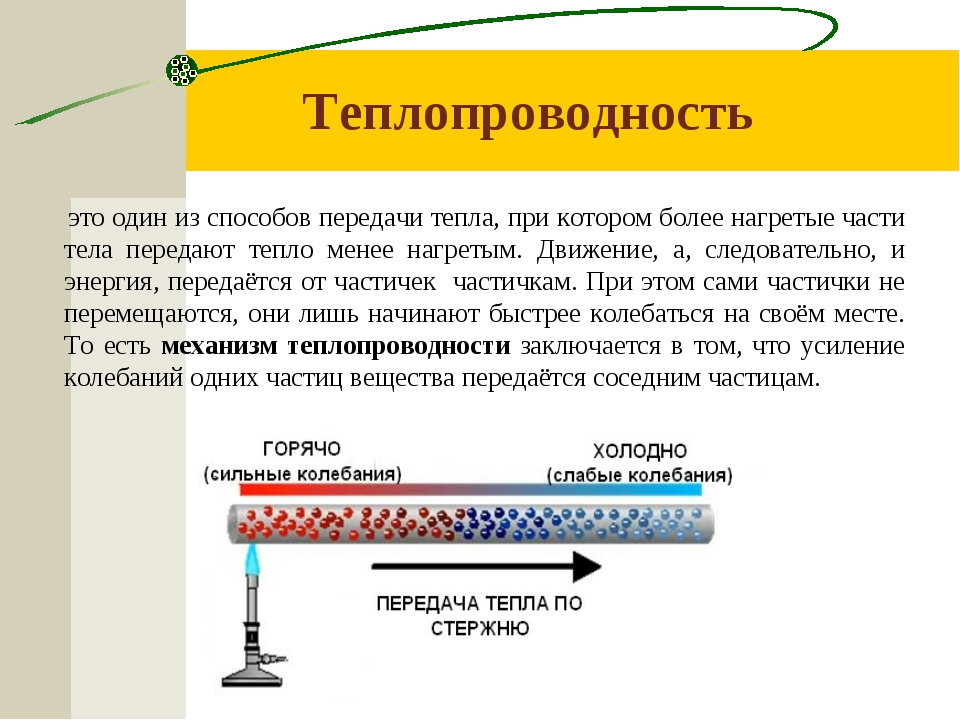 C. Колвард, Т.A. Gant, M.V. Klein, R. Merlin, R. Fischer, H. Morkoc, and A.C. Gossard, Phys. Ред. B 31 (4), 2080 (1985). https://doi.org/10.1103/physrevb.31.2080 Чтобы отличить этот вид локализации от локализации, вызванной деструктивной интерференцией свернутых собственных мод между различными единицами СР, мы сравнили PR, взвешенную PR и передачу шести периодических SL с каждым периодов (p = 1–6 мк) в градуированных СР к таковым в градуированных СР на рис. -складывание во всех случаях.С увеличением длины периода в периодических СР высокочастотные фононы более сильно локализованы из-за конфайнмента и становятся почти полностью локализованными при p = 5 uc и p = 6 uc, как показано на рис. 6(а) и 6(б), что должно быть доминирующей причиной локализации в высокочастотном диапазоне в градуированных СЛ. Однако для фононов умеренной частоты PR и взвешенный PR в периодических СР более или менее не зависят от длины периода. Как только различные единицы SL соединяются, чтобы составить градуированные SL, PR и взвешенный PR значительно уменьшаются и меньше, чем любые из периодических SL.
C. Колвард, Т.A. Gant, M.V. Klein, R. Merlin, R. Fischer, H. Morkoc, and A.C. Gossard, Phys. Ред. B 31 (4), 2080 (1985). https://doi.org/10.1103/physrevb.31.2080 Чтобы отличить этот вид локализации от локализации, вызванной деструктивной интерференцией свернутых собственных мод между различными единицами СР, мы сравнили PR, взвешенную PR и передачу шести периодических SL с каждым периодов (p = 1–6 мк) в градуированных СР к таковым в градуированных СР на рис. -складывание во всех случаях.С увеличением длины периода в периодических СР высокочастотные фононы более сильно локализованы из-за конфайнмента и становятся почти полностью локализованными при p = 5 uc и p = 6 uc, как показано на рис. 6(а) и 6(б), что должно быть доминирующей причиной локализации в высокочастотном диапазоне в градуированных СЛ. Однако для фононов умеренной частоты PR и взвешенный PR в периодических СР более или менее не зависят от длины периода. Как только различные единицы SL соединяются, чтобы составить градуированные SL, PR и взвешенный PR значительно уменьшаются и меньше, чем любые из периодических SL.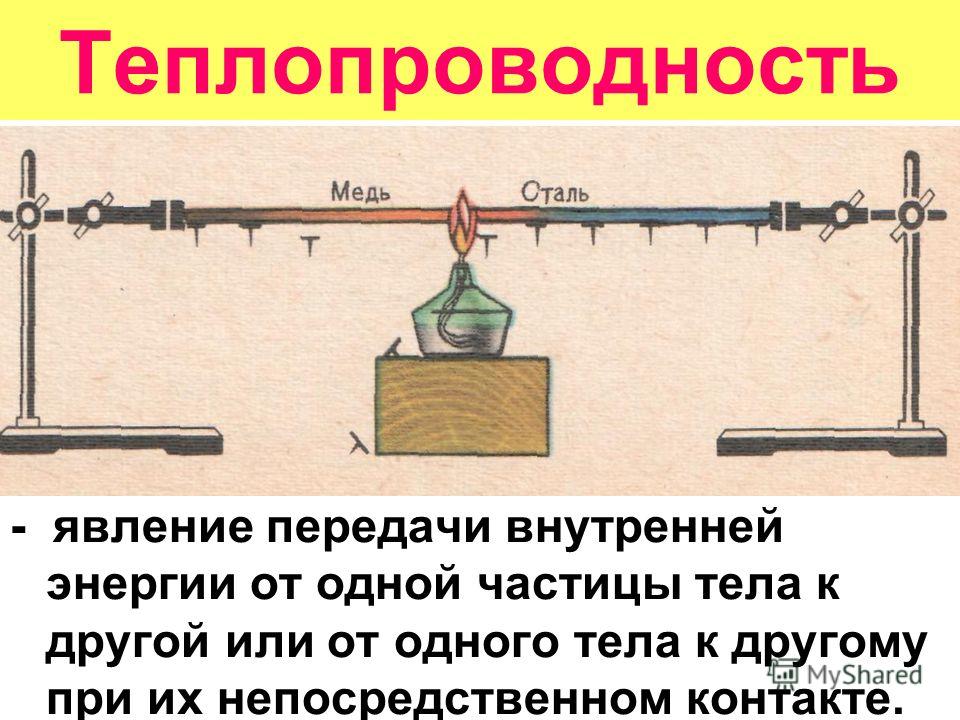 Уменьшение должно происходить из-за интерференции свернутых мод в разных блоках SL, что приводит к чрезвычайно сильному ослаблению передачи в диапазоне средних частот, как показано на рис. 6(c). Об этом также можно судить по результатам общей плотности состояний на рис. 7, где плотность состояний градуированных СЛ довольно близка к таковым для периодических СЛ в диапазоне умеренных частот. Большое снижение передачи в этом диапазоне в градуированных SL должно быть вызвано интерференцией мод в разных блоках SL.В высокочастотном диапазоне суммарная ПЭС значительна только в периодических СЛ с p = 1 и p = 2 и пренебрежимо мала (за исключением очень немногих частотных точек) в СЛ с большей длиной периода (p = 3- 6 ус). В основном это вызвано тем, что высокочастотные моды не могут поддерживаться в сегменте Ge, когда он приближается к объемному состоянию по мере увеличения его толщины. В результате эти высокочастотные моды в градиентных СЛ могут оставаться только в первых двух блоках СЛ с короткими длинами периодов (p = 1–2 мкс).
Уменьшение должно происходить из-за интерференции свернутых мод в разных блоках SL, что приводит к чрезвычайно сильному ослаблению передачи в диапазоне средних частот, как показано на рис. 6(c). Об этом также можно судить по результатам общей плотности состояний на рис. 7, где плотность состояний градуированных СЛ довольно близка к таковым для периодических СЛ в диапазоне умеренных частот. Большое снижение передачи в этом диапазоне в градуированных SL должно быть вызвано интерференцией мод в разных блоках SL.В высокочастотном диапазоне суммарная ПЭС значительна только в периодических СЛ с p = 1 и p = 2 и пренебрежимо мала (за исключением очень немногих частотных точек) в СЛ с большей длиной периода (p = 3- 6 ус). В основном это вызвано тем, что высокочастотные моды не могут поддерживаться в сегменте Ge, когда он приближается к объемному состоянию по мере увеличения его толщины. В результате эти высокочастотные моды в градиентных СЛ могут оставаться только в первых двух блоках СЛ с короткими длинами периодов (p = 1–2 мкс). С этой точки зрения эти моды можно было бы назвать «градонами», которые представляют собой ограниченные моды в некоторых частях градуированных систем из-за их отсутствия в других частях. 61,62 61. J. Xiao, K. Yakubo, K. Yu, Phys. Ред. B 73 (5), 054201 (2006 г.). https://doi.org/10.1103/physrevb.73.05420162. J. J. Xiao, K. Yakubo, K. W. Yu, J. Phys.: Condens. Материя 19 (2), 026224 (2006). https://doi.org/10.1088/0953-8984/19/2/026224 На рис.8. «Градоны» в диапазоне 13–15 ТГц аналогичны и здесь не показаны. «Градоны» почти равномерно возбуждаются внутри ограниченной области и резко затухают на границе этой области, что согласуется с ранее описанными особенностями. 61 61. J. Xiao, K. Yakubo, K. Yu, Phys. Ред. B 73 (5), 054201 (2006 г.). https://doi.org/10.1103/physrevb.73.054201 Поскольку «градоны» по существу являются ограниченными модами, подобными локализованным модам, индуцированным примесями, 61 61. J. Xiao, K.Якубо, К.
С этой точки зрения эти моды можно было бы назвать «градонами», которые представляют собой ограниченные моды в некоторых частях градуированных систем из-за их отсутствия в других частях. 61,62 61. J. Xiao, K. Yakubo, K. Yu, Phys. Ред. B 73 (5), 054201 (2006 г.). https://doi.org/10.1103/physrevb.73.05420162. J. J. Xiao, K. Yakubo, K. W. Yu, J. Phys.: Condens. Материя 19 (2), 026224 (2006). https://doi.org/10.1088/0953-8984/19/2/026224 На рис.8. «Градоны» в диапазоне 13–15 ТГц аналогичны и здесь не показаны. «Градоны» почти равномерно возбуждаются внутри ограниченной области и резко затухают на границе этой области, что согласуется с ранее описанными особенностями. 61 61. J. Xiao, K. Yakubo, K. Yu, Phys. Ред. B 73 (5), 054201 (2006 г.). https://doi.org/10.1103/physrevb.73.054201 Поскольку «градоны» по существу являются ограниченными модами, подобными локализованным модам, индуцированным примесями, 61 61. J. Xiao, K.Якубо, К. Ю. // Физ. Ред. B 73 (5), 054201 (2006 г.). https://doi.org/10.1103/physrevb.73.054201 они почти не способствуют переносу тепла. Поэтому нас в основном интересует локализация фононов умеренной частоты за счет когерентного обратного рассеяния и интерференции. Частичная фононная локализация в этой работе представляет собой слабую локализацию, т. е. слабую версию сильной локализации в смысле Андерсона. 22 22. P. Sheng, Введение в рассеяние волн, локализацию и мезоскопические явления (Springer, Heidelberg, 2006).Тенденции как PR, так и передачи в зависимости от длины в градуированных SL с другими конфигурациями в таблице I довольно схожи. PR, взвешенный PR и пропускание на длине сходимости (Np = 4) для различных конфигураций показаны на рис. 9(а)–9(в) соответственно. С увеличением количества единиц СР и уровня беспорядка PR, взвешенный PR и пропускание уменьшаются во всем спектре, особенно в диапазоне умеренных частот, где локализация фононов наиболее сильна. Нормированная функция накопления теплопроводности в зависимости от частоты на рис.
Ю. // Физ. Ред. B 73 (5), 054201 (2006 г.). https://doi.org/10.1103/physrevb.73.054201 они почти не способствуют переносу тепла. Поэтому нас в основном интересует локализация фононов умеренной частоты за счет когерентного обратного рассеяния и интерференции. Частичная фононная локализация в этой работе представляет собой слабую локализацию, т. е. слабую версию сильной локализации в смысле Андерсона. 22 22. P. Sheng, Введение в рассеяние волн, локализацию и мезоскопические явления (Springer, Heidelberg, 2006).Тенденции как PR, так и передачи в зависимости от длины в градуированных SL с другими конфигурациями в таблице I довольно схожи. PR, взвешенный PR и пропускание на длине сходимости (Np = 4) для различных конфигураций показаны на рис. 9(а)–9(в) соответственно. С увеличением количества единиц СР и уровня беспорядка PR, взвешенный PR и пропускание уменьшаются во всем спектре, особенно в диапазоне умеренных частот, где локализация фононов наиболее сильна. Нормированная функция накопления теплопроводности в зависимости от частоты на рис. 9(d) подтверждает локализацию фононов с другой точки зрения. С ростом уровня беспорядка наклон в диапазоне 4–6 ТГц (основная часть диапазона умеренных частот) постепенно уменьшается, что отражает уменьшение вклада в перенос тепла от частично локализованных состояний. Локализация становится достаточно сильной, чтобы теплопроводность уменьшалась с длиной на шести и семи единицах СР, где также появляются два небольших плато около 1 и 6,5 ТГц. частотные точки на рис.10. Частотные точки выбираются из тех, у которых низкий PR на рис. 5(а). Получен четкий экспоненциальный спад пропускания с длиной, который широко используется в качестве доказательства локализации фононов. 32–35,37–39 32. I. Savić, N. Mingo, and D.A. Stewart, Phys. Преподобный Летт. 101 (16), 165502 (2008). https://doi.org/10.1103/physrevlett.101.16550233. T. Yamamoto, K. Sasaoka, and S. Watanabe, Phys. Преподобный Летт. 106 (21), 215503 (2011). https://doi.org/10.1103/физревлетт.106.21550334. J. Mendoza и G.
9(d) подтверждает локализацию фононов с другой точки зрения. С ростом уровня беспорядка наклон в диапазоне 4–6 ТГц (основная часть диапазона умеренных частот) постепенно уменьшается, что отражает уменьшение вклада в перенос тепла от частично локализованных состояний. Локализация становится достаточно сильной, чтобы теплопроводность уменьшалась с длиной на шести и семи единицах СР, где также появляются два небольших плато около 1 и 6,5 ТГц. частотные точки на рис.10. Частотные точки выбираются из тех, у которых низкий PR на рис. 5(а). Получен четкий экспоненциальный спад пропускания с длиной, который широко используется в качестве доказательства локализации фононов. 32–35,37–39 32. I. Savić, N. Mingo, and D.A. Stewart, Phys. Преподобный Летт. 101 (16), 165502 (2008). https://doi.org/10.1103/physrevlett.101.16550233. T. Yamamoto, K. Sasaoka, and S. Watanabe, Phys. Преподобный Летт. 106 (21), 215503 (2011). https://doi.org/10.1103/физревлетт.106.21550334. J. Mendoza и G. Chen, Nano Lett. 16 (12), 7616–7620 (2016). https://doi.org/10.1021/acs.nanolett.6b0355035. R. Hu и Z. Tian, Phys. Ред. B 103 (4), 045304 (2021). https://doi.org/10.1103/physrevb.103.04530437. S. Hu, Z. Zhang, P. Jiang, J. Chen, S. Volz, M. Nomura, and B. Li, J. Phys. хим. лат. 9 (14), 3959–3968 (2018). https://doi.org/10.1021/acs.jpclett.8b0165338. Juntunen T., Vänskä O., Tittonen I. // Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105. Y. Ni, H. Zhang, S. Hu, H. Wang, S. Volz, and S. Xiong, Int. J. Тепломассообмен 144 , 118608 (2019). https://doi.org/10.1016/j.ijheatmasstransfer.2019.118608 Однако одно существенное отличие заключается в том, что в режиме сильной локализации передача затухает до ненулевой константы вместо нуля. 34,35,38 34. J. Mendoza and G. Chen, Nano Lett. 16 (12), 7616–7620 (2016). https://дои.org/10.1021/acs.nanolett.6b0355035. R. Hu и Z. Tian, Phys.
Chen, Nano Lett. 16 (12), 7616–7620 (2016). https://doi.org/10.1021/acs.nanolett.6b0355035. R. Hu и Z. Tian, Phys. Ред. B 103 (4), 045304 (2021). https://doi.org/10.1103/physrevb.103.04530437. S. Hu, Z. Zhang, P. Jiang, J. Chen, S. Volz, M. Nomura, and B. Li, J. Phys. хим. лат. 9 (14), 3959–3968 (2018). https://doi.org/10.1021/acs.jpclett.8b0165338. Juntunen T., Vänskä O., Tittonen I. // Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105. Y. Ni, H. Zhang, S. Hu, H. Wang, S. Volz, and S. Xiong, Int. J. Тепломассообмен 144 , 118608 (2019). https://doi.org/10.1016/j.ijheatmasstransfer.2019.118608 Однако одно существенное отличие заключается в том, что в режиме сильной локализации передача затухает до ненулевой константы вместо нуля. 34,35,38 34. J. Mendoza and G. Chen, Nano Lett. 16 (12), 7616–7620 (2016). https://дои.org/10.1021/acs.nanolett.6b0355035. R. Hu и Z. Tian, Phys. Ред. B 103 (4), 045304 (2021). https://doi.org/10.1103/physrevb.103.04530438. Juntunen T., Vänskä O., Tittonen I. // Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105901 Это особенность частичной локализации, которая может быть вызвана либо декогеренцией некоторых фононов, как было указано в предыдущих работах 37,38 37. S. Hu, Z. Чжан, П. Цзян, Дж. Чен, С. Волц, М.Nomura и B. Li, J. Phys. хим. лат. 9 (14), 3959–3968 (2018). https://doi.org/10.1021/acs.jpclett.8b0165338. Juntunen T., Vänskä O., Tittonen I. // Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105901 или недостаточная сила беспорядка в настоящей работе. Из-за умеренного беспорядка некоторая часть фононов на определенной частоте все еще может проходить через градиентные СР, даже если длина системы непрерывно увеличивается.Ненулевое постоянное пропускание фононов приводит к тому, что теплопроводность градиентных СР увеличивается с длиной при Np ≥ 4–5 в разд.
Ред. B 103 (4), 045304 (2021). https://doi.org/10.1103/physrevb.103.04530438. Juntunen T., Vänskä O., Tittonen I. // Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105901 Это особенность частичной локализации, которая может быть вызвана либо декогеренцией некоторых фононов, как было указано в предыдущих работах 37,38 37. S. Hu, Z. Чжан, П. Цзян, Дж. Чен, С. Волц, М.Nomura и B. Li, J. Phys. хим. лат. 9 (14), 3959–3968 (2018). https://doi.org/10.1021/acs.jpclett.8b0165338. Juntunen T., Vänskä O., Tittonen I. // Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105901 или недостаточная сила беспорядка в настоящей работе. Из-за умеренного беспорядка некоторая часть фононов на определенной частоте все еще может проходить через градиентные СР, даже если длина системы непрерывно увеличивается.Ненулевое постоянное пропускание фононов приводит к тому, что теплопроводность градиентных СР увеличивается с длиной при Np ≥ 4–5 в разд. . В недавней статье 38 38. Juntunen T., Vänskä O. and Tittonen I. Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105901 Поправочный член, учитывающий фононную декогерентность, был добавлен к обычной формуле экспоненциального затухания передачи, что хорошо согласуется с их прямыми результатами моделирования МД.Мы не пытаемся подогнать зависящее от длины фононное пропускание на рис. 10 феноменологической формулой 38 38. Juntunen T., Vänskä O., Tittonen I. Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105901, так как здесь частичная локализация вызвана другим механизмом. Желательна соответствующая теоретическая модель, которая соответствовала бы настоящим результатам во всем диапазоне длины, и она будет в центре нашей будущей работы. По сравнению с локализацией электрона, которую легче достичь, 42 42.С. Датта, Электронный транспорт в мезоскопических системах (издательство Кембриджского университета, Великобритания, 1997).
. В недавней статье 38 38. Juntunen T., Vänskä O. and Tittonen I. Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105901 Поправочный член, учитывающий фононную декогерентность, был добавлен к обычной формуле экспоненциального затухания передачи, что хорошо согласуется с их прямыми результатами моделирования МД.Мы не пытаемся подогнать зависящее от длины фононное пропускание на рис. 10 феноменологической формулой 38 38. Juntunen T., Vänskä O., Tittonen I. Phys. Преподобный Летт. 122 (10), 105901 (2019). https://doi.org/10.1103/physrevlett.122.105901, так как здесь частичная локализация вызвана другим механизмом. Желательна соответствующая теоретическая модель, которая соответствовала бы настоящим результатам во всем диапазоне длины, и она будет в центре нашей будущей работы. По сравнению с локализацией электрона, которую легче достичь, 42 42.С. Датта, Электронный транспорт в мезоскопических системах (издательство Кембриджского университета, Великобритания, 1997). локализацию фононов в теплопроводности обычно труднее наблюдать из-за ее широкополосности. Таким образом, требуется дальнейшее теоретическое исследование локализации парциальных фононов, особенно ее зависимости от силы беспорядка.
локализацию фононов в теплопроводности обычно труднее наблюдать из-за ее широкополосности. Таким образом, требуется дальнейшее теоретическое исследование локализации парциальных фононов, особенно ее зависимости от силы беспорядка.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.
Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.

- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Комплект для измерения теплопроводности
Есть вопросы? Обратитесь в службу поддержки клиентов.406-256-0990 или Живой чат
- Возраст 11+
- На складе, готово к отправке
- Нужно быстро? Варианты доставки смотрите в корзине.

Изучите теплопроводность, сравнив скорость теплопередачи для следующих металлов: алюминий, углеродистая сталь, медь, латунь и нержавеющая сталь из сплава никеля. Читать Подробнее
участников My Science Perks зарабатывают не менее 0,32 доллара США за этот товар. Войдите или создайте Бесплатный HST Аккаунт, чтобы начать зарабатывать сегодня
ОПИСАНИЕ
Изучите теплопроводность путем сравнения скоростей теплопередачи для следующих металлов: алюминий, углеродистая сталь, медь, латунь и нержавеющая сталь из никелевого сплава.В этот комплект входят пять металлических стержней длиной 10 см, ручной зажим и свеча. Полные инструкции включают советы по обучению маленьких детей теплопроводности.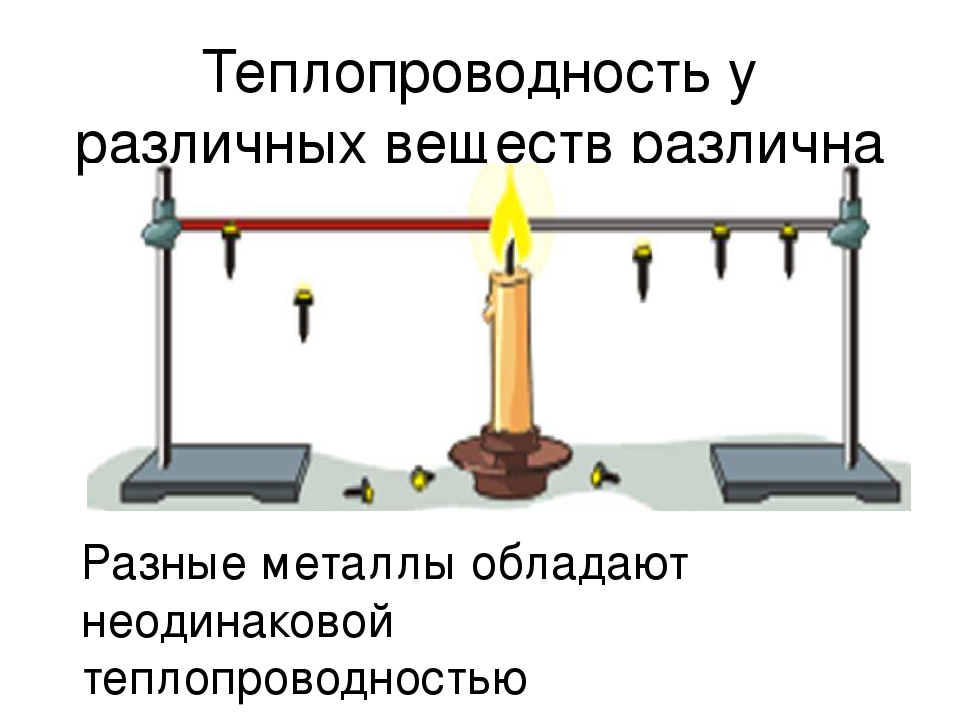
Следующие вопросы могут помочь вам придумать хороший проект для научной выставки: Какие металлы лучше всего проводят тепло? Как их можно использовать наиболее эффективно? (Ищите повседневные образцы.)
Примечание. Этот набор может содержать следы свинца. Контакт кожи со свинцом не опасен; однако, чтобы избежать потенциального переваривания, всегда мойте руки после работы.
БЛОК ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ
СОДЕРЖАНИЕ
ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ Мы хотим, чтобы этот предмет был живым, когда вы его получите! Поэтому нам нужно
знать, когда вы будете дома, чтобы получить его (минимизируя
воздействие элементов). Физика и инженерия/Сила и движение/Силовое и двигательное оборудование /физика-техника/,/физика-техника/сила-движение/,/физика-техника/сила-движение/сила-движение-оборудование/ Мы поняли. Наука может быть грязной. Но продукты и услуги Home Science Tools справятся с этим. Наши продукты долговечны, надежны и доступны по цене, чтобы доставить вас из поля в лабораторию на кухню. Они не подведут вас, с чем бы они ни столкнулись. Будь то (чрезмерно) нетерпеливые молодые ученые из года в год или строгие требования, которые возникают раз в жизни. И если ваш научный запрос пойдет не так, как ожидалось, вы можете рассчитывать на помощь нашей службы поддержки клиентов. Рассчитывайте на дружелюбные голоса на другом конце телефона и советы экспертов в своем почтовом ящике. Укажите дату доставки, среда
— Пятница, это по крайней мере 7 дней с сегодняшнего дня.
Укажите дату доставки, среда
— Пятница, это по крайней мере 7 дней с сегодняшнего дня.

 Эти знания необходимы при изучении процесса теплопроводности. Тепловой поток твердого тела определяется только его теплопроводностью, но в жидкостях и газах процессы теплопроводности, конвекции и теплового излучения действуют одновременно.
Эти знания необходимы при изучении процесса теплопроводности. Тепловой поток твердого тела определяется только его теплопроводностью, но в жидкостях и газах процессы теплопроводности, конвекции и теплового излучения действуют одновременно.
