Теплопроводность — это… Что такое Теплопроводность?
Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела ( атомами, молекулами, электронами и т.п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.
Численная характеристика теплопроводности материала равна количеству теплоты, проходящей через материал площадью 1 кв.м за единицу времени (секунду) при единичном температурном градиенте.
Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением объектов занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.
Закон теплопроводности Фурье
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
где — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, — коэффициент теплопроводности (иногда называемый просто теплопроводностью), — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]
Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
где — полная мощность тепловых потерь, — площадь сечения параллелепипеда, — перепад температур граней, — длина параллелепипеда, то есть расстояние между гранями.
Коэффициент теплопроводности измеряется в Вт/(м·K).
Коэффициент теплопроводности вакуума
Коэффициент теплопроводности вакуума почти ноль (чем глубже вакуум, тем ближе к нулю). Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, тепло в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Связь с электропроводностью
Связь коэффициента теплопроводности с удельной электрической проводимостью в металлах устанавливает закон Видемана — Франца:
где — постоянная Больцмана, — заряд электрона.
Коэффициент теплопроводности газов
Коэффициент теплопроводности газов определяется формулой[2]
Где: i — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5, для одноатомного i=3), k — постоянная Больцмана, M — молярная масса, T — абсолютная температура, d — эффективный диаметр молекул, R — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из не радиоактивных газов — у ксенона).
Обобщения закона Фурье
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело.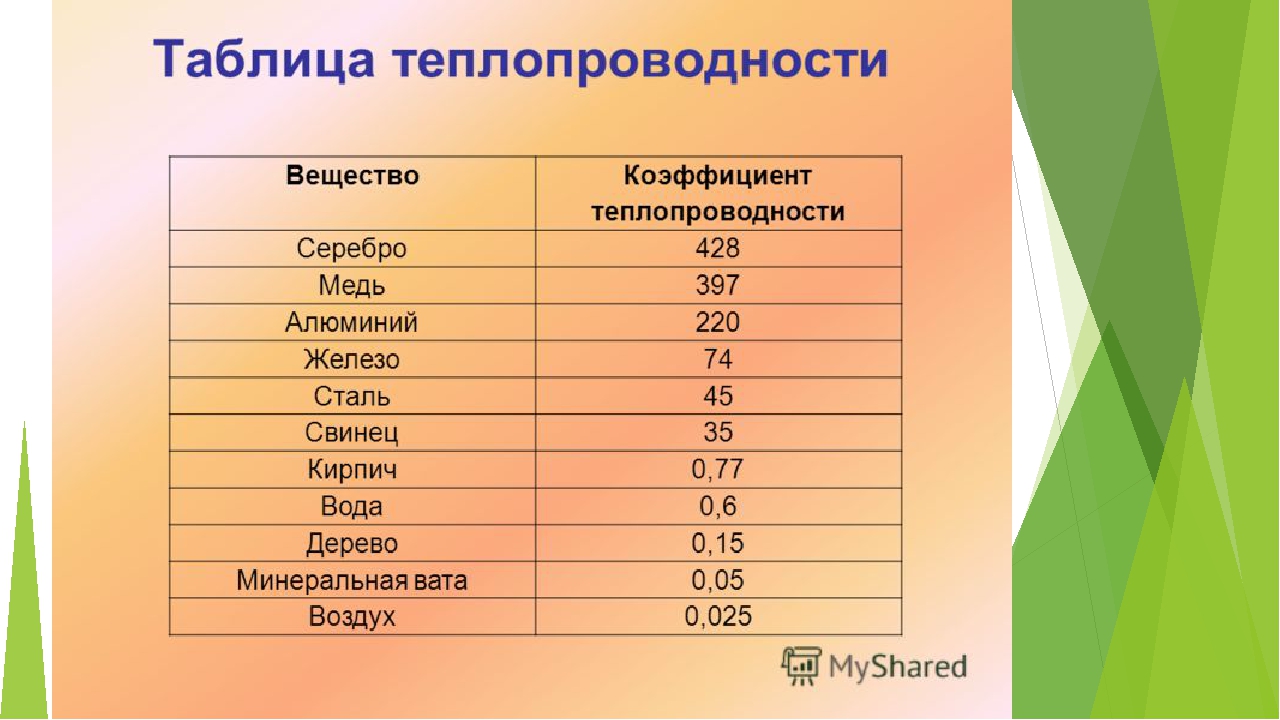 Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т.п. Инерционность в уравнения переноса первым ввел Максвелл
Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т.п. Инерционность в уравнения переноса первым ввел Максвелл
Если время релаксации пренебрежимо мало, то это уравнение переходит в закон Фурье.
Коэффициенты теплопроводности различных веществ
| Материал | Теплопроводность, Вт/(м·K) |
|---|---|
| Графен | (4840±440) — (5300±480) |
| Алмаз | 1001—2600 |
| Графит | 278,4—2435 |
| Карбид кремния | 490 |
| Серебро | 430 |
| Медь | 382—390 |
| Оксид бериллия | 370 |
| Золото | 320 |
| Алюминий | 202—236 |
| Нитрид алюминия | 200 |
| Нитрид бора | 180 |
| Кремний | 150 |
| Латунь | 97—111 |
| Хром | 93,7 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Оксид цинка | 54 |
| Сталь | 47 |
| Кварц | 8 |
| Стекло | 1-1,15 |
| КПТ-8 | 0,7 |
| Вода при нормальных условиях | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Силиконовое масло | 0,16 |
| Пенобетон | 0,14—0,3 |
| Древесина | 0,15 |
| Нефтяные масла | 0,12 |
| Свежий снег | 0,10—0,15 |
| Вата | 0,055 |
| Воздух (300 K, 100 кПа) | 0,026 |
| Вакуум (абсолютный) | 0 (строго) |
другие вещества
| Материал | Теплопроводность, Вт/(м·K) |
|---|---|
| 201 | |
| Бериллий | 201 |
| Вольфрам | 173 |
| Магний | 156 |
| Родий | 150 |
| Иридий | 147 |
| Молибден | 138 |
| Рутений | 117 |
| Хром | 93,9 |
| Осмий | 87,6 |
| Титан | 21,9 |
| Тефлон | 0,25 |
| Бумага | 0,14 |
| Полистирол | 0,082 |
| Шерсть | 0,05 |
| Минеральная вата | 0,045 |
| Пенополистирол | 0,04 |
| Стекловолокно | |
| Пробковое дерево | 0,035 |
| Пеноизол | 0,035 |
| Каучук вспененный | 0,03 |
| Аргон | 0,0177 |
| Аэрогель | 0,017 |
| Ксенон | 0,0057 |
На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений.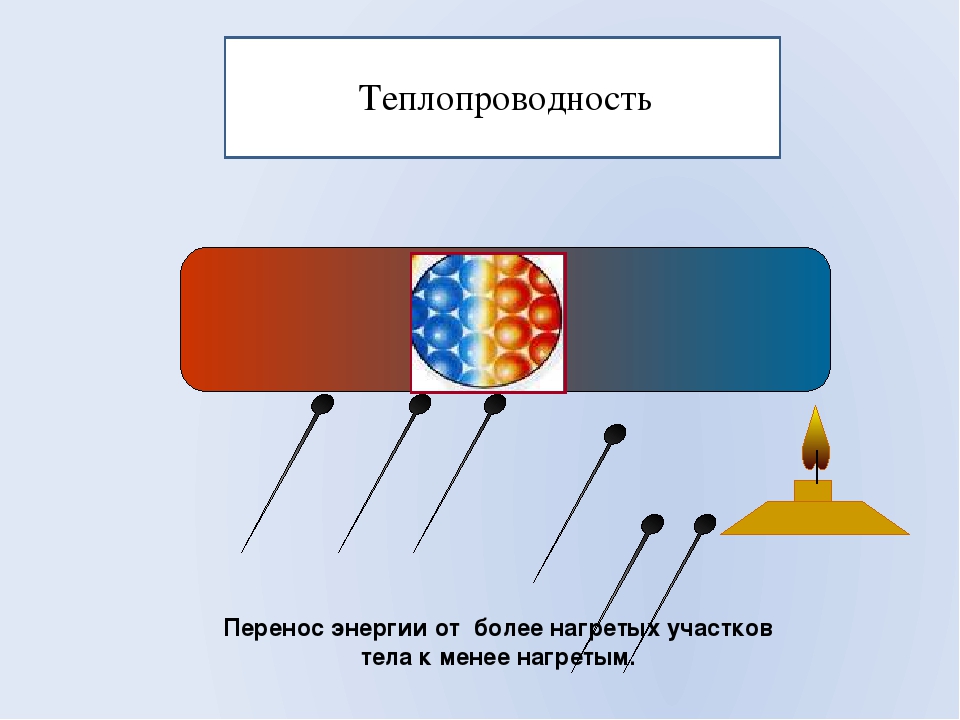 Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы). Так же в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепла, даже если зазоры представляют собой идеальный вакуум.
Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы). Так же в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепла, даже если зазоры представляют собой идеальный вакуум.
Примечания
См. также
Ссылки
Теплопроводность — это… Что такое Теплопроводность?
Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела ( атомами, молекулами, электронами и т.п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.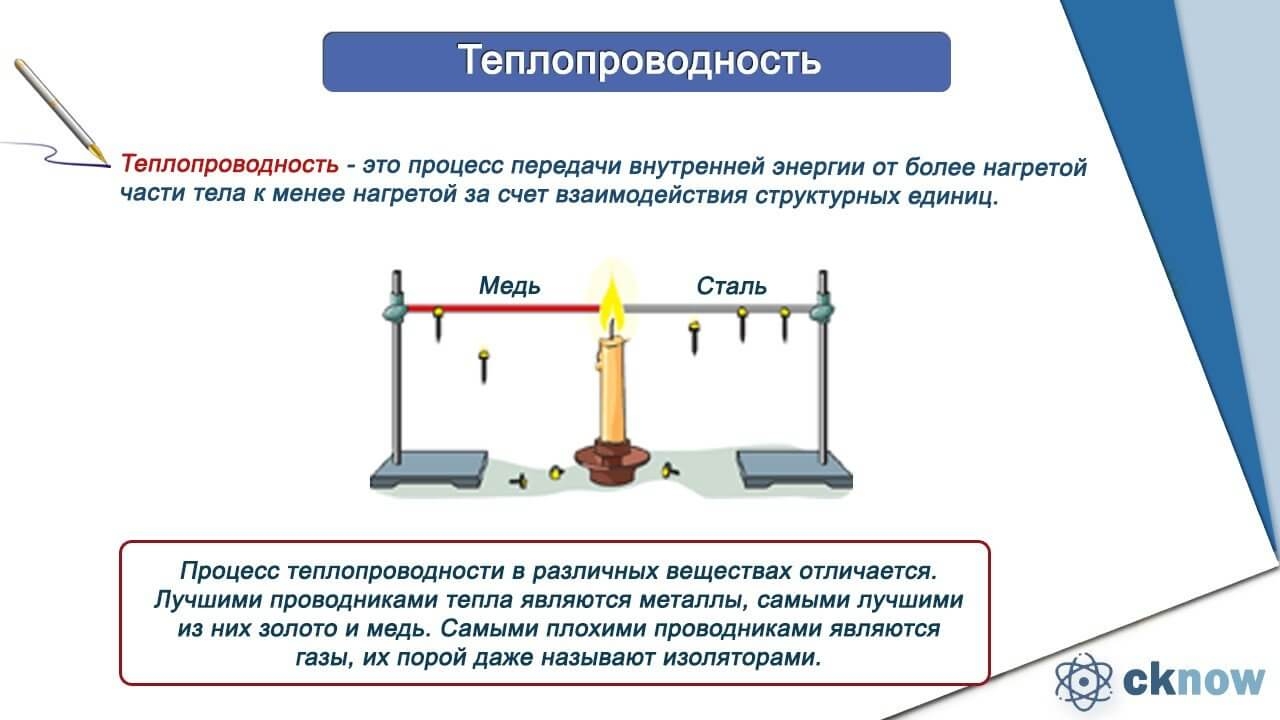
Численная характеристика теплопроводности материала равна количеству теплоты, проходящей через материал площадью 1 кв.м за единицу времени (секунду) при единичном температурном градиенте. Данная численная характеристика используется для расчета теплопроводности для калибрования и охлаждения профильных изделий.
Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением объектов занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.
Закон теплопроводности Фурье
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
где — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, — коэффициент теплопроводности (иногда называемый просто теплопроводностью), — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
где — полная мощность тепловых потерь, — площадь сечения параллелепипеда, — перепад температур граней, — длина параллелепипеда, то есть расстояние между гранями.
Коэффициент теплопроводности измеряется в Вт/(м·K).
Коэффициент теплопроводности вакуума
Коэффициент теплопроводности вакуума почти ноль (чем глубже вакуум, тем ближе к нулю). Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, тепло в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Связь с электропроводностью
Связь коэффициента теплопроводности с удельной электрической проводимостью в металлах устанавливает закон Видемана — Франца:
где — постоянная Больцмана, — заряд электрона.
Коэффициент теплопроводности газов
Коэффициент теплопроводности газов определяется формулой[2]
Где: i — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5, для одноатомного i=3), k — постоянная Больцмана, M — молярная масса, T — абсолютная температура, d — эффективный диаметр молекул, R — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из не радиоактивных газов — у ксенона).
Обобщения закона Фурье
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т.п. Инерционность в уравнения переноса первым ввел Максвелл[3], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[4]
Если время релаксации пренебрежимо мало, то это уравнение переходит в закон Фурье.
Коэффициенты теплопроводности различных веществ
| Материал | Теплопроводность, Вт/(м·K) |
|---|---|
| Графен | (4840±440) — (5300±480) |
| Алмаз | 1001—2600 |
| Графит | 278,4—2435 |
| Карбид кремния | 490 |
| Серебро | 430 |
| Медь | 382—390 |
| Оксид бериллия | 370 |
| Золото | 320 |
| Алюминий | 202—236 |
| Нитрид алюминия | 200 |
| Нитрид бора | 180 |
| Кремний | 150 |
| Латунь | 97—111 |
| Хром | 93,7 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Оксид цинка | 54 |
| Сталь | 47 |
| Кварц | 8 |
| Стекло | 1-1,15 |
| КПТ-8 | 0,7 |
| Вода при нормальных условиях | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Силиконовое масло | 0,16 |
| Пенобетон | 0,14—0,3 |
| Древесина | 0,15 |
| Нефтяные масла | 0,12 |
| Свежий снег | 0,10—0,15 |
| Вата | 0,055 |
| Воздух (300 K, 100 кПа) | 0,026 |
| Вакуум (абсолютный) | 0 (строго) |
другие вещества
| Материал | Теплопроводность, Вт/(м·K) |
|---|---|
| Кальций | 201 |
| Бериллий | 201 |
| Вольфрам | 173 |
| Магний | 156 |
| Родий | 150 |
| Иридий | 147 |
| Молибден | 138 |
| Рутений | 117 |
| Хром | 93,9 |
| Осмий | 87,6 |
| Титан | 21,9 |
| Тефлон | 0,25 |
| Бумага | 0,14 |
| Полистирол | 0,082 |
| Шерсть | 0,05 |
| Минеральная вата | 0,045 |
| Пенополистирол | 0,04 |
| Стекловолокно | 0,036 |
| Пробковое дерево | 0,035 |
| Пеноизол | 0,035 |
| Каучук вспененный | 0,03 |
| Аргон | 0,0177 |
| Аэрогель | 0,017 |
| Ксенон | 0,0057 |
На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы). Так же в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепла, даже если зазоры представляют собой идеальный вакуум.
Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы). Так же в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепла, даже если зазоры представляют собой идеальный вакуум.
Примечания
См. также
Ссылки
Что такое теплопроводность
Сергей Дворянинов
«Квантик» №2, 2019
Отчего, когда в оттепель идёт снег, он тает на руке, а на шубе остаётся?
Л. Н. Толстой, «Тепло» (Рассуждение)
Третий лишний
Вспомним одну старую задачку. Есть автобус, трамвай, троллейбус. Что здесь лишнее?
Лишний автобус, так как он работает на бензине, а не на электричестве, как трамвай и троллейбус. А можно считать лишним трамвай, потому что его колёса не «обуты» в резиновые шины.
А можно считать лишним трамвай, потому что его колёса не «обуты» в резиновые шины.
А теперь новая задача. Из трёх словосочетаний: тёплый осенний день, тёплое море, тёплая одежда — какое лишнее?
Мы называем день или море тёплыми, если у них соответствующая температура. Называя пальто или куртку тёплой, мы никак не связываем это качество одежды с её температурой как материального предмета. Следовательно, лишняя здесь тёплая одежда.
Называть одежду тёплой позволяет некоторая её физическая характеристика, о которой и расскажем.
Коэффициент теплопроводности
Наступила зима. В квартире батареи центрального отопления нагревают воздух. Почему же температура в комнатах повышается не до температуры батареи, а до меньшего уровня? Да потому, что тепло через стены уходит наружу, на улицу. Что это значит? Тепло — не какой-то физический объект. Но из жизненного опыта вы знаете, что горячее тело нагревает окружающие его холодные тела (а холодное — остужает горячие), и удобно считать, что при этом от горячих тел к холодным передаётся тепло.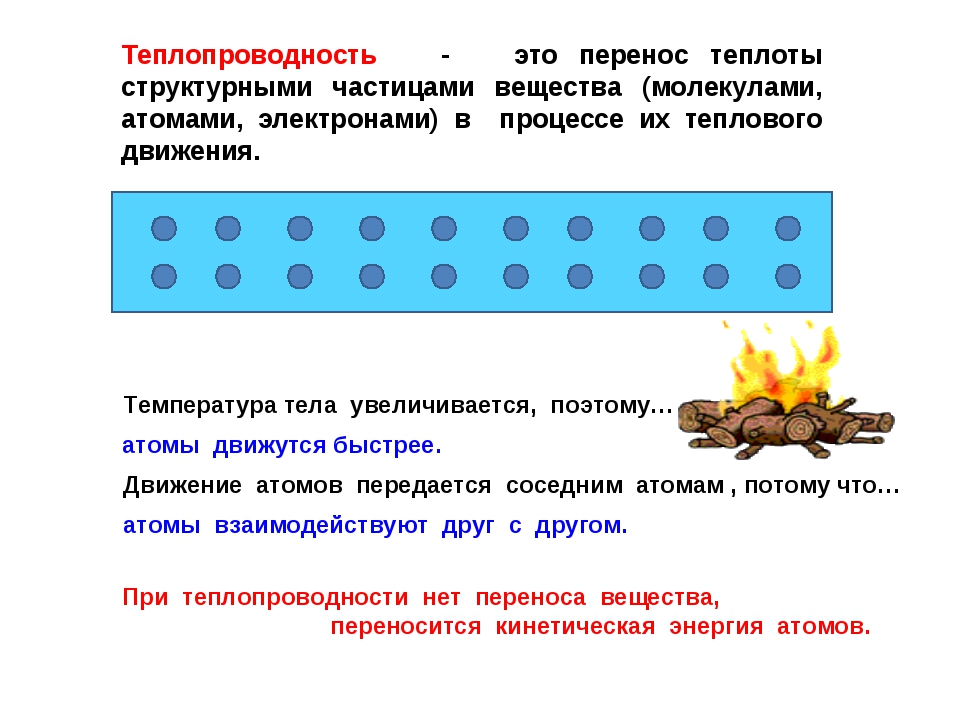
Как тепло распространяется в одном теле, от уже нагретых частей к более холодным? Разные материалы проводят тепло по-разному — одни хуже, другие лучше. Поэтому у каждого материала есть свой коэффициент теплопроводности k, равный количеству тепла, которое за 1 секунду проходит через стену из этого материала площадью 1 кв. метр и толщиной 1 метр при разности температур 1 градус.
Понятно, что через стену в два раза большей площади проходит в два раза большее количество тепла, а через стену удвоенной толщины — вдвое меньшее (подумайте, почему?). А ещё оказывается, что чем больше разность температур, тем быстрее передаётся тепло.
Количество тепла, как и любой энергии, измеряют в джоулях (Дж). Например, чтобы вскипятить 1 литр воды комнатной температуры, необходимо «передать воде» 350 000 Дж = 350 кДж. А скорость передачи тепла измеряют в ваттах (Вт). Передача 1 Дж тепла за 1 с соответствует 1 Вт. Например, мощность чайника примерно равна 2 кВт = 2000 Вт.
У силикатного (или белого) кирпича k = 0,81 (далее эту размерность будем опускать), то есть, например, для квадратного метра кирпичной стены толщиной 50 см потери тепла на 1 градус разницы температур составят 1,62 джоуля в секунду (или 1,62 ватта). У дерева k = 0,2, и потому при той же толщине стен деревянный дом теплее кирпичного в 4 раза. В частности, поэтому кирпичные стены делают толще деревянных. А у бетона k = 1,75, и панельный дом, построенный из бетонных плит, получается вдвое холоднее кирпичного с той же толщиной стен. Стены можно утеплять пенопластом — его коэффициент 0,04. Вспомним детский стишок:
Ох, беда, беда, беда,
Наступили холода.
На стекле горюет муха:
«Выпал снег белее пуха!
Если бы мне валенки,
Пусть подшиты, стареньки,
Да суконные штаны —
Дожила бы до весны!»
Дело в том, что у шерстяного войлока (то есть у тех же валенок) k = 0,045. Зимой в валенках намного теплее, чем в кожаных ботинках. Конечно, валенки ноги не греют, а лишь препятствуют большим потерям тепла.
Конечно, валенки ноги не греют, а лишь препятствуют большим потерям тепла.
У хлопковой ваты k = 0,055. Потому испокон веков ватные халаты защищали жителей Средней Азии от нестерпимой летней жары. Температура тела человека 36,7°C, температура воздуха 40–45°C. В этом случае ватный халат в минимальной степени способствует подводу тепла к телу, предохраняя человека от перегрева. Точно так же меховые рукавицы защищают руки кузнеца, держащего раскалённую заготовку.
У минеральной ваты k = 0,045–0,055. Её используют для термоизоляции труб отопления.
Газы — плохие проводники тепла, у них коэффициент теплопроводности мал, например у воздуха k = 0,022. Поэтому оконные рамы делали двойными, и в современных стеклопакетах тоже есть воздух между стёклами: можно сказать, что тепло в доме сохраняет не стекло, а воздух внутри рамы. Но газы могут передавать тепло конвекцией, то есть перемешиваться. По этой причине особенно хорошими теплоизоляционными свойствами обладают пористые материалы — поры в них препятствуют конвекции.
Многие птицы зимой во время сильных морозов зарываются в снег. Рыхлый снег почти не проводит тепло и сохраняет примерно одинаковую температуру даже при сильных ночных заморозках. Так спасаться от морозов, да и от хищников, научились глухари, тетерева, куропатки, рябчики. Птицы способны проводить под снегом без движения несколько дней, при этом их потери энергии минимальны. Да и медведи спят в берлогах, занесённых снегом, словно тёплым одеялом.
Среди металлов рекордсменом по теплопроводности можно считать серебро — у него k = 430. У железа k = 92. Если серебряную ложку опустить в кипяток, то удержать её в руках, пожалуй, не удастся: она очень быстро станет нестерпимо горячей. Металлы очень хорошо проводят тепло (гораздо лучше неметаллов), потому что в них есть свободные электроны, которые быстро перемещаются и переносят тепло.
Возвращаясь к тёплой одежде, скажем, что она не греет, а препятствует потерям тепла. Теперь вы легко объясните, какую одежду мы называем холодной.
Напоследок — две задачи.
1. В некоторых современных квартирах делают тёплые полы. Для этого вдоль всего пола прокладывают нагревательные элементы, питающиеся электричеством. А в новых вагонах московского метро появились «тёплые поручни», которые не требуют электропитания. Можете догадаться, как они устроены?
2. Эта задача очень старая. Два полярника вышли из палатки на лёд. Падающий сверху снег на комбинезоне одного потихоньку таял, а у другого — нет, делая человека похожим на снеговика. У кого одежда теплее?
Ответы
1. «Тёплые поручни» — это обычные никелированные поручни, покрытые тонким слоем пластика. Пластик плохо проводит тепло, и поэтому тепло от человеческих рук не распространяется вдоль такого поручня. Это создаёт ощущение, что поручень тёплый.
2. Если снежинки на комбинезоне тают, то температура на его поверхности плюсовая. Стало быть, такой комбинезон плохо сохраняет тепло человеческого тела и отводит его в окружающую среду. Теплее одежда у того полярника, который похож на снеговика.
Теплее одежда у того полярника, который похож на снеговика.
Художник Максим Калякин
Что такое теплопроводность и теплопередача. Теплопроводность металлов и других материалов.
• написать лс• профиль
5.0
Оценка статьи
Всего голосов: 1
Репутация автора
• повысить репутацию
• история репутации
Как и все другие виды энергии, теплота может передаваться от тела к телу. Происходит это всегда, когда есть тела разной температуры. При этом им необязательно даже находиться в соприкосновении, так существует несколько способов передачи тепла. А именно:
Теплопроводность. Это передача тепла при непосредственном контакте двух тел. (Тело может быть и одно, если его части разной температуры.
 ) При этом чем больше разность температур тел и чем больше площадь их контакта — тем больше тепла передаётся каждую секунду. Помимо этого, количество передаваемого тепла зависит от материала — например, большинство металлов хорошо проводят тепло, а дерево и пластик — гораздо хуже. Величину, характеризующую эту способность передавать тепло, тоже называют теплопроводностью (более корректно – коэффициент теплопроводности), что может приводить к некоторой путанице.
) При этом чем больше разность температур тел и чем больше площадь их контакта — тем больше тепла передаётся каждую секунду. Помимо этого, количество передаваемого тепла зависит от материала — например, большинство металлов хорошо проводят тепло, а дерево и пластик — гораздо хуже. Величину, характеризующую эту способность передавать тепло, тоже называют теплопроводностью (более корректно – коэффициент теплопроводности), что может приводить к некоторой путанице.Если необходимо измерить теплопроводность какого-либо материала, то обычно это проводят в следующем эксперименте: изготовляется стержень из интересующего материала и один его конец поддерживается при одной температуре, а другой — при отличной, например более низкой, температуре. Пусть, например, холодный конец будет помещён в воду со льдом — таким образом будет поддерживаться постоянная температура, а измеряя скорость таяния льда можно судить о количестве полученного тепла. Деля количество тепла (а вернее — мощность) на разность температур и поперечное сечение стержня и умножая на его длину, получаем коэффициент теплопроводности, измеряющийся, как следует из вышенаписанного, в Дж*м/К*м2*с, то есть в Вт/К*м.
 Ниже вы видите таблицу теплопроводности некоторых материалов.
Ниже вы видите таблицу теплопроводности некоторых материалов.| Материал | Теплопроводность, Вт/(м·K) |
| Алмаз | 1001—2600 |
| Серебро | 430 |
| Медь | 401 |
| Оксид бериллия | 370 |
| Золото | 320 |
| Алюминий | 202—236 |
| Кремний | 150 |
| Латунь | 97—111 |
| Хром | 107 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Оксид цинка | 54 |
| Сталь | 47 |
| Оксид алюминия | 40 |
| Кварц | 8 |
| Гранит | 2,4 |
| Бетон сплошной | 1,75 |
| Базальт | 1,3 |
| Стекло | 1-1,15 |
| Термопаста КПТ-8 | 0,7 |
| Вода при нормальных условиях | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Древесина | 0,15 |
| Нефтяные масла | 0,12 |
| Свежий снег | 0,10—0,15 |
| Стекловата | 0,032-0,041 |
| Каменная вата | 0,034-0,039 |
| Воздух (300 K, 100 кПа) | 0,022 |
Как видно, теплопроводность различается на много порядков. Удивительно хорошо проводят тепло алмаз и оксиды некоторых металлов (по сравнению с другими диэлектриками), плохо проводят тепло воздух, снег и термопаста КПТ-8.
Но мы привыкли считать, что воздух хорошо проводит тепло, а вата — нет, хотя она может на 99% состоять из воздуха. Дело в конвекции. Горячий воздух легче холодного, и «всплывает» наверх, порождая постоянную циркуляцию воздуха вокруг нагретого или сильно охлаждённого тела. Конвекция на порядок улучшает теплопередачу: при её отсутствии было бы очень затруднительно вскипятить кастрюлю воды, не перемешивая её постоянно. А в диапазоне от 0°С до 4°С вода при нагревании сжимается, что приводит к конвекции в противоположном от привычного направлении. Это приводит к тому, что независимо от температуры воздуха, на дне глубоких озёр температура всегда устанавливается равной 4°C
Для уменьшения теплоотдачи из пространства между стенками термосов откачивают воздух. Но надо отметить, что теплопроводность воздуха мало зависит от давления вплоть до 0,01мм рт.ст, то есть границы глубокого вакуума. Этот феномен объясняется теорией газов.
Ещё один способ теплопередачи — это излучение. Все тела излучают энергию в виде электромагнитных волн, но только достаточно сильно нагретые (~600°С) излучают в видимом нами диапазоне. Мощность излучения даже при комнатной температуре достаточно большая — порядка 40мВт с 1см2. В пересчёте на площадь поверхности человеческого тела (~1м2) это составит 400Вт. Спасает лишь то, что в привычном нам окружении все тела вокруг также излучают с примерно той же мощностью. Мощность излучения, кстати, сильно зависит от температуры (как T4) , согласно закону Стефана-Больцмана. Расчёты показывают, что, например, при 0°С мощность теплового излучения примерно в полтора раза слабее, чем при 27°С.
В отличие от теплопроводности, излучение может распространяться в полном вакууме — именно благодаря нему живые организмы на Земле получают энергию Солнца. Если теплопередача излучением нежелательна, то её минимизируют, ставя непрозрачные перегородки между холодным и горячим объектами, либо уменьшают поглощение излучения (и испускание, кстати, в ровно той же степени), покрывая поверхность тонким зеркальным слоем металла, например, серебра.
- Данные по теплопроводности взяты из Wikipedia, а туда они попали из справочников, таких, как:
- «Физические величины» под ред. И. С. Григорьева
- CRC Handbook of Chemistry and Physics
- Более строгое описание теплопроводности можно найти в учебнике по физике, например в «Общей физике» Д.В.Сивухина (Том 2). В 4 томе есть глава, посвящённая тепловому излучению (в т.ч. закону Стефана-Больцмана)
понятие о термине, единица измерения, коэффициент для разных материалов
При возведении здания строители стараются добиться его энергоэффективности, чтобы условия в помещениях были комфортными. Для этого учитывают теплопроводность строительных материалов. Но, если принято решение самостоятельно заниматься этим процессом, то понадобится изучить все понятия о термине и единице его измерения, чтобы правильно подобрать теплоизоляцию. В связи с тем, что коэффициент теплопроводности разный для материалов, к вопросу нужно подойти ответственно, чтобы избежать ошибки при их выборе.
Теплопроводность – что это такое
Теплопроводностью называется способность всех видов газов, жидкости или материалов передавать тепло. Это значит, что когда объект нагревается с одной стороны, он трансформируется в теплопроводник, т.к. передает свою энергию дальше. При охлаждении процесс происходит также.
Например, если во время приготовления пищи перемешивать продукты деревянной лопаткой, то изменений в температуре не последует. Но, если для этих целей использовать кухонную утварь из металла, то она быстро нагреется так, что держать ее станет в руке невозможно. Таких примеров теплопроводности привести можно немало.
Объяснение этого с точки зрения физики: тепловая энергия стремится от среды с высокой температурой к среде с низкой температурой. Причем ей требуется время, чтобы пройти через стройматериал. Чем больше его нужно, тем ниже скорость передачи тепла.
Внимание!Если температура по обе стороны используемого материала одинаковая, то переход тепловой энергии не состоится.
Так,
- теплопроводность кирпича и стали составляет 0,56 и 58Вт/м●К соответственно;
- древесины – 0,09-0,1;
- песка – 0,35
Можно заметить, что не все материалы обладают одинаковой теплоэффективностью, это зависит от факторов:
- Пористая структура свидетельствует о ее неоднородности и наличии воздуха в порах.
- Структура пор – небольшие размеры и их замкнутость приводит к снижению теплового потока.
- Плотность – чем она выше, тем больше коэффициент проводимости тепла.
- Влажность – негативный фактор, который повышает скорость теплопередачи. Поэтому надо качественно произвести гидроизоляцию сооружения, правильно сделать вентиляцию и использовать влагоустойчивые стройматериалы.
Формула теплопроводности создана с учетом воздействия температуры на это свойство материала. Выглядит она так:
λ=λ0●(1+b●t), где
- λ0 — коэффициент теплопроводности при 0°С, измеряется который в Вт/м●℃;
- b – справочная величина температуры;
- t – непосредственно температура.
Коэффициент теплопроводности
Зачастую в паспорте стройматериалов указан коэффициент теплопроводности – единица измерения которого Вт/(м●℃). Она характеризует любой материал как проводник тепла. В формуле она определяется греческой буквой λ.
Внимание!Часто в формулах можно увидеть не градусы по Цельсию, а по Кельвину, обозначающиеся как K. Суть от этого не меняется.
Данный коэффициент демонстрирует способность используемого материала передавать тепло на определенную дистанцию за время. При этом показатель определяет именно сырье, а его размеры значения не имеют.
Рассчитать коэффициент теплообмена можно для материала строительного и иного назначения. Например, коэффициент теплоотдачи стали использовать как теплоотвод или теплообменник. Но для больше части стройматериалов ситуация обратная – чем меньше этот показатель для стен, тем меньше тепла здание потеряет зимой.
Сопротивление теплопередаче
Коэффициент теплопередачи – это показатель, характеризующий используемый материал. Но, как показывает практика, лучше оперировать какой-то величиной, которая будет описывать теплопроводные способности определенного сооружения. Иными словами, учитываться должны особенности его строения и параметров.
Термическое сопротивление – это и есть такая величина. Можно считать, что она обратная коэффициенту теплопроводности и учитывающая толщину стройматериала. Для этого показателя существует следующее обозначение – R. Формула при этом выглядит следующим образом:
R = h/λ, где
- R — сопротивление теплопередаче однослойной однородной ограждающей конструкции, м²•℃/Вт;
- h — толщина этого слоя в метрах;
- λ — коэффициент теплопроводности материала конструкции, Вт/(м•℃).
Часто стены сооружают многослойными, один слой при этом – утеплитель с низким коэффициентом теплопроводности. Благодаря такому подходу нужный показатель повышается. Это связано с тем, что надо прибавить все слои сопротивления теплопередаче, из которых состоит ограждающая конструкция. Не стоит забывать и о суммировании приграничных слоев воздуха внутри и снаружи сооружения.
Таблица теплопроводности материалов
Для стен, перекрытий, и полов используют разные материалы, но часто теплопроводность гипсокартона и других строительных материалов сравнивают с кирпичом. Его знают все, поэтому проводить аналогии с ним намного проще. Но для кирпичных стен надо выбрать теплоизоляцию, т.к. они обладают высокой теплопроводностью.
Строительные материалы
Коэффициент теплопроводности строительных материалов указан в таблице. В ней отражены нормативные показатели, демонстрирующие теплоизоляционные свойства.
| Строительный материал | Плотность, кг/м³ | Теплопроводность, Вт/м•К |
| Бетон | 2400 | 1,51 |
| Железобетон | 2500 | 1,69 |
| Керамзитобетон | 500 | 0,14 |
| 1800 | 0,66 | |
| Пенобетон | 300 | 0,08 |
| Пеностекло | 400 | 0,11 |
Эти значения используют, если надо рассчитать:
- теплоизоляцию фасадов;
- общестроительную изоляцию;
- сколько понадобится изоляционных материалов при устройстве крыши;
- техническую изоляцию.
Такие простые вычисления уже в начале проектирования позволят определить более подходящие материалы и их количество.
Показатель теплопроводности металлов (железа, алюминия и пр.) тоже имеет значение в строительстве, например, при выборе батареи в помещение. Кроме этого, эти значения пригодятся в процессе сварки ответственных сооружений, производстве полупроводников и изоляторов разного типа. Таблица теплопроводности металлов поможет быстро найти нужное значение.
| Металл | Коэффициент теплопроводности при температуре, °C | ||||
| -100 | 0 | 100 | 300 | 700 | |
| Алюминий | 2,45 | 2,38 | 2,3 | 2,26 | 0,9 |
| Бериллий | 4,1 | 2,3 | 1,7 | 1,25 | 0,9 |
| Ванадий | — | — | 0,31 | 0,34 | — |
| Висмут | 0,11 | 0,08 | 0,07 | 0,11 | 0,15 |
| Вольфрам | 2,05 | 1,9 | 1,65 | 1,45 | 1,2 |
| Гафний | — | — | 0,22 | 0,21 | — |
| Железо | 0,94 | 0,76 | 0,69 | 0,55 | 0,34 |
| Золото | 3,3 | 3,1 | 3,1 | — | — |
| Индий | — | 0,25 | — | — | — |
| Иридий | 1,51 | 1,48 | 1,43 | — | — |
| Кадмий | 0,96 | 0,92 | 0,9 | 0,95 | 0,44 |
| Калий | — | 0,99 | — | 0,42 | 0,34 |
| Кальций | — | 0,98 | — | — | — |
| Кобальт | — | 0,69 | — | — | — |
Таблица теплопроводности воздуха поможет правильно рассчитать показатель теплообмена. Все расчеты зависят от температуры окружающей среды.
| Температура, °C | Теплопроводность, Вт/м•град |
| -50 | 0,0204 |
| -40 | 0,0212 |
| -30 | 0,022 |
| -20 | 0,0228 |
| -10 | 0,0236 |
| 0 | 0,0244 |
| 10 | 0,0251 |
| 20 | 0,0259 |
| 30 | 0,0267 |
| 40 | 0,0276 |
| 50 | 0,0283 |
Судя по данным из таблицы, с увеличением температуры показатель теплопроводности также растет.
Теплоизоляционные материалы
В основном надо учитывать показатель теплопроводности изоляционных материалов. Важно помнить, что если у металлов он зависит от температуры воздуха, то у утеплителей главную роль играет плотность. По этой причине в таблице расставлены результаты с учетом плотности используемого материала.
| Теплоизоляция | Плотность, кг/м³ | Теплопроводность, Вт/м•К |
| Минеральная вата (базальтовая) | 50 | 0,048 |
| 100 | 0,056 | |
| 200 | 0,07 | |
| Стекловата | 155 | 0,041 |
| 200 | 0,044 | |
| Пенополистирол | 40 | 0,038 |
| 100 | 0,041 | |
| 150 | 0,5 | |
| Пенополистирол экструдированный | 33 | 0,031 |
| Пенополиуретан | 32 | 0,023 |
| 40 | 0,029 | |
| 60 | 0,035 | |
| 80 | 0,041 |
Перед тем, как сделать окончательный выбор, надо взять во внимание тот факт, что некоторые из представленных материалов при повышенной влажности значительно лучше проводят тепло. В случае, когда во время его использования существует вероятность наступления такой ситуации надолго, для расчета надо применять теплопроводность именно для такого состояния.
Для чего рассчитывается теплопроводность
Коэффициент теплопередачи поможет рассчитать без ошибок толщину несущих стен с учетом утеплителей. Процент потери тепла в здании составляет:
- по 30% через кровлю и стены;
- 10% — сквозь полы;
- 20% приходится на окна и двери.
Утечка тепла происходит через несколько ограждающих конструкций в строящемся здании.
Иными словами, при неправильном расчете, жители такого дома будут использовать только 10% тепловой энергии, исходящей от радиаторов отопления.
Как рассчитать толщину стены
Для этого понадобится суммировать коэффициенты теплопроводности всех материалов, которые были использованы при возведении стены. Это неудивительно, т.к. часто этот элемент возводят в несколько слоев. Так, коэффициент теплопроводности кирпича, наружного слоя штукатурки и облицовки надо учесть, как и выравнивающие материалы, используемые для внутренних работ (листы из гипсокартона, плиты, панели и пр.). Показателем воздушной прослойки тоже не стоит пренебрегать.
Существует удельная теплопроводность для каждого региона страны, которую берут за основу вычислений. Важно помнить, что расчетная величина не должна быть больше удельной. В таблице приведены значения по городам, которые рассчитывались с учетом средней температуры и уровня влажности:
| Населенный пункт | Теплопроводность |
Москва | 3,14 |
Санкт-Петербург | 3,18 |
Ростов-на-Дону | 2,75 |
Сочи | 2,1 |
Чем южнее, тем показатель должен быть меньше. Следовательно, толщину стены можно уменьшить.
Определение теплопроводности стройматериалов — важный этап при возведении зданий. Благодаря ему в помещении можно обеспечить комфортные условия проживания: зимой в нем не будет холодно, а летом — жарко. Поэтому пренебрегать им не стоит. Кроме этого, нужно знать, от чего зависит теплопроводность.
Теплопроводность
Что такое теплопроводностьВ предыдущей главе мы рассматривали явление передачи тепла от одного предмета к другому, явление передачи внутренней энергии. Также внутренняя энергия может передаваться от одной части тела к другому. Если нагреть гвоздь с одного конца, то через некоторое время и другой его конец тоже нагреется.
Итак, теплопроводность — это процесс передачи внутренней энергии от одной части тела к другой или от одного тела к другому при их контакте.
Какой теплопроводностью обладают веществаКаждый предмет или объект в природе состоит из разного вещества. В каждом веществе молекулы находятся на разном расстоянии между собой. Следовательно, исходя из этого упрощенного варианты, можно прийти к выводу о том, что каждое тело (вещество) обладает разной теплопроводностью.
Если нагреть палку с одной стороны, то через время вторая сторона не нагревается или нагревается очень слабо, но если тот же опыт провести с гвоздем, то через время вторая сторона гвоздя также станет горячей. Можно сделать вывод о том, что дерево обладает малой теплопроводностью, а железо, из которого сделан гвоздь — большой.
Жидкости обладают меньшей теплопроводностью. Самой малой теплопроводностью обладают газы. Ну и почти отсутствует теплопроводность в вакууме, так как в нем расстояние между частицами очень велико. По такому принципу построены термосы, которые могут сохранять температуру внутри продолжительное время. Дело в том, что между стенками термоса откачан воздух и содержится практически вакуум. Из-за этого от одной стенки к другой внутренняя энергия передается очень медленно из-за очень низкой теплопроводности.
Рассмотрим на видеоролике эксперимент теплопроводности для разных сред. Три банки с водой охлаждаются в холодильнике, во льду и в холодной соленой воде со льдом. Какая из трех банок охладится быстрее? В какой среде теплопроводность выше?
Коэффициент теплопроводности материалов таблица, формулы
Термин «теплопроводность» применяется к свойствам материалов пропускать тепловую энергию от горячих участков к холодным. Теплопроводность основана на движении частиц внутри веществ и материалов. Способность передавать энергию тепла в количественном измерении – это коэффициент теплопроводности. Круговорот тепловой энергопередачи, или тепловой обмен, может проходить в любых веществах с неравнозначным размещением разных температурных участков, но коэффициент теплопроводности зависим от давления и температуры в самом материале, а также от его состояния – газообразного, жидкого или твердого. Эквивалентная теплопроводимость строительных материалов и утеплителей
Физически теплопроводность материалов равняется количеству тепла, которое перетекает через однородный предмет установленных габаритов и площади за определенный временной отрезок при установленной температурной разнице (1 К). В системе СИ единичный показатель, который имеет коэффициент теплопроводности, принято измерять в Вт/(м•К).
Как рассчитать теплопроводность по закону Фурье
В заданном тепловом режиме плотность потока при передаче тепла прямо пропорциональна вектору максимального увеличения температуры, параметры которой изменяются от одного участка к другим, и по модулю с одинаковой скоростью увеличения температуры по направлению вектора:
q → = − ϰ х grad х (T), где:
- q → – направление плотности предмета, передающего тепло, или объем теплового потока, который протекает по участку за заданную временную единицу через определенную площадь, перпендикулярный всем осям;
- ϰ – удельный коэффициент теплопроводности материала;
- T – температура материала.
Знак «-» в формуле перед «ϰ» указывает, что тепло движется в противоположном направлении от вектора grad х (T)/ – в направлении уменьшения температуры предмета. Эта формула отражает закон Фурье. В интегральном выражении коэффициент теплопередачи согласно закону Фурье будет выглядеть как формула:
- P = − ϰ х S х ΔT / l, выражается в (Вт/(м•К) х (м2•К) / м = Вт/(м•К) х (м•К) = Вт), где:
- P – общая мощность потерь теплоотдачи;
- S – сечение предмета;
- ΔT – разница температуры по стыкам сторон предмета;
- l – расстояние между стыками сторон предмета – длина фигуры.
Электропроводность и коэффициент теплопередачи
Собственно, коэффициент теплопроводности металлов «ϰ» связан с их удельной электропроводимостью «σ» согласно закону Видемана-Франца, в соответствии с которым коэффициент теплопроводности металлов зависит от удельной электропроводимости прямо пропорционально температуре:
Κ / σ = π2 / 3 х (К / e)2 х T, где:
- К – постоянный коэффициент Больцмана, устанавливающий закономерность между тепловой энергией тела и его температурой;
- e – заряд электрона;
- T – термодинамическая температура предмета.
Коэффициент теплопроводности газовой среды
В газовой среде коэффициент теплопроводности воздуха может рассчитываться по приблизительной формуле:
ϰ ~ 1/3 х p х cv х Λλ х v–, где:
- pv – плотность газовой среды;
- cv – удельная емкость тепловой энергии при одном и том же объеме тела;
- Λλ – расстояние свободного перемещения молекул в газовой среде;
- v– – скорость передачи тепла.
Или:
ϰ = I x К / 3 x π3/3 x d2 √ RT / μ, где:
- i – результат суммирования уровней свободы прямого движения и вращения молекул в газовой среде (для 2-атомных газов i=5, для 1-атомных i=3;
- К – коэффициент Больцмана;
- μ – отношение массы газа к количеству молей газа;
- T – термодинамическая температура;
- d – ⌀ молекул газа;
- R – универсальный коэффициент для газовой среды.
Согласно формуле минимальная теплопроводность материалов существует у тяжелых инертных газов, максимально эффективная теплопроводность строительных материалов – у легких.
Теплопроводимость в газовой разреженной среде
Газовая среда и теплопроводность
Результат по выкладкам выше, по которым делают расчет теплопроводности для газовой среды, от давления не зависит. Но в очень разреженной газовой среде расстояние свободного перемещения молекул зависит не от столкновений частиц, а от препятствий в виде стен резервуара. При этом ограничение перемещения молекул в соответствующих единицах измерения называют высоковакуумной средой, при которой степень теплообмена уменьшается в зависимости от плотности материала и прямо пропорциональна значению давления в резервуаре:
ϰ ~ 1/3 х p х cv х l х v–, где:
i – объем резервуара;
Р – уровень давления в резервуаре.
Согласно этой формуле теплопроводность в вакуумной среде стремится к нулевой отметке при глубоком вакууме. Это объясняется тем, что в вакууме частицы, которые передают тепловую энергию, имеют низкую плотность на единицу площади. Но тепловая энергия в вакуумной среде перетекает посредством излучения. В качестве примера можно привести обычный термос, в котором для уменьшения потерь тепловой энергии стенки должны быть двойными и посеребренными, без воздуха между ними. Что такое тепловое излучение
При применении закона Фурье не принимают во внимание инерционность перетекания тепловой энергии, а это значит, что имеется в виду мгновенная передача тепла из любой точки на любое расстояние. Поэтому формулу нельзя использовать для расчетов передачи тепла при протекании процессов, имеющих высокую частоту повторения. Это ультразвуковое излучение, передача тепловой энергии волнами ударного или импульсного типа и т.д. Существует решение по закону Фурье с релаксационным членом:
τ х ∂q / ∂t = − (q + ϰ х ∇T) .
Если релаксация τ мгновенная, то формула превращается в закон Фурье.
Ориентировочная таблица теплопроводности материалов:
| Основа | Значение теплопроводности, Вт/(м•К) |
| Жесткий графен | 4840 +/– 440 – 5300 +/– 480 |
| Алмаз | 1001-2600 |
| Графит | 278,4-2435 |
| Бора арсенид | 200-2000 |
| SiC | 490 |
| Ag | 430 |
| Cu | 401 |
| BeO | 370 |
| Au | 320 |
| Al | 202-236 |
| AlN | 200 |
| BN | 180 |
| Si | 150 |
| Cu3Zn2 | 97-111 |
| Cr | 107 |
| Fe | 92 |
| Pt | 70 |
| Sn | 67 |
| ZnO | 54 |
| Черная сталь | 47-58 |
| Pb | 35,3 |
| Нержавейка | Теплопроводность стали – 15 |
| SiO2 | 8 |
| Высококачественные термостойкие пасты | 5-12 |
| Гранит (состоит из SiO2 68-73 %; Al2O3 12,0-15,5 %; Na2O 3,0-6,0 %; CaO 1,5-4,0 %; FeO 0,5-3,0 %; Fe2O3 0,5-2,5 %; К2О 0,5-3,0 %; MgO 0,1-1,5 %; TiO2 0,1-0,6 %) | 2,4 |
| Бетонный раствор без заполнителей | 1,75 |
| Бетонный раствор со щебнем или с гравием | 1,51 |
| Базальт (состоит из SiO2 – 47-52%, TiO2 – 1-2,5%, Al2O3 – 14-18%, Fe2O3 – 2-5%, FeO – 6-10%, MnO – 0,1-0,2%, MgO – 5-7%, CaO – 6-12%, Na2O – 1,5-3%, K2O – 0,1-1,5%, P2O5 – 0,2-0,5 %) | 1,3 |
| Стекло (состоит из SiO2, B2O3, P2O5, TeO2, GeO2, AlF3 и т.д.) | 1-1,15 |
| Термостойкая паста КПТ-8 | 0,7 |
| Бетонный раствор с наполнителем из песка, без щебня или гравия | 0,7 |
| Вода чистая | 0,6 |
| Силикатный или красный кирпич | 0,2-0,7 |
| Масла на основе силикона | 0,16 |
| Пенобетон | 0,05-0,3 |
| Газобетон | 0,1-0,3 |
| Дерево | Теплопроводность дерева – 0,15 |
| Масла на основе нефти | 0,125 |
| Снег | 0,10-0,15 |
| ПП с группой горючести Г1 | 0,039-0,051 |
| ЭППУ с группой горючести Г3, Г4 | 0,03-0,033 |
| Стеклянная вата | 0,032-0,041 |
| Вата каменная | 0,035-0,04 |
| Воздушная атмосфера (300 К, 100 кПа) | 0,022 |
| Гель на основе воздуха | 0,017 |
| Аргон (Ar) | 0,017 |
| Вакуумная среда | 0 |
Приведенная таблица теплопроводности учитывает теплопередачу посредством теплового излучения и теплообмена частиц. Так как вакуум не передает тепло, то оно перетекает при помощи солнечного излучения или другого типа генерации тепла. В газовой или жидкой среде слои с разной температурой смешиваются искусственно или естественным способом.
Таблица теплопроводимости стройматериалов
Проводя расчет теплопроводности стены, необходимо принимать во внимание, что теплопередача сквозь стеновые поверхности меняется от того, что температура в здании и на улице всегда разная, и зависит от площади всех поверхностей дома и от теплопроводности стройматериалов.
Чтобы количественно оценить теплопроводность, ввели такое значение, как коэффициент теплопроводности материалов. Он показывает, как тот или иной материал способен передавать тепло. Чем выше это значение, например, коэффициент теплопроводности стали, тем эффективнее сталь будет проводить тепло.
- При утеплении дома из древесины рекомендуется выбирать стройматериалы с низким коэффициентом.
- Если стена кирпичная, то при значении коэффициента 0,67 Вт/(м2•К) и толщине стены 1 м при ее площади 1 м2 при разнице наружной и внутридомовой температуры 10С кирпич будет пропускать 0,67 Вт энергии. При разнице температур 100С кирпич будет пропускать 6,7 Вт и т.д.
Стандартное значение коэффициента теплопроводимости теплоизоляции и других строительных материалов верно для толщины стены 1 м. Чтобы провести расчет теплопроводности поверхности другой толщины, следует коэффициент поделить на выбранное значение толщины стены (метры). Ориентировочные показатели коэффициентов теплопроводимости
В СНиП и при проведении расчетов фигурирует термин «тепловое сопротивление материала», он означает обратную теплопроводность. То есть при теплопроводности листа пенопласта 10 см и его теплопроводности 0,35 Вт/(м2•К) тепловое сопротивление листа – 1 / 0,35 Вт/(м2•К) = 2,85 (м2•К)/Вт.
Ниже – таблица теплопроводности для востребованных строительных материалов и теплоизоляторов:
| Стройматериалы | Коэффициент теплопроводимости, Вт/(м2•К) |
| Плиты из алебастра | 0,47 |
| Al | 230 |
| Шифер асбоцементный | 0,35 |
| Асбест (волокно, ткань) | 0,15 |
| Асбоцемент | 1,76 |
| Асбоцементные изделия | 0,35 |
| Асфальт | 0,73 |
| Асфальт для напольного покрытия | 0,84 |
| Бакелит | 0,24 |
| Бетон с заполнителем щебнем | 1,3 |
| Бетон с заполнителем песком | 0,7 |
| Пористый бетон – пено- и газобетон | 1,4 |
| Сплошной бетон | 1,75 |
| Термоизоляционный бетон | 0,18 |
| Битумная масса | 0,47 |
| Бумажные материалы | 0,14 |
| Рыхлая минвата | 0,046 |
| Тяжелая минвата | 0,05 |
| Вата – теплоизолятор на основе хлопка | 0,05 |
| Вермикулит в плитах или листах | 0,1 |
| Войлок | 0,046 |
| Гипс | 0,35 |
| Глиноземы | 2,33 |
| Гравийный заполнитель | 0,93 |
| Гранитный или базальтовый заполнитель | 3,5 |
| Влажный грунт, 10% | 1,75 |
| Влажный грунт, 20% | 2,1 |
| Песчаники | 1,16 |
| Сухая почва | 0,4 |
| Уплотненный грунт | 1,05 |
| Гудроновая масса | 0,3 |
| Доска строительная | 0,15 |
| Фанерные листы | 0,15 |
| Твердые породы дерева | 0,2 |
| ДСП | 0,2 |
| Дюралюминиевые изделия | 160 |
| Железобетонные изделия | 1,72 |
| Зола | 0,15 |
| Известняковые блоки | 1,71 |
| Раствор на песке и извести | 0,87 |
| Смола вспененная | 0,037 |
| Природный камень | 1,4 |
| Картонные листы из нескольких слоев | 0,14 |
| Каучук пористый | 0,035 |
| Каучук | 0,042 |
| Каучук с фтором | 0,053 |
| Керамзитобетонные блоки | 0,22 |
| Красный кирпич | 0,13 |
| Пустотелый кирпич | 0,44 |
| Полнотелый кирпич | 0,81 |
| Сплошной кирпич | 0,67 |
| Шлакокирпич | 0,58 |
| Плиты на основе кремнезема | 0,07 |
| Латунные изделия | 110 |
| Лед при температуре 00С | 2,21 |
| Лед при температуре -200С | 2,44 |
| Лиственное дерево при влажности 15% | 0,15 |
| Медные изделия | 380 |
| Мипора | 0,086 |
| Опилки для засыпки | 0,096 |
| Сухие опилки | 0,064 |
| ПВХ | 0,19 |
| Пенобетон | 0,3 |
| Пенопласт марки ПС-1 | 0,036 |
| Пенопласт марки ПС-4 | 0,04 |
| Пенопласт марки ПХВ-1 | 0,05 |
| Пенопласт марки ФРП | 0,044 |
| ППУ марки ПС-Б | 0,04 |
| ППУ марки ПС-БС | 0,04 |
| Лист из пенополиуретана | 0,034 |
| Панель из пенополиуретана | 0,024 |
| Облегченное пеностекло | 0,06 |
| Тяжелое вспененное стекло | 0,08 |
| Пергаминовые изделия | 0,16 |
| Перлитовые изделия | 0,051 |
| Плиты на цементе и перлите | 0,085 |
| Влажный песок 0% | 0,33 |
| Влажный песок 0% | 0,97 |
| Влажный песок 20% | 1,33 |
| Обожженный камень | 1,52 |
| Керамическая плитка | 1,03 |
| Плитка марки ПМТБ-2 | 0,035 |
| Полистирол | 0,081 |
| Поролон | 0,04 |
| Раствор на основе цемента без песка | 0,47 |
| Плита из натуральной пробки | 0,042 |
| Легкие листы из натуральной пробки | 0,034 |
| Тяжелые листы из натуральной пробки | 0,05 |
| Резиновые изделия | 0,15 |
| Рубероид | 0,17 |
| Сланец | 2,100 |
| Снег | 1,5 |
| Хвойная древесина влажностью 15% | 0,15 |
| Хвойная смолистая древесина влажностью 15% | 0,23 |
| Стальные изделия | 52 |
| Стеклянные изделия | 1,15 |
| Утеплитель стекловата | 0,05 |
| Стекловолоконные утеплители | 0,034 |
| Стеклотекстолитовые изделия | 0,31 |
| Стружка | 0,13 |
| Тефлоновое покрытие | 0,26 |
| Толь | 0,24 |
| Плита на основе цементного раствора | 1,93 |
| Цементно-песчаный раствор | 1,24 |
| Чугунные изделия | 57 |
| Шлак в гранулах | 0,14 |
| Шлак зольный | 0,3 |
| Шлакобетонные блоки | 0,65 |
| Сухие штукатурные смеси | 0,22 |
| Штукатурный раствор на основе цемента | 0,95 |
| Эбонитовые изделия | 0,15 |
Кроме того, необходимо учитывать теплопроводность утеплителей из-за их струйных тепловых потоков. В плотной среде возможно «переливание» квазичастиц из одного нагретого стройматериала в другой, более холодный или более теплый, через поры субмикронных размеров, что помогает распространять звук и тепло, даже если в этих порах будет абсолютный вакуум.
4.3: Теплопроводность — Physics LibreTexts
На рисунке IV.1 показан поток тепла со скоростью dQ / dt вдоль полосы материала площадью поперечного сечения A . По длине планки наблюдается перепад температур (поэтому по ней течет тепло). На расстоянии х от конца стержня температура Т ; на расстоянии x + δ x это T + δ T . Обратите внимание, что если тепло течет в положительном направлении, как показано, δ T должно быть отрицательным.То есть, ближе к правому концу планки холоднее. Температурный градиент dT / dx отрицательный. Тепло течет в направлении, противоположном градиенту температуры.
Отношение скорости теплового потока на единицу площади к отрицательному градиенту температуры называется теплопроводностью материала:
\ [\ frac {dQ} {dt} = -KA \ frac {dT} {dx}. \]
Я использую символ K для обозначения теплопроводности. Другие часто встречающиеся символы — это k или λ.Его единица СИ — Вт · м −1 K −1 .
Я определил это в одномерной ситуации и для изотропной среды, и в этом случае тепловой поток противоположен градиенту температуры. Можно представить, что в анизотропной среде скорость теплового потока и градиент температуры могут быть разными параллельно разным кристаллографическим осям. В этом случае тепловой поток и температурный градиент не могут быть строго антипараллельными, а теплопроводность является тензорной величиной.Такая ситуация не будет касаться нас в этой главе.
Если в нашем одномерном примере нет утечки тепла по сторонам стержня, тогда скорость потока тепла вдоль стержня должна быть одинаковой по всей длине стержня, что означает, что градиент температуры является однородным. по длине проволоки. Возможно, проще представить отсутствие потерь тепла с боков, чем добиться этого на практике. Если бы стержень был расположен в вакууме, не было бы потерь на теплопроводность или конвекцию, а если бы стержень был очень блестящим, потери на излучение были бы незначительными.
Значения по порядку величины теплопроводности обычных веществ
Воздух 0,03 Вт м −1 K −1
Вода 0,6
Стекло 0,8
Fe 80
Al 240
Cu 400
Легко представить, как тепло может проводиться по твердому телу, когда колебания атомов на одном конце твердого тела передаются следующим атомам, когда один атом подталкивает следующий, и так далее. Однако из таблицы видно, и во всяком случае общеизвестно, что одни вещества (металлы) проводят тепло намного лучше, чем другие.Действительно, среди металлов существует тесная корреляция между теплопроводностью и электропроводностью (при данной температуре). Это говорит о том, что механизм теплопроводности в металлах такой же, как и для электропроводности. Тепло в металле переносится в основном электронами.
Было бы интересно найти в Интернете или других источниках значения теплопроводности и электропроводности ряда металлов. Можно обнаружить, что значения теплопроводности, K , иногда указываются в незнакомых «практических» единицах, таких как БТЕ в час на квадратный фут для температурного градиента 1 F ° на дюйм, и переводят их в единицы СИ, Вт · м. −1 K −1 может быть немного сложной задачей.Электропроводность σ несколько уменьшается с повышением температуры (как и теплопроводность, но в меньшей степени), поэтому было бы важно найти их все при одинаковой температуре. Тогда вы сможете увидеть, действительно ли отношение K / σ одинаково для всех металлов при данной температуре. 2 = 2.{-1}. \]
Здесь k — постоянная Больцмана, а e — заряд электрона. Было обнаружено, что это предсказание хорошо выполняется при комнатной температуре и выше, но при низких температурах электропроводность быстро увеличивается с понижением температуры, и отношение начинает падать значительно ниже значения, предсказанного уравнением 4.2.2, приближаясь к нулю при 0 К.
Читатель может быть знаком со следующими терминами в области электричества
Электропроводность σ
Электропроводность G
Удельное сопротивление ρ
Сопротивление R
Они связаны соотношением G = 1/ R , σ = 1 / ρ, R = ρ l / A , G = σ A / l ,
, где l и A — длина и площадь поперечного сечения проводника.Читатель, вероятно, также знает, что сопротивления складываются последовательно, а проводимости складываются параллельно. Мы можем определить некоторые аналогичные величины, относящиеся к тепловому потоку. Таким образом, удельное сопротивление обратно пропорционально проводимости, сопротивление составляет л / А, в раз больше удельного сопротивления, проводимость составляет А / л, в раз больше проводимости, и так далее. Эти концепции могут пригодиться в следующем жанре задач, любимых экзаменаторами.
Помещение имеет стены площадью A 1 , толщина d 1 , теплопроводность K 1 , дверь площадью A 2 , толщина d 2 , теплопроводность K 2 , а площадь окна A 3 , толщина d 3 , теплопроводность K 3 , температура внутри T 1 и температура на улице Т 2 .Какова скорость потери тепла из помещения?
У нас есть три параллельных проводимости: \ (\ frac {K_1 A_1} {d_1}, ~ \ frac {K_2 A_2} {d_2}, \) и \ (\ frac {K_3 A_3} {d_3} \), и так что у нас
\ [\ frac {dQ} {dt} = \ left (\ frac {K_1 A_1} {d_1} + \ frac {K_2 A_2} {d_2} + \ frac {K_3 A_3} {d_3} \ right) (T_2 — Т_1). \]
Конечно, проблема не должна быть именно такой. Возможно, вам задали показатель теплопотерь и попросили найти площадь окна. Но вы понимаете общую идею и, вероятно, сможете сами придумать несколько примеров.Скорость теплового потока аналогична току, а разница температур подобна ЭДС батареи.
Материалы с экстремальной теплопроводностью, разработанные фононами
Киттель, К. Введение в физику твердого тела 7-е изд. (Wiley, 1996).
Peierls, R. Zur kinetischen Theorie der Wärmeleitung in Kristallen. Ann. Phys. 395 , 1055–1101 (1929).
Артикул Google ученый
Аллен П. Б. и Фельдман Дж. Л. Теплопроводность неупорядоченных гармонических твердых тел. Phys. Ред. B 48 , 12581–12588 (1993).
CAS Статья Google ученый
Клеменс П. Г. Рассеяние низкочастотных волн решетки на статических дефектах. Proc. Phys. Soc. А 68 , 1113 (1955).
Артикул Google ученый
Каллавей Дж. Модель решеточной теплопроводности при низких температурах. Phys. Ред. , , 113, , 1046–1051 (1959).
CAS Статья Google ученый
Cahill, D. G. et al. Наноразмерный тепловой перенос. J. Appl. Phys. 93 , 793 (2003).
CAS Статья Google ученый
Cahill, D. G. et al.Наноразмерный тепловой перенос. II. 2003–2012 гг. Заявл. Phys. Ред. 1 , 011305 (2014).
Артикул CAS Google ученый
Dresselhaus, M. S. et al. Новые направления низкоразмерных термоэлектрических материалов. Adv. Матер. 19 , 1043–1053 (2007).
CAS Статья Google ученый
Volz, S.Г. и Чен, Г. Молекулярно-динамическое моделирование теплопроводности кристаллов кремния. Phys. Ред. B 61 , 2651 (2000).
CAS Статья Google ученый
МакГоги, А. Дж. Х. и Ларкин, Дж. М. Прогнозирование свойств фононов на основе моделирования равновесной молекулярной динамики. Annu. Преподобный Тепло. Трансф. 17 , 49–87 (2014).
Артикул Google ученый
Бройдо Д. А., Малорни М., Бирнер Г., Минго Н. и Стюарт Д. А. Собственная решеточная теплопроводность полупроводников из первых принципов. Заявл. Phys. Lett. 91 , 231922 (2007).
Артикул CAS Google ученый
Чжан В., Фишер Т. и Минго Н. Метод атомистической функции Грина: эффективный подход к моделированию переноса фононов в нанометровом масштабе. Номер. Нагревать.Трансф. B 51 , 333–349 (2007).
CAS Статья Google ученый
Марколонго А., Умари П. и Барони С. Микроскопическая теория и квантовое моделирование атомного переноса тепла. Нат. Phys. 12 , 80–84 (2015).
Артикул CAS Google ученый
Барток, А. П., Пейн, М. К., Кондор, Р. и Чани, Г.Потенциалы гауссовского приближения: точность квантовой механики без электронов. Phys. Rev. Lett. 104 , 136403 (2010).
Артикул CAS Google ученый
Дай Дж. И Тиан З. Строгий формализм ангармонической атомистической функции Грина для трехмерных интерфейсов. Phys. Ред. B 101 , 041301 (R) (2020).
Артикул Google ученый
Minnich, A.J. et al. Метод спектроскопии теплопроводности для измерения длины свободного пробега фононов. Phys. Rev. Lett. 107 , 095901 (2011).
CAS Статья Google ученый
Siemens, M. E. et al. Квазибаллистический перенос тепла от границ раздела наноразмеров, наблюдаемый с помощью сверхбыстрых когерентных пучков мягкого рентгеновского излучения. Нат. Матер. 9 , 26–30 (2010).
CAS Статья Google ученый
Канг, Дж. С., Ли, М., Ву, Х., Нгуен, Х. и Ху, Ю. Экспериментальное наблюдение высокой теплопроводности в арсениде бора. Наука 361 , 575–578 (2018).
CAS Статья Google ученый
Tian, F. et al. Необычно высокая теплопроводность в объемных кристаллах арсенида бора. Наука 361 , 582–585 (2018).
CAS Статья Google ученый
Li, S. et al. Высокая теплопроводность в кубических кристаллах арсенида бора. Наука 361 , 579–581 (2018).
CAS Статья Google ученый
van Roekeghem, A., Carrete, J., Oses, C., Curtarolo, S. & Mingo, N. Высокопроизводительный расчет теплопроводности высокотемпературных твердых фаз: случай оксида и фторидные перовскиты. Phys. Ред. 6 , 041061 (2016).
Артикул Google ученый
Сейф, Х. Р. и др. Переосмысление фононов: проблема беспорядка. npj Comput. Матер. 3 , 49 (2017).
Артикул CAS Google ученый
Kim, W. et al. Снижение теплопроводности и повышение термоэлектрической добротности за счет внедрения наночастиц в кристаллические полупроводники. Phys.Rev. Lett. 96 , 045901 (2006).
Артикул CAS Google ученый
Poudel, B. et al. Высокие термоэлектрические характеристики массивных сплавов наноструктурированного теллурида сурьмы висмута. Наука 320 , 634–638 (2008).
CAS Статья Google ученый
Лукьянова М.Н. и др. Когерентная фононная теплопроводность в сверхрешетках. Наука 338 , 936–939 (2012).
CAS Статья Google ученый
Ravichandran, J. et al. Кроссовер от некогерентного к когерентному рассеянию фононов в эпитаксиальных оксидных сверхрешетках. Нат. Матер. 13 , 168–172 (2014).
CAS Статья Google ученый
Лукьянова М.Н. и др. Локализация фононов в теплопроводности. Sci. Adv. 4 , eaat9460 (2018).
CAS Статья Google ученый
Ферми Э., Паста П., С., У. и Цингоу М. Исследования нелинейных задач (Калифорнийский университет, 1955).
Huberman, S. et al. Наблюдение второго звука в графите при температурах выше 100 К. Science 364 , 375–379 (2019).
CAS Статья Google ученый
Слак, Г. А. Неметаллические кристаллы с высокой теплопроводностью. J. Phys. Chem. Твердые вещества 34 , 321–335 (1973).
CAS Статья Google ученый
Линдсей, Л., Бройдо, Д. А. и Рейнеке, Т. Л. Определение из первых принципов сверхвысокой теплопроводности арсенида бора: конкурента алмаза? Phys. Rev. Lett. 111 , 025901 (2013).
CAS Статья Google ученый
Равичандран, Н. К. и Бройдо, Д. Фонон-фононные взаимодействия в твердых телах с сильными связями: правила отбора и процессы высшего порядка. Phys. Ред. 10 , 021063 (2020).
CAS Статья Google ученый
Фен Т., Линдсей Л. и Руан X. Четырехфононное рассеяние значительно снижает внутреннюю теплопроводность твердых тел. Phys. Ред. B 96 , 161201 (R) (2017).
Артикул Google ученый
Lv, B. et al. Экспериментальное исследование предложенного сверхтеплопроводника: БА. Заявл. Phys. Lett. 106 , 074105 (2015).
Артикул CAS Google ученый
Линдси, Л., Бройдо, Д. А. и Рейнеке, Т. Л. Фононно-изотопное рассеяние и теплопроводность в материалах с большим изотопным эффектом: исследование из первых принципов. Phys. Ред. B 88 , 144306 (2013).
Артикул CAS Google ученый
Zheng, Q. et al. Теплопроводность GaN, 71 GaN и SiC от 150 К до 850 К. Phys. Rev. Mater. 3 , 014601 (2019).
CAS Статья Google ученый
Гу, X., Wei, Y., Yin, X., Li, B. & Yang, R.Фононно-тепловые свойства двумерных материалов. Ред. Мод. Phys. 90 , 041002 (2018).
CAS Статья Google ученый
Линдсей, Л., Бройдо, Д. А. и Минго, Н. Решеточная теплопроводность однослойных углеродных нанотрубок: за пределами приближения времени релаксации и правил отбора фонон-фононного рассеяния. Phys. Ред. B 80 , 125407 (2009).
Артикул CAS Google ученый
Линдси, Л., Бройдо, Д. А., Минго, Н. Изгибные фононы и тепловой перенос в графене. Phys. Ред. B 82 , 115427 (2010).
Артикул CAS Google ученый
Ким П., Ши Л., Маджумдар А. и Макьюэн П. Л. Измерения переноса тепла отдельных многослойных нанотрубок. Phys. Rev. Lett. 87 , 215502 (2001).
CAS Статья Google ученый
Маруяма, С. Молекулярно-динамическое моделирование теплопроводности в ОСНТ конечной длины. Phys. B 323 , 193–195 (2002).
CAS Статья Google ученый
Баландин А.А. и др. Превосходная теплопроводность однослойного графена. Nano Lett. 8 , 902–907 (2008).
CAS Статья Google ученый
Шмидт А. Дж., Чен X. и Чен Г. Накопление импульсов, радиальная теплопроводность и анизотропная теплопроводность в переходном термоотражении накачки и зонда. Rev. Sci. Instrum. 79 , 114902 (2008).
Артикул CAS Google ученый
Минго, Н. и Бройдо, Д. А. Зависимость теплопроводности углеродных нанотрубок от длины и «проблема длинных волн». Nano Lett. 5 , 1221–1225 (2005).
CAS Статья Google ученый
Лепри, С. Теплопроводность в классических низкоразмерных решетках. Phys. Rep. 377 , 1–80 (2003).
CAS Статья Google ученый
Чанг, К. В., Окава, Д., Гарсия, Х., Маджумдар, А. и Зеттл, А. Нарушение закона Фурье в теплопроводниках из нанотрубок. Phys.Rev. Lett. 101 , 075903 (2008).
CAS Статья Google ученый
Xu, X. et al. Зависимая от длины теплопроводность в подвешенном однослойном графене. Нат. Commun. 5 , 3689 (2014).
CAS Статья Google ученый
Takabatake, T., Suekuni, K., Nakayama, T. & Kaneshita, E. Электронно-кристаллические термоэлектрические клатраты фононного стекла: эксперименты и теория. Ред. Мод. Phys. 86 , 669–716 (2014).
CAS Статья Google ученый
Кларк, Д. Р. и Филпот, С. Р. Материалы термобарьерных покрытий. Mater. Сегодня 8 , 22–29 (2005).
CAS Статья Google ученый
Weathers, A. et al. Стеклоподобная теплопроводность в наноструктурах сложного анизотропного кристалла. Phys. Ред. B 96 , 214202 (2017).
Артикул Google ученый
Christensen, M. et al. Исключение пересечения мод дремоты в термоэлектрических материалах. Нат. Матер. 7 , 811–815 (2008).
CAS Статья Google ученый
Сейлз, Б. К., Мандрус, Д. и Уильямс, Р. К. Заполненные антимониды скуттерудита: новый класс термоэлектрических материалов. Наука 272 , 1325–1328 (1996).
CAS Статья Google ученый
Mukhopadhyay, S. et al. Двухканальная модель сверхнизкой теплопроводности кристаллического Tl 3 VSe 4 . Наука 360 , 1445–1458 (2018).
Артикул CAS Google ученый
Хугебум-Пот, К.M. et al. Новый режим переноса тепла в наномасштабе: коллективная диффузия увеличивает эффективность рассеивания. Proc. Natl Acad. Sci. США 112 , 4846–4851 (2015).
CAS Статья Google ученый
Lee, S. et al. Резонансное соединение приводит к низкой теплопроводности решетки. Нат. Commun. 5 , 3525 (2014).
Артикул Google ученый
Delaire, O. et al. Гигантское ангармоническое рассеяние фононов в PbTe. Нат. Матер. 10 , 614–619 (2011).
CAS Статья Google ученый
Tian, Z. et al. Фононная проводимость в PbSe, PbTe и PbTe 1− x Se x из расчетов из первых принципов. Phys. Ред. B 85 , 184303 (2012).
Артикул CAS Google ученый
Li, C. W. et al. Гигантский фононный ангармонизм, управляемый орбитой, в SnSe. Нат. Phys. 11 , 1063–1069 (2015).
CAS Статья Google ученый
Ma, H. et al. Сверхкомпактный и мягкий (CH 3 NH 3 ) 3 Bi 2 I 9 кристалл со сверхнизкой теплопроводностью. Phys. Rev. Lett. 123 , 155901 (2019).
CAS Статья Google ученый
Qian, X., Gu, X. & Yang, R. Решеточная теплопроводность органо-неорганического гибридного перовскита CH 3 NH 3 PbI 3 . Заявл. Phys. Lett. 108 , 063902 (2016).
Артикул CAS Google ученый
Pisoni, A. et al. Сверхнизкая теплопроводность в органо-неорганическом гибридном перовските CH 3 NH 3 PbI 3 . J. Phys.Chem. Lett. 5 , 2488–2492 (2014).
CAS Статья Google ученый
Чжу Т. и Эртекин Е. Смешанный фононный и нефононный транспорт в гибридных перовскитах галогенида свинца: двойственность стекла и кристалла, динамический беспорядок и ангармонизм. Energy Environ. Sci. 12 , 216–229 (2019).
CAS Статья Google ученый
Иоффе А.Ф. Полупроводниковые термоэлементы и термоэлектрическое охлаждение. Phys. Сегодня 12 , 42 (1959).
Артикул Google ученый
Тамура С. Изотопное рассеяние дисперсионных фононов в Ge. Phys. Ред. B 27 , 858–866 (1983).
CAS Статья Google ученый
Гарг, Дж., Бонини, Н., Козинский Б. и Марзари Н. Роль беспорядка и ангармонизма в теплопроводности кремний-германиевых сплавов: исследование из первых принципов. Phys. Rev. Lett. 106 , 045901 (2011).
Артикул CAS Google ученый
Мураками Т., Шига Т., Хори Т., Эсфарджани К. и Шиоми Дж. Важность локальных силовых полей для снижения теплопроводности решетки в PbTe 1− x Se x сплавов. Europhys. Lett. 102 , 46002 (2013).
Артикул CAS Google ученый
Арригони М., Каррете Дж., Минго Н. и Мэдсен Г. К. Количественное предсказание решеточной теплопроводности в случайных полупроводниковых сплавах из первых принципов: роль беспорядка силовых постоянных. Phys. Ред. B 98 , 115205 (2018).
CAS Статья Google ученый
Симончелли М., Марзари Н. и Маури Ф. Единая теория теплопереноса в кристаллах и стеклах. Нат. Phys. 15 , 809–813 (2019).
CAS Статья Google ученый
Исаева, Л., Барбалинардо, Г., Донадио, Д. и Барони, С. Моделирование переноса тепла в кристаллах и стеклах на основе единого решеточно-динамического подхода. Нат. Commun. 10 , 3853 (2019).
Артикул CAS Google ученый
Янг Р. и Чен Г. Моделирование теплопроводности периодических двумерных нанокомпозитов. Phys. Ред. B 69 , 195316 (2004).
Артикул CAS Google ученый
Казимир, Х. Б. Г. Замечание о теплопроводности кристаллов. Physica 5 , 495–500 (1938).
Артикул Google ученый
Chiritescu, C. et al. Сверхнизкая теплопроводность в неупорядоченных слоистых кристаллах WSe 2 . Наука 315 , 351–353 (2007).
CAS Статья Google ученый
Vaziri, S. et al. Сверхвысокая теплоизоляция неоднородно-слоистых двумерных материалов. Sci. Adv. 5 , eaax1325 (2019).
CAS Статья Google ученый
Чен, Г. Теплопроводность и перенос баллистических фононов в поперечном направлении сверхрешеток. Phys. Ред. B 57 , 14958 (1998).
CAS Статья Google ученый
Маджумдар А. Микромасштабная теплопроводность в тонких диэлектрических пленках. J. Heat. Трансф. 115 , 7–16 (1993).
Артикул Google ученый
Chen, G. in Последние тенденции в исследованиях термоэлектрических материалов III Vol. 71 (изд. Тритт, Т. М.) Гл. 5, 203–259 (Elsevier, 2001).
Венкатасубраманян Р. Уменьшение решеточной теплопроводности и поведение, подобное локализации фононов в сверхрешеточных структурах. Phys. Ред. B 61 , 3091 (2000).
CAS Статья Google ученый
Чен Г. Теплопроводность фононных волн в тонких пленках и сверхрешетках. J. Heat. Трансф. 121 , 945–953 (1999).
Артикул Google ученый
Ян Б. и Чен Г. Частично когерентная фононная теплопроводность в сверхрешетках. Phys. Ред. B 67 , 195311 (2003).
Артикул CAS Google ученый
Maire, J. et al. Настройка теплопроводности волновой природой фононов. Sci. Adv. 3 , e1700027 (2017).
Артикул CAS Google ученый
Сперлинг, Л. Х. Введение в физику полимеров (Wiley, 2005).
Лю, Дж. И Ян, Р. Зависимая от длины теплопроводность одиночных протяженных полимерных цепей. Phys. Ред. B 86 , 104307 (2012).
Артикул CAS Google ученый
Zhang, T. & Luo, T. Влияние морфологии теплопроводности одиночных цепей полиэтилена и кристаллических волокон. J. Appl. Phys. 112 , 094304 (2012).
Артикул CAS Google ученый
Генри А. и Чен Г. Высокая теплопроводность одиночных полиэтиленовых цепей с использованием моделирования молекулярной динамики. Phys. Rev. Lett. 101 , 235502 (2008).
Артикул CAS Google ученый
Zhang, T., Wu, X. & Luo, T. Полимерные нановолокна с выдающейся теплопроводностью и термостабильностью: фундаментальная связь между молекулярными характеристиками и макроскопическими термическими свойствами. J. Phys. Chem. С 118 , 21148–21159 (2014).
CAS Статья Google ученый
Шулумба, Н., Хеллман, О. и Минних, А. Дж. Решеточная теплопроводность молекулярных кристаллов полиэтилена из первых принципов, включая ядерные квантовые эффекты. Phys. Rev. Lett. 119 , 185901 (2017).
Артикул Google ученый
Ван Х., Кавиани М. и Хуанг Б. Фононная связь и транспорт в отдельных полиэтиленовых цепях: сравнительное исследование с объемным кристаллом. Наноразмер 9 , 18022–18031 (2017).
CAS Статья Google ученый
Ван Х., Хо В., Сегалман Р. А. и Кэхилл Д. Г. Теплопроводность высокомодульных полимерных волокон. Макромолекулы 46 , 4937–4943 (2013).
CAS Статья Google ученый
Шен, С., Генри, А., Тонг, Дж., Чжэн, Р. и Чен, Г. Полиэтиленовые нановолокна с очень высокой теплопроводностью. Нат. Nanotechnol. 5 , 251–255 (2010).
CAS Статья Google ученый
Shrestha, R. et al. Кристаллические полимерные нановолокна со сверхвысокой прочностью и теплопроводностью. Нат. Commun. 9 , 1664 (2018).
Артикул CAS Google ученый
Xu, Y. et al. Наноструктурированные полимерные пленки с металлоподобной теплопроводностью. Нат. Commun. 10 , 1771 (2019).
Артикул CAS Google ученый
Singh, V. et al. Высокая теплопроводность цепочечного аморфного политиофена. Нат. Nanotechnol. 9 , 384–390 (2014).
CAS Статья Google ученый
Ronca, S., Igarashi, T., Forte, G. & Rastogi, S. Металлическая теплопроводность в легком изоляторе: ленты и пленки из сверхвысокомолекулярного полиэтилена, обработанные в твердом состоянии. Полимер 123 , 203–210 (2017).
CAS Статья Google ученый
Zhu, B. et al. Новые полиэтиленовые волокна с очень высокой теплопроводностью благодаря аморфной реструктуризации. САУ Омега 2 , 3931–3944 (2017).
CAS Статья Google ученый
Смит М. К., Сингх В., Калаитциду К. и Кола Б. А. Поверхности массива поли (3-гексилтиофен) нанотрубок с регулируемым смачиванием и контактным переносом тепловой энергии. ACS Nano 9 , 1080–1088 (2015).
CAS Статья Google ученый
Lu, C. et al. Теплопроводность электропрядения из оксида полиэтилена с ориентированной цепью (ПЭО). Полимер 115 , 52–59 (2017).
CAS Статья Google ученый
Kurabayashi, K., Asheghi, M. & Goodson, K. E. Измерение анизотропии теплопроводности в полиимидных пленках. J. Microelectromech. Syst. 8 , 180–191 (1999).
CAS Статья Google ученый
Wei, X., Zhang, T. & Luo, T. Зависимая от конформации цепи теплопроводность аморфных полимерных смесей: влияние меж- и внутрицепочечных взаимодействий. Phys. Chem. Chem. Phys. 18 , 32146–32154 (2016).
CAS Статья Google ученый
Shanker, A. et al. Высокая теплопроводность аморфных полимеров, полученных электростатическим способом. Sci. Adv. 3 , e1700342 (2017).
Артикул CAS Google ученый
Xie, X. et al. Высокая и низкая теплопроводность аморфных макромолекул. Phys. Ред. B 95 , 035406 (2017).
Артикул Google ученый
Xu, Y. et al. Конъюгированный полимер, полученный методом молекулярной инженерии, с высокой теплопроводностью. Sci. Adv. 4 , eaar3031 (2018).
Артикул CAS Google ученый
Kim, G.H. et al. Высокая теплопроводность в смесях аморфных полимеров за счет искусственных межцепочечных взаимодействий. Нат. Матер. 14 , 295–300 (2015).
CAS Статья Google ученый
Миядзаки, Ю., Нишияма, Т., Такахаши, Х., Ктагири, Ж.-И. & Такезава Ю. Разработка высокотеплопроводных эпоксидных композитов. В 2009 Конференция IEEE по электрической изоляции и диэлектрическим явлениям 638–641 (IEEE, 2009).
Cui, L. et al. Теплопроводность переходов одиночных молекул. Nature 572 , 628–633 (2019).
CAS Статья Google ученый
Wang, Z. et al. Сверхбыстрая мгновенная теплопроводность молекулярных цепочек. Наука 317 , 787–790 (2007).
CAS Статья Google ученый
Русс, Б., Глауделл, А., Урбан, Дж. Дж., Чабиник, М. Л. и Сегалман, Р. А. Органические термоэлектрические материалы для сбора энергии и контроля температуры. Нат. Rev. Mater. 1 , 16050 (2016).
Дуда, Ю.К., Хопкинс, П. Е., Шен, Ю. и Гупта, М. С. Исключительно низкая теплопроводность пленок производного фуллерена PCBM. Phys. Rev. Lett. 110 , 015902 (2013).
Артикул CAS Google ученый
Liu, J. et al. Сверхнизкая теплопроводность тонких пленок органического и неорганического цинкона, осажденных атомарным / молекулярным слоем. Nano Lett. 13 , 5594–5599 (2013).
CAS Статья Google ученый
Ong, W.-L. И Мален, Дж. А. Тепловой перенос в наноструктурированных органо-неорганических гибридных материалах. Annu. Преподобный Тепло. Трансф. 19 , 67–126 (2016).
CAS Статья Google ученый
Yang, J. et al. Тонкие сверхатомные пленки, обрабатываемые в растворе. J. Am. Chem. Soc. 141 , 10967–10971 (2019).
CAS Статья Google ученый
Li, R., Lee, E. & Luo, T. Единый потенциал глубокой нейронной сети, способный предсказывать теплопроводность кремния в различных фазах. Mater. Сегодня Phys. 12 , 100181 (2019).
Артикул Google ученый
Qian, X., Peng, S., Li, X., Wei, Y. & Yang, R. Моделирование теплопроводности с использованием потенциалов машинного обучения: приложение к кристаллическому и аморфному кремнию. Mater. Сегодня Phys. 10 , 100140 (2019).
Артикул Google ученый
Ju, S. et al. Создание наноструктур для транспорта фононов с помощью байесовской оптимизации. Phys. Ред. 7 , 021024 (2017).
Артикул Google ученый
Wu, S. et al. Обнаружение полимеров с высокой теплопроводностью с помощью машинного обучения с использованием алгоритма молекулярного дизайна. npj Comput. Матер. 5 , 66 (2019).
Артикул CAS Google ученый
Каррет, Дж., Ли, В., Минго, Н., Ван, С. и Куртароло, С. Обнаружение полупроводников Half-Heusler с беспрецедентно низкой теплопроводностью с помощью моделирования материалов с высокой производительностью. Phys. Ред. 4 , 011019 (2014).
CAS Статья Google ученый
Cho, J. et al. Электрохимически регулируемая теплопроводность оксида лития-кобальта. Нат. Commun. 5 , 4035 (2014).
CAS Статья Google ученый
Tomko, J. A. et al. Настраиваемый перенос тепла и обратимое переключение теплопроводности в топологически связанных биологических материалах. Нат. Nanotechnol. 13 , 959–964 (2018).
CAS Статья Google ученый
Ihlefeld, J. F. et al. Фононная теплопроводность, регулируемая по напряжению при комнатной температуре, через реконфигурируемые границы раздела в тонких сегнетоэлектрических пленках. Nano Lett. 15 , 1791–1795 (2015).
CAS Статья Google ученый
Shin, J. et al. Световое переключение теплопроводности в азобензольных полимерах. Proc. Natl Acad. Sci. США 116 , 5973–5978 (2019).
CAS Статья Google ученый
Lu, Q. et al. Двунаправленная настройка переноса тепла в SrCoO x с электрохимически индуцированными фазовыми переходами. Нат. Матер. 19 , 655–662 (2020).
CAS Статья Google ученый
Менихарт, К. и Крарти, М. Потенциальная экономия энергии от развертывания динамических изоляционных материалов для жилых зданий в США. Сборка. Environ. 114 , 203–218 (2017).
Артикул Google ученый
Hao, M., Li, J., Park, S., Moura, S. & Dames, C. Эффективное терморегулирование литий-ионных аккумуляторов с пассивным терморегулятором на границе раздела на основе сплава с памятью формы . Нат. Энергетика 3 , 899–906 (2018).
CAS Статья Google ученый
Lyeo, H.-K. и другие. Теплопроводность материала с фазовым переходом Ge 2 Sb 2 Te 5 . Заявл. Phys. Lett. 89 , 151904 (2006).
Артикул CAS Google ученый
Caccia, M. et al. Металлокерамические композиты для теплообменников в солнечных электростанциях. Природа 562 , 406–409 (2018).
CAS Статья Google ученый
Глассбреннер, К. Дж. И Слак, Г. А. Теплопроводность кремния и германия от 3 ° К до точки плавления. Phys. Ред. 134 , A1058 – A1069 (1964).
Артикул Google ученый
Аллен П. Б., Фельдман Дж. Л., Фабиан Дж. И Вутен Ф. Диффузоны, локоны и пропагоны: характер атомных колебаний в аморфном Si. Philos. Mag. B 79 , 1715–1731 (1999).
CAS Статья Google ученый
Помпе, Г.& Хегенбарт, Э. Теплопроводность аморфного Si при низких температурах. Phys. Статус Solidi B 47 , 103–108 (1988).
Артикул Google ученый
Кэхилл, Д. Г., Фишер, Х. Э., Клитснер, Т., Шварц, Э. Т. и Поль, Р. О. Теплопроводность тонких пленок: измерения и понимание. J. Vac. Sci. Technol. А 7 , 1259–1266 (1989).
CAS Статья Google ученый
Кэхилл Д. Г., Катияр М. и Абельсон Дж. Р. Теплопроводность тонких пленок и -Si: H. Phys. Ред. B 50 , 6077–6081 (1994).
CAS Статья Google ученый
McGaughey, A.J.H., Jain, A. & Kim, H.-Y. Фононные свойства и теплопроводность из первых принципов, динамики решетки и уравнения переноса Больцмана. J. Appl. Phys. 125 , 011101 (2019).
Артикул CAS Google ученый
Шиоми, Дж., Эсфарджани, К. и Чен, Г. Теплопроводность соединений полугейслера на основе расчетов из первых принципов. Phys. Ред. B 84 , 104302 (2011).
Артикул CAS Google ученый
Johnson, J. A. et al. Прямое измерение недиффузионного переноса тепла при комнатной температуре на микронные расстояния в силиконовой мембране. Phys. Rev. Lett. 110 , 025901 (2013).
Артикул CAS Google ученый
Ху, Й., Зенг, Л., Минних, А. Дж., Дрессельхаус, М. С. и Чен, Г. Спектральное картирование теплопроводности посредством баллистического переноса в нанометровом масштабе. Нат. Nanotechnol. 10 , 701–706 (2015).
CAS Статья Google ученый
Chen, K. et al. Сверхвысокая теплопроводность в кубическом нитриде бора, обогащенном изотопами. Наука 367 , 555–559 (2020).
CAS Статья Google ученый
Морелли Д. Т. и Слэк Г. А. в статье «Материалы с высокой теплопроводностью» (ред. Шинде, С. Л. и Гоэла, Дж. С.), гл. 2, 37–68 (Springer, 2005).
Dames, C. Подтверждение сверхвысокой теплопроводности арсенида бора. Наука 361 , 549–550 (2018).
CAS Статья Google ученый
Гири, А. и Хопкинс, П. Достижение лучшего проводника тепла. Нат. Матер. 19 , 481–490 (2020).
Артикул CAS Google ученый
Канг, Дж. С., Ву, Х. и Ху, Ю. Тепловые свойства и фононная спектральная характеристика синтетического фосфида бора для применений с высокой теплопроводностью. Nano Lett. 17 , 7507–7514 (2017).
CAS Статья Google ученый
Qian, X., Jiang, P. & Yang, R. Анизотропная теплопроводность карбида кремния 4H и 6H, измеренная с использованием термоотражения во временной области. Mater. Сегодня Phys. 3 , 70–75 (2017).
Артикул Google ученый
Кафф, Дж.и другие. Восстановление вкладов фононов в среднюю длину свободного пробега в теплопроводность с использованием наноразмерных мембран. Phys. Ред. B 91 , 245423 (2015).
Артикул CAS Google ученый
Лю В. и Ашеги М. Измерение теплопроводности ультратонких слоев монокристаллического кремния. J. Heat. Трансф. 128 , 75–83 (2006).
CAS Статья Google ученый
Ашеги М., Леунг Ю. К., Вонг С. и Гудсон К. Э. Фононно-граничное рассеяние в тонких слоях кремния. Заявл. Phys. Lett. 71 , 1798–1800 (1997).
CAS Статья Google ученый
Гудсон, К. Э. и Джу, Ю. С. Теплопроводность в новых электронных пленках. Annu. Rev. Mater. Sci. 29 , 261–293 (1999).
CAS Статья Google ученый
Li, D. et al. Теплопроводность индивидуальных кремниевых нанопроволок. Заявл. Phys. Lett. 83 , 2934–2936 (2003).
CAS Статья Google ученый
Дэймс, К. и Чен, Г. Теоретическая фононная теплопроводность нанопроволок сверхрешетки Si / Ge. J. Appl. Phys. 95 , 682–693 (2004).
CAS Статья Google ученый
Чой, К. Л., Вонг, Ю. У., Янг, Г. В. и Канамото, Т. Модуль упругости и теплопроводность ультра вытянутого полиэтилена. J. Polym. Sci. B 37 , 3359–3367 (1999).
CAS Статья Google ученый
Пиро, Л., Кинани-Алауи, М., Исси, Дж. П., Бегин, Д. и Бийо, Д. Теплопроводность ориентированной полиацетиленовой пленки. Solid State Commun. 79 , 427–429 (1989).
Артикул Google ученый
Андерсон П. В., Гальперин Б. И., Варма К. М. Аномальные низкотемпературные термические свойства стекол и спиновых стекол. Philos. Mag. 25 , 1–9 (1972).
CAS Статья Google ученый
Кэхилл Д., Уотсон С. и Поль Р. Нижний предел теплопроводности неупорядоченных кристаллов. Phys. Ред. B 46 , 6131–6140 (1992).
CAS Статья Google ученый
Ван Х., Лиман К. Д., Трит Н. Д., Чабиниц М. Л. и Кэхилл Д. Г. Сверхнизкая теплопроводность производных фуллерена. Phys. Ред. B 88 , 075310 (2013).
Артикул CAS Google ученый
Chen, Z.И Дэймс, С. Анизотропная модель минимальной теплопроводности. Заявл. Phys. Lett. 107 , 193104 (2015).
Артикул CAS Google ученый
Джаноцци П., де Жиронколи С., Павоне П. и Барони С. Ab initio расчет фононной дисперсии в полупроводниках. Phys. Ред. B 43 , 7231–7242 (1991).
CAS Статья Google ученый
Зиман Дж. М. Электроны и фононы: теория явлений переноса в твердых телах (Oxford Univ. Press, 2001).
Debernardi, A., Baroni, S. & Molinari, E. Время жизни ангармонических фононов в полупроводниках из теории возмущений функционала плотности. Phys. Rev. Lett. 75 , 1819–1822 (1995).
CAS Статья Google ученый
Li, W., Carrete, J., А. Катчо, Н. и Минго, Н. ShengBTE: решатель уравнения переноса Больцмана для фононов. Comput. Phys. Commun. 185 , 1747–1758 (2014).
CAS Статья Google ученый
Ян Ф. и Деймс К. Спектры средней длины свободного пробега как инструмент для понимания теплопроводности в объеме и наноструктурах. Phys. Ред. B 87 , 035437 (2013).
Артикул CAS Google ученый
Dames, C. & Chen, G. в справочнике по термоэлектричеству : от макросов до нано (ред. Роу, Д. М.), гл. 42 (Тейлор и Фрэнсис, 2006).
Эсфарджани К., Чен Г. и Стокс Х. Т. Перенос тепла в кремнии на основе расчетов из первых принципов. Phys. Ред. B 84 , 085204 (2011).
Артикул CAS Google ученый
Ли, С., Бройдо, Д., Эсфарджани, К. и Чен, Г.Гидродинамический перенос фононов в подвешенном графене. Нат. Commun. 6 , 6290 (2015).
CAS Статья Google ученый
Cepellotti, A. et al. Фононная гидродинамика в двумерных материалах. Нат. Commun. 6 , 6400 (2015).
CAS Статья Google ученый
Минго, Н., Хаузер, Д., Кобаяши, Н. П., Плиссонье, М., Шакури, А. Подход «наночастицы в сплаве» к эффективным термоэлектрикам: силициды в SiGe. Nano Lett. 9 , 711–715 (2009).
CAS Статья Google ученый
Тадано Т. и Цунеюки С. Самосогласованные фононные расчеты динамических свойств решетки в кубическом SrTiO 3 с ангармоническими силовыми постоянными из первых принципов. Phys.Ред. B 92 , 054301 (2015).
Артикул CAS Google ученый
Liao, B. et al. Значительное уменьшение решеточной теплопроводности за счет электрон-фононного взаимодействия в кремнии с высокими концентрациями носителей: исследование из первых принципов. Phys. Rev. Lett. 114 , 115901 (2015).
Артикул CAS Google ученый
Zhou, J. et al. Ab initio оптимизация эффекта фононного увлечения для низкотемпературного термоэлектрического преобразования энергии. Proc. Natl Acad. Sci. США 112 , 14777–14782 (2015).
CAS Статья Google ученый
Кэхилл Д. и Поль Р. О. Теплопроводность аморфных твердых тел над плато. Phys. Ред. B 35 , 4067–4073 (1987).
CAS Статья Google ученый
Dames, C. Измерение теплопроводности тонких пленок: Омега 3 и родственные электротермические методы. Annu. Преподобный Тепло. Трансф. 16 , 7–49 (2013).
Артикул Google ученый
Кэхилл, Д. Г. Анализ теплового потока в слоистых структурах для определения термоотражения во временной области. Rev. Sci. Instrum. 75 , 5119–5122 (2004).
CAS Статья Google ученый
Schmidt, A.J., Cheaito, R. & Chiesa, M. Метод термоотражения в частотной области для характеристики тепловых свойств. Rev. Sci. Instrum. 80 , 094901 (2009).
Артикул CAS Google ученый
Мазнев А.А., Джонсон Дж. А. и Нельсон К.А. Возникновение недиффузионного фононного транспорта при нестационарном распаде тепловой решетки. Phys. Ред. B 84 , 195206 (2011).
Артикул CAS Google ученый
Jiang, P., Qian, X. & Yang, R. Учебное пособие: термоотражение во временной области (TDTR) для определения тепловых свойств объемных и тонкопленочных материалов. J. Appl. Phys. 124 , 161103 (2018).
Артикул CAS Google ученый
Qian, X., Ding, Z., Shin, J., Schmidt, A.J.И Чен, Г. Точное измерение плоской теплопроводности слоистых материалов без датчика на металлической пленке с использованием термоотражения в частотной области. Rev. Sci. Instrum. 91 , 064903 (2020).
CAS Статья Google ученый
Кох, Ю. К. и Кэхилл, Д. Г. Частотная зависимость теплопроводности полупроводниковых сплавов. Phys. Ред. B 76 , 075207 (2007).
Артикул CAS Google ученый
Хуа К., Чен X., Равичандран Н. К. и Миннич А. Дж. Экспериментальная метрология для получения коэффициентов передачи тепловых фононов на твердых границах раздела. Phys. Ред. B 95 , 205423 (2017).
Артикул Google ученый
Ляо Б., Мазнев А. А., Нельсон К. А. и Чен Г. Фотовозбужденные носители заряда подавляют суб-терагерцовую фононную моду в кремнии при комнатной температуре. Нат. Commun. 7 , 13174 (2016).
CAS Статья Google ученый
Zhou, J. et al. Прямое наблюдение большого влияния электрон-фононного взаимодействия на перенос фононного тепла. Нат. Commun. 11 , 6040 (2020).
CAS Статья Google ученый
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Что такое испытание на теплопроводность?
Теплопроводность — это фундаментальное свойство материала, связанное с легкостью, с которой тепловая энергия передается через конкретный материал.Материалы, которые легко проводят тепло с небольшим наложенным температурным градиентом, имеют более высокую теплопроводность, чем материалы, которые более устойчивы (с большей изоляцией) к потоку тепла. Точное знание теплопроводности материала необходимо для прогнозирования теплопередачи за счет теплопроводности.
Теплопроводность — это чистое свойство материала, не зависящее от площади проводимости или толщины материала. ASTM D5470 стандартизирует метод двустороннего, одномерного теплового потока для измерения теплопроводности, так что полученные данные будут отражать только свойства материала безотносительно к конкретному используемому испытательному оборудованию.
ASTM D5470 рассматривает теплопроводность «тонких» материалов, которые часто называют «материалами с термоинтерфейсом». «Тонкие» материалы — это примерно те материалы, которые имеют толщину менее 1-2 см. Этот метод определяет теплопроводность как отношение теплового потока к соответствующему градиенту температуры в условиях одномерной теплопроводности. Это измерение можно представить как теплопроводность между двумя параллельными изотермическими поверхностями площадью A при температурах T H и T C , разделенных слоем испытуемого материала толщиной X с установившейся мощностью Q .Таким образом, теплопроводность, k , определяется как
.k = Q * X / ((T H — T C ) * A)
Самыми популярными единицами измерения теплопроводности являются ватт / метр Кельвина (Вт / мК). Термическое сопротивление просто определяется как величина, обратная теплопроводности. Альтернативное выражение для k можно получить, используя термическое сопротивление R образца материала между параллельными горячей и холодной поверхностями, определенное:
R = (T H — T C ) / Q
Объединение этих значений дает более простую форму определения теплопроводности:
k = X / (R * A)
Часто термоинтерфейсные материалы поставляются в листах номинальной толщины, где спецификации теплопроводности для материала представлены в форме RA , а не k .Для этих ситуаций
RA = X / k
Теплопроводность — это свойство материала, которое не зависит от какого-либо конкретного применения, поскольку в идеале свойства материала не зависят от применения. Когда конкретный материал реализуется в качестве термоинтерфейса в приложении для электронной упаковки, влияние материала на общие тепловые характеристики собранного корпуса зависит от многих технических деталей, только одна из которых — проводимость интерфейсного материала.Такие вопросы, как геометрия конструкции, поверхностные контактные сопротивления и тепловое сопротивление других элементов в сборке, имеют решающее значение при оценке общих тепловых характеристик любого конкретного приложения для упаковки электроники. Для этой цели программа Analysis Tech Semiconductor Thermal Testing может определить общее тепловое сопротивление упакованного полупроводникового устройства в зависимости от типа используемого материала термоинтерфейса.
Теплопроводность и закон Видемана-Франца
Теплопередача за счет теплопроводности включает передачу энергии внутри материала без какого-либо движения материала в целом.Скорость теплопередачи зависит от температурного градиента и теплопроводности материала. Теплопроводность — это довольно простое понятие, когда вы обсуждаете потери тепла через стены вашего дома, и вы можете найти таблицы, которые характеризуют строительные материалы и позволяют делать разумные расчеты.
Более фундаментальные вопросы возникают, когда вы исследуете причины значительных колебаний теплопроводности. Газы передают тепло путем прямых столкновений между молекулами, и, как и следовало ожидать, их теплопроводность низкая по сравнению с большинством твердых тел, поскольку они являются разбавленными средами.Неметаллические твердые тела передают тепло посредством колебаний решетки, так что нет чистого движения среды при прохождении энергии. Такой перенос тепла часто описывают в терминах «фононов», квантов колебаний решетки. Металлы являются гораздо лучшими проводниками тепла, чем неметаллы, потому что те же самые подвижные электроны, которые участвуют в электропроводности, также участвуют в передаче тепла.
Концептуально теплопроводность можно рассматривать как контейнер для зависящих от среды свойств, которые связывают скорость потери тепла на единицу площади со скоростью изменения температуры.
Для идеального газа скорость теплопередачи пропорциональна средней молекулярной скорости, длине свободного пробега и молярной теплоемкости газа.
Для неметаллических твердых тел теплопередача рассматривается как передача посредством колебаний решетки, поскольку атомы, колеблющиеся более энергично в одной части твердого тела, передают эту энергию менее энергичным соседним атомам. Это может быть усилено совместным движением в форме распространяющихся решеточных волн, которые в квантовом пределе квантуются как фононы.На практике неметаллические твердые тела настолько изменчивы, что мы обычно просто характеризуем вещество с помощью измеренной теплопроводности при выполнении обычных расчетов.
У металлов достаточно высокая теплопроводность, и те металлы, которые являются лучшими электрическими проводниками, также являются лучшими проводниками тепла. При заданной температуре теплопроводность и электрическая проводимость металлов пропорциональны, но повышение температуры увеличивает теплопроводность при одновременном уменьшении электропроводности.Это поведение количественно выражено в законе Видеманна-Франца:
., где коэффициент пропорциональности L называется числом Лоренца. Качественно это соотношение основано на том факте, что и тепло, и электрический перенос связаны со свободными электронами в металле. Теплопроводность увеличивается со средней скоростью частиц, поскольку это увеличивает прямой перенос энергии. Однако электропроводность уменьшается с увеличением скорости частиц, потому что столкновения отвлекают электроны от прямого переноса заряда.Это означает, что отношение теплопроводности к электрической проводимости зависит от квадрата средней скорости, который пропорционален кинетической температуре.
Теплопроводность | TORELINA ™ | ТОРЕЙ ПЛАСТИК
Техническая информация | Тепловые свойства | Теплопроводность
Явления теплопередачи, которые заставляют объекты, подверженные разнице температур, принимать однородную температуру, в основном подразделяются на теплопроводность, конвекцию и излучение, в зависимости от состояния пути потока, по которому течет тепло, и других факторов.Теплопроводность — это явление, при котором тепло перемещается через твердый или неподвижный газ (или жидкость). Теплопроводность — это свойство, указывающее на легкость, с которой тепло может проходить через твердое тело, такое как формованное изделие. Носители (среды) для переноса тепла включают свободные электроны, колебания решетки и колебания молекул. Эффект теплопередачи свободных электронов очень высок, поэтому такие металлы, как алюминий и медь, обладают высокой теплопроводностью. С другой стороны, пластмассовые материалы, такие как TORELINA, являются изоляционными материалами, которые не имеют свободных электронов, поэтому имеют более низкую теплопроводность, чем металлы, и превосходят их по своим теплоизоляционным свойствам.
Ⅰ. Измерение теплопроводности
Существуют различные методы измерения теплопроводности твердого тела. Их можно разделить на установившиеся методы, при которых температура образца находится в установившемся состоянии, а теплопроводность определяется по количеству (тепловой поток, Вт / м 2 ), которое проходит через единицу поперечного сечения. площадь в единицу времени и нестационарные методы, в которых теплопроводность определяется по скорости распространения тепла через образец (коэффициент температуропроводности, м 2 S -1 ).В последнее время чаще всего используются нестационарные методы, с помощью которых можно быстро получить измерения. Эти методы включают метод лазерной вспышки и метод горячего диска. Теплопроводность можно определить, используя плотность образца и удельную теплоемкость при температуре измерения в дополнение к температуропроводности, определенной нестационарным методом, в соответствии с формулой 6.1. Обычно для измерения теплопроводности используется плоская пластина, так что с помощью стационарного метода и метода лазерной вспышки можно определить теплопроводность в направлении толщины, а с помощью метода горячего диска можно определить теплопроводность в плоском направлении. в дополнение к этому по толщине.Существует еще один метод, с помощью которого теплопередачу фактического формованного продукта проверяют визуально с помощью термографии, которая анализирует инфракрасные лучи, испускаемые формованным продуктом, и затем выражается в диаграмме распределения температуры.
Ⅱ. Теплопроводность TORELINA
Коэффициент теплопроводности TORELINA в направлении толщины, определенный стационарным методом, приведен в таблице. 6.3. Армированный ППС имеет более высокую теплопроводность, чем неармированный ППС.Армирование из стекловолокна и минерального наполнителя имеет более высокую теплопроводность, чем полимер PPS, поэтому теплопроводность различается в зависимости от типа и содержания добавленного армирования.
Таблица. 6.3 Теплопроводность TORELINA (устойчивый метод, 80 ℃)
| Товар | Квартир | Армированный стекловолокном | Стекло + наполнитель армированное | Улучшение эластомера | Неармированный | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| A504X90 | A604 | A310MX04 | A610MX03 | A673M | A575W20 | A495MA1 | A900 | A670T05 | ||
| Теплопроводность (направление толщины) | Вт / м ・ K | 0.3 | 0,3 | 0,5 | 0,5 | 0,3 | 0,3 | 0,4 | 0,2 | 0,2 |
Ⅲ. PPS
с высокой теплопроводностьюPPS с высокой теплопроводностью подходит для продления срока службы электрических и электронных компонентов, таких как системы светодиодного освещения, а также для проектирования теплового излучения в таких целях, как снижение потерь энергии в обмотках, используемых в автомобильных двигателях.TORELINA предлагает линейку TORELINA H501B, электропроводящего типа, теплопроводность которого значительно улучшена по сравнению с обычным PPS, и H718LB, который сохраняет свои изоляционные свойства. (Таблица 6.4)
Таблица. 6.4 PPS с высокой теплопроводностью (23 ℃)
| Товар | Направление измерения | Шт. | Армированный стекловолокном | Высоконаполненная | PPS | с высокой теплопроводностьюМетод измерения | |
|---|---|---|---|---|---|---|---|
| Тип изоляции | Тип электропроводящего | ||||||
| A504X90 | A310MX04 | H718LB | H501B | ||||
| Теплопроводность | Планарное направление | Вт / м ・ K | 0.4 | 0,7 | 1,0 | 10,0 | Метод горячего диска |
| Удельное объемное сопротивление | – | Ом ・ м | 2 × 10 14 | 1 × 10 14 | 5 × 10 13 | 5 × 10 0 | – |
Рис. 6.7 Термографический анализ
При термическом анализе с использованием термографии (рис.6.7) источник тепла (3,4 Вт) размещается в центре плоской пластины (80 × 80 × 3 мм t), а наблюдение ведется с противоположной стороны. На рис. 6.8 сравниваются графики распределения температуры, полученные при нагревании обычных марок PPS, армированных стекловолокном (A504X90), и марок PPS с высокой теплопроводностью (H501B и H718LB) в течение пяти минут. Можно видеть, что для марки PPS, армированной стекловолокном, которая имеет низкую теплопроводность, тепло от источника тепла трудно рассеивать, образуя горячую точку, тогда как для марок PPS с высокой теплопроводностью тепло распространяется в окружающую среду, тем самым ограничивая размер горячей точки.
Рис. 6.8 Распределение температуры высокотеплопроводных марок PPS (термография)
Разница между теплопроводностью, коэффициентом диффузии, пропусканием, сопротивлением и коэффициентом теплопередачи
Узнайте больше в этой статье о различиях и важности теплопроводности, температуропроводности, коэффициента теплопередачи, теплопередачи и теплового сопротивления и т. Д.
Теплопроводность
Теплопроводность \ (\ lambda \) описывает передачу тепла в установившемся состоянии за счет теплопроводности из-за градиента температуры \ (\ frac {\ delta T} {\ delta x} \).Закон Фурье применяется к тепловому потоку \ (\ dot q \) (скорость теплового потока на единицу площади):
\ begin {align}
& \ boxed {\ dot q = \ lambda \ cdot \ frac {\ Delta T} {\ Delta x}} ~~~~~ \ text {закон Фурье} \\ [5px]
\ конец
Более подробную информацию о теплопроводности можно найти в статье Теплопроводность (закон Фурье).
Коэффициент теплопроводности и термическое сопротивление проводимости
Если теплопроводность \ (\ lambda \) связана с толщиной объекта \ (\ Delta x \), через который передается тепло, получается коэффициент теплопроводности для \ (\ Lambda \):
\ begin {align}
& \ dot q = \ underbrace {\ frac {\ lambda} {\ Delta x}} _ {\ text {коэффициент теплопередачи} \\ {\ text {проводимости} \ Lambda}} \ cdot \ Delta T \\ [5px]
\ end {align}
Закон Фурье в данном случае:
\ begin {align}
& \ boxed {\ dot q = \ Lambda \ cdot \ Delta T} ~~~ \ text {where} ~~ \ boxed {\ Lambda = \ frac {\ lambda} {\ Delta x} } ~~ \ text {коэффициент теплопроводности} \\ [5px]
\ end {align}
В то время как теплопроводность является характеристической величиной, которая зависит только от материала (величина, зависящая от материала), коэффициент теплопроводности зависит от размера объекта, поскольку он учитывает фактическую толщину объекта (величина, зависящая от компонента) !
Величина, обратная коэффициенту теплопередачи (проводимости), называется тепловым сопротивлением (проводимости) \ (R \):
\ begin {align}
& R: = \ frac {1} {\ Lambda} \\ [5px]
& \ boxed {R = \ frac {\ Delta x} {\ lambda}} ~~~ \ text {термический сопротивление проводимости} \\ [5px]
\ end {align}
Как величина, зависящая от компонента, тепловое сопротивление проводимости описывает изолирующий эффект компонента в отношении теплопроводности!
Температуропроводность
Температуропроводность \ (a \) связана с теплопроводностью.Температуропроводность определяется плотностью \ (\ rho \) и удельной теплоемкостью материала \ (c \):
\ begin {align}
& \ boxed {a = \ frac {\ lambda} {\ rho \ cdot c}} ~~~~~ \ text {коэффициент температуропроводности} \\ [5px]
\ end {align}
В отличие от теплопроводности (установившееся состояние теплопроводности), температуропроводность описывает передачу тепла для теплопроводности в установившемся состоянии и , то есть распространение температуры во времени внутри объекта.2}} ~~~ \ text {одномерное уравнение теплопроводности} \\ [5px]
\ end {align}
С помощью уравнения теплопроводности можно, например, определить распространение температуры вдоль стержня во времени.
Анимация: Распределение температуры во времени вдоль нагреваемого тонкого стержняКоэффициент теплопередачи и тепловое сопротивление конвекции
Коэффициент теплопередачи \ (\ alpha \) описывает теплопередачу за счет тепловой конвекции между жидкостью (газом или жидкостью) и твердым телом из-за разницы температур между этими средами.Такой перенос тепла имеет большое значение, например, в трубе, по которой протекает вода. Между водой и стенкой трубы тепло передается за счет конвекции, если, например, труба теплее воды. Тепловой поток \ (\ точка q \) на границе раздела между твердым телом («стенкой») и жидкостью можно рассчитать по следующей формуле:
\ begin {align}
& \ boxed {\ dot q = \ alpha \ cdot (T_w-T_f)} \\ [5px]
\ end {align}
В этой формуле температура жидкости обозначается как \ (T_f \), а температура непосредственно на поверхности твердой стенки обозначается как \ (T_w \).Более подробную информацию о коэффициенте теплопередачи можно найти в статье Коэффициент теплопередачи для тепловой конвекции.
Коэффициент, обратный коэффициенту теплопередачи, называется тепловое сопротивление конвекции сопротивление теплопередаче \ (R_ \ text {s} \):
\ begin {align}
\ label {rk}
& \ boxed {R_ \ text {s} = \ frac {1} {\ alpha}} ~~~ \ text {тепловое сопротивление конвекции} \\ [5px]
\ end {align}
Как величина, зависящая от компонента, тепловое сопротивление конвекции описывает изолирующий эффект объекта по отношению к тепловой конвекции!
Коэффициент теплопередачи (значение U)
Коэффициент теплопередачи (общий) \ (U \), также называемый U-значением или U-фактором , описывает теплопередачу между двумя жидкостями, разделенными твердым телом.Тепловой поток \ (\ dot q \) через твердое тело зависит от разницы температур \ (\ Delta T \) жидкостей:
\ begin {align}
& \ boxed {\ dot q = U \ cdot \ Delta T} \\ [5px]
\ end {align}
Коэффициент теплопроводности играет важную роль в строительстве, где, например, стена здания отделяет воздух внутри здания от воздуха снаружи. Особую роль играют два механизма теплопередачи, поэтому всю теплопередачу можно разделить на три этапа:
- тепловая конвекция от жидкости к одной стороне разделяющего объекта («внутренность»)
→ тепловое сопротивление конвекции \ (R_ \ text {si} \) - теплопроводность через разделяющий объект
→ тепловое сопротивление теплопроводности \ (R \) - тепловая конвекция с противоположной стороны разделяющего объекта («снаружи») на жидкость
→ тепловое сопротивление конвекции \ (R_ \ text {se} \)
Сумма отдельных тепловых сопротивлений в конечном итоге дает общее тепловое сопротивление \ (R_ \ text {T} \) через компонент (аналогично электрическому сопротивлению):
\ begin {align}
& \ boxed {R_ \ text {T} = R_ \ text {si} + R + R_ \ text {se}} ~~~ \ text {общее тепловое сопротивление} \\ [5px]
\ end {align}
Таким образом, полное тепловое сопротивление описывает изолирующий эффект компонента, разделяющего две жидкости (например,грамм. воздух). Обратное значение общего теплового сопротивления в конечном итоге соответствует U-значению (общий коэффициент теплопередачи):
\ begin {align}
& \ boxed {U = \ frac {1} {R_ \ text {T}} = \ frac {1} {R_ \ text {si} + R + R_ \ text {se}}} ~~~ \ text {значение U} \\ [5px]
\ end {align}
Сводка
| количество | описание … | Примечание |
|---|---|---|
| теплопроводность \ (\ лямбда \) | теплопроводность в устойчивом состоянии материал | теплопроводность в установившемся режиме | свойство компонента |
| тепловое сопротивление проводимости \ (R \) | изоляционный эффект теплопроводности | обратная величина теплового коэффициент теплопроводности |
| коэффициент температуропроводности \ (a \) | распространение температуры за счет теплопроводности (нестационарное состояние) | см. akson-quick.ru © 2019
|
