ЗОЛОТАЯ ПРОПОРЦИЯ. НОВЫЙ ВЗГЛЯД | Наука и жизнь
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Золотую пропорцию в школе не «проходят». И когда один из авторов предлагаемой ниже статьи (кандидат технических наук В. Белянин) рассказал о золотом сечении абитуриентке, собравшейся поступать в МАДИ, в процессе подготовки к экзаменам в институт, задача неожиданно вызвала живой интерес и массу вопросов, на которые «с ходу» не было ответов. Решили искать их вместе, и тогда обнаружились тонкости в золотой пропорции, ускользавшие от исследователей ранее.
Узоры математики, как и узоры художника или узоры поэта, должны быть красивы;
идеи, как и краски или слова, должны сочетаться гармонически. Красота является первым критерием: в мире нет места для безобразной математики.
Дж. Х. Харди
Красота математической задачи служит одним из важнейших стимулов ее нескончаемого развития и причиной порождения многочисленных приложений. Порой проходят десятки, сотни, а иногда и тысячи лет, но люди вновь и вновь находят неожиданные повороты в хорошо известном решении и его интерпретации. Одной из таких долгоживущих и увлекательных задач оказалась задача о золотом сечении (ЗС), отражающая элементы изящества и гармонии окружающего нас мира. Нелишне напомнить, кстати, что, хотя сама пропорция была известна еще Евклиду, термин «золотое сечение» ввел Леонардо да Винчи (см.
Геометрически золотое сечение подразумевает деление отрезка на две неравные части так, чтобы большая часть была средним пропорциональным между всем отрезком и меньшей частью (рис. 1).
Алгебраически это выражается следующим образом:
, или ,
или (1)
Исследование этой пропорции еще до ее решения показывает, что между отрезками a и b существуют по крайней мере два удивительных соотношения. Например, из пропорции (1) легко получается выражение,
которое устанавливает пропорцию между отрезками a, b, их разностью и суммой. Поэтому о золотом сечении можно сказать иначе: два отрезка находятся в гармоничном соотношении, если их разность относится к меньшему отрезку так, как больший отрезок относится к их сумме.
Второе соотношение получается, если исходный отрезок принять равным единице: a + b = 1, что очень часто используется в математике. В таком случае
a2 — b2 = a — b = ab.
Из этих результатов следуют два удивительных соотношения между отрезками а и b:
a2 — b2 = a — b = ab,(2)
которые будут использованы в дальнейшем.
Перейдем теперь к решению пропорции (1). На практике используют две возможности.
1. Обозначим отношение a/b через . Тогда получим уравнение
x2 — x — 1 = 0, (3)
которое имеет иррациональные корни
Обычно рассматривают только положительный корень x1, дающий простое и наглядное деление отрезка в заданной пропорции. Действительно, если принять целый отрезок за единицу, то, используя значение этого корня x1, получим a ≈ 0,618, b ≈ 0,382.
Именно положительный корень x1 уравнения (3) наиболее часто называют золотой пропорцией или пропорцией золотого сечения. Соответствующее геометрическое деление отрезка называют золотым сечением (точка С на рис. 1).
1).
Для удобства дальнейшего изложения обозначим x1
Оставляемый по обыкновению в стороне отрицательный корень x2 приводит к менее наглядному делению отрезка на две неравные части. Дело в том, что он дает делящую точку С, которая лежит вне отрезка (так называемое внешнее деление). Действительно, если a + b = 1, то, используя корень x2, получим a ≈ -1,618, b ≈ 2,618. Поэтому отрезок a необходимо откладывать в отрицательном направлении (рис. 2).
2. Второй вариант решения пропорции (1) принципиально не отличается от первого. Будем считать неизвестным отношение
y2 + y -1 = 0 , (4)
которое имеет иррациональные корни
Если a + b = 1, то, используя корень y1, получим a = y1 ≈ 0,618, b ≈ 0,382. Для корня y2 получим a ≈ -1,618, b ≈ 2,618. Геометрическое деление отрезка в пропорции золотого сечения с использованием корней y1 и y2 полностью идентично предыдущему варианту и соответствует рис. 1 и 2.
Для корня y2 получим a ≈ -1,618, b ≈ 2,618. Геометрическое деление отрезка в пропорции золотого сечения с использованием корней y1 и y2 полностью идентично предыдущему варианту и соответствует рис. 1 и 2.
Положительный корень y1 непосредственно дает искомое решение задачи, и его также называют золотой пропорцией .
Для удобства обозначим значение корня y1 = d.
Таким образом, в литературе золотую пропорцию математически выражают числом D1,618 или числом d0,618, между которыми существуют две изумительные связи:
Dd = 1 и D — d = 1. (5)
Доказано, что другой подобной пары чисел, обладающих этими свойствами, не существует.
Используя оба обозначения для золотой пропорции, запишем решения уравнений (3) и (4) в симметричном виде: =
Необычные свойства золотого сечения достаточно подробно описаны в литературе [1-4]. Они настолько удивительны, что покоряли разум многих выдающихся мыслителей и создали вокруг себя ореол таинственности.
Они настолько удивительны, что покоряли разум многих выдающихся мыслителей и создали вокруг себя ореол таинственности.
Золотая пропорция встречается в конфигурации растений и минералов, строении частей Вселенной, музыкальном звукоряде. Она отражает глобальные принципы природы, пронизывая все уровни организации живых и неживых объектов. Ее используют в архитектуре, скульптуре, живописи, науке, вычислительной технике, при проектировании предметов быта. Творения, несущие в себе конфигурацию золотого сечения, представляются соразмерными и согласованными, всегда приятны взгляду, да и сам математический язык золотой пропорции не менее изящен и элегантен.
Кроме равенств (5) из соотношения (2) можно выделить три интересные соотношения, которые обладают определенным совершенством, выглядят вполне привлекательно и эстетично:
(6)
Величие и глубину природы можно ощущать не только, например, при созерцании
звезд или горных вершин, но и вглядываясь в некоторые удивительные формулы,
очень ценимые математиками за их красоту. К ним можно отнести изящные соотношения
золотой пропорции, фантастическую формулу Эйлера
К ним можно отнести изящные соотношения
золотой пропорции, фантастическую формулу Эйлера
После решения пропорции (1) ее идея кажется довольно простой, но, как это часто бывает со многими на первый взгляд простыми задачами, в ней скрыто немало тонкостей. Одной из таких замечательных тонкостей, мимо которой до сих пор проходили исследователи, является связь корней уравнений (3) и (4) с углами трех замечательных треугольников.
Чтобы убедиться в этом, рассмотрим, каким образом одномерный отрезок, разделенный в пропорции золотого сечения, может быть легко преобразован в двумерный образ в виде треугольника. Для этого, используя вначале рис. 1, отложим на отрезке
 Получим две точки С1 и С2, делящие отрезок АВ с разных концов в пропорции золотого сечения (рис. 3). Считая равные отрезки АС1 и ВС2 радиусами, а точки А и В центрами окружностей, проведем две дуги до их пересечения в верхней точке С. Соединив точки А и С, а также
Получим две точки С1 и С2, делящие отрезок АВ с разных концов в пропорции золотого сечения (рис. 3). Считая равные отрезки АС1 и ВС2 радиусами, а точки А и В центрами окружностей, проведем две дуги до их пересечения в верхней точке С. Соединив точки А и С, а также По теореме косинусов
(АВ)2 = 2(АС)2(1 — cos β).
Подставив численные значения отрезков АВ и АС в эту формулу, получим
(7)
Аналогично получаем
(8)
Выход золотой пропорции на двумерный образ позволил связать корни уравнений (3) и (4) с углами треугольника АВС, который можно назвать первым треугольником золотой пропорции.
Выполним аналогичное построение, используя рис. 2. Если на продолжении отрезка АВ отложить от точки В вправо отрезок, равный по величине отрезку a, и повернуть вокруг центров А и В вверх оба отрезка как радиусы до их соприкосновения, то получим второй треугольник золотой пропорции (рис. 4). В этом равнобедренном треугольнике сторона АВ = a + b = 1, сторона АС = ВС = D ≈1,618, и поэтому по формуле теоремы косинусов получаем
(9)
Угол a при вершине С равен 36о и связан с золотой пропорцией соотношением (8). Как и в предыдущем случае, углы этого треугольника связаны с корнями уравнений (3) и (4).
Второй треугольник золотой пропорции служит основным составляющим элементом правильного выпуклого пятиугольника и задает пропорции правильного звездчатого пятиугольника (пентаграммы), свойства которых подробно рассмотрены в книге [3].
Звездчатый пятиугольник — фигура симметричная, и в то же время в соотношениях ее отрезков проявляется асимметрическая золотая пропорция. Подобное сочетание противоположностей всегда притягивает глубоким единством, познание которого позволяет проникнуть в скрытые законы природы и понять их исключительную глубину и гармонию. Пифагорейцы, покоренные созвучием отрезков в звездчатом пятиугольнике, выбрали его символом своего научного сообщества.
Подобное сочетание противоположностей всегда притягивает глубоким единством, познание которого позволяет проникнуть в скрытые законы природы и понять их исключительную глубину и гармонию. Пифагорейцы, покоренные созвучием отрезков в звездчатом пятиугольнике, выбрали его символом своего научного сообщества.
Со времен астронома И. Кеплера (XVII век) иногда высказываются различные точки зрения относительно того, что обладает большей фундаментальностью — теорема Пифагора или золотая пропорция. Теорема Пифагора лежит в основании математики, это один из ее краеугольных камней. Золотое сечение лежит в основании гармонии и красоты мироздания. На первый взгляд оно несложно для понимания и не обладает значительной основательностью. Тем не менее некоторые его неожиданные и глубокие свойства постигаются только в последнее время [1], что говорит о необходимости с почтением относиться к его скрытой тонкости и возможной универсальности. Теорема Пифагора и золотая пропорция в своем развитии тесно переплетаются одна с другой и геометрическими и алгебраическими свойствами. Между ними нет ни пропасти, ни принципиальных различий. Они не конкурируют, у них разные предназначения.
Между ними нет ни пропасти, ни принципиальных различий. Они не конкурируют, у них разные предназначения.
Вполне возможно, что обе точки зрения равноправны, так как существует прямоугольный треугольник, содержащий в себе разнообразные особенности золотой пропорции. Другими словами, существует геометрическая фигура, достаточно полно объединяющая два математических восхитительных факта — теорему Пифагора и золотую пропорцию.
Чтобы построить такой треугольник, достаточно продолжить сторону ВС треугольника АВС (рис. 4) до пересечения в точке Е с перпендикуляром, восстановленным в точке А к стороне АВ (рис. 5).
Во внутреннем равнобедренном треугольнике АСЕ угол φ (угол АСЕ) равен 144о, а угол ψ (углы ЕАС и АЕС) равен 18о. Сторона АС = СЕ = СВ = D. Используя теорему Пифагора, легко получить, что длина катета
Используя этот результат, легко приходим к соотношению(10)
Итак, найдена непосредственная связь корня y2 уравнения (4) — последнего из корней уравнений (3) и (4) — с углом 144о. В связи с этим треугольник АСЕ можно назвать третьим треугольником золотой пропорции.
В связи с этим треугольник АСЕ можно назвать третьим треугольником золотой пропорции.
Если в замечательном прямоугольном треугольнике АВЕ провести биссектрису угла САВ до пересечения со стороной ЕВ в точке F, то увидим, что вдоль стороны АВ располагаются четыре угла: 36о, 72о, 108о и 144о, с которыми корни уравнений золотой пропорции имеют непосредственную связь (соотношения (7) — (10)). Таким образом, в представленном прямоугольном треугольнике содержится вся плеяда равносторонних треугольников, обладающих особенностями золотого сечения. Кроме того, весьма примечательно то, что на гипотенузе любые два отрезка, ЕС = D и СF = 1,0 находятся в соотношении золотой пропорции с FВ = d. Угол ψ связан с корнями D и d уравнений (3) и (4) соотношениями
.
В основу представленных выше построений равнобедренных треугольников, углы которых связаны с корнями уравнений золотой пропорции, положены исходный отрезок АВ и его части a и b. Однако золотое сечение позволяет моделировать не только описанные выше треугольники, но и различные другие геометрические фигуры, несущие в себе элементы гармоничных отношений.
Однако золотое сечение позволяет моделировать не только описанные выше треугольники, но и различные другие геометрические фигуры, несущие в себе элементы гармоничных отношений.
Приведем два примера подобных построений. В первом — рассмотрим отрезок АВ, представленный на рис. 1. Пусть точка С — центр окружности, отрезок b — радиус. Проведем радиусом b окружность и касательные к ней из точки А (рис. 6). Соединим точки касания E и F с точкой С. В результате получим асимметричный ромб АЕСF, в котором диагональ АС делит его на два равных прямоугольных треугольника АСЕ и АСF.
Обратим более пристальное внимание на один из них, например на треугольник АСЕ. В этом треугольнике угол АЕС — прямой, гипотенуза АС = a, катет СЕ = b и катет АЕ = √ab ≈ 0,486, что следует из соотношения (2). Следовательно, катет АЕ является средним геометрическим (пропорциональным) между отрезками a и b, то есть выражает геометрический центр симметрии между числами a ≈ 0,618 и b ≈ 0,382.
Найдем значения углов этого треугольника:
Как и в предыдущих случаях, углы δ и ε связаны через косинус с корнями уравнений (3) и (4).
Заметим, что асимметричный ромб, подобный ромбу AECF, получается при проведении касательных из точки В к окружности радиуса a и c центром в точке А.
Асимметричный ромб AECF получен иным путем в книге [1] при анализе формообразования и явлений роста в живой природе. Прямоугольный треугольник АЕС назван в этой работе «живым» треугольником, так как способен порождать наглядные образы, соответствующие различным структурным элементам природы, и служить ключом при построении геометрических схем начала развития некоторых живых организмов.
Второй пример связан с первым и третьим треугольниками золотого сечения. Образуем из двух равных первых треугольников золотой пропорции ромб с внутренними углами 72о и 108о. Аналогично объединим два равных третьих треугольника золотой пропорции в ромб с внутренними углами 36о и 144о. Если стороны этих ромбов равны между собой, то ими можно заполнить бесконечную плоскость без пустот и перекрытий. Соответствующий алгоритм заполнения плоскости разработал в конце 70-х годов ХХ века физик-теоретик из Оксфордского университета Р. Пенроуз. Причем выяснилось, что в получающейся мозаике невозможно выделить элементар ную ячейку с целым числом ромбов каждого вида, трансляция которой позволяла бы получить всю мозаику. Но самым замечательным оказалось то, что в бесконечной мозаике Пенроуза отношение числа «узких» ромбов к числу «широких» точно равно значению золотой пропорции d = 0,61803…!
Если стороны этих ромбов равны между собой, то ими можно заполнить бесконечную плоскость без пустот и перекрытий. Соответствующий алгоритм заполнения плоскости разработал в конце 70-х годов ХХ века физик-теоретик из Оксфордского университета Р. Пенроуз. Причем выяснилось, что в получающейся мозаике невозможно выделить элементар ную ячейку с целым числом ромбов каждого вида, трансляция которой позволяла бы получить всю мозаику. Но самым замечательным оказалось то, что в бесконечной мозаике Пенроуза отношение числа «узких» ромбов к числу «широких» точно равно значению золотой пропорции d = 0,61803…!
В этом примере удивительным образом соединились все корни золотого сечения, выраженные через углы, с одним из случаев нетривиального заполнения бесконечной плоскости двумя элементарными фигурами — ромбами.
В заключение отметим, что приведенные выше разнообразные примеры связи корней уравнений золотой пропорции с углами треугольников иллюстрируют тот факт, что золотая пропорция более емкая задача, чем это представлялось ранее. Если прежде сферой приложения золотой пропорции считались в конечном итоге соотношения отрезков и различные последовательности, связанные с численными значениями ее корней (числа Фибоначчи), то теперь обнаруживается, что золотая пропорция может генерировать разнообразные геометрические объекты, а корни уравнений имеют явное тригонометрическое выражение.
Если прежде сферой приложения золотой пропорции считались в конечном итоге соотношения отрезков и различные последовательности, связанные с численными значениями ее корней (числа Фибоначчи), то теперь обнаруживается, что золотая пропорция может генерировать разнообразные геометрические объекты, а корни уравнений имеют явное тригонометрическое выражение.
Авторы отдают себе отчет, что высказанная выше точка зрения относительно изящества математических соотношений, связанных с золотой пропорцией, отражает личные эстетические переживания. В современной философской литературе понятия эстетики и красоты трактуются довольно широко и используются скорее на интуитивном уровне. Эти понятия отнесены главным образом к искусству. Содержание научного творчества в эстетическом плане в литературе практически не рассматривается. В первом приближении к эстетическим параметрам научных исследований можно отнести их сравнительную простоту, присущую им симметрию и способность порождать наглядные образы. Всем этим эстетическим параметрам отвечает задача, получившая название «золотая пропорция». В целом же проблемы эстетики в науке далеки от своего решения, хотя и представляют большой интерес.
Всем этим эстетическим параметрам отвечает задача, получившая название «золотая пропорция». В целом же проблемы эстетики в науке далеки от своего решения, хотя и представляют большой интерес.
Интуитивно чувствуется, что золотая пропорция все еще скрывает свои тайны. Некоторые из них, вполне возможно, лежат на поверхности, ожидая необычного взгляда своих новых исследователей. Знание свойств золотой пропорции может служить творческим людям хорошим фундаментом, придавать им уверенность и в науке и в жизни.
ЛИТЕРАТУРА
1. Шевелев И. Ш., Марутаев И. А., Шмелев И. П. Золотое сечение: Три взгляда на природу гармонии. — М.: Стройиздат, 1990. — 343 с.
2. Стахов А. П. Коды золотой пропорции. — М.: Радио и связь, 1984. — 152 с.
3. Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238 с.
4. Коробко В. И. Золотая пропорция: Некоторые философские аспекты гармонии. — М. — Орел: 2000. — 204 с.
— Орел: 2000. — 204 с.
5. Урманцев Ю. А. Золотое сечение // Природа, 1968, № 11.
6. Попков В. В., Шипицын Е. В. Золотое сечение в цикле Карно // УФН, 2000, т. 170, № 11.
7. Константинов И. Фантазии с додекаэдром // Наука и жизнь, 2001, № 2.
8. Шевелев И. Ш. Геометрическая гармония // Наука и жизнь, 1965, № 8.
9. Гарднер М. От мозаик Пенроуза к надежным шифрам. — М. : Мир, 1993.
Золотая пропорция. новый взгляд. Золотое сечение: как это работает
Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве – во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.
ОПРЕДЕЛЕНИЕ
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая — ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.
Это соотношение действует в формах пространства и времени.
Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.
ИСТОРИЯ
Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой дух.
Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи — это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.
д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи — это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.
Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего, именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.
Впрочем, его «математическое эстетство» вызывало много критики.
ПРИРОДА
Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.
Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.
ЧЕЛОВЕК
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек – это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.
В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.
Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.
В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.
В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела – 8:5.
ИСКУССТВО ПРОСТРАНСТВЕННЫХ ФОРМ
Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следовали этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.
Искусствовед Ф.В.Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.
Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.
И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.
СЛОВО, ЗВУК И КИНОЛЕНТАФормы временно?го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи – 5, 8, 13, 21, 34.
Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.
В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.
Советский музыковед Э.К.Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.
Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух – в Одессе. Переход на сцены в городе и есть золотая середина фильма.
Ещё в древнем Египте было известно Золотое сечение , Леонардо да Винчи и Евклид изучали свойства его. Зрительное восприятие человека устроено таким образом, что он различает по форме все предметы, которые его окружают. Его интерес к предмету или его форме, продиктован иногда необходимостью, или этот интерес могла вызвать красота предмета. Если в самой основе построения формы, использовано сочетание золотого сечения и законы симметрии, то это наилучшее сочетание для визуального восприятия человеком, который ощущает гармонию и красоту. Всё целое состоит из частей, больших и малых, и эти разной величины части имеют определённое отношение, как друг к другу, так и к целому. А высшее проявление функционального и структурного совершенства в природе, науке, искусстве, архитектуре и технике это Принцип золотого сечения . Понятие о золотом сечении ввел в научный обиход древнегреческий математик и философ (VI в. до н.э.) Пифагор. Но само знание о золотом сечении он позаимствовал у древних египтян. Пропорции всех построек храмов, пирамиды Хеопса, барельефов, предметы быта и украшения из гробниц показывают, что соотношение золотого сечения активно использовалось древними мастерами ещё задолго до Пифагора.
Его интерес к предмету или его форме, продиктован иногда необходимостью, или этот интерес могла вызвать красота предмета. Если в самой основе построения формы, использовано сочетание золотого сечения и законы симметрии, то это наилучшее сочетание для визуального восприятия человеком, который ощущает гармонию и красоту. Всё целое состоит из частей, больших и малых, и эти разной величины части имеют определённое отношение, как друг к другу, так и к целому. А высшее проявление функционального и структурного совершенства в природе, науке, искусстве, архитектуре и технике это Принцип золотого сечения . Понятие о золотом сечении ввел в научный обиход древнегреческий математик и философ (VI в. до н.э.) Пифагор. Но само знание о золотом сечении он позаимствовал у древних египтян. Пропорции всех построек храмов, пирамиды Хеопса, барельефов, предметы быта и украшения из гробниц показывают, что соотношение золотого сечения активно использовалось древними мастерами ещё задолго до Пифагора. Как пример: барельеф из храма Сети I в Абидосе и в барельефе Рамзеса использован принцип золотого сечения в пропорциях фигур. Выяснил это архитектор Ле Корбюзье. На деревянной доске извлечённой из гробницы Зодчего Хесира, изображен рельефный рисунок, на котором виден сам зодчий, держащий в руках инструменты для измерений, которые изображены в положении фиксирующем принципы золотого сечения . Знал о принципах золотого сечения и Платон (427…347 гг. до н.э.). Диалог «Тимей» тому доказательство,так как он посвящен вопросам золотого деления , эстетическим и математическим воззрениям школы Пифагора. Принципы Золотого сечения использованы древнегреческими архитекторами в фасаде храма Парфенона. Циркули которые применяли в своей работе древние архитекторы и скульпторы античного мира были обнаружены при раскопках храма Парфенона.
Как пример: барельеф из храма Сети I в Абидосе и в барельефе Рамзеса использован принцип золотого сечения в пропорциях фигур. Выяснил это архитектор Ле Корбюзье. На деревянной доске извлечённой из гробницы Зодчего Хесира, изображен рельефный рисунок, на котором виден сам зодчий, держащий в руках инструменты для измерений, которые изображены в положении фиксирующем принципы золотого сечения . Знал о принципах золотого сечения и Платон (427…347 гг. до н.э.). Диалог «Тимей» тому доказательство,так как он посвящен вопросам золотого деления , эстетическим и математическим воззрениям школы Пифагора. Принципы Золотого сечения использованы древнегреческими архитекторами в фасаде храма Парфенона. Циркули которые применяли в своей работе древние архитекторы и скульпторы античного мира были обнаружены при раскопках храма Парфенона.
Парфенон, Акрополь., Афины В Помпеях (музей в Неаполе) пропорции золотого деления так же имеются в наличии. В античной литературе дошедшей до нас принцип золотого сечения упоминается впервые в «Началах» Евклида. В книге «Начал» во второй части дается геометрический принцип золотого сечения . Последователями Евклида стали Папп (III в. н.э.) Гипсикл (II в. до н.э.), и др. В средневековую Европу с принципом золотого сечения познакомились по переводам с арабского Евклидовских «Начал». Принципы золотого сечения были известны только узкому кругу посвященных,они ревностно оберегались, хранились в строгой тайне. Наступила эпоха возрождения и интерес к принципам золотого сечения увеличивается в среде учёных и художников так как этот принцип применим и в науке, и в архитектуре, и в искусстве. И Леонардо Да Винчи стал использовать эти принципы в своих произведениях, даже более того он начал писать книгу по геометрии, но но в это время появилась книга монаха Луки Пачоли, который опередил его и выпустил в свет книгу «Божественная пропорция» после чего Леонардо оставил свой труд не законченным.
В античной литературе дошедшей до нас принцип золотого сечения упоминается впервые в «Началах» Евклида. В книге «Начал» во второй части дается геометрический принцип золотого сечения . Последователями Евклида стали Папп (III в. н.э.) Гипсикл (II в. до н.э.), и др. В средневековую Европу с принципом золотого сечения познакомились по переводам с арабского Евклидовских «Начал». Принципы золотого сечения были известны только узкому кругу посвященных,они ревностно оберегались, хранились в строгой тайне. Наступила эпоха возрождения и интерес к принципам золотого сечения увеличивается в среде учёных и художников так как этот принцип применим и в науке, и в архитектуре, и в искусстве. И Леонардо Да Винчи стал использовать эти принципы в своих произведениях, даже более того он начал писать книгу по геометрии, но но в это время появилась книга монаха Луки Пачоли, который опередил его и выпустил в свет книгу «Божественная пропорция» после чего Леонардо оставил свой труд не законченным. По оценкам историков науки и современников, Лука Пачоли являлся настоящим светилом, гениальным Итальянским математиком в проживавшим в период между Галилеем и Фибоначчи. Являясь учеником художника Пьеро делла Франчески, Лука Пачоли написал две книги, «О перспективе в живописи», название одной из них. Он по мнению многих является творцом начертательной геометрии. Лука Пачоли по приглашению герцога Моро в 1496 г приезжает в Милан, и читает там лекции по математике. Леонардо да Винчи в это время работал при дворе Моро. Изданная в 1509 году в Венеции книга Луки Пачоли «Божественная пропорция» стала восторженным гимном золотой пропорции , с иллюстрациями прекрасно выполненными, есть все основания полагать что иллюстрации выполнил сам Леонардо да Винчи. Монах Лука Пачоли, как одно из достоинств золотой пропорции выделял её «божественную суть». Понимая научную и художественную ценность золотого сечения,Леонардо да Винчи посвящал много времени для его изучения. Выполняя сечение стереометрического тела, состоящего из пятиугольников, он получал прямоугольники с отношениями сторон в соответствии с золотым сечением .
По оценкам историков науки и современников, Лука Пачоли являлся настоящим светилом, гениальным Итальянским математиком в проживавшим в период между Галилеем и Фибоначчи. Являясь учеником художника Пьеро делла Франчески, Лука Пачоли написал две книги, «О перспективе в живописи», название одной из них. Он по мнению многих является творцом начертательной геометрии. Лука Пачоли по приглашению герцога Моро в 1496 г приезжает в Милан, и читает там лекции по математике. Леонардо да Винчи в это время работал при дворе Моро. Изданная в 1509 году в Венеции книга Луки Пачоли «Божественная пропорция» стала восторженным гимном золотой пропорции , с иллюстрациями прекрасно выполненными, есть все основания полагать что иллюстрации выполнил сам Леонардо да Винчи. Монах Лука Пачоли, как одно из достоинств золотой пропорции выделял её «божественную суть». Понимая научную и художественную ценность золотого сечения,Леонардо да Винчи посвящал много времени для его изучения. Выполняя сечение стереометрического тела, состоящего из пятиугольников, он получал прямоугольники с отношениями сторон в соответствии с золотым сечением . И название он ему дал “золотое сечение ”. Которое держится до сих пор. Альбрехт Дюрер,так же занимается изучением золотого сечения в Европе, встречается с монахом Лукой Пачоли. Иоган Кеплер величайший астроном того времени, первым обращает внимание на значение золотого сечения для ботаники называя его сокровищем геометрии. Он называл золотую пропорцию продолжающей саму себя «Она так устроена, – он говорил, – сумма двух младших членов нескончаемой пропорции дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
И название он ему дал “золотое сечение ”. Которое держится до сих пор. Альбрехт Дюрер,так же занимается изучением золотого сечения в Европе, встречается с монахом Лукой Пачоли. Иоган Кеплер величайший астроном того времени, первым обращает внимание на значение золотого сечения для ботаники называя его сокровищем геометрии. Он называл золотую пропорцию продолжающей саму себя «Она так устроена, – он говорил, – сумма двух младших членов нескончаемой пропорции дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
Что бы найти отрезки золотой пропорции нисходящего и восходящего рядов воспользуемся пентаграммой.
Рис. 5. Построение правильного пятиугольника и пентаграммы
Для того чтобы построить пентаграмму нужно начертить правильный пятиугольник по разработанному немецким живописцем и графиком Альбрехтом Дюрером, способом построения. Если O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Используя циркуль, отметим отрезок на диаметре CE = ED. Тогда длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Затем через один угол соединяем углы пятиугольника диагоналями и получим пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Если O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Используя циркуль, отметим отрезок на диаметре CE = ED. Тогда длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Затем через один угол соединяем углы пятиугольника диагоналями и получим пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения. Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.
Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.
Рис. 6. Построение золотого
треугольника
Золотое сечение и Золотое СечениеВ математике и искусстве, две величины находятся в золотой пропорции, если соотношение между суммой этих величин и большиего такое же, как соотношение между большего и меньшего. Выразил алгебраически: Золотое сечение часто обозначается греческой буквой фи (? или?). фигура золотого сечения иллюстрирует геометрические отношения, которые определяют эту константу. Золотое сечение является иррациональной математической константой, примерно 1,6180339887.
Золотой прямоугольникЗолотой прямоугольник представляет собой прямоугольник, длины сторон находятся в золотой пропорции, 1: ? (один-к-фи), то есть 1: или примерно 1:1. 618. Золотой прямоугольник может быть построен только с линейкой и циркулем: 1. Построить простой квадрат 2. Нарисуйте линию от середины одной стороны площади к противоположному углу 3. Используйте эту линию в качестве радиуса, чтобы нарисовать дугу, которая определяет высоту прямоугольника 4. Завершить золотой прямоугольник
618. Золотой прямоугольник может быть построен только с линейкой и циркулем: 1. Построить простой квадрат 2. Нарисуйте линию от середины одной стороны площади к противоположному углу 3. Используйте эту линию в качестве радиуса, чтобы нарисовать дугу, которая определяет высоту прямоугольника 4. Завершить золотой прямоугольник
В геометрии, золотой спиралью является логарифмическая спираль, фактор роста которой b связано с ? , золотым сечением. В частности, золотая спираль становится более широкой (дальше от места ее начала) на коэффициент ? для каждой четверти оборота который она делает.
Последовательные точки деления золотого прямоугольника на квадраты, лежат на логарифмической спирали, которая иногда известна как золотая спираль.
Золотое сечение в архитектуре и искусстве.Многие архитекторы и художники свои работы исполняли в соответствии с пропорциями золотого сечения, особенно в виде золотого прямоугольника, в котором отношение большей стороны к меньшей имеет пропорции золотого сечения, полагая, что это соотношение будет эстетично. [ Источник: Wikipedia.org ]
[ Источник: Wikipedia.org ]
Вот несколько примеров:
Парфенон, Акрополь., Афины . Этот древний храм подходит почти точно в золотой прямоугольник.
Витрувианский Человек Леонардо да Винчи можно сделать много линий прямоугольников в эту цифру. Затем, существуют три различных набора золотых прямоугольников: Каждый набор для области головы, туловища, и ног. Рисунок Леонардо Да Винчи Витрувианский Человек иногда путают с принципами «золотого прямоугольника», однако, это не так. Построение Витрувианского Человека основано на рисовании круга с диаметром, равным диагонали квадрата, перемещая его вверх таким образом, что он будет касаться основания квадрата и составление окончательного круга между основанием площади и средней точке между площадью центра квадрата и центра круга: Подробное объяснение о геометрических строительство >>
Золотое сечение в природе.
Адольф Цейзинг, чьи основные интересы были математика и философия, нашел золотую пропорцию в расположении ветвей вдоль стебля растения и прожилок в листьях. Он расширил свои исследования и от растений перешёл к животным, изучая скелеты животных и разветвлений их вен и нервов, а так же в пропорциях химических соединений и геометрии кристаллов, вплоть до использования золотого сечения в изобразительном искусстве. В этих явлениях, он увидел, что золотая пропорция используется везде в качестве универсального закона, Цейзинг написал в 1854 году.: Золотое сечение является универсальным законом, в котором содержится основной принцип формирующий стремление к красоте и полноте в таких областях, как природы, так и искусства, которая пронизывает, как первостепенный духовный идеал, всех структур, форм и пропорций, будь то космическое или физическое лицо, органическое или неорганическое, акустическое или оптическое, но свою наиболее полную реализацию принцип золотого сечения находит, в человеческой форме.
Примеры:
Срез оболочки Nautilus открывает золотой принцип построения спирали.
Моцарт разделил свои сонаты на две части, длины которых отражают золотое сечение , хотя существует много споров о том, сознательно ли он это сделал. В более современные времена, венгерский композитор Бела Барток и французский архитектор Ле Корбюзье целенаправленно включали принцип золотой пропорции в свои работы. Даже сегодня, золотое сечение окружает нас повсеместно в искусственных предметах. Посмотрите на практически любой христианский крест, отношение вертикальной части к горизонтальной золотая пропорция. Чтобы найти золотой прямоугольник, посмотрите в своём бумажнике, и вы найдёте там кредитные карты. Несмотря на эти многочисленные доказательства приведённые в произведениях искусства созданные на протяжении веков, в настоящее время ведутся дискуссии среди психологов о том, действительно ли люди воспринимают золотые пропорции, в частности, золотой прямоугольник, как более красивым, чем другие формы. В 1995 году статье в журнале, профессор Кристофер Грин,
из Йоркского университета в Торонто, обсуждает ряд экспериментов на протяжении многих лет, которые не показали какого либо предпочтение форме золотой прямоугольник, но отмечает, что некоторые другие представили доказательства того, что такое предпочтение не существует.
Но независимо от науки, золотое сечение сохраняет свою загадочность, отчасти потому, что отлично применяется во многих неожиданных местах в природе. Спираль раковины моллюска Наутилус удивительно близка к золотому сечению , и отношение длины грудной клетки и живота у большинства пчел почти золотое сечение . Даже сечения из наиболее распространенных форм человеческой ДНК прекрасно вписывается в золотой десятиугольник. Золотое сечение и его родственники также появляются во многих неожиданных контекстах, в математике, и они продолжают вызвать интерес математических сообществ. Д-р Стивен Марквардт, бывший пластический хирург, использовал эту загадочную пропорцию золотое сечение , в своей работе, которое уже давно отвечает за красоту и гармонию, чтобы сделать маску, которую он считал самой красивой формой человеческого лица которое только может быть.
В 1995 году статье в журнале, профессор Кристофер Грин,
из Йоркского университета в Торонто, обсуждает ряд экспериментов на протяжении многих лет, которые не показали какого либо предпочтение форме золотой прямоугольник, но отмечает, что некоторые другие представили доказательства того, что такое предпочтение не существует.
Но независимо от науки, золотое сечение сохраняет свою загадочность, отчасти потому, что отлично применяется во многих неожиданных местах в природе. Спираль раковины моллюска Наутилус удивительно близка к золотому сечению , и отношение длины грудной клетки и живота у большинства пчел почти золотое сечение . Даже сечения из наиболее распространенных форм человеческой ДНК прекрасно вписывается в золотой десятиугольник. Золотое сечение и его родственники также появляются во многих неожиданных контекстах, в математике, и они продолжают вызвать интерес математических сообществ. Д-р Стивен Марквардт, бывший пластический хирург, использовал эту загадочную пропорцию золотое сечение , в своей работе, которое уже давно отвечает за красоту и гармонию, чтобы сделать маску, которую он считал самой красивой формой человеческого лица которое только может быть.
Маска совершенного человеческого лица
Египетская царица Нефертити (1400 до н.э.)
лицо Иисуса копия с Туринской плащанице и исправлено в соответствии с маской д-ра Стивена Марквардта.
«Усредненное» (синтезированное) лицо из числа знаменитостей. С пропорциями золотого сечения.
Использовались материалы сайта: http://blog.world-mysteries.com/
Геометрия — точная и достаточно сложная наука, которая при всем этом является своеобразным искусством. Линии, плоскости, пропорции — все это помогает создавать много действительно прекрасных вещей. И как ни странно, в основе этого лежит именно геометрия в самых разных ее формах. В этой статье мы рассмотрим одну очень необычную вещь, которая непосредственно связанна с этим. Золотое сечение — это именно тот геометрических подход, о котором пойдет речь.
Форма предмета и ее восприятие
Люди чаще всего ориентируются на форму предмета для того, чтобы распознавать его среди миллионов других. Именно по форме мы определяем, что за вещь лежит перед нами или стоит вдали. Мы в первую очередь узнаем людей по форме тела и лица. Поэтому с уверенностью можем утверждать, что сама форма, ее размеры и вид — одна из самых важных вещей в восприятии человека.
Именно по форме мы определяем, что за вещь лежит перед нами или стоит вдали. Мы в первую очередь узнаем людей по форме тела и лица. Поэтому с уверенностью можем утверждать, что сама форма, ее размеры и вид — одна из самых важных вещей в восприятии человека.
Для людей форма чего бы то ни было представляет интерес по двум главным причинам: либо это диктуется жизненной необходимостью, либо же вызывается эстетическим наслаждением от красоты. Самое лучшее зрительное восприятие и ощущение гармонии и красоты чаще всего приходит, когда человек наблюдает форму, в построении которой использовались симметрия и особое соотношение, которое и называется золотым сечением.
Понятие золотого сечения
Итак, золотое сечение — это золотая пропорция, которая также является гармоническим делением. Для того чтобы объяснить это более понятно, рассмотрим некоторые особенности формы. А именно: форма является чем-то целым, ну а целое, в свою очередь, всегда состоит из некоторых частей. Эти части, вероятнее всего, обладают разными характеристиками, по крайней мере разными размерами.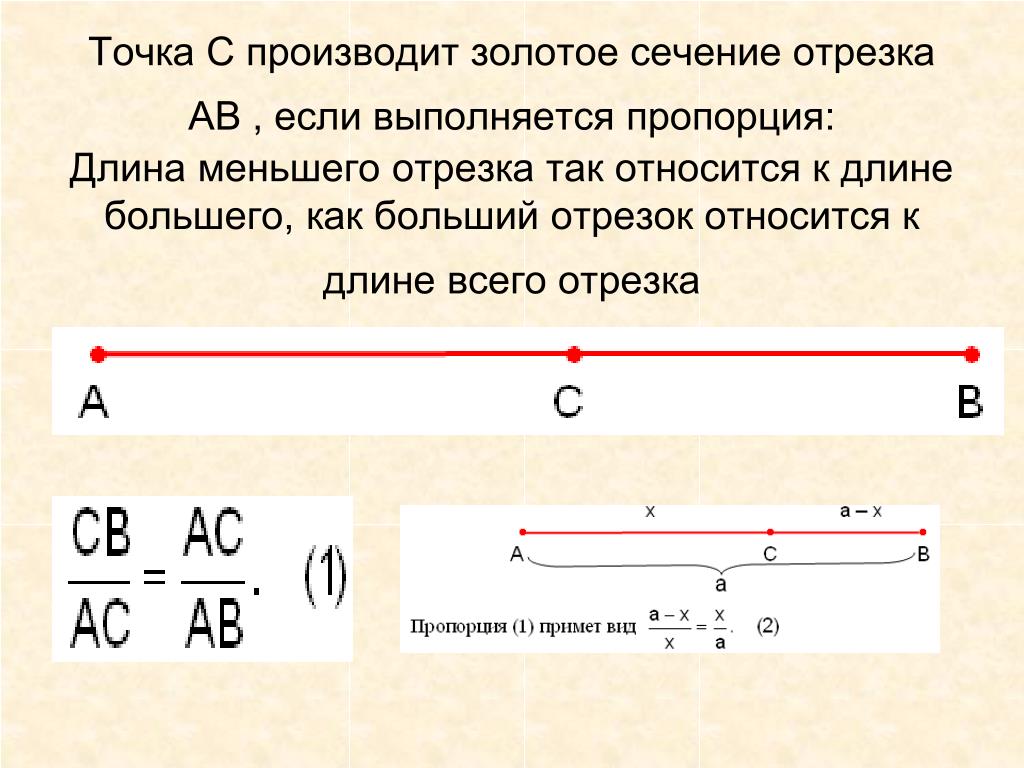 Ну а такие размеры всегда находятся в определенном соотношении как между собой, так и по отношению к целому.
Ну а такие размеры всегда находятся в определенном соотношении как между собой, так и по отношению к целому.
Значит, другими словами, мы можем утверждать, что золотое сечение — это соотношение двух величин, которое имеет свою формулу. Использование такого соотношения при создании формы помогает сделать ее максимально красивой и гармоничной для человеческого глаза.
Из древней истории золотого сечения
Соотношение золотого сечения часто используют в самых разных сферах жизни прямо сегодня. Но история этого понятия уходит еще в древние времена, когда только зарождались такие науки, как математика и философия. Как научное понятие золотое сечение вошло в обиход во времена Пифагора, а именно в VI веке до нашей эры. Но еще до того знания о подобном соотношении на практике использовали в Древнем Египте и Вавилоне. Ярким свидетельством этого являются пирамиды, для построения которых использовали именно такую золотую пропорцию.
Новый период
Эпоха Возрождения стала новым дыханием для гармонического деления, особенно благодаря Леонардо да Винчи. Это соотношение все больше начали использовать как в таких как геометрия, так и в искусстве. Ученные и художники стали более глубоко изучать золотое сечение и создавать книги, рассматривающие этот вопрос.
Это соотношение все больше начали использовать как в таких как геометрия, так и в искусстве. Ученные и художники стали более глубоко изучать золотое сечение и создавать книги, рассматривающие этот вопрос.
Одна из самых важных исторических работ, связанных с золотой пропорцией, — это книга Луки Панчоли под названием «Божественная пропорция». Историки подозревают, что иллюстрации этой книги были выполнены самим Леонардо до Винчи.
золотой пропорции
Математика дает очень четкое определение пропорции, которое говорит о том, что она является равенством двух соотношений. Математически это можно выразить таким равенством: а:b=с:d, где а, b, с, d — это некоторые определенные значения.
Если рассматривать пропорцию отрезка, разделенного на две части, то можем встретить всего несколько ситуаций:
- Отрезок разделен на две абсолютно ровные части, а значит, АВ:АС= АВ:ВС, если АВ — это точна начала и конца отрезка, а С — точка, которая и разделяет отрезок на две равные части.

- Отрезок разделен на две неравные части, которые могут находиться в самом разном соотношении между собой, а значит, здесь они абсолютно непропорциональны.
- Отрезок разделен так, что АВ:АС= АС:ВС.
Что же касается золотого сечения, то это такое пропорциональное деление отрезка на неравные между собой части, когда весь отрезок относится к большей части, как и сама большая часть относится к меньшей. Существует и другая формулировка: меньший отрезок так относится к большему, как и больший ко всему отрезку. В математическом соотношении это выглядит следующим образом: а:b = b:с или с:b = b:а. Именно такой вид имеет формула золотого сечения.
Золотая пропорция в природе
Золотое сечение, примеры которого мы сейчас рассмотрим, относится к невероятным явлениям в природе. Это очень красивые примеры того, что математика — это не просто цифры и формулы, а наука, которая имеет более чем реальное отражение в природе и нашей жизни вообще.
Для живых организмов одна из главных жизненных задач — это рост. Такое стремление занять свое место в пространстве, по сути, осуществляется в нескольких формах — рост вверх, практически горизонтальное расстилание по земле или закручивание по спирали на некой опоре. И как бы ни было это невероятно, много растений растут в соответствии с золотой пропорцией.
Такое стремление занять свое место в пространстве, по сути, осуществляется в нескольких формах — рост вверх, практически горизонтальное расстилание по земле или закручивание по спирали на некой опоре. И как бы ни было это невероятно, много растений растут в соответствии с золотой пропорцией.
Еще один почти невероятный факт — это соотношения в теле ящериц. Их тело выглядит достаточно приятно для человеческого глаза, и это возможно благодаря тому же золотому соотношению. Если быть точнее, то длина их хвоста относится к длине всего тела как 62: 38.
Интересные факты о правилах золотого сечения
Золотое сечение — это поистине невероятное понятие, а значит, на протяжении всей истории мы можем встретить много действительно интересных фактов о такой пропорции. Представляем вам некоторые из них:
Золотое сечение в человеческом теле
В этом разделе нужно упомянуть очень значимую персону, а именно — С. Цейзинга. Это немецкий исследователь, который провел огромнейшую работу в сфере изучения золотой пропорции. Он опубликовал труд под названием «Эстетические исследования». В своей работе он представил золотое сечение как абсолютное понятие, которое является универсальным для всех явлений как в природе, так и в искусстве. Здесь можно вспомнить золотое сечение пирамиды наряду с гармоничной пропорцией человеческого тела и так далее.
Он опубликовал труд под названием «Эстетические исследования». В своей работе он представил золотое сечение как абсолютное понятие, которое является универсальным для всех явлений как в природе, так и в искусстве. Здесь можно вспомнить золотое сечение пирамиды наряду с гармоничной пропорцией человеческого тела и так далее.
Именно Цейзинг смог доказать, что золотое сечение, по сути, есть средним статистическим законом для человеческого тела. Это было показано на практике, ведь во время своей работы ему пришлось измерять очень много человеческих тел. Историки считают, что в этом опыте принимали участие более двух тысяч людей. По исследования Цейзинга, главный показатель золотого соотношения — это деление тела точкой пупка. Так, мужское тело со средним соотношением 13:8 немного ближе к золотому сечению, чем женское, где число золотого сечения составляет 8:5. Также золотую пропорцию можно наблюдать в других частях тела, таких как, например, рука.
О построении золотого сечения
На самом деле, построение золотого сечения — дело нехитрое. Как мы видим, еще древние люди справлялись с этим довольно легко. Что уже говорить о современных знаниях и технологиях человечества. В этой статье мы не будем показывать, как подобное можно сделать просто на листке бумаги и с карандашом в руках, но с уверенностью заявим, что это, на самом деле, возможно. Более того, сделать это можно далеко не одним способом.
Как мы видим, еще древние люди справлялись с этим довольно легко. Что уже говорить о современных знаниях и технологиях человечества. В этой статье мы не будем показывать, как подобное можно сделать просто на листке бумаги и с карандашом в руках, но с уверенностью заявим, что это, на самом деле, возможно. Более того, сделать это можно далеко не одним способом.
Так как это достаточно несложная геометрия, золотое сечение является довольно простым для построения даже в школе. Поэтому информацию об этом можно легко найти в специализированных книгах. Изучая золотое сечение 6 класс полностью способен понять принципы его построения, а значит, даже дети достаточно умны для того, чтобы осилить подобную задачу.
Золотая пропорция в математике
Первое знакомство с золотым сечением на практике начинается с простого деления отрезка прямой все в тех же пропорциях. Чаще всего это реализуется с помощью линейки, циркуля и, конечно же, карандаша.
Отрезки золотой пропорции выражают как бесконечную иррациональную дробь AE = 0,618. .., если АВ принимается за единицу, ВЕ = 0,382… Для того чтобы сделать эти вычисления более практическими, очень часто используют не точные, а приближенные значения, а именно — 0,62 и 0,38. Если же отрезок АВ принимать за 100 частей, то большая его часть будет равна 62, ну а меньшая — 38 частям соответственно.
.., если АВ принимается за единицу, ВЕ = 0,382… Для того чтобы сделать эти вычисления более практическими, очень часто используют не точные, а приближенные значения, а именно — 0,62 и 0,38. Если же отрезок АВ принимать за 100 частей, то большая его часть будет равна 62, ну а меньшая — 38 частям соответственно.
Главное свойство золотого соотношения можно выразить уравнением: х 2 -х-1=0. При решении мы получаем следующие корни: х 1,2 =. Хотя математика и есть точной и строгой наукой, как и ее раздел — геометрия, но именно такие свойства, как закономерности золотого сечения, наводят таинственность на эту тему.
Гармония в искусстве через золотое сечение
Для того чтобы подвести итоги, рассмотрим коротко то, о чем уже говорили.
В основном под правило золотого соотношения подпадает много образцов искусства, где соблюдается соотношение близкое к 3/8 и 5/8. Это и есть грубая формула золотого сечения. В статье уже очень много упоминалось о примерах использования сечения, но мы еще раз посмотрим на него через призму древнего и современного искусства. Итак, самые яркие примеры из древних времен:
Итак, самые яркие примеры из древних времен:
Что касается уже наверняка сознательного использования пропорции, то, начиная с времен Леонардо да Винчи, она вошла в использование практически во всех отраслях жизни — от науки и до искусства. Даже биология и медицина доказали, что золотое соотношение работает даже в живых системах и организмах.
«Золотое сечение» уже давно стало синонимом слова «гармония». Словосочетание «золотое сечение» обладает просто магическим действием. Если вы выполняете какой-то художественный заказ (неважно, картина это, скульптура или дизайн), фраза «работа сделана в полном соответствии с правилами золотого сечения » может стать прекрасным аргументом в вашу пользу – проверить заказчик скорее всего не сможет, а звучит это солидно и убедительно. При этом немногие понимают, что же скрывается под этими словами. Между тем, разобраться, в том, что такое золотое сечение и как оно работает, достаточно просто.
Золотое сечение – это такое деление отрезка на 2 пропорциональные части, при котором целое так относится к большей части, как большая к меньшей . Математически эта формула выглядит так: с : b = b : а или a : b = b : c .
Математически эта формула выглядит так: с : b = b : а или a : b = b : c .
Итогом алгебраического решения данной пропорции будет иррациональное число Ф (Ф в честь древнегреческого скульптора Фидия).
Я не буду приводить само уравнение, чтобы не загружать текст. При желании, его можно легко найти в сети. Скажу только, что Ф будет приблизительно равным 1,618. Запомните эту цифру, это числовое выражение золотого сечения .
Итак, золотое сечение – это правило пропорции, оно показывает соотношение частей и целого.
На любом отрезке можно найти «золотую точку» — точку, которая делит этот отрезок на части, воспринимаемые как гармоничные. Соответственно, так же можно разделить любой объект. Для примера построим прямоугольник, поделенный в соответствии с «золотой» пропорцией:
Отношение большей стороны получившегося прямоугольника к меньшей будет приблизительно равно 1,6 (заметьте, меньший прямоугольник, получившийся в результате построений, также будет золотым).
Вообще, в статьях, объясняющих принцип золотого сечения , встречается множество подобных рисунков. Объясняется это просто: дело в том, что найти «золотую точку» путем обычного измерения проблематично, поскольку число Ф, как мы помним, иррациональное. Зато, такие задачи легко решаются геометрическими методами, с помощью циркуля и линейки.
Однако, наличие циркуля для применения закона на практике совсем не обязательно. Есть ряд чисел, которые принято считать арифметическим выражением золотого сечения. Это ряд Фибоначчи . Вот этот ряд:
0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.
Запоминать эту последовательность не обязательно, ее можно легко вычислить: каждое число в ряду Фибоначчи равно сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21: 34 = 0,617, а 34: 55 = 0,618.
Один из самых древних (и не потерявших свою привлекательность до сих пор) символов, пентаграмма – прекрасная иллюстрация принципа золотого сечения .
В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны). (цитата из Википедии).
Почему же «золотая пропорция» представляется такой гармоничной?
У теории золотого сечения есть масса как сторонников, так и противников. Вообще, идея о том, что красоту можно измерить и просчитать с помощью математической формулы, симпатична далеко не всем. И, возможно, эта концепция действительно казалась бы надуманной математической эстетикой, если бы не многочисленные примеры природного формообразования, соответствующие золотому сечению .
Сам термин «золотое сечение » ввел Леонардо да Винчи. Будучи математиком, да Винчи также искал гармоничное соотношение для пропорций человеческого тела.
“Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.
Деление тела точкой пупа – важнейший показатель золотого сечения . Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8: 5 = 1,6. У новорожденного пропорция составляет отношение 1: 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Постепенно, золотое сечение превратилось в академический канон, и когда в искусстве назрел бунт против академизма, про золотое сечение на время забыли. Однако, в середине XIX века эта концепция вновь стала популярной благодаря трудам немецкого исследователя Цейзинга. Он проделал множество измерений (около 2000 человек), и сделал вывод, что золотое сечение выражает средний статистический закон.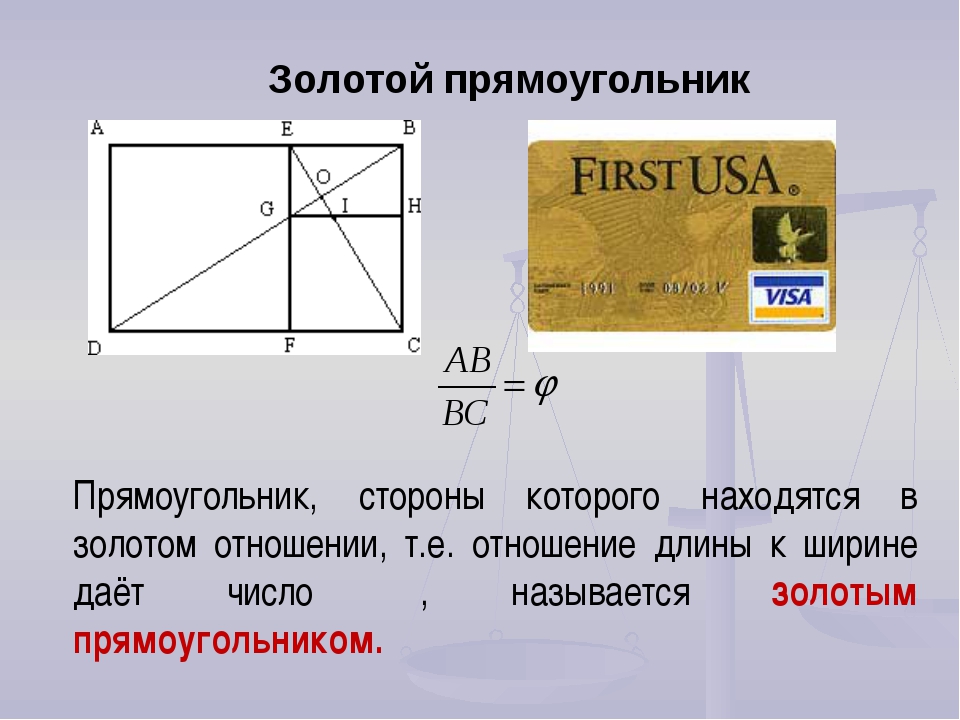 Помимо людей, Цейзинг исследовал архитектурные сооружения, вазы, растительный и животный мир, стихотворные размеры и музыкальные ритмы. Согласно его теории, золотое сечение является абсолютом, универсальным правилом для любых явлений природы и искусства.
Помимо людей, Цейзинг исследовал архитектурные сооружения, вазы, растительный и животный мир, стихотворные размеры и музыкальные ритмы. Согласно его теории, золотое сечение является абсолютом, универсальным правилом для любых явлений природы и искусства.
Принцип золотой пропорции применяется в разных сферах, не только в искусстве, но и в науке и в технике. Будучи настолько универсальной, она, конечно, подвергается множеству сомнений. Часто проявления золотого сечения объявляются результатом ошибочных вычислений или простого совпадения, (а то и подтасовки). В любом случае, к любым замечаниям, как сторонников теории, так и противников, стоит относиться критически.
А о том, как этот принцип применять на практике, можно прочитать .
Золотое сечение просто, как все гениальное. Представьте отрезок АВ, разделенный точкой С. Вам нужно лишь поставить точку С так, чтобы можно было составить равенство СВ/АС = АС/АВ = 0,618. То есть число, полученное при делении самого маленького отрезка СВ на длину среднего отрезка АС должно совпадать с числом, полученным при делении среднего отрезка АС на длину большого отрезка АВ. Числом этим будет 0,618. Это и есть золотая, или, как говорили в древности, божественная пропорция — ф (греческая «фи»). Индекс совершенства.
Числом этим будет 0,618. Это и есть золотая, или, как говорили в древности, божественная пропорция — ф (греческая «фи»). Индекс совершенства.
Трудно сказать, когда именно и кем было замечено, что следование этой пропорции дает ощущение гармонии. Но как только люди стали что-то создавать собственными руками, то интуитивно старались соблюсти это соотношение. Здания, возведенные с учетом ф , всегда выглядели более гармонично по сравнению с теми, в которых пропорции золотого сечения нарушены. Это неоднократно проверялось всевозможными тестами.
В геометрии существуют два объекта, неразрывно связанных с ф : правильный пятиугольник (пентаграмма) и логарифмическая спираль. В пентаграмме каждая линия, пересекаясь с соседней, делит ее в золотой пропорции, а в логарифмической спирали диаметры соседних витков относятся друг к другу так же, как отрезки АС и СВ на нашей прямой АВ. Но ф работает не только в геометрии. Считается, что части любой системы (например, протоны и нейтроны в ядре атома) могут находиться между собой в пропорции, соответствующей золотому числу. В этом случае, полагают ученые, система оказывается оптимальной. Правда, для научного подтверждения гипотезы требуется еще не один десяток лет исследований. Там, где ф нельзя измерить инструментальным методом, применяют так называемый числовой ряд Фибоначчи, в котором каждое последующее число является суммой двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. Особенность этого ряда заключается в том, что при делении любого его числа на следующее за ним получается результат, максимально приближенный к 0,618. Например, возьмем числа 2,3 и 5. 2/3 = 0,666, а 3/5 = 0,6. По сути, здесь присутствует то же соотношение, что и между составляющими нашего отрезка АВ. Таким образом, если измерительные характеристик какого-то объекта или явления можно вписать в числовой ряд Фибоначчи, это означает, что в их строении соблюдена золотая пропорция. А таких объектов и систем бессчетное множество, и современная наука открывает все новые и новые. Так что вопрос, не является ли ф действительно божественной пропорцией, на которой держится наш мир, вовсе не риторический.
В этом случае, полагают ученые, система оказывается оптимальной. Правда, для научного подтверждения гипотезы требуется еще не один десяток лет исследований. Там, где ф нельзя измерить инструментальным методом, применяют так называемый числовой ряд Фибоначчи, в котором каждое последующее число является суммой двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. Особенность этого ряда заключается в том, что при делении любого его числа на следующее за ним получается результат, максимально приближенный к 0,618. Например, возьмем числа 2,3 и 5. 2/3 = 0,666, а 3/5 = 0,6. По сути, здесь присутствует то же соотношение, что и между составляющими нашего отрезка АВ. Таким образом, если измерительные характеристик какого-то объекта или явления можно вписать в числовой ряд Фибоначчи, это означает, что в их строении соблюдена золотая пропорция. А таких объектов и систем бессчетное множество, и современная наука открывает все новые и новые. Так что вопрос, не является ли ф действительно божественной пропорцией, на которой держится наш мир, вовсе не риторический.
Золотая пропорция соблюдена и в природе, причем уже на самых простейших уровнях. Взять например, белковые молекулы, из которых состоят ткани всех живых организмов. Отличаются молекулы друг от друга по массе, которая зависит от числа входящих в них аминокислот. Не так давно было установлено, что наиболее распространенными являются белки с массами 31; 81,2; 140,6; 231; 319 тыс. единиц. Ученые отмечают, что этот ряд почти соответствует ряду Фибоначчи — 3, 8,13, 21, 34 (здесь ученые не учитывают десятичную разницу этих рядов).
Наверняка при дальнейших исследованиях будет найден белок, масса которого будет коррелировать с 5. Эту уверенность дает даже устройство простейших — многие вирус имеют пентагональную структуру. Стремятся к ф и пропорции химических элементов. Ближе всего к ней плутоний: соотношение числа протонов в его ядре с нейтронами равно 0,627. Дальше всего — водород. В свою очередь, число атомов в химических соединениях удивительно часто кратно числам ряда Фибоначчи. Особенно это касается окислов урана и соединений металлов.
Особенно это касается окислов урана и соединений металлов.
Если вы разрежете нераскрывшуюся почку дерева, то обнаружите там две спирали, направленные в разные стороны. Это зачатки листьев. Соотношение количества витков между этими двумя спиралями всегда будет 2/3, или 3/5, или 5/8 и т. д. То есть опять по Фибоначчи. Кстати, ту же самую закономерность мы видим и в расположении семечек подсолнуха, и в строении шишек хвойных деревьев. Но вернемся к листьям. Когда они раскроются, то не потеряют своей связи с ф , поскольку будут располагаться на стебле или ветке по логарифмической спирали. Но и это еще не все. Существует понятие «угла расхождения листьев» — это угол, под которым находятся листья относительно друг друга. Вычислить этот угол не составляет большого труда. Представьте, что в стебель вписана призма с пятиугольным основанием. Теперь пустите по стеблю спираль. Точки, в которых спираль будет касаться граней призмы, соответствуют тем точкам, откуда растут листья. А теперь от первого листа проведите прямую линию вверх и посмотрите, сколько листьев будет лежать на этой прямой. Их число в биологии обозначается буквой n (в нашем случае это два листа). Теперь посчитайте количество витков, описываемых спиралью вокруг стебля. Полученное число называется листовым циклом и обозначается буквой p (в нашем случае оно равно 5). Теперь умножаем максимальный угол — 360 градусов на 2 (n) и делим на 5 (p). Получаем искомый угол расхождения листьев — 144 градуса. Соотношение n и p пиру каждого растения или дерева свое, но все они не выходят из ряда Фибоначчи: 1/2; 2/5; 3/8; 5/13 и т. д. Биологи установили, что углы, образованные по этим пропорциям, в бесконечности стремятся к 137 градусам — оптимальному углу расхождения, при котором равномерно распределяется солнечный свет по веткам и листьям. Да и в самих листьях мы можем заметить соблюдение золотой пропорции, как, впрочем, и в цветках — легче всего ее заметить в тех, что имеют форму пентаграммы.
А теперь от первого листа проведите прямую линию вверх и посмотрите, сколько листьев будет лежать на этой прямой. Их число в биологии обозначается буквой n (в нашем случае это два листа). Теперь посчитайте количество витков, описываемых спиралью вокруг стебля. Полученное число называется листовым циклом и обозначается буквой p (в нашем случае оно равно 5). Теперь умножаем максимальный угол — 360 градусов на 2 (n) и делим на 5 (p). Получаем искомый угол расхождения листьев — 144 градуса. Соотношение n и p пиру каждого растения или дерева свое, но все они не выходят из ряда Фибоначчи: 1/2; 2/5; 3/8; 5/13 и т. д. Биологи установили, что углы, образованные по этим пропорциям, в бесконечности стремятся к 137 градусам — оптимальному углу расхождения, при котором равномерно распределяется солнечный свет по веткам и листьям. Да и в самих листьях мы можем заметить соблюдение золотой пропорции, как, впрочем, и в цветках — легче всего ее заметить в тех, что имеют форму пентаграммы.
ф не обошла и животный мир. По мнению ученых, присутствие золотой пропорции в строении скелета живых организмов решает очень важную задачу. Так достигается максимально возможная прочность остова при минимально возможном весе, что, в свою очередь, позволяет рационально распределить материю по частям тела. Это касается почти всех представителей фауны. Так, морские звезды — совершенные пятиугольники, а раковины многих моллюсков представляют собой логарифмические спирали. Соотношение длины хвоста стрекозы к ее корпусу тоже равно ф . Да и комар не прост: у него три пары ног, брюшко делится на восемь сегментов, а на голове пять усиков-антенн — все тот же ряд Фибоначчи. Число позвонков у многих животных, например у кита или лошади, равно 55. Число ребер — 13, а количество костей в конечностях — 89. А конечности сами имеют трехчастную структуру. Общее же число костей этих животных, считая зубы (которых, 21 пара) и косточки слухового аппарата,- 233 (число Фибоначчи). Чему тут удивляться, когда даже яйцо, из которого, как многие народы считают, все и произошло, можно вписать в прямоугольник золотого сечения — длина такого прямоугольника в 1,618 раза превышает его ширину.
По мнению ученых, присутствие золотой пропорции в строении скелета живых организмов решает очень важную задачу. Так достигается максимально возможная прочность остова при минимально возможном весе, что, в свою очередь, позволяет рационально распределить материю по частям тела. Это касается почти всех представителей фауны. Так, морские звезды — совершенные пятиугольники, а раковины многих моллюсков представляют собой логарифмические спирали. Соотношение длины хвоста стрекозы к ее корпусу тоже равно ф . Да и комар не прост: у него три пары ног, брюшко делится на восемь сегментов, а на голове пять усиков-антенн — все тот же ряд Фибоначчи. Число позвонков у многих животных, например у кита или лошади, равно 55. Число ребер — 13, а количество костей в конечностях — 89. А конечности сами имеют трехчастную структуру. Общее же число костей этих животных, считая зубы (которых, 21 пара) и косточки слухового аппарата,- 233 (число Фибоначчи). Чему тут удивляться, когда даже яйцо, из которого, как многие народы считают, все и произошло, можно вписать в прямоугольник золотого сечения — длина такого прямоугольника в 1,618 раза превышает его ширину.
©При частичном или полном использовании данной статьи — активная гиперссылка ссылка на познавательный журнал сайт ОБЯЗАТЕЛЬНА
Золотое сечение в фотографии и правило третей.
Золотое сечение в фотографии одно из основных понятий и главных правил для построения правильной и гармоничной композиции. Создание фотографии бесспорно творческий процесс, но, как и в любой другой области искусства, здесь также присутствуют свои правила и принципы. И хотя в наши дни они очень часто нарушаются или игнорируются, в целях создания гипер авангардных фотоснимков, все-таки их нужно знать.
Правило золотого сечения или «божественная пропорция», было впервые открыто итальянским математиком Леонардо Фибоначчи (приблизительно в 1200 г.), который первый заметил, что в окружающей природе существует своего рода схема-дизайн, которая невероятным образом очень приятно воспринимается человеческим глазом. Со времен Ренессанса, художники уже активно использовали правило золотого сечения и создавали свои картины, применяя главную цифру правила в отношении соотношения сторон — 1:1,618. Использование данного правила помогает создавать сильную композицию органичным и естественным способом.
Использование данного правила помогает создавать сильную композицию органичным и естественным способом.
Принцип золотого сечения нашел свое выражение в двух схемах-фигурах, известных как Спираль Фибоначчи и Сетка Фибоначчи.
Использование спирали во время компоновки кадра, позволяет создать гармоничную композицию, и при ее просмотре взгляд зрителя будет естественным образом скользит вдоль фотографии.
В чем главное отличие этих двух понятий? Посмотрите на следующие фотографии.
Главное отличие в соотношение сторон. Параметры золотого сечения 1:0.618:1, а правило третей – 1:1:1. Вывод можно сделать такой: правило третей немного более упрощенная версия правила золотого сечения, в его классическом варианте. Оно было впервые озвучено в 1797 г. Согласно данному правилу, кадр делиться воображаемыми линиями по горизонтали и вертикали на трети, где главные композиционные детали располагаются на точках пересечения линий. Применение данного правила создает более динамичную композицию, тем самым открывая зрителю глубокий смысл фотографии, приглашая его к активному взаимодействию во время просмотра. Чтобы понять данное правило в действие рассмотрим следующие фотографии.
Применение данного правила создает более динамичную композицию, тем самым открывая зрителю глубокий смысл фотографии, приглашая его к активному взаимодействию во время просмотра. Чтобы понять данное правило в действие рассмотрим следующие фотографии.
Многие исследования доказали, что во время просмотра фотографии, для человеческого взгляда более естественно концентрироваться на одной из точек пересечения, чем в центре кадра. Если на фотографии вы хотите сделать акцент, на определенном предмете, то его необходимо расположить на одной из четырех точек. Желаете сделать акцент на переднем плане фотографии? Тогда лучше, сформировать кадр так, чтобы линия горизонта проходила вдоль верхней линии сетки (соотношение 2:1) и наоборот. Хотите показать красивый узор на небе? Тогда линия горизонта, должна проходить вдоль нижней линии сетки.
В видоискателе большинства современных, профессиональных фотоаппаратов можно увидеть сетку, созданную по принципу правила третей, она значительно облегчает фокусирование и правильное распределение акцентов.
Есть такое популярное выражение «Правила создана для того, чтобы их нарушать». И в свадебной фотографии, правило третей очень часто нарушается, в целях создания интересных кадров. Чтобы расти в артистическом плане, я считаю, что правило иногда нужно нарушать, только в любом случае их надо знать и уметь хорошо применять их на практике.
Золотое сечение — Энциклопедия по экономике
Первая часть Божественной пропорции посвящена вопросам золотого сечения , вторая — правильным многогранникам, третья — архитектуре. [c.205]Название книги дало золотое сечение , известное в геометрии со времен Евклида. [c.205]
Лука Пачоли был близок к Леонардо да Винчи, а принципы двойной бухгалтерии он позаимствовал у купцов Генуи и Венеции. Интересно, что в то время в арифметике ещё не было даже общепринятых символов + и — для обозначения сложения и вычитания. В одной из своих других работ Лука Пачоли описал знаменитый принцип золотого сечения. [c.662]
[c.662]
Я не буду утомлять читателя длинными пассажами о числах Фибоначчи, лежащих в основе окружающего нас мира, а просто сошлюсь на многочисленные учебники и статьи, посвященные описанию этой числовой последовательности и так называемого золотого сечения. Я лишь еще раз подчеркну важность числовой последовательности Фибоначчи, включающей в себя следующие числа 1,2, 3, 5, 8, 13, 21, 34, 55 — и т. д. Каждое последующее число ряда получается путем сложения двух предыдущих чисел. По мере роста номера числа в последовательности отношение предшествующего числа к последующему приближается к 0,618, а отношение последующего числа к предшествующему стремится к 1,618. Такая особенность присуща только членам данной последовательности. [c.46]
В этой главе мы не собираемся подвергать исчерпывающему анализу такие понятия, как «золотые сечения», «золотые прямоугольники» и «логарифмические спирали», не говоря уже о математических основах теории волн и собственно числовой последовательности Фибоначчи. Тем не менее необходимо упомянуть о том, что на основе «золотого коэффициента» можно построить так называемую «логарифмическую спираль», каковая, как полагают, отчасти объясняет универсальный принцип роста, некий закон — общий для всей нашей вселенной. Считается, что спираль сохраняет постоянную форму, в каком бы виде она ни представала.
[c.350]
Тем не менее необходимо упомянуть о том, что на основе «золотого коэффициента» можно построить так называемую «логарифмическую спираль», каковая, как полагают, отчасти объясняет универсальный принцип роста, некий закон — общий для всей нашей вселенной. Считается, что спираль сохраняет постоянную форму, в каком бы виде она ни представала.
[c.350]
Деление двух любых стоящих рядом чисел из ряда Фибоначчи приводило в среднем к числу 0.618, которое считалось числом золотого сечения в древнегреческой и древнеегипетской культурах. Именно это число и стало основой для применения в техническом анализе линий Фибоначчи, где 0.618 превратилось в 61,8%. [c.132]
Числа Фибоначчи тесно связаны с золотым сечением в геометрии. Золотое сечение хорошо известно в математике и архитектуре со времен Древней Греции. Если разделить отрезок единичной длины на две части так, чтобы отношение длины отрезка к большей части равнялось отношению большей части к меньшей, то длина этой большей части ф равна
[c. 183]
183]
Пропорции золотого сечения в анализе графиков описывают соотношения тенденций (5 волн 1,2,3,4,5) и коррекций (3 волны А, В, С). Оказывается, их использование вместо обычных пропорций 1/3, 1/2, 2/3, дает более точный результат. [c.185]
Отметим, что числа 1.618, 0.618 называются золотым сечением , золотой серединой или золотым коэффициентом . Эти числа являются решением задачи о разделении отрезка на части так, чтобы меньшая часть относилась к большей, как большая ко всему отрезку. [c.125]
Методика прогностических расчетов с использованием чисел Фибоначчи строится на том, что численное соотношение движения и отката должно давать коэффициенты «золотого сечения», то есть [c.166]
Чтобы лучше понять, как ФИ Фибоначчи геометрически встраивается в ФИ-спирали и ФИ-эллипсы, начнем с описания золотого сечения линии и прямоугольника и их соответствующих отношений к ФИ. [c.14]
Линия АВ длиной L разделена на два отрезка точкой С. Пусть длины АС и СВ будут равны а и b соответственно. Если С являет ся такой точкой, что частное L-т- а равно частному a -s-b, то С золотое сечение АВ. Отношение L -ь а или а -А b называется золотым отношением.
[c.14]
Если С являет ся такой точкой, что частное L-т- а равно частному a -s-b, то С золотое сечение АВ. Отношение L -ь а или а -А b называется золотым отношением.
[c.14]
Конечная точка О называется полюсом равноугольной спирали, которая проходит через золотые сечения D, Е, G, J и так далее. [c.16]
ФИ-спираль — самая красивая из математических кривых. Эта спираль на протяжении миллионов лет встречается в естественном мире на каждом шагу. Ряд суммирования Фибоначчи и золотое сечение, представленное в Главе 1 как геометрический эквивалент ряда суммирования Фибоначчи, очень тесно ассоциируются с этой замечательной кривой. Последовательные камеры раковины наутилуса развиваются по ФИ-спирали. По мере роста раковины размер ее камер увеличивается, но их форма остается неизменной. Два сегмента спирали могут быть различны по размеру, но не по форме. Спираль не имеет конечной точки. Рисунок 6.1 показывает рентгенограмму раковины камерного наутилуса («кораблика»). Камеры раковины наутилуса растут согласно «божественной пропорции», которая и есть ФИ Фибоначчи (отношение 1. 618).
[c.147]
618).
[c.147]
Не только египетские пирамиды построены в соответствии с совершенными пропорциями золотого сечения, то же самое явление обнаружено и у мексиканских пирамид. Возникает мысль, что как египетские, так и мексиканские пирамиды были возведены приблизительно в одно время людьми общего происхождения. Пример важной роли скрытой пропорции Ф=1.618 представлен на рис. 1-2а и Ь. [c.5]
Золотое сечение отрезка [c.7]
Греческий математик Евклид применил золотое сечение к отрезку прямой (рис. 1-4). Отрезок АВ длины L делится точкой С на две части. Пусть длины отрезков АС и СВ будут равны соответственно а и Ь. Если точка С такова, что L a равняется а Ь, то С — золотое сечение отрезка АВ. Отношение L a или а Ь называется «золотым отношением». Другими словами, точка С делит отрезок АВ на две части таким образом, что отношения этих частей равны 1.618 и 0.618. [c.7]
| Рис. 1-4 Золотое сечение отрезка. |
 7]
7]| Рис. 1-5 Золотое сечение прямоугольника. |
ЦИРКУЛЬ ЗОЛОТОГО СЕЧЕНИЯ [c.117]
Рис. А-1 Циркуль золотого сечения. [c.118]
Последовательность Фибоначчи содержит и другие любопытные соотношения, или коэффициенты, но те, которые мы только что привели — самые важные и известные. Как мы уже подчеркнули выше, на самом деле Фибоначчи не является первооткрывателем своей последовательности. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам, которые называли его «золотым коэффициентом» или «золотым сечением». Его следы мы находим в музыке, изобразительном искусстве, архитектуре и биологии. Греки использовали принцип «золотого сечения» при строительстве Парфенона, египтяне — Великой пирамиды в Гизе. Свойства «золотого коэффициента» были хорошо известны Пифагору, Платону и Леонардо-да-Винчи.
[c.349]
Как мы уже подчеркнули выше, на самом деле Фибоначчи не является первооткрывателем своей последовательности. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам, которые называли его «золотым коэффициентом» или «золотым сечением». Его следы мы находим в музыке, изобразительном искусстве, архитектуре и биологии. Греки использовали принцип «золотого сечения» при строительстве Парфенона, египтяне — Великой пирамиды в Гизе. Свойства «золотого коэффициента» были хорошо известны Пифагору, Платону и Леонардо-да-Винчи.
[c.349]
Он основан на пропорциях золотого сечения. А само золотое сечение очень тесно связано в математике с числами Фибоначчи. Поэтому-то никто и не удивляется, что подход получил название метода проекций и откатов Фибоначчи. www.fx iub.org [c.180]
Странные цифры. Красивые цифры. Эти соотношения указывают на тесную связь, существующую между золотым сечением и числами Фибоначчи. Пусть это и странное, и неожиданное для нематиматиков свойство, но зато как интригует . . www.fx iub.org
[c.184]
. www.fx iub.org
[c.184]
Пропорции золотого сечения дают ориентиры не только возможных уровней отката, но и указывают возможную величину хода в случае продолжения тенденции (proje tion). Бывает, что после хода некоторого размаха Н рынок откатывается, а затем продолжает ход в том же направлении. В типичном случае после этого величина продолженного хода может составить 1,618 х Н. [c.187]
Чтобы наложить на график дуги Фиболаччи, отыскивается значимый по величине проход рынка (например, падение от 117 до 108,50 на рис. 6.6). Соответствующие экстремумы соединяются отрезком, который затем делится в пропорциях золотого сечения. Через точки деления отрезка затем проводятся окружности с центром во втором экстремуме. [c.187]
На самом деле Фибоначчи вообще-то не является первооткрывателем этих пропорций. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам. Они называли его «золотым коэффициентом» или «золотым сечением». Его глубокие следы можно обнаружить в музыке, изобразительном искусстве, архитектуре и биологии. Так, греки использовали принцип «золотого сечения» при строительстве Парфенона, египтяне — Великой пирамиды в Гизе. К тому же, свойства «золотого коэффициента» были хорошо известны Пифагору, Платону и Леонардо да Винчи. В общем, многие уважаемые господа знали об этих магических цифрах. Но возникает вопрос а не могут ли они пригодиться и нам И если да, то как же пользоваться таким великим открытием
[c.163]
Его глубокие следы можно обнаружить в музыке, изобразительном искусстве, архитектуре и биологии. Так, греки использовали принцип «золотого сечения» при строительстве Парфенона, египтяне — Великой пирамиды в Гизе. К тому же, свойства «золотого коэффициента» были хорошо известны Пифагору, Платону и Леонардо да Винчи. В общем, многие уважаемые господа знали об этих магических цифрах. Но возникает вопрос а не могут ли они пригодиться и нам И если да, то как же пользоваться таким великим открытием
[c.163]
Это отношение стало обрастать разными особыми именами еще даже до того, как другой средневековый математик Лука Па-чиоли (1445—1514) назвал его «божественной пропорцией». Среди его современных названий — «золотое сечение» и » золотая середина». Немецкий астроном Иоганн Кеплер (1571 — 1630) назвал отношение Фибоначчи одним из сокровищ геометрии. В алгебре оно, как правило, обозначается греческой буквой ФИ (ср), а именно [c.10]
Греческий математик Евклид Мегарский (450—370 гг. до н. э.) — первый ученый, написавший о золотом сечении и, таким образом, сосредоточившийся на анализе прямой линии (рисунок 1.3).
[c.14]
до н. э.) — первый ученый, написавший о золотом сечении и, таким образом, сосредоточившийся на анализе прямой линии (рисунок 1.3).
[c.14]
| Рисунок 1.3 Золотое сечение линии. Источник FAM Resear h, 2000. |
Золотое сечение прямоугольника лучше всего продемонстрировать, начертив квадрат, геометрическую конфигурацию, послужившую фундаментом Пирамиды Гизы. Этот квадрат можно затем преобразовать в золотой прямоугольник, как это схематично показано на рисунке 1.4. [c.15]
Сторона АВ квадрата AB D на рисунке 1.4 делится пополам. Чертится дуга круга с центром в точке Е и радиусом ЕС, отсекающая продление АВ в точке F. Перпендикулярно AF чертится линия FG, пресекающая продление D в точке G. AFGD — золотой прямоугольник. Согласно формальному определению, геометрическое представление золотого сечения в прямоугольнике означает, что длина прямоугольника этой формы в 1,618 раз больше, чем его ширина. И вновь появляется отношение Фибоначчи ФИ, на сей раз в пропорциях золотого прямоугольника.
[c.15]
Перпендикулярно AF чертится линия FG, пресекающая продление D в точке G. AFGD — золотой прямоугольник. Согласно формальному определению, геометрическое представление золотого сечения в прямоугольнике означает, что длина прямоугольника этой формы в 1,618 раз больше, чем его ширина. И вновь появляется отношение Фибоначчи ФИ, на сей раз в пропорциях золотого прямоугольника.
[c.15]
Единственной математической кривой следующей модели естественного роста является спираль, выраженная в таких природных феноменах, как Spira mirabilis или раковина наутилуса. ФИ-спираль называют самой красивой математической кривой. Этот тип спирали часто встречается в природе. Ряд суммирования Фибоначчи и золотое сечение, представленное выше как его геометрический эквивалент, очень хорошо ассоциируются с этой замечательной кривой. [c.16]
Наш анализ времени основан на открытиях Евклида Мегар-ского и изобретенном им золотого сечения. Об этом уже говорилось ранее в представлении отношения Фибоначчи в геометрии и золотого сечения линии. [c.27]
[c.27]
Читатели в принципе познакомились с анализом временных целей Фибоначчи в Главе 1. Чтобы правильно рассчитать дни временных целей Фибоначчи, используем работу греческого математика Евклида Мегарского и изобретенный им «золотой срез» (также называемый золотым сечением), связывающий закон природы с геометрией. [c.197]
Особые названия этому соотношению начали давать еще до того, как Лука Пачиоли (средневековый математик) назвал его Божественной пропорцией. Среди его современных названий есть такие, как Золотое сечение, Золотое среднее и Отношение вертящихся квадратов. Кеплер назвал это соотношение «одним из сокровищ геометрии». В алгебре общепринято его обозначение греческой буквой фи (Ф = 1.618). [c.3]
В Великой пирамиде прямоугольный пол царской усыпальницы иллюстрирует золотое сечение (рис. 1-5). Лучше всего «золотой прямоугольник» показывать, начав с квадрата — основания пирамиды в Гизе. Сторона АВ квадрата AB D на рис. 1-5 делится пополам. Проводится дуга окружности с центром Е и радиусом ЕС, пересекающая продолжение отрезка АВ в точке F. Перпендикулярно отрезку AF проводится отрезок FG до пересечения с продолжением отрезка D в точке G. Получаем AFGD — золотой прямоугольник. Согласно определению, длина прямоугольника золотого сечения в 1.618 раза превышает ширину. Следовательно, соотношение его пропорций — это число Ф
[c.7]
Перпендикулярно отрезку AF проводится отрезок FG до пересечения с продолжением отрезка D в точке G. Получаем AFGD — золотой прямоугольник. Согласно определению, длина прямоугольника золотого сечения в 1.618 раза превышает ширину. Следовательно, соотношение его пропорций — это число Ф
[c.7]
Когда выбрана правильная величина фильтра, этот метод должен очень хорошо работать на трендовых рынках. На боковых рынках он должен сильно ограничить «напрасные дергания» (whipsawing). Примеры минимальных величин фильтра для некоторых товаров приведены ниже. Эти значения были получены «вручную» в 1983г. как часть материала к семинару на тему «Золотое сечение». Последняя проверка показала, насколько это возможно, что эти минимальные значения не изменились. Если в соотношениях Фибоначчи есть смысл, эти числа не зависят от времени. [c.79]
Циркуль золотого сечения был представлен на семинарах, проводившихся автором в 1983г. Это необходимый инструмент для каждого инвестора, интересующегося теорией Фибоначчи. Кроме того, он очень легок в использовании.
[c.117]
Кроме того, он очень легок в использовании.
[c.117]
Циркуль золотого сечения — это превращение суммационной последовательности Фибоначчи в инвестиционный инструмент. Как и у циркуля, его «ножки» могут быть сведены уже или разведены шире (рис. А-1). Эти три ножки всегда остаются разведенными в соответствии с соотношением Фибоначчи, таким образом, всегда возможна динамическая адаптация к циклам. Это инструмент для приложения соотношений 0.618 и 1.618 к любому методу анализа чартов из представленных в этой книге, за исключением спирального (выполнять который необходимо на компьютере). Он поможет работать с [c.117]
Золотое сечение в веб дизайне
Одной из основных характеристик эффективного дизайна является четкая структура контента. Все элементы должны быть хорошо и гармонично сбалансированы, чтобы пользователи могли легко воспринимать информацию на экране и взаимодействовать с продуктом без усилий.
Для создания композиции профессионалы применяют различные методы.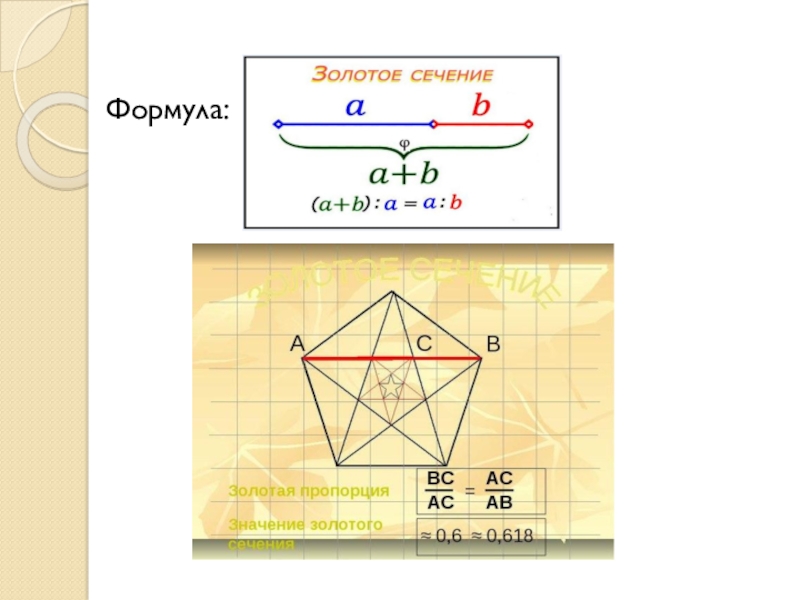 Золотое сечение в веб дизайне — одно из общих инструментов для создания приятной композиции, это математическая пропорция, называемая золотым соотношением. В статье мы определим суть этого метода и посмотрим, как его можно использовать.
Золотое сечение в веб дизайне — одно из общих инструментов для создания приятной композиции, это математическая пропорция, называемая золотым соотношением. В статье мы определим суть этого метода и посмотрим, как его можно использовать.
Что такое золотое соотношение?
Все в мире стремится к гармонии и равновесию. Даже природа создает формы, близкие к совершенству. Стремясь открыть тайны идеальных пропорций, математики вычислили формулу, которая появляется в большинстве вещей на Земле.
Золотое соотношение представляет собой математическую пропорцию между элементами разных размеров, которые считаются наиболее эстетически привлекательными для глаз человека. Золотое соотношение равно 1: 1,618, и его часто иллюстрируют спиралью, похожей на морскую раковину.
Итак, как точно рассчитанть идеальную пропорцию? Во-первых, вам нужно определить длину меньшего элемента. Затем умножьте его на золотое соотношение, равное 1,618, и результатом будет идеальная длина большего элемента.
Большинство знаменитых произведения искусства подчиняются золотому соотношению. Леонардо да Винчи и Сальвадор Дали были известны как последователи теории золотого сечения, и они использовали его в качестве ключевого инструмента для своих удивительных работ. Сегодня золотое соотношение применяется в различных областях, включая архитектуру, искусство, фотографию и дизайн.
Золотое сечение в веб дизайне
Эффективная композиция является основой хорошего дизайна. Все элементы должны работать вместе, чтобы максимизировать приятный опыт. Более того, каждый отдельный элемент, даже маленький, как иконка, должен быть созданы с гармонией. Золотое сечение оказывает положительное влияние на визуальное восприятие, поэтому многие дизайнеры применять его в своем рабочем процессе.
Дизайн логотипа или иконки требует глубокого внимания к деталям. Золотое сечение позволяет создавать иллюстрации, в которых каждый элемент помещается в гармонию и соответствующую пропорцию с другими элементами. Кроме того, дизайн логотипа — это сердце бренда, поэтому дизайнеры стремятся представить его самым убедительным образом.
Кроме того, дизайн логотипа — это сердце бренда, поэтому дизайнеры стремятся представить его самым убедительным образом.
Пользовательский интерфейс должен иметь четкую визуальное композицию, чтобы люди могли без проблем использовать продукт. Золотое сечение часто применяется для эффективного размещения элементов пользовательского интерфейса. Прежде всего, его можно использовать на этапе проектирования макета. Таким образом, вы можете планировать структуру макетов и размеров компонентов пользовательского интерфейса в соответствии с золотой пропорциями. Кроме того, схема золотое сечение поможет использовать изображения для веб-дизайна, балансируя в соответствии общей структурой сайта или приложения.
Как золотое сечение поможет улучшить дизайн интерфейса?
Математические вычисления могут показаться скучными и отнимающими много времени, поэтому может возникнуть вопрос, стоит ли это усилий. Давайте посмотрим, какое золотое сечение может помочь проекту.
Хорошо сбалансированный контент
Дизайнеры часто сталкиваются с ситуацией, когда продукт должен содержать большое количество различного контента, и каждая его часть жизненно важна и не может быть заменена. Чтобы объединить все компоненты в приятной композиции, можно применить золотое сечение. Разделите макет на части в соотношении 1: 1.618, и поместите контент в секторах в соответствии с их важностью. Такая композиция приятна для восприятия и помогает организовать все компоненты.
Чтобы объединить все компоненты в приятной композиции, можно применить золотое сечение. Разделите макет на части в соотношении 1: 1.618, и поместите контент в секторах в соответствии с их важностью. Такая композиция приятна для восприятия и помогает организовать все компоненты.
Эффективная визуальная иерархия
Говоря об организации контента, мы не должны забывать о визуальной иерархии. Как мы упоминали в наших предыдущих статьях, это метод эффективного структурирования компонентов контента. Объединяя принципы этих двух методов, дизайнеры максимизируют возможности создания хорошей дизайнерской композиции.
Уровни типографии
Для создания эффективной типографии дизайнеры должны разделить содержимое копии на разные уровни. Обычно они включают в себя различные виды текста, включая заголовки, подзаголовки, основной контент и т. д. Применение золотого соотношения может быстро определить соответствующую пропорцию между типографскими уровнями, например, вы можете выбрать определенный размер для заголовка, а затем разделить его на 1,618. Результат покажет вам наиболее подходящий размер для подзаголовков.
Результат покажет вам наиболее подходящий размер для подзаголовков.
Приятное первое впечатление
Когда пользователи впервые видят продукт, они просматривают пользовательский интерфейс, чтобы понять, нравится он им или нет. Принцип психологии, известный как висцеральная реакция, утверждает, что люди решают, нравится ли им что-то или нет в течение нескольких секунд. Эта реакция протекает быстрее, чем наше сознание, поэтому мы даже не осознаем этого. Вот почему важно, чтобы первое впечатление от продукта было приятным. Золотое сечение в веб дизайне оказывает положительное влияние на разум пользователей и их зрительное восприятие, и это работает с первого взгляда на продукт.
Дизайн, представляющий естественный баланс компонентов, не может быть незамеченным. Хорошо структурированная компоновка является одной из основных частей мощного пользовательского интерфейса. Золотое соотношение приносит гармонию в дизайн и делает продукт приятным для пользователей. Не бойтесь математической формулы. Это не так сложно, как может показаться. Более того, золотой коэффициент может помочь создать удобные цифровые продукты, которые будут сочетать полезность и эстетику.
Это не так сложно, как может показаться. Более того, золотой коэффициент может помочь создать удобные цифровые продукты, которые будут сочетать полезность и эстетику.
Источник
Веб-дизайн как у Да Винчи. Оформляем сайт с помощью золотого сечения
21 мая 2021 г.
Время чтения: 4 минуты
У больших компаний есть свой секрет создания идеального логотипа и красивого дизайна сайта. Некоторые знакомые нам страницы и логотипы известных брендов выверены с помощью правила золотого сечения. Эта сугубо математическое явление помогает вычислить гармоничные размеры любого объекта и сделать его приятным глазу.
Золотое сечение — это фиксированная пропорция. Чтобы её получить, нужно разделить прямой отрезок произвольной длины с учётом следующего условия: длинная часть отрезка относится к короткой так же, как весь отрезок относится к длинной части. Эта пропорция всегда равна 1,618 и у этого числа есть собственное название, «фи».
Это значение было известно ещё в Древнем Египте и существует теория, что его использовали при сооружении пирамид. А наиболее широкую популярность метод золотого сечения приобрёл в Средние века. По мнению исследователей, композиция величайшего шедевра живописи «Мона Лиза» авторства Леонардо да Винчи была построена именно с использованием числа «фи».
Рассмотрим, каким образом золотое сечение применяется в дизайне. На основе отрезка, разделённого на две части в пропорции 1 к 1,618, построим квадрат и прямоугольник.
В результате мы получим прямоугольник с золотым сечением, который также называют золотым. Правая его часть тоже представляет собой золотой прямоугольник. Если выделить в нём квадрат, то оставшаяся часть снова окажется прямоугольником с золотым сечением — и так до бесконечности.
Если плавной линией соединить по два противоположных угла каждого из квадратов, то мы получим идеальную спираль, созданную по правилу золотого сечения.
Чтобы получить несколько кругов, которые относятся друг к другу в соотношении 1 к 1,1618, тоже воспользуемся квадратами.
Полученные элементы можно применять в проектировании макетов страниц и логотипов.
Разделение макета на зоны
Чтобы провести границы между блоками на будущей веб-странице, используйте число «фи». Самое простое решение — разделить область страницы на две части по вертикали так, чтобы значения ширины получившихся прямоугольников имели то самое соотношение 1 к 1,618.
Например, если нам необходимо разделить область шириной 1080 пикселей, то делим 1080 на число «фи» и получаем 668 пикселей — ширину большего прямоугольника. Осталось вычесть это значение из общей ширины и получить ширину меньшего прямоугольника. Теперь можно приступать к наполнению макета.
Известный пример использования золотого сечения в веб-дизайне — сайт журнала National Geographic.
Регулирование «воздуха»
Профессиональные дизайнеры знают, что правильно расставить акценты в изображении помогает свободное пространство вокруг его элементов. Чтобы понять, сколько «воздуха» необходимо рядом с каждым из элементов, наложите на макет один или несколько золотых прямоугольников. Для этого можно использовать такой шаблон.
Чтобы понять, сколько «воздуха» необходимо рядом с каждым из элементов, наложите на макет один или несколько золотых прямоугольников. Для этого можно использовать такой шаблон.
К слову, готовые шаблоны с прямоугольниками, кругами и спиралью можно скачать, например, здесь или здесь.
Если вы расположите элементы по углам и краям квадратов, то свободного пространства между ними будет именно столько, сколько необходимо. Афиша фестиваля Bregenzer Festspiele была оформлена именно по этому принципу.
Направление взгляда пользователя
Чтобы расположить элементы в нужном порядке, необязательно размещать их строго сверху вниз или справа налево. Золотая спираль, построенная по углам квадратов золотого прямоугольника, поможет выстроить нестандартную траекторию движения глаз пользователей по странице.
Привяжите элементы к разным участкам спирали: начните повествование в её самой длинной части, а завершите рассказ в её центре. Дизайнер Тим Роузиль при оформлении своего персонального сайта поступил именно так.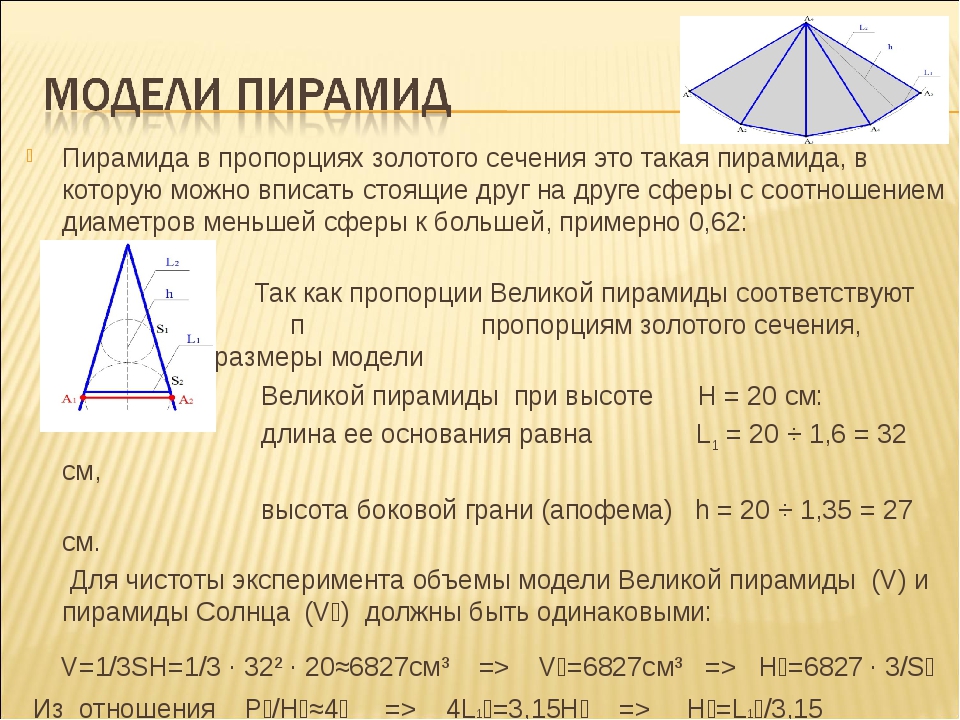
Создание логотипов
Здесь мы вспомним об окружностях, вписанных в квадраты золотого прямоугольника. Их можно использовать в разработке аккуратных логотипов. Располагайте произвольным образом внутри большого круга круги поменьше и формируйте ту фигуру, которая вам необходима. Логотип Pepsi — один из ярких примеров использования кругов с золотым сечением.
Выбор размера текста
И ещё один полезный совет по использованию золотого сечения. На страницах мы используем фрагменты текста с разным кеглем. Чтобы подобрать оптимальные размеры шрифта для заголовков, подзаголовков и основного текста, также потребуется число «фи». К примеру, разделите выбранный вами размер заголовка на 1,618 и вы получите подходящий размер для подзаголовков.
Кстати, для вычисления «золотых» величин можно воспользоваться онлайн-калькуляторами Phiculator и Golden Ratio Calculator.
Подведём итоги и кратко опишем полезные свойства золотого сечения в веб-дизайне. Оно позволяет:
- структурировать контент на странице,
- сбалансированно располагать элементы,
- облегчать восприятие информации и взаимодействие со страницей,
- создавать гармоничные логотипы,
- вызывать позитивные эмоции у пользователей.

Что представляет собой золотое сечение в математике и науке
Золотое сечение в математике и науке представляет собой пропорциональное деление некого отрезка на части разные по длине, но при этом каждый получившийся отрезок имеет такое отношение к большей части, как эта большая часть относится ко всей длине.
Соотношение отрезков можно выразить бесконечной дробью 0,618033…
Математика дает нам такое понятие как золотая пропорция. Вычислить ее возможно с помощью числа Непера – lim(1+(1/x))x. Необходимо для этого число Пи помножить на комплексное число і, а после разделить на 5. Полученное значение является степенью, в которую необходимо возвести число Непера. Полученное значение далее необходимо сложить с числом Непера, возведенном в ту же степень, только с отрицательным значением. Результатом вычислений и будет золотая пропорция.
Золотое сечение и ряд Фибоначчи
Имя Фибоначчи тесно связано с исследованиями сути золотого сечения. Он задался вопросом, как развивается идеальная популяция кроликов. По его идее существовали изначально самец и самка, которые на втором месяце жизни начали спариваться, ежемесячно самка рожала новую пару крольчат. Если принять за условие, что эти идеальные кролики никогда не умирают, то, сколько же пар будет через год? Ища ответ на этот вопрос, Фибоначчи получил ряд чисел, а именно 0, 1, 1, 2, 3, 5, 8 и так до бесконечности. Эта последовательность, позволяющая понять золотое сечение, названа его именем – ряд Фибоначчи.
По его идее существовали изначально самец и самка, которые на втором месяце жизни начали спариваться, ежемесячно самка рожала новую пару крольчат. Если принять за условие, что эти идеальные кролики никогда не умирают, то, сколько же пар будет через год? Ища ответ на этот вопрос, Фибоначчи получил ряд чисел, а именно 0, 1, 1, 2, 3, 5, 8 и так до бесконечности. Эта последовательность, позволяющая понять золотое сечение, названа его именем – ряд Фибоначчи.
Элементарная математика позволяет определить, в чем особенность ряда. Так каждое число, начиная с третьего, является равным двух чисел, стоящих перед ним. Действительно, 2++3=5, а 3+5=8. При этом если разделить смежные числа, то получится значение золотого сечения. Ряд демонстрирует тот же принцип, что и золотое сечение – меньший отрезок имеет такое отношение к большему, как этот больший относится ко всей длине. Наука математика сформулировала также золотое соотношение – это выражение значения 0,618033… с помощью дроби.
Итак, математика этого явления понятно, но как же наука и жизнь используют полученные знания?
Наука и золотое сечение
Золотое сечение нашей планеты это параллель, которая имеет широту 55,62 градуса. Можно отметить, что широте золотого сечения находится Москва и много других городов России. Более того, обычно это города-миллионники! Является ли это совпадение случайным при условии, что все живое в мире тяготеет к соблюдению принципа золотого сечения.
Можно отметить, что широте золотого сечения находится Москва и много других городов России. Более того, обычно это города-миллионники! Является ли это совпадение случайным при условии, что все живое в мире тяготеет к соблюдению принципа золотого сечения.
Такая наука как астрономия говорит нам, что орбиты всех планет нашей Солнечной системы между собой соотносятся точно также как целые степени числа всем известного золотого сечения!
Наука биология подтверждает, что и в растительном мире пропорции цветов, количество лепестков их размер соотносятся аналогичным образом. Даже строение ДНК соблюдает этот закон всего живого! Строение идеального человеческого тела, такого, которое мы привыкли считать красивым, если его разбить на части, имеет необходимые пропорции. Это соотношения длины рук, ног и других частей тела, расстояние между глазами, ушами и носом на человеческом лице. Эти знания активно используют художники и модельеры.
Наука математика помогла обнаружить «золотой принцип» даже в величайших архитектурных сооружениях земли, например, пирамиде Хеопса. Люди искусства проектировали предметы интерьера, здания, целые комплексы сооружений, руководствуясь знаниями, открытыми учеными средневековья или же подражая природе, которая негласно соблюдает этот закон.
Люди искусства проектировали предметы интерьера, здания, целые комплексы сооружений, руководствуясь знаниями, открытыми учеными средневековья или же подражая природе, которая негласно соблюдает этот закон.
Конечно, без такой науки, как математика, люди не смогли бы сформулировать этот принцип, но внутреннее они, как и все живое в нашей вселенной, тяготеют к нему, что отражается в их творчестве.
Золотое сечение — Учебное пособие
Золотое сечение часто упоминается в отношении композиции изображения. Но что такое золотое сечение и каковы его математические основы? Этот урок содержит все, что вам нужно знать о золотом сечении.
Что такое золотое сечение?
Золотое сечение — это эмпирическое правило композиции, восходящее к древности. Он описывает пропорции, которые люди находят особенно приятными. Золотое сечение часто встречается в природе и даже в человеческом теле и с большим успехом используется в искусстве, архитектуре и даже типографике.
Математическая сторона золотого сечения
Математика золотого сечения относительно проста. Линия делится на две части «а» и «б» так, что отношение большего участка (а) к меньшему участку (б) равно отношению всей длины (а + b) к большему участку . Это приводит к формуле: a / b = (a + b) / a. Результатом этой формулы является иррациональное число, которое в математике часто называют «золотым числом» или фи. Золотое число фи примерно равно 1.618. Евклид был первым, кто дал письменное описание золотого сечения ок. 360-280 гг. до н.э.
Золотое сечение и последовательность Фибоначчи
В 1202 году математик Леонардо Фибоначчи описал ряд рациональных чисел, которые дают наиболее близкое приближение числа фи, когда соседние члены вводятся в формулу золотого сечения. Последовательность Фибоначчи можно наблюдать в природе, не только в росте популяции кроликов, как он предполагал, но и в естественных явлениях, таких как расположение листьев у растений. Последовательность Фибоначчи начинается с числа 1 (или иногда с 0), и каждое число представляет собой сумму двух предыдущих членов. Таким образом, первые числа будут 1, 1, 2, 1 + 2 = 3, 2 + 3 = 5, 8, 13… и так далее.
Последовательность Фибоначчи начинается с числа 1 (или иногда с 0), и каждое число представляет собой сумму двух предыдущих членов. Таким образом, первые числа будут 1, 1, 2, 1 + 2 = 3, 2 + 3 = 5, 8, 13… и так далее.
Этот ряд чисел напрямую связан с золотым сечением. Чем больше число в последовательности, тем ближе его пропорции к соседнему числу будут к золотому числу фи.
Золотое сечение в фотографии
В фотографии вы можете использовать золотое сечение как полезный инструмент для создания гармоничных и приятных композиций.Поскольку центр изображения часто воспринимается как статичный или неинтересный, такое разделение пространства часто используется в визуальной композиции. Фотография разделена на девять прямоугольников по двум горизонтальным и вертикальным линиям в соответствии с золотым сечением. Это широко известно как фи-сетка.
Затем изображение состоит из важных элементов вдоль линий и на их пересечениях. Например, горизонт расположен по одной из вертикальных линий, а человек на переднем плане расположен по одной из вертикальных линий.
Совет: вы можете скомпоновать изображение вне фи-сетки, чтобы привлечь внимание людей — это нарушит гармонию и создаст дополнительное напряжение. С помощью этого метода вы можете превратить любую осеннюю фотографию в произведение искусства!
Золотое сечение в искусстве
Золотое сечение, также известное как божественная пропорция, встречается на протяжении всей истории искусства, начиная с древних времен. Например, знаменитая скульптура Венеры Милосской богини Афродиты была сделана между 100 и 130 годами до нашей эры и содержит золотые пропорции.
В композиции эпохи Возрождения Леонардо да Винчи также мастерски использует божественную пропорцию. Его картина «Тайная вечеря» построена по золотым пропорциям.
Всемирно известная Мона Лиза также составлена из «золотого треугольника» — равнобедренного треугольника, в котором длина сторон и основание образуют золотое сечение.
Попробуйте эту композицию для своих портретных фотографий и поэкспериментируйте с золотым треугольником. Это создает впечатляющую композицию, которую люди считают сбалансированной и гармоничной.Наш совет? После того, как вы определились с композицией, настройте акриловую фотопечать с помощью высококачественной фотобумаги Kodak Pro Endura для ярких цветов и ярких контрастов.
Это создает впечатляющую композицию, которую люди считают сбалансированной и гармоничной.Наш совет? После того, как вы определились с композицией, настройте акриловую фотопечать с помощью высококачественной фотобумаги Kodak Pro Endura для ярких цветов и ярких контрастов.
Золотые пропорции являются общей чертой работ великих мастеров, таких как итальянский художник Рафаэль . Его «Триумф Галатеи» состоит из двух разделов. Чуб Галатеи Рафаэля не только отделяет небо от земли, но и отмечает золотые сечения произведения. В его «Сикстинской Мадонне» также можно найти невидимое разделение — на этот раз вдоль пупка Мадонны.
Немецкий художник Автопортрет Альбрехта Дюрера в шубе (примерно 1500 г.) изображает художника в позе, которая традиционно предназначалась для Иисуса или монархов. Волосы Дюрера образуют треугольник, который делит произведение на золотые секции. Лицо художника также обрамлено вертикальными линиями, которые структурируют картину в соответствии с золотым сечением.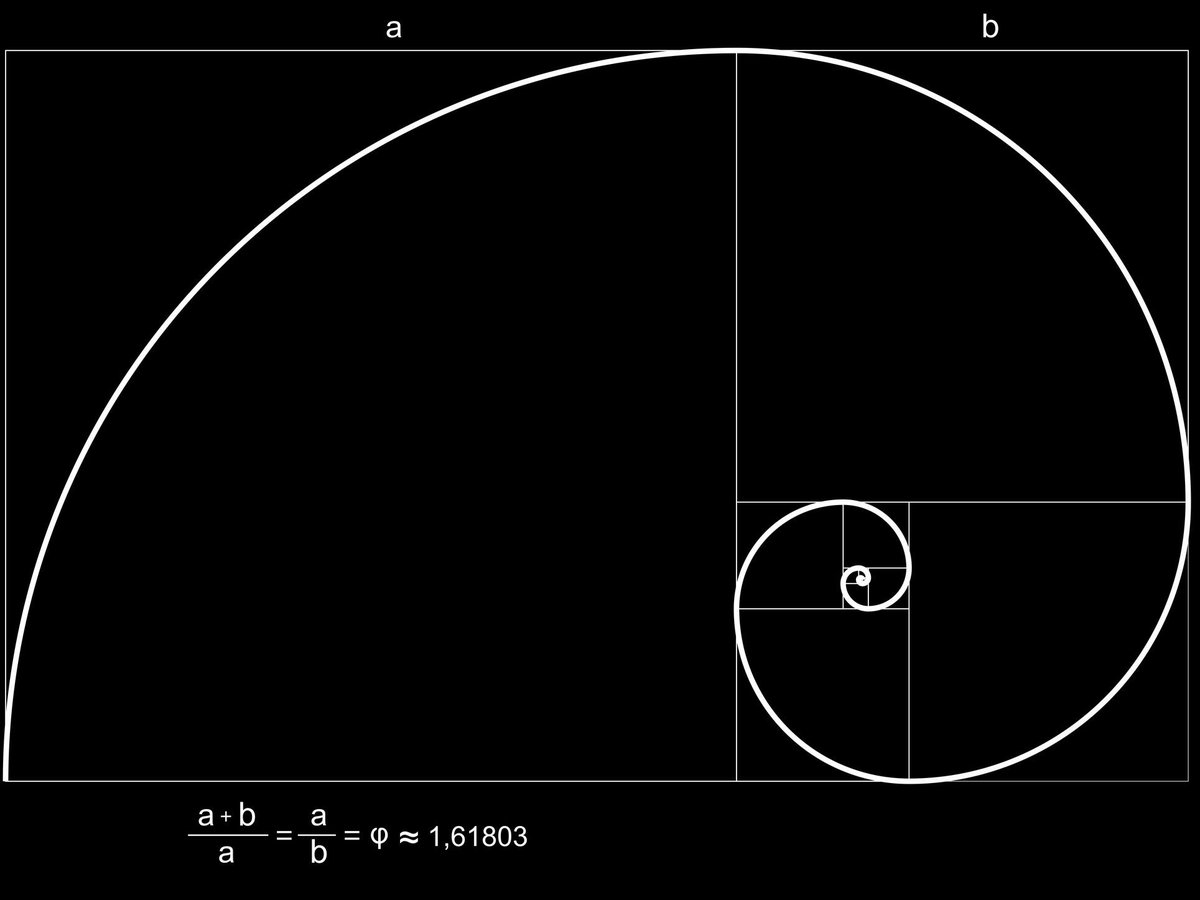
Золотое сечение в лицах и телах
В своем «Витрувианском человеке» Леонардо да Винчи создал впечатляющую систему измерения золотого сечения, основанную на человеческом теле.
Сегодня пластическая хирургия основана на золотом сечении, так как она воспринимается как особенно приятная и красивая. Чем ближе пропорции тела и лица к божественному соотношению, тем более привлекательным считается человек. Согласно исследованиям американского пластического хирурга Стивена Марквардта, люди считают идеальным, когда ширина носа, умноженная на фи, равняется ширине рта.
Золотое сечение в известной архитектуре
Древние храмы уже строились по золотому сечению.Например, Великая пирамида в Гизе (ок. 2590–2470 гг. до н. э.) имеет идеальные пропорции по сегодняшним меркам. Парфенон в Афинах, построенный около 450 г. до н.э., также близко соответствует пропорциям золотого сечения.
Собор Святого Петра и Кёльнский собор также созданы по божественной пропорции.
Золотые пропорции в природе: Золотая спираль Наутилуса
Если разбить прямоугольник по золотому сечению, затем таким же образом разделить меньшую половину и так далее, то в итоге получится несколько вложенных четырехугольников.Как и в последовательности Фибоначчи, длины сторон будут равны сумме длин двух прямоугольников, на которые она была разделена. Если углы соединяются изогнутой линией, получается логарифмическая спираль, также известная как золотая спираль.
Раковина наутилуса растет по похожей спирали, которая не меняет своей изогнутой формы, даже когда увеличивается в размерах. Эта симметричная спираль часто встречается в природе: в ураганах, папоротниках и даже целых галактиках.
Совет: используйте спираль для собственных фотографий, чтобы создать напряженную композицию.Продемонстрируйте изображение в крупноформатном произведении искусства, превратив его в печать на холсте!
Будь то в животном мире или в человеческом теле, золотое сечение — увлекательное явление, происхождение которого остается неизвестным. Немецкий физик и философ Карл Фридрих фон Вайцзекер резюмировал тайну, сказав: «Возможно, вездесущая, скрытая математика природы является причиной существования всей красоты».
Немецкий физик и философ Карл Фридрих фон Вайцзекер резюмировал тайну, сказав: «Возможно, вездесущая, скрытая математика природы является причиной существования всей красоты».
15 сверхъестественных примеров золотого сечения в природе
Знаменитая последовательность Фибоначчи веками пленяла математиков, художников, дизайнеров и ученых.Также известное как Золотое сечение, его повсеместное распространение и поразительная функциональность в природе предполагает его важность как фундаментальной характеристики Вселенной.
Мы уже говорили о рядах Фибоначчи и о золотом сечении, но стоит сделать краткий обзор. Последовательность Фибоначчи начинается так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и так далее до бесконечности. Каждое число является суммой двух предшествующих ему чисел. Это простая модель, но она кажется встроенной в космос системой нумерации.Вот 15 поразительных примеров фи в природе.
Леонардо Фибоначчи придумал последовательность при расчете идеальных пар кроликов расширения в течение одного года. Сегодня его возникающие закономерности и соотношения (фи = 1,61803…) можно наблюдать на микро- и макроуровне, вплоть до биологических систем и неодушевленных объектов. Хотя золотое сечение не объясняет каждых структур или паттернов во Вселенной, оно, безусловно, играет важную роль. Вот несколько примеров.
Сегодня его возникающие закономерности и соотношения (фи = 1,61803…) можно наблюдать на микро- и макроуровне, вплоть до биологических систем и неодушевленных объектов. Хотя золотое сечение не объясняет каждых структур или паттернов во Вселенной, оно, безусловно, играет важную роль. Вот несколько примеров.
1. Лепестки цветка
Количество лепестков в цветке соответствует последовательности Фибоначчи. Известные примеры включают лилию с тремя лепестками, лютики с пятью (на фото слева), цикорий с 21, маргаритку с 34 и так далее. Фи появляется в лепестках благодаря идеальному расположению упаковки, выбранному дарвинистскими процессами; каждый лепесток расположен на 0,618034 оборота (из круга 360 °), что обеспечивает наилучшее воздействие солнечного света и других факторов.
2. Головки семян
Головка цветка также подвержена процессам Фибоначчи. Как правило, семена образуются в центре, а затем мигрируют наружу, чтобы заполнить все пространство. Подсолнухи представляют собой отличный пример этих спиралевидных узоров.
В некоторых случаях семенные головки расположены настолько плотно, что их общее количество может быть довольно большим — до 144 и более. И при подсчете этих спиралей сумма имеет тенденцию соответствовать числу Фибоначчи. Интересно, что для оптимизации заполнения требуется очень иррациональное число (а именно такое, которое не будет хорошо представлено дробью).Фи отвечает всем требованиям довольно хорошо.
3. Сосновые шишки
Подобным образом семенные коробочки на сосновой шишке расположены по спирали. Каждый конус состоит из пары спиралей, каждая из которых закручивается вверх в противоположных направлениях. Количество шагов почти всегда будет соответствовать паре последовательных чисел Фибоначчи. Например, конус 3-5 — это конус, который встречается сзади через три шага по левой спирали и через пять шагов по правой.
4. Фрукты и овощи
Подобные спиралевидные узоры можно найти на ананасах и цветной капусте.
5. Ветви дерева
Последовательность Фибоначчи также можно увидеть в том, как формируются или расщепляются ветви деревьев. Основной ствол будет расти до тех пор, пока не создаст ответвление, создающее две точки роста. Затем один из новых стеблей разветвляется на два, а другой остается в состоянии покоя. Этот образец ветвления повторяется для каждого из новых стеблей. Хорошим примером является чихалка. Корневая система и даже водоросли демонстрируют этот образец.
Основной ствол будет расти до тех пор, пока не создаст ответвление, создающее две точки роста. Затем один из новых стеблей разветвляется на два, а другой остается в состоянии покоя. Этот образец ветвления повторяется для каждого из новых стеблей. Хорошим примером является чихалка. Корневая система и даже водоросли демонстрируют этот образец.
6. Раковины
Еще одним примером являются уникальные свойства Золотого прямоугольника.Эта форма, прямоугольник, в котором отношение сторон a/b равно золотой середине (фи), может привести к процессу вложения, который может повторяться до бесконечности и который принимает форму спирали. Это называется логарифмической спиралью, и она изобилует в природе.
Раковины улиток и наутилусов следуют по логарифмической спирали, как и улитка внутреннего уха. Его также можно увидеть в рогах некоторых коз и в форме паутины некоторых пауков.
7. Спиральные галактики
Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет собой логарифмическую спираль с углом наклона около 12 градусов. Интересно отметить, что спиральные галактики бросают вызов ньютоновской физике. Еще в 1925 году астрономы поняли, что, поскольку угловая скорость вращения галактического диска меняется с расстоянием от центра, радиальные рукава должны искривляться по мере вращения галактик. Впоследствии, после нескольких оборотов, вокруг галактики должны начать закручиваться спиральные рукава. Но они этого не делают — отсюда и так называемая проблема намотки.Звезды снаружи, казалось бы, движутся со скоростью выше ожидаемой — уникальная черта космоса, помогающая сохранять свою форму.
Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет собой логарифмическую спираль с углом наклона около 12 градусов. Интересно отметить, что спиральные галактики бросают вызов ньютоновской физике. Еще в 1925 году астрономы поняли, что, поскольку угловая скорость вращения галактического диска меняется с расстоянием от центра, радиальные рукава должны искривляться по мере вращения галактик. Впоследствии, после нескольких оборотов, вокруг галактики должны начать закручиваться спиральные рукава. Но они этого не делают — отсюда и так называемая проблема намотки.Звезды снаружи, казалось бы, движутся со скоростью выше ожидаемой — уникальная черта космоса, помогающая сохранять свою форму.
8. Ураганы
9. Лица
Лица, как человеческие, так и нечеловеческие, изобилуют примерами золотого сечения. Рот и нос расположены в золотых секциях на расстоянии между глазами и нижней частью подбородка. Подобные пропорции видны сбоку, и даже сам глаз и ухо (которые следуют по спирали).
Стоит отметить, что тело каждого человека отличается, но средние значения среди населения имеют тенденцию к фи. Также было сказано, что чем ближе наши пропорции соответствуют фи, тем более «привлекательными» воспринимаются эти черты. Например, самые «красивые» улыбки — это те, в которых центральные резцы в 1,618 раза шире боковых резцов, которые в 1,618 раза шире клыков, и так далее. Вполне возможно, что с эво-психологической точки зрения мы склонны любить физические формы, соответствующие золотому сечению — потенциальному показателю репродуктивной пригодности и здоровья.
10. Пальцы
Глядя на длину наших пальцев, каждая часть — от кончика основания до запястья — больше предыдущей примерно на пропорцию фи.
11. Тела животных
Даже наши тела имеют пропорции, соответствующие числам Фибоначчи. Например, измерение от пупка до пола и от макушки до пупка является золотым сечением. Тела животных проявляют аналогичные тенденции, включая дельфинов (глаз, плавники и хвост падают на Золотое сечение), морских звезд, морских ежей, муравьев и медоносных пчел.
12. Репродуктивная динамика
Говоря о медоносных пчелах, они следуют Фибоначчи и другими интересными способами. Самый глубокий пример — это деление количества самок в колонии на количество самцов (самок всегда больше, чем самцов). Ответ обычно очень близок к 1,618. Кроме того, генеалогическое древо медоносных пчел также следует знакомой схеме. У самцов один родитель (самка), а у самок два (самка и самец). Таким образом, когда дело доходит до генеалогического древа, у мужчин есть 2, 3, 5 и 8 бабушек и дедушек, прадедов, гр-гр-дедушек и гр-гр-гр-дедушек соответственно.По той же схеме у женщин 2, 3, 5, 8, 13 и так далее. И, как уже отмечалось, физиология пчел также довольно хорошо следует Золотой кривой.
13. Схемы борьбы животных
Когда ястреб приближается к своей добыче, его самый острый взгляд находится под углом к направлению их полета — угол, равный шагу спирали.
14. Матка
По словам Джаспера Вегутса, гинеколога университетской клиники Левена в Бельгии, врачи могут определить, выглядит ли матка нормальной и здоровой, на основании ее относительных размеров — размеров, которые приблизительно соответствуют золотому сечению. Из Guardian :
Из Guardian :
За последние несколько месяцев он измерил матки 5000 женщин с помощью УЗИ и составил таблицу среднего отношения длины матки к ее ширине для разных возрастных групп.
Данные показывают, что это соотношение составляет около 2 при рождении, а затем оно неуклонно снижается в течение жизни женщины до 1,46 в пожилом возрасте.
Доктор Вергутс был взволнован, обнаружив, что когда женщины наиболее фертильны, в возрасте от 16 до 20 лет, отношение длины матки к ширине равно 1.6 — очень хорошее приближение к золотому сечению.
«Это первый раз, когда кто-то смотрит на это, поэтому я рад, что все получилось так хорошо», — сказал он.
15. Молекулы ДНК
Даже микроскопическое царство не защищено от Фибоначчи. Молекула ДНК имеет длину 34 ангстрема и ширину 21 ангстрем для каждого полного цикла своей двойной спирали. Эти числа, 34 и 21, являются числами ряда Фибоначчи, и их отношение 1,61
очень близко к Фи, 1. 6180339.
6180339.
Спасибо Кельвину Дворски за помощь со статьей!
Источники и изображения: Вверху: Лоскутников/Shutterstock; Motorcup: Motorolka / ShutterStock, , , , Galaxy , Galaxy: , Galaxy: , , Американский музей естественной истории и здесь , Mody Bee , Ураган : MNN , Faces: Goldennumber и здесь , ДНК .
Золотое сечение | Винодельня Мира
Поместье Mira Winery спроектировано в соответствии с золотым сечением, в чем можно убедиться, посетив наш новый Дом гостеприимства и Винный завод в Юнтвилле.
Золотое сечение лучше всего аппроксимируется последовательностью Фибоначчи и лежит в основе архитектуры, искусства и природы. Это также лежит в основе Mira с момента нашего первого знакомства, дизайна нашего поместья и нашего Ovum, деревянного ферментера винодельни в форме яйца.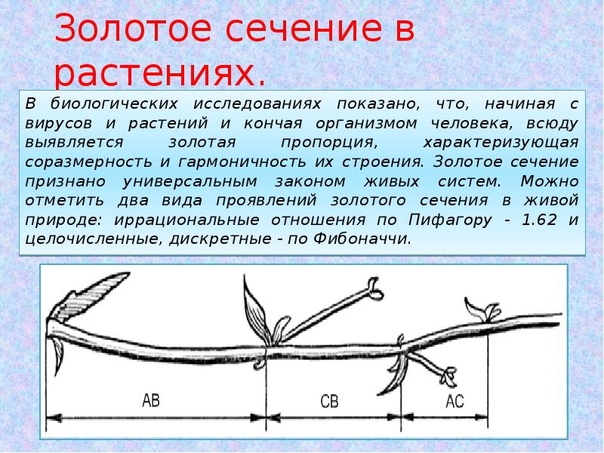 Яйцо воплощает Золотое сечение как по форме, так и по функциям, позволяя ферментации естественным образом смешиваться внутри яйца.
Яйцо воплощает Золотое сечение как по форме, так и по функциям, позволяя ферментации естественным образом смешиваться внутри яйца.
Финансы
«Восстановление Фибоначчи» — это инструмент, который технические аналитики используют для определения своих взглядов на поведение покупателей и продавцов на рынках. Этот метод назван в честь знаменитой последовательности Фибоначчи, набора чисел со свойствами, связанными со многими природными явлениями. Хотя использование этих чисел для прогнозирования движений рынка гораздо менее надежно, чем их использование для расчета моделей семян подсолнуха, появление последовательности в области финансов является еще одним свидетельством ее способности захватывать человеческое воображение.
Архитектура
Ракушка и роза
Последовательность Фибоначчи часто используется в архитектуре и искусстве, потому что считается, что она создает эстетически приятные деления и пропорции. Во многих случаях золотое сечение применялось позже при анализе произведения искусства/здания, и глаз видит то, что хочет видеть.
Природа
Многие примеры чисел Фибоначчи встречаются в фенотипических структурах растений и животных. Действительно, числа Фибоначчи часто проявляются в количестве лепестков цветов, спиралей на раковине подсолнуха или наутилуса, морских звезд и дробях, фигурирующих в филлотаксисе [4, 18, 10].
Еще один простой пример, в котором можно найти последовательность Фибоначчи в природе, дается количеством лепестков цветов. У большинства их три (например, лилии и ирисы), пять (парнасия, шиповник) или восемь (космея), 13 (некоторые ромашки), 21 (цикорий), 34, 55 или 89 (сложноцветные).
Арт
Одна очень известная картина, известная как Мона Лиза, написанная Леонардо да Винчи, нарисована в соответствии с золотым сечением. Если мы разделим этот прямоугольник линией, проведенной через ее глаза, мы получим еще один золотой прямоугольник, а это означает, что соотношение длины ее головы и ее глаз является золотым.
Ключ к сбалансированному веб-дизайну: золотое сечение
Естественный баланс — это концепция, которую веб-дизайнеры вложили в базовые принципы дизайна. Помимо математического соотношения, золотое сечение проистекает из корней и пропорций природы. Мы углубимся в то, что такое золотое сечение и как вы можете использовать его для гармонизации своих проектов.
Помимо математического соотношения, золотое сечение проистекает из корней и пропорций природы. Мы углубимся в то, что такое золотое сечение и как вы можете использовать его для гармонизации своих проектов.
Золотое сечение является фундаментальным аспектом дизайнерской работы.Он встречается почти повсюду в природе и восходит к древним грекам.
Посмотрим на ГЕОМ…
На протяжении всей истории отношение длины прямоугольников к ширине 1,61803 39887 49894 84820 считалось наиболее приятным для глаз.
Это соотношение было названо греками золотым сечением. В мире математики числовое значение называется «фи» по имени греческого скульптора Фидия . Пространство между колоннами образует золотые прямоугольники.В этой структуре, которая находится в Афинах, Греция, есть золотые прямоугольники.
Он ваял многие вещи, в том числе полосы скульптур, которые проходят над колоннами Парфенона.
Фидий широко использовал золотое сечение в своих скульптурных произведениях. Внешние размеры Парфенона в Афинах, построенного примерно в 440 г. до н.э., образуют идеальный золотой прямоугольник.
Внешние размеры Парфенона в Афинах, построенного примерно в 440 г. до н.э., образуют идеальный золотой прямоугольник.
Леонардо да Винчи называл это «божественной пропорцией» и изображал на многих своих картинах.Ниже представлена знаменитая «Мона Лиза». Попробуйте нарисовать прямоугольник вокруг ее лица. Соответствуют ли измерения золотой пропорции?
Вы можете продолжить изучение этого вопроса, разделив прямоугольник, образованный ее глазами, в качестве горизонтального разделителя. Он провел полное исследование человеческого тела и соотношения длин различных частей тела.
http://www.geom.uiuc.edu/~demo5337/s97b/art.htm
Золотое сечение в веб-дизайне
Ясно, что золотое сечение использовалось на протяжении всей истории, но сейчас возникает желание творчески приспособить это соотношение к виртуальной среде.
По этому принципу можно оформить свой лендинг, а также все остальные страницы и мелкие детали внутри них.
Это интерпретируется как спираль, которая начинается широкой и экспоненциально сужается по мере закручивания внутрь. Золотое сечение также выражается как 1:1,61.
Во-первых, вам нужно определить длину маленького элемента. Затем умножьте его на золотое сечение, которое равно 1,618, и результатом будет идеальная длина большего элемента.
Процесс разработан, чтобы помочь с пропорциями. Все элементы должны работать вместе, чтобы максимизировать пользовательский опыт в этом случае.
Зачем использовать золотое сечение? —
Хорошо сбалансированный контент!Дизайнеры часто сталкиваются с ситуацией, когда продукт должен содержать большое количество разнообразного контента, который невозможно заменить. Чтобы смешать все компоненты в приятном сочетании, можно применить золотое сечение.
Разделите макет на разные части в пропорции 1:1.618 и распределите содержимое по секторам в соответствии с их важностью.
 Такой композиции достаточно для восприятия пользователями, и она помогает организовать все компоненты.
Такой композиции достаточно для восприятия пользователями, и она помогает организовать все компоненты.
Кроме того, каждый отдельный элемент, например, икона, должен быть создан в гармонии с собой. Золотое сечение положительно влияет на визуальное восприятие и является основной причиной, по которой многие графические дизайнеры и дизайнеры пользовательского интерфейса применяют его в своем рабочем процессе.
Другой пример:Возьмите ширину 1000 пикселей и разделите ее на 1.618, чтобы получить высоту около 618 пикселей.
Затем добавьте квадрат 618 x 618 с правой стороны холста, оставив прямоугольник 382 x 618 с левой стороны – еще один золотой прямоугольник.
Как вы поняли, «золотой прямоугольник» — это прямоугольник, длина которого в 1,6180 раз больше ширины.
*Золотой прямоугольник чаще всего используется для визуализации золотого сечения, но вы также можете использовать круги и треугольники очень похожим образом. — Этот пример предоставлен Apiumhub
— Этот пример предоставлен Apiumhub
Вы можете использовать The Golden Ration для логотипов, типографики, изображений, макетов веб-дизайна и многого другого!
Вы часто будете видеть веб-сайты с панелью навигации и изображением заголовка вверху, которое занимает значительную часть экрана. Многие веб-сайты разбиты на две колонки, одна из которых в два раза шире другой.
Это не только удобно, потому что облегчает навигацию по веб-сайту, но и создает первый элемент золотого сечения.
Инструменты
Эти инструменты сделают всю работу за вас. Так легко!
PHICULATOR — простой виджет для панели инструментов Mac OSX, который при задании любого числа вычисляет соответствующее значение с использованием золотого сечения.
PHIMATRIX — ПО для проектирования и анализа для Windows и Mac. Принимайте отличные решения по композиции за считанные секунды с бесконечным количеством приложений. Программа накладывает на любое изображение на экране десятки настраиваемых сеток и шаблонов.
AREAWARE — Физический продукт для ежедневного творчества! Используйте искатель золотого сечения, карманное устройство для наблюдения, чтобы найти пропорциональное совершенство в вашем окружении.
Когда вы понимаете лежащую в его основе теорию, использование золотого сечения становится простым и понятным. Дайте нам знать, что вы думаете о золотом сечении в комментариях!
Хотите изменить дизайн своего веб-сайта, чтобы он соответствовал золотому сечению? Свяжитесь с Blue Archer сегодня, чтобы начать разговор.
Золотое сечение и как его использовать в графическом дизайне
Искусство и дизайн крайне субъективны. Мусор одного человека может стать шедевром для другого. Но, к счастью, существует старинное число, которое может помочь превратить ваши проекты в научно доказанную красоту: золотое сечение.
Мусор одного человека может стать шедевром для другого. Но, к счастью, существует старинное число, которое может помочь превратить ваши проекты в научно доказанную красоту: золотое сечение.
Вы когда-нибудь тайно задавались вопросом: «Что такого замечательного в Моне Лизе?» Ответ — это золотое сечение.
Также известное как Золотое сечение, Золотое сечение или греческая буква «фи», золотое сечение — это очень удобное число, которое помогает создавать красивые, идеально сбалансированные конструкции, которые эстетически удовлетворяют на глубоком мозговом уровне. Круто, да?
Хотя искусство и дизайн часто руководствуются инстинктом и творчеством, Золотое сечение использует математику, чтобы изменить процесс создания изображений, макета, типографики и многое другое. Итак, давайте углубимся в это.
Что такое золотое сечение?
—
Золотое сечение — это число, используемое, когда две величины делятся таким образом, что их отношение равно отношению их суммы к большей из двух величин. Это число 1,618, также называемое Фи.
Это число 1,618, также называемое Фи.
Самый простой способ продемонстрировать это — использовать последовательность Фибоначчи. Не вдаваясь в подробности и , эта последовательность представляет собой сумму двух чисел, стоящих перед ней. Итак: 0,1,1,2,3,5,8,13,21…во веки веков (и присно). Когда-то греки использовали последовательность Фибоначчи, чтобы сформировать визуальный паттерн в помощь своим проектам. Когда вы превращаете последовательность в квадраты и кладете их бок о бок, чтобы получились прямоугольники, начинает формироваться спираль (называемая Золотой Спиралью).
Пусть вас не пугают несколько уравнений! Золотое сечение на самом деле намного проще, чем кажется. И встречается везде. Золотая спираль появляется в природе повсюду вокруг нас. От ураганов до цветов, от галактик до ракушек… и даже от тех странных мутировавших цветных капуст, которые иногда можно найти в продуктовом магазине.
Золотое сечение в природе Мате Маршалко через средуКак использовать золотое сечение в графическом дизайне
—
Одна из лучших особенностей золотого сечения заключается в том, что оно дает вам простое число, помогающее структурировать выразительный характер дизайна. Просто умножьте размер элемента на 1,618, чтобы определить размер другого элемента, или наложите золотую спираль, чтобы отрегулировать их расположение. Вы можете использовать Золотое сечение, чтобы ориентироваться в своих макетах, типографике, изображениях и многом другом.
Просто умножьте размер элемента на 1,618, чтобы определить размер другого элемента, или наложите золотую спираль, чтобы отрегулировать их расположение. Вы можете использовать Золотое сечение, чтобы ориентироваться в своих макетах, типографике, изображениях и многом другом.
Мы собрали четыре совета и рекомендации о том, как использовать золотое сечение, чтобы максимизировать научную красоту в ваших проектах в стиле да Винчи.
1. Иерархия типографики
При создании любого дизайна, в котором используется текст, всегда учитывайте иерархию сообщений в макете.Будь то постер, приглашение на свадьбу или макет веб-сайта, вы можете использовать золотое сечение, чтобы определить размер типографики.
Например, предположим, когда вы разрабатываете свою иерархию копий для действительно важного текста (A), вашего типа важного текста (B) и вашего не очень важного текста (C). Если ваш наименьший размер шрифта для (C) составляет 10 пикселей, умножьте его на 1,618, чтобы получить приблизительное руководство для больших размеров.
2.Композиция изображения
При рассмотрении гармонии ваших изображений всегда полезно остановиться, сделать шаг назад и вернуться со свежим взглядом. Но если у вас нет времени обдумывать свои произведения искусства, более быстрая альтернатива — Золотая спираль. Наложите спираль на свои изображения, чтобы увидеть, какие элементы расположены где и действительно ли они создают гармонию.
Используя Золотую спираль, вы можете решить, где должны быть фокусы, как центрировать заголовок для максимального воздействия или какие элементы нужно сместить, чтобы придать дизайну больше энергии.
Иллюстрация ночного неба от Alerim3. Дизайн логотипа
Хорошо продуманный логотип жизненно важен для вашего бренда, чтобы люди могли понять основную идею практически с первого взгляда. Вот почему это отличная идея учитывать золотое сечение при разработке логотипа, чтобы мгновенно привлечь людей и помочь им установить связь. На самом деле, многие крупнейшие мировые бренды используют золотое сечение для создания своих логотипов: Pepsi, Apple и Twitter, и это лишь некоторые из них.
На самом деле, многие крупнейшие мировые бренды используют золотое сечение для создания своих логотипов: Pepsi, Apple и Twitter, и это лишь некоторые из них.
Например, логотип Green in Blue для хлебопекарного бизнеса «Голодный гном» — это идеально сбалансированный логотип в стиле современного китча, в котором используется золотое сечение для управления размещением изображения и размером текста.
Логотип Rahajoe для Little Spoon использует круги в золотом сечении в качестве сетки, определяющей их дизайн.
графический логотип золотого сечения от Rahajoe
При разработке логотипа вы даже можете представить последовательность Фибоначчи в виде ряда кругов, а затем переставить их, чтобы сформировать сетку, которая станет основой для вашего логотипа. Это основа многих логотипов, в том числе птицы Twitter.
Последовательность Фибоначчи, показанная через круги Мостафы Амина и Brandology Studio4.Макеты
Когда вам нужно совмещать множество разных вещей в одном макете, всегда полезно использовать Золотую спираль, чтобы ориентироваться при размещении каждого элемента. Нас естественным образом тянет к центру спирали, поэтому часто лучше всего поместить туда самое важное сообщение.
Нас естественным образом тянет к центру спирали, поэтому часто лучше всего поместить туда самое важное сообщение.
Например, в дизайне плаката Green in Blue для вечеринки Summer of Love спираль идеально облегает лицо и цветок, делая его хорошо сбалансированным и интригующим фокусом.
Запомните это число: 1.618
—
Этот номер — твой новый лучший друг. Умножьте размер шрифта или элемент дизайна на золотое сечение, и вы станете на один шаг ближе к тому, чтобы ваш макет начал складываться воедино. Или вы всегда можете наложить Золотую спираль в качестве удобного ориентира.
Из-за научного и даже универсального характера золотого сечения дизайнеры часто используют его, знают они об этом или нет. Тем не менее, всегда полезно проверить, соответствуют ли ваши проекты магии 1.618, так что вы можете поднять их на новый уровень удивительности!
Прочтите нашу статью Design 101, если хотите узнать больше об основах графического дизайна.
Хотите получить красивый дизайн, вдохновленный золотым сечением?
Работайте с одним из наших талантливых дизайнеров, чтобы это произошло!
Золотое сечение и его влияние на воспринимаемую визуальную привлекательность фотографий
Ахтаруззаман, М., и Шафи, А.А. (2012). Геометрическое обоснование числа Фи, золотое сечение и барокко в природе, архитектуре, дизайне и технике.Международный журнал искусств, 1 (1), 1–22. doi: 10.5923/j.arts.20110101.01
Беллос, А. (2014, 25 февраля). Золотое сечение: художники-графики изображают золотое сечение – в картинках | Алекс Беллос. Получено с https://www.theguardian.com/science/alexs-adventures-in-numberland/gallery/2014/feb/25/golden-meaning-graphic-artists-golden-ratio-pictures
.Бенджафилд, Дж. (1976). Золотой прямоугольник: некоторые новые данные. Американский журнал психологии, 89(4), 737. doi: 10.2307/1421471
Брэндон, Дж.(2019, 2 августа). Божественная композиция с коэффициентом Фибоначчи (правило третей на стероидах). Получено с https://digital-photography-school.com/divine-composition-with-fibonaccis-ratio-the-rule-of-therts-on-steroids/
Получено с https://digital-photography-school.com/divine-composition-with-fibonaccis-ratio-the-rule-of-therts-on-steroids/
Казинс, К. (2015, 9 февраля). Глядя на изображения: Phi Grid против правила третей. Получено с https://designshack.net/articles/layouts/looking-at-images-phi-grid-vs-rule-of-therts/
Елизаров В. (2019, 16 мая). Что такое золотое сечение в фотографии и как его использовать.Получено с https://www.phototraces.com/golden-ratio-in-photography/
.Фальбо, К. (2005). Золотое сечение: противоположная точка зрения. The College Mathematics Journal, 36 (2), 123. doi: 10.2307/30044835
Фехнер, Г. (1971). Königliche Gesellschaft der Wissenschaften (Академия Wissenschaften) Геттинген, Bayerische Akademie der Wissenschaften München. дои: 10.1515/9783111433868
Фаулер, Д. Х. (1982). Обобщение золотого сечения. Уорикский университет, Ковентри, Англия.Получено с https://www.fq.math.ca/Scanned/20-2/fowler.pdf
. Годкевич, М. (1974). Золотое сечение: артефакт диапазона стимулов и мера предпочтения. Американский журнал психологии, 87 (1/2), 269. doi: 10.2307/1422021
Золотое сечение: артефакт диапазона стимулов и мера предпочтения. Американский журнал психологии, 87 (1/2), 269. doi: 10.2307/1422021
Грин, CD (1995). Все, что блестит: обзор психологических исследований эстетики золотого сечения. Восприятие, 24 (8), 937–968. дои: 10.1068/p240937
Грин, CD (2012). Как найти опровержение золотого сечения, не прилагая особых усилий.Эмпирические исследования искусств, 30 (1), 115–122. doi: 10.2190/em.30.1.h
Гросс, Р. (2016, 23 августа). Что такое золотое сечение? Что нужно знать и как это использовать. Получено с https://www.canva.com/learn/what-is-the-golden-ratio/
.Ливио, М. (2008). Золотое сечение: история самого удивительного числа в мире Фи. Нью-Йорк: Бродвейские книги.
Макроссон, В.Д.К., и Стюарт, ЧП (1997). Склонность художников к разделению отрезков в золотом сечении.Перцептивные и двигательные навыки, 84 (3), 707–713. doi: 10.2466/pms.1997.84.3.707
Марковский, Г. (1992). Заблуждения о золотом сечении. The College Mathematics Journal, 23(1), 2. doi: 10.2307/2686193
The College Mathematics Journal, 23(1), 2. doi: 10.2307/2686193
Нюрнберг Т., Лесун Дж. Дж., Фальконер Д., Ольга и Гопи Т. (2018 г., 6 марта). Как использовать золотое сечение, чтобы улучшить свои фотографии. Получено
Штекер, К. (1980). Гипотеза золотого сечения. Американский журнал психологии, 93 (3), 467. doi: 10.2307/1422725
Позаментье, А.С. и Леманн И. (2012). Великолепное золотое сечение. Амхерст, Нью-Йорк: Книги Прометея.
Сугаард, М. (2020, декабрь). Золотое сечение — Принципы формы и компоновки. Получено с https://www.interaction-design.org/literature/article/the-golden-ratio-principles-of-form-and-layout
.Спаркман, Дж. (2016, 25 октября). Почему золотое сечение лучше, чем правило третей. Получено с https://petapixel.com/2016/10/24/golden-ratio-better-rule-therts/
.Персонал, К.Б. (2019, 22 октября). Золотое сечение: руководство дизайнера. Получено с https://www.creativebloq.com/design/designers-guide-golden-ratio-12121546
.
Стигер, Стефан и Вирен Свами. «Время отпустить? Никакого автоматического эстетического предпочтения золотого сечения в художественных фотографиях». Психология эстетики, творчества и искусства, т. 1, с. 9, нет. 1, 2015, стр. 91–100., doi: 10.1037/a0038506.
Штейнбах, П. (1997). Золотые поля: Дело о семиугольнике. Математический журнал, 70 (1), 22.дои: 10.2307/2691048
Виттевен, В., Виттевен, А., и Чайлдресс, Д. Х. (2016). Великая пирамида Гизы: современный взгляд на древние знания. Амстердам: Frontier Publishing.
Уэллс, Д. (1992). Скрытые связи с двойным смыслом. Кембридж: Издательство Кембриджского университета.
Золотое сечение. Внесите баланс в дизайн пользовательского интерфейса. | by tubik
Одной из основных характеристик эффективного дизайна является понятный пользовательский интерфейс. Все элементы должны быть хорошо сбалансированы и гармонично расположены, чтобы пользователи могли легко воспринимать информацию на экране и без усилий взаимодействовать с продуктом.
Чтобы создать эффективную дизайнерскую композицию, профессионалы применяют различные приемы и методы из области искусствоведения, а также основные математические теории. Одним из распространенных инструментов, помогающих создавать приятные дизайнерские композиции, является математическая пропорция, называемая золотым сечением. В статье мы определим суть этой техники и посмотрим, как ее можно использовать в дизайне.
Все в мире стремится к гармонии и равновесию. Даже матушка-природа приводит вещи в формы, близкие к совершенным.Людям нравится все, что имеет естественный оттенок, и они всегда стремятся реализовать эти модели и формы в своем результате. В погоне за раскрытием секретов творения математики вычислили формулу, которая присутствует в большинстве вещей на Земле.
Золотое сечение — это математическое соотношение между элементами разного размера, которое считается наиболее эстетичным для человеческого глаза. Золотое сечение равно 1:1,618 и часто изображается спиралями в форме ракушек, которые вы наверняка видели в Интернете.
Итак, как именно рассчитывается идеальная асимметрия? Во-первых, нужно определиться с длиной маленького элемента. Затем умножьте его на золотое сечение, которое равно 1,618, и результатом будет идеальная длина большего элемента.
ИсточникСчитается, что теория золотого сечения существует уже более 4000 лет. Ученые обнаружили, что большинство старинных зданий, а также известные произведения искусства подчиняются золотому сечению.Леонардо да Винчи и Сальвадор Дали были известны как последователи теории золотого сечения и использовали ее как ключевой инструмент для своих удивительных работ. Сегодня золотое сечение применяется в различных областях, включая архитектуру, искусство, фотографию и дизайн.
Эффективная композиция является основной частью дизайна. Все элементы должны работать вместе, чтобы максимизировать приятное впечатление. При этом каждый отдельный элемент, даже такой маленький, как икона, должен создаваться в гармонии внутри себя. Золотое сечение оказывает положительное влияние на визуальное восприятие, поэтому многие графические дизайнеры и дизайнеры пользовательского интерфейса применяют его в своем рабочем процессе.
Золотое сечение оказывает положительное влияние на визуальное восприятие, поэтому многие графические дизайнеры и дизайнеры пользовательского интерфейса применяют его в своем рабочем процессе.
Графические дизайнеры больше склонны применять золотое сечение. Дело в том, что преподаватели рисования часто объясняют теорию золотого сечения, чтобы помочь ученикам разобраться, как работать с пропорциями. Вот почему многие дизайнеры продолжают применять этот инструмент при создании различной графики, особенно для небольших, но значимых элементов дизайна, таких как логотип.
Дизайн логотипов и иконок требует особого внимания к деталям.Золотое сечение позволяет создавать иллюстрации, в которых каждый элемент находится в гармонии и соответствующей пропорции с другими. Более того, дизайн логотипа является сердцем бренда, поэтому дизайнеры стремятся представить его наиболее привлекательным образом. Золотая пропорция может придать логотипу эстетическую привлекательность и повысить популярность бренда.
Пользовательский интерфейс должен иметь четкое визуальное представление компонентов, чтобы люди могли без проблем использовать продукт. Золотое сечение часто применяется для эффективного размещения элементов пользовательского интерфейса.В первую очередь его можно использовать на этапе каркасного моделирования. Таким образом, вы можете спланировать структуру размещения макета и размеров компонентов пользовательского интерфейса в соответствии с золотой пропорцией. Кроме того, схема золотого сечения может помочь профессионалам обрезать изображения для веб-дизайна, чтобы композиция фотографии оставалась сбалансированной.
Графический дизайн для Промо-ролик Opera SoftwareМатематические расчеты могут показаться скучными и трудоемкими, поэтому может возникнуть вопрос, а стоит ли это усилий.Давайте посмотрим, что золотое сечение может привнести в дизайн.
Сбалансированный контент
Дизайнеры часто сталкиваются с ситуацией, когда продукт должен содержать большое количество разнообразного контента и каждая его часть жизненно необходима и не может быть заменена. Чтобы объединить все компоненты в приятную композицию, можно применить золотую пропорцию. Разделите макет на разные секции, используя пропорцию 1:1,618, и разместите контент в секторах в соответствии с их важностью. Такая композиция контента достаточна для восприятия пользователями и помогает организовать все компоненты.
Чтобы объединить все компоненты в приятную композицию, можно применить золотую пропорцию. Разделите макет на разные секции, используя пропорцию 1:1,618, и разместите контент в секторах в соответствии с их важностью. Такая композиция контента достаточна для восприятия пользователями и помогает организовать все компоненты.
Эффективная визуальная иерархия
Говоря об организации контента, нельзя забывать о визуальной иерархии. Как мы упоминали в наших предыдущих статьях, это метод эффективного структурирования компонентов контента. Сочетая принципы этих двух методов, дизайнеры максимизируют шансы на создание мощной дизайнерской композиции.
Отслеживающий виджетМощные уровни типографики
Чтобы создать эффективную типографику, дизайнеры должны разделить копируемый контент на разные уровни.Обычно они включают в себя различные виды текста, включая заголовки, подзаголовки, основной текст, заголовок и т. д. Специалисты по золотому сечению могут быстро определить подходящую пропорцию между уровнями типографики, например, вы можете выбрать определенный размер для заголовка, а затем разделить его на 1. 618. Результат покажет вам наиболее подходящий размер подзаголовков.
618. Результат покажет вам наиболее подходящий размер подзаголовков.
Приятное первое впечатление
Когда пользователи впервые пробуют продукт, они просматривают пользовательский интерфейс, чтобы понять, нравится он им или нет.Принцип психологии, известный как висцеральная реакция, гласит, что люди решают, нравится им что-то или нет, в течение нескольких секунд, глядя на что-то. Эта реакция идет быстрее, чем наше сознание, поэтому мы даже не осознаем этого. Вот почему так важно, чтобы первое впечатление о продукте было приятным. Дизайн, созданный с использованием золотого сечения, оказывает положительное влияние на сознание пользователей и их визуальное восприятие и работает с первого взгляда на продукт.
Соответствующее пустое пространство
Белое пространство — это пространство между элементами в композиции дизайна.Дизайнеры всегда должны заботиться о количестве пустого пространства в пользовательском интерфейсе, поскольку от него в значительной степени зависит единство композиции.




 Такой композиции достаточно для восприятия пользователями, и она помогает организовать все компоненты.
Такой композиции достаточно для восприятия пользователями, и она помогает организовать все компоненты.