Соотношение золотое сечение: Attention Required! | Cloudflare

Что такое «золотое сечение»?. На протяжении веков «золотое сечение»… | by Сергей Базанов | Paradox Review

«Золотое сечение», называемое также «золотая пропорция» или «золотое соотношение», было обнаружено во многих самых знаменитых творениях человечества — от древнегреческого Парфенона до творений Сальвадора Дали. Возможно, вы уже читали на эту тему статью «Нереализованное влияние золотого сечения».

Не важно, считаете ли вы, что эта божественная пропорция является поистине знамением красоты или просто предвзятым выбором, но, без сомнения, это одно из самых интригующих чисел в мире. Поэтому, сейчас мы поговорим о математической основе «золотого сечения».

Впервые о «золотом сечении» упоминает древнегреческий математик Евклид около 300 лет до нашей эры. В шестой книге своего трактата «Начала» Евклид дает определение «золотого сечения». Он поручает нам взять отрезок линии и разделить его на два меньших сегмента так, что отношение всей линии (a + b) к отрезку a будет таким же, как отношение отрезка a к сегменту b:

Что эквивалентно пропорции:

Евклид использовал «золотое сечение» для построения правильного пятиугольника. Отношение диагонали правильного пятиугольника к его стороне равно золотому сечению. Правильный пятиугольник (пентагон) еще называют «золотой пятиугольник».

«Золотое сечение» часто представляют как «Золотой прямоугольник» — прямоугольник с отношением длин сторон примерно 1,618:1.

Этот прямоугольник обладает тем свойством, что если от него отрезать квадрат, то снова получится золотой прямоугольник меньшего размера и так до бесконечности.

Золотой прямоугольник.

На самом деле, соотношение сторон «золотого прямоугольника» — это иррациональное значение 1,618034…, т.е. бесконечная десятичная дробь, не имеющая периода.

Это число и есть пропорция «золотого сечения», оно обозначается греческой буквой Фи в честь древнегреческого скульптора и архитектора Фидия, мастера, воплотившего его в своих работах.

Чтобы найти значение 1,618034…, мы должны решить пропорцию, показанную выше. Для простоты предположим, что b = 1 и a = x и найдем решение для x.

a = x, b = 1

Шаг 1. Сделаем перекрестное умножение:

Шаг 2. Приведем уравнение к 0:

Шаг 3. Решим квадратное уравнение:

Поскольку мы работаем с длинами, нам нужно только положительное решение:

Решение найдено! «Золотое сечение» выражается, как дробь.
Для проверки подставим a = 1.618 и b = 1, чтобы убедиться, что наша пропорция верная:

Обратите внимание, как интересно: мы можем написать «золотое соотношение» при помощи самого себя. Это потрясающе!

Что эквивалентно:

Пойдем дальше… Заменим φ = 1 + 1 / φ для φ в знаменателе:

И еще дальше!

Мы могли бы продолжать делать это бесконечно. Оказывается, «Золотое сечение» может быть записано как бесконечная цепная дробь.

Мы можем использовать непрерывную дробь, чтобы раскрыть связь «золотого сечения» с последовательностью Фибоначчи.

Для начала мы немного изменим нашу бесконечную дробь — добавим индексы, чтобы показать, как следующее значение φ(n+1) может быть получено из предыдущего значения φ(n).

Так как это бесконечная цепная дробь, с ростом n искомое значение приближается к истинному значению φ.

Теперь допустим, что φ(0) = 1 и найдем φ(1).

Продолжим вычислять следующеезначение — φ(2)

И далее… φ(3), φ(4)…

Посмотрите! Это же последовательность Фибоначчи! Каждое приближение — это отношение двух соседних чисел Фибоначчи.

По мере продвижения к каждому новому последовательному вычислению мы обнаруживаем, что наше искомое значение все ближе и ближе приближается к его истинному «Золотому сечению».

На девятом члене последовательности Фибоначчи мы уже получаем значения «золотого сечения», с тремя верными цифрами после запятой.

В самом деле, limit F(n+1)/F(n) при n→∞ (где F(n) и F(n+1) представляют n и n+1 числа в последовательности Фибоначчи) сходится к φ.

Если визуализировать этот процесс, то мы увидим, как последовательность Фибоначчи создает прямоугольники всё ближе и ближе к «Золотому прямоугольнику».

Прямоугольник Фибоначчи.

Хотя в мире дизайна продолжаются споры о том, является ли «золотое сечение» оптимальной пропорцией или нет, можно с уверенностью сказать, что оно математически совершенно и не перестает нас удивлять.

Что такое золотое сечение и правда ли оно повсюду

Что такое золотое сечение

Это ^{соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.}

Наиболее известные графические представления золотого сечения — это прямоугольник с соотношением сторон примерно 62:48 и построенная в нём спираль.

«Золотой прямоугольник» можно разделить на такие же, только меньшего размера. Изображение: Dicklyon / Wikimedia Commons

«Золотая спираль» (красная), вписанная в «золотой прямоугольник». Изображение: Silverhammermba & Jahobr / Wikimedia Commons

Золотое сечение тесно связано с числами Фибоначчи. Это ряд чисел, каждое из которых равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Чем дальше продолжается этот ряд, тем ближе соотношение соседних чисел в нём к 1,618. Например, 3/2=1,5; 8/5=1,6, а 34/21= 1,619.

Почему золотое сечение так популярно

Впервые им заинтересовались ^{ещё древнегреческие математики Пифагор и Евклид. Они считали, что на числах построено всё мироздание и с их помощью можно объяснить любой феномен. Неудивительно, что элегантное соотношение так заинтересовало античных мыслителей.}

Вслед за ними золотым сечением увлеклись многие выдающиеся учёные и деятели искусства. Например, Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.

Его считают «божественной пропорцией»

Название «золотое сечение» придумал немецкий математик XIX века Мартин Ом. До него это соотношение именовали ^{«божественной пропорцией».}

Из‑за приписываемых характеристик золотое сечение старались применять как можно чаще. Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.

Некоторые и поныне считают эту пропорцию секретом привлекательности и примером универсальной гармонии, приятной человеческому глазу. Например, о золотом сечении любят говорить пластические хирурги. А ещё это число популярно ^{как никакое другое в математике.}

Его можно встретить в природе

Числа Фибоначчи и спирали, подобные золотому сечению, часто обнаруживаются в природе. Например, в количестве лепестков у цветов или форме растений.

Часть растения эониума. Фото: Max Ronnersjö / Wikimedia Commons

Его обнаруживают в произведениях архитектуры и искусства

Например, «божественные пропорции» находят в Парфеноне и египетских пирамидах. Также широко распространено заблуждение, что «Мона Лиза» написана в соответствии с числом φ.

Почему универсальность золотого сечения — миф

Однако при тщательном изучении становится понятно, что эта пропорция не так уж всеобъемлюща.

Божественность золотого сечения преувеличивается

Золотому сечению придают больше значения, чем есть в действительности. Красивые узоры и налёт таинственности сделали ^{из обычного геометрического соотношения математический миф, который, к примеру, очень любят нумерологи.}

Чаще всего вещи причисляют к золотому сечению с большими допущениями. Ни о какой точности и математической универсальности в таком случае говорить не приходится. Поэтому при желании можно обнаружить «божественные пропорции» где угодно.

В природе золотое сечение не так уж распространено

Его находят далеко не ^{везде. Например, у маков всегда четыре лепестка, а в ряд Фибоначчи четвёрка не входит. Также нередко встречается четырёхлистный клевер. Раковины морских моллюсков похожи на спираль золотого сечения, но всё-таки другие . У них больше витков, и расстояние между ними меньше. Ни у одного моллюска коэффициент скручивания раковины и близко не равен 1,62. Это видно даже невооружённым глазом:}

Спираль морского моллюска. Изображение: Florian Elias Rieser / Wikimedia Commons

Спираль Фибоначчи, близкая к золотому сечению. Изображение: Jahobr / Wikimedia Commons

В человеческом теле же столько точек, от которых можно производить измерение, что при желании реально найти золотое сечение где угодно. Вот только с большой вероятностью у разных людей «божественную пропорцию» придётся искать в разных местах, так как мы можем сильно отличаться друг от друга.

В искусстве оно тоже встречается не так уж часто

Изучение 565 картин выдающихся художников показало ^{, что в среднем соотношение сторон в работах составляет 1,34. Это явно не дотягивает до золотого сечения. Учёные не находят его даже в произведениях Леонардо да Винчи.}

Археологические исследования не подтверждают ^{и того, что древние греки могли использовать золотое сечение при постройке Парфенона. Из более чем 100 памятников древнегреческой архитектуры это число нашлось в пропорциях только четырёх объектов: башни, алтаря, гробницы и надгробия. Не могли пользоваться золотым сечением и древние египтяне, не обладавшие достаточным уровнем технологий, чтобы точно высчитывать пропорции.}

Кому золотое сечение может быть полезно на самом деле

Современная математика использует ^{золотое сечение и числа Фибоначчи при описании фракталов — фигур, которые проявляют самоподобие.}

Фрактальная форма кочана капусты Романеско. Фото: Ivar Leidus / Wikimedia Commons

Знание о числе φ играет важную роль в изучении хаоса и изменяющихся (динамических) систем. Оно помогает понять, как природа развивается и самоорганизуется.

Также числа Фибоначчи полезны при решении некоторых сложных задач. Например, с помощью этих чисел советский математик Юрий Матиясевич доказал ^{, что не существует универсального алгоритма решения уравнений с как минимум двумя неизвестными.}

Читайте также 💆‍♂️👩‍🔬

Калькулятор золотого сечения (золотой пропорции) онлайн

Золотое сечение — это особое соотношение сторон фигуры, которое наиболее приятно для созерцания. Это число известно с античных времен, а ученые эпохи Возрождения называли его божественной пропорцией. Число Фи — золотое сечение, приблизительно равное 1,618.

История

Особую красоту деления отрезка на стороны в соотношении 1/1,618 заметили еще античные ученые. Евклид в своих началах использовал этот метод при построении пентагона, а пифогорейцы рассматривали весь мир как царство математической гармонии и уделяли большое внимание соотношению 1/1,618. В 1202 году Леонардо Фибоначчи вывел особую последовательность, отношение членов которой стремилось к числу Фибоначчи. Лука Пачоли, один из величайших алгебраистов Италии, назвал это соотношение божественной пропорцией, связав свойства бога с числом Фи. Именно с этого момента золотое сечение начало активно использоваться в работах художников эпохи Возрождения и получило буквально мистический статус. По словам Кеплера, число Фи — бесценная жемчужина математики.

Число Фи в математике

Золотое сечение часто встречается в геометрии. Золотой прямоугольник — фигура на плоскости, длина и ширина которой соотносятся как 1/1,618. Примечательное свойство такого прямоугольника состоит в том, что при удалении из фигуры любого квадрата образуется новый прямоугольник с точно таким же соотношением сторон. Стоит упомянуть и пентаграмму — звездчатый многоугольник, стороны которого пересекаются в соответствии с правилом золотого сечения.

В арифметике число Фи встречается в упоминаемой выше последовательности Фибоначчи, так как lim(Fn/Fn-1) -> Фи. Кроме того, золотое сечение имеет интересное представление в других формах записи. Так, Фи представляется как бесконечная цепочка квадратных корней из единицы. А если привести Фи к цепному виду, то получится бесконечная дробь вида [1; 1, 1, 1, 1, 1…]

Число Фи в реальности

Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм». Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.

После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи.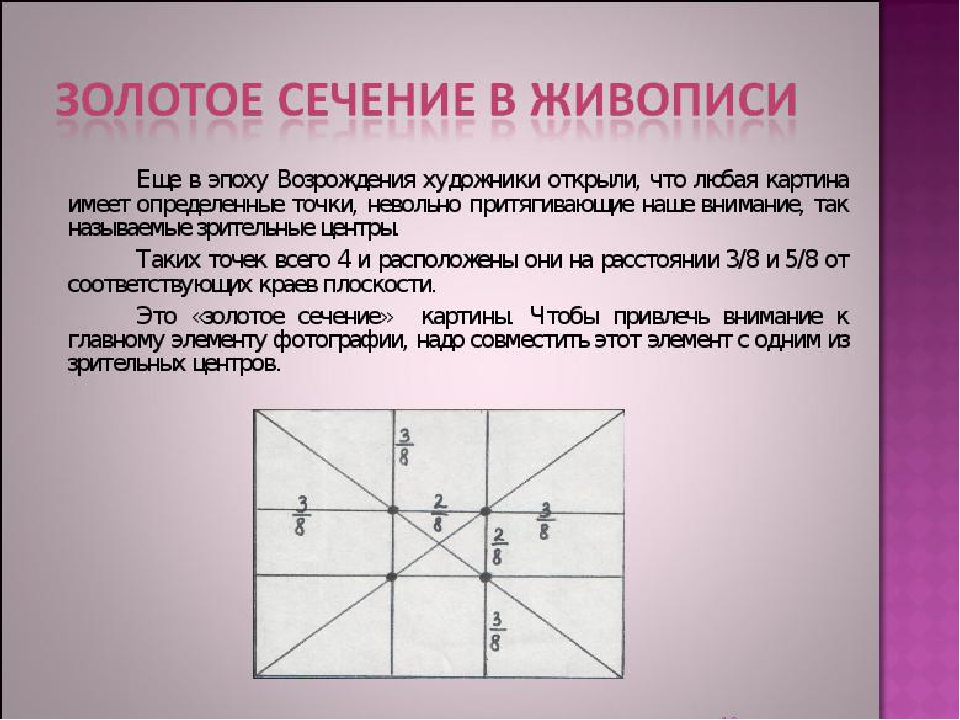 Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.

Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.

Калькулятор золотого сечения

Если вы хотите использовать божественную пропорцию в своей работе, то наш калькулятор к вашим услугам. Для определения сторон золотого прямоугольника вам понадобится ввести одну из сторон, а программа определит вторую, соответствующую правилу золотого сечения. Прелесть калькулятора состоит в том, что он не просто умножает сторону на 1,618, а подбирает целое значение. Именно поэтому вам потребуется оперировать целыми числами, что удобно на практике.

Пример из реальной жизни

Живопись

Допустим, вы хотите сделать приятную с точки зрения математики картину, следовательно, вам нужно нарисовать ее на золотом прямоугольнике. Вам потребуется заказать холст определенного размера, и чтобы определить его размеры, используйте наш калькулятор. Пусть вы хотите писать на холсте, длина которого составит 120 см. Как узнать необходимую ширину? Введите это значение в ячейку A и получите ответ, равный 74 см.

Заключение

Божественная пропорция — мистическое соотношение, которое занимает умы математиков уже несколько тысячелетий. Возможно, именно число Фи содержит ответы на вечные вопросы о тайнах мироздания. Если вам потребуется создать объекты, соответствующие золотому сечению, используйте наш калькулятор, при помощи которого вы сможете подобрать целые числа.

Что такое золотое сечение? | Вечные вопросы | Вопрос-Ответ

«Золотое сечение — это пропорциональное деление отрезка на две неравные части, при котором меньший отрезок так относится к большему, как больший ко всему», — указывает Научно-технический энциклопедический словарь. Это выражается формулой AC/BC = BC/AВ, где АС — меньший отрезок, а ВС — больший.

Считается, что эта пропорция является проявлением гармонии и порядка мирового устройства, идеальной моделью Вселенной. Монах Лука Пачоли в книге «Божественная пропорция» писал, что в золотом сечении проявляется божественное триединство: малый отрезок олицетворяет Сына, большой — Отца, а целое — Святой дух.

 В чём еще проявляется золотое сечение?

Существует  концепция, согласно которой, золотое сечение является универсальным правилом, воплощается  во всём, что окружает человека. Немецкий исследователь золотого сечения, профессор Адольф Цейзинг считал, что части растений и пропорции человеческого тела подчинены правилу золотого сечения. Обмерив около двух тысяч людей, он пришёл к выводу, что части человеческого тела относятся друг к другу примерно в одинаковом отношении. Свои наблюдения он проверил на античных статуях, где эта закономерность подтвердилась, что означало осведомлённость древних о законе золотого сечения.

Исследователи природы находят «идеальную пропорцию» в строении различных живых систем. Самый известный пример — это структура спирали, которая подчиняется математическому закону золотого сечения и находит воплощение, например, в форме рогов горных козлов или раковинах моллюсков.

Золотое сечение в раковине моллюска. Фото: Shutterstock.com

Принципы золотого сечения можно найти в архитектуре древних людей, например, египтян или вавилонян. После измерения пропорций пирамиды Хеопса, храмов и барельефов из гробницы Тутанхамона стало известно, что древние архитекторы основывали расчеты на этой закономерности.

В эпоху Возрождения принцип золотого сечения начинают намеренно использовать художники и скульпторы, отдавая таким образом дань античным традициям. Одним из последователей этого правила считается Леонардо да Винчи, которому, кстати, часто предписывают появление самого термина «золотое сечение». Искусствоведы находят проявление золотого сечения на многих его картинах, в частности, в композиции «Тайной вечери» и в пропорции частей тела «Витрувианского человека».

В математике, помимо основного закона, касающегося соотношения отрезков, примером золотого сечения является Ряд Фибоначчи. Это такая последовательность чисел, при которой каждое последующее число равно сумме двух предыдущих чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. При этом отношение смежных чисел ряда приближается к отношению золотого сечения. Считается, что эта последовательность возникла в качестве ответа на загадку: «Сколько пар кроликов в один год от одной пары родится?»

Смотрите также:

Золотое сечение | Блог 4brain

Золотым сечением называют число, полученное путем деления линии на две части таким образом, что более длинная часть (а), разделенная на меньшую часть (b), равна полной длине линии (а+b), разделенной на более длинную часть (а). Такое отношение часто символизируют с помощью литеры Ф (читается как «фи») – 21-й буквы греческого алфавита. В форме уравнения это выглядит так:

a / b = (a + b) / a = 1. 6180339887498948420…

Как и в случае с π (пи, отношение длины окружности к ее диаметру), число Ф является бесконечным. Обычно его округляют до значения 1,618.

История открытия золотой середины

Это число было найдено и открыто много раз, поэтому у него так много разных названий — золотая середина, золотое сечение, божественная пропорция и т.д. Исторически его можно увидеть в архитектуре многих древних творений, таких как Великие Пирамиды и Парфенон. В пирамиде Гизы длина каждой стороны основания составляет 230,5 метров при высоте 146,6 метров. Отношение основания к высоте составляет примерно 1,5717, что близко к золотой пропорции.

Фидий (500 г. до н.э. — 432 г. до н.э.) был греческим скульптором и математиком, который, как считается, применил Ф, создавая скульптуры для Парфенона. Платон (428 г. до н.э. — 347 г. до н.э.) считал, что золотое сечение является наиболее универсальным связующим звеном математических отношений. Позднее Евклид (365 г. до н.э. — 300 г.

до н.э.) связал золотое сечение с построением пентаграммы.

Последовательность Фибоначчи и золотое сечение

Около 1200 года математик Леонардо Фибоначчи открыл уникальные свойства последовательности Фибоначчи. Эта последовательность непосредственно связана с золотым сечением, потому что если взять любые два последовательных числа Фибоначчи, их отношение будет очень близко к золотому сечению. По мере того как числа возрастают, соотношение приближается к значению 1,618. Например, соотношение 3 к 5 составляет 1,666. Но соотношение 13 к 21 составляет 1,625. Возрастая, соотношение 144 к 233 составляет 1,618. Все эти числа являются последовательными числами в последовательности Фибоначчи.

Такие соотношения из ряда Фибоначчи, близкие к значению золотого сечения, могут быть применены к пропорциям прямоугольника, называемого золотым прямоугольником. Он известен как одна из наиболее визуально совершенных из всех геометрических форм — следовательно, правило золотого сечения очень широко применяется во всех видах визуального искусства. Золотой прямоугольник также связан с золотой спиралью, которая создается путем создания смежных квадратов измерений Фибоначчи.

Пропорции золотого сечения в материальном мире

В 1509 году Лука Пачоли написал книгу, которая называет число Ф «Божественной пропорцией», что было наглядно показано Леонардо да Винчи. Позже да Винчи назвал эту пропорцию золотым сечением. Оно использовалось для достижения баланса и красоты во многих картинах и скульптурах эпохи Возрождения.

Да Винчи сам использовал золотое сечение, чтобы определить все пропорции в «Тайной вечере», включая размеры стола, пропорции стен и деталей интерьера. Золотое сечение также появляется в «Витрувианском Человеке» да Винчи и «Мона Лизе». Считается, что золотое сечение использовали и другие великие художники, включая Микеланджело, Рафаэля, Рембрандта, Сьюрата и Сальвадора Дали.

Термин «фи» был придуман американским математиком Марком Барром в 1900-х годах. Ф продолжал применяться в математике и физике, в том числе в плитках Пенроуза 1970-х годов, которые позволяли мозаичным поверхностям иметь пятикратную симметрию.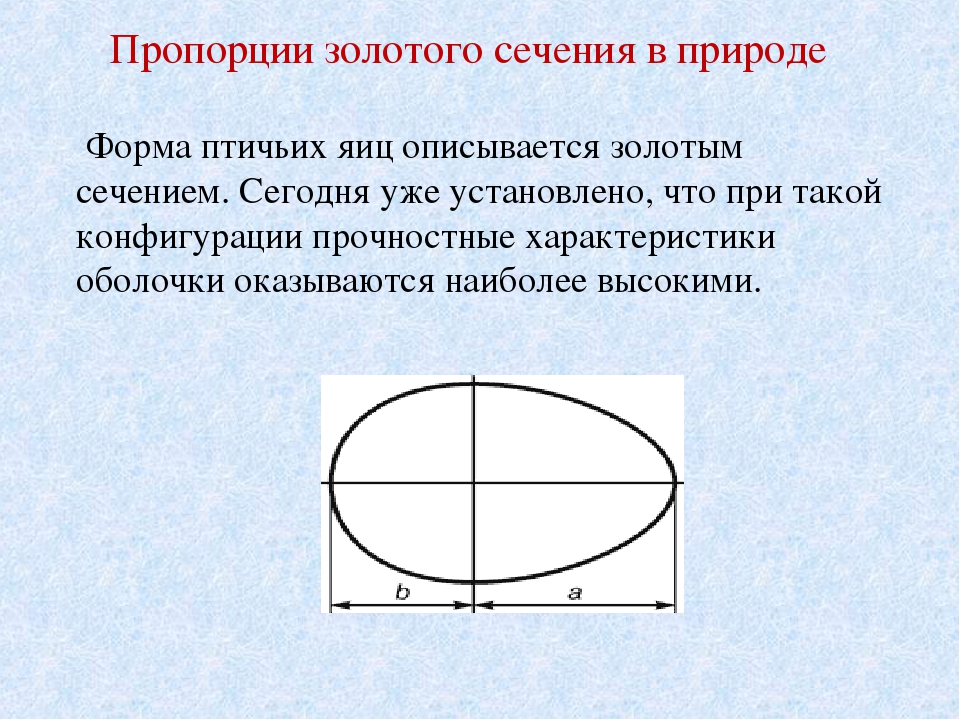

В 1980-х годах Ф появился в квазикристаллах – недавно открывшейся форме материи.

Фи — более чем загадочный и неясный термин в математике и физике. Он появляется вокруг нас в нашей повседневной жизни, даже в наших эстетических взглядах. Исследования показали, что когда испытуемые видят случайные лица, они считают наиболее привлекательными те, которые имеют четкие параллели с золотым сечением. Лица, оцененные как наиболее привлекательные, показывают золотые соотношения между шириной лица и шириной глаз, носа и бровей. Испытуемые не были математиками или физиками, знакомыми с правилом золотого сечения (они были просто среднестатистическими людьми), и оно вызвало инстинктивную реакцию.

Золотое сечение также проявляется во всех видах природы и науки. Ниже приведены примеры самых неожиданных мест, в которых можно его встретить.

• Цветочные лепестки. Количество лепестков на некоторых цветах соответствует последовательности Фибоначчи. С точки зрения теории Дарвина считается, что каждый лепесток помещается таким образом, чтобы обеспечить максимально возможное воздействие солнечного света и других факторов.
• Семенные головки. Семена цветка часто начинают произрастать в центре семенной головки и мигрируют наружу, заполняя свободное пространство. Например, семечки подсолнухов следуют этой схеме.
• Сосновые шишки. Семенные коробочки сосновых шишек наполнены семенами, которые растут спирально вверх, в противоположных направлениях. Количество шагов, которые делают спирали, как правило, соответствует числам Фибоначчи.
• Ветви дерева. То, как ветки дерева формируются или расщепляются, является примером последовательности Фибоначчи. Корневые системы и водоросли также придерживаются такого способа формирования.
• Раковины. Многие раковины, в том числе раковины улитки и раковины наутилуса, являются прекрасными примерами золотой спирали.
• Спиральные галактики. Млечный путь имеет несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль примерно 12 градусов. Форма спирали идентична золотой спирали, а золотой прямоугольник можно нарисовать над любой спиральной галактикой.
• Ураганы. Внутреннее строение ураганов часто следует правилу золотой спирали.
• Пальцы руки человека. Каждый участок пальца от кончика основания до запястья больше, чем предыдущий, примерно на соотношение Ф.
• Тела человека и животных. Расстояние от пупка человека до пола и от макушки головы до пупка – это золотое сечение. Но человек не единственный пример золотого сечения в животном мире. Дельфины, морские звезды, морские ежи, муравьи и пчелы также демонстрируют эту пропорцию.
• Молекулы ДНК. Молекула ДНК имеет размеры 34 ангстрем на 21 ангстрем на каждом полном цикле спирали в виде сдвоенной спирали. В рядах Фибоначчи 34 и 21 являются последовательными числами.

Таким образом, примеров, где встречаются пропорции и соотношения, следующие правилу золотого сечения, более чем достаточно. Кроме перечисленных примеров, число «Фи» часто встречается в математике, физике, астрономии, биологии и иных сферах деятельности человека. Можно смело утверждать, что название «Божественное сечение» по праву присвоено числу Ф – видимо им руководствовался создатель, наполняя эту Вселенную всем живым и неживым.

Основополагающий принцип природы – «Золотое сечение»

В быту часто советуют найти «золотую середину», но такой середины в природе не существует, однако, есть «золотое сечение» или «золотое число». 

Пн 23 июля 2018, 10:07

Фото: thejizn.com

Золотое сечение это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве – во всем, с чем может соприкоснуться человек. Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.

Что может быть общего между древнеегипетскими пирамидами, картиной Леонардо да Винчи «Мона Лиза», подсолнухом, улиткой, сосновой шишкой и пальцами человека? Связывает их удивительные числа, которые были открыты итальянским математиком средневековья Леонардо Пизанским, более известным по именем Фибоначчи (родился около 1170 — умер после 1228). После его открытия числа эти так и стали называться его именем. Удивительная закономерность последовательности чисел Фибоначчи состоит в том, что каждое число в этой последовательности получается из суммы двух предыдущих чисел, которые представляют бесконечную последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, … Эту схему расположения чисел можно увидеть повсюду в природе. Когда большее число из этой последовательности разделить на меньшее, расположенное рядом число, то соотношение приблизительно получается 1.618; и если меньшее число разделить на большее число, стоящее рядом, то получается примерно 0.618. Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Существует большое количество способов математически выразить золотое соотношение, и во всех этих методах имеется своя определенная простота, точность и обаяние. Но история этого понятия уходит еще в древние времена, когда только зарождались такие науки, как математика и философия.

Как научное понятие золотое сечение вошло в обиход во времена Пифагора, а именно в VI веке до нашей эры. Но еще до того знания о подобном соотношении на практике использовали в Древнем Египте и Вавилоне. Ярким свидетельством этого являются пирамиды, для построения которых использовали именно такую золотую пропорцию. Эпоха Возрождения стала новым дыханием для гармонического деления, особенно благодаря Леонардо да Винчи. Это соотношение все больше начали использовать как в точных науках, таких как геометрия, так и в искусстве. Ученные и художники стали более глубоко изучать золотое сечение и создавать книги, рассматривающие этот вопрос. Одна из самых важных исторических работ, связанных с золотой пропорцией, – это книга Луки Панчоли под названием «Божественная пропорция». 

Правило золотого сечения активно применялось в построении пирамид. Например, всемирно известные гробницы Тутанхамона и Хеопса возводили с использованием такого соотношения. И золотое сечение пирамиды до сих пор остается загадкой, ведь по сей день не известно, случайно или же специально выбирались такие размеры для их оснований и высот. 

Правило золотого сечения четко видно в фасаде Парфенона – одного из самых красивых сооружений в архитектуре Древней Греции. То же касается здания собора Парижской Богоматери (Нотр-Дам де Пари), то здесь не только фасады, но и другие части конструкции возводили, опираясь на эту невероятную пропорцию. Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве – во всем, с чем может соприкоснуться человек.

Почему Фидий (греческий скульптор) и другие мастера древней Греции и Египта, часто использовали этот коэффициент при создании многих своих произведений искусства? Все потому, что было обнаружено, что при таком коэффициенте человеку наиболее приятно смотреть на предмет дизайна, который образует так называемый Золотой прямоугольник. Если короткая сторона прямоугольника равна 1, то его длинная сторона будет равна 1.618.

Здание ООН – это Золотой прямоугольник. Многие вещи, которыми мы пользуемся, в своей основе имеют приблизительный Золотой прямоугольник: кредитные карточки, игральные карты, открытки, блокноты, карточки каталога 3 х 5 и 5 х 8 и т.д.

Когда мы понимаем, что информация, необходимая для образования спиралей и чисел в живых организмах, хранится в ДНК, то должно ли нас удивлять, что ширина молекулы ДНК составляет 21 ангстрем (1А =10^-10 м), а длина одного полного поворота её спирали равна 34 ангстремам (причем оба числа относятся к последовательности чисел Фибоначчи)? Молекула ДНК представляет собой одну длинную цепь золотых сечений. Их можно обнаружить как в живой, так и в неживой природе. Их симметрия, красота и математическая точность присутствуют в каждой сфере природы, но любое творение лишено полного совершенства (возможно, из-за греха Адама).

Вы задумывались, можно ли определить меру красоте? Оказывается, с математической точки зрения возможно. Простая арифметика даёт понятие об абсолютной гармонии, которая и отображается в безупречной красоте, благодаря принципу Золотого сечения. Архитектурные сооружения древнего Египта и Вавилона первыми начали соответствовать данному принципу. Но сформулировал принцип первым Пифагор. По ряду Фибоначчи устроена шишка, ракушка, ананас, подсолнух, ураган, паутина, молекула ДНК, яйцо, стрекоза, Красота природных форм рождается во взаимодействии двух физических сил — тяготения и инерции. «Золотая пропорция» символ этого взаимодействия, поскольку диктуемое ею отношение большей части целого к самому целому выражает основные моменты живого роста: стремительный взлет легкого юного побега до зрелости и замедленный рост «по инерции» до момента цветения, когда достигшее полной силы растение готовится дать жизнь новому побегу. «Золотое сечение» — один из этих основополагающих принципов природы.

Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Они используют мерки с тела человека, сотворенного также по принципу золотой сечения. Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными. Пример золотого сечения в строении тела человека: если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618. Кто любит чудеса — сотворите волшебное действо: умножьте свой рост на магическое число 0,618 и вы выйдете на пуп! Если получится — то вы идеальный человек по Леонардо да Винчи. Таким образом, человеческие представления о красивом формируются явно под влиянием того, какие воплощения порядка и гармонии человек видит в живой природе.

В Москве в 2017 году мэром города Сергеем Собяниным был запущен проект реновации жилого комплекса столицы. Казалось бы, что подобная мера должна быть встречена с воодушевлением среди жителей города. Ведь взамен квартир в старых пятиэтажках, которые подлежат сносу, горожанам предлагают переселиться в новые, комфортные дома. Однако подобная инициатива со стороны руководства столицей вызвала негативную реакцию и люди начали выходить на митинги против сноса старых сооружений. Инженер-физик Алексей Золотарев, предполагает, что разгадка заключается в том, что хрущёвки Москвы строились именно по золотым пропорциям. Скорее всего, предполагает ученый, люди это чувствуют, жить в пятиэтажках очень комфортно, люди меньше болеют и поэтому не хотят переезжать куда-либо. Физик утверждает, что существует особые «космические» пропорции построения всех жилых систем, который имеет цифровое выражение — 1,618. Эта цифра имеет сакральный, мистический смысл. Во время правления Хрущева по всей стране развернулось строительство малогабаритных пятиэтажек. В них также можно усмотреть золотое сечение, соотношение высоты, длины, ширины 1, 618, однако приравнивать эти постройки к произведениям искусства достаточно проблематично.

Валериан Чупин

Источник информации: Чайковские.Новости

Комментарии (4)

Спокуха, клава…

Да чтоб вы знали.
Хотя бы из этого источника — лучше поздно, чем никогда.
Чернуха уже душу режет.
А «Эта информация», 23 июля 2018 19:52 · Я, душу греет, что не всё ещё потеряно нашей цивилизацией. Вроде эволюция, как нас уверяли , — это движение вперёд и вверх по спирали? И, если в 6 веке д. н.э. об этом думали и смогли найти положительный момент в окружающем нас мире, то нам то уж предстоят великие открытия.
Правда, всё ещё дверь никто не может отыскать, которую стоит распахнуть, чтобы совершить рывок вперёд и вверх, всё не те открывают и не те двери.

Эта информация как связана с чайковскими новостями? Пи-пи-пи…

Традиции: Рождественская кухня

Рождество Христово уже завтра, сегодня – сочельник. Давайте вместе с порталом Культура.рф вспомним (а кто-то и узнает), какие традиционные блюда готовили в России к этим праздникам.

Чт 06 января 2022, 09:45

Комментариев: 0

Чайковец ответит за «интимные переписки» со школьницами

54-летний житель Чайковского округа отправлял несовершеннолетним собеседницам в одной из социальных сетей различные сообщения интимного характера. За это и поплатился – суд приговорил его к реальному сроку.

Пт 14 января 2022, 11:18

Комментариев: 0

В каникулы – в виртуальный зал!

Чайковский историко-художественный музей  подготовил в новогодние каникулы для чайковцев большую концертную программу. Концерты для детей и взрослых пройдут в виртуальном концертном зале музея.

Пн 03 января 2022, 10:55

Комментариев: 0

ЛЕНТА НОВОСТЕЙ

Николай Киселев вернулся в «Чайковский Водоканал» Редакция  это пропустила, но наверстывает упущенное. Николай Киселев, работавший замглавы администрации Чайковского городского округа по инфраструктуре, ушел с занимаемой должности и вновь вернулся на прежнее место работы — в «Чайковский Водоканал». Чт 27 января 2022, 11:37 Комментариев: 5
Кто ушел на карантин? В Чайковском на дистанционное обучение в связи с ростом заболеваемости ОРВИ и коронавирусом, по имеющейся в  информации, отправлены восемь классов разных школ округа. Пт 28 января 2022, 11:17 Комментариев: 0	Долг за капремонт в наследство Новый владелец квартиры обязан уплатить взносы на капремонт за предыдущего собственника, сообщает Минфин РФ. Пн 07 августа 2017, 12:57 Комментариев: 6

Золотое сечение – это… Золотое сечение пирамиды. Формула золотого сечения

Геометрия – точная и достаточно сложная наука, которая при всем этом является своеобразным искусством. Линии, плоскости, пропорции – все это помогает создавать много действительно прекрасных вещей. И как ни странно, в основе этого лежит именно геометрия в самых разных ее формах. В этой статье мы рассмотрим одну очень необычную вещь, которая непосредственно связанна с этим. Золотое сечение – это именно тот геометрических подход, о котором пойдет речь.

Форма предмета и ее восприятие

Люди чаще всего ориентируются на форму предмета для того, чтобы распознавать его среди миллионов других. Именно по форме мы определяем, что за вещь лежит перед нами или стоит вдали. Мы в первую очередь узнаем людей по форме тела и лица. Поэтому с уверенностью можем утверждать, что сама форма, ее размеры и вид – одна из самых важных вещей в восприятии человека.

Для людей форма чего бы то ни было представляет интерес по двум главным причинам: либо это диктуется жизненной необходимостью, либо же вызывается эстетическим наслаждением от красоты. Самое лучшее зрительное восприятие и ощущение гармонии и красоты чаще всего приходит, когда человек наблюдает форму, в построении которой использовались симметрия и особое соотношение, которое и называется золотым сечением.

Понятие золотого сечения

Итак, золотое сечение – это золотая пропорция, которая также является гармоническим делением. Для того чтобы объяснить это более понятно, рассмотрим некоторые особенности формы. А именно: форма является чем-то целым, ну а целое, в свою очередь, всегда состоит из некоторых частей. Эти части, вероятнее всего, обладают разными характеристиками, по крайней мере разными размерами. Ну а такие размеры всегда находятся в определенном соотношении как между собой, так и по отношению к целому.

Значит, другими словами, мы можем утверждать, что золотое сечение – это соотношение двух величин, которое имеет свою формулу. Использование такого соотношения при создании формы помогает сделать ее максимально красивой и гармоничной для человеческого глаза.

Из древней истории золотого сечения

Соотношение золотого сечения часто используют в самых разных сферах жизни прямо сегодня. Но история этого понятия уходит еще в древние времена, когда только зарождались такие науки, как математика и философия. Как научное понятие золотое сечение вошло в обиход во времена Пифагора, а именно в VI веке до нашей эры. Но еще до того знания о подобном соотношении на практике использовали в Древнем Египте и Вавилоне. Ярким свидетельством этого являются пирамиды, для построения которых использовали именно такую золотую пропорцию.

Новый период

Эпоха Возрождения стала новым дыханием для гармонического деления, особенно благодаря Леонардо да Винчи. Это соотношение все больше начали использовать как в точных науках, таких как геометрия, так и в искусстве. Ученные и художники стали более глубоко изучать золотое сечение и создавать книги, рассматривающие этот вопрос.

Одна из самых важных исторических работ, связанных с золотой пропорцией, – это книга Луки Панчоли под названием «Божественная пропорция». Историки подозревают, что иллюстрации этой книги были выполнены самим Леонардо до Винчи.

Математическое выражение золотой пропорции

Математика дает очень четкое определение пропорции, которое говорит о том, что она является равенством двух соотношений. Математически это можно выразить таким равенством: а:b=с:d, где а, b, с, d – это некоторые определенные значения.

Если рассматривать пропорцию отрезка, разделенного на две части, то можем встретить всего несколько ситуаций:

• Отрезок разделен на две абсолютно ровные части, а значит, АВ:АС= АВ:ВС, если АВ – это точна начала и конца отрезка, а С – точка, которая и разделяет отрезок на две равные части.
• Отрезок разделен на две неравные части, которые могут находиться в самом разном соотношении между собой, а значит, здесь они абсолютно непропорциональны.
• Отрезок разделен так, что АВ:АС= АС:ВС.

Что же касается золотого сечения, то это такое пропорциональное деление отрезка на неравные между собой части, когда весь отрезок относится к большей части, как и сама большая часть относится к меньшей. Существует и другая формулировка: меньший отрезок так относится к большему, как и больший ко всему отрезку. В математическом соотношении это выглядит следующим образом: а:b = b:с или с:b = b:а. Именно такой вид имеет формула золотого сечения.

Золотая пропорция в природе

Золотое сечение, примеры которого мы сейчас рассмотрим, относится к невероятным явлениям в природе. Это очень красивые примеры того, что математика – это не просто цифры и формулы, а наука, которая имеет более чем реальное отражение в природе и нашей жизни вообще.

Для живых организмов одна из главных жизненных задач – это рост. Такое стремление занять свое место в пространстве, по сути, осуществляется в нескольких формах – рост вверх, практически горизонтальное расстилание по земле или закручивание по спирали на некой опоре. И как бы ни было это невероятно, много растений растут в соответствии с золотой пропорцией.

Еще один почти невероятный факт – это соотношения в теле ящериц. Их тело выглядит достаточно приятно для человеческого глаза, и это возможно благодаря тому же золотому соотношению. Если быть точнее, то длина их хвоста относится к длине всего тела как 62 : 38.

Интересные факты о правилах золотого сечения

Золотое сечение – это поистине невероятное понятие, а значит, на протяжении всей истории мы можем встретить много действительно интересных фактов о такой пропорции.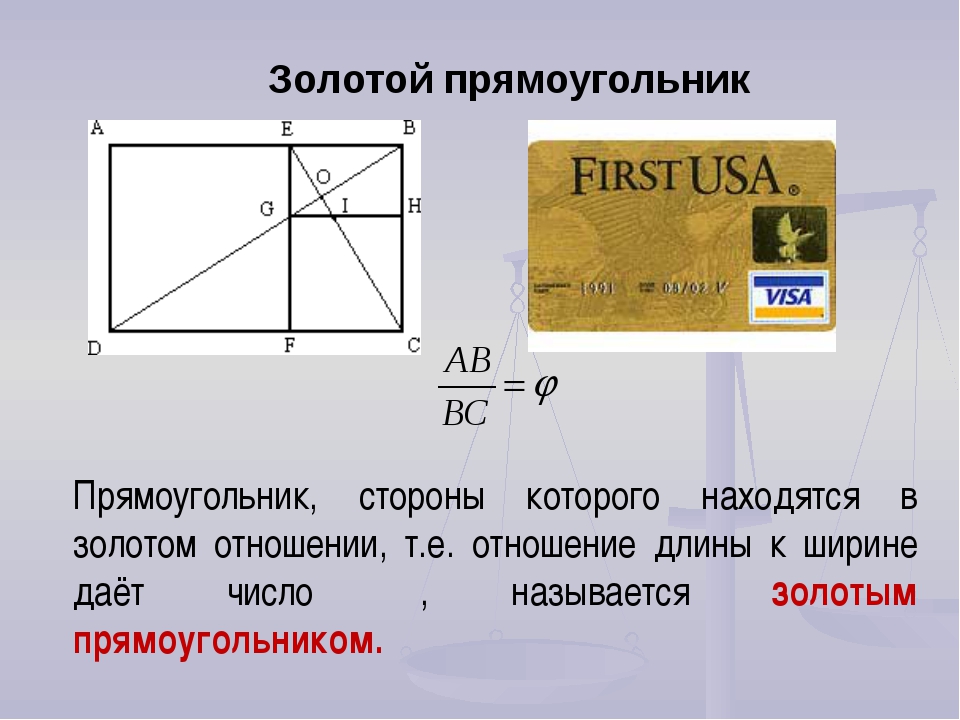 Представляем вам некоторые из них:

• Правило золотого сечения активно применялось в построении пирамид. Например, всемирно известные гробницы Тутанхамона и Хеопса возводили с использованием такого соотношения. И золотое сечение пирамиды до сих пор остается загадкой, ведь по сей день не известно, случайно или же специально выбирались такие размеры для их оснований и высот.
• Правило золотого сечения четко видно в фасаде Парфенона – одного из самых красивых сооружений в архитектуре Древней Греции.
• То же касается здания собора Парижской Богоматери (Нотр-Дам де Пари), то здесь не только фасады, но и другие части конструкции возводили, опираясь на эту невероятную пропорцию.
• В русской архитектуре можно встретить невероятно много примеров зданий, полностью соответствующих золотому сечению.
• Гармоничное деление присуще также и человеческому телу, а значит, и скульптуре, в частности, статуям людей. Например Аполлон Бельведерский – статуя, где у человека рост делится пупочной линией в золотом сечении.
• Живопись – отдельная история, особенно если учесть роль Леонарда да Винчи в истории золотого соотношения. Его известная Джоконда, конечно же, подлежит этому закону.

Золотое сечение в человеческом теле

В этом разделе нужно упомянуть очень значимую персону, а именно – С. Цейзинга. Это немецкий исследователь, который провел огромнейшую работу в сфере изучения золотой пропорции. Он опубликовал труд под названием «Эстетические исследования». В своей работе он представил золотое сечение как абсолютное понятие, которое является универсальным для всех явлений как в природе, так и в искусстве. Здесь можно вспомнить золотое сечение пирамиды наряду с гармоничной пропорцией человеческого тела и так далее.

Именно Цейзинг смог доказать, что золотое сечение, по сути, есть средним статистическим законом для человеческого тела. Это было показано на практике, ведь во время своей работы ему пришлось измерять очень много человеческих тел. Историки считают, что в этом опыте принимали участие более двух тысяч людей. По исследования Цейзинга, главный показатель золотого соотношения – это деление тела точкой пупка. Так, мужское тело со средним соотношением 13:8 немного ближе к золотому сечению, чем женское, где число золотого сечения составляет 8:5. Также золотую пропорцию можно наблюдать в других частях тела, таких как, например, рука.

О построении золотого сечения

На самом деле, построение золотого сечения – дело нехитрое. Как мы видим, еще древние люди справлялись с этим довольно легко. Что уже говорить о современных знаниях и технологиях человечества. В этой статье мы не будем показывать, как подобное можно сделать просто на листке бумаги и с карандашом в руках, но с уверенностью заявим, что это, на самом деле, возможно. Более того, сделать это можно далеко не одним способом.

Так как это достаточно несложная геометрия, золотое сечение является довольно простым для построения даже в школе. Поэтому информацию об этом можно легко найти в специализированных книгах. Изучая золотое сечение 6 класс полностью способен понять принципы его построения, а значит, даже дети достаточно умны для того, чтобы осилить подобную задачу.

Золотая пропорция в математике

Первое знакомство с золотым сечением на практике начинается с простого деления отрезка прямой все в тех же пропорциях. Чаще всего это реализуется с помощью линейки, циркуля и, конечно же, карандаша.

Отрезки золотой пропорции выражают как бесконечную иррациональную дробь AE = 0,618…, если АВ принимается за единицу, ВЕ = 0,382… Для того чтобы сделать эти вычисления более практическими, очень часто используют не точные, а приближенные значения, а именно – 0,62 и 0,38. Если же отрезок АВ принимать за 100 частей, то большая его часть будет равна 62, ну а меньшая – 38 частям соответственно.

Главное свойство золотого соотношения можно выразить уравнением: х²-х-1=0. При решении мы получаем следующие корни: х_1,2=. Хотя математика и есть точной и строгой наукой, как и ее раздел – геометрия, но именно такие свойства, как закономерности золотого сечения, наводят таинственность на эту тему.

Гармония в искусстве через золотое сечение

Для того чтобы подвести итоги, рассмотрим коротко то, о чем уже говорили.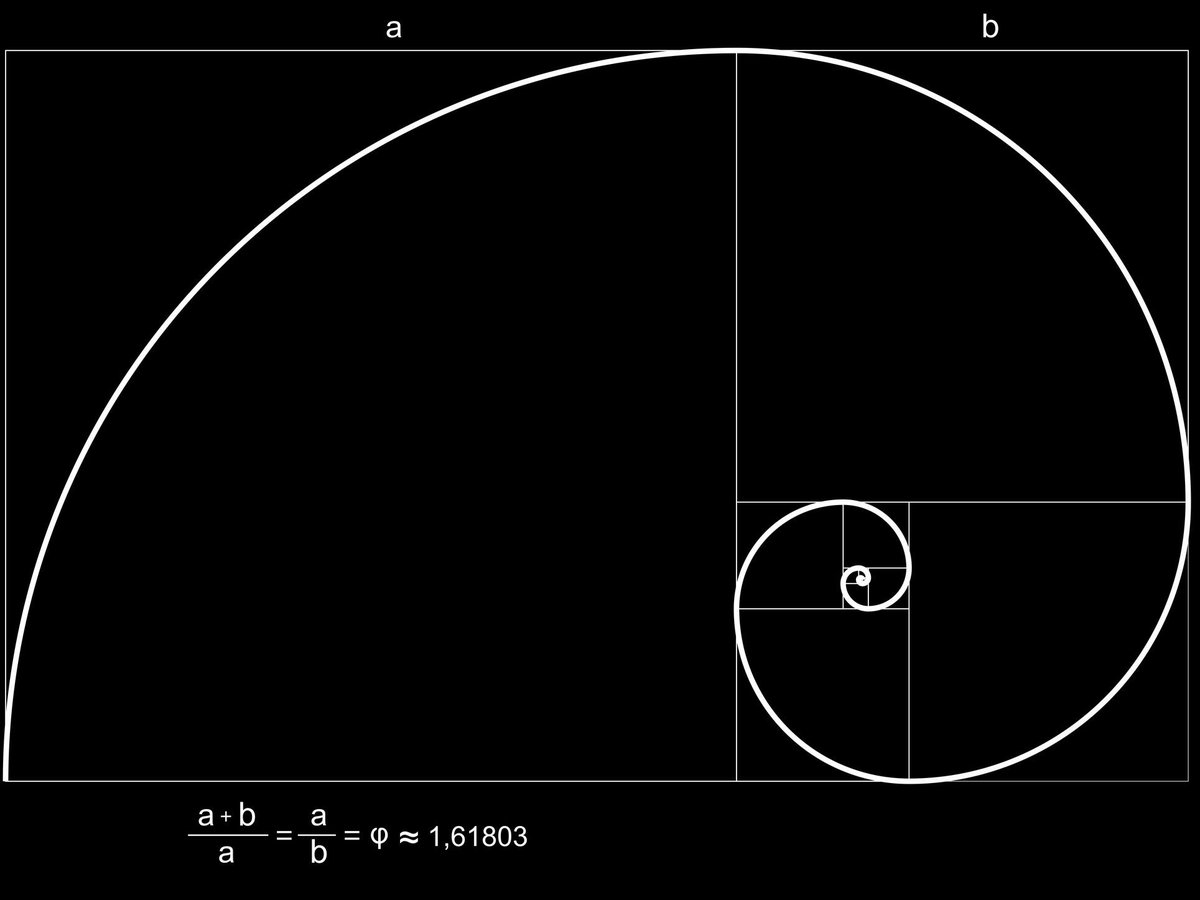

В основном под правило золотого соотношения подпадает много образцов искусства, где соблюдается соотношение близкое к 3/8 и 5/8. Это и есть грубая формула золотого сечения. В статье уже очень много упоминалось о примерах использования сечения, но мы еще раз посмотрим на него через призму древнего и современного искусства. Итак, самые яркие примеры из древних времен:

• Золотое сечение пирамиды Хеопса и Тутанхамона выражается буквально во всем: храмы, барельефы, предметы быта и, конечно же, украшения самых гробниц.
• Храм фараона Сети І в Абидосе славится рельефами с разными изображениями, и все это соответствует все тому же закону.

Что касается уже наверняка сознательного использования пропорции, то, начиная с времен Леонардо да Винчи, она вошла в использование практически во всех отраслях жизни – от науки и до искусства. Даже биология и медицина доказали, что золотое соотношение работает даже в живых системах и организмах.

Золотое сечение

Золотое сечение

Золотое сечение

На протяжении всей истории отношение длины прямоугольников к ширине 1,61803 39887 49894 84820 считалось наиболее приятным для глаз. Греки назвали это соотношение золотым сечением. В мире математики числовое значение называется «фи» в честь греческого скульптора Фидия. Пространство между колоннами образуют золотые прямоугольники. В этой структуре, которая находится в Афинах, Греция, есть золотые прямоугольники.

Он создал множество скульптур, в том числе скульптурные полосы, которые проходят над колоннами Парфенона. Вы можете посетить слайд-шоу Парфенона, изображенного выше.

Фидий широко использовал золотое сечение в своих скульптурных произведениях. Внешние размеры Парфенона в Афинах, построенного примерно в 440 г. до н.э., образуют идеальный золотой прямоугольник. Сколько примеров золотых прямоугольников вы можете найти на плане этажа Парфенона ниже? Вы можете распечатать схему и измерить расстояния с помощью линейки.

Ниже приведены другие примеры искусства и архитектуры, в которых использовался золотой прямоугольник. Считается, что этому первому образцу Великой пирамиды в Гизе 4600 лет, то есть задолго до появления греков. Его размеры также основаны на золотом сечении. Сайт о пирамиде дает очень подробную информацию об этом.

Эту пропорцию использовали многие художники, жившие после Фидия.Леонардо да Винчи называл это «божественной пропорцией» и изображал на многих своих картинах. Слева находится знаменитая «Мона Лиза». Попробуйте нарисовать прямоугольник вокруг ее лица. Соответствуют ли измерения золотой пропорции? Вы можете дополнительно изучить это, разделив прямоугольник, образованный с помощью ее глаз в качестве горизонтального разделителя. Он провел полное исследование человеческого тела и соотношения длин различных частей тела.

Табличка Золотого сечения 1, 1993 г.
Флетчер Кокс
клен птичий глаз, шпатлеванный
шпон красного дуба, бубинга, венге и клена; токарная обработка
31 х 4 см
Предоставлено Белым домом
подарок художника
Фотография Джона Бигелоу Тейлора

Выше приведен пример современного художника, который интересуется золотым сечением. Он назвал свою работу «Золотое сечение», что является просто другим названием соотношения, что означает, что она разделена на части золотой пропорции.

следущая страница

Как скомпоновать свои фотографии как художник

Если вы готовы расти как фотограф, используя технику композиции, которую сложно применять, но которую стоит освоить, пришло время начать экспериментировать с золотым сечением. Золотое сечение можно применять к вашим композициям по-разному, с целью создания естественно поразительной композиции.

Никогда не слышал о золотом сечении? Возможно, вы знаете его под одним из многочисленных псевдонимов: золотая середина, фи-сетка, спираль Фибоначчи или божественная пропорция. Называйте это как хотите, но обязательно попробуйте эту технику, чтобы улучшить свои композиции.

Что такое золотое сечение в фотографии?

Вы уже узнали, что золотое сечение — это руководство по композиции, но знаете ли вы, что в основе золотого сечения лежит математика? Но не волнуйтесь, вам не нужно будет решать какие-либо уравнения, чтобы использовать эту технику!

Золотое сечение — это отношение примерно 1. 618 к 1. Он веками использовался художниками, архитекторами и музыкантами, но его также можно найти повсюду в мире природы. Чтобы использовать золотое сечение в фотографии, вы просто применяете его к размещению объектов в своей композиции. Ниже мы поговорим подробнее о конкретных способах применения золотого сечения к вашим фотографиям.

Почему это называется золотым сечением?

Золотое сечение необычайно, потому что его можно визуализировать во всех аспектах жизни, от человеческого тела до знаменитых произведений искусства и всего, что между ними.Хотя эта математика существовала независимо от человечества задолго до письменной истории, художники начали использовать ее в качестве основы для композиций в 1500-х годах. Художники эпохи Возрождения стали называть его золотым сечением или божественной пропорцией из-за его способности достигать баланса и красоты.

Спираль Фибоначчи

Спираль Фибоначчи основана на последовательности Фибоначчи, открытой Леонардо Фибоначчи около 1200 года. Это последовательность чисел, начинающаяся с 0 и 1.Сложите два вместе, чтобы получить 1. Каждое число в последовательности является суммой двух предшествующих ему чисел. Итак, последовательность: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее.

Отношение любых двух последовательных чисел Фибоначчи очень близко к золотому сечению, которое приблизительно равно 1,618034. И если вы используете числа Фибоначчи для создания сетки с квадратами, представляющими ширину чисел Фибоначчи, вы получите спираль Фибоначчи.

Фи-сетка

Фи-сетка — еще один способ визуализации золотого сечения.Прямоугольники можно накладывать на изображение в сетке с соотношением сторон 1:1,618. Эта «фи-сетка» делит вашу сцену на трети как по горизонтали, так и по вертикали. Но в отличие от более популярного правила третей, центральные линии Фи-решетки расположены ближе друг к другу. Это перемещает более важные элементы вашей фотографии ближе к центру.

Чем золотое сечение лучше правила третей?

Правило третей в основном является упрощением золотого сечения. Его очень легко визуализировать, и поэтому начинающим фотографам проще использовать его без особых предусмотрительности.Золотое сечение, напротив, немного более технично. В этом сценарии вы имеете дело с более точными соотношениями, поэтому выровнять композицию не так просто. Использование золотого сечения в фотографии полезно для того, чтобы направлять взгляд зрителя вокруг вашего изображения таким образом, чтобы оно было естественным и сбалансированным.

То, что вы решите использовать для данной композиции, во многом будет зависеть от сцены, которую вы пытаетесь запечатлеть. Правило третей отлично подходит для минималистичных фотографий, где у вас есть один объект.Золотое сечение полезно для позиционирования нескольких объектов в композиции или для акцентирования движения.

Как использовать золотое сечение в фотографии на iPhone

Теперь пришло время использовать золотое сечение для создания собственных композиций. Вот несколько идей и советов по компоновке фотографий с использованием золотого сечения на iPhone. Это требует практики, но со временем вы начнете видеть линии сетки мысленным взором, когда будете кадрировать кадр.

Как сочинять золотое сечение

Золотое сечение можно применять ко многим различным сценам, используя фи-сетку или спираль Фибоначчи.Как узнать, какой из них использовать?

Ищите направляющие линии или естественные кривые в сцене. Сильные направляющие линии лучше всего размещать с помощью фи-сетки, а изогнутые, органичные линии лучше работают со спиралью Фибоначчи. Правило третей — это упрощенная версия золотого сечения, поэтому, если у вас возникли проблемы с представлением наложения сетки при кадрировании кадра, не бойтесь использовать правило третей.

Если на камере iPhone не активировано наложение сетки по правилу третей, вы можете включить его в настройках.Просто перейдите в «Настройки»> «Камера»> «Сетка» и включите его. Попытка представить спираль Фибоначчи, выровненную по вашей фотографии, поначалу трудна, но со временем становится легче.

Если вы используете спираль Фибоначчи, поместите объект дальше, чем правило пересечения третей. Если вы выбрали фи-сетку, поместите объект ближе к центру изображения по сравнению с правилом пересечения третей.

Попробуйте снимать с разных точек зрения, чтобы подчеркнуть золотое сечение.Возможно, вам придется присесть или стрелять сверху. Если вы не уверены, какая композиция работает лучше всего, сделайте много изображений, а затем используйте программу редактирования, чтобы обрезать их позже.

Как использовать обрезку золотого сечения в Lightroom

Используете ли вы приложение Lightroom на своем iPhone? При использовании камеры Lightroom вы можете использовать различные наложения сетки, включая правило третей и фи-сетку. Находясь в режиме просмотра камеры, коснитесь трех точек в правом верхнем углу, чтобы включить эту опцию.

Чтобы использовать обрезку золотого сечения во время постобработки, вам придется использовать настольную версию Lightroom. Кроме того, мы надеемся, что они в конечном итоге добавят эту функцию в Lightroom Mobile. А пока, вот как обрезать фотографию, используя золотое сечение с Lightroom на вашем компьютере:

1. Откройте Lightroom на своем компьютере и переключитесь в режим разработчика.
2. Нажмите кнопку обрезки на левой панели инструментов, чтобы открыть инструмент обрезки.
3. Используйте клавишу «O» для переключения между различными наложениями кадрирования.Вы увидите сетку правила третей, фи-сетку и спираль Фибоначчи, а также некоторые другие.
4. Используйте любое выбранное вами наложение сетки, чтобы указать, что нужно обрезать.
5. Когда вы будете довольны результатами, экспортируйте фотографию в свои файлы или перетащите ее обратно на iPhone с помощью Airdrop.

Использование золотого сечения в фотографии поможет вам усовершенствовать технику композиции и сделать вас лучшим фотографом. Хотя этому сложно научиться, как только вы начнете использовать золотое сечение для составления своих изображений, вы будете на крючке!

История золотого сечения в искусстве

Леонардо да Винчи, Тайная вечеря (1494-99). Изображение: Википедия.

Мир искусства веками ощущал на себе влияние золотого сечения. Этот математический принцип, также известный как «Золотое сечение» или «Божественная пропорция», является выражением отношения двух сумм, при котором их отношение равно большей из двух величин.

В эпоху Возрождения художник и рисовальщик Леонардо да Винчи использовал пропорции, установленные золотым сечением, для создания своих шедевров. Сандро Боттичелли, Микеланджело, Жорж Сёра и другие использовали эту технику в своих работах.

Гэри Мейснер в блоге Golden Number нанес на карту геометрические основы избранных картин с помощью программного обеспечения, которое можно увидеть ниже:

Сандро Боттичелли, Рождение Венеры (1483-85). Изображение: Википедия.

Изображение: Гэри Мейснер, thegoldennumber.net.

Микеланджело, Сотворение Адама (1508-12). Изображение: Википедия.

Изображение: Гэри Мейснер, thegoldennumber.net.

В 19 веке художники Жорж Сёра и Эдвард Бёрн-Джонс организовали свои композиции с помощью геометрии.

Постимпрессионистская картина Сёра Купальщицы в Асинере (1884 г.) можно разделить на три прямоугольника, например, разграничивающие передний, средний и задний план. А арка лестницы Бёрн-Джонса является фокусом Золотая лестница (1876-1880), вокруг которой расположены остальные элементы.

Жорж Сёра, Купальщицы в Аньере (1884 г.). Изображение: Википедия.

Эдвард Бёрн-Джонс, Золотая лестница (1876-1880).Изображение: Википедия.

Хотя модернизм отходит от строгого использования золотого сечения, геометрия широко используется во многих движениях того времени. Чистые линии и формы в основных цветах наполняют картины и графику, о чем свидетельствуют конструктивизм, супрематизм и де Стиль.

Казимир Малевич, Супрематическая композиция (1916). Изображение: Википедия.

Пит Мондриан, Композиция с желтым, синим и красным (1937–42)
Предоставлено: Коллекция Тейт

Переходя к трем измерениям, геометрия играла важную роль в двадцатом веке. Скульпторы Константин Бранкузи, Барбара Хепворт и Генри Мур работают абстрактно, но с простыми линиями и формами.

Константин Бранкузи, Птица в космосе (1927). Изображение: LACMA/© Constantin Brancusi Estate/Artist Rights Society (ARS), Нью-Йорк/ADAGP, Париж.

Барбара Хепуорт, Волна (1943-44). Изображение: © Bowness, Hepworth Estate/National Galleries Scotland.

Генри Мур, Three Points (1939-40). Изображение: © Фонд Генри Мура/Тейт.

Бразильский неоконкретизм в значительной степени опирается на простоту геометрии: работы Лигии Кларк и Хелио Оититики представляют собой массу углов и блоков цвета.

Lygia Clark, Planos em superfície modulada no. 2, версия 01 ( Плоскости на модулированной поверхности № 2, версия 1 ) (около 1957 г.). Изображение: WNYC/Eurides Лула Родригес Кардосо.

Helio Oiticica, Metaesquema (1958). Изображение: ВикиАрт.

И последнее, но не менее важное: художник Сальвадор Дали воскрешает «божественные пропорции» да Винчи в своем сюрреалистическом посвящении Таинство Тайной вечери (1955), возвращая нас к тому, с чего мы начали.

Сальвадор Дали, Таинство Тайной Вечери (1955).Изображение: ВикиАрт.

Следите за новостями Artnet на Facebook:

Хотите быть впереди мира искусства? Подпишитесь на нашу рассылку, чтобы получать последние новости, поучительные интервью и острые критические выводы, которые продвигают обсуждение вперед.

Золотое сечение — определение, формула, примеры

Золотое сечение, которое часто называют золотым сечением, божественной пропорцией или золотым сечением, является особым атрибутом, обозначаемым символом ϕ, и примерно равен 1.618. Изучение многих особых формаций может быть выполнено с использованием специальных последовательностей, таких как последовательность Фибоначчи, и атрибутов, таких как золотое сечение.

Это соотношение встречается в различных искусствах, архитектуре и дизайне. Многие замечательные архитектурные сооружения, такие как Великая пирамида Египта, Парфенон, были частично или полностью спроектированы так, чтобы отражать в своей структуре золотое сечение. Великие художники, такие как Леонардо да Винчи, использовали золотое сечение в нескольких своих шедеврах, и в 1500-х годах оно было известно как «Божественная пропорция».Давайте узнаем больше о золотом сечении в этом уроке.

Что такое золотое сечение?

Золотое сечение, также называемое золотым сечением, божественной пропорцией или золотым сечением, существует между двумя величинами, если их отношение равно отношению их суммы к большей величине между ними. Со ссылкой на это определение, если мы разделим линию на две части, части будут в золотом сечении, если:

Отношение длины более длинной части, скажем «a», к длине более короткой части, скажем, «b» равно отношению их суммы «(a + b)» к большей длине.

Обратитесь к следующей диаграмме для лучшего понимания вышеуказанной концепции:

Обозначается греческой буквой ϕ, произносимой как «фи». Приблизительное значение ϕ равно 1,61803398875 . Оно находит применение в геометрии, искусстве, архитектуре и других областях. Таким образом, следующее уравнение устанавливает соотношение для расчета золотого сечения: два.

Определение золотого сечения

Когда линия делится на две части, длинная часть, которая делится на короткую часть, равна всей длине, деленной на длинную часть, определяется как золотое сечение. Ниже приведены примеры золотого сечения в архитектуре и искусстве.

Есть много применений золотого сечения в области архитектуры. Многие архитектурные чудеса, такие как Великая мечеть Кайруана, были построены с учетом золотого сечения в их структуре.Такие художники, как Леонардо да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах.

Формула золотого сечения

Формулу золотого сечения можно использовать для расчета значения золотого сечения. Уравнение золотого сечения выведено, чтобы найти общую формулу для расчета золотого сечения.

Уравнение золотого сечения

Из определения золотого сечения,

а/б = (а + б)/а = ϕ

Из этого уравнения получаем два уравнения:

а/б = ϕ → (1)

(а + b)/а = ϕ → (2)

Из уравнения (1),

а/б = ϕ

⇒ а = б

Подставьте это в уравнение (2),

(bϕ + b)/bϕ = ϕ

б( ф + 1)/бф = ф

(ϕ + 1)/ϕ = ϕ

1 + 1/ϕ = ϕ

1 + 1/ϕ = ϕ

Как рассчитать золотое сечение?

Значение золотого сечения можно рассчитать разными методами. Начнем с основного.

Метод проб и ошибок

Мы угадаем произвольное значение константы, а затем выполним следующие шаги, чтобы вычислить более близкое значение на каждой итерации.

• Вычислите мультипликативную обратную величину угаданного вами значения, т. е. 1/значение. Это значение будет нашим первым термином.
• Вычислите другой член, добавив 1 к мультипликативному, обратному этому значению.
• Оба условия, полученные на предыдущих шагах, должны быть равны.Если нет, мы будем повторять процесс, пока не получим примерно равное значение для обоих членов.
• Для второй итерации мы будем использовать предполагаемое значение, равное члену 2, полученному на шаге 2, и так далее.

Например,

Поскольку ϕ = 1 + 1/ϕ, оно должно быть больше 1. Начнем со значения 1,5 в качестве нашего первого предположения.

• Член 1 = мультипликативный, обратный 1,5 = 1/1,5 = 0,6666… ​​
• Член 2 = Мультипликативное значение, обратное 1. 5 + 1 = 0,6666.. + 1 = 1,6666… ​​

Поскольку оба термина не равны, мы повторим этот процесс снова, используя предполагаемое значение, равное term 2 .

В следующей таблице приведены данные расчетов для всех принятых значений, пока мы не получим желаемые равные условия:

Итерация	Предполагаемое значение	Термин 1 (1/значение)	Термин 2 (1/значение + 1)
1.	1,5	11,511,5 = 0,6666..	0,6666.. + 1 = 1,6666..
2.	1.6666..	11,666..11,666.. = 0,6	0,6 + 1 = 1,6
3.	1,6	11,611,6 = 0,625	0,625 + 1 = 1,625
4.	1,625	11.62511.625 = 0,61538..	0,61538.. + 1 = 1,61538..
5.	1.61538..	..	.. и так далее

Чем больше итераций вы выполните, тем ближе приблизительное значение будет к точному. Другие методы обеспечивают более эффективный способ вычисления точного значения.

Уравнение золотого сечения

Другой метод расчета значения золотого сечения заключается в решении уравнения золотого сечения.2 — 4ас}}{2а}\)

Подставляя значения a = 1, b = -1 и c = -1, получаем,

ϕ = \(\frac{1 \pm \sqrt{( 1 + 4 )}}{2}\)

Решение можно упростить до положительного значения, что даст:

ϕ = 1/2 + √5/2

Обратите внимание, что мы не рассматриваем отрицательное значение, так как \(\phi\) — это отношение длин, и оно не может быть отрицательным.

Следовательно, ϕ = 1/2 + √5/2

Что такое золотой прямоугольник?

В геометрии золотой прямоугольник определяется как прямоугольник, длины сторон которого находятся в золотом сечении. Золотой прямоугольник демонстрирует совершенно особую форму самоподобия. Все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.

Построение золотого прямоугольника

Мы можем построить золотой прямоугольник, используя следующие шаги:

• Шаг 1: Сначала нарисуем квадрат из 1 единицы. На одной из его сторон нарисуйте точку посередине. Теперь мы проведем линию от этой точки до угла другой стороны.

• Шаг 2: Используя эту линию в качестве радиуса и точку, проведенную посередине, в качестве центра, нарисуйте дугу, идущую вдоль стороны квадрата.Длину этой дуги можно рассчитать по теореме Пифагора: √(1/2) ² + (1) ² = √5/2 единиц.
• Шаг 3: Используйте пересечение этой дуги и стороны квадрата, чтобы нарисовать прямоугольник, как показано на рисунке ниже:

Это золотой прямоугольник, потому что его размеры находятся в золотом сечении. т. е. ϕ = (√5/2 + 1/2)/1 = 1,61803

Что такое последовательность Фибоначчи?

Последовательность Фибоначчи — это особый ряд чисел, в котором каждый член (начиная с третьего члена) является суммой двух предыдущих его членов.Для нахождения последовательности Фибоначчи можно использовать следующие шаги:

• Начнем с того, что возьмем 0 и 1 в качестве первых двух членов.
• Таким образом, третий член 1 вычисляется путем сложения 0 и 1.
• Точно так же следующий член = 1 + 2 = 3 и так далее.

Последовательность Фибоначчи задается как 0, 1, 1, 2, 3, 5, 8, 13, 21,… и так далее. Последовательность Фибоначчи и золотое сечение имеют между собой особую связь. Когда мы начинаем вычислять отношения двух последовательных членов ряда Фибоначчи, значение каждого последующего отношения становится ближе к точному значению ϕ.

Например,

В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ. В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ.

Срок 1	Срок 2	Соотношение = Клемма 2 / Клемма 1
2	3	1,5
3	5	1.6666..
5	8	1,6
8	13	1,625
13	21	1,61538

☛Связанные темы 

Ниже приведен список тем, тесно связанных с золотым сечением. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.

Часто задаваемые вопросы о золотом сечении

Что такое золотое сечение простыми словами?

Золотое сечение — это математическое отношение, которое существует между двумя величинами, если их отношение равно отношению их суммы к большей величине из двух. Другими словами, когда линия разделена на две части и более длинная часть «а», разделенная на меньшую часть «b», равна сумме (а + b), деленной на «а», это означает, что линия отражающее золотое сечение, равное 1.618.

Что вы подразумеваете под золотым прямоугольником?

В геометрии золотой прямоугольник определяется как прямоугольник, длины сторон которого находятся в золотом сечении. Золотой прямоугольник демонстрирует совершенно особую форму самоподобия. Все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.

Почему золотое сечение красиво?

Золотое сечение — это соотношение, которое при использовании в различных областях для проектирования объектов делает объекты эстетически привлекательными и приятными на вид.Поэтому золотое сечение называют красивым атрибутом. Его можно заметить в различных узорах природы, например, в спиралевидном расположении цветов и листьев. Есть много применений золотого сечения в области архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре, например, Великая пирамида Египта и Великая мечеть Кайруана.

Почему золотое сечение важно?

Золотое сечение — это математическое соотношение, которое часто встречается в природе и используется в различных областях.Он используется в нашей повседневной жизни, искусстве и архитектуре. Объекты, созданные с учетом золотого сечения в своей структуре и дизайне, более приятны и эстетичны для глаз. Это можно заметить по спиралевидному расположению цветков и листьев.

Где в реальной жизни используется золотое сечение?

Есть много применений золотого сечения в области искусства и архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре.Такие художники, как Лео да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах. Его можно использовать для изучения структуры многих объектов в нашей повседневной жизни, которые напоминают определенный узор.

Кто открыл золотое сечение?

Древнегреческие математики первыми упомянули о золотом сечении в своих работах. Математики V века до нашей эры Гиппакус и Евклид внесли большой вклад в свои исследования по этому вопросу.

Что такое формула золотого сечения?

Формулу золотого сечения можно использовать для расчета значения золотого сечения.Формула для расчета золотого сечения дается как,

1 + 1/ϕ = ϕ

, где ϕ обозначает золотое сечение.

Золотое сечение

: что это такое и почему вы должны использовать его в дизайне | by Pratik Hegde

Золотое сечение находит широкое применение в полиграфическом дизайне, например, в плакатах, маркетинговых материалах, визитных карточках и т. д. Это обсуждение больше вращается вокруг того, как мы можем эффективно использовать золотое сечение в нашей работе в качестве дизайнеров пользовательского интерфейса . Давайте разберемся.

1.Золотые формы для использования

Наиболее часто используемые золотые формы в дизайне — это золотые прямоугольники, золотые круги, золотая спираль и золотые треугольники. Часто они используются в сочетании для создания завораживающих дизайнерских композиций. Если вы новичок, я призываю вас пройти онлайн-уроки, чтобы понять, как создавать золотые фигуры.

Золотые прямоугольники, спирали, круги, треугольники

2. Установка размеров макета с золотым сечением

Макет в веб-дизайне или графическом дизайне используется для размещения визуальных элементов на странице.Он включает в себя организацию художественной композиции для достижения конкретных коммуникативных целей. Здесь можно использовать золотое сечение для определения ширины панелей, боковых панелей или даже высоты представлений. Например, макет шириной 960 пикселей. Разделив это на 1,618, мы примерно получим 594 пикселя (593,325..), что вполне можно определить как высоту вашего представления. Два отдельных раздела также могут быть сделаны с размерами 594 пикселей и 366 пикселей (960–594), которые могут формировать макет страницы из двух разделов. Мы можем пойти дальше, разделив пространство по золотой середине, чтобы получить больше сеток.

Структурирование макета с использованием золотого сечения

Определение высоты любого представления очень важно в графическом дизайне по сравнению с веб-дизайном, поскольку контент является фактором, определяющим высоту страницы в веб-дизайне.

3. Определение интервала между содержимым с использованием золотого сечения

Много раз мы используем стандартные отступы и поля для определения отступов и интервалов между блоками содержимого независимо от размера макета. Управление этими положительными или отрицательными пространствами часто влияет на конечный результат или разрушает его.Однако можно использовать золотые прямоугольники, чтобы убедиться, что межмакетные пространства пропорциональны и рассчитаны.

«Совет: используйте квадраты большего размера, такие как блоки 8 и 13, для определения макетов. Используйте меньшие квадраты единицы 1, 2 или 3, чтобы определить отступы и интервалы содержимого»

4. Использование золотого сечения в типографике

Если вам трудно определить размеры различных текстовых иерархий в вашей композиции дизайна, вы можете используйте золотое сечение в качестве руководства, чтобы определить лучший размер для каждого из них. Допустим, основной текст имеет размер 10 пикселей. Умножив его на 1,618, вы получите 16,18. Размер текста заголовка может быть 16px. Если у вас есть заголовок размером 24 пикселя и вам интересно, какой размер лучше всего подходит для основного текста, это правильно! Разделите его на 1,618, что даст 14,83, которое вы можете округлить до 15 или 14 пикселей. Ну вот! Использование золотого сечения упрощает принятие решения при определении размеров текстовой иерархии.

Использование золотого сечения в типографике

5. Дизайн значков/логотипов с использованием золотого сечения

Золотые формы, такие как треугольники, квадраты, круги и спирали, широко используются при разработке значков или логотипов.Правильное использование золотых форм может обеспечить правильный баланс и превратить хороший дизайн в великолепный. Мы не будем вдаваться в подробности этого раздела, так как это отдельный большой раздел. Однако ниже приведены несколько примеров использования золотого сечения в значках и логотипах.

Изображения взяты из Google для иллюстраций

Золотое сечение и дизайн пользовательского интерфейса

Пропорциональные системы основаны на соотношениях и веками использовались в архитектуре и искусстве.Золотое сечение было впервые упомянуто еще около 500 г. до н.э. Фидием, Платоном, а затем Евклидом. Справедливо предположить, что это соотношение было открыто несколько раз на протяжении всей истории — отсюда и его многочисленные названия, включая золотую середину, золотое сечение, золотое сечение, божественную пропорцию (придуманную Леонардо да Винчи) и греческий символ φ.

Точное математическое определение выглядит следующим образом (согласно Википедии):

Золотое сечение: Две величины a и b (a>b) относятся к золотому сечению φ , если их отношение равно отношению их суммы к большей из двух величин:

Два отрезка в золотом сечении (a/b = φ)

Можно показать, что золотое сечение φ обладает особым свойством:

и равно 1. 618033… (иррациональное число). (Вы можете проверить, что 1/0,618=1,618.)

Исследование Джакомо Риццолатти и Чинции Ди Дио предполагает, что человеческий мозг запрограммирован на предпочтение человеческих тел с пропорциями золотого сечения. В ходе исследования участникам, не имевшим никакого отношения к искусству, показывали оригинальное изображение и искаженные версии статуи. Пропорции оригинальной статуи отражали золотое сечение. Исходное изображение сильно активировало наборы клеток мозга, которых не было на искаженных изображениях, что позволяет предположить, что красота является отчасти врожденным качеством.

Золотое сечение использовалось для анализа величин, встречающихся в природе, архитектуре, живописи и музыке. Часто предполагается, что при его использовании создается органичная, сбалансированная и эстетически приятная композиция, которая, как считается, приятна человеческому глазу.

Примеры зданий и произведений искусства, пропорции которых соответствуют золотому сечению, включают пирамиды в Гизе, Парфенон в Афинах и Мону Лизу да Винчи.

Мона Лиза Леонардо да Винчи: длина и ширина головы (сегменты a ₁ и b ₁ ), а также длина и ширина туловища (начиная от линии глаз вниз к рукам — сегменты a ₂ и b ₂ ) находятся в золотом сечении.

Золотой прямоугольник и спираль

 

T Золотой прямоугольник — это просто прямоугольник, стороны которого пропорциональны золотому сечению.

Стороны золотого прямоугольника находятся в золотом сечении (a/b = φ).  

Золотой прямоугольник имеет интересное свойство: если разделить его на квадрат со стороной, равной меньшему размеру прямоугольника, и еще один прямоугольник (как на изображении ниже), то окажется, что меньший прямоугольник также является золотым прямоугольником.(Это свойство непосредственно выводится из свойства золотого сечения, описанного в предыдущем разделе.)

Когда вы делите золотой прямоугольник на квадрат и меньший прямоугольник, как на изображении выше, меньший прямоугольник также является золотым прямоугольником.

Вы можете повторять этот процесс бесконечно, разделив каждый золотой прямоугольник на квадрат и еще один золотой прямоугольник. В результате получится золотая спираль — полученная путем соединения противоположных углов каждого из квадратов.

Чтобы получить золотую спираль, начните с деления золотого прямоугольника ABCD на квадрат ABEF и меньший золотой прямоугольник EFDC. Затем повторите процесс для меньшего золотого прямоугольника EFDC. Золотая спираль образуется путем соединения противоположных углов получившихся квадратов.

Золотая спираль встречается во многих природных элементах, таких как растения, и в погодных явлениях, таких как ураганы.

Примеры золотого сечения в дизайне пользовательского интерфейса

Как золотое сечение используется в дизайне интерфейсов? Рассмотрим пару типичных примеров:

Размеры текста

Различные размеры шрифта могут быть в золотом сечении.Допустим, размер основного шрифта на вашем сайте составляет 16 пикселей. Размер шрифта заголовка может быть кратным размеру вашего тела в золотом отношении, то есть он может составлять 16 φ = 16 x 1,618 = 25,88 или примерно 26 пикселей.

Некоторые также используют золотое сечение для определения высоты строки, необходимой для того, чтобы определенный размер шрифта соответствовал золотому сечению. (Высота строки — это высота шрифта плюс пробел между строками текста — она в основном определяет, насколько плотно расположены строки текста в абзаце.) Например, если у вас был размер шрифта 16 пикселей для основного текста, высота строки может быть 16 φ = 16 x 1.618 = 25,88 или, опять же, примерно 26 пикселей.

Высота строки — это высота шрифта плюс расстояние между строками текста. Верх: размеры заголовка и основного текста соответствуют золотому сечению. Высота строки также находится в золотом соотношении с размером шрифта. Увеличение высоты строки облегчает чтение. Внизу: в этом текстовом блоке не используется золотое сечение.

Однако оказывается, что все немного сложнее, потому что по мере увеличения длины строки высота строки также должна увеличиваться, чтобы сохранить удобочитаемость. Например, исследование, проведенное в 2004 году в Университете Рединга, пришло к выводу, что длинные строки требуют большего межстрочного интервала, чтобы глаза могли легко найти следующую строку вниз. Если вы действительно хотите разработать свою типографику с учетом золотого сечения, вы можете использовать типографский калькулятор золотого сечения, который даст вам идеальную высоту строки для заданного размера шрифта и ширины строки.

Обрезка изображения

Композиция важна при создании привлекательных образов. Быстрый и простой способ обрезать изображения и создать эффектную композицию — применить золотую спираль к фокусу изображения.

Сильная композиция создается путем размещения спирали в фокусе изображения, а затем соответствующей обрезки изображения, как в примере слева. Как использовать золотую спираль для обрезки изображения.

Макет веб-страницы

Макет с двумя столбцами естественным образом создается при разделении золотого прямоугольника на квадрат и меньший золотой прямоугольник. Полученный макет идеально подходит для области основного контента и боковой панели. Небрежное следование этому макету создает структуру и баланс интерфейса.Однако на современных адаптивных веб-сайтах будет сложно полностью поддерживать золотое сечение для всех размеров области просмотра. Если вы сосредоточитесь на создании базовой сетки на основе соотношения и выравнивании компонентов по ней, вы сможете получить основные преимущества соотношения по крайней мере на экранах некоторых размеров.

Базовая структура веб-сетки, в которой используется золотое сечение слева. Как создать свободную сетку страниц с использованием золотого сечения   ​​​​​.

Заключение

Некоторые дизайнеры очарованы золотым сечением и используют его для создания и редактирования всевозможных элементов дизайна интерфейса.Другие считают, что золотое сечение не более достоверно, чем любой другой метод, используемый для определения размеров и пропорций. Тем не менее, золотое сечение может быть полезной ссылкой для новых визуальных дизайнеров или дизайнеров, желающих улучшить свои навыки с помощью конкретного математического подхода.

Узнайте больше на нашем курсе «Основы визуального дизайна» на конференции UX.

 

Ссылки

Ди Дио, К., Макалузо, Э., и Риццолатти, Г. (2007). Золотая красавица: реакция мозга на классические скульптуры и скульптуры эпохи Возрождения.ПЛОС ОДИН. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0001201

Дайсон, М. К., и Хазелгроув, М. (2001). Влияние скорости чтения и длины строки на эффективность чтения с экрана. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.108.4346&rep=rep1&type=pdf

Пирсон, К. (2019). Секретная симфония: введение в типографику золотого сечения. Персонифицированный. https://pearsonified.com/golden-ratio-typography-intro/

Почему золотое сечение лучше, чем правило третей

Давным-давно, когда я был молодым студентом-художником, мне рассказали о «Правиле третей».«Мне сказали, что это одна из самых важных основ искусства и фотографии, поскольку она помогает вам получить правильную композицию на ваших изображениях.

Наложите сетку крестиков и крестиков на изображение и обрежьте или переместите изображение так, чтобы «точки интереса» лежали на линиях или пересечениях линий. Звучит достаточно просто. Он был основой бесчисленных миллионов изображений на протяжении веков. Но идеально ли это? Нет! Есть ли лучший, более крутой ** брат в сети? Да! Введите золотое сечение.

Чтобы немного замедлить процесс, вот как выглядит правило третей (далее я буду называть его сеткой ROT) на простом черном фоне. Скорее всего, вы знакомы с ним, вы видели, как он появляется в видоискателе вашей камеры или как наложение в Photoshop или Lightroom.

Сетка отлично подходит для того, чтобы убедиться, что ваши горизонты прямые, чтобы убедиться, что объекты равномерно распределены по всему кадру, и в целом придает немного спокойствия и порядка сцене.

Вот его лучший, мудрый и неуловимый брат: Золотое сечение, также иногда называемое спиралью Фибоначчи.Это результат того, что вы выполняете некоторые сложные математические операции над прямоугольником, например: a/b = (a+b)/a = 1,61803398875. Нет необходимости запоминать это, вы можете найти оверлеи повсюду в Интернете, чтобы загрузить и вставить свои изображения, а также встроенные (но очень хорошо спрятанные) в Lightroom.

Чтобы получить доступ к этой спирали, нажмите R, чтобы открыть функцию обрезки, затем прокручивайте доступные наложения с помощью O, пока не найдете спираль. Переворачивать его можно нажатием Shift+O.Есть восемь его вариаций.

Выглядит довольно забавно, тугая спираль заканчивается не по центру и обеспечивает большое количество линий, по которым можно выровнять изображение.

Если я наложу два слоя друг на друга, вы увидите, как они пересекаются. Плотная спираль синего соотношения почти соединяется с нижним правым пересечением красного наложения. Есть причина, по которой золотое сечение часто отбрасывают, потому что одновременное отображение всех восьми его вариаций на экране — это убийство.

Нижний правый угол пересечения красных линий находится довольно близко к тугому завитку спирали. Вот почему они не накладывают спираль на камеру. Спираль всего в четырех из восьми возможных направлений.

Итак, если с золотым сечением проблем больше, чем с сеткой ROT, почему я должен волноваться об этом? Все сводится к длинной размашистой дуге спирали. Размещение объектов по изогнутой линии, а не по прямым линиям сетки, привлекает внимание зрителей к изображению, заставляя его приблизиться к тугому витку спирали, где вы разместили интересующую вас точку.Это похоже на гигантский подсознательный дорожный знак, указывающий глазам туда, куда вы хотите, чтобы они шли.

Надеюсь, я еще не потерял тебя. Вот несколько реальных примеров применения золотого сечения на нескольких моих изображениях, одно без наложения и одно с наложением. Надеюсь, вы видите, сколько раз изображения следуют за широкими кривыми и заканчиваются фокусом изображения в тугой катушке.

Линия повторяет форму тела мужчины на кровати и заканчивается взглядом женщины.

Это изображение фокусируется на ребенке, доминирующем на изображении на переднем плане, крупнее взрослой матери.

На этот раз спираль проходит через объекты фона, такие как стул и штатив, вокруг освещения и на сгибе ноги фотографа на полу.

Фокус переносится на открытую дверь автомобиля, заставляя зрителя задаться вопросом «почему?»

Золотое сечение можно использовать по-разному — от портретов до пейзажей… даже спортивной и уличной фотографии.Начните искать золотое сечение при редактировании ваших фотографий в вашей любимой программе постобработки кадрирования и посмотрите, как она может поднять ваши фотографии с «да» до «о, да!»

Должен признаться, как только я обнаружил свою любовь к Ratio, я начал пролистывать съемки последних нескольких лет, чтобы повторно кадрировать изображения в Ratio. На мой взгляд, эти недавно обрезанные картинки кажутся гораздо более динамичными и интересными и насильно ведут взгляд по картинкам.

Как всегда, вы можете последовать моему совету, но я просто хочу показать, что в мире искусства есть нечто большее, чем просто перекрещивание линий.