Золотое сечение в архитектуре храмов
Авторы исследовательской работы в 5 классе «Золотое сечение в архитектуре храмов» исследуют теорию золотого сечения и его применение в архитектуре храмов, проводят замеры сооружений и математические вычисления, позволяющие им на практике применить способ золотого сечения при проектировании храма.
В проекте «Золотое сечение в архитектуре храмов» авторами были поставлены и реализованы цели выявить наличие «золотого сечения» в архитектуре храмов и проверить, возможно ли при построении макета храма без точных расчетов выдержать основные пропорции.
Проект по математике «Золотое сечение в архитектуре храмов» — это хороший способ расширить свой кругозор познавательной информацией из истории золотого сечения. Золотое сечение присутствует во всех сферах: в архитектуре, музыке, живописи, литературе, прикладных искусствах, в общей композиции произведения и в соотношении его частей вплоть до самых малых. Данная работа позволяет понять как золотое сечение применено в архитектуре храмов.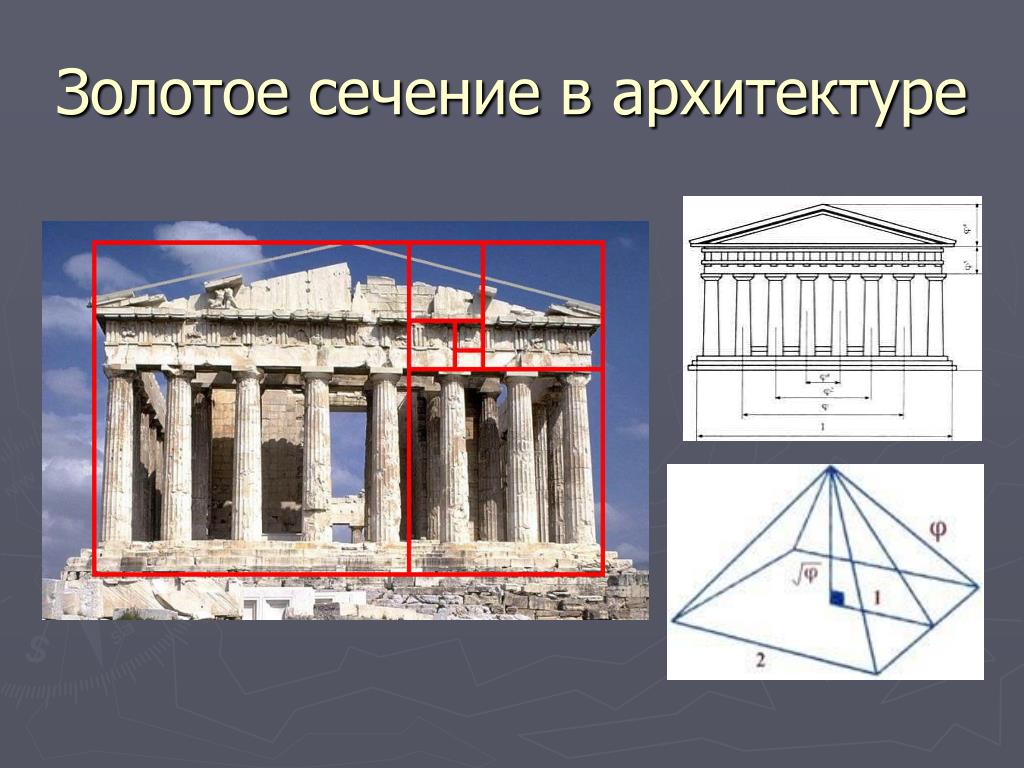
Оглавление
Введение
1. Что такое золотое сечение?
2. Золотое сечение в архитектуре?
3. Исследование золотого сечения на примере архитектуры храмов.
Заключение
Литература
Введение
Мы находим золотое сечение всюду: в архитектуре, музыке, живописи, литературе, прикладных искусствах, в общей композиции произведения и в соотношении его частей вплоть до самых малых.
«Золотое сечение» применялось и применяется в архитектуре с древнейших времён до наших дней. Секрет могучего эмоционального воздействия, которое эти здания оказывают на зрителя, многие искусствоведы искали и находили в соотношениях «
Мы выдвинули гипотезу, что пропорции различных частей храмов составляют число, очень близкое к золотому сечению.
Кроме того, нас заинтересовал вопрос, возможно ли при построении макета храма без точных расчетов выдержать основные пропорции. Мы предположили, что это возможно.
Мы предположили, что это возможно.
Цель исследования:
- выявить наличие «золотого сечения» в архитектуре храмов;
- проверить, возможно ли при построении макета храма без точных расчетов выдержать основные пропорции.
Задачи:
- познакомиться с понятием золотого сечения и рассмотреть примеры золотого сечения в окружающей нас действительности, строении храмов;
- провести математические расчеты в вычислении пропорций «золотого сечения»;
- обобщить полученные результаты.
Для решения данных задач, использованы такие методы исследования:
- анализ литературы, ресурсов сети Интернет;
- математические расчеты пропорциональных отношений;
- сопоставление полученных данных.
Практическая значимость работы
Для проведения своего исследования мы обратились к современному источнику информации – к Интернету и изучили информацию о золотом сечении. Информацию для проверки нашей гипотезы мы не нашли, поэтому свои выводы сделали, основываясь на результатах исследования.
Что такое золотое сечение?
На первом этапе исследования мы изучили понятие «золотое сечение». Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
Если принять весь отрезок с за 1, то отрезок a будет равен 0,618, а отрезок b=0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1.618).
Математические расчеты древних ученых позволили выяснить, что золотое сечение встречается очень часто, и в окружающем мире все стремится к правилу золотого сечения.
Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, зрительные центры.
Это открытие у художников того времени получило название «золотое сечение» картины.
В музыке также есть следы золотого сечения. Многие музыкальные инструменты созданы по правилу золотого сечения.
В исследованиях по биологии в 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая гармоничность их строения. Золотое сечение признано универсальным законом живых систем.
Исследовательский проект «Золотое сечение вокруг нас» Оглавление
Исследовательский проект
«Золотое сечение
вокруг нас»
Оглавление.
Вступление…………………………………………………….
 3
3Глава1 . История золотого сечения
Золотое сечение в математике. …………………………….5
Глава 2. Золотое сечение в искусстве…………………….….7
Глава 3. Золотое сечение в природе……………………..…..10
Глава 4. Золотое сечение вокруг нас………………….……..11
Глава 4. Эксперимент…………………………………………14
Заключение……………………………………………………..15
Литература……………………………………………………..15
Приложение ……………………………………………..……16
Вступление.
«Геометрия обладает двумя великими
сокровищами. Первое — это теорема Пифагора,
второе — деления отрезка в крайнем и среднем
отношениях. Первое сравнимо с мерой золота,
Первое сравнимо с мерой золота,
второе же больше напоминает драгоценный камень»
Иоганн Кеплер
Рассматривая на уроке математики тему «Пропорция» учитель привел примеры золотого сечения, назвав ее «божественной пропорцией». Увлекшись этой темой, я узнал, что «Божественной пропорцией» золотое сечение назвал средневековый итальянский математик Лука Пачоли, написав книгу о золотом сечении, которую так и назвал «Божественная пропорция». По его мнению, даже Бог использовал принцип золотого сечения для создания Вселенной.
Золотое сечение встречается везде: в искусстве, природе, окружающем нас мире. Тема интересна и современна, она не потерялась во времени. И поэтому является темой моего исследования.
В
моем выборе меня поддержали родители
и учитель математики. В
исследовательской работе мы постарались
эту тему изучить подробнее, доказать
присутствие золотого сечения в окружающем
нас мире.
В
исследовательской работе мы постарались
эту тему изучить подробнее, доказать
присутствие золотого сечения в окружающем
нас мире.
Что же такое – «золотое сечение»?
Гипотеза: «Золотое сечение» — гармоническая пропорция.
Объект исследования: репродукции картин, фотографии и рисунки знаменитых архитектурных сооружений, скульптур, современные строения и окружающий нас мир.
Предмет исследования: форма и строение исследуемых предметов.
Цель: Показать, что великое открытие – ЗОЛОТОЕ СЕЧЕНИЕ, пройдя множество веков живо, актуально и востребовано по сей день.
Задачи работы:
Мы попытаемся проанализировать историю «золотого сечения».
Мы исследуем репродукции картин знаменитых художников, архитектурных сооружений и скульптур на предмет «золотого сечения».

Мы попробуем найти «золотое сечение» в природе и окружающем нас мире.
Проведем эксперимент на выявление предпочтения пропорциям «золотого сечения».
Новизна исследования: раскрытие учащимся нашей школы понятия «золотого сечения» в окружающем нас мире.
Ход исследования:
Подобрать материалы по истории «золотого сечения» в библиотеке и в Интернете.
Изучить подобранный материал.
Подобрать фотографии и рисунки.
Провести эксперимент и проанализировать собранный материал.
Сделать выводы.
Практическая значимость:
Использование приобретенных знаний и навыков исследовательской работы при изучении геометрии, биологии, изобразительного искусства, истории, астрономии.

Использование работы при составлении стенда: «Золотое сечение вокруг нас» в кабинете математики.
Методы исследования: наблюдение, измерение, анализ, эксперимент.
Умения и навыки: подбирать необходимую литературу и делать выводы по собранной информации, работать в Интернете, проводить эксперимент, оформлять работу.
Глава1 . История золотого сечения. Золотое сечение в математике.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. a : b= b : c или с : b= b : а.
Обозначаемое греческой буквой «фи» (φ), золотое сечение выражается числом
͌
0, 618 (обратное ему 1,618) и обладаем рядом
любопытных свойств. φ – первая буква
в имени великого
древнегреческого скульптора Фидия,
который часто использовал золотое
сечение в своих произведениях, а термин
ввел великий художник, ученый и
изобретатель Леонардо да Винчи (1452-1519)
φ – первая буква
в имени великого
древнегреческого скульптора Фидия,
который часто использовал золотое
сечение в своих произведениях, а термин
ввел великий художник, ученый и
изобретатель Леонардо да Винчи (1452-1519)
История “Золотого сечения” — это история человеческого развития мира.
Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор и его ученики свое знание золотого сечения позаимствовали у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, предметов быта свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
Греки были
искусными геометрами. Даже арифметике
обучали своих детей при помощи
геометрических фигур. Вся древнегреческая
культура развивалась под знаком золотой
пропорции. Греки первые установили:
пропорции хорошо сложенного человеческого
тела подчиняются ее законам, что особенно
хорошо видно на примере античных статуй
(Аполлон Бельведерский, Венера Милосская). Античный Парфенон — исполнены гармонии
золотой пропорции. В наши дни интерес
к золотой пропорции возрос с новой
силой. Рассмотрим основные геометрические
фигуры, в которых присутствует «золотое
сечение».
Античный Парфенон — исполнены гармонии
золотой пропорции. В наши дни интерес
к золотой пропорции возрос с новой
силой. Рассмотрим основные геометрические
фигуры, в которых присутствует «золотое
сечение».
Числа Фибоначчи и золотое сечение.
В 1202 г вышел в свет его математический труд “Книга об абаке” (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила “Сколько пар кроликов в один год от одной пары родится”. Размышляя на эту тему, Леонардо Фибоначчи выстроил такой ряд цифр:
0, 1, 1, 2, 3, 5, 8,
13, 21, 34, 55, 89, 144, и т.д.
Он известен, как
ряд Фибоначчи. Особенность последовательности
чисел состоит в том, что каждый ее член,
начиная с третьего, равен сумме двух
предыдущих 2 + 3= 5; 3 + 5= 8; 5 + 8= 13, 8 + 13= 21; 13 +
21= 34 и т.д., а если разделить каждое из
них на предыдущее, то получится: 1:1=1;
2:1=2; 3:2=1,5; 5:3=1,666 666; 8:5=1,6; 13:8=1,625; 21:13=1,615384…
Если делить все большие и большие числа
Фибоначчи, то можно приблизиться к
отношению золотого сечения. Несмотря
на то , что книга была опубликована в
1202 году числа Фибоначчи, привлекают
математиков до сих пор.
Несмотря
на то , что книга была опубликована в
1202 году числа Фибоначчи, привлекают
математиков до сих пор.
Золотое сечение в математике.
«Золотой» равнобедренный треугольник. Это равнобедренный треугольник, отношение боковой стороны к основанию равно 1,618 | |
«Золотой» прямоугольный треугольник. Прямоугольный треугольник, в котором стороны относятся как 1,618:√1,618: 1, называется «золотым» прямоугольным треугольником. | |
«Золотой» прямоугольник . Длина такого прямоугольника больше его ширины примерно в 1,618 раз | |
Пентаграмма — правильный пятиугольник. Точки
пересечения диагоналей в пентаграмме
всегда являются точками золотого
сечения диагоналей. |
Глава 2. Золотое сечение в искусстве.
Золотое сечение в картине И. И. Шишкина»Сосновая роща»
На знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия. | |
Картина Н. Н. Ге
«Александр Сергеевич Пушкин в селе
Михайловском». Н. Ге
«Александр Сергеевич Пушкин в селе
Михайловском». | |
В этой картине фигура Пушкина также поставлена художником слева на линии золотого сечения. Голова военного, с восторгом слушающего чтение поэта, находится на другой вертикальной линии золотого сечения. | |
Золотое сечение в картине Леонардо да Винчи «Джоконда» | |
Портрет Моно Лизы привлекает тем, что композиция рисунка построена на»золотых треугольниках» (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника) | |
Статуя Аполлона Бельведерского Статуя Венеры Милосской
Известно,
что знаменитая скульптура создана по
принципу золотого сечения. Точка С делит
отрезок AD, точка В делит
отрезок АС в отношении приближенно
равно 1,618.
Парфенон (древнегреческая архитектура)
Древние греки Иктинас, Колликрэйтс, и Фидиас, совместно создали Парфенон, в Афинах приблизительно в 440 г. до нашей эры. Если фасад Парфенона вписать в прямоугольник, то стороны прямоугольника образуют золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза.
Великая Пирамида фараона Хеопса
Среди грандиозных пирамид Египта особое место занимает Великая Пирамида фараона Хеопса (Хуфу). Гениальные создатели египетских пирамид стремились поразить далеких потомков глубиной своих знаний, и они достигли этого, выбрав в качестве «главной геометрической идеи» для пирамиды Хеопса — «золотой» прямоугольный треугольник.
Застывшая музыка русских храмов
Трудно
найти человека, который бы не знал и не
видел собора Василия Блаженного на
Красной площади Москвы. Для композиции
построек собора характерно гармоническое
сочетание симметричных и асимметричных
пропорций. Храм, симметричный в своей
основе, содержит много геометрических
«неправильностей». Так, центральный
объем шатра смещен на 3 м к западу от
геометрического центра всей композиции.
Однако неточность делает композицию
более живописной, «живой» и она
выигрывает в целом. Для архитектурного
убранства собора характерно нарастание
декоративных форм ввысь; формы вырастают
одна из другой, тянутся вверх, подымаясь
то крупными элементами, то образуя
группы, состоящие из более мелких
декоративных частей.
Храм, симметричный в своей
основе, содержит много геометрических
«неправильностей». Так, центральный
объем шатра смещен на 3 м к западу от
геометрического центра всей композиции.
Однако неточность делает композицию
более живописной, «живой» и она
выигрывает в целом. Для архитектурного
убранства собора характерно нарастание
декоративных форм ввысь; формы вырастают
одна из другой, тянутся вверх, подымаясь
то крупными элементами, то образуя
группы, состоящие из более мелких
декоративных частей.
Исследователи обнаружили в нем пропорцию, основанную на ряде золотого сечения:
1: 0,618:0,6182:0,6183:0,6184:0,6185:0,6186:0,6187
Пентаграмма и «Пентагон»
Пентаграмма вызывала особое восхищение у пифагорейцев и считалась их главным опознавательным знаком.
Здание
военного ведомства США имеет форму
пентаграммы и получило название
«Пентагон», что значит правильный
пятиугольник.
Изучив литературу по данной теме, мы пришли к выводу, что издревле людей интересовала «золотая пропорция». Мы так же узнали, что люди давно использовали «золотую пропорцию» на практике при строительстве различных домашних строений и храмов, использовали при изготовлении домашней утвари, применяли при создании механизмов, которые облегчали труд человека. В этой главе мы привели наиболее интересные, по-нашему мнению, примеры , связанные с золотым сечением.
Глава 3. Золотое сечение в природе.
Изучив литературу, мы узнали, что у многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.
В ящерице с
первого взгляда улавливаются приятные
для нашего глаза пропорции – длина ее
хвоста так относится к длине остального
тела, как 62 к 38. Можно заметить золотые
пропорции, если внимательно посмотреть
на яйцо птицы. В природе встречается
«пентагональная» симметрия»:
Можно заметить золотые
пропорции, если внимательно посмотреть
на яйцо птицы. В природе встречается
«пентагональная» симметрия»:
китайская роза яблоко в разрезе морская звезда кактус
Мы узнали, что человеческое тело создано по законам золотого сечения. Оказывается, талия делит совершенное человеческое тело в отношении золотого сечения. Ученые обнаружили, что для взрослых мужчин это отношение
равно в среднем примерно 13/8 = 1,625, а для взрослых женщин оно составляет 8/5 = 1,6. Так что пропорции мужчин ближе к «золотому сечению», чем пропорции женщин (однако женщина в обуви на каблуках может оказаться ближе к «золотым» пропорциям). У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году у мужчин равняется 1,625. Пропорции золотого сечения проявляются и в отношении других частей тела — длина плеча, предплечья и кисти, кисти и пальцев..
Таким
образом, природа подчиняется принципу
«золотой пропорции» (строение человеческого
тела, ящерицы, бабочки, листья и цветы
многих растений и т. д.).
д.).
Глава 4. Золотое сечение вокруг нас
Мы исследовали окружающий нас мир на наличие золотого сечения. И нашли много интересных фактов, подтверждающих, что золотое сечение живет рядом с нами.
Мемориал Памяти с. Ребриха Высота солдата относится к высоте девочки приблизительно равно 1,66 | |
Районный краеведческий музей. Отношение длины здания к высоте приблизительно равно 1,53 | |
Ст. Ребриха Ул. Касмалинская Высота дома относится к его длине как: 1,77 | |
Высота изображенных лошадей относится к длине изображенных лошадей, как: 1,7 | |
Рис. 1 Рис. 2 Рис.3 | Мы
исследовали расположение листьев
комнатных растений вдоль стебля и
измерили расстояние между листьями,
нашли отношения соответственных
расстояний (рис. Такой же принцип роста мы обнаружили и у других растений. На данных фотографиях показано, что точка В делит отрезок АС в отношении : 1,4 (рис.1), и 1,3(рис.2) |
Исследуем ученика 6 класса:
Таблица№1. Золотое сечение и человек
|
Из таблицы
видно, что пропорции тела приближены к
золотому сечению, но до идеальной
пропорции необходимо еще расти.
Исследуем Солнечную систему
Листая справочные материалы и энциклопедии, мы обнаружили таблицы с характеристиками планет солнечной системы (приложение1). И решили проверить солнечную систему на содержание золотого сечения. К нашему удивлению, мы ее обнаружили. Данные приводим в таблице №2
Таблица№2.
Планеты | Отношение расстояний от Солнца до планет | Отношение больших полуосей орбит |
Венера-Меркурий | 1,87 | 1,57 |
Земля-Венера | 1,38 | 1,4 |
Марс-Земля | 1,52 | 1,61 |
Юпитер-Марс | 3,41 | 3,28 |
Сатурн-Юпитер | 1,83 | 1,85 |
Уран-Сатурн | 2,01 | 1,99 |
Нептун-Уран | 1,57 | 1,51 |
Плутон-Нептун | 1,32 | 1,62 |
Среднее арифметическое | 1,86 | 1,85 |
Среднее арифметическое с планетой Фаэтон | 1,65 | 1,65 |
Заметим,
что отношение между планетами Марсом
и Юпитером заметно отличается от других. Практически в два раза. В литературе
указано, что между этими планетами
находится пояс астероидов. Меня
заинтересовал этот вопрос. Рассмотрев
различные источники информации,
оказалось, что немецкий физик и математик
И. Тициус в 1766 году нашел числовую
закономерность в расстояниях планет
от Солнца. Согласно этому
Практически в два раза. В литературе
указано, что между этими планетами
находится пояс астероидов. Меня
заинтересовал этот вопрос. Рассмотрев
различные источники информации,
оказалось, что немецкий физик и математик
И. Тициус в 1766 году нашел числовую
закономерность в расстояниях планет
от Солнца. Согласно этому
правилу, между орбитами Марса и Юпитера должна была существовать какая-то планета. Считается, что древние греки называли ее Фаэтон и ее орбита находилась между орбитами Марса и Юпитера. До сих пор идут споры о ее существовании.
Мы, полагаясь на данную таблицу (среднее арифметическое отношение расстояний планет от Солнца, включая планету Фаэтон- равно 1,6 ) — считаем, что планета была!!!
Глава 4. Эксперимент
В этой главе мы проводим эксперименты на выявление предпочтения пропорциям «золотого сечения» учениками нашей школы.
Эксперимент
№1. Мы попросили испытуемых выбрать среди
11 прямоугольников наиболее привлекательный,
причем лишь два из них являются золотыми
. Данные приводим ниже в таблице №3.
Таблица №3
Данные приводим ниже в таблице №3.
Таблица №3
Класс | Кол-во опрошенных | Кол-во человек, которые выбрали золотой прямоугольник | % выбора золотых прямоугольников учениками | % золотых прямоугольников первоначально 2:11 | |
5-6 | 27 | 8 | 27% | 18% | |
9,11 | 14 | 6 | 42% | 18% |
Из таблицы
видно, что выбор золотого прямоугольника
увеличился у старшеклассников.
Эксперимент №2. Мы предложили ученикам 5-6 классов (всего 17 человек), побыть немного художниками и изобразить горизонт будущей своей картины. При подсчете итогов, заметили, что линия горизонта делит на всех рисунках в среднем ͌ 1,65.
Эксперименты подтвердили, что большее предпочтение отдается золотым пропорциям.
Заключение.
Тема
«Золотое сечение вокруг нас» интересна
и современна, она не потерялась во
времени. Золотое сечение, действительно, можно
называть «Божественной пропорцией». Оно, не
только окружает нас вокруг и распространено
в Солнечной системе, но и события,
происходящие с нами, тоже происходят
согласно золотой пропорции. Например,
возрастные кризисы людей. В обществознании
есть закон уплотнения истории – с каждым
новым этапом скорость развития общества
увеличивается. Эта тема отдельной
исследовательской работы.
Важным результатом изучения данной темы является, то, что принцип золотого сечения используется везде: в искусстве, науке, природе, человеке, гармонично объединяя весь в мир в единое целое. Накопленный материал, пригодиться в дальнейшей исследовательской работе. Можно подробнее изучить на предмет золотого сечения здания, находящиеся на территории Ребрихинского района. Не менее увлекательным будет для старшеклассников путешествие в мир золотого сечения в математике.
Литература.
Еженедельная учебно-методическая газета «Математика» №13, 2008 г.- Издательский дом «Первое сентября» гл. ред. А.Соловейчик.
Я познаю мир: Математика: Дет. энцикл./авт.сост.А.П.Савин,2004.
Что мы знаем о планетах. Мн., «Народная асвета», 1977г
Земля / Пер. с ит. И.Горелой; — М.:ЗАО «Планета детства», 2001
Лэнгдон Н, Снейп Ч.
 С математикой в путь: Пер. с
англ.-М.:Педагогика, 1987
С математикой в путь: Пер. с
англ.-М.:Педагогика, 1987Большая серия знаний. Изобразительное искусство. –М.:ООО «ТД «Издательство Мир книги», 2005.
Большая серия знаний. Вселенная. –М.:ООО «ТД «Издательство Мир книги», 2005.
/
/konkurs/tarhov/russian/stages.htm
Исследовательский проект «Золотое сечение»
Муниципальное общеобразовательное бюджетное учреждение
«Средняя общеобразовательная школа №17»
Пожарского муниципального района
Индивидуальный итоговый проект
«Золотое сечение»
Выполнила:
Богачёва Галина Андреевна
ученица 9 класса
Куратор проекта:
Циплакова Лариса Владимировна
учитель математики
с. Новостройка
Новостройка
2020г
Содержание
стр | ||
1. | Введение………………………………………………………………… | 3 |
2. | Цель и задачи исследования…………………………………………… | 4 |
3. | История возникновения «Золотого сечения»………………………… | 5 |
4. | Определение понятия «Золотое сечение»…………………………….. | 6-12 |
5. | Деление отрезка прямой по правилу «Золотого сечения»…………… | 13-19 |
6. | Золотая спираль………………………………………………………… | 20-32 |
7. | «Золотое сечение» в архитектуре древности…………………………. | 33-37 |
8. | «Золотое сечение» на примере башен московского Кремля………… | 38-39 |
9. | Выводы…………………………………………………………………… | 40 |
10. | Литература………………………………………………………………. | 41 |
Вашему вниманию представляется исследовательская работа по теме «Золотое сечение».
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида.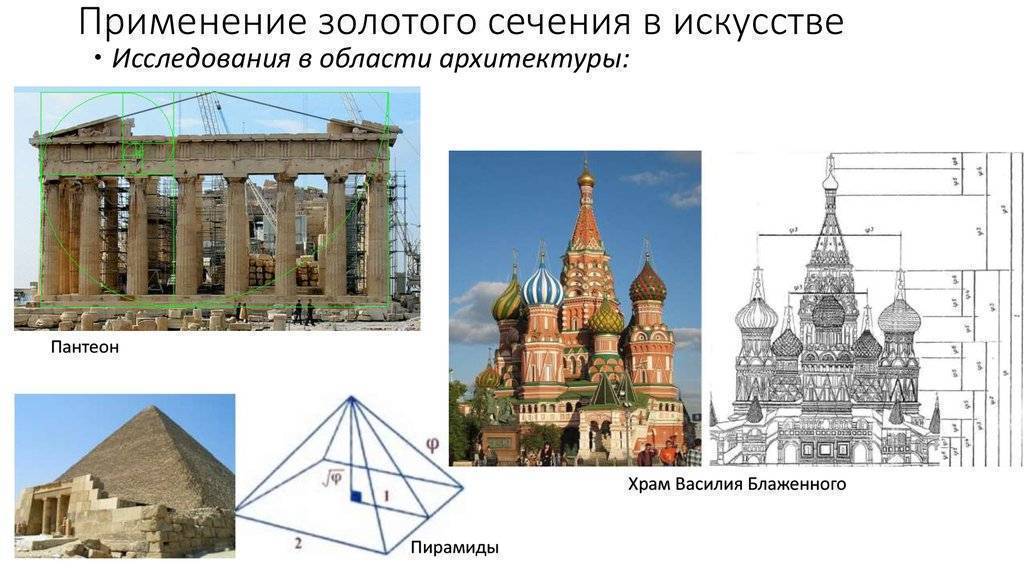 Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием занимались многие ученые. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным. Что же такое «золотое сечение»?
Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием занимались многие ученые. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным. Что же такое «золотое сечение»?
Практическая значимость проекта заключается в том, чтобы уделить больше внимания столь необходимой теме, чем это делает школьная программа. «Золотое сечение» — одна из самых важных тем не только в математике, но и в других областях, но дети слишком мало ознакомлены с этим явлением.
Целью моей работы является изучение теоретической информации по выбранной теме, формирование навыков самостоятельной исследовательской деятельности, решения ключевой проблемы в процессе сотрудничества и создания продукта, а также обучение работе с информацией и медиа средствами для расширения кругозора и развития творческих способностей.
В соответствии с поставленной целью необходимо решить следующие задачи:
Подобрать литературу по теме «Золотое сечение»
Провести исследования по следующим направлениям:
Ознакомиться с историей золотого сечения
Сформулировать понятие «золотое сечение», рассмотреть алгебраический и геометрический смысл
Сформулировать понятие гармонии и математической гармонии
Исследовать пропорции тела человека по Цейзингу
Определить пропорции тела человека на примере обучающихся МОБУ СОШ №17
Найти подтверждение наличия золотого сечения в природе
Рассмотреть применение золотого сечения в искусстве (скульптура, живопись)
Ознакомиться с применением золотого сечения в архитектуре
Проанализировать объекты архитектуры
Сделать выводы по исследуемой теме
Начать свою работу мне бы хотелось с исторических фактов по теме моего исследования. Понятие «Золотое сечение» тесно связано с понятием «Гармония», которая, в свою очередь, имеет два определения:
Понятие «Золотое сечение» тесно связано с понятием «Гармония», которая, в свою очередь, имеет два определения:
«Гармония – соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое. В гармонии получают внешнее выявление внутренняя упорядоченность и мера бытия»
Математическая гармония — это равенство или соразмерность частей друг с другом и части с целым. Понятие математической гармонии тесно связано с понятиями пропорции и симметрии.
«Золотое сечение» не зря называют гармонией математики. Об этом свидетельствуют представленные формулы, которые доставляют «эстетическое наслаждение» и вызывают неосознанное чувство ритма.
Понятие «Золотой пропорции» связано с тремя очень известными людьми: Леонардо да Винчи, Леонардо Фибоначчи и Иоганн Кеплер.
Леонардо да Винчи был одним из первых, кто ввёл сам термин «Золотое сечение». Леонардо Фибоначчи составил ряд чисел, известный как «Ряд Фибоначчи», а Иоганн Кеплер установил связь между двумя этими явлениями, доказав, что последовательность отношений соседних чисел Фибоначчи в пределе стремится к золотой пропорции.
Изучив «Золотое сечение» в геометрии, я рассмотрела задачу о делении отрезка в золотом соотношении и пришла к выводу, что точка Е является искомой и производит золотое сечение отрезка АВ.
Также «Золотое сечение» можно наблюдать и в природе на примере объектов, представленных в презентации.
Также в своём проекте мне хотелось бы показать интересные фигуры, которые тоже связаны с «Золотой пропорцией»: золотой треугольник, золотой прямоугольник и пентаграмма. Их объединяет то, что они так или иначе находятся в золотом соотношении.
Далее нам представляется ещё одно очень увлекательное явление – «Золотая спираль». Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый по четверти окружности, мы получаем золотую логарифмическую спираль. Её можно часто наблюдать в повседневной жизни в подсолнечниках, в шишках сосны, ананасах, кактусах, бивнях и рогах животных, а также во многом другом.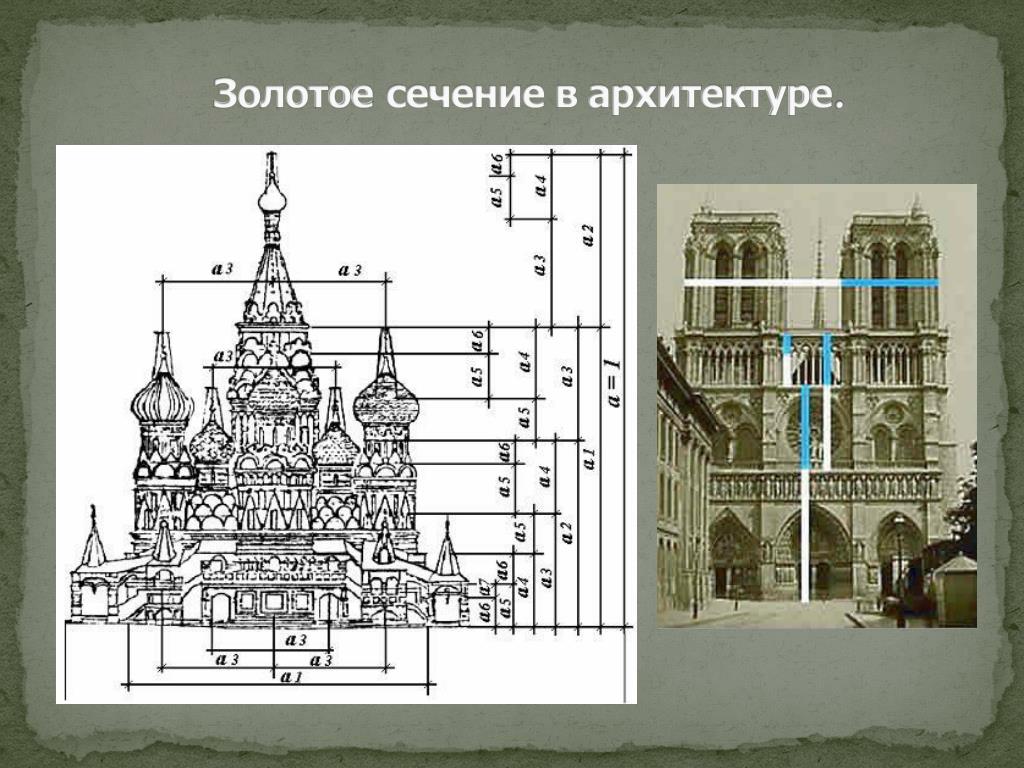
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он измерил около двух тысяч человеческих тел и пришел к выводу, что пропорции золотого сечения проявляются в отношении частей тела человека – длина плеча, предплечья и кисти, кисти и пальцев и т.д. Деление тела точкой пупа – важнейший показатель золотого сечения. Это исследование назвали «Математической эстетикой Цейзинга».
Я решила проверить «Золотое сечение» на некоторых своих одноклассниках и результаты меня удивили. Человеческое тело действительно находится в «Золотом отношении», а также составленная таблица помогла убедиться в действительности теории Цейзинга о том, что пропорции тела у мальчиков ближе к показателю золотого сечения, чем у девочек.
«Золотое сечение» используется в живописи, архитектуре, скульптуре и фотографии, о чём свидетельствуют представленные изображения знаменитых статуй, картин и сооружений.
Чтобы полностью удостовериться в полученной информации и доказать её верность в своём проекте, я решила изучить «Золотое сечение» на примере башен московского Кремля: Арсенальная и Тайницкая. Выполнив необходимые расчёты, я убедилась в том, что в строительстве обеих башен соблюдалась «Золотая пропорция».
Подводя итог вышесказанному, можно сделать следующие выводы:
Принципы «золотого сечения» лежат в основе архитектурных пропорций многих замечательных произведений мирового зодчества.
Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – одно из замечательных проявлений структурного и функционального совершенства целого и его частей в архитектуре
Золотое сечение выражает средний статистический закон.
Деление тела «точкой пупа» важнейший показатель «Золотого сечения».
Пропорции мужского тела колеблются в пределах среднего значения 13:8=1, 625 и несколько ближе подходят к «Золотому сечению», чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8:5=1,6.
Таким образом, основная цель проекта и поставленные задачи достигнуты.
РазделыАвторы работА Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Э Ю Я Руководители работА Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Э Ю Я |
|
Золотое сечение в архитектуре и искусстве
Строительством храма Парфенон руководил архитектор Фидий (краткое сообщение о этом произведении).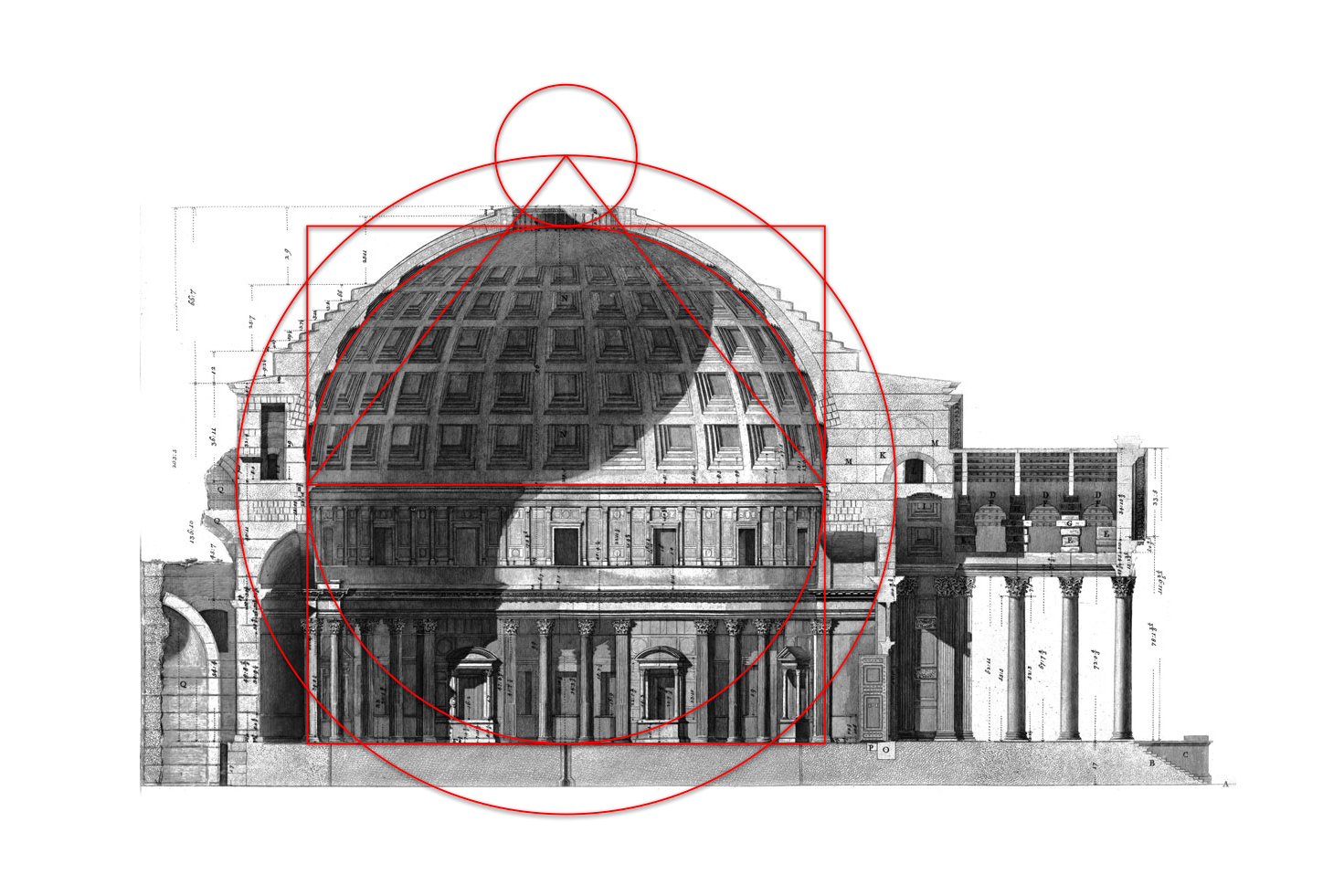
Парфенон — главный храм в древних Афинах, посвященный покровительнице этого города и всей Аттики, богине Афине-Девственнице. Он красовался на самом высоком пункте афинского акрополя, там, где перед тем стоял не вполне достроенный храм той же богини, заложенный еще до нашествия. По окончании персидских войн, в правление Перикла, приступили к сооружению, на месте прежнего святилища, нового, более обширного и роскошного храма, при чем пущено в ход искусство лучших из тогдашних художников и употреблены огромные денежные средства. Строителями П. называют Иктина и Калликрата; первому, по-видимому, принадлежал проект этого здания, а второй заведовал производством строительных работ. Велики скульптор Фидий и сам Перикл наблюдали за постройкой, продолжавшейся около десяти лет, с 448 по 438 г. До Р. Хр. На прямоугольной платформе (в 68,4 м длины и в 30,38 м ширины), сложенной из пирейского камня и на которую можно было со всех сторон подниматься по трем ступеням, высился построенный из пентелийского мрамора величественный периптер дорического стиля с восемью колоннами в каждом коротком фасе и с семнадцатью в каждом длинном. Вышиной эти колонны были в 11 м, диаметр их разреза в нижнем конце равнялся 1,8 м. Окруженный этой колоннадой, стоит и посей день.
Вышиной эти колонны были в 11 м, диаметр их разреза в нижнем конце равнялся 1,8 м. Окруженный этой колоннадой, стоит и посей день.
Другим примером из архитектурной древности является Пантеон, храм всех богов в Риме.
Известный русский архитектор Казаков Матвей Федорович в своем творчестве широко использовал “золотое сечение”. Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например золотое сечение можно обнаружить в архитектуре здания сената в Кремле. По проекту Казакова построена в Москве Голицынская больница, которая в настоящее время называется “Первая клиническая” больница имени Пирогова.
Еще один архитектурный шедевр Москвы – дом Пашкова (1786 г.)– является одним из наиболее совершенным произведением архитектуры Василия Ивановича Баженова.
Прекрасное творение прочно вошло в ансамбль центра современной Москвы. Наружный вид сохранился почти без изменения до наших дней, ныне Российская государственная библиотека.
Многие высказывания зодчего заслуживают внимания и в наши дни. О своем любимом искусстве В. Баженов говорил: “Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания … К достижению сего служит руководством знание пропорции , перспективы , механики или вообще физики ,а всем им общим вождем является рассудок”
Внимание людей издавна привлекала совершенство формы пятиконечная звезда.
Пятиконечной звезде — около 3000 лет. Ее первые изображения донесли до нас вавилонские глиняные таблички. Из древней Вавилонии в Средиземноморье, как полагают, звездчатый пятиугольник перевез Пифагор и сделал его символом жизни и здоровья, а также тайным опознавательным знаком.
Сегодня пятиконечная звезда реет на флагах едва ли не половины стран мира. Чем же объясняется такая популярность? Тем, что совершенная форма этой фигуры радует глаз. Звездчатый пятиугольник буквально соткан из пропорций, и прежде всего золотой пропорции.
Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей их подвиги и деяния.
Известно, что еще в древности основу скульптуры составляла теория пропорции. Отношение частей человеческого тела связывалось с формулой “золотого сечения”.
Пропорции “золотого сечения” создают впечатления гармонии красоты, поэтому скульпторы использовали их в своих произведениях.
Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения”. Так например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям.
Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих произведениях.
Самая знаменитая из них была статуя Зевса Олимпийского, которая считалась одним из чудес света и статуя Афины Парфенос.
Измерения нескольких тысяч человеческих тел позволило обнаружить, что для взрослых мужчин это отношение равно 13:8=1,625, а взрослых женщин оно составляет 8:5 = 1,6. Так что пропорции мужчин ближе к “золотому сечению”.
“Золотое сечение” в изобразительном искусстве.
Особый вид изобразительного искусства Древней Греции следует выделить изготовление и роспись всевозможных сосудов. В изящной форме легко угадываются пропорции золотого сечения .
В живописи и скульптуре храмов, на предметах домашнего обихода древние египтяне чаще всего изображали богов и фараонов. Были установлены каноны изображения стоящего человека идущего, сидящего и т.д. Художники обязаны были заучивать отдельные формы и схемы изображения по таблицам и образцам. Художники Древней Греции совершали специальные путешествия в Египет, чтобы поучиться умению пользоваться каноном.3D проект дома по золотому сечению в архитектуре стиля модерн
Пример проекта небольшого двухэтажного дома с рациональным дизайном архитектурных элементов, выполненных по правилам золотого сечения. Золотая пропорция в архитектуре позволяет строить самые прочные конструкции зданий одновременно с привлекательным эстетическим видом.
Скачать 3D модель небольшого двухэтажного домика по золотой пропорции
| Технические характеристики | |
| Архитектура в стиле: | модерн |
| Дом размером: | 11×19 м |
| Общая жилая площадь: | 160 м2 |
| Этажность здания: | двухэтажный |
| Материал несущих стен: | кирпич |
| Тип крыши: | чердак |
| Гараж: | с гаражом |
Краткий обзор основных преимуществ и особенности планировки проекта:
- Применение золотой пропорции в архитектурных элементах здания.

- Небольшой и эргономичный план двухэтажного дома.
- Большая ванная комната с разделенным санузлом.
- Кухня на втором этаже.
- Большая крытая терраса.
Идеология планирования в этом небольшом двухэтажном доме:
- лаконичность и минимализм;
- практичность и энергоэффективность;
- эргономичность и современная эстетичность.
Дом идеально подходит для небольшой молодой семьи с небольшим бюджетом на частное строительство своего жилья.
Правило золотого сечения в архитектуре стиля модерн
Большая часть элементов архитектуры в небольшом двухэтажном доме спроектированы по правилам золотого сечения. Как ее еще называют божественная пропорция. Ее формула определяется как соотношением меньшей величины к большей, как большая к целому. Коэффициент золотого сечения равен числу 1,6180339887. Но золотую пропорцию проще воспринимать в процентном соотношении 38/62.
Где:
- доля меньшей величины занимает – 38%;
- большая величина – 68%;
- целое – 100%.

Из этого следует:
- 38/62*100≈60% (соотношением меньшей величины к большей)
- 62/100*100≈60% (как большая к целому).
В кулуарах математиков золотое сечение называют асимметрической симметрией.
Правила золотого сечения были известны еще в древнем Египте до нашей эры. Именно в золотой пропорции были построены египетские пирамиды, которые доказали свою прочность на протяжении тысячелетий. Эту математическую гармонию также активно применяли в древнегреческой архитектуре.
Божественная пропорция постоянно встречается во всех живых организмах, например, пропорции человеческого тела, структуры ДНК, раковины улитки, семена подсолнуха и т.д.
Интересный факт! Золотое сечение придает не только прочность конструкциями, но и вызывает чувство спокойствия, безопасности и удовольствие от эстетической красоты у зрителя, который любуется результатом архитектурного произведения искусства. Именно поэтому многие художники, скульпторы и архитекторы часто применяют это правило в своих шедеврах произведения искусства.
В современной архитектуре сегодня популярен минимализм и поэтому все чаще стали применять архитектурные элементы конструкции здания спроектированных по правилам золотого сечения, чтобы одновременно придать прочность структуры и украсить дизайн формы дома.
Золотое сечение. Принципы формообразования в природе
Золотое сечение в искусстве
Под « правилом золотого сечения » в архитектуре и искусстве обычно понимаются асимметричные композиции , не обязательно содержащие золотое сечение математически.
Многие утверждают, что объекты, содержащие в себе « золотое сечение », воспринимаются людьми как наиболее
гармоничные . Обычно такие исследования не выдерживают строгой критики. В любом случае ко всем этим утверждениям следует относиться с осторожностью, поскольку во многих случаях это может оказаться результатом подгонки или совпадения. Есть основание считать, что значимость золотого сечения в
искусстве преувеличена и основывается на ошибочных расчётах. Некоторые из таких утверждений:
Некоторые из таких утверждений:
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе , изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению . В фасаде древнегреческого храма также присутствуют золотые пропорции . В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления , и т. д. и т. п.
- Результаты исследования золотого сечения в музыке впервые изложены в докладе Эмилия Розенова (1903) и позднее развиты в его статье «Закон золотого сечения в поэзии и музыке» (1925). Розенов показал действие данной пропорции в музыкальных формах эпохи Барокко и классицизма на примере произведений Баха , Моцарта , Бетховена .
При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов
бумаги и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино и телевизионных экранов — например, 3:4 или 9:16) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции « слишком вытянутыми ».
Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции « слишком вытянутыми ».
Начиная с Леонардо да Винчи , многие художники сознательно использовали пропорции « золотого сечения ». Российский зодчий Жолтовский также использовал золотое сечение в своих проектах.
Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам золотого сечения. Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения . Да и в каждой части есть свой перелом, происходящий по закону золотого сечения . В кадре, сцене, эпизоде происходит некий скачок в развитии темы:
сюжета , настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения , он воспринимается как наиболее закономерный и естественный.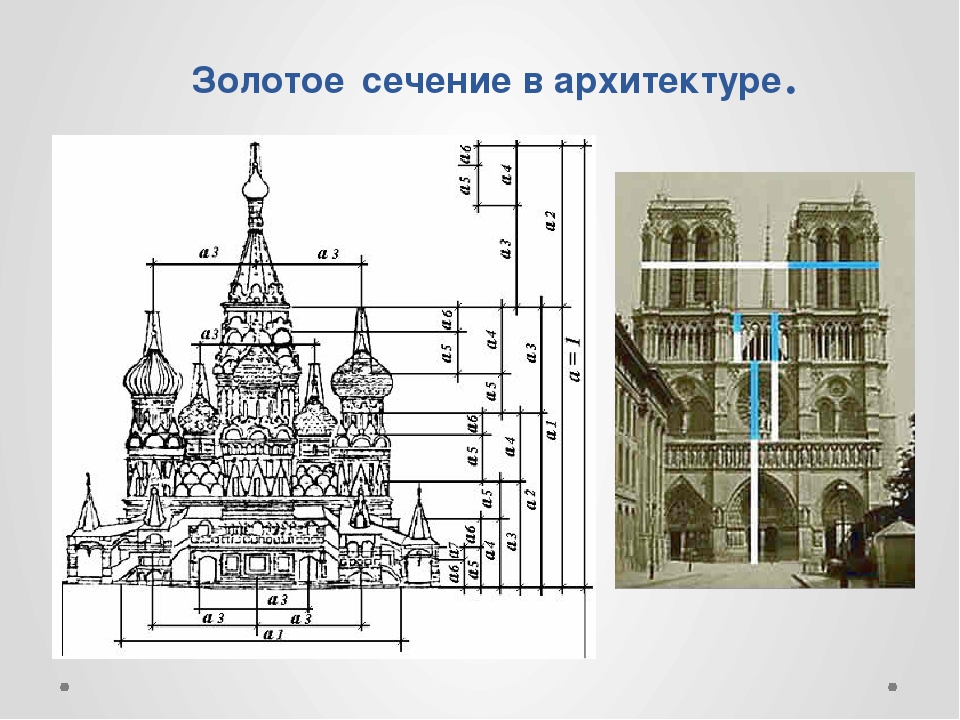
Другим примером использования правила «золотого сечения » в киноискусстве служит расположение основных компонентов кадра в особых точках — «зрительных центрах». Часто используются четыре точки, расположенные на расстоянии 3/8 и 5/8 от соответствующих краёв плоскости.
Золотое сечение в скульптуре
Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния.
Известно, что еще в древности основу скульптуры составляла теория пропорций . Отношения частей человеческого тела связывались с формулой золотого сечения .
Пропорции “золотого сечения” создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях.
Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения” . Так, например, знаменитая
статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям . Великий
древнегреческий
скульптор Фидий часто использовал “золотое сечение” в своих произведениях. Самыми знаменитыми из них были
статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.
Великий
древнегреческий
скульптор Фидий часто использовал “золотое сечение” в своих произведениях. Самыми знаменитыми из них были
статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.
Золотое сечение в архитектуре
В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре , как и в живописи , все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение” , то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин.
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в
греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для
скульптуры.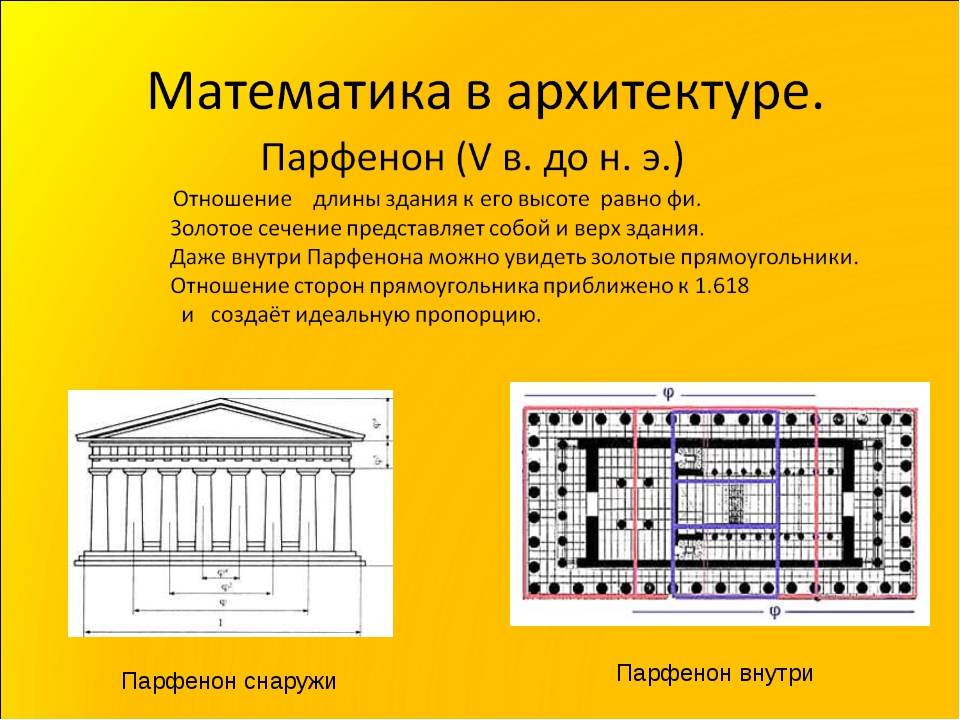 Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению” , то получим те или иные выступы фасада.
Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению” , то получим те или иные выступы фасада.
Другим примером из архитектуры древности является Пантеон.
Известный русский архитектор М. Казаков в своем творчестве широко использовал “золотое сечение” . Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова (Ленинский проспект, д. 5).
Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова.
Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г.
При восстановлении здание приобрело более массивные формы . Не сохранилась и внутренняя планировка здания, о которой дают представления только чертеж нижнего этажа.
Многие высказывания зодчего заслуживают внимание и в наши дни. О своем любимом искусстве В. Баженов говорил:
“ Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания… К достижению сего служит руководством знание пропорции , перспектива , механика или вообще физика, а всем им общим вождем является рассудок ”.
Золотое сечение в живописи
Каждый рисующий определяет отношения величин и, не удивляйтесь, отличает среди них отношение «золотого — сечения» . Такой характер зрительного восприятия подтверждается многочисленными опытами, проводившимися в разное время в ряде стран мира.
Немецкий психолог Густав Фехнер в 1876 г. провел ряд экспериментов, показывая мужчинам и женщинам, юношам и девушкам, а также детям нарисованные на
бумаге фигуры различных прямоугольников, предлагая выбрать из них только один, но производящий на каждого испытуемого самое приятное впечатление. Все выбрали прямоугольник, показывающий
отношение двух его сторон в
пропорции «золотого сечения» . Опыты иного рода продемонстрировал перед студентами нейрофизиолог из США Уоррен Мак-Каллок в 40-х годах нашего века, когда попросил нескольких добровольцев из числа будущих специалистов привести продолговатый предмет к предпочтительной
форме . Студенты некоторое время работали, а затем вернули профессору предметы. Почти на всех из них отметки были нанесены точно в районе
отношения «золотого сечения », хотя молодым людям совершенно не было ничего известно об этой « божественной
пропорции ». Мак-Каллок потратил два года на подтверждение этого феномена, так как сам лично не верил, что все люди выбирают эту
пропорцию или устанавливают ее в любительской работе по изготовлению всевозможных поделок.
Все выбрали прямоугольник, показывающий
отношение двух его сторон в
пропорции «золотого сечения» . Опыты иного рода продемонстрировал перед студентами нейрофизиолог из США Уоррен Мак-Каллок в 40-х годах нашего века, когда попросил нескольких добровольцев из числа будущих специалистов привести продолговатый предмет к предпочтительной
форме . Студенты некоторое время работали, а затем вернули профессору предметы. Почти на всех из них отметки были нанесены точно в районе
отношения «золотого сечения », хотя молодым людям совершенно не было ничего известно об этой « божественной
пропорции ». Мак-Каллок потратил два года на подтверждение этого феномена, так как сам лично не верил, что все люди выбирают эту
пропорцию или устанавливают ее в любительской работе по изготовлению всевозможных поделок.
Интересное явление наблюдается при посещении зрителями музеев и выставок
изобразительного искусства
. Многие люди, сами не рисовавшие, с поразительной точностью улавливают даже малейшие неточности в принципа.
“ Пусть никто, не будучи математиком, не дерзнет читать мои труды ”.
Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.
Нет сомнений, что
Леонардо да Винчи
был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится “обо всем на свете”.
Он писал справа налево неразборчивым почерком и левой рукой. Это самый известный из существующих образец зеркального письма.
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что
композиция рисунка основана на золотых треугольниках , являющихся частями правильного звездчатого пятиугольника.
Существует очень много версий об истории этого
портрета . Вот одна из них.
Вот одна из них.
Жил-был один бедный человек, было у него четыре сына: три умных, а один из них и так, и сяк. И вот пришла за отцом смерть. Перед тем, как расстаться с жизнью, он позвал к себе детей и сказал: “Сыны мои, скоро я умру. Как только вы схороните меня, заприте хижину и идите на край света добывать себе счастья. Пусть каждый из вас чему-нибудь научится, чтобы мог кормить сам себя”. Отец умер, а сыновья разошлись по свету, договорившись спустя три года вернуться на поляну родной рощи. Пришел первый брат, который научился плотничать, срубил дерево и обтесал его, сделал из него женщину, отошел немного и ждет. Вернулся второй брат, увидел деревянную женщину и, так как он был портной, в одну минуту одел ее: как искусный мастер он сшил для нее красивую шелковую одежду. Третий сын украсил женщину золотом и драгоценными камнями – ведь он был ювелир. Наконец, пришел четвертый брат. Он не умел плотничать и шить, он умел только слушать, что говорит земля, деревья, травы, звери и птицы, знал ход небесных тел и еще умел петь чудесные песни. Он запел песню, от которой заплакали притаившиеся за кустами братья. Песней этой он оживил женщину, она улыбнулась и вздохнула. Братья бросились к ней и каждый кричал одно и то же: “Ты должна быть моей женой”. Но женщина ответила: “Ты меня создал – будь мне отцом. Ты меня одел, а ты украсил – будьте мне братьями.
Он запел песню, от которой заплакали притаившиеся за кустами братья. Песней этой он оживил женщину, она улыбнулась и вздохнула. Братья бросились к ней и каждый кричал одно и то же: “Ты должна быть моей женой”. Но женщина ответила: “Ты меня создал – будь мне отцом. Ты меня одел, а ты украсил – будьте мне братьями.
А ты, что вдохнул в меня душу и научил радоваться жизни, ты один мне нужен на всю жизнь”.
Кончив сказку, Леонардо взглянул на Монну Лизу, ее лицо озарилось светом, глаза сияли. Потом, точно пробудившись от сна, она вздохнула, провела по лицу рукой и без слов пошла на свое место, сложила руки и приняла обычную позу. Но дело было сделано – художник пробудил равнодушную
статую ; улыбка блаженства, медленно исчезая с ее лица, осталась в уголках рта и трепетала, придавая лицу изумительное, загадочное и чуть лукавое выражение, как у человека, который узнал тайну и, бережно ее храня, не может сдержать торжество. Леонардо молча работал, боясь упустить этот момент, этот луч солнца, осветивший его скучную модель. .. портрета . Толковали о естественности выражения, о простоте позы, о красоте рук. Художник сделал еще небывалое: на картине изображен воздух, он окутывает фигуру прозрачной дымкой. Несмотря на успех, Леонардо был мрачен, положение во Флоренции показалось художнику тягостным, он собрался в дорогу. Не помогли ему напоминания о нахлынувших заказах.
.. портрета . Толковали о естественности выражения, о простоте позы, о красоте рук. Художник сделал еще небывалое: на картине изображен воздух, он окутывает фигуру прозрачной дымкой. Несмотря на успех, Леонардо был мрачен, положение во Флоренции показалось художнику тягостным, он собрался в дорогу. Не помогли ему напоминания о нахлынувших заказах.
20.05.2017
Золотое сечение – это то, о чем должен знать каждый дизайнер. Мы объясним, что это такое, и как вы можете его использовать.
Существует общее математическое соотношение, найденное в природе, которое может быть использовано в дизайне для создания приятных, натурально-выглядящих композиций. Его называют Золотым Сечением или греческой буквой “фи”. Если вы иллюстратор, арт директор или графический дизайнер, вам определенно стоит использовать Золотое Сечение в каждом проекте.
В этой статье мы объясним, как его использовать, а также поделимся несколькими отличными инструментами для дальнейшего вдохновения и изучения.
Тесно связанная с Последовательностью Фибоначи (Fibonacci Sequence), которую вы, возможно, помните из уроков математики или романа Дэна Брауна “Код Да Винчи”, Золотое Сечение описывает идеально симметричное взаимоотношение между двумя пропорциями.
Приблизительно равное соотношению 1: 1.61, Золотое Сечение может быть иллюститровано как Золотой Прямоугольник: большой прямоугольник, включающий квадрат (в котором стороны равны длине самой короткой стороны прямоугольника) и прямоугольник поменьше.
Если убрать квадрат из прямоугольника, останется другой, маленький Золотой Прямоугольник. Этот процесс может продолжаться до бесконечности, как и цифры Фибоначи, которые работают в обратном порядке. (Добавление квадрата со сторонами, равными длине самой длинной стороны прямоугольника, приближает вас к Золотому Прямоугольнику и Золотому Сечению.)
Золотое Сечение в действии
Считается, что Золотое Сечение используется уже около 4000 лет в искусстве и дизайне. Однако, многие люди соглашаются, что при строительстве Египетских Пирамид также использовался этот принцип.
Однако, многие люди соглашаются, что при строительстве Египетских Пирамид также использовался этот принцип.
В более современные времена это правило может быть замечено в музыке, искусстве и дизайне вокруг нас. Применяя аналогичную рабочую методологию, вы можете привнести в свою работу те же особенности дизайна. Давайте взглянем на несколько вдохновляющих примеров.
Греческая архитектура
В древнегреческой архитектуре Золотое Сечение использовалось для определения приятных пространственных отношений между шириной здания и его высотой, размером портика и даже положением колонн, поддерживающих структуру.
В результате получается идеально пропорциональное строение. Движение неоклассической архитектуры также использовало эти принципы.
Тайная вечеря
Леонардо Да Винчи, как и многие другие художники прошлых лет, часто использовал Золотое Сечение для создания приятных композиций.
В Тайной вечере фигуры расположены в нижних двух третях (самая большая из двух частей Золотого Сечения), а Иисус идеально зарисован между золотых прямоугольников.
Золотое сечение в природе
Существует множество примеров Золотого Сечения в природе – их вы можете обнаружить вокруг себя. Цветы, морские раковины, ананасы и даже пчелиные соты демонстрируют одинаковое соотношение.
Как рассчитать Золотое Сечение
Рассчет Золотого Сечения достаточно прост, и начинается с простого квадрата:
01. Нарисуйте квадрат
Он образует длину короткой стороны прямоугольника.
02. Разделите квадрат
Разделите квадрат пополам с помощью вертикальной линии, образуя два прямоугольника.
03. Проведите диагональ
В одном из прямоугольников проведиде линию из одного угла в противоположный.
04. Поверните
Поверните эту линию так, чтобы она легла горизонтально по отношению к первому прямоугольнику.
05. Создайте новый прямоугольник
Создайте прямоугольник, используя новую горизонтальную линию и первый прямоугольник.
Как использовать Золотое Сечение
Использовать этот принцип проще, чем вы думаете. Существует пара быстрых трюков, которые вы можете использовать в своих макетах, или потратить немного больше времени и полностью раскрыть концепт.
Существует пара быстрых трюков, которые вы можете использовать в своих макетах, или потратить немного больше времени и полностью раскрыть концепт.
Быстрый способ
Если вы когда-нибудь сталкивались с “Правилом третей”, то вам будет знакома идея разделения пространства на равные трети по вертикали и горизонтали, при этом места пересечения линий создают естественные точки для объектов.
Фотограф размещает ключевой объект на одной из этих пересекающихся линий, чтобы создать приятную композицию. Этот прицип может также использоваться в вашей разметке страниц и дизайне постеров.
Правило третей можно применять к любой форме, но если вы примените его к прямоугольнику с пропорциями примерно 1: 1.6, вы окажетесь очень близко к золотому прямоугольнику, что сделает композицию более приятной для глаз.
Полная реализация
Если вы хотите реализовать Золотое Сечение в вашем дизайне в полной мере, то просто расположите основной контент и сайдбар (в веб дизайне) в соотношении равном 1: 1. 61.
61.
Можно округлить значения в меньшую или большую стороны: если контент-зона равна 640px, а сайдбар 400px, то эта разметка вполне подойдет под Золотое Сечение.
Разумеется, вы также можете разделить области контента и боковой панели на одно и то же отношение, а связь между заголовком веб-страницы, областью содержимого, футером и навигацией также может быть спроектирована с использованием того же приципа.
Полезные инструменты
Вот несколько инструментов, которые помогут вам в использовании Золотого Сечения в дизайне и создании пропорциональных проектов.
GoldenRATIO – это приложение для создания дизайна веб сайтов, интерфейсов и шаблонов, подходящих под Золотое Сечение. Доступно в Mac App Store за 2,99$. Включает визуальный калькулятор Золотого Сечения.
Так же в приложении есть функция “Избранное”, которое сохраняет настройки для повторяющихся задач и “Click-thru” мод, позволяющий сворачивать приложение в Photoshop.
Этот калькулятор Золотого Сечения от Pearsonified помогает в создании идеальной типографики для вашего сайта. Введите размер шрифта, ширину контейнера в поле, и нажмите кнопку Set my type! Если вам нужно оптимизировать количество букв в строчке, вы можете дополнительно ввести значение CPL.
Введите размер шрифта, ширину контейнера в поле, и нажмите кнопку Set my type! Если вам нужно оптимизировать количество букв в строчке, вы можете дополнительно ввести значение CPL.
Это простое, полезное и бесплатное приложение доступно для Mac и PC. Введите любое число, и приложение вычислит вторую цифру в соответствии с приципом Золотого Сечения.
Это приложение позволяет проектировать с золотыми пропорциями, экономя кучу времени на вычислениях.
Вы можете менять формы и размеры, фокусируясь на работе над своим проектом. Постоянная лицензия стоит 49$, но вы можете скачать бесплатную версию на месяц.
Обучение Золтому Сечению
Вот несколько полезных туториалов по Золотому Сечению (английский язык):
В этом туториале для Digital Arts Роберто Маррас (Roberto Marras) показывает, как использовать Золотое Сечение в художественной работе.
Туториал от Tuts+, рассказывающий, как использовать золотые принципы в веб дизайн проектах.
Туториал от Smashing Magazine, рассказывающий о пропорциях и правиле третей.
Эта гармония поражает своими масштабами…
Здравствуйте, друзья!
Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?
Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.
Да, в статье много изображений, формул, как-никак, золотое сечение — это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)
Что такое золотое сечение?
Если по-простому, то золотое сечение — это определенное правило пропорции, которое создает гармонию ?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.
Но, кроме этого, золотое сечение — это математика: у него есть конкретная формула и конкретное число. Многие математики, вообще, считают его формулой божественной гармонии, и называют «асимметричной симметрией».
До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.
Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1. 6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.
6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.
В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:
Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:
Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.
Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:
Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:
Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.
Ряд Фибоначчи и золотое сечение
Продолжаем творить и наблюдать за магией математики и золотого сечения. В средние века был такой товарищ — Фибоначчи (или Фибоначи, везде по-разному пишут). Любил математику и задачи, была у него и интересная задачка с размножением кроликов =) Но не в этом суть. Он открыл числовую последовательность, числа в ней так и зовутся «числа Фибоначчи».
Сама последовательность выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… и дальше до бесконечности.
Если словами, то последовательность Фибоначчи — это такая последовательность чисел, где каждое последующее число, равно сумме двух предыдущих.
Причем здесь золотое сечение? Сейчас увидите.
Спираль Фибоначчи
Чтобы увидеть и прочувствовать всю связь числового ряда Фибоначчи и золотого сечения, нужно снова взглянуть на формулы.
Иными словами, с 9-го члена последовательности Фибоначчи мы начинаем получать значения золотого сечения. И если визуализировать всю эту картину, то мы увидим, как последовательность Фибоначчи создает прямоугольники все ближе и ближе к золотому прямоугольнику. Вот такая вот связь.
Теперь поговорим о спирали Фибоначчи, ее еще называют «золотой спиралью».
Золотая спираль — логарифмическая спираль, коэффициент роста которой равен φ4, где φ — золотое сечение.
В общем и целом, с точки зрения математики, золотое сечение — идеальная пропорция. Но на этом ее чудеса только начинаются. Принципам золотого сечения подчинен почти весь мир, эту пропорцию создала сама природа. Даже эзотерики, и те, видят в ней числовую мощь. Но об этом точно не в этой статье будем говорить, поэтому, чтобы ничего не пропустить, можете подписаться на обновления сайта.
Золотое сечение в природе, человеке, искусстве
Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.
И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.
Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.
Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.
Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.
Все надо рассчитывать, относительно чего-то другого.
Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:
от плеч до макушки к размеру головы = 1:1.618
от пупка до макушки к отрезку от плеч до макушки = 1:1.618
от пупка до коленок и от коленок до ступней = 1:1.618
от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618
Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».
Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.
Золотое сечение в природе и ее явлениях
Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:
в завитках человеческого уха мы можем увидеть золотую спираль;
ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;
и в молекуле ДНК;
по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.
Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.
Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:
Смотрите:
Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.
Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.
Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.
Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.
По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.
Абсолютно во всем живом и не живом можно прочесть высшую красоту и гармонию.
Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет. Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил.
Золотое сечение в искусстве
Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.
Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.
В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.
В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.
Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.
Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.
Золотые котики Фибоначчи
Ну и, наконец, о котиках! Вы задумывались о том, почему все так любят котеек? Они же ведь заполонили Интернет! Котики везде и это чудесно =)
А все дело в том, что кошки — идеальны! Не верите? Сейчас докажу вам это математически!
Видите? Тайна раскрыта! Котейки идеальны с точки зрения математики, природы и Вселенной =)
* Я шучу, конечно. Нет, кошки, действительно, идеальны) Но математически их никто не измерял, наверное.
Нет, кошки, действительно, идеальны) Но математически их никто не измерял, наверное.
На этом, в общем-то, все, друзья! Мы увидимся в следующих статьях. Удачи вам!
P. S. Изображения взяты с сайта medium.com.
/ Forens.Ru — 2008.
библиографическое описание:
Золотое сечение в анатомии человека / Forens.Ru — 2008.
Последние поступления в библиотеку
Аспекты молекулярно-генетического исследования волос человека в зависимости от их морфологических характеристик. II. Особенности генотипирования / Александрова В.Ю., Богатырева Е.А., Куклев М.Ю., Лапенков М.И., Плахина Н.В. // Судебно-медицинская экспертиза. — М., 2019. — №2. — С. 22-25.
Возможность определения расстояния выстрела из охотничьего оружия 12-го калибра по признакам повреждений одежды и соответствующим им математическим моделям / Суворов А.С., Белавин А.В., Макаров И.Ю., Страгис В.Б., Райзберг С.А., Гюльмамедова Н.Д. // Судебно-медицинская экспертиза. — М., 2019. — №2. — С. 19-21.
— №2. — С. 19-21.
Комплексная судебная экспертиза изображений внешнего облика человека / Россинская Е.Р., Зинин А.М. // Судебно-медицинская экспертиза. — М., 2019. — №2. — С. 15-18.
Структура смертельной механической травмы в России (по материалам 2003-2017 гг.) / Ковалев А.В., Макаров И.Ю., Самоходская О.В., Куприна Т.А. // Судебно-медицинская экспертиза. — М., 2019. — №2. — С. 11-14.
Методологические подходы к производству судебно-медицинской экспертизы состояния здоровья детей в случаях пренебрежения их нуждами / Ковалев А.В., Кеменева Ю.В. // Судебно-медицинская экспертиза. — М., 2019. — №2. — С. 4-10.
Каждый человек, сталкивающийся с геометрией объектов в пространстве, хорошо знаком с методом золотого сечения. Его применяют в искусстве, дизайне интерьеров и архитектуре. Еще в прошлом столетии золотое сечение оказалось таким популярным, что теперь многие сторонники мистического видения мира дали ему другое название — универсальное гармоническое правило. Особенности этого метода стоит рассмотреть подробнее. Это поможет узнать, почему он пользуется интересом сразу в нескольких сферах деятельности — искусстве, архитектуре, дизайне.
Особенности этого метода стоит рассмотреть подробнее. Это поможет узнать, почему он пользуется интересом сразу в нескольких сферах деятельности — искусстве, архитектуре, дизайне.
Суть универсальной пропорции
Принцип золотого сечения является всего лишь зависимостью чисел. Однако многие относятся к нему предвзято, приписывая этому явлению какие-то мистические силы. Причина кроется в необычных свойствах правила:
- Многие живые объекты обладают пропорциями туловища и конечностей, приближенными к показаниям золотого сечения.
- Зависимости 1,62 или 0,63 определяют отношения размеров лишь для живых существ. Объекты, относящиеся к неживой природе, очень редко соответствуют значению гармонического правила.
- Золотые пропорции строения туловища живых существ представляют собой неотъемлемое условие выживания многих биологических видов.
Золотое сечение можно найти в строении тел различных животных, стволов деревьев и корней кустарников. Сторонники универсальности этого принципа стараются доказать, что его значения жизненно важны для представителей живого мира.
Можно объяснить метод золотого сечения, используя образ куриного яйца. Отношение отрезков от точек скорлупы, в равной степени удаленных от центра тяжести, равно показателю золотого сечения. Самым важным для выживания птиц показателем яйца является именно его форма, а не прочность скорлупы.
Важно! Золотое сечение рассчитано на основе измерений множества живых объектов.
Происхождение золотого сечения
Об универсальном правиле было известно еще математикам Древней Греции. Ее использовал Пифагор и Евклид. В известном архитектурном шедевре — пирамиде Хеопса отношение размеров основной части и длины сторон, а также барельефов и декоративных деталей соответствуют гармоническому правилу.
Метод золотого сечения взяли на вооружение не только архитекторы, но и художники. Тайна гармонической пропорции считалась одной из величайших загадок.
Первым, документально заверившим универсальную геометрическую пропорцию, был монах-францисканец Лука Пачоли. Его способности к математике были блестящи. Широкое признание золотое сечение получило после публикации результатов исследований золотого сечения Цейзинга. Он изучал пропорции тела человека, древние памятники скульптуры, растения.
Его способности к математике были блестящи. Широкое признание золотое сечение получило после публикации результатов исследований золотого сечения Цейзинга. Он изучал пропорции тела человека, древние памятники скульптуры, растения.
Как рассчитали золотое сечение
Разобраться, что такое золотое сечение, поможет объяснение, основанное на длинах отрезков. К примеру, внутри большого находится несколько маленьких. Тогда длины небольших отрезков относятся к общей длине большого отрезка, как 0,62. Такое определение помогает разобраться, на сколько частей можно поделить определенную линию, чтобы она соответствовала гармоническому правилу. Еще один плюс использования этого метода — можно узнать, каким должно быть отношение самого большого отрезка к длине всего объекта. Это соотношение равняется 1,62.
Такие данные можно представить, как пропорции измеряемых объектов. Сначала их выискивали, подбирая опытным путем. Однако теперь точные соотношения известны, поэтому построить объект в соответствии с ними не составит труда. Золотое сечение находят такими путями:
Золотое сечение находят такими путями:
- Построить прямоугольный треугольник. Разбить одну из его сторон, а затем провести перпендикуляры с секущими дугами. При проведении вычислений следует от одного конца отрезка построить перпендикуляр, равный ½ его длины. Затем достраивают прямоугольный треугольник. Если отметить точку на гипотенузе, которая покажет длину перпендикулярного отрезка, то радиус, равняющийся оставшейся части линии, рассечет основание на две половины. Получившиеся линии будут соотноситься друг с другом согласно золотому сечению.
- Универсальные геометрические значения получают и другим способом — выстраивая пентаграмму Дюрера. Она является звездой, которая помещена в окружность. В ней находится 4 отрезка, длины которых соответствуют правилу золотого сечения.
- В архитектуре гармоническая пропорция применяется в модифицированном виде. Для этого прямоугольный треугольник следует разбивать по гипотенузе.
Важно!
Если сравнивать с классическим понятием метода золотого сечения, версия для архитекторов имеет соотношение 44:56.
Если в традиционном толковании гармонического правила для графики, его рассчитывали как 37:63, то для архитектурных сооружений чаще использовали 44:56. Это обусловлено необходимостью сооружать высотные постройки.
Секрет золотого сечения
Если в случае с живыми объектами золотое сечение, проявляющееся в пропорциях тела людей и животных можно объяснить необходимостью приспосабливаться к среде, то в использование правила оптимальных пропорций в 12 веке для постройки домов было в новинку.
Парфенон, сохранившийся со времен Древней Греции, был возведен по методу золотого сечения. Множество замков вельмож средних веков создавали с параметрами, соответствующими гармоническому правилу.
Золотое сечение в архитектуре
Множество построек древности, которые сохранились до сих пор, служат подтверждением тому, что архитекторы из эпохи средневековья были знакомы с гармоническим правилом. Очень хорошо заметно стремление соблюсти гармоническую пропорцию при сооружении церквей, значимых общественных зданий, резиденций королевских особ.
К примеру, собор Парижской Богоматери возведен таким образом, что многие из его участков соотносится с правилом золотого сечения. Можно найти немало произведений архитектуры 18 века, которые были построены в согласии с этим правилом. Правило применяли и многие русские архитекторы. Среди них был и М. Казаков, который создавал проекты усадеб и жилых зданий. Он проектировал здание сената и Голицынскую больницу.
Естественно, дома с таким отношением частей возводили и до открытия правила золотого сечения. Например, к таким зданиям относится церковь Покрова на Нерли. Красота здания приобретает еще большую загадочность, если учесть, что здание покровской церкви было возведено в XVIII веке. Однако современный вид постройка приобрела после реставрации.
В трудах о золотом сечении упоминается, что в архитектуре восприятие объектов зависит от того, кто наблюдает. Пропорции, образованные при помощи золотого сечения, дают максимально спокойное соотношение частей строения относительно друг друга.
Ярким представителем из ряда строений, соответствующих универсальному правилу, является памятник архитектуры Парфенон, возведенный еще в пятом веке до н. э. Парфенон устроен с восьмью колоннами по меньшим фасадам и с семнадцатью — по большим. Храм возведен из благородного мрамора. Благодаря этому использование раскраски ограничено. Высота строения относится к его длине 0,618. Если разделить Парфенон по пропорциям золотого сечения, получатся определенные выступы фасада.
Все эти сооружения имеют одно сходство — гармоничность сочетания форм и отменное качество строительства. Это объясняется использованием гармонического правила.
Важность золотого сечения для человека
Архитектура древних построек и средневековых домов довольно интересна и для дизайнеров современности. Это объясняется такими причинами:
- Благодаря оригинальному оформлению домов можно не допустить надоевших штампов. Каждое такое здание является архитектурным шедевром.
- Массовое применение правила для украшения скульптур и статуй.

- Благодаря соблюдению гармонических пропорций взгляд притягивается к более важным деталям.
Важно! При создании проекта постройки и создании внешнего облика архитекторы средневековья применяли универсальные пропорции, опираясь на закономерности человеческого восприятия.
Сегодня психологи пришли к выводу, что принцип золотого сечения — не что иное, как человеческая реакция на определенное соотношение размеров и форм. В одном эксперименте группе испытуемых предложили согнуть бумажный лист таким образом, чтобы стороны получились с оптимальными пропорциями. В 85 результатах из 100 люди сгибали лист практически в точном соответствии с гармоническим правилом.
Как утверждают современные ученые, показатели золотого сечения относятся скорее к сфере психологии, нежели характеризуют закономерности физического мира. Это объясняет, почему к нему проявляется такой интерес со стороны мистификаторов. Однако при построении объектов согласно этому правилу человек воспринимает их более комфортно.
Использование золотого сечения в дизайне
Принципы использования универсальной пропорции все чаще используют при строительстве частных домов. Особое внимание уделяется соблюдению оптимальных пропорций конструкции. Немало внимания уделяют правильному распределению внимания внутри дома.
Современная интерпретация золотого сечения уже не относится лишь к правилам геометрии и формы. Сегодня принципу гармонических пропорций подчиняются не только размеры деталей фасада, площадь комнат или длины фронтонов, но и цветовая палитра, используемая при создании интерьера.
Соорудить гармоничное строение на модульном основании гораздо проще. Многие отделения и помещения в этом случае выполняются как отдельные блоки. Они проектируются в строгом соответствии с гармоническим правилом. Возвести здание как набор отдельных модулей, значительной проще, чем создавать единую коробку.
Многие фирмы, занимающиеся сооружением загородных домов, при создании проекта соблюдают гармоническое правило. Это позволяет создать у клиентов впечатление, что конструкция здания детально проработана. Такие дома обычно описывают, как наиболее гармоничные и комфортные в использовании. При оптимальном выборе площадей комнат жильцы психологически ощущают успокоение.
Это позволяет создать у клиентов впечатление, что конструкция здания детально проработана. Такие дома обычно описывают, как наиболее гармоничные и комфортные в использовании. При оптимальном выборе площадей комнат жильцы психологически ощущают успокоение.
Если дом возведен без учета гармонических пропорций, можно создать планировку, которая будет по соотношению размеров стен приближена к показателю 1:1,61. Для этого в комнатах устанавливают дополнительные перегородки, или переставляют предметы мебели.
Аналогично меняют габариты дверей и окон таким образом, чтобы проем имел ширину, показатель которой меньше значения высоты в 1,61 раза.
Сложнее подбирать цветовые решения. В этом случае можно соблюдать упрощенное значение золотого сечения — 2/3. Основным цветовым фоном следует занять 60% пространства комнаты. Оттеняющий оттенок занимает 30% помещения. Оставшаяся площадь поверхностей закрашивается близкими друг к другу тонами, усиливающими восприятие выбранного цвета.
Внутренние стены комнат делят горизонтальной полосой. Ее располагают в 70 см от пола. Высота мебели должна находиться в гармоническом соотношении с высотой стен. Это правило относится и к распределению длин. К примеру, диван должен иметь габариты, которые бы оказались не меньше 2/3 длины простенка. Площадь помещения, которая занята предметами мебели, тоже должна иметь определенное значение. Она относится к общей площади всего помещения как 1:1,61.
Золотая пропорция сложно применима на практике ввиду наличия всего одного числа. Именно поэтому. Проектирую гармоничные строения, пользуются рядом чисел Фибоначчи. Благодаря этому обеспечивается разнообразие вариантов форм и пропорций деталей строения. Ряд чисел Фибоначчи также носит название золотого. Все значения строго соответствуют определенной математической зависимости.
Кроме ряда Фибоначчи, в современной архитектуре применяют и другой метод проектирования — принцип, заложенный французским архитектором Ле Корбюзье.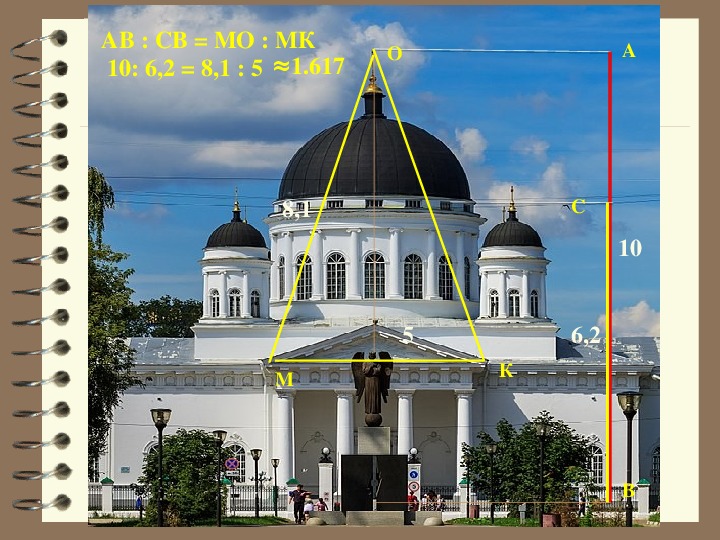 При выборе этого способа отправной единицей измерения выступает рост владельца дома. Исходя из этого показателя рассчитывают размеры здания и внутренних помещений. Благодаря этому подходу дом получается не только гармоничным, но и приобретает индивидуальность.
При выборе этого способа отправной единицей измерения выступает рост владельца дома. Исходя из этого показателя рассчитывают размеры здания и внутренних помещений. Благодаря этому подходу дом получается не только гармоничным, но и приобретает индивидуальность.
Любой интерьер приобретет более завершенный вид, если в нем использовать карнизы. При использовании универсальных пропорций можно вычислить его размер. Оптимальными показателями являются 22,5, 14 и 8,5 см. Устанавливать карниз следует по правилам золотого сечения. Маленькая сторона декоративного элемента должна относиться к большей так, как относится к сложенным значениям двух сторон. Если большая сторона будет равна 14 см, то маленькую стоит сделать 8,5 см.
Придать помещению уюта можно путем деления стеновых поверхностей при помощи гипсовых зеркал. Если стена поделена бордюром, от оставшейся большей части стены следует отнять высоту карнизной планки. Для создания зеркала оптимальной длины от бордюра и карниза следует отступить одинаковое расстояние.
Заключение
Дома, построенные по принципу золотого сечения, действительно получаются очень удобными. Однако цена постройки таких строений довольно высока, поскольку стоимость стройматериалов ввиду нетипичных размеров увеличивается на 70%. Этот подход совершенно не нов, поскольку большинство домов прошлого века создавали исходя из параметров хозяев.
Благодаря использованию метода золотого сечения в строительстве и дизайне здания получаются не только комфортабельными, но и долговечными. Они выглядят гармонично и привлекательно. Интерьер тоже оформляют по универсальной пропорции. Это позволяет грамотно использовать пространство.
В таких комнатах человек ощущает себя максимально комфортно. Соорудить дом с использованием принципа золотого сечения можно самостоятельно. Главное — рассчитать нагрузки на элементы строения, и правильно выбрать материалы.
Метод золотого сечения используют в дизайне интерьера, размещая в комнате декоративные элементы определенных размеров. Это позволяет придать помещению уюта. Цветовые решения тоже выбирают в соответствии с универсальными гармоническими пропорциями.
Это позволяет придать помещению уюта. Цветовые решения тоже выбирают в соответствии с универсальными гармоническими пропорциями.
Золотое сечение в архитектуре —
Золотое сечение в архитектуре
Опубликовано [email protected] 18 июля 2014 г. / 0 комментариев+Что такое золотое сечение?
«Витрувианский человек» Леонардо да Винчи, демонстрирующий золотое сечение в размерах тела.
Золотое сечение, или Божественная пропорция, относится к количеству пространства между объектами или отношениям между числами.Золотое сечение, встречающееся в природе, чаще всего в раковине наутилуса, применяется во множестве контекстов: в искусстве, математике, дизайне и архитектуре, и при соблюдении правил делает эти объекты наиболее визуально привлекательными.
Это в основном то же самое, на что ссылаются фотографы, говоря о правиле третей. При съемке изображения фотограф делит их композицию на трети, а затем выстраивает объект в перекрестие перекрестия 1/3. Если бы они взяли это правило немного дальше, ближе к 1:1.618, это будет соответствовать Божественному Соотношению.
Если бы они взяли это правило немного дальше, ближе к 1:1.618, это будет соответствовать Божественному Соотношению.
Золотой прямоугольник показывает соотношение 1:1,68
Архитекторы используют золотое сечение в дизайне, потому что красота — это наука.
+Где вы находите применение золотого сечения в архитектуре?
- Золотое сечение применялось в Древнем Риме.
- Золотое сечение, используемое в проектах жилых домов.
- Золотое сечение используется пуристами, такими как швейцарский архитектор Лекрузье.
+Как использовать золотое сечение в своих проектах?
Я пурист. Я считаю архитектуру академическим искусством, наукой. Когда я проектирую пространство для клиента, я сначала смотрю, каковы физические требования. После этого я проектирую на основе психологических требований.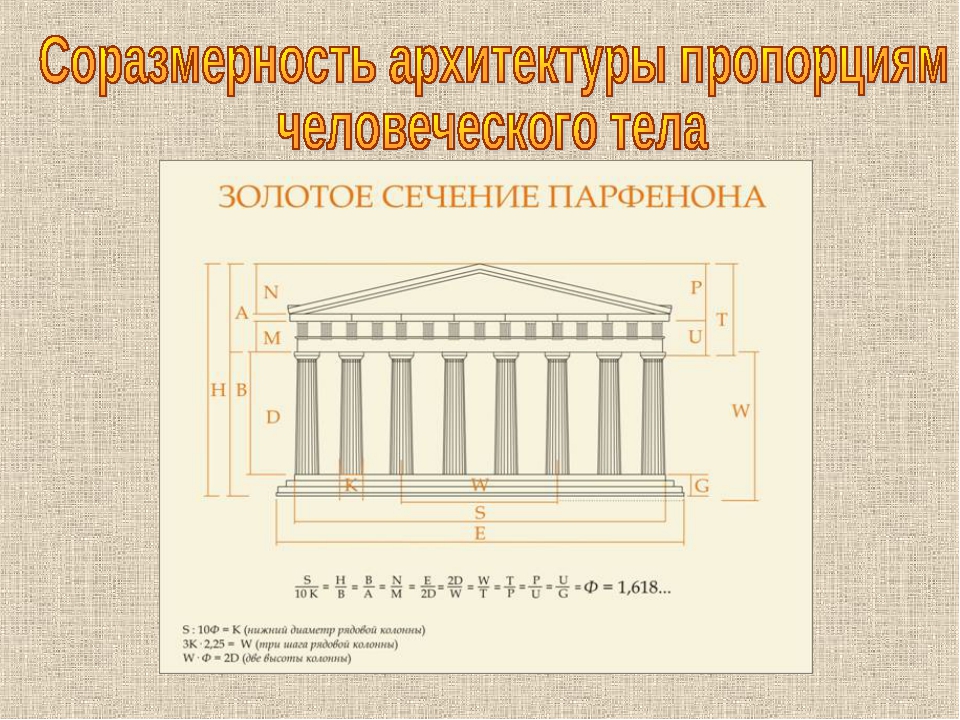 Как цвета влияют на ваше настроение, так и пропорции.Ритм вашего жизненного пространства так же важен для того, чтобы вы чувствовали себя как дома. В пространстве, которое имеет для нас значение, существует особый порядок. Этот порядок основан на концепции Божественного или Золотого сечения.
Как цвета влияют на ваше настроение, так и пропорции.Ритм вашего жизненного пространства так же важен для того, чтобы вы чувствовали себя как дома. В пространстве, которое имеет для нас значение, существует особый порядок. Этот порядок основан на концепции Божественного или Золотого сечения.
Где размещать окна, как располагать двери и т. д. — все определяется золотой пропорцией.
+ Забавный факт
Если вы измерите расстояние от пола до пупка, а затем умножите это на 1,618, вы получите более или менее свой рост. На самом деле, чем больше вы соответствуете божественному соотношению, тем вы привлекательнее.
(PDF) Как изучить золотое сечение в архитектуре и проектировании Город
Wezha Hawez Baiz. Междунар. Journal of Engineering Research and Application www.ijera.com
ISSN: 2248-9622, Vol. 6, выпуск 8, (часть -4) август 2016 г., стр. 01-07
,
VII. ИСПОЛЬЗОВАНИЕ ЗОЛОТОЙ СПИРЛИ В ГОРОДЕ
ДИЗАЙН
На двух рисунках ниже (13) и (14)
показано, как концепция городского распределения получает
выгоду от формы наутилуса. Например,
Например,
прямых линий пересечения кривых наутилуса
могут создавать различные требования к
городу, такие как уличная сеть, пешеходы, каналы,
городские бульвары как доступ к центральной части города,
парки, и так далее. так как ясно, что в линейном и
круглые размеры городских кварталов становятся меньше в центральном городе
и плотность более интенсивна, то же самое верно для спирального города
, плотность которого
увеличивается и размеры блоков становятся на
меньше в центре города.Кроме того, пересечение
прямых линий и кривых линий
позволяет городу обеспечить жилые районы,
объекты, услуги и парки, даже больше,
меньших кривых линий позволяют жителям обеспечить
передвижение и транспортная деятельность
по всему городу даже на велосипеде или
мобильность. Большие транспортные маршруты во внешней части города
создадут огромные зеленые насаждения.
Рисунок (13): показан спиральный заголовок Рисунок (14): показан план города в виде золотой спирали
Источник: веб-сайт The Guardian, 2015 г. Источник: веб-сайт The Guardian, 2015 г.
VIII. ЗАКЛЮЧЕНИЕ И
РЕКОМЕНДАЦИЯ
Исходя из того, что было объяснено выше,
правил и принципов следует учитывать для
эстетических целей. Дизайн — это не просто набросок
и поиск красивой формы. Нет никаких сомнений в том, что на проектирование зданий
влияют многие факторы, такие как форма земли,
местоположение, окружающая среда и так далее.По сути, есть
несколько принципов, которые дизайнеры должны учитывать при создании эскизов и
проектов. В этом исследовании рассматривается одна из основных
частей, а именно золотое сечение.
В этом исследовании выясняется, что существуют
принципы и основы проектирования архитектуры,
связанные с математикой в целом. Очевидно,
, что математика обладает особой эстетикой, если она относительно более правильно использовала
при проектировании зданий. Эта математика
Эта математика
касается не только чисел, она
также касается отношения и соотношения между числами
. Золотое сечение для архитекторов — это глобальный термин
, используемый в различных областях, таких как
. мебель, малоэтажное строительство и небоскребы.
Практические примеры и доказательства показывают, что золотое сечение
оказывает влияние на архитектуру. В
реальности золотое сечение касается не только уравнения
и правил, но и может быть применено к очень подробной
архитектуре в различных масштабах.Во многих случаях
архитектуры рассматривают красоту и аргументы
в их дизайне нуждаются в доказательствах. В основном математические
представляют доказательства и истину. Во многих случаях дизайнеры
могут использовать математику в качестве золотого сечения для проверки
своих работ. Можно сделать вывод, что понимание принципов
почти очень важно для архитектуры
.
БИБЛИОГРАФИЯ
[1]. Чинг, Ф.Д. К. (2007), Архитектура: форма,
пространство и порядок. 3-е издание. Канада:
John Wiley & Sons, Inc.
[2]. Чинг, Ф.Д. К. (1995) визуальный словарь
архитектуры. Канада: John Wiley &
Sons, Inc.
[3]. Вайднер, Д. (2012), Дом с золотым сечением: конструкция формы
. Магистр диссертации. Политехнический институт Вирджинии
и Государственный университет
.
[4]. Ла Вин, Л., (2001) Механика и
Значение в архитектуре. Лондон:
Университет Миннесоты.
[5]. Эдвардс, Б. и др. (2006). Двор
Жилье: прошлое, настоящее, будущее. США:
Тейлор и Фрэнсис.
[6]. Мд. Ахтаруззаман*, Амир А. Шафи
(2011). Геометрическое обоснование Фи,
Золотое сечение и барокко
Природа, Архитектура, Дизайн и
Инженерия.Международный журнал искусств
2011; 1(1): 1-22 DOI:
10.5923/j.arts.20110101.01.
[7].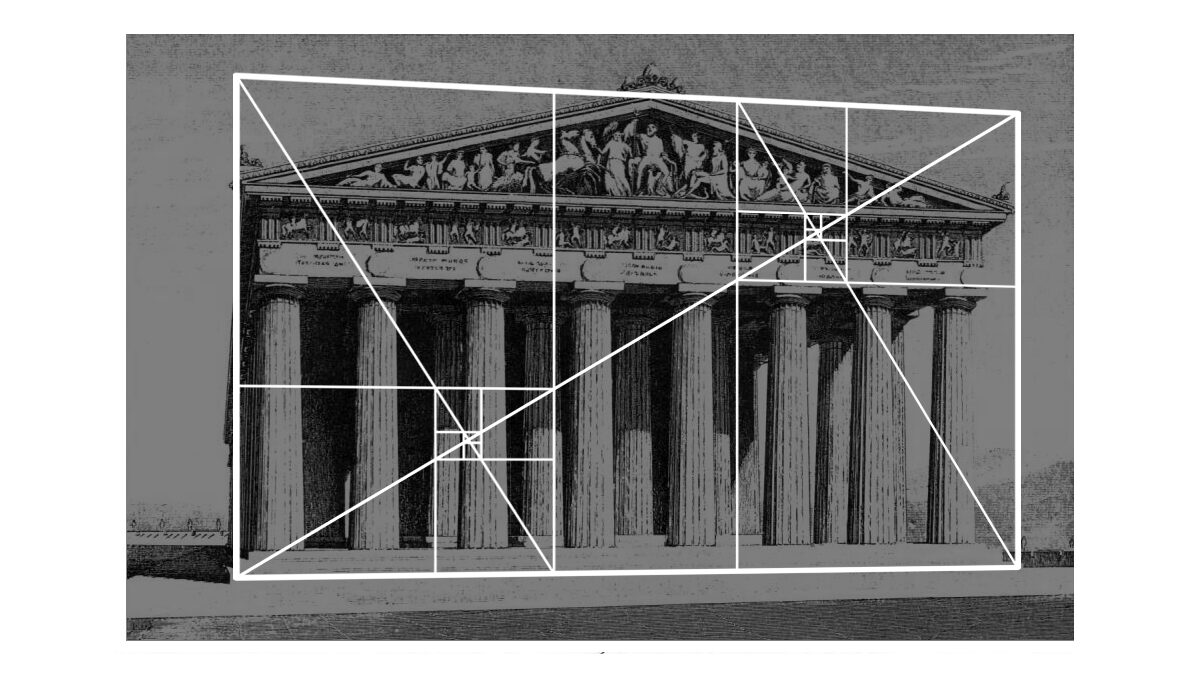 Бозинофф, М. (2015). Откуда
Бозинофф, М. (2015). Откуда
знания о взаимосвязи между математикой
чисел Фибоначчи и золотым сечением в искусстве, архитектуре и музыке
чисел Фибоначчи и золотым сечением в искусстве, архитектуре и музыкеВ этом разделе представлены некоторые появления ряда Фибоначчи и золотого сечения в архитектуры, искусства и музыки.
Содержание этой страницы
Значок означает в конце раздела есть что нужно сделать.1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..Больше..
Золотое сечение в архитектуре.
Парфенон и греческая архитектура
Древние греки знали о прямоугольнике, стороны которого находятся в золотом
пропорция (1 : 1.618, что соответствует 0,618:1). Это происходит естественным образом
в некоторых
пропорции Пяти Платоновых Тел
(как мы уже видели). Конструкция для
точка золотого сечения находится в
Элементы Евклида.
Золотой прямоугольник, как предполагается, появляется во многих пропорциях этого знаменитого
древнегреческий храм Парфенон на Акрополе в Афины , Греция, но нет оригинальных документальных свидетельств того, что это было преднамеренно
разработан в. (Есть копия оригинального здания (с точностью до одной восьмой дюйма!)
Нэшвилл
который называет себя «Афины Южной Америки».)
(Есть копия оригинального здания (с точностью до одной восьмой дюйма!)
Нэшвилл
который называет себя «Афины Южной Америки».)
Акрополь (видеть схематический план или План Роя Джорджа Парфенона с активными точками, по которым можно щелкнуть для просмотра фотографий), в центре Афин находится обнажение скалы возвышается над древним городом. Его самым известным памятником является Парфенон, храм богини. Афина построена вокруг 430 или 440 г. до н.э.Он в значительной степени находится в руинах, но сейчас проходит некоторую реставрацию (см. на сайте Роя Джорджа по ссылке выше).
Опять же, оригинальных планов самого Парфенона нет. Похоже, построен на схеме золотых прямоугольников и прямоугольников корня-5:
- вид спереди (см. схему выше): золотой прямоугольник, ширина которого в Phi больше высоты
- вид сверху: 5, пока передняя часть широкая поэтому площадь пола равна квадратному корню из 5 прямоугольник
 чтобы противодействовать оптической иллюзии изогнутых линий уровня, это только приблизительные
меры, но достаточно хорошие.
чтобы противодействовать оптической иллюзии изогнутых линий уровня, это только приблизительные
меры, но достаточно хорошие.| Изображение Панфенона здесь показывает четкие золотые сечения в расположении трех горизонтальных линий. но общая форма и другие характерные черты соответствуют пропорциям золотого сечения 90 272, а не 90 273. | Пантеон, Либеро Патриньяни |
Ссылки
Современная архитектура
Новое учебное здание проекта «Эдем»
Проект Эдем в с.Остел, между Плимутом и Пензансом на юго-западе Англии и в 50 милях от Лендс-Энда, есть несколько удивительно впечатляющих теплиц, основанных на геодезических куполах (называемых биомами), построенных в старый карьер. Он отмечает тысячелетие в 2000 году и в настоящее время является одной из самых популярных туристических достопримечательностей на юго-западе Англии.
Новые 15 миллионов фунтов стерлингов Образовательный центр под названием The Core был разработан с использованием чисел Фибоначчи и спиралей растений отражать характер участка – растения из по всему миру.
 На логотипе изображен рисунок панелей на крыше.
На логотипе изображен рисунок панелей на крыше. Что имеет возраст 300 миллионов лет, весит 70 тонн и является самым большим в мире? Это новая скульптура под названием «Семя». в центре Ядра, который был открыт в День летнего солнцестояния 2007 года (23 июня). Дизайн Питера Рэндалла-Пейджа основан на спиралях, найденных в семенах. и подсолнухи и сосновые шишки.
Калифорнийский политехнический инжиниринг Плаза
Инженерный колледж в Калифорнии Политехнический государственный университет планирует новая Инженерная Плаза на основе чисел Фибоначчи и нескольких геометрических диаграмм вы также видел на других страницах здесь.Также есть страница картинки нового здания.Говорит дизайнер Plaza и бывший студент Калифорнийского политехнического университета Джеффри Гордон Смит.
В качестве направляющего элемента мы выбрали спираль ряда Фибоначчи, или золотую середину, как представление инженерных знаний.Начало строительства в настоящее время запланировано на конец 2005 или начало 2006 года.

Здание Организации Объединенных Наций в Нью-Йорке
Архитектор Ле Корбюзье намеренно включил несколько золотых прямоугольников как формы окон или других аспектов зданий, которые он спроектировал.Одним из них (не спроектированным Ле Корбюзье) является здание Организации Объединенных Наций в Нью-Йорке, которое имеет L-образную форму. Хотя в некоторых книгах вы прочтете, что «вертикальная часть буквы L имеет стороны в золотом сечении, и на этой более высокой части есть отличительные отметки, которые делят высоту по золотому сечению», когда я смотрел фотографии здания, я не мог найти эти измерения. А вы?
[С благодарностью Бьорну Сместаду из колледжа Финнмарк, Норвегия, за упоминание этих ссылок.]Дополнительные ссылки по архитектуре
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..Больше..
Золотое сечение и искусство
Лука Пачоли (1445-1517) в своей работе Divina propore (О божественной пропорции) писал о золотое сечение также называют золотой серединой или божественной пропорцией : Прямая АВ делится в точке М так, что отношение две части, меньший MB к большему AM является такое же, как отношение большей части AM ко всему AB.
Мы видели на предыдущих страницах этого сайта что это дает два соотношения: AM:AB, которое также является BM:AM и равно 0,618… которое мы называем фи (начиная с маленький р). Другое соотношение равно AB:AM = AM:MB = 1/phi= 1,618… или Фи (обратите внимание на заглавную П). Оба они по-разному называются золотым числом или золотое сечение , золотое сечение , золотая середина или божественная пропорция .Другие страницы этого сайта объясняют намного больше об этом и его удивительном математические свойства и их связь с числами Фибоначчи.Работа Пачоли повлияла Леонардо да Винчи (1452-1519) и Альбрехта Дюрера (1471-1528) и можно увидеть в некоторых работах Жоржа Сёра, Поль Синьяк и Мондриан, например.
Много книг по масляной живописи и акварели в вашей местной библиотеке.
укажет, что объекты лучше располагать не по центру
изображения, но в одну сторону или «примерно на одну треть» пути, и
использовать линии, которые делят изображение на трети. Это, кажется, делает
дизайн изображения более приятный для глаз и снова опирается на идею
золотое сечение является «идеальным».
Это, кажется, делает
дизайн изображения более приятный для глаз и снова опирается на идею
золотое сечение является «идеальным».
Искусство Леонардо
Веб-сайт галереи Уффици во Флоренции, Италия, имеет виртуальная комната какой-то картин и рисунков Леонардо да Винчи. Предлагаю для самостоятельного анализа следующие две картины Леонардо да Винчи:- Благовещение
- — это изображение, которое выглядит так, как будто оно находится в кадре формы 1:sqrt(5) (прямоугольник корня-5).Распечатайте его и измерьте — это прямоугольник с корнем 5?
Разделите его на квадрат слева и еще один справа. (Если это root-5
прямоугольник, эти линии отмечают два прямоугольника золотого сечения как оставшиеся части
после удаления квадрата). Также отметьте в
линии на картинке, которые составляют 0,618 пути вверх и 0,618 пути вниз
Это. Также отметьте вертикальными линиями, которые
0,618 пути с обоих концов.
 Вы увидите, что эти
линии выделяют значимые части изображения или проходят через важные
объекты. Затем вы можете попробовать провести линии, которые делят эти части на
их золотые сечения тоже.
Вы увидите, что эти
линии выделяют значимые части изображения или проходят через важные
объекты. Затем вы можете попробовать провести линии, которые делят эти части на
их золотые сечения тоже. - Леонардо Мадонна с младенцем и святыми
- в квадратной рамке. Посмотрите на линии золотого сечения (0,618 пути вниз и вверх по кадру и 0,618 пути поперек от слева и справа) и посмотрите, выделяют ли эти линии значимые части изображение.Выглядят ли другие подразделения как дальнейшие золотые сечения?
Современное искусство
Гобелен Грэма Сазерленда в соборе Ковентри
| | Огромный гобелен Грэма Сазерленда (1903-1980) с изображением Христа-Царя за алтарем в
Ковентри
кафедральный собор
вот на фото сделал
Роб Орланд. Кажется, он был разработан с некоторыми четкими золотыми сечениями, как я показал. на фото Роба:
Ссылки: |
Ссылки, специально относящиеся к числам Фибоначчи или золотому сечению (Phi):
Ссылки на
основных источников искусства в Интернете :Работы современных художников с использованием золотого сечения
Когда я выступал с докладом в The Eden Project в Корнуолле в июле 2007 г., Патрисия Беннеттс и Мэри Миллер из Фалмута познакомила меня с использованием Числа Фибоначчи в дизайне Quilt .(Наведите указатель мыши на их имена, чтобы увидеть их адреса электронной почты.)Их два дизайна основаны на шаблоне в середина, где полосы в нижней половине имеют ширину 1, 2, 3, 5, 8 и 13 коричневого цвета которые чередуются с более светлые полосы той же ширины, но в порядке убывания.

| Woolly Thoughts — веб-сайт Стива Пламмера и Пэта Эшфорта с многие проекты по вязанию спицами и крючком, вдохновленные математикой, в том числе проекты, основанные на числах Фибоначчи, золотая спираль, треугольники Пифагора, флексагоны и многое другое.Они много лет работают в школы дают новый поворот в математике с их практическим подходом к проектированию с использованием школьной математики. Отличный ресурс для учителей, которые хотят по-новому вовлечь учащихся в математику, а также для математиков интересует вязание спицами и крючком. | |
Билли Рут Саддат — североамериканская художница, специализирующаяся на
работа с корзиной, которая сейчас известна во всем мире.Ее дизайн основан на
Числа Фибоначчи и золотое сечение — см. ее веб-страницу
JABOBs (просто куча корзин).
Преподавание математики в середине
В школе есть
хорошее онлайн введение
к ее работе (январь 1999 г. ). ). | |
| Кес ван Проойен Калифорнийский университет использовал ряд, аналогичный ряду Фибоначчи — один из добавив предыдущие три термина в качестве основы для своего искусства. |
Фибоначчи и Фи для изготовления мебели
| Пьетро Малусарди и Карен Уоллес имеют страница в Интернете демонстрируя некоторые элегантные применения золотого сечения в дизайне мебели. | |
| Решения для нестандартной мебели имеют Медиа-кабинет разработан с использованием пропорций золотого сечения. | |
Недавнее издание (январь/февраль 2003 г.) журнала Ancient Egypt Magazine содержало
статья о деревообработке в Древнем
Египет, где автор, Джеффри Киллен, объясняет, как коробка (сундук) демонстрирует
золотое сечение в его дизайне, но не уверен, совпадение это или дизайн. | |
| Флетчер Кокс это мастер по дереву, который использовал золотое сечение в своей клен с высоты птичьего полета деревянная тарелка. |
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..Больше..
Русский Сергей Эйзенштейн снял классический немой фильм 1925 года Броненосец Потемкин (DVD или видео теперь доступна версия этого 75-минутного фильма в формате PAL).Он разделил фильм, используя точки золотого сечения, чтобы начать важные сцены в фильме, измеряя они по длине на целлулоидной пленке.Джонатан Бергер из Стэнфордского университета Центр компьютерных исследований в области музыки и акустики использовал это как иллюстрацию чисел Фибоначчи в курс лекций.
Денес Надь в увлекательной статье, озаглавленной Золотое сечение (изм): от математики к теории искусства и музыковедение, часть 1 в Симметрия, культура и наука , том 7, номер 4, 1996, страницы 337-448 говорит о том, можем ли мы воспринять момент золотого сечения без изначально осознавая весь временной интервал.
 Он ссылается на свою собственную работу по
Восприятие золотого сечения и в видеоарте (стр. 418 вышеуказанной статьи).
Он ссылается на свою собственную работу по
Восприятие золотого сечения и в видеоарте (стр. 418 вышеуказанной статьи).1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..Больше..
Первый раздел здесь вдохновлен книгой доктора Рэйчел Холл. Программа курса мультикультурной математики в Университете Святого Иосифа в Филадельфии, США. (Подробнее об этом с некоторыми хорошими математическими головоломками в этом pdf-документе.)Ударение, метр и санскритская поэзия
В английском языке мы склонны думать о поэзии как о строках текста, которые рифмуются , то есть строки, которые заканчиваются на , звучат так же, как в этой детской песенке:Мерцай, мерцай, маленькая звездочкаТакже у нас есть ритма отдельных звуков (называемых слогами). Такие слова, как twinkle состоит из двух слогов: twin- и -kle , тогда как такие слова, как звезда есть только одна.
Как я же потрясен тем, кто ты есть.
Над миром, так высоко
Как бриллиант в небе
…
 Некоторые слоги выделены ударением
больше, чем другие, чтобы они звучали
громче (например, TWIN- в мерцании), тогда как другие безударны и тише
(например, -kle в мерцании).Словари часто показывают, как произносится слово.
путем разделения его на
слоги, ударные части показаны заглавными буквами, как мы сделали здесь, напр.
DIC-tion-ar-y, чтобы показать, что в нем 4 слога, причем ударение только на первом из них.
Некоторые слоги выделены ударением
больше, чем другие, чтобы они звучали
громче (например, TWIN- в мерцании), тогда как другие безударны и тише
(например, -kle в мерцании).Словари часто показывают, как произносится слово.
путем разделения его на
слоги, ударные части показаны заглавными буквами, как мы сделали здесь, напр.
DIC-tion-ar-y, чтобы показать, что в нем 4 слога, причем ударение только на первом из них. Если мы позволим S обозначать ударный слог и с безударный, затем ударение каждой строчки песни или стихотворения это его метров (ритм). В песне над каждой строкой есть метр СссСссС.
В санскритской поэзии слоги бывают либо длинными, либо короткими.
В английском мы замечаем это в некоторых словах, но не в целом — все слоги в песне
выше занимает примерно одинаковое время, чтобы сказать, находятся ли они в состоянии стресса или нет, поэтому все
строки занимают одинаковое количество времени, чтобы сказать.
тем не мение облачное небо состоит из двух слов и трех слогов CLOW-dee SKY ,
но первый и третий слоги имеют ударение и произносятся дольше, чем другие
слог.
Предположим, что длинные слоги произносятся вдвое дольше, чем короткие.
Итак, мы можем задать вопрос:
в санскритской поэзии, если всем строкам требуется одинаковое время, чтобы сказать, какие комбинации короткие (S) и длинные (L) слоги у нас могут быть?
Это просто еще одна головоломка того же типа, что и в простых головоломках Фибоначчи. страницу на этом сайте. На одну единицу времени у нас есть только один краткий слог, чтобы сказать: S = 1 way
Для двух единиц времени у нас может быть два коротких или один длинный слог: СС и Л.
= 2 способа
Для трех единиц мы можем иметь: SSS, SL или LS = 3 направления
Любые предположения для строк из 4 единиц времени? Четыре казалось бы разумным — но неправильно! Уже пять!
SSSS, SSL, SLS, LSS и LL;
общий ответ заключается в том, что линии, которые произносятся за n единиц времени, могут быть сформированы в Fib (n)
способы.
Это заметил Ачарья Хемачандра около 1150 г. н.э. или 70 лет до н. э.
до того, как Фибоначчи опубликовал свое первое издание Liber Abaci в 1202 году!
э.
до того, как Фибоначчи опубликовал свое первое издание Liber Abaci в 1202 году!
Ачарья Хемачандра и (так называемые) Числа Фибоначчи Междунар. Журнал математического образования , том 20 (1986), страницы 28–30.
Вергилий
Энеида Мартин Гарднер в главе «Числа Фибоначчи и Лукаса» в Математический цирк (Penguin books, 1979 или Mathematical Assoc.Америки 1996) упоминает Книга профессора Джорджа Экеля Дакворта Структурные модели и пропорции в «Энеиде» Вергилия: исследование в математическая композиция (Издательство Мичиганского университета, 1962 г.). Дакворт утверждает, что Вергилий сознательно использовал числа Фибоначчи. структурировать свою поэзию, как и другие римские поэты того времени.1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..Больше..
Фибоначчи и музыка
Trudi H Garland [см. ниже] отмечает, что на
5-тоновая шкала (черные ноты на фортепиано), 8-тональная гамма (белые
ноты на фортепиано) и гамму из 13 нот (полная октава в полутонах,
с двумя нотами, отстоящими друг от друга на октаву).Однако это немного искажает правду,
так как, чтобы получить и 8, и 13, мы должны считать одну и ту же ноту дважды (C…C в обоих случаях).
Да, это
называется окт авеню, потому что мы обычно поем или играем восьмую ноту, которая
завершает цикл, повторяя начальную ноту «на октаву выше».
и, возможно, звучит более приятно для слуха. Но реально всего 12 разных банкнот
в нашей октаве, а не 13!
ниже] отмечает, что на
5-тоновая шкала (черные ноты на фортепиано), 8-тональная гамма (белые
ноты на фортепиано) и гамму из 13 нот (полная октава в полутонах,
с двумя нотами, отстоящими друг от друга на октаву).Однако это немного искажает правду,
так как, чтобы получить и 8, и 13, мы должны считать одну и ту же ноту дважды (C…C в обоих случаях).
Да, это
называется окт авеню, потому что мы обычно поем или играем восьмую ноту, которая
завершает цикл, повторяя начальную ноту «на октаву выше».
и, возможно, звучит более приятно для слуха. Но реально всего 12 разных банкнот
в нашей октаве, а не 13!
Различные композиторы использовали числа Фибоначчи при сочинении музыки, а некоторые авторы находят золотое сечение еще в Средневековье (10 век) (см., например, The Golden Section In The Early Notated Western Music P Larson Fibonacci Quarterly 16 (1978), стр. 513-515).
Золотые сечения в конструкции скрипки
Раздел «Скрипка» в Новый Оксфордский компаньон к музыке, том 2, показывает, как Страдивари знал о золотом сечении и использовал его для поместите эфы в его знаменитые скрипки.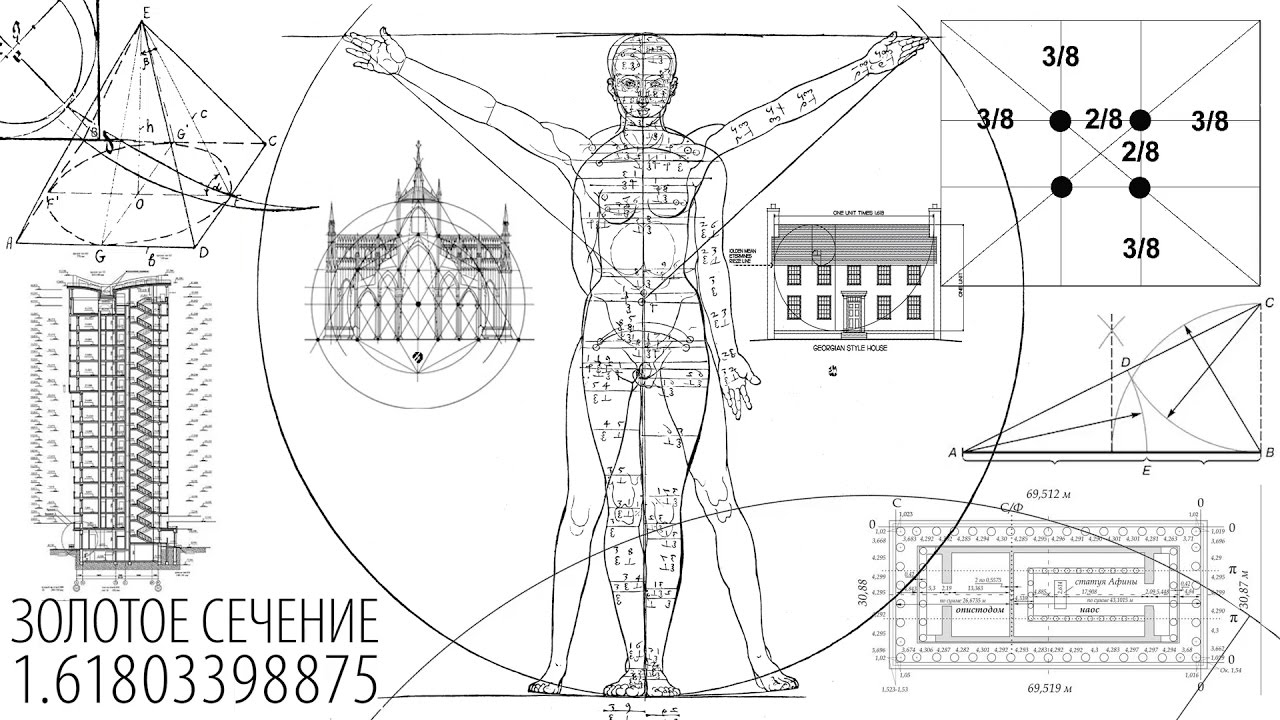
Метод Багинского построения скрипок также основан на золотых сечениях.
Использовал ли Моцарт золотую середину?
Это название статьи в Американский ученый марта/апреля 1996 г. Майк Мэй.Он сообщает об анализе Джоном Путцем многих сонат Моцарта. Джон Путц обнаружил значительное отклонение от золотого разделение на разделы и что любая близость к золотым сечениям может быть объясняется ограничениями самой сонатной формы, а не целенаправленным соблюдение золотого сечения.The Mathematics Magazine Том 68 № 4, страницы 275-282, октябрь 1995 г. статья Путца о Моцарте и золотом сечении в его музыке.
Фи в Пятой симфонии Бетховена?
В Mathematics Teaching том 84 в 1978 году, Дерек Хейлок пишет о Золотом сечении в пятой части Бетховена на страницах 56-57. Он утверждает, что знаменитый вступительный «девиз» (нажмите на музыку, чтобы прослушать)
происходит точно в точке золотой середины 0,618 в такте 372 из 601
и снова в такте 228, который является другой точкой золотого сечения (0. 618034 с конца куска)
но он должен использовать 601 бар, чтобы получить эти цифры. Он делает это, игнорируя последние 20 тактов.
происходящие после окончательного появления девиза, а также игнорирование бара
387.
618034 с конца куска)
но он должен использовать 601 бар, чтобы получить эти цифры. Он делает это, игнорируя последние 20 тактов.
происходящие после окончательного появления девиза, а также игнорирование бара
387.
Взгляните на полную партитуру на сайте The Hector Berlioz.
о Берлиозе: предшественники и современники
странице, если вы перейдете по ссылке Scores Available . Плагин для браузера также позволяет вам услышать его.
Обратите внимание, что повторяющиеся 124 такта в начале не учитываются при подсчете тактов на
музыкальные очки.
Тим Бенджамин указывает, что Но там 626 баров, а не 601!
Поэтому точки золотого сечения на самом деле находятся на 239-м такте.
(показан как такт 115, так как количество не включает повторение)
и 387 (также отмечены как 263 полоса).
Как отмечает британский композитор Тим Бенджамин:
626 тактов состоят из повторяющихся секций из 124 тактов. это первые 248 тактов повторяющейся секции, «экспозиции» — затем 354 раздела «развитие», затем 24 такта «перепросмотр» (стандартная «форма первой части»).Поэтому там не может быть ничего существенного в 239, потому что в тот момент бывает дважды. Однако в 387 есть что-то довольно странное — это инверсия основного девиза. У вас большая оркестровая деятельность, потом тишина, потом эта тихая инверсия девиза, потом тишина, затем снова большая активность.
Также вы должны иметь в виду, что номера баров начинаются с 1, а не с 0, поэтому вам нужно искать что-то, происходящее на 387,9 (округление на 1dp), а не 386.9. Вот что на самом деле происходит — странное инверсия проходит от 387,25 до 388,5.
Но такт 387 — это именно тот, на который Хейлок решил не обращать внимания!
Так это Бетховенское « phi -fth» или просто старое доброе «Fifth»?
Барток, Дебюсси, Шуберт, Бах и Сати
Есть несколько увлекательных статей и книг, которые объясняют, как эти композиторы могли намеренно использовать золотое сечение в своей музыке:| Двойственность и синтез в музыке Белы Бартока Э. 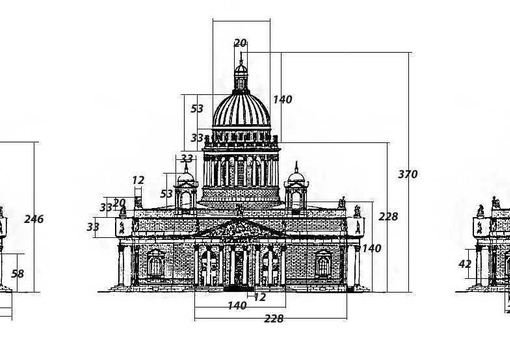 Лендваи на страницах 174-193 модуля , пропорции, симметрии, ритма Г. Кепеса (редактор),
Джордж Бразиль, 1966 год; Лендваи на страницах 174-193 модуля , пропорции, симметрии, ритма Г. Кепеса (редактор),
Джордж Бразиль, 1966 год; | |
| Некоторые поразительные пропорции в музыке Белы Бартока в Fibonacci Quarterly Vol 9, часть 5, 1971, страницы 527-528 и 536-537. | |
| Бела Барток: анализ его музыки Эрно Лендваи, опубликовано Kahn & Averill, 1971; имеет более подробный взгляд на использование Бартока золотой середины. | |
| Дебюсси в пропорции — музыкальный анализ Рой Ховат, Кембриджский унив. Пресса, 1983 г., ISBN = 0 521 23282 1. | |
Веб-сайт концертирующего пианиста Роя Ховата
имеет больше информации о своей книге Дебюсси в пропорции и других работах и ссылках. | |
| Адамс, Катни С. Эрик Сати и анализ золотого сечения. в Музыка и письма , Oxford University Press, ISSN 0227-4224, том 77, номер 2 (май 1996 г.), страницы 242-252 | |
| Исследования Шуберта ,
(редактор Брайан Ньюбоулд) Лондон: Ashgate Press, 1998 есть глава Архитектура как драма у позднего Шуберта Рой Ховат, страницы 168 — 192, о золотых сечениях Шуберта в его поздняя соната ля мажор (Д.959). | |
| Пропорциональный дизайн Дж.С. Две итальянские кантаты Баха , Tushaar Power, Музыкальная практика , Том 1, № 2. Осень 1994 г., стр. 35-46. Это часть докторской диссертации автора J.S. Бах и божественная пропорция представлен на музыкальном факультете Университета Дьюка в марте 2000 года.  | |
| Пропорции в музыке Хьюго Нордена в Fibonacci Quarterly vol
2 (1964) стр. 219-222 рассказывает о первой фуге в опере И. С. Баха Искусство фуги и показывает, как числа Фибоначчи и числа Люка появляются в его организации. | |
| «Канон» Пера Норгорда Хьюго Нордена в Fibonacci Quarterly том 14 (1976), страницы 126-128 говорится в заглавной части является «примером музыки, полностью и до мельчайших деталей основанной на числах Фибоначчи». | |
| Серия Фибоначчи в музыке двадцатого века Дж. Крамер, Журнал теории музыки 17 (1973), страницы 110-148 |
Существует очень полезный набор математических ссылок на Искусство и музыка веб-ресурсы из математических архивов на это стоит посмотреть.

Золотая струна как Music
Золотая нить — это фрактальная цепочка из нулей и единиц, которая растет в способом, подобным Фибоначчи, следующим образом:1После первых двух строк все остальные составляются из двух последних строк аналогичным образом. чтобы каждое число Фибоначчи было суммой двух предшествующих ему.Каждая строка (список 0 и 1) здесь является копией строки над ней , за которой следует . тот, что выше этого. В результате получается бесконечно длинная строка Золотая нить или слово Фибоначчи или последовательность кролика. Интересно послушать в музыкальном виде и даю два пути в разделе Услышьте золотую последовательность на этой странице. В этом же разделе я упоминаю Лондонская группа Perfect Fifth who использовали его в статье под названием Фибоначчи которые вы можете услышать в Интернете тоже.
10
101
10110
10110101
1011010110110
101101011011010110101
…
Другая музыка, связанная с Фибоначчи и Фи
Джон Байлз, ученый-компьютерщик из Рочестерского университета в штате Нью-Йорк использовали серию, которая количество наборов чисел Фибоначчи, сумма которых равна n для создания музыкального произведения. Он писал об этом и имеет ссылку на
услышать произведение онлайн. Серия выглядит так:
Он писал об этом и имеет ссылку на
услышать произведение онлайн. Серия выглядит так: Он обладает некоторыми фрактальными свойствами в том смысле, что график можно увидеть в секциях, каждая из которых начинается и заканчивается, когда график опускается до самых низких точек на линии y=1.Каждый раздел начинается с и заканчивается копия раздела два перед ним (и немного сдвинулись вверх), а между ними находится копия предыдущего раздела снова переместилась вверх.
Я написал больше об этой серии в разделе под названием Суммируя числа Фибоначчи на Базы Фибоначчи и другие способы представления целых чисел.
1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..Больше..
разных, забавных и странных мест, где можно найти Фи и числа Фибоначчи
телевизионных станций в Галифаксе, Канада
В Галифаксе, Новая Шотландия, есть 4 канала некабельного телевидения, и они пронумерованы. 3, 5, 8 и 13! проф. Об этом сообщил Карл Дилчер.
совпадение на Восьмой международной конференции по числам Фибоначчи и их приложениям
летом 1998 года.
Об этом сообщил Карл Дилчер.
совпадение на Восьмой международной конференции по числам Фибоначчи и их приложениям
летом 1998 года.Электростанция Турку, Финляндия
Йорг Вигельс из Дюссельдорфа сказал мне, что он был поражен увидеть числа Фибоначчи, ярко светящиеся в ночном небе во время визита в Турку в Финляндии. То дымоход электростанции Турку имеет Числа Фибоначчи на ней в неоновом свете высотой 2 метра! Это была первая комиссия Проект экологического искусства города Турку в 1994 году.Художник Марио Мерц (Италия) называет его Последовательность Фибоначчи 1-55 и говорит, что «это метафора человеческого поиска порядка и гармонии среди хаоса».Фотография здесь была сделана доктором Чинг-Куанг Шене из Мичиганского технологического университета. и воспроизводится здесь с его любезного разрешения от его страница фотографий его поездки в Финляндию.
Разработано в?
- Если вы измерите кредитную карту, вы обнаружите, что это идеальный золотой прямоугольник .

- Золотой прямоугольный значок National Geographic также тоже кажется прямоугольником золотого сечения.
- Брайан Агрон из Фэрфакса, Калифорния, нашел золотое сечение в дизайне его горный велосипед, Трек Топливо 90 показано выше с отмеченными золотыми сечениями.
- Брайан также говорит, что форма больших дверей в больницах кажется золотым прямоугольником.
- Джон Харрисон Массачусетс нашел золотой прямоугольник в форме Шоколадная вафля Kit-Kat — большая плитка с четырьмя пальцами в старой упаковке, как показано выше.
Два мифа о часах и золотом сечении времени
Иногда вы будете читать, что часы, настроенные на 90 268 десять против двух 90 269, имеют свои особенности. руки расположены так, чтобы образовать золотой прямоугольник, и что это «эстетично».Но нетрудно подсчитать, что угол между руками в это время составляет 0,3238 оборота (или больший угол составляет 0,6762 оборота), оба из которых далеки от углов золотого сечения 0.
 618 и 0,382 (= 1–0,618) оборота.
618 и 0,382 (= 1–0,618) оборота. В любом 12-часовом периоде имеется одиннадцати различных периодов времени когда стрелки часов отмечают золотое сечение на окружности.
Какое время они?
Какое расположение наиболее симметрично?
Что легче всего запомнить?
Что ближе всего к кратному 5 минутам?
- мы измеряем часы как десятичную дробь, так что 2:30 равно 2.5 часов и 12:00 и 0:00 это 0,0 часов и
- , если мы измеряем углы от 12 часов в долях оборота, а не в радианах или градусов так, чтобы, например, часовая стрелка находилась на 0,25 оборота в 3 часа
Другие авторы говорят, что стрелки на 1:50 или 10:08 образуют золотой прямоугольник , используя точки на
обод.
Это тоже неверно даже если бы можно было представить их спроецированными на обод и затем
сделать прямоугольник — не простое визуальное упражнение!
Вот часы с вытянутыми к ободу стрелками и золотым прямоугольником
накладывается на часы. Когда часовая стрелка указывает на нужное место, это примерно 10:04, а когда
минутная стрелка становится в правильное положение, это примерно 10 ч 9 м 35 с, но тогда часовая стрелка не
указать на нужное место.
Когда часовая стрелка указывает на нужное место, это примерно 10:04, а когда
минутная стрелка становится в правильное положение, это примерно 10 ч 9 м 35 с, но тогда часовая стрелка не
указать на нужное место.
Момент, когда стрелки стоят точно симметрично, равен
10 часов 9 минут 13.8462… секунд, а также
1 час 50 минут 46,1538 секунды.
Таким образом, 10:09 и 1:51 достаточно близки, но даже с учетом визуальной гимнастики это маловероятно.
что глаз распознает такое
золотая прямоугольная конструкция того времени, по моему математическому мнению!
Список задач
- Какие еще логотипы можно найти в виде золотых прямоугольников?
- Где еще вы нашли золотой прямоугольник?
1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..Больше..
Есть много книг и статей, в которых говорится, что золотой прямоугольник 90 268 — самая приятная форма 90 269. и укажите, как оно использовалось в формах знаменитых зданий, в структуре некоторых музыкальных произведений и в
дизайн некоторых известных произведений искусства. Действительно, такие люди, как Корбюзье и Барток, сознательно
и сознательно использовали золотое сечение в своих проектах.
и укажите, как оно использовалось в формах знаменитых зданий, в структуре некоторых музыкальных произведений и в
дизайн некоторых известных произведений искусства. Действительно, такие люди, как Корбюзье и Барток, сознательно
и сознательно использовали золотое сечение в своих проектах.Однако идея «наиболее приятной формы» подвергается критике. Золотое сечение как понятие изучалось греческими геометрами за несколько сотен лет до Рождества Христова, как упоминалось на предыдущих страницах этого сайта, Но представление о нем как о , приятном или красивой форме, возникло только в конце 1800-х годов и не по-видимому, не имеет никаких письменных текстов (древнегреческих, египетских или вавилонских), поддерживающих твердые свидетельство.
В лучшем случае золотое сечение, используемое в дизайне, просто один из нескольких возможных методов «теории дизайна», которые помогают людям структурировать то, что они создают.В худшем случае, некоторые люди пытались возвысить золотое сечение за пределы того, что мы можем проверить с научной точки зрения.
 Древние
Египтяне действительно используют его как основное «число» для форм пирамид? Мы не знаем.
Обычно формы
таких зданий не совсем квадратные и, возможно, как в случае с пирамидами и Парфеноном,
части зданий
были разрушены эрозией или разрушены, и поэтому мы не знаем, какова была их первоначальная длина.
Действительно, если вы посмотрите, где я провел линии
на картинке Парфенона выше видно, что их вряд ли можно назвать точными поэтому любые измерения, указанные авторами, являются довольно приблизительными!
Древние
Египтяне действительно используют его как основное «число» для форм пирамид? Мы не знаем.
Обычно формы
таких зданий не совсем квадратные и, возможно, как в случае с пирамидами и Парфеноном,
части зданий
были разрушены эрозией или разрушены, и поэтому мы не знаем, какова была их первоначальная длина.
Действительно, если вы посмотрите, где я провел линии
на картинке Парфенона выше видно, что их вряд ли можно назвать точными поэтому любые измерения, указанные авторами, являются довольно приблизительными!Итак, на этой странице много спекулятивного материала, и, возможно, он мог бы стать хорошим проектом для научной ярмарки, исследовать, действительно ли золотое сечение объясняет некоторые основные особенности дизайна важных произведений искусства, будь то архитектура, живопись, скульптура, музыка или поэзия.На этом вам конец!
| Джордж Марковски Заблуждения о золотом сечении в The College Mathematics Journal Том 23, январь 1992 г.  , страницы 2-19 — важная статья, в которой
слабые места в части
Теория «золотое сечение — самая приятная форма». , страницы 2-19 — важная статья, в которой
слабые места в части
Теория «золотое сечение — самая приятная форма». Это читабельно и хорошо представлено. Возможно, слишком много людей просто принимают (недопустимые?) замечания других и включать их в свои работы? Вы можете согласиться или не согласиться с все, что говорит Марковский, но это хорошая статья, которая пытается развенчать упрощенное и ненаучный «культовый» статус, придаваемый Фи, видя его там, где его на самом деле нет! Это не отрицание того, что Фи, безусловно, — это , действительно присутствующее в большей части ботаники, и математические причины этого объясняются на предыдущих страницах этого сайта. | |
| Как найти «золотое число» без особых усилий Роджер Фишлер, Fibonacci Quarterly , 1981, том 19, страницы 406–410. Еще один важный документ, в котором показано, как проводить измерения и их усреднение.  почти всегда будет давать среднее значение, близкое к Фи. Тематические исследования – это данные о
Великая пирамида Хеопса и различные теории, выдвигаемые для объяснения ее
размеры, золотое сечение в архитектуре, его использование Ле Корбюзье и Сера
и в изобразительном искусстве.Он заключает, что несколько работ, направленных
чтобы показать, что использовалось Фи, на самом деле ошибочны и «без каких-либо оснований». почти всегда будет давать среднее значение, близкое к Фи. Тематические исследования – это данные о
Великая пирамида Хеопса и различные теории, выдвигаемые для объяснения ее
размеры, золотое сечение в архитектуре, его использование Ле Корбюзье и Сера
и в изобразительном искусстве.Он заключает, что несколько работ, направленных
чтобы показать, что использовалось Фи, на самом деле ошибочны и «без каких-либо оснований». | |
| Чертежная доска Фибоначчи Проект Великой пирамиды в Гизе Полковник Р. С. Борода в Fibonacci Quarterly vol 6, 1968, страницы 85–87; имеет три отдельные теории (только одна из которых связана с золотым сечением). что довольно хорошо согласуется с размерами, измеренными в 1880 году. | |
Золотое сечение (изм): от математики к теории искусства
и музыковедение, часть 1 , Денес Надь в Симметрия, культура и наука ,
том 7, номер 4, 1996, стр.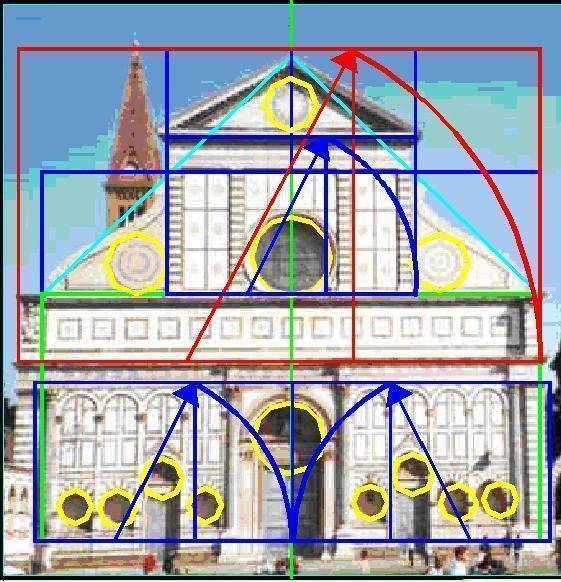 337-448 337-448 В разделе 2.1 говорится, что существует как минимум девять различных теорий о форме Великой пирамиды. фараона Хуфу (Великая пирамида Хеопса), две из которых относятся к золотому сечению: Угол наклона граней равен
|
Ссылки и ссылки на золотое сечение в музыке и искусстве
| Ключ: | ||
|---|---|---|
| книга | ||
| статья в журнале или статья в научном журнале | ||
| веб-сайт | ||
Музыка
| Увлекательные Фибоначчи Труди Хаммель Гарланд, публикации Дейла Сеймура, 1987 год — отличное введение в ряд Фибоначчи с лотами.  полезных идей для занятий.Включает в себя
раздел Музыка. полезных идей для занятий.Включает в себя
раздел Музыка. | |
| Пример чисел Фибоначчи, используемых для генерации
Ритмические ценности в современной музыке в Fibonacci Quarterly Vol 9, часть 4, 1971, страницы 423-426; |
Ссылки на другие музыкальные веб-сайты
Музыка гамеланаДругая музыка
Гамелан
— перкуссионная музыка Индонезии.То Американский институт гамелана содержит много информации, в том числе Гонгкаст записал музыку онлайн, чтобы вы могли сами послушать музыку Gamelan.Новая музыка
от Дэвида Кэнрайта с кафедры математики Военно-морской школы последипломного образования в Монтерее, США; сочетание ряда Фибоначчи с музыкальными формами индонезийского гамелана.Некоторые компакт-диски
на Gamelan музыка Центральной Явы (индонезийский остров не софт!).
Искусство
Мартин Моргенштерн имеет большой и интересный список книги и статьи о золотом сечении и музыка с рефератами, некоторые из которых на немецком языке. Последовательность Фибоначчи
— это название ансамбля классической музыки. всемирно известных солистов, музыкантов в резиденции в Кингстонском университете (Кингстон-на-Темзе, Суррей, Великобритания).Базируясь в районе Лондона (Великобритания), их актуальная программа мероприятий находится на веб-сайте по ссылке выше.Кейси Монговен Композитор, который использовал числа Фибоначчи и золотые сечения в своих собственных музыкальные композиции. Вы можете услышать их и прочитать больше на его веб-сайт. У Кейси впечатляюще большой набор фрагментов, большинство из которых длится всего несколько секунд, но они увлекательная для прослушивания и очень отличается от обычной музыки.То высота тона его нот часто основана на степенях Фи, а их порядок фиксируется числом. последовательности, такие как числа Фибоначчи или R(n) — количество представлений Фибоначчи n или во многих других последовательностях которые описаны здесь, на моем сайте Фибоначчи.
Его партитуры тоже являются изображениями, которые проиллюстрировать многие из серий, которые вы увидите здесь. Вы можете поэкспериментировать для себя с помощью визуализатора последовательности Фибоначчи который был разработан специально для работ Кейси.Тед Фроберг объясняет, как он использовал числа Фибоначчи «mod 7» (то есть остатки когда мы делим каждое число Фибоначчи на 7), чтобы создать «тему», которую он затем гармонизирует и превратился в вальс Фибоначчи.
© 1996-2010 Доктор Рон Нотт
Математическая история Золотое число Роджера Герц-Фишлера, Дувр, 1998 г., ISBN 0486400077.Научное исследование всех основных источников в попытке проследить самые ранние ссылки на «золотое сечение», его названия и т.д. Образование через искусство (3-е издание) H Read,
Книги Пантеона, 1956 г., страницы 14–22;Новый пейзаж в искусстве и науке Г. Кепеш
P Theobald and Co, 1956, стр. 329 и 294;Х. Э. Хантли, Божественная пропорция: исследование математической красоты,
— переиздание старой классики в Дувре 1970 года.CF Linn, Золотая середина: математика и изящные искусства ,
Даблдей 1974.Дьёрдь Доци, Сила пределов: пропорциональные гармонии в природе, Искусство и архитектура
Shambala Press, (новое издание 1994 г.).М. Боулс, Золотые отношения: искусство, математика, природа , 2-е изд.,
Пифагорейская пресса, 1987 г.
обновлено 22 сентября 2010 г.
| [1] | К. Элам. Геометрия дизайна, этюды пропорций и композиции. Princeton Architectural Press, 37 East 7 th Street, New York 10003. |
| [2] | Х. Э. Хантли. Божественная пропорция: исследование математической красоты. Dover Publications, Inc. 31 East 2 nd Street, Mineola, NY 11501. Библиотека конгресса, номер карточки в каталоге: 70-93195. 31 East 2 nd Street, Mineola, NY 11501. Библиотека конгресса, номер карточки в каталоге: 70-93195. |
| [3] | К. К. Тунг. Темы математического моделирования. Princeton University Press, 31 марта 2007 г. |
| [4] | Ливио, Марио (2002). Золотое сечение: история числа Фи, самого удивительного числа в мире.Нью-Йорк: Бродвейские книги. |
| [5] | Доци, Дьёрдь (1994). Сила ограничений: пропорциональные гармонии в природе, искусстве и архитектуре. Бостон: Shambhala Publications, Inc. |
| [6] | Гика, Матила (1977). Геометрия искусства и жизни, 2-е издание. Дуврские публикации. |
| [7] | Р. Х. Фишлер. Дольф Цейзинг, 1810–1876: жизнь и творчество немецкого интеллектуала. Январь 2004 г., Mzinhigan Publications. |
| [8] | Т. Кассабова, Режиссер: профессор М.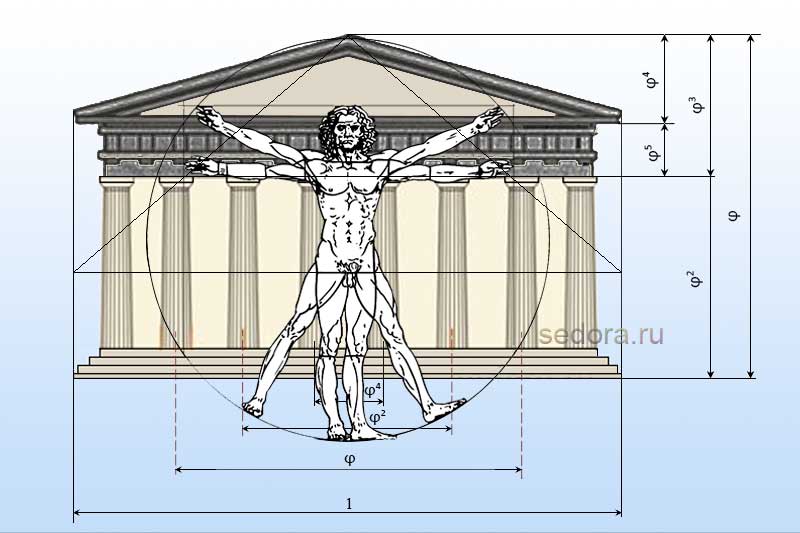 Розен, танцевальный факультет. Где цвета сливаются со звуками. Диссертация представлена на факультет Высшей школы Университета штата Мэриленд, Колледж-Парк, при частичном выполнении требований для получения степени МИД, 2009 г. Розен, танцевальный факультет. Где цвета сливаются со звуками. Диссертация представлена на факультет Высшей школы Университета штата Мэриленд, Колледж-Парк, при частичном выполнении требований для получения степени МИД, 2009 г. |
| [9] | А. Бежан. Золотое сечение предсказало: зрение, познание и передвижение как единый замысел в природе. Международный журнал дизайна, природы и экодинамики.Том. 4, № 2, 2009, 97–104. |
| [10] | Л. Лакассань, А. Манзанера, Ж. Денуле, А. Мериго. Высокопроизводительное обнаружение движения: некоторые тенденции в отношении новых встроенных архитектур для систем машинного зрения. Журнал обработки изображений в реальном времени, 2009 г., Springer. 127 – 146. |
| [11] | C. Bauckhage, J.K. Tsotsos, F.E. Bunn. Автоматическое обнаружение аномальной походки. Журнал Image and Vision Computing 27, 2009 г., Science Direct. 108-115. |
| [12] | М. У. Г. Хан, А. Саид. Обнаружение человека в видео. Journal of Theoretical and Applied Information Technology, 2005 — 2009. 212 – 220. У. Г. Хан, А. Саид. Обнаружение человека в видео. Journal of Theoretical and Applied Information Technology, 2005 — 2009. 212 – 220. |
| [13] | Ю. Капуста. Квадрат, круг и золотая пропорция: новый класс геометрических построений. ВЕБ-журнал ФОРМА 2004, Vol. 19, (№ 4), 293-313. http://www.scipress.org/journals/forma/toc/1904.html. |
| [14] | Дж. Каппрафф. Введение: В поисках золотой середины. ВЕБ-журнал ФОРМА 2004, Vol.19 (№ 4), 287 – 289. http://www.scipress.org/journals/forma/toc/1904.html. |
| [15] | C. D. Зеленый. Все, что блестит: обзор психологических исследований эстетики золотого сечения. Журнал ВОСПРИЯТИЯ 1995, Vol. 24. 937-968. http://htpprints.yorku.ca/archive/00000003/00/goldrev3.htm. |
| [16] | Ахратуцзаман М. и Шафи А.А. Продвижение Android и вклад разных стран в исследования и разработку гуманоидной платформы. Международный журнал робототехники и автоматизации (IJRA), том (1): выпуск (2), 2010 г. Журнал компьютерных наук (CSC Journal), Малайзия. 43-57. Международный журнал робототехники и автоматизации (IJRA), том (1): выпуск (2), 2010 г. Журнал компьютерных наук (CSC Journal), Малайзия. 43-57. |
| [17] | Е.И. Левин, Б.Ч. D. Стоматологическая эстетика и золотая пропорция. Журнал ортопедической стоматологии, съемное протезирование. Том. 40, номер 3, сентябрь 1978 г., стр. 244–252. |
| [18] | С. Кинг, Ф. Бек и У. Латтге. О тайне золотого угла в филлотаксисе. Завод, клетка и окружающая среда, Blackwell Publishing Ltd.2004, 27. 685-695. |
| [19] | Дж. Х. Э. Картрайт, Д. Л. Гонсалезиз, О. Пирокс, Д. Станциал. Эстетика, динамика и музыкальные гаммы: золотая связь. Дж. Новое музыкальное исследование 2002, 31. 51–58. |
| [20] | Н. Э. Друри. Красота только поверхностна. Журнал Королевского медицинского общества. Том. 93, февраль 2000 г. 89-92. |
| [21] | М. Чиассон и Дж. Роджерс. Beauty Bare: форма сонета, геометрия и эстетика.Журнал литературы и науки, Vol. 2, № 1 (2009), 48-64. Чиассон и Дж. Роджерс. Beauty Bare: форма сонета, геометрия и эстетика.Журнал литературы и науки, Vol. 2, № 1 (2009), 48-64. |
| [22] | С. Гелдарт, Д. Маурер и Х. Хендерсон. Влияние высоты внутренних черт лица на эстетические оценки взрослых и время взгляда 5-месячных детей. Восприятие, 1999, Том. 28, 839-850. |
| [23] | Т. Якобсен. Индивидуальное и групповое моделирование стратегий эстетического суждения. Британский журнал психологии (2004 г.), Vol. 95, 41-56. |
| [24] | Г.Марковский. Заблуждения о золотом сечении. Математический журнал колледжа, Vol. 23, № 1, январь 1992 г. 1-19. |
| [25] | В. Я. Конечный. Ваза на каминной полке: золотое сечение в контексте. Эмпирические исследования искусств, Vol. 15 (2), 1997. 177-207. |
| [26] | П. Сингх. Так называемые числа Фибоначчи в древней и средневековой Индии. Журнал Historia Mathematica, Vol. 12 (1984). 229-244. Журнал Historia Mathematica, Vol. 12 (1984). 229-244. |
| [27] | В.А. Лефевр и Ю. Н. Ефремов. Возможные аналоги когнитивных процессов в картинах рентгенологической изменчивости быстрого барстера. Astronomical & Astrophysical Transactions: Журнал Евразийского астрономического общества, 1476-3540, Vol. 18, выпуск 2, 1999, 335-342. |
| [28] | Р. Гейровска. Золотое сечение в творениях природы возникает в строении атомов и ионов. Инновации в химической биологии. Springer Science and Business Media B.V.2009. 133-139 |
| [29] | Дж. Ф. Солис и Ф. М. Риос. Отжиг золотого сечения для задач выполнимости с использованием схем динамического охлаждения. ОСНОВЫ ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМ, Конспект лекций по информатике, Springer-Verlag Berlin Heidelberg 2008, Vol. 4994/2008, 215224 |
| [30] | Ю. Х. Чан и С. А. Р. Абу-Бакар. Система обнаружения лиц, основанная на информации о цвете, основанной на признаках. Материалы Международной конференции по компьютерной графике, изображениям и визуализации (CGIV 2004).153-158. Материалы Международной конференции по компьютерной графике, изображениям и визуализации (CGIV 2004).153-158. |
| [31] | К. Сандип и А. Н. Раджагопалан. Обнаружение человеческого лица на загроможденных цветных изображениях с использованием информации о цвете кожи и границах. Материалы Индийской конференции по компьютерному зрению, графике и обработке изображений (ICVGIP’02), декабрь 2002 г., Ахмадабад, Индия. 230-235. |
| [32] | М. Хофри и З. Росберг. Задержка пакетов согласно взвешенной политике TDM золотого сечения в канале с множественным доступом. IEEE Transactions on Infopmation Theory, vol.Это-33, нет. 3, май 1987 г., стр. 341–349. |
| [33] | К. Сюэ и П. Шеу. Оптимальное планирование пути без столкновений двух мобильных роботов. Семинар IEEE по языкам для автоматизации: симбиотические и интеллектуальные роботы, 29–31 августа 1988 г., стр. 63–68. |
| [34] | М. Ахтаруззаман и А. А. Шафи. Геометрический анализ гуманоидной системы BIOLOID, стоящей на одной ноге. Материалы 4-й Международной конференции по мехатронике (ICOM `11) 2011 г., 17-19 мая 2011 г., Куала-Лумпур, Малайзия. Ахтаруззаман и А. А. Шафи. Геометрический анализ гуманоидной системы BIOLOID, стоящей на одной ноге. Материалы 4-й Международной конференции по мехатронике (ICOM `11) 2011 г., 17-19 мая 2011 г., Куала-Лумпур, Малайзия. |
| [35] | С. Как. Золотая середина и физика эстетики. Архив физики: физика/0411195, 2004. |
| [36] | С. Обара. Золотое сечение в искусстве и архитектуре. Университет Джорджии, факультет математического образования, Дж. Уилсон, EMAT 4690/6690. http://jwilson.coe.uga.edu/EMT668/EMAT6680.2000/Obara/Emat6690/Golden%20Ratio/golden.html. |
| [37] | Некоторые твердые (трехмерные) геометрические факты о золотом сечении; Квазикристаллы и фи.http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/phi3DGeom.html#quasi. |
| [38] | Э. Леонг. Электронная книга по фотографии Глава 16 — Золотое сечение. http://photoinf. com/Golden_Mean/Edwin_Leong/Camera_Hobby_-_e-Book_on_the_Golden_Ratio.htm. com/Golden_Mean/Edwin_Leong/Camera_Hobby_-_e-Book_on_the_Golden_Ratio.htm. |
| [39] | Дж. А. Ньето. Связь между черными дырами и золотым сечением. Препринт arXiv:1106.1600, 2011, 1–10. |
| [40] | М. Ахтаруззаман, А. А. Шафи и М.Рашид. Стратегия выбора компонентов для антропоморфного робота. Национальная конференция аспирантов (NPC) 2011, Малайзия. 19-20 сентября 2011 г. |
| [41] | Ахтаруззаман М. и Шафи А.А. Попытка разработки двуногой интеллектуальной машины BIM-UIA. Материалы 4-й Международной конференции по мехатронике (ICOM `11) 2011 г., 17-19 мая 2011 г., Куала-Лумпур, Малайзия. |
| [42] | H. Вентилятор. Новый комбинированный алгоритм оптимизации роя частиц, основанный на стратегии золотого сечения.Передовые исследования материалов, Vol. 308-310, 2011, 1099-1105 |
| [43] | Дж. Фан, В.Д.Ю. Фрактальный анализ орто- и паракортексов шерстяного волокна. Передовые исследования материалов (тома 197–198), 2011 г., стр. 86–89. Фан, В.Д.Ю. Фрактальный анализ орто- и паракортексов шерстяного волокна. Передовые исследования материалов (тома 197–198), 2011 г., стр. 86–89. |
| [44] | Д. К. Вс. Анализ устойчивости систем адаптивного управления золотого сечения для поддержания ориентации космического аппарата с неизвестными параметрами. Прикладная механика и материалы, Vol. 80-81, 2011, 1096-1102. |
| [45] | М.А. Ахтер. Накопление исследований. LAP Lambert Academic Publishing, 2011. |
| [46] | P. Sandhaus, M. Rabbath2 и S. Boll. Использование эстетических принципов для автоматического макета фотокниги. Достижения в мультимедийном моделировании, 2011 г., часть I, LNCS 6523, Springer-Verlag Berlin Heidelberg, 2011 г. 84–95. |
| [47] | Г. Мейснер. Золотое сечение: фи, 1,618. Интернет-источник (2011 г.): http://www.goldennumber.net. |
| [48] | Г. Мейснер. PhiMatrix, программное обеспечение для проектирования и анализа золотого сечения. Интернет-источник (2011 г.): http://www.phimatrix.com. Мейснер. PhiMatrix, программное обеспечение для проектирования и анализа золотого сечения. Интернет-источник (2011 г.): http://www.phimatrix.com. |
| [49] | Р. Нотт. Числа Фибоначчи и золотое сечение в искусстве, архитектуре и музыке. Интернет-источник (2010 г.): http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibInArt.html. |
| [50] | Филлотаксис, числа Фибоначчи — Золотой угол. Интернет-источник (2011 г.): http://www.science.smith.edu/phyllo/About/fibogolden.html#Фибоначчи. |
| [51] | Что такое Фи? Интернет-источник (2011 г.): http://phieengineering.com/what_is_phi.htm. |
Коврики Тойо Ито и Рафаэля Монео в стиле Золотого сечения
Тойо Ито и Рафаэль Монео разработали шелковые ковры на основе золотого сечения
Созданные по инициативе Phillips и ARTinD, ковры ушли с молотка на распродаже 20th Century & Contemporary Art
Лауреаты Притцкеровской премии архитекторы Тойо Ито и Рафаэль Монео внесли последний вклад в проект Golden Ratio, инициативу аукционного дома Phillips и кураторской платформы ARTinD Оливы Сартого, которая пригласила десять архитекторов создать уникальный шелковый ковер, вдохновленный этой темой. Серия исследует пересечение искусства, дизайна и архитектуры, используя золотое сечение как композиционный инструмент, объединяющий области.
Серия исследует пересечение искусства, дизайна и архитектуры, используя золотое сечение как композиционный инструмент, объединяющий области.
‘Архитекторам было предложено использовать золотое сечение в качестве инструмента для обоснования своего предложения. Таким образом, все их проекты были разными по дизайну и формату, но в то же время они смогли придать уникальный характер всей коллекции», — говорит Сартого. «Все архитекторы отреагировали по-разному; некоторые использовали Ratio как пропорцию, некоторые как визуальный образ, некоторые как историческую справку.
В данном случае узор Ито основан на сегментированном навесе здания библиотеки, который он спроектировал для Колледжа социальных наук Тайваньского университета. Сократив здание до его основных компонентов — небольшого количества точек, представляющих колонны, поддерживающие части крыши с кувшинками, — японский архитектор создал спирографический узор из изогнутых линий. Мотив повторяется, бледно-зеленые нити расходятся наружу, соединяя и стирая точки в текучей композиции.
Дизайн ковра Тойо Ито
Отрывок, взятый из текста 16-го века о перспективе, La Pratica della Perspettiva итальянского архитектора и покровителя Андреа Палладио Даниэле Барбаро, является отправной точкой в дизайне Монео.Описание 32-гранного многогранника отражено в его узоре из треугольников землистых тонов и пятиугольников, которые разворачиваются, как сеть на кремовом фоне.
Moneo описывает процесс как «приятное занятие» в видеоинтервью, сопровождавшем выставку в Phillips в Mayfair. «Я не представлял, что получится так красиво», — говорит испанский архитектор. «По некоторым причинам мне всегда приятны естественные цвета».
Ковер Рафаэля Монео, вдохновленный эссе XVI века Даниэле Барбаро.
Графические интерпретации золотого сечения покойного Алессандро Мендини, Нормана Фостера, Бена ван Беркеля, Питера Эйзенмана, Су Фуджимото, Пьеро и Натали Сартого, Тома Мейна и Питера Цумтора были воссозданы из шелка ручной работы, чтобы сформировать первую коллекцию в серия, которая была продана на аукционе Phillips прошлой весной. Эти последние произведения Ито и Монео были проданы вместе с рисунками в рамах на распродаже 20th Century & Contemporary Art в аукционном доме Phillips Berkeley Square за 40 000 и 37 500 фунтов стерлингов соответственно.
Эти последние произведения Ито и Монео были проданы вместе с рисунками в рамах на распродаже 20th Century & Contemporary Art в аукционном доме Phillips Berkeley Square за 40 000 и 37 500 фунтов стерлингов соответственно.
«В своей практике ARTinD соединяет архитектуру с миром искусства, и вместе с Phillips мы даем коллекционерам доступ к уникальным творениям крупных современных архитекторов», — объясняет Сартого о проекте. Хотя продажа знаменует собой завершение трехлетней инициативы, ее успех заставил Phillips подготовиться к открытию нового сотрудничества, которое снова объединит архитектуру, дизайн и искусство.§
Руководство дизайнера по золотому сечению [с 14 примерами]
Что общего между раковинами улиток, ураганами, Парфеноном и Моной Лизой?
Все они следуют золотому сечению.
Вот в чем дело: независимо от того, являетесь ли вы дизайнером или нет, исследования показали, что ваш мозг, скорее всего, запрограммирован на то, чтобы отдавать предпочтение природе и произведениям искусства, которые следуют золотому сечению. На самом деле искусство, которое следует золотому сечению, часто считается самым красивым. Поэтому, даже если вы не знаете, что это такое, вы, несомненно, видели его в некоторых из ваших любимых дизайнов и архитектур.
На самом деле искусство, которое следует золотому сечению, часто считается самым красивым. Поэтому, даже если вы не знаете, что это такое, вы, несомненно, видели его в некоторых из ваших любимых дизайнов и архитектур.
В математике (предмет, в котором я никогда не был так силен) существует золотое сечение, когда линия делится на две части, и длинная часть (а), деленная на меньшую часть (б), равна сумме обеих частей. (а) + (б), разделить на (а). Оно должно равняться примерно 1,618.
Понял? И я нет. Но для наших целей мы сосредоточимся на Золотом Узоре в том виде, в каком он существует в искусстве — например, в древнеримской архитектуре или картинах Леонардо да Винчи.
Изображение предоставлено Музеем науки . Если золотое сечение действительно является обязательным условием для захватывающего дух искусства, само собой разумеется, что вы, как человек, занимающийся дизайн-проектом, должны знать о нем все. Здесь мы разберем примеры золотого сечения в природе, дизайне и даже человеческом лице, чтобы вы могли подумать, как включить золотое сечение в свои собственные маркетинговые проекты.
Что такое золотое сечение в дизайне?
Золотое сечение, также известное как Золотое сечение, Золотое сечение или Фи, представляет собой математическое соотношение, которое можно использовать для создания некоторых из самых красивых произведений искусства и архитектуры, таких как Мона Лиза или Парфенон.Наш мозг запрограммирован на то, чтобы предпочитать изображения, соответствующие золотому сечению, которое можно найти во многих элементах природы и даже в человеческом лице, и поэтому оно выглядит чистым и органичным.
Золотое сечение в природеЗолотое сечение появилось во многих заметных и очевидных объектах природы, включая деревья, сосновые шишки и семена клубники.
Однако его также можно увидеть в абстрактных местах, таких как точка в черной дыре, где температура меняется с положительной на отрицательную.Его постоянное присутствие может означать, что золотое сечение является фундаментальной константой природы, что может объяснить, почему наш мозг, кажется, запрограммирован лучше реагировать на визуальные эффекты, соответствующие золотому сечению.
Здесь мы рассмотрим лишь несколько примеров золотого сечения в природе:
1. Лепестки цветов
2. Ураганы
3. Спиральные галактики
4. Раковины Наутилуса
5.Семена цветов
6. Сосновые шишки
Значение золотого сечения для человеческого лицаТеперь, когда мы изучили, как природа следует золотому сечению, давайте посмотрим на золотое сечение, как оно проявляется на человеческом лице.
Предположительно, голова образует золотой прямоугольник с глазами в середине, а рот и нос — в виде золотых участков расстояния между глазами и подбородком. Золотое сечение можно найти даже в наших зубах и профиле, когда мы поворачиваем голову в сторону.
Исследование показало, что лица, наиболее близкие к золотому сечению, считаются самыми красивыми.
Доктор Стивен Р.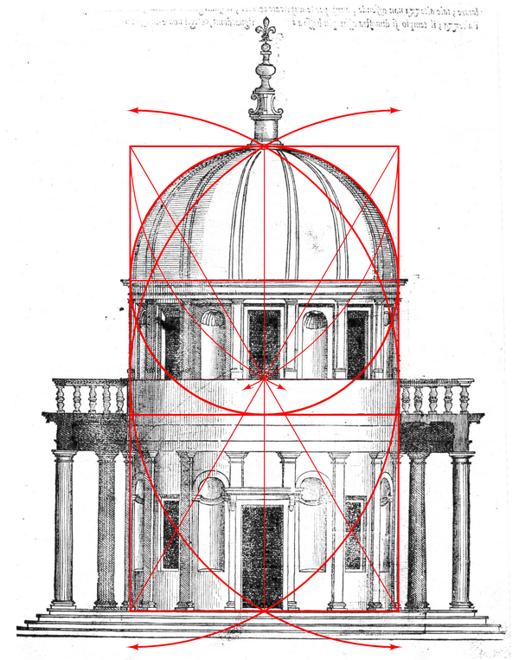 Марквардт, получивший докторскую степень в Калифорнийском университете в Лос-Анджелесе и занимающийся исследованиями человеческой привлекательности, считает, что золотое сечение — это математическая формула, описывающая красоту лица.
Марквардт, получивший докторскую степень в Калифорнийском университете в Лос-Анджелесе и занимающийся исследованиями человеческой привлекательности, считает, что золотое сечение — это математическая формула, описывающая красоту лица.
Примеры золотого сечения
- «Мона Лиза» Леонардо да Винчи
- Парфенон
- Раковины улиток
- Ураганы
- Высевающие головки
- Лепестки цветов
- Сосновые шишки
- «Тайная вечеря» Леонардо да Винчи
- Ветки деревьев
- Человеческое лицо
- Спиральная галактика
- «Сотворение Адама» Микеланджело
- молекул ДНК
- «Таинство Тайной вечери» Сальвадора Дали
Следующий курс был разработан совместно с Институтом цифрового маркетинга:
[PDF] How toExplore Golden Ratio in Architecture and Design City
ПОКАЗЫВАЕТ 1-10 ИЗ 17 РЕФЕРЕНЦИЙ
СОРТИРОВАТЬ ПОРелевантностиНаиболее влиятельные документыНедавность
Дом с золотым сечением: конструкция формы
Дом с золотым сечением в первую очередь из куба, который является необходимой исходной точкой для этого проекта. Подобно правилам изобретательства, его цель состоит в том, чтобы… Развернуть
Подобно правилам изобретательства, его цель состоит в том, чтобы… Развернуть
Золотое сечение
В статье о восприятии эстетики верхних резцов1 не упоминалось о золотом сечении, соотношении 1,61:1, которое встречается в природе и науке и имеет использовался в архитектуре; по общему мнению, Парфенон был построен в таких пропорциях. Expand- Посмотреть 2 выдержки, справочная информация
Применение золотой середины в архитектуре
Золотое сечение, иррациональное число, связанное с последовательностью Фибоначчи, возникает при изучении биологического роста и иерархических систем.Совершенно отличается от природных структур, которые демонстрируют такие… Expand
Архитектурная форма, пространство и порядок
Серия цифровых презентаций, связывающих концептуальные и перцептивные аспекты архитектуры путем наложения фотографий и рисунков со схемами, помогающими зрителю идентифицировать элементы и абстрактные принципы от того, что видно в книге или на мониторе.

 3
3

 При этом эти точки
образуют новую пентаграмму FGHKL. В
новой пентаграмме можно провести
диагонали, пересечение которых образуют
новую пентаграмму.
При этом эти точки
образуют новую пентаграмму FGHKL. В
новой пентаграмме можно провести
диагонали, пересечение которых образуют
новую пентаграмму. 1)
1) С математикой в путь: Пер. с
англ.-М.:Педагогика, 1987
С математикой в путь: Пер. с
англ.-М.:Педагогика, 1987
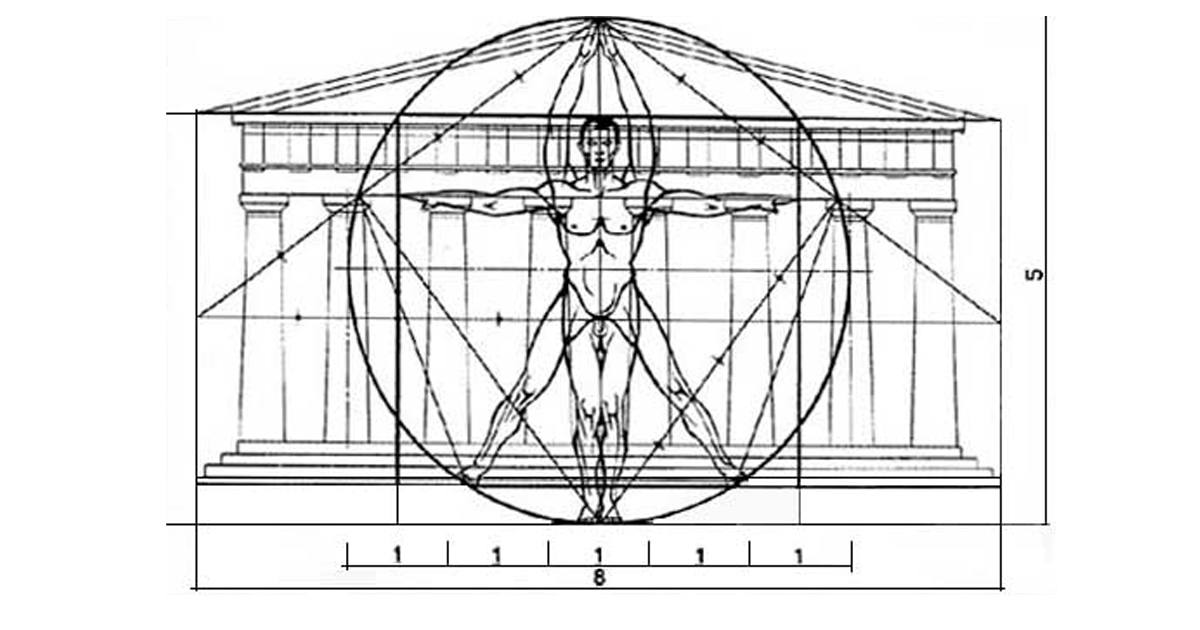 4 «Отношения и пропорции». Дается обзор некоторых применений золотого сечения в науке и искусстве на протяжении истории человечества.
4 «Отношения и пропорции». Дается обзор некоторых применений золотого сечения в науке и искусстве на протяжении истории человечества. Рассмотрению особенностей проявления золотой пропорции – от объектов природы до произведений искусства посвящена данная работа. Практическая значимость материала состоит в том, что на его основе может быть создан интереснейший элективный курс как для учащихся 6-7-х классов, так и для учеников старшей школы.
Рассмотрению особенностей проявления золотой пропорции – от объектов природы до произведений искусства посвящена данная работа. Практическая значимость материала состоит в том, что на его основе может быть создан интереснейший элективный курс как для учащихся 6-7-х классов, так и для учеников старшей школы. В ней показано применение золотого сечения в архитектуре, скульптуре и живописи.
В ней показано применение золотого сечения в архитектуре, скульптуре и живописи. Рассказано о «золотых» геометрических фигурах и о золотом сечении в природе, искусстве и архитектуре. Работа сопровождается презентацией и исследовательским материалом по изучению золотого сечения в архитектуре г. Владивостока.
Рассказано о «золотых» геометрических фигурах и о золотом сечении в природе, искусстве и архитектуре. Работа сопровождается презентацией и исследовательским материалом по изучению золотого сечения в архитектуре г. Владивостока.
 Материалы представлены в виде таблиц, схем, диаграмм. Большое внимание уделяется эстетике восприятия «золотых» фигур.
Материалы представлены в виде таблиц, схем, диаграмм. Большое внимание уделяется эстетике восприятия «золотых» фигур. Автор применяет полученные знания при исследовании пропорций астраханских церквей и соборов на наличие пропорций золотого сечения.
Автор применяет полученные знания при исследовании пропорций астраханских церквей и соборов на наличие пропорций золотого сечения. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии.
Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Форма, в основе построения которой лежит золотое сечение, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Цель работы – узнать и показать взаимодействие и взаимообогащение науки математики и природы, искусства. В работе автор изучила пропорцию золотого сечения; провела ряд исследований, показывающих присутствие золотого сечения в нас самих и вокруг нас; познакомилась с учеными, внесшими весомый вклад в изучение золотого сечения.
Форма, в основе построения которой лежит золотое сечение, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Цель работы – узнать и показать взаимодействие и взаимообогащение науки математики и природы, искусства. В работе автор изучила пропорцию золотого сечения; провела ряд исследований, показывающих присутствие золотого сечения в нас самих и вокруг нас; познакомилась с учеными, внесшими весомый вклад в изучение золотого сечения. В школьной программе данная тема изучается недостаточно полно, но я, занимаясь в Дизайн-студии ДТДиМ, заинтересовался этим вопросом. В жизни мы ежедневно встречаемся с золотым сечением, но большинство людей об этом и не подозревают.
В школьной программе данная тема изучается недостаточно полно, но я, занимаясь в Дизайн-студии ДТДиМ, заинтересовался этим вопросом. В жизни мы ежедневно встречаемся с золотым сечением, но большинство людей об этом и не подозревают. Казани, столицы Татарстана. На основе этих примеров автор делает вывод, что «золотое сечение» можно назвать формулой красоты.
Казани, столицы Татарстана. На основе этих примеров автор делает вывод, что «золотое сечение» можно назвать формулой красоты.

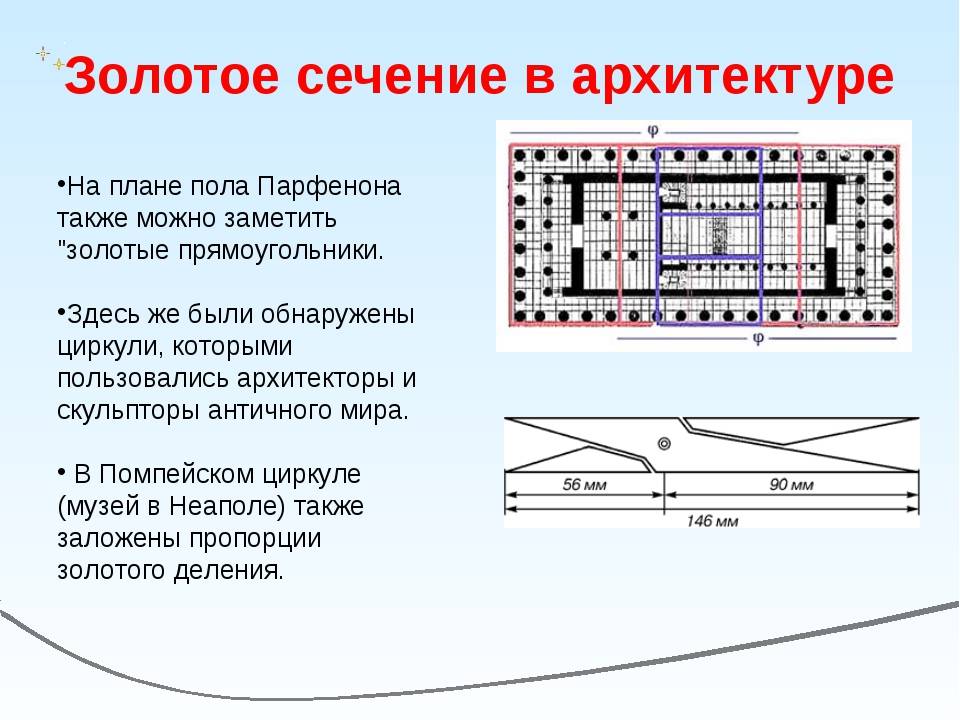

 Вы увидите, что эти
линии выделяют значимые части изображения или проходят через важные
объекты. Затем вы можете попробовать провести линии, которые делят эти части на
их золотые сечения тоже.
Вы увидите, что эти
линии выделяют значимые части изображения или проходят через важные
объекты. Затем вы можете попробовать провести линии, которые делят эти части на
их золотые сечения тоже. В точке золотого сечения
по вертикали пупок указан в самом узком месте талии, а также внизу
край пояса (пояса или пояса) показан синими стрелками.
В точке золотого сечения
по вертикали пупок указан в самом узком месте талии, а также внизу
край пояса (пояса или пояса) показан синими стрелками.
 Поэтому там
не может быть ничего существенного в 239, потому что в тот момент
бывает дважды. Однако в 387 есть что-то довольно странное — это
инверсия основного девиза. У вас большая оркестровая деятельность,
потом тишина, потом эта тихая инверсия девиза, потом тишина,
затем снова большая активность.
Поэтому там
не может быть ничего существенного в 239, потому что в тот момент
бывает дважды. Однако в 387 есть что-то довольно странное — это
инверсия основного девиза. У вас большая оркестровая деятельность,
потом тишина, потом эта тихая инверсия девиза, потом тишина,
затем снова большая активность.

 Вы можете услышать их и прочитать больше на
его веб-сайт. У Кейси впечатляюще большой
набор фрагментов, большинство из которых длится всего несколько секунд, но они увлекательная для прослушивания и очень отличается от обычной музыки.То
высота тона его нот часто основана на степенях Фи, а их порядок фиксируется числом.
последовательности, такие как числа Фибоначчи или R(n) —
количество представлений Фибоначчи n
или во многих других последовательностях
которые описаны здесь, на моем сайте Фибоначчи.
Вы можете услышать их и прочитать больше на
его веб-сайт. У Кейси впечатляюще большой
набор фрагментов, большинство из которых длится всего несколько секунд, но они увлекательная для прослушивания и очень отличается от обычной музыки.То
высота тона его нот часто основана на степенях Фи, а их порядок фиксируется числом.
последовательности, такие как числа Фибоначчи или R(n) —
количество представлений Фибоначчи n
или во многих других последовательностях
которые описаны здесь, на моем сайте Фибоначчи. 
