Лимб и алидада теодолита — Морской флот
Теодолит — середины 20 го века Теодолит измерительный прибор для измерения горизонтальных и вертикальных углов при геодезических работах, топографических, геодезических и маркшейдерских съёмках, в строительстве и т. п. Основной рабоч … Википедия
Лимб (инструмент) — Эта статья слишком короткая. Пожалуйста … Википедия
Корпус военных топографов — Основание Указ императора Александра I 28 января 1822 года Ликвидация Постановление СНК СССР 1918 год Корпус военных топографов (КВТ) (до 1866 Корпус топографов) был организован в 1822 году для централизов … Википедия
Теодолит — геодезический инструмент (См. Геодезические инструменты) для определения направлений и измерения горизонтальных и вертикальных углов при геодезических работах, топографических и маркшейдерских съёмках, в строительстве и т. п. (см.… … Большая советская энциклопедия
Магнитные приборы* — для наблюдения земного магнетизма: I) для абсолютных наблюдений, II) для вариационных и III) магнитограф. I. М. приборы для абсолютных измерений элементов земного магнетизма (см.). Простейший прибор для определения склонения буссоль склонения,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
I. М. приборы для абсолютных измерений элементов земного магнетизма (см.). Простейший прибор для определения склонения буссоль склонения,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Магнитные приборы — для наблюдения земного магнетизма: I) для абсолютных наблюдений, II) для вариационных и III) магнитограф. I. М. приборы для абсолютных измерений элементов земного магнетизма (см.). Простейший прибор для определения склонения буссоль склонения,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ГЕОДЕЗИЯ — (греч. geodaisia, от ge Земля и daio делю, разделяю), наука об определении положения объектов на земной поверхности, о размерах, форме и гравитационном поле Земли и других планет. Это отрасль прикладной математики, тесно связанная с геометрией,… … Энциклопедия Кольера
геодезия — наука, изучающая форму, размеры и гравитационное поле Земли, а также технические средства и методы измерений на местности. Геодезия зародилась в странах Древнего Востока и в Египте, где задолго до н. э. были известны методы измерения земельных… … Географическая энциклопедия
Геодезия зародилась в странах Древнего Востока и в Египте, где задолго до н. э. были известны методы измерения земельных… … Географическая энциклопедия
Универсальный инструмент — универсал в астрономии и геодезии, переносный угломерный инструмент, служащий для измерения углов в вертикальной и горизонтальной плоскостях. С помощью У. и. по наблюдениям звёзд и Солнца определяют географические координаты места,… … Большая советская энциклопедия
Теодолит состоит из (рис. 5 а, б): подставки с тремя подъемными винтами, которая крепится к головке штатива становым (закрепительным) винтом через трегер, представляющий собой пластину со втулкой, в которой имеется резьба. В подставке вращается алидадная часть теодолита, состоящая из лимба, цилиндрическая ось которого входит в полость подставки и собственно алидады, ось которой, в свою очередь, входит в цилиндрическую полость лимба. Между стойками закреплена на оси и может вращаться зрительная труба, состоящая из объектива, окуляра и расположенной между ними фокусирующей линзы, которая может перемещаться в небольших пределах с помощью винта фокусировки. В окулярном колене зрительной трубы расположена, заключенная в оправу, стеклянная пластина, закрепленная четырьмя юстировочными винтами, на которой методом гравировки нанесена сетка нитей. Окулярное кольцо при вращении перемещает линзу, заключенную в обойму, и позволяет фокусировать изображение сетки нитей зрительной трубы в соответствии со зрением. На корпусе зрительной трубы закреплены оптические визиры, позволяющие осуществлять грубое наведение теодолита на цель.
В окулярном колене зрительной трубы расположена, заключенная в оправу, стеклянная пластина, закрепленная четырьмя юстировочными винтами, на которой методом гравировки нанесена сетка нитей. Окулярное кольцо при вращении перемещает линзу, заключенную в обойму, и позволяет фокусировать изображение сетки нитей зрительной трубы в соответствии со зрением. На корпусе зрительной трубы закреплены оптические визиры, позволяющие осуществлять грубое наведение теодолита на цель.
На одной из стоек расположен установочный цилиндрический уровень, один конец которого заделан шарнирно, а дугой закреплен между двумя юстировочными винтами (или винтом и пружиной).
На другой стойке закреплен вертикальный круг, состоящий из лимба, скрепленного со зрительной трубой и алидады, скрепленной со стойкой, линия нулей которой перпендикулярна оси вращения теодолита или устанавливается горизонтально автоматически с помощью компенсатора.
Горизонтальный и вертикальный угломерные круги теодолита одинаковые по размерам и изготовлены в виде колец из стекла. На посеребренном крае угломерного круга нанесены градусные деления. Изображения горизонтального и вертикального угломерных кругов с помощью оптической системы теодолита предается в поле зрения оптического шкалового микроскопа, расположенного рядом с окуляром зрительной трубы. В поле зрения шкалового микроскопа видны изображения горизонтального и вертикального угломерных кругов, а также шкалы верньеров, с помощью которых производится отсчет. Окулярное кольцо шкалового микроскопа позволяет фокусировать изображения делений лимба и алидады и их оцифровку.
На посеребренном крае угломерного круга нанесены градусные деления. Изображения горизонтального и вертикального угломерных кругов с помощью оптической системы теодолита предается в поле зрения оптического шкалового микроскопа, расположенного рядом с окуляром зрительной трубы. В поле зрения шкалового микроскопа видны изображения горизонтального и вертикального угломерных кругов, а также шкалы верньеров, с помощью которых производится отсчет. Окулярное кольцо шкалового микроскопа позволяет фокусировать изображения делений лимба и алидады и их оцифровку.
Теодолит имеет ряд закрепительных и наводящих винтов: лимба, алидады, зрительной трубы. Обычно, перпендикулярно закрепительному винту расположен наводящий винт. Центрирование теодолита над вершиной измеряемого угла осуществляется с помощью нитяного отвеса, который крепится к специальному крючку станового винта или с помощью оптического отвеса, вмонтированного в подставку.
Рис. 5 а. Теодолит 4Т30П. 1 – трегер, 2 – подъемные винты подставки, 3 – оптический центрир, 4 – подставка, 5 – алидадная часть теодолита, 6 – винт вращения лимба, совмещения нулей лимба и алидады, 7 – цилиндрический, установочный уровень, 8 – юстировочные винты цилиндрического уровня, 9 – стойки, 10 – зеркало подсветки оптической системы, 11 –наводящий винт зрительной трубы, 12 – оптический визир, 13 – вертикальный круг, 14 – винт фокусировки, 15 – зрительная труба (объектив), 16 – зажимной винт зрительной трубы, 17 – цилиндрический уровень при зрительной трубе, 18 – закрепительный винт ориентир – буссоли, 19 – ориентир – буссоль, 20 – зеркало
Рис.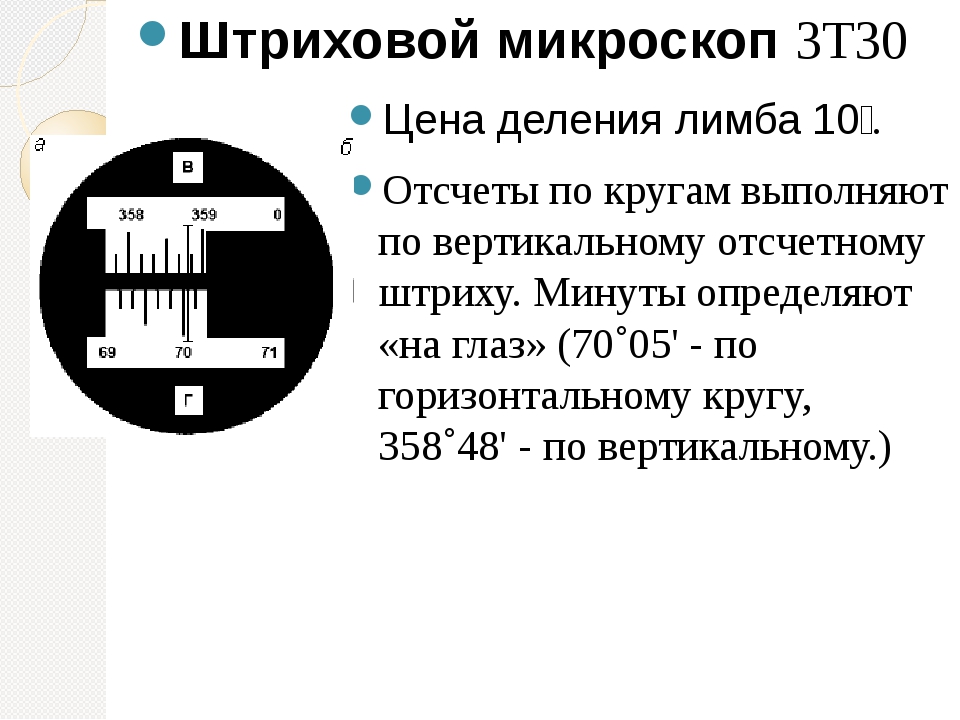 5 б. Теодолит 3Т15П. 1 – трегер, 2 – подъемные винты подставки, 3 – подставка, 4 – закрепительный винт лимба, 5 – наводящий винт алидады, 6 – закрепительный винт алидады, 7 – винт вращения лимба, совмещения нулей лимба и алидады, 8 – цилиндрический уровень, 9 – юстировочные винты цилиндрического уровня, 10 – микрометренный винт шкалового микроскопа, 11 –наводящий винт зрительной трубы, 12 – стойки, 13 – зеркало подсветки оптической системы, 14 – оптический визир, 15 – вертикальный круг, 16 – винт фокусировки, 17 – ось зрительной трубы, 18 – зрительная труба (объектив), 19 – зажимной винт зрительной трубы, 20 – цилиндрический уровень при зрительной трубе
5 б. Теодолит 3Т15П. 1 – трегер, 2 – подъемные винты подставки, 3 – подставка, 4 – закрепительный винт лимба, 5 – наводящий винт алидады, 6 – закрепительный винт алидады, 7 – винт вращения лимба, совмещения нулей лимба и алидады, 8 – цилиндрический уровень, 9 – юстировочные винты цилиндрического уровня, 10 – микрометренный винт шкалового микроскопа, 11 –наводящий винт зрительной трубы, 12 – стойки, 13 – зеркало подсветки оптической системы, 14 – оптический визир, 15 – вертикальный круг, 16 – винт фокусировки, 17 – ось зрительной трубы, 18 – зрительная труба (объектив), 19 – зажимной винт зрительной трубы, 20 – цилиндрический уровень при зрительной трубе
Лимб горизонтального круга представляет собой стеклянный угломерный круг. Стеклянные лимбы выполняются обычно в виде колец, на которые нанесены деления от 0 до 360°. Размеры лимба зависят от требуемой точности измерения углов. Чем выше требуемая точность, тем больше диаметр лимба.Деления на лимбе наносятся с помощью специальной делительной машины. Цифры наносятся на шкале, как правило через 1°. Количество делений, содержащихся в одном градусе, определяет цену деления лимба.
Цифры наносятся на шкале, как правило через 1°. Количество делений, содержащихся в одном градусе, определяет цену деления лимба.
Подставка предназначена для крепления теодолита к штативу и состоит из следующих основных частей: собственно подставки с цилиндрической полостью, трех подъемных винтов, трегера и пружины (современные теодолиты пружины не имеют). Подъемные винты служат для установки оси вращения теодолита в отвесное положение. В центре трегера укреплена втулка с резьбой для станового винта, которым подставка крепится к головке штатива.
Алидада горизонтального круга представляет собой круг или два диаметрально противоположных сектора, центры которых должны совпадать с центром лимба. Один из диаметров алидады принимается за начальный и обозначается «». От нуля по ходу часовой стрелки нанесена специальная шкала – верньер, разделяющая один градус на определенное количество делений, определяемое точностью прибора.
Отсчитывание углов по лимбу и алидаде производится с помощью специального оптического отсчетного устройства – шкалового микроскопа.
Алидада горизонтального круга имеет меньший диаметр, чем лимб, и расположена в конической полости оси лимба. Теодолиты, конструкция осей которых позволяет независимо вращать алидаду и лимб, называются повторительными.
Цилиндрический уровень (рис. 6) служит для точной установки осей прибора в горизонтальное или вертикальное положение. Основным элементом уровня является стеклянная трубка 1, называемая ампулой. Ампулу заполняют разогретым эфиром. При остывании эфир уменьшается в объеме, и в ампуле образуется пространство 4, заполненное парами эфира, которое называют пузырьком уровня. Внутреннюю поверхность ампулы уровня тщательно шлифуют под определенным радиусом кривизны R. Наивысшая точка поверхности ампулы называется нуль-пунктом (точка О на рис. 6). На наружной поверхности ампулы нанесены деления 5, по которым определяется положение пузырька уровня. Когда концы пузырька располагаются симметрично относительно нуль-пункта, принято говорить, что пузырек находится в нуль-пункте.
6). На наружной поверхности ампулы нанесены деления 5, по которым определяется положение пузырька уровня. Когда концы пузырька располагаются симметрично относительно нуль-пункта, принято говорить, что пузырек находится в нуль-пункте.
Касательная UU1 к дуге АОВпродольного сечения внутренней поверхности ампулы в нуль-пункте (рис. 6, в) называется осью цилиндрического уровня. Когда пузырек уровня находится в нуль-пункте, ось уровня занимает горизонтальное положение.
Рис. 6. Цилиндрический уровень: а – вертикальный разрез: 1 – ампула; 2 – корпус; 3 – юстировочные гайки; 4 – пузырек уровня: 5 – верх ампулы с делениями; 6 – оправа уровня; б – вид сверху: в – принцип работы цилиндрического уровня.
Угол τ, на который наклоняется ось уровня при перемещении пузырька на одно деление ампулы, называется ценой деления уровня. Цена деления уровня служит мерой чувствительности уровня. Чем меньше цена деления, тем выше его чувствительность. Ампула уровня помещается в специальную оправу 6, один конец которой шарнирно соединен с корпусом2 уровня, а другой закреплен двумя юстировочнымигайками (или винтами) 3, с помощью которых можно изменять наклон оси уровня относительно его корпуса.
Чем меньше цена деления, тем выше его чувствительность. Ампула уровня помещается в специальную оправу 6, один конец которой шарнирно соединен с корпусом2 уровня, а другой закреплен двумя юстировочнымигайками (или винтами) 3, с помощью которых можно изменять наклон оси уровня относительно его корпуса.
Зрительная труба (рис. 7а) служит для наведения теодолита на удаленные точки местности, построения направления и проектирования его на горизонтальный круг. Зрительная труба состоитизобъектива и окуляра, заключенных в общий корпус. Для получения отчетливого изображения при различных удалениях наблюдаемого предмета между объективом и окуляром помещается фокусирующая линза, которая может перемещаться в небольших пределах. Процесс получения отчетливого изображения путем перемещения фокусирующей линзы называется фокусированием.
| Рис. 7. Устройство зрительной трубы с внутренним фокусированием | Диафрагма и сетка нитей |
В зрительной трубе различают геометрическую, оптическую, визирную оси и ось вращения.Зрительные трубы геодезических приборов обеспечивают точность наведения на предметы, расположенные на расстоянии, которое в 2 раза больше фокусного расстояния объектива. У современных оптических теодолитов зрительные трубы имеют внутреннее фокусирование и увеличение 20 – 25 крат.
Поскольку геометрическая и оптическая оси (геометрической осью называют прямую, соединяющую центры входного и выходного отверстий, оптической осью называют прямую, соединяющую оптические центры объектива и окуляра) не совпадают и, кроме того, ничем не зафиксированы, пользоваться ими для точного наведения трубы на точки местности практически невозможно. Для получения в поле зрения трубы постоянной фиксированной точки, служащей для наведения трубы на предмет, перед окуляром с помощью винтов крепится диафрагма 4со стекломна котором выгравировано несколько пересекающихся прямых линий. Средние из них, пересекаясь, образуют крест сетки нитей К. Пластина заключена в специальную оправу-диафрагму, которая может перемещаться в небольших пределах с помощью винтов(рис. 7 б).
Для получения в поле зрения трубы постоянной фиксированной точки, служащей для наведения трубы на предмет, перед окуляром с помощью винтов крепится диафрагма 4со стекломна котором выгравировано несколько пересекающихся прямых линий. Средние из них, пересекаясь, образуют крест сетки нитей К. Пластина заключена в специальную оправу-диафрагму, которая может перемещаться в небольших пределах с помощью винтов(рис. 7 б).
Визирной осью трубы называется прямая, соединяющая оптический центр объектива с крестом сетки нитей. При наведении креста сетки нитей на изображение точки местности, видимой в поле зрения (этот процесс называется визированием), происходит построение направления от исходной точки на искомую.
Для того чтобы спроектировать это направление на горизонтальный круг, труба должна вращаться в плоскости, перпендикулярной к плоскости штрихов лимба и проходящей через центр угломерного круга (лимба). При повороте трубы вокруг оси вращения визирная ось описывает плоскость, которая носит название коллимационной. Коллимационная плоскость должна проходить через нуль горизонтального круга. Поворот трубы вокруг оси вращения, в результате которого окуляр становится в положение, занимаемое до этого объективом, называется переводом зрительной трубы через зенит.
При повороте трубы вокруг оси вращения визирная ось описывает плоскость, которая носит название коллимационной. Коллимационная плоскость должна проходить через нуль горизонтального круга. Поворот трубы вокруг оси вращения, в результате которого окуляр становится в положение, занимаемое до этого объективом, называется переводом зрительной трубы через зенит.
Вертикальный круг служит для измерения углов наклона. Он состоит из лимба вертикального круга, скрепленного со зрительной трубой и алидады вертикального круга, скрепленной со стойкой.Современные теодолиты снабжены устройствами – компенсаторами – (взамен уровня) для автоматической установки горизонтально линии нулей верньера вертикального круга. При отсутствии компенсатора горизонтальность линии нулей обеспечивается конструкцией теодолита.
Если визирную ось трубы установить горизонтально, то нули лимба должны совместиться с нулями верньера алидады.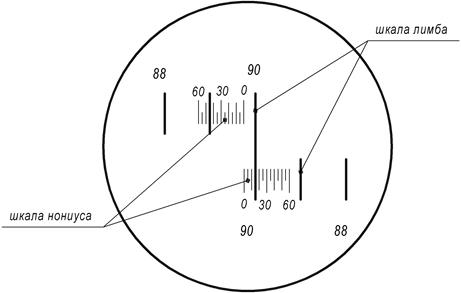 Отсчет по лимбу вертикального круга при горизонтальном положении визирной оси называется местом нуля вертикального круга и обозначается МО. В процессе измерения вертикальных углов этот угол должен оставаться постоянным.
Отсчет по лимбу вертикального круга при горизонтальном положении визирной оси называется местом нуля вертикального круга и обозначается МО. В процессе измерения вертикальных углов этот угол должен оставаться постоянным.
Штативслужит для установки теодолита (или любого другого геодезического прибора) над точкой местности. Основными частями штатива являются:
головка, на которой устанавливается инструмент при измерении;
ножки (металлические или деревянные), которые крепятся шарнирно к головке штатива с помощью болтов с гайками.
Верхние части ножек оправлены металлом, на нижние концы набиваются металлические наконечники. Ножки штатива могут быть постоянной длины или раздвижными. Раздвижные ножки позволяют быстро устанавливать инструмент над точкой при работе на наклонных участках местности и на нужной высоте над точкой местности. В центре головки штатива имеется отверстие, через которое с помощью станового винта крепится подставка теодолита. Ось симметрии станового винта совпадает с осью вращения теодолита. Соблюдение этого условия необходимо для центрирования теодолита над точкой местности. Центрирование осуществляется с помощью нитяного или оптического отвеса.
Ось симметрии станового винта совпадает с осью вращения теодолита. Соблюдение этого условия необходимо для центрирования теодолита над точкой местности. Центрирование осуществляется с помощью нитяного или оптического отвеса.
Нитяной отвес подвешивается за крючок станового винта на шнуре. Отвес представляет собой цилиндр с коническим окончанием, причем вершина конуса совпадает с осью симметрии станового винта.
Оптический отвес (рис. 8) состоит из окуляра1, в поле зрения которого на сетку нитей 2 через призму 3 передается изображение точки местности 4. Оптический отвес с помощью специальных винтов 5 крепится либо к подставке, либо к нижней поверхности цилиндрической оси вращения теодолита. Он устанавливается так, чтобы ось, проходящая через перекрестие сетки нитей 6, была перпендикулярна к оси 7вращения прибора. Установка сетки нитей производится с помощью юстировочных винтов 8.
Рис.8. Оптический отвес: 1 – окуляр; 2 – сетка нитей; 3 – призма; 4 – закрепленная точка местности; 5 – винт; 6 – перекрестие сетки нитей:7 – ось вращения прибора; 8 – юстировочные винты
С точки зрения входящих в комплект частей, устройство теодолита простое. Трудности возникают в процессе настройки прибора. Дело это тонкое и требуют постоянные проверки. Однако в строительстве и проектировании прибор просто незаменим. Геодезисты знают об этом, мы же попробуем описать, так сказать, строение теодолита и его работу более популярным языком.
Основные части теодолита
Приспособление позволяет с высокой точностью замерять углы в пространстве и работать в горизонтальной или вертикальной плоскости. Как правило, выбирается относительный метод, когда за основу принимается эталонный объект, а по нему уже отсчитывается искомый угол. Измерение таким способом известно с XIX века, но сегодняшние теодолиты — это усовершенствованные приспособления, которых существует несколько разновидностей.
Шкала. Этот элемент, представленный горизонтально или вертикально расположенным кругом, показывает результат. Находится на подставке, имеющей регулировочные винты для управления главными узлами. Измеритель смотрит в окуляр, управляемый винтами, которые позволяют навести окуляр на объект и закрепить его, когда найдена контрольная точка.
Лимб и алидада. Части горизонтального круга, активно использующиеся при измерении горизонтальных углов.
- Лимб — это стационарное стеклянное кольцо с делениями на 360°.
- Алидада — элемент, вращающийся с примыкающей частью прибора и выставляющий отсчет.
Для фиксации отсчета и дальнейшего проведения измерений относительно него закрепляется специальный винт и отпускается лимб, корпус в этом случае останется неподвижным, двигаться же будут лимб и алидада.
Это и есть главные части теодолита. Но снимать показания помогают и другие устройства, с которыми тоже будет полезно познакомиться. Степень горизонтальности установки теодолита контролируется с помощью цилиндрического уровня, а точку отсчета потерять не дает оптический центрир. Отсчеты снимаются по микроскопу, и это финальная стадия работы замерщика.
Виды устройств
Имеются следующие виды устройств:
- Механические. Наиболее простой по конструкции и самый дешевый тип, однако у него и самая низкая точность, поэтому для серьезной работы он не подходит.
- Электронные. Электронный теодолит удобен, потому что оснащен устройством для считывания и обработки результатов, геодезисту остается правильно выставить его, а остальное прибор сделает сам.
- Оптические. Наиболее широкое распространение получил теодолит оптический. Он не производит расчеты, как электронный, но стоимость устройства и качество измерения привлекают.
- Лазерные. Эти теодолиты самые дорогие, но и более совершенные устройства. Позволяют делать измерения с большой точностью и удобны в использовании, но приобретать их имеет смысл лишь для постоянных работ, где высоки требования к результату.
Два принципиально разных вида теодолитов отличаются по подвижности алидады и лимба. В повторительных типах данные элементы могут закреплять поочередно, а показания снимать методом последовательных повторений. Обыкновенные варианты этого не допускают, так как алидада с осью представляют в них единое неподвижное целое, и для каждого измерения требуется отдельная настройка.
Маркировка
Марка теодолита — это совокупность букв и цифр. В каждой есть связка литеры «Т» с какой-либо цифрой. Буква указывает на то, что прибор — теодолит, цифры показывают погрешность измерения в секундах, чем они больше, тем больше и погрешность.
- Цифрой 1 маркируются высокоточные приборы.
- Цифрами 2 и 5 маркируются точные теодолиты.
- Цифрами 15 и 30 маркируются технические приборы.
Стоит цифра точности после литеры «Т», а если перед буквой есть другая цифра, она служит для обозначения поколения прибора или его модификации в категории марки.
Требования перед работой
Перед измерением углов теодолит проверяется. Нужно проверять специальную отметку или пломбу, а также периодически — геометрические параметры, так как ошибка в пару градусов со временем может привести к катастрофе!
- Важна абсолютная вертикальность оси алидады и ее перпендикулярность цилиндрическому уровню.
- Визирная ось зрительной трубы должна быть перпендикулярна ей, не выполнив этого коллимационного условия, четкая система отсчета невозможна.
- Оси трубы и алидады должны быть перпендикулярными.
- Проверяем, насколько измерительная сетка расположена в вертикальной коллимационной плоскости.
Использование теодолита
Приемов профессионального использования приборов много, и им учат на специальных курсах, здесь же приведем основные из них.
- Установка теодолита. Первым шагом станет нахождение точки отсчета. На местности находим ровную поверхность, по которой центрируем прибор на подставке уровнями и зажимными винтами. В итоге положение прибора должно получиться строго горизонтальным.
- Ловим объект. Визиром отыскиваем цель и точнее наводим винтами измерительную сетку, чтобы установить центр объекта. На это смотрим через окуляр, а если света недостаточно, улучшить ситуацию поможет специальное зеркальце (как в случае с микроскопом). После выставления центра окуляром фиксируется его значение.
- Обработка результатов. Лучше сделать не одно, а несколько измерений. Новый отсчет рекомендуется на известную величину, к примеру, 90°. Если новые измерения отличаются от предыдущих на 90°, то результат можно фиксировать, если нет — производится еще пара подобных измерений с разным отсчетом и вычисляется среднее значение.
История приборов
Первые теодолиты в центре угломерного круга на острие иголки имели линейку, способную вращаться на этом острие свободно (подобно стрелке компаса). В линейке делались вырезы, в которых натягивались нити, служащие отсчетными индексами. Центр угломерного круга помещался в вершину измеряемого угла, где и закреплялся.
Поворачивая линейку, ее совмещали с первой стороной угла и по шкале круга брали отсчет N1. Потом линейку совмещали со второй стороной угла и брали отсчет N2. Разность N2 и N1 равнялась значению угла. Подвижную линейку назвали алидадой, а угломерный круг — лимбом. Совмещение линейки-алидады со сторонами угла осуществлялось с помощью примитивных визиров.
Современные теодолиты существенно отличаются от предшественников.
- Совмещение алидады со сторонами угла производится с помощью зрительной трубы, которая может вращаться по высоте и азимуту.
- Для отсчета по шкале лимба применяется отсчетное приспособление.
- Конструкцию покрывает прочный металлический кожух.
- Прочее.
Плавное вращение алидады и лимба обеспечивает система осей, а регулируются вращения наводящими и зажимными винтами.
Установки теодолита производятся с помощью специального штатива. Центр лимба с отвесной линией, которая проходит через вершину измеряемого угла, осуществляется оптическим центриром или нитяным отвесом.
Коллимационная плоскость образуется визирной осью окуляра при вращении зрительной трубы вокруг собственной оси. Стороны угла проектируются на лимб подвижной вертикальной плоскостью, называющейся коллимационной плоскостью. Плоскость эта образуется визирной осью зрительной трубы, когда труба вращается вокруг своей оси.
Визирной осью трубы (визирной линией) называется воображаемая линия, которая проходит через центр сетки нитей и оптический центр объектива трубы.
ТЕОДОЛИТ | МобиСтрой
Теодолитом называют геодезический оптический прибор для измерения и построения на местности горизонтальных углов. Конструкции многих теодолитов позволяют измерять и вертикальные углы, но с меньшей точностью, чем горизонтальные. Различают теодолит ы высокоточные, точные и технические (малой точности).
Схема устройства и основные элементы теодолита: 1 — исходная станция {вершина угла), 2 — подставка, 3 — подъемный винт, 4 и 5 — лимб и алидада горизонтального круга, 6 — подставка трубы, 7 и 8 — вертикальный круг, 9 — зрительная труба, 10 — визирная ось трубы, 11 — ось вращения трубы, 12 — цилиндрический уровень, 13 — ось уровня, 14 — зажимные винты горизонтального круга, 15 — штатив, 16 — становой винт, 17 — нитяной отвес
Конструктивные ‘элементы теодолита: подставка-треножник (трегер) 2 с тремя подъемными винтами, горизонтальный круг (лимб 4 и алидада 5), подставка трубы (колонки) 6, вертикальный круг (алидада 7 и лимб 8), зрительная труба 9, цилиндрический уровень 12 при горизонтальном круге. Прибор крепится к штативу 15 с помощью станового винта 16. Для крепления частей прибора в нужном положении служат зажимные винты 14. В вершине измеряемого угла, над точкой стояния (станцией) 1, теодолит центрируется по отвесу 17. Точность центрирования нитяным отвесом равна 3-5 мм, оптическим центри-ром — в пределах 1 — 2 мм.
Зрительная труба 9 имеет три оси: геометрическую (ось цилиндра трубы), оптическую (линия, соединяющая оптические центры объектива и окуляра) и визирную 10 (линия, связывающая оптический центр объектива и точку пересечения нитей сетки).
Горизонтальный круг состоит из двух частей: лимба 4 и алидады 5. Лимб — это металлическое или стеклянное кольцо, по внешнему краю которого нанесены градусные и минутные деления. Деления отсчитываются по ходу часовой стрелки. Наименьшее расстояние между двумя делениями — цена деления лимба. Алидада — это концентрически связанный с лимбом круг или двойной сектор, на котором расположены отсчетные приспособления. На кожухе алидады крепится подставка 6 зрительной трубы. При измерении горизонтальных углов лимб остается неподвижным, а трубу вместе с алидадой устанавливают в заданном направлении. Подъемные винты 3 служат для установки плоскости горизонтального круга (и оси 13 цилиндрического уровня) строго горизонтально. Алидада вместе с подставкой и зрительной трубой может вращаться относительно лимба, который при необходимости также можно поворачивать. После грубого предварительного наведения и закрепления алидады теодолит точно наводят на наблюдаемую точку специальными наводящими винтами, обеспечивающими плавное его вращение.
Вертикальный круг, служащий для измерения вертикальных углов, состоит из лимба 8, наглухо соединенного со зрительной трубой, и алидады 7, жестко связанной с осью 11 вращения трубы. В рабочее положение круг часто устанавливается с помощью специального уровня или маятникового компенсатора.
Принцип работы теодолита
Особенности конструкции и инструкция, как пользоваться теодолитом. Классификация инструмента и последовательное пояснение по выполнению работ. Установка прибора, ловля объекта и обработка полученных результатов.
Основные части теодолита
Приспособление позволяет с высокой точностью замерять углы в пространстве и работать в горизонтальной или вертикальной плоскости. Как правило, выбирается относительный метод, когда за основу принимается эталонный объект, а по нему уже отсчитывается искомый угол. Измерение таким способом известно с XIX века, но сегодняшние теодолиты — это усовершенствованные приспособления, которых существует несколько разновидностей.
Шкала. Этот элемент, представленный горизонтально или вертикально расположенным кругом, показывает результат. Находится на подставке, имеющей регулировочные винты для управления главными узлами. Измеритель смотрит в окуляр, управляемый винтами, которые позволяют навести окуляр на объект и закрепить его, когда найдена контрольная точка.
Лимб и алидада. Части горизонтального круга, активно использующиеся при измерении горизонтальных углов.
- Лимб — это стационарное стеклянное кольцо с делениями на 360°.
- Алидада — элемент, вращающийся с примыкающей частью прибора и выставляющий отсчет.
Для фиксации отсчета и дальнейшего проведения измерений относительно него закрепляется специальный винт и отпускается лимб, корпус в этом случае останется неподвижным, двигаться же будут лимб и алидада.
Это и есть главные части теодолита. Но снимать показания помогают и другие устройства, с которыми тоже будет полезно познакомиться. Степень горизонтальности установки теодолита контролируется с помощью цилиндрического уровня, а точку отсчета потерять не дает оптический центрир. Отсчеты снимаются по микроскопу, и это финальная стадия работы замерщика.
Что такое геодезия
Геодезия — это наука, занимающаяся точным измерением земной поверхности, созданием рабочих чертежей или карт и прочими прикладными задачами. Для всех этих направлений созданы специальные разделы геодезии, но наиболее ощутимой и важной для повседневной жизни является инженерная геодезия.
Именно этот раздел занимается съемкой местности для постройки зданий и сооружений, для прокладки дорог, для определения точности проходки шахтных выработок или тоннелей. Задачи, решаемые этой отраслью, носят чисто прикладной характер, тесно соприкасающийся со строительством или картографией.
Определение расстояния теодолитом с помощью дальномерной рейки
С помощью теодолита можно определить и расстояние до точки взятия отсчётов, с погрешностью примерно в 10 см. Устанавливаем дальномерную рейку на точку, до которой хотим измерить расстояние. В визирной сетки теодолита есть 2 дальномерных штриха, расположенных сверху и снизу. Измерение расстояние производится просто. Считаем количество сантиметров от одного горизонтального дальномерного штриха до другого и умножаем полученное значение на дальномерный коэффициент трубы, который обычно равен 100.
Определение расстояния теодолитом при помощи дальномерной рейки по дальномерным нитям
На приведённом примере расстояния до рейки будет примерно 19,4 метра.
Виды устройств
Имеются следующие виды устройств:
- Механические. Наиболее простой по конструкции и самый дешевый тип, однако у него и самая низкая точность, поэтому для серьезной работы он не подходит.
- Электронные. Электронный теодолит удобен, потому что оснащен устройством для считывания и обработки результатов, геодезисту остается правильно выставить его, а остальное прибор сделает сам.
- Оптические. Наиболее широкое распространение получил теодолит оптический. Он не производит расчеты, как электронный, но стоимость устройства и качество измерения привлекают.
- Лазерные. Эти теодолиты самые дорогие, но и более совершенные устройства. Позволяют делать измерения с большой точностью и удобны в использовании, но приобретать их имеет смысл лишь для постоянных работ, где высоки требования к результату.
Два принципиально разных вида теодолитов отличаются по подвижности алидады и лимба. В повторительных типах данные элементы могут закреплять поочередно, а показания снимать методом последовательных повторений. Обыкновенные варианты этого не допускают, так как алидада с осью представляют в них единое неподвижное целое, и для каждого измерения требуется отдельная настройка.
Маркировка
Марка теодолита — это совокупность букв и цифр. В каждой есть связка литеры «Т» с какой-либо цифрой. Буква указывает на то, что прибор — теодолит, цифры показывают погрешность измерения в секундах, чем они больше, тем больше и погрешность.
- Цифрой 1 маркируются высокоточные приборы.
- Цифрами 2 и 5 маркируются точные теодолиты.
- Цифрами 15 и 30 маркируются технические приборы.
Стоит цифра точности после литеры «Т», а если перед буквой есть другая цифра, она служит для обозначения поколения прибора или его модификации в категории марки.
Порядок работы с теодолитом
Работать с теодолитом можно двумя способами:
- Полярным. В основе проведения измерений лежат две точки с известными значениями. Расчёты производят от второй точки на первую. Далее вымеряют расстояние между ними. Завершающий этап – привязка теодолитного хода к каждой из отметок.
- Используя створы с перпендикулярами. Данный метод применяют при производстве разбивочных работ. Он заключается в откладывании прямых углов на местности при поэтапном прохождении прибором каждой отметки.
В инструкции для теодолита чётко говорится о том, что прежде, чем начать работать с прибором, его нужно настроить. Подготовительный этап включает в себя:
- Центрирование.
- Горизонтирование.
- Фокусировку.
Повторительный теодолит[править | править код]
Повторительные теодолиты или оптические имеют специальную повторительную систему осей лимба и алидады, позволяющую лимбу вместе с алидадой вращаться независимо вокруг собственной оси раздельно и/или совместно. Такой теодолит позволяет последовательным вращением алидады несколько раз откладывать (повторять) на лимбе величину измеряемого горизонтального угла, что увеличивает точность измерений, брать отсчеты по двум диаметрально противоположным сторонам. Такие приборы так же именуются оптическими чтобы отличить от механических теодолитов. Лимб изготовлен из стекла.[5][6]
Требования перед работой
Перед измерением углов теодолит проверяется. Нужно проверять специальную отметку или пломбу, а также периодически — геометрические параметры, так как ошибка в пару градусов со временем может привести к катастрофе!
- Важна абсолютная вертикальность оси алидады и ее перпендикулярность цилиндрическому уровню.
- Визирная ось зрительной трубы должна быть перпендикулярна ей, не выполнив этого коллимационного условия, четкая система отсчета невозможна.
- Оси трубы и алидады должны быть перпендикулярными.
- Проверяем, насколько измерительная сетка расположена в вертикальной коллимационной плоскости.
Как проверить теодолит
Для правильной, точной работы прибора требуется качественная настройка его положения и соответствия осей. Для этого проводятся регулярные проверки и юстировки, позволяющие точно установить прибор, обеспечить правильное положение осей и плоскостей.
Проверка производится поэтапно:
- Установка на точку. Положение треноги настраивается таким образом, чтобы отвес точно указывал на точку с известными параметрами (точку стояния), отмеченную на грунте.
- Установка горизонтальной плоскости. Производится настройка горизонтали по пузырьковому уровню, затем прибор разворачивается на 180° и вновь настраивается. Приемлемым положением считается несоответствие положения пузырька не более 1 деления.
- Установка визирной оси. Выбирается и замеряется отдаленная точка. Затем труба поворачивается на 180°, прибор разворачивается и вновь производятся измерения (иначе говоря, производится измерение параметров точки при положениях КП или КЛ). Затем лимб открепляют и разворачивают на 180°, после чего все операции повторяются. Полученные значения рассчитываются по специальной методике, результат должен соответствовать паспортным значениям. При обнаружении расхождений производится настройка перпендикулярности визирной оси или оси вращения трубы.
Все проверки или юстировки производятся перед тем, как пользоваться теодолитом. Для настройки оптики прибор направляется в специализированную мастерскую или на завод.
Использование теодолита
Приемов профессионального использования приборов много, и им учат на специальных курсах, здесь же приведем основные из них.
- Установка теодолита. Первым шагом станет нахождение точки отсчета. На местности находим ровную поверхность, по которой центрируем прибор на подставке уровнями и зажимными винтами. В итоге положение прибора должно получиться строго горизонтальным.
- Ловим объект. Визиром отыскиваем цель и точнее наводим винтами измерительную сетку, чтобы установить центр объекта. На это смотрим через окуляр, а если света недостаточно, улучшить ситуацию поможет специальное зеркальце (как в случае с микроскопом). После выставления центра окуляром фиксируется его значение.
- Обработка результатов. Лучше сделать не одно, а несколько измерений. Новый отсчет рекомендуется на известную величину, к примеру, 90°. Если новые измерения отличаются от предыдущих на 90°, то результат можно фиксировать, если нет — производится еще пара подобных измерений с разным отсчетом и вычисляется среднее значение.
Ссылки[править | править код]
- Устройство теодолита
- Теодолит на сайте о геодезии и геоприборах
Правила эксплуатации теодолита
Для выполнения высокоточных измерений важно знать все тонкости при обращении с геодезическим прибором. От навыков геодезиста во многом зависит, в какой степени полученные при измерении цифры будут соответствовать реальному положению вещей, окажется ли достаточно прочной и долговечной возводимая конструкция.
Данный геодезический прибор имеет ряд преимуществ:
- С его помощью можно проводить точнейшие угловые измерения, невзирая на экстремальные климатические условия и специфику местности. Без помех работает в интервале температур от -25 до 50 градусов.
- На точность полученных данных не оказывают влияние нестандартные условия работы, поэтому теодолит можно брать даже в экспедиции.
- Компактный размер облегчает транспортировку прибора.
- Элементарная и быстрая калибровка и юстировка.
3 — Основные части геодезических приборов
Основные части геодезических приборов
По назначению геодезические приборы делятся на:
1. Приборы для угловых измерений – теодолиты.
2. Приборы для линейных измерений – рулетки, мерные ленты и проволоки, дальномеры.
3. Приборы для измерения превышений – нивелиры.
4. Приборы для съемочных работ – тахеометры, кипрегели, фототеодолиты и др.
5. Приборы для аэро–, фото– съемки – стереокомпараторы, аэрофото аппарата, стереометры.
Зрительная труба – это увеличительный прибор для наблюдения удаленных объектов. Астрономическая труба дает обратное изображение, земная – прямое.
Основными частями зрительной трубы является: объектив 1, окуляр 2, внутренняя фокусирующая линза 3, которая перемещается внутри трубы вращением кремальеры 4 (кремальерного винта или кольца) и сетки нитей 5.
Объектив и окуляр трубы располагают т.о. чтобы при установки трубы на бесконечность передний фокус окуляра совпадал с задним фокусом объектива и плоскостью сетки нитей. В окулярной части трубы находиться сетка нитей на которую проектируется изображение наблюдаемого предмета, между объективом и окуляром располагается двояковогнутая фокусирующая линза, которая перемещается при помощи кремальеры.
Зрительная труба имеет 3 основные оси.
– визирная ось, прилегая проходит через оптический центр объектива и центр сетки нитей; вертикальная плоскость проходящая через визирную ось называется коллимационной.
– оптическая ось проходит через центр объектива и окуляра.
– геометрическая ось – прямая проходящая через центры поперечных сечений объективной части трубы.
При установке зрительной трубы по глазу необходимо получить отчетливое изображение сетки нитей и наблюдение объекта, для этого зрительную трубу наводят на светлый фон и вращением окулярного кольца добиваются отчетливого изображения нити сетей.
Для наведения резкости на предмет при помощи кремальеры перемещают фокусирующую линзу до совпадения изображения предмета с плоскостью сетки нитей.
После установки зрительной трубы следует убедиться в отсутствии параллакса сетки нитей – кажущегося смещения изображения относительно сетки при перемещении глаза наблюдателя относительно окуляра, устраняется дополнительной фокусировкой.
Увеличение зрительной трубы это отношение угла под которым предмет виден в зрительную трубу к углу, под которым предмет виден невооруженным глазом, на практике за увеличение зрительной трубы принимают соотношение фокусного расстояния объектива и окуляра.
Ход лучей в зрительной трубе
Более совершенными являются трубы с внутренней фокусировкой; в них применяется дополнительная подвижная рассеивающая линза L2, образующая вместе с объективом L1 эквивалентную линзу L. При перемещении линзы L2 изменяется расстояние между линзами l и, следовательно, изменяется фокусное расстояние f эквивалентной линзы. Изображение предмета, находящееся в фокальной плоскости линзы L, также перемещается вдоль оптической оси, и когда оно попадает на плоскость сетки нитей становится четко видным в окуляре трубы. Трубы с внутренней фокусировкой короче; они герметичны и позволяют наблюдать близкие предметы; в современных измерительных приборах применяются в основном такие зрительные трубы.
В технических приборах увеличение 20–30 крат.
Полем зрения трубы называется пространство, которое видно в зрительную трубу при ее неподвижном положении.
Уровни предназначены для приведения в горизонтальное положение отдельных частей приборов, в геодезических приборах применяются жидкостные уровни.
Круглый уровень – представляет собой стеклянную ампулу округлой формы заключенной в металлической оправу и заполненную жидкостью так, чтобы оставалось свободное пространство, заполненное парами жидкости – пузырек.
На верхней внешней поверхности ампулы нанесены концентрические окружности – центр этих окружностей – нуль пункт.
Внутренняя верхняя поверхность ампулы представляет собой сферу большего радиуса. Осью круглого уровня называется прямая, походящая через нуль–пункт перпендикулярно к внутренним верхним поверхностям ампулы. Круглый уровень имеет небольшую точность, и применятся для предварительной установки прибора.
Цилиндрический уровень – стеклянная ампула цилиндрической формы, заключенная в металлическую оправу, заполненная жидкостью и имеет пузырек.
На верхней поверхности ампулы нанесены деления – середина нуль–пункт. Внутренняя и верхняя поверхность ампулы представляет собой дугу большего радиуса.
Касательная к внутренней и верхней поверхности ампулы, проходящий через нуль–пункт, называется осью уровня.
Для повышения точности установки приборов используется контактные уровни, это цилиндрические уровни с системой призм, позволяющих получать изображение концов пузырька уровня в поле зрения трубы.
Положению пузырька в нуль–пункте считается установка оптический контакт концов его изображения.
Цена деления уровня это угол, на который нужно изменить наклон оси уровня, чтобы пузырек переместился на одно деление.
Горизонтальный круг теодолита
Предназначен для измерения горизонтальных углов, состоит из лимба и алидады.
Лимб – плоское, стеклянное или металлическое кольцо по скошенному краю которого нанесены деления от 0о до 360о по часовой стрелке.
Алидада – это вспомогательное приспособление, позволяющее брать отсчеты по лимбу. Оси вращения лимба и алидады совпадают. Их принимают за основную вертикальную ось теодолита zz1. На алидаде имеется индекс (штрих) или шкала при помощи которых берут отсчет по лимбу.
Отсчет – это дуга лимба от 0о до 0о алидады по часовой стрелке.
При измерении горизонтальных углов лимб обычно движется и лежит в горизонтальной плоскости, а алидада скреплена с трубой и вращается вместе с ней.
Вертикальный круг
Вертикальный круг предназначен для измерения вертикальных углов (угол наклона). Состоит из лимба и алидады.
Лимб вертикального круга может иметь разную оцифровку от 0о до 360о по часовой стрелке или против часовой стрелки секторную оцифровку, т.е. от 0о до ±90о, ±75о, ±60о. Лимб вертикального круга скреплен с трубой и вращается вместе с ней.
Алидада вертикального круга обычно снабжена цилиндрическим уровнем для приведения ее нулевых штрихов в горизонтальное положение, в процессе измерения алидада неподвижна.
Отсчетные приспособления
Штриховой микроскоп – это индекс (штрих) на алидаде, при помощи которого берут отсчеты по лимбу.
Шкаловый микроскоп – это вспомогательная шкала на алидаде, длина которой равна минимальному делению основной шкалы лимба. Направление оцифровки основной и вспомогательной шкалы противоположны.
Верньер – это вспомогательная шкала на алидаде n–делений которых соответствует n–1 делению основной шкалы лимба. Направление оцифровки вспомогательной шкалы совпадает с основной.
Отсчет вычисляют по формуле:
A=A0+it.
А0 – отсчет по нулевому указателю Верньера, который был пройден этим указателем от начала лимба и номер штриха Верньера совпадающий со штрихом лимба.
i – номер штриха верньера совпадающий со штрихом лимба
t – точность Верньера.
Подставка геодезических приборов (триер) снабжена тремя подъемными винтами для горизонтирования. Все подвижные части приборов снабжены закрепительными (стопорными) винтами, которые предназначены для фиксирования этих частей в неподвижном положении.
Наводящие (микрометренные) винты предназначены для плавного и медленного поворота частей прибора, работают только при завернутых закрепленных винтах.
Угловые измерения
В геодезии измеряют горизонтальные и вертикальные углы.
Измерение горизонтальных углов, их сущность: пусть на местности закреплена точки А, В, С, находящиеся на разной высоте над уровнем моря. Необходимо измерить горизонтальный угол между АВ и АС местности.
Проведем через А, В, С отвесные линии, которые при пересечении с горизонтальной плоскостью Р дадут их проекции а, в, с. , лежащий в горизонтальной плоскости будет являться горизонтальным углом. Для получения численного значения горизонтального необходимо установить угломерный прибор так, чтобы его ось проходила через А в В и С. Установить вешки и взять отсчеты по горизонтальному кругу прибора в‘ и с‘. Значение равно разности отсчетов: = в‘–с‘.
Горизонтальные углы измеряют при помощи горизонтального круга теодолита.
Классификация теодолитов
Теодолиты по точности делятся на:
1. Высокоточные, позволяющие измерять углы со средней квадратической погрешностью 0,5″–1″
2. Точные, СКП 2″–10″
3. Технические, СКП 15″–30″
По материалам изготовления кругов и устройству отсчетных приспособлений Верньер:
1. С металлическими кругами и Верньерами
2. Со стеклянными кругами – отсчетное приспособление – штриховой или школвый микроскоп и оптический микрометр.
По конструкции на:
1. Простые теодолиты, у которых лимб и алидада могут вращаться только отдельно.
2. Повторительные, у которых лимб и алидада имеют как независимое так и совместное вращение.
По назначению на:
1. Маркшейдерские.
2. Проектировочные
и т.д.
Принципиальная схема теодолита
1- лимб ГК
2- алидада ГК
3- колонки
4- алидада ВК
5- лимб ВК
6- зрительная труба
7- цилиндрический уровень
8- подставка
9- подъемные винты
10- становой винт
II1– основная (вертикальная) ось теодолита
НН1– ось вращения зрительной трубы
Теодолит должен соответствовать определенным оптико–механическим и геометрическим условиям. Оптико–механическое условие гарантирует завод изготовитель, а геометрические условия подвержены изменениям в процессе работы, транспортировки и хранения приборов.
Геометрические условия необходимо проверять после длительного хранения прибора и регулярно во время работы.
Основные геометрические условия теодолита
1. Основная ось теодолита должна быть отвесна
2. Лимб ГК должен быть горизонтален, визирная плоскость не должна быть отвесна. Для соблюдения выполнения этих условий производят поверки теодолита.
Поверки теодолита
Поверка 1.
Ось цилиндрического уровня при алидаде ГК (uu1) должна быть перпендикулярна основной оси теодолита zz1.
Горизонтирование
Уровень устанавливают параллельно двум винтам подставки и их вращением в противоположные стороны приводят пузырек уровня в нуль–пункт. Уровень поворачивают на 180о и проверяют положение пузырька. Если пузырек остался в нуль–пункте или сместился не более чем на одно деление – условие поверки выполнено. В противном случае половину схода устраняют подъемочными винтами подставки, а вторую половину исправительными винтами уровня. Поверку исправления выполняют до тех пор, пока условие ее не будет выполняться.
Перед выполнением остальных поверок теодолит тщательно горизонтируют, т.е. его основную ось приводят в отвесное положение, для этого уровень устанавливают параллельно двум винтам подставки и приводят пузырек в нуль–пункт. Уровень поворачивают на 90о и третьим винтом приводят пузырек в нуль–пункт.
Эти действия повторяют до тех пор, пока при любом положение ампулы пузырек не будет располагаться в нуль–пункте, либо смещаться на одно деление.
Поверка 2.
Визирная ось трубы vv1 должна быть перпендикулярна горизонтальной оси вращения трубы hh1.
Нарушение этого условия ведет к коллимационной ошибки (с).
Для выполнения поверки визируют на удаленную точку и берут отсчеты по лимбу ГК при КЛ и КП. При соблюдении условий отсчеты будут различаться равно на 180о, т.е. КЛ–КП±180о=0
Если условие нарушено вычисляют коллимационную погрешность , величина которая не должна превышать удвоенной точности отсчетного приспособления с≤2t. При нарушении этого условия производят исправления. Для этого вычисляют полусумму отсчетов , которую устанавливают по ГК, действую наводящим винтом алидады ГК, при этом сетка нитей сместиться с наблюдаемой точки.
Действую горизонтальными исправительными винтами сетки, совмещают ее центр с наблюдаемой точкой (предварительно ослабляют вертикальные исправительные винты, чтобы дать возможность передвигаться сетки в горизонтальном направлении). После исправления вертикальные винты затягивают.
Поверку исполняют до тех пор, пока не будет выполняться условие.
Поверка 3.
Горизонтальная ось вращения трубы должна быть перпендикулярна к основной оси прибора zz1.
Для выполнения поверки теодолит устанавливают на расстоянии 20–30 м от здания и визируют верхней части стены точку. Трубу опускают до примерно горизонтального положения и на стене фиксируют проекцию центра сетки нитей.
Эти же действия повторяют при другом положении ВК. Если проекции сетки центра совпали или расстояние между ними не превышает ширины биссектора сетки – условие считают выполненным. Нарушение условия говорит о неравенстве подставок зрительной трубы, исправление которой производят на заводе – изготовителе или в специализированных мастерских.
Поверка 4.
Одна из нитей сетки должна быть вертикальна, а вторая горизональна.
Для выполнения поверки визируют на удаленную точку и действуя наводящим винтом алидады и действуя наводящим винтом алидады ГК поварачивают прибор вокруг его оси вращения. Если изображение точки остается на горизонтальной нити сетки – условие считается выполненным, в противном случае сетку исправляют, ослабив горизононтальные и вертикальные исправительные винты, совмещают изображение точки с горизонтальной нитью.
Если производились исправления, то повторяют поверку 2.
Эксцентриситет алидады
В плоскости лимба горизонтального круга имеются три характерных точки:
D – центр круга делений лимба,
A – центр вращения алидады,
L – центр вращения лимба.
В идеальном теодолите все три точки должны совпадать, но в действительности они не совпадают. Несовпадение точки A с точкой D называется эксцентриситетом алидады, несовпадение точки L с точкой D называется эксцентриситетом лимба, несовпадение точек A и L называется эксцентриситетом осей.
Рассмотрим влияние эксцентриситета алидады на отсчеты по лимбу. Отрезок AD называется линейным элементом эксцентриситета алидады и обозначается буквой l.
Некоторые теодолиты имеют два отсчетных устройства, отстоящих одно от другого на 180o. Вследствие эксцентриситета алидады отсчет по одному отсчетному индексу будет меньше правильного отсчета на угол ε:
N’1 = N1 – ε
по другому отсчетному индексу – больше правильного на угол ε:
N’2 = N2 + ε
Средний отсчет будет свободен от влияния эксцентриситета:
N = 0.5*(N1‘ + N2‘) = 0.5*(N1 + N2) .
Чтобы получить численное значение эксцентриситета, нужно из отсчета N2′ вычесть отсчет N1‘:
N2‘ – N1′ = N2 – N1 + 2*ε,
но N2 – N1 = 180o, поэтому:
ε = 0.5*(N’2 – N’1 + 180o).
При вращении алидады взаимное положение линейного элемента эксцентриситета алидады и отсчетных индексов изменяется, и величина ошибки отсчета ε’ зависит от угла γ:
ε’ = ε * sin(γ) .
У теодолитов с односторонним отсчитыванием отсчет по лимбу искажается на величину ε’ с одним знаком при КЛ и с другим знаком при КП; в среднем отсчете влияние эксцентриситета исключается.
Из всех ошибок отсчитывания по лимбу, возникающих вследствие нарушения геометрических условий, можно выделить симметричные ошибки, то–есть такие, которые имеют разные знаки при КЛ и КП и влияние которых в среднем отсчете устраняется, и несимметричные ошибки, влияние которых в среднем отсчете не устраняется. К симметричным ошибкам относятся коллимационная ошибка, ошибка из–за неравенства подставок, ошибка эксцентриситета. К несимметричным ошибкам относятся ошибка наклона оси вращения алидады, ошибки делений лимба и некоторые другие.
Способы измерения горизонтальных углов
Перед началом измерения теодолит устанавливают в рабочее положение в вершине угла, а в точках, на которых будет вестись визирование, вертикально устанавливают вешки.
Установка прибора в рабочее положение подразумевает его центрирование, горизонтирование и установка трубы по глазу.
Центрирование – это приведение основной оси теодолита в вершину измеряемого угла. При выполнении работ технической точности центрирование выполняют нитевым отвесом, для этого теодолит на штативе сначала устанавливают на точкой приближенно, стараясь, чтобы верхняя поверхность головки штатива была примерно горизонтальна, ножки штатива закрепляют в пункте. Ослабляют становой винт и перемещением прибора по штативу совмещают острие отвеса с вершиной угла, становой винт затягивают. Точность центрирования 2–5 мм.
Горизонтирование см. поверку 1.
Установка зрительной трубы по глазу см. устройство зрительной трубы.
Способ приемов
Состоит из двух полуприемов, которые выполняются при разных положениях вертикального круга. Для измерения угла в полуприеме закрепляют лимб ГК, открепляют алидаду ГК, визируют на правую точку и, закрепив алидаду, берут отсчет по лимбу ГК. Открепляют алидаду, визируют на левую точку и, закрепив алидаду, берут еще один отсчет. Разность отсчетов даст величину измеряемого угла. Для выполнения второго полуприема трубу переводят через зенит и смещают лимб ГК примерно на 60о, 90о. Выполняют аналогично.
Второй полуприем выполняют для контроля измерения и снижения влияния инструментальных ошибок.
Значения углов в полуприемах должно различаться не более удвоенной точности отсчетного приспособления теодолита. Если условие выполняется за окончательно значение принимают среднее из двух измерений. Для повышения точности измерения можно выполнить несколькими приемами, смещая между ними лимб на величину , где n – число приемов.
Способ круговых приемов
Применяется в тех случаях, когда нужно измерить углы, между тремя и более направлениям на станции.
Теодолит устанавливают в т.О и приводят его в рабочее положение.
Ориентируют лимб по направлению на какую–либо точку, например А (направляют 0о лимба ГК на точку А).
Для этого открепляют алидаду и ее вращением устанавливают отсчет = 0о, закрепляют ее, открепляют лимб и визируют на точку А, закрепляют.
Открепляют алидаду ее вращением по часовой стрелке последовательно визируют на точку В, С, Д и берут отсчеты по лимбу ГК.
В конце проверяют неподвижность лимба, т.е. визируют снова на точку А и берут отсчет.
Отсчет может изменяться до 2t, эти действия составляют полуприем.
Трубу переводят через зенит и выполняют еще один полуприем при другом положении ВК, но визируя против часов стрелки (т.А–Д–С–А–В).
2С – удвоенная коллимационная погрешность.
Колебание удвоенной коллимационной погрешности 2С, допускается в пределах удвоенной точности отсчетного приспособления (1′) теодолита.
Для повышения точности измерения можно выполнить несколькими приемами, переставляя между ними лимб на величину , где n–число приемов.
Способ повторений
Дает возможность повысить точность измерений за счет уменьшения влияния ошибки отсчитывания.
Прибор приводят в рабочее положения в вершине угла и выполняют измерение в процессе которого последовательно откладывают на лимбе измеряемый угол 2k – раз, k – число повторений.
Предположим, что угол измеряется двумя повторениями.
Ориентируют лимб отсчетом близким к 0, на точку А и записывают этот отсчет (n1).
Открепляют алидаду визируют на точку В и берут контрольный отсчет n2.
Открепляют лимб визирую на точку А, отсчет не берут.
В результате лимб переместился против часовой стрелки на угол β.
Открепляют алидаду визируют на точку В, и снова не берут отсчет. Теперь на лимбе отложен угол =2β.
Если необходимо сделать больше двух повторений, то эти условия продолжают до тех пор, пока на лимбе не будет отложен угол β столько раз сколько нужно повторения.
Далее трубу переводят через зенит, открепляют лимб и визируют на точку А. Отсчте при этом не изменяется. Открепляет алидаду, визируют на точку В, на лимбе отложен угол 3β.
Снова открепляют лимб визируют на точку А, открепляют алидаду, визируют на точку В, на лимбе отложен угол 4β.
Берут отсчет n2. Вычисляют угол β по формуле:, (k – число повторений) сравнивая его с контрольным.
Измерение вертикальных углов
Методика измерений зависит от конструкции и оцифровки ВК теодолита.
1 способ
Если ВК не имеет уровень при алидаде, то после приведения прибора в рабочее положение, визируют на определяемую точку. Например, при КЛ, наводящим винтом алидады вертикального круга приводят в 0–пункт уровень при ВК и берут отсчет по лимбу ВК.
Трубу переводят через зенит и действия повторяют при другом положении вертикального круга.
Вычисляют вертикальный угол и МО.
Контролем правильности измерений служит постоянство МО, колебания которого могуб быть в пределах удвоенной точности прибора. (МО=const, ∆MO≤2t).
2 способ
В случае, если алидада ВЕ не имеет уровня, и его функции выполняет уровень при алидаде ГК (Т30, 2Т30). Прибор приводят в рабочее положение, предварительно визируют на опредямую точку, подъемным винтом подставки расположенным ближе все к визирной оси, приводят в 0–пункт пузырек уровня при ГК, производят точное визирвание и берут отсчет по вертикальному кругу. Действие повторяют при другом положении ВК.
Вычисляют вертикальный угол и МО, контроль МО=const.
3 способ
Если алидада ВК не имеет уровня и вместо него используется компенсатор (алидада автоматически становится горизонтально).
Порядок измерений:
Прибор приводят в рабочее положение, визируют на определяемую точку и берут отсчет по ВК. Трубу переводят через зенит и действия повторяют. Вычисляют вертикальный угол и МО, МО=const.
Формулы для вычисления вертикального угла и МО
1. от 0º до 360º (лимб) по часовой стрелке:
МО=½(КЛ+КП)
V=КП–МО=МО–КЛ=½(КП–КЛ)
2. от 0º до 360º (лимб) против часовой стрелке (Т30):
МО=½(КЛ+КП+180º)
V=КЛ–Мо=МО–КП–180º=½(КЛ–КП–180º)
от 0º до ±90º | МО=½(КЛ–КП) |
от 0º до ±75º от 0º до ±60º | v=КЛ–МО=МО–КП=½(КЛ–КП) |
3.
Место нуля вертикального круга
При нарушении геометрических условий ВК возникает инструментальная ошибка, называется место нуля ВК.
Место нуля – это отсчет по ВК в момент, когда визирная ось трубы горизонтальная, а пузырек уровня при ВК находиться в нуль–пункте.
При соблюдении геометрических условий этот отсчет равен нулю, при нарушении отличается от нуля.
Геометрические условия. Место нуля – величина постоянная для прибора, его колебания может быть в пределах 2t. Желательно чтобы МО≤2t, в противном случаю его исправляют.
Исправление места нуля
Если место нуля получается большим, то при основном положении круга нужно навести трубу на точку и микрометренным винтом алидады установить отсчет, равный углу наклона; при этом пузырек уровня отклонится от нуль–пункта. Исправительными винтами уровня привести пузырек в нуль–пункт.
Измерение угла наклона местности
В точке А устанавливают теодолит. Приводят его в рабочее положение и при помощи рулетки измеряют высоту инструмента i.
i – это расстояние от оси вращения трубы до точки, над которой установлен прибор.
В точке В вертикально устанавливают рейку, на которой отмечают i. Визируют на высоту инструмента и измеряют вертикальный угол, который будет равен углу наклона местности.
Измерение длин линий
Определение расстояния между точками земной поверхности называется линейными измерениями.
Линейные измерения делятся на непосредственные и косвенные.
К непосредственным измерениям относят такие измерения, при которых мерный прибор укладывают непосредственно в створе измеряемой линии.
Створ – вертикальная плоскость, соединяющая начало и конец измеряемой линии.
Если невозможно измерить длину линии непосредственно, прибегают к косвенным измерениям. В этом случае определяемую длину находят как функцию других измеряемых величин.
Для линейных измерений используют механические и физико–оптические мерные приборы.
Механические рулетки:
– Стальные (25–100 м), эти рулетки имеющие метровые, дециметровые сантиметровые и миллиметровые деления;
– Тесьмяные рулетки (10 м) – сантиметровые, дециметровые, миллиметровые. Используются для съема контура местности.
– Стальные мерные ленты (20 м) имеющие метровые, полуметровые, дециметровые деления. В комплект входят шпильки, которые фиксируют концы ленты. Погрешность 1:2000.Используется для линейных измерений в съемках.
– Инварные проволоки (24 м) с десяти сантиметровыми и миллиметровыми шкалами на концах. Измерение производят при помощи подвесного базисного прибора. Применяется для высокоточных линейных измерений. Погрешность 1:1000000.
Достоинства: высокая точность измерений, простота устройства, не высокая стоимость, возможность откладывания проектных длин.
Недостаток: высокая трудоемкость измерений.
Физико–оптические мерные приборы – это различные лазерные, свето–, радио–, оптико–, дальномеры.
Измерения этими приборами основаны на косвенном способе.
Их достоинствами является точность и быстрота измерений, возможность измерения больших расстояний.
Недостатки: невозможность откладывать проектные расстояния, высокая цена, сложность устройства.
Измерение длин линий механическим прибором (на примере мерной ленты)
Для измерения расстояния обычно не достаточно закрепить на местности начало и конец измеряемой линии, необходимо в створе линии установить дополнительные вешки, этот процесс называется провешиванием или вешением линии. Вешение может производиться при помощи теодолита или на глаз.
Для провешивания линии АВ на глаз, в точках А и В закрепляют вешки, наблюдатель становиться возле точки А так, чтобы вешки в точках А и В совпали. Его помощник движется от точки А к точке В и устанавливает в точках 1, 2, …, n дополнительные вешки, руководясь указаниями наблюдателя.
При вешении теодолита в точке А устанавливают теодолит, в точку В вешку. Вертикальная нить сетки совмещают с вешкой в точке В, закрепляют горизонтальный круг и трубу, вспомогательные вешки устанавливают по вертикальной нити сетки.
Если между точками А и В нет прямой видимости, вешение выполняется следующим образом: выбирают две вспомогательные точки, таким образом, чтобы они обе были видны и из точки А и из точки В, и в них устанавливают вешки.
Методом последовательных приближений перемещают вешки из точки D1 в C1, C1 вD2 , D2 в C2 и т.д., до тех пор пока все вешки не будут на одной прямой.
Порядок измерения линий
После провешивания закрепляют точки перегиба местности, попадающие в створ линии. При помощи рулетки измеряют наклонные участки D1, D2, … и углы наклона местности ν1, ν2, ….
Вычисление горизонтальных проекций измеренных расстояний
d1, d2– горизонтальные проложения:
di=Dicos νi
Общая сумма горизонтального проложения АВ:
d=Σdi
Каждое наклонное расстояние измеряют следующим образом: нулевой штрих ленты прикладывают к началу измеряемой линии, ленту укладывают в створе, встряхивают в горизонтальной и вертикальной плоскостях, натягивают и вставляют шпильку в вырез в конце ленты, снимают ленту со шпильки, одевают на шпильку нулевой вырез ленты и действия повторяют. В конце измеряют длину неполного пролета. Измеренная наклонная длина вычисляется по формуле:
D1=n∙l+r
r – длина неполного пролета
n – число полных проложений ленты
Для контроля длину измеряют в обратном направлении D2, за окончательно значение длины принимают среднее из двух измерений, если разница между ними не превышает 1:2000 от длины линии:
Поправки, вводимые в длины линии, измеренные механическими приборами:
1. За температуру вводят в тех случаях, когда температура измерений отличается от нормально (+20ºС). Номинальную длину мерного прибора определяют при нормальной температуре, его длина увеличивается или уменьшается в зависимости от внешней температуры:
D –измеренная длина
l – длина мерного прибора
α – коэффициент линейного расширения
t – температура измерения
t0 – нормальная температура
2. За наклон линии вводится в тех случаях. Когда угол наклона местности превышает 2º. Иногда необходимо на наклонной поверхности отложить расстояние так, чтобы его горизонтальное проложение было равно заданной величине.
Сначала от точки А откалывают горизонтальные проложения, а затем удлиняют его на поправку:
3. За компарирование – это определение истинной длины мерного приора, при компарировании мерным прибором измеряют заранее известную длину линии и сравнивают результаты измерений с известной величиной, а затем вычисляют поправку мерного прибора. Эта поправка вводиться в том случае если номинальная длина отличается от длины.
Измерение расстояний при помощи физико–оптических мерных приборов
(на примере нитяного дальномера)
Нитяной дальномер это две вспомогательные горизонтальные нити на сетке.
Ход лучей в нитяном дальномере Поле зрения трубы
Определения расстояний нитяным дальномером
Для определения расстояния между точками А и В, над точкой А устанавливают прибор так, чтобы его ось вращения проходила через точку А, а в точке В вертикально устанавливают рейку с сантиметровыми делениям. Предположим, что визирная ось трубы горизонтальна и введем обозначения:
Р – расстояние между дальномерными нитями
σ – расстояние от оси вращения прибора до оптического центра объектива
f – фокусное расстояние объектива
F – передний фокус объектива
n – расстояние по рейке меду дальномерными нитями
Поскольку визирная ось горизонтальна, лучи параллельны ей и проходящие через дальномерные нити пересекут передний фокус объектива и, пройдя его, спроектируются на реку, т.е. в трубу можно будет видеть рейку, и изображение дальномерных нитей. Поскольку на рейке нанесены сантиметровые деления, можно будет определить расстояние между дальномерными нитями по рейке, т.е. взять отсчет n.
Из чертежа видно, что расстояние между точками: d = σ + f + E
σ и f постоянны, для каждого прибора и из можно заменить на постоянное слагаемое:
d = c + E (c=0.1 м)
Е – определяют из подобия треугольников:
Поскольку f и Р постоянные величины, то их можно заменить коэффициентами дальномера:
Е = kn (k=100)
D = kn + c
Поскольку точность определения расстояния при помощи дальномера ≈ 1:300 от длины линии, слагаемым с можно пренебречь:
D = kn
100 фото конструкции и особенностей теоделитной съемки
Геодезия – одна из самых древних наук. Уже в XVII в. появились первые устройства для проведения промеров. В их числе был и оптический теодолит.
Краткое содержимое статьи:
Описание прибора. Его виды
Теодолит называется геодезический прибор, служащий для измерения как вертикальных, так и горизонтальных углов на местности. Принято выделять теодолиты следующих видов:
- Техназначения.
- Точного измерения.
- Высокоточные.
В зависимости от сложности конструкционного решения геодезические приборы могут быть:
Простого типа. Здесь алидада и вертикальная цилиндрическая ось связаны между собой.
Повторительного типа. Вращение лимба и алидады может быть как совместным, так и раздельным. Благодаря приборам подобного типа можно проводить измерения углов не только по классической методике, но и способом повторений.
Теодолиты могут быть оснащены самой разнообразной оптикой, начиная с фотоаппарата и кончая видеокамерой. Отсюда и соответствующие названия – фототеодолит и кинотеодолит.
Современные теодолиты весьма высокоточны и технологичны. Например, гиротеодолит позволяет производить измерения азимута во всех направлениях.
Самым популярным сегодня видом теодолита является электронный теодолит. Во всём, что касается точности измерений, он гораздо лучше своего оптического аналога. Подобные приборы оснащены электронным дисплеем и встроенной памятью.
Оптический теодолит
Достоинства оптического теодолита:
- Надёжность.
- Устойчивость к разным климатическим условиям.
- Отсутствие необходимости в аккумуляторе.
- Стойкость к температурным перепадам.
Недостатки:
- Необходимость специальных знаний для получения точных результатов.
- Значительная продолжительность замеров.
Электронный теодолит
К положительным сторонам электронного теодолита относятся:
- Удобный дисплей.
- Более быстрое проведение измерений.
- Позволяет работать в сумерки.
- Не требует от человека особых навыков.
Минусы:
- Ограниченность возможного температурного диапазона. При температуре ниже 20°С нельзя снимать отсчёты.
- Требуется возможность подключаться к электросети для зарядки.
Правила работы с теодолитом
Как же пользоваться теодолитом? Это не так сложно, как кажется на первый взгляд.
Вначале необходимо поместить прибор в вершину угла, который вы хотите измерить. Причём лимб должен быть своим центром в данной точке.
Затем воспользуйтесь алидадой (вращаемой линейкой) – совместите её с одной из сторон угла и отмечайте показания по кругу.
Далее переместите алидаду ко второй стороне угла и зафиксируйте получившуюся цифру. Разница этих двух показаний и будет равна величине угла. Вот и весь принцип работы теодолита.
Конструкция теодолита
Как показывают фото данного прибора, в его состав входят:
- Лимб. Это плоский стеклянный диск, на поверхность которого нанесена шкала углов от 0 до 360 градусов.
- Алидада. Это схожий стеклянный диск с отсчётной насечкой, расположенный на одной оси с лимбом. Алидада может свободно вращаться.
- Оптический прибор. Состоит из объектива, фокусирующей линзы и сетки нитей, изготовленной из стекла. Насечки на последней используют для ориентирования при наведении на угол.
- Уровни. Применяются при установке устройства в вертикальном положении.
- Подъёмные винты. С их помощью происходит регулировка прибора.
Все рассмотренные выше составные детали помещены в корпус, устанавливаемый на треногу.
Теодолитная съёмка
Теодолитная съёмка – это группа мероприятий, проводимых при помощи теодолита с целью построения контурного плана местности. Она состоит из двух этапов:
- Вначале создаётся геодезическое обоснование, прокладываются все теодолитные ходы по всему периметру исследуемой территории.
- Далее измеряются диагонали внутри участка.
Рассмотрим инструкцию для проведения теодолитной съёмки:
- Определите и зафиксируйте опорные точки. На их подборку значительное влияние оказывают особенности рельефа участка. Шаг между точками обычно колеблется от 100 до 400 м.
- Установите обоснования и восстановите межевые знаки.
- Подготовьте ходы к проведению измерений. Очистите местность от кустов, поросли и кустарников, мешающих промеру.
- Измерьте при помощи теодолита необходимые линии и углы.
- Проведите съёмку ситуации (диагоналей).
Фото теодолита
Также рекомендуем посетить:
Измерение горизонтальных углов. | Инженерная геодезия. Часть 1.
Измерение горизонтального угла выполняют способом приемов. При измерении нескольких углов, имеющих общую вершину, применяют способ круговых приемов.Работу начинают с установки теодолита над центром знака (например, колышка), закрепляющим вершину угла, и визирных целей (вех, специальных марок на штативах) на концах сторон угла.
Установка теодолита в рабочее положение состоит из центрирования прибора, горизонтирования его и фокусирования зрительной трубы.
Центрирование выполняют с помощью отвеса. Устанавливают штатив над колышком так, чтобы плоскость его головки была горизонтальна, а высота соответствовала росту наблюдателя. Закрепляют теодолит на штативе, подвешивают отвес на крючке станового винта и, ослабив его, перемещают теодолит по головке штатива до совмещения острия отвеса с центром колышка. Точность центрирования нитяным отвесом 3 – 5 мм.
Пользуясь оптическим центриром, теодолита (если такой у теодолита имеется), сначала надо выполнить горизонтирование, а затем центрирование. Точность центрирования оптическим центриром 1 – 2 мм.
Горизонтирование теодолита выполняют в следующем порядке. Поворачивая алидаду, устанавливают ее уровень по направлению двух подъемных винтов, и, вращая их в разные стороны, приводят пузырёк уровня в нуль-пункт. Затем поворачивают алидаду на 90º и третьим подъёмным винтом снова приводят пузырёк в нуль-пункт.
Фокусирование зрительной трубы выполняют “по глазу” и “по предмету”. Фокусируя “по глазу”, вращением диоптрийного кольца окуляра добиваются четкого изображения сетки нитей. Фокусируя “по предмету”, вращая рукоятку кремальеры, добиваются четкого изображения наблюдаемого предмета. Фокусирование должно быть выполнено так, чтобы при покачивании головы наблюдателя изображение не перемещалось относительно штрихов сетки нитей.
Измерение угла способом приемов. Прием состоит из двух полуприемов. Первый полуприем выполняют при положении вертикального круга слева от зрительной трубы. Закрепив лимб и открепив алидаду, наводят зрительную трубу на правую визирную цель. После того как наблюдаемый знак попал в поле зрения трубы, зажимают закрепительные винты алидады и зрительной трубы и, действуя наводящими винтами алидады и трубы, наводят центр сетки нитей на изображение знака и берут отсчёт по горизонтальному кругу. Затем, открепив трубу и алидаду, наводят трубу на левую визирную цель и берут второй отсчёт. Разность первого и второго отсчётов даёт величину измеряемого угла. Если первый отсчёт оказался меньше второго, то к нему прибавляют 360º.
Второй полуприем выполняют при положении вертикального круга справа, для чего переводят трубу через зенит. Чтобы отсчёты отличались от взятых в первом полуприеме, смещают лимб на несколько градусов. Затем измерения выполняют в той же последовательности, как в первом полуприеме.
Если результаты измерения угла в полуприёмах различаются не более двойной точности прибора (то есть 1¢ для теодолита Т30), вычисляют среднее, которое и принимают за окончательный результат.
Понятие об измерении способом круговых приемов нескольких углов, имеющих общую вершину. Одно из направлений принимают за начальное. Поочередно, по ходу часовой стрелки, при круге слева наводят трубу на все визирные цели и берут отсчеты. Последнее наведение вновь делают на начальное направление. Затем, переведя трубу через зенит, вновь наблюдают все направления, но в обратном порядке – против часовой стрелки. Из отсчетов при круге слева и круге справа находят средние и вычитают из них среднее значение начального направления. Получают список направлений – углов, отсчитываемых от начального направления.
| Главная » Статьи и полезные материалы » Микроскопы » Статьи о микроскопах, микропрепаратах и исследованиях микромира » Устройство оптического микроскопа у теодолита Прежде чем говорить об устройстве оптического микроскопа у теодолита, необходимо разобраться, что это за прибор. Теодолиты – это геодезические инструменты, предназначенные для измерения горизонтальных и вертикальных углов на местности. Они бывают оптическими, электронными, лазерными и специального назначения. Теодолит состоит из штатива, измерительных кругов (лимбов), измерительной линейки (алидады), зрительной трубы, визира и отсчетного микроскопа. Микроскоп оптического теодолита бывает трех видов. Наиболее распространены штриховой и шкаловой микроскопы. Однако самые точные теодолиты снабжены микроскопами с оптическим микрометром. Микроскоп теодолита предназначен для снятия показаний с измерительного прибора. Упрощенная схема работы с оптическим теодолитом такова: устанавливаем прибор на ровную поверхность, наводим зрительную трубу на объект изучения, снимаем измерения. Теодолиты широко применяют в строительных работах, при составлении топографических карт и планов. Шкаловой микроскоп теодолитаЗначения горизонтальных и вертикальных углов высчитываются по лимбам – измерительным кругам, помещенным в колонку и основание теодолита. Чтобы снять с них показания, необходимо воспользоваться шкаловым микроскопом теодолита. Он представляет собой небольшую оптическую трубку, расположенную рядом с основной зрительной трубой. Заглянув в окуляр, мы увидим два полукруга с горизонтальными шкалами. Верхний полукруг показывает значения вертикальных углов, нижний – горизонтальных. Эти значения еще называют «отсчетами», и они исчисляются градусами, минутами и секундами. В каждом полукруге шкалового микроскопа теодолита расположены две шкалы: подвижная (шкала лимба) и неподвижная (шкала алидады). По подвижной шкале мы определяем градусы в диапазоне от 0° до 360°, по неподвижной – минуты в диапазоне от 0 до 60. Значение шкалы лимба меняется при изменении положения теодолита. Та риска подвижной шкалы, которая попала на шкалу алидады, и есть искомое значение градуса. Эта же риска указывает нам и на значение минут – берем мы его уже с неподвижной шкалы. Немного сложнее с секундами. У каждого теодолита есть своя точность измерений. Высокоточные измерительные приборы отличаются погрешностью менее 10 секунд. Техническим теодолитам свойственна точность в 15, 30 или 60 секунд. Предположим, у нашего измерительного прибора точность 30 секунд. Никаких промежуточных значений, кроме 0 и 30 секунд, наши измерения принимать не смогут. Поэтому если риска шкалы лимба попадает точно на риску шкалы алидады, принято считать, что значение секунд равно 0. Если она попадает между двух рисок шкалы алидады, значит, значение секунд равно 30. Оптические теодолиты, снабженные микроскопами, одни из самых неприхотливых. Они не боятся отрицательных температур и не требуют дополнительного питания. Однако тем, кто не знаком с геодезическими приборами, стоит обратить внимание на электронные теодолиты. Они самостоятельно высчитывают значения углов и выводят результаты измерений на встроенный экран. Пользоваться ими намного проще. 4glaza.ru Использование материала полностью для общедоступной публикации на носителях информации и любых форматов запрещено. Разрешено упоминание статьи с активной ссылкой на сайт www.4glaza.ru. Производитель оставляет за собой право вносить любые изменения в стоимость, модельный ряд и технические характеристики или прекращать производство изделия без предварительного уведомления. Рекомендуемые товары
Другие обзоры и статьи о микроскопах, микропрепаратах и микромире:
|
3 Требования к геодезии для наук о Земле | Точная геодезическая инфраструктура: национальные требования к общему ресурсу
Эпохав гидрологии суши, открывающая важные новые перспективы для исследований земного водного цикла, прогнозирования наводнений и водных ресурсов.
ПОГОДАСпутниковые изображения, показываемые по телевидению, могут создать впечатление, что прогнозы погоды основаны на этих изображениях, но на самом деле прогнозы основаны на физических моделях тропосферы , самых нижних 14 километров атмосферы.Эти модели должны постоянно получать измерения состояния атмосферы (давления, температуры, влажности и ветра) на разных высотах вокруг планеты, чтобы соответствовать реальным атмосферным условиям. Способность предсказывать как серьезность, так и временную и пространственную протяженность погодных изменений, особенно осадков, имеет решающее значение для общественной безопасности и сельского хозяйства, и правительства всего мира сотрудничают для сбора данных, используемых в прогнозах. На протяжении десятилетий исходные данные для этих моделей предоставлялись радиозондами, более известными как метеозонды.К сожалению, пространственное распределение пунктов приема радиозондов ограничено как из-за недостаточного покрытия океанов, так и из-за значительного сокращения числа пунктов в южном полушарии. Увеличение количества запусков радиозондов в день сдерживается стоимостью оборудования, которое нельзя использовать повторно. Геодезисты, сосредоточенные на точном позиционировании, используют поправки для устранения атмосферных эффектов, которые считаются источником шума в их измерениях. И наоборот, эти же поправки могут использоваться метеорологами для лучшего понимания атмосферы.Таким образом, улучшение геодезической инфраструктуры приносит пользу обеим областям науки.
Наземные измеренияЭффекты атмосферной рефракции уже давно признаны важным источником ошибок в геодезии. Вместо того, чтобы полагаться на неопределенные модели, методы космической геодезии, такие как GNSS / GPS, оценивают тропосферные вариации вместе с интересующими параметрами позиционирования. В конце концов, проблему удалось обратить вспять; предполагая, что положение станции точно определено, ученые могли бы использовать «мешающий» сигнал в оценках GNSS / GPS, чтобы восстановить изменяющееся во времени поведение атмосферы (Ware et al., 2000). В отличие от радиозондов, которые измеряют атмосферные условия на нескольких высотах, наземные GNSS / GPS измеряют только «интегрированное» влияние атмосферы, то есть насколько атмосфера задерживает измерение в целом. Примерно 80 процентов задержки (известной как «сухая тропосфера») можно предсказать, если измерить приземное давление. После устранения задержки в сухой тропосфере можно восстановить задержку из-за водяного пара, которая может быть масштабирована до так называемого осажденного водяного пара (PWV).Измерения PWV оценивают модели переноса влаги и скрытого тепла, которые имеют решающее значение для прогнозов погоды. Однако, чтобы быть полезными для прогнозирования погоды, данные должны быть доступны в режиме, близком к реальному времени.
Поскольку PWV изменяется как в пространстве, так и во времени, необходимы глобально распределенные и часто собираемые данные. Для текущего созвездия, состоящего примерно из 30 спутников, один приемник GNSS / GPS обычно принимает сигналы от 6 до 12 спутников. Эти данные в основном используются для оценки PWV в воздушном столбе над приемником GNSS / GPS.Но, в принципе, наличие измерений с более чем одного направления означает, что GNSS / GPS имеет азимутальную, а также вертикальную чувствительность. Чем больше спутников передают сигналы с заданного направления, тем выше будет чувствительность. Это также означает, что комбинация сигналов от нескольких систем, таких как Galileo, ГЛОНАСС и КОМПАС, даст даже более чувствительные возможности мониторинга атмосферы, чем те, которые доступны только с помощью GPS США. Кроме того, поскольку приемники GNSS / GPS работают непрерывно, зондирование атмосферы GNSS / GPS имеет исключительную временную чувствительность, что особенно важно для мониторинга и прогнозирования поведения сильных погодных явлений.
Поскольку атмосферная задержка неразрывно связана с тем, насколько хорошо может быть определено положение, для исследований тропосферы GNSS / GPS требуется такая же инфраструктура: точное определение орбиты вдоль
Студент геодезического института отбыл год в зоне боевых действий после потери ноги
Кто мог подумать, что Станислав Стовбан, молодой человек из Прикарпатья, Калуш, прочтет «Сказку о реальном человеке» Бориса Полиовий на одном дыхании.Людям старшего поколения известна драматическая и одновременно оптимистичная история летчика Алексея Маресьева. Во время советско-германской войны его самолет был сбит. Пилот несколько дней полз по заснеженному лесу, чтобы добраться до товарищей. Из-за обморожения ему ампутировали обе ноги. Однако Алексей Маресьев не только научился танцевать на протезах, но и начал пилотировать боевой самолет …
Станислав Стовбан, коммандос-пулеметчик, кавалер ордена Богдана Хмельницкого, имеет похожую, но другую историю.В тот день, когда сепаратисты взорвали терминал Донецкого аэропорта, когда украинские киборги переходили с этажа на этаж, плита пола сломала этому молодому человеку ребра и сломала ему обе ноги. Одну ногу хирурги соединили вместе, а другую пришлось ампутировать, так как была повреждена главная артерия. Когда спецназовец оправился от тяжелого ранения, какой-то врач принес ему книгу «Сказка о реальном человеке». Они пытались заставить его понять, что даже без ног можно вести продуктивную жизнь.
Сказка об этом реальном человеке, которая еще не написана, имеет интересное довоенное начало.Мне удалось поговорить с спецназовцем, когда он приехал в Институт геодезии Львовского политехнического института со своей военной базы, чтобы сдавать определенные экзамены и тесты индивидуально. Раньше Станислав учился на дневном отделении, и так мог и дальше учиться…
Впрочем, послушаем самого Станислава:
— Должен признать, что геодезия была мечтой всей моей жизни. Я с детства всегда хотел стать военным. Я пытался поступить в Академию Сухопутных войск, но у меня не получилось из-за жесткой конкуренции.Я выбрал Институт геодезии, наверное, потому, что геодезисты хорошо ориентируются на местности. Это очень важно для военных. Кстати, свои знания в области оптики и навыки работы с картой я использовал в армии. Я проучился два с половиной года, а потом взял академический отпуск, чтобы служить в армии.
— Вы сделали это добровольно? Что сказали твои друзья? Многие студенты мечтают «уклониться» от армии. А как твои родители это восприняли?
— Они были в шоке.Я их единственный сын. Но мое решение было непреклонным. Я понимал, что военную карьеру нужно начинать с службы рядовым. Я служил в Старичах, на Яворовском полигоне. Я учил студентов нашей Академии водить десантно-штурмовую машину. После демобилизации я несколько месяцев искал работу. В конце концов я возобновил учебу в геодезическом институте, но уже на заочном отделении. И началась российская агрессия на Донбассе.
— Вас призвали в армию?
— Нет, не было.Я не дождался своей мобилизационной волны. Я сам пришел в военкомат. Мне дали два дня, чтобы попрощаться с родителями. На тот же Яворовский полигон меня направили в 3-й батальон 80-й -й -й отдельной десантно-штурмовой бригады. После согласования боевых действий мы прибыли в Константиновку, что в 68 км от Донецка. Вот и была наша точка вывиха. В декабре начались серьезные бои в зоне Донецкого аэропорта. В эту зону входил сам аэропорт, Водяное, Опытное, Писки… Самые тяжелые бои шли в аэровокзале 20 января 2015 года.Мой пулемет работал без перерыва 8 часов. Из-за перегрева сгорели три ствола пулемета. Вы уже говорили о моих раненых ногах…
— Я знаю, что после завершения лечения и протезирования вы продолжили службу. Когда я рассказывал вашу историю своим коллегам-репортерам, они сомневались: «Как они могли забрать человека с ампутированным поводом обратно в армию? Должны быть какие-то военно-медицинские комиссии… ».
— Я избежал этой проблемы, потому что я не прекращал службу в Вооруженных Силах Украины, поэтому мне не пришлось проходить медицинское обследование.На самом деле от командира подразделения зависит очень многое. Он подает рапорт старшему командованию, что ему нужен конкретный солдат на определенную должность, и, как правило, получает положительный ответ. Я продолжил службу по контракту «до конца особого срока».
— Я знаю, что вы год находитесь в зоне боевых действий с ампутированной ногой. Не могли бы вы попросить, чтобы вас перевели куда-нибудь подальше от линии фронта?
— Не смог! Напротив, меня попросили отправить в зону боевых действий.Были определенные препятствия, но мне удалось их преодолеть. Сейчас я служу в Житомире старшиной эскадрильи, где проходят подготовку спецназовцы. Помимо своих основных обязанностей, я учу молодых солдат стрелять из всех видов стрелкового оружия.
— Я слышал много жалоб, что наших солдат плохо кормят…
— Это зависит от командиров. В тех местах, где я обслуживала, еда всегда была адекватной.
— Как вы относитесь к алкоголю? Не секрет, что у некоторых в армии есть проблемы с алкоголем…
— Мягко говоря.Люди много пьют … А я вообще не употребляю алкоголь принципиально. Я даже не пью пиво или шампанское в канун Нового года. Правда, я курил очень давно, но полтора года назад бросил.
— Честно говоря, Станислав, я думал, что преподаватели в вашем институте, зная ваш рассказ, автоматически ставят вам хорошие оценки. Вам просто нужно прийти лично. Но доцент Богдан Поляница, декан института, доказал, что я не прав.
— Я завершаю учебную программу.Я ко всему отношусь серьезно. У вас не может быть слишком много знаний.
— Что вы видите в своем будущем?
— После получения степени бакалавра я смогу пройти ускоренный курс для получения офицерского звания в Одесской военной академии на факультете подготовки специалистов-десантников высокой мобильности.
— А у десантников имеется ввиду, что надо прыгать с парашютом? Сложно представить, как можно приземлиться на протез…
— У меня уже 5 прыжков с парашютом.Однако я сделал их до того, как мне ампутировали ногу. Но в апреле у меня будет первый прыжок с протезом. У меня уже есть разрешение. У меня был такой протез, который минимизирует вероятность травм во время прыжков, сделанный в Киеве. Я должен сказать, что в передовых армиях мира есть программы адаптации солдат-инвалидов к военной службе. Есть примеры, когда солдаты с искусственными руками становятся хорошими снайперами, например, в США.
— Многие бывшие военнослужащие, служившие в АТО, оказались вовлечены в политику, стали народными депутатами.У вас может быть такой же шанс…
— Дай бог! Меня совсем не привлекает политика. Мы знаем, как люди доверяют политикам. Каждый должен заниматься своим делом, которое он знает и любит. Это может звучать грандиозно, но есть такая поговорка: «Есть такая профессия, чтобы защищать свою Родину…».
typhon.geodesy — документация Typhon 0.8.0dev
# - * - кодировка: utf-8 - * -
"" "Функции для работы с географическими системами координат
и справочные эллипсоиды.
Если не указано иное, функции перенесены из atmlab-2-3-181."" "
импортировать numpy как np
из констант импорта тифона
__all__ = [
'эллипсоидные модели',
'ellipsoid_r_geodetic',
'ellipsoid_r_geocentric',
'ellipsoid2d',
'ellipsoidcurvradius',
'синд',
'cosd',
'танд',
'asind',
'в диапазоне',
'cart2geocentric',
'geocentric2cart',
'cart2geodetic',
'geodetic2cart',
'geodetic2geocentric',
'geocentric2geodetic',
'great_circle_distance',
'geographic_mean',
'cartposlos2geocentric',
'geocentricposlos2cart',
'сфера_плоскость_пересечение',
'tunnel_distance',
]
[документы] def sind (x):
"" "Синус аргумента в градусах."" "
вернуть np.sin (np.deg2rad (x))
[документы] def cosd (x):
"" "Косинус аргумента в градусах." ""
вернуть np.cos (np.deg2rad (x))
[документы] def tand (x):
"" "Тангенс аргумента в градусах." ""
вернуть np.tan (np.deg2rad (x))
[документы] def asind (x):
"" "Обратный синус в градусах." ""
вернуть np.arcsin (np.deg2rad (x))
[документы] def inrange (x, minx, maxx, exclude = 'none', text = None):
"" "Проверить, находится ли x в заданных пределах.
Параметры:
x: переменная для тестирования.
minx: нижняя граница.
maxx: верхняя граница.exclude (str): исключить границы. Возможные значения:
"нет", "нижний", "верхний" и "оба"
text (str): Дополнительный текст предупреждения.
Повышает:
Исключение: если значение выходит за допустимые пределы.
"" "
compare = {'none': (np.greater_equal, np.less_equal),
'нижний': (np.greater, np.less_equal),
'верхний': (np.greater_equal, np.less),
'оба': (np.greater, np.less),
}
больше, меньше = сравнить [исключить]
если меньше (x, minx) или больше (x, maxx):
если текст None:
Raise Exception ('Диапазон вне пределов [{}, {}]'.формат (minx, maxx))
еще:
поднять исключение (
'Диапазон вне границы [{}, {}]: {}'. Формат (minx, maxx, текст)
)
[документы] класс ellipsoidmodels ():
"" "Предоставьте данные для различных справочных эллипсоидов.
Охватываются следующие модели:
* SphericalEarth (радиус установлен как constants.earth_radius)
* WGS84
* SphericalVenus (радиус такой же, как в ARTS)
* SphericalMars (радиус такой же, как в ARTS)
* EllipsoidMars
* Сферический Юпитер (радиус такой же, как в ARTS)
Примеры:
>>> e = эллипсоидные модели ()
.. Портировано из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
[документы] def __init __ (self):
self._data = {
"SphericalEarth": (constants.earth_radius, 0),
«WGS84»: (6378137, 0,08181916),
"SphericalVenus": (6051800.0, 0),
«СферикалМарс»: (3389500.0, 0),
"EllipsoidMars": (3396190.0, 0.1083),
«Сферический Юпитер»: (690.0, 0),
}
def __getitem __ (я, модель):
вернуть self.get (модель)
[документы] def get (self, model = 'WGS84'):
"" "Возвращает данные для различных справочных эллипсоидов.Параметры:
model (str): Модель эллипсоида.
Возврат:
кортеж: Экваториальный радиус (r), эксцентриситет (e)
Примеры:
>>> e ['WGS84']
(6378137, 0,08181916)
>>> e.get ('WGS84')
(6378137, 0,08181916)
>>> ellipsoidmodel () ['WGS84']
(6378137, 0,08181916)
"" "
если модель в self._data:
вернуть self._data .__ getitem __ (модель)
еще:
Raise Exception ('Неизвестная модель эллипсоида "{}".'.format (модель))
@имущество
def модели (self):
"" "Список доступных моделей.
Примеры:
>>> Электронные модели
['SphericalVenus',
«Сферический Марс»,
'WGS84',
'Сферический Юпитер',
"Эллипсоид Марс",
'SphericalEarth']
"" "
список возврата (self._data.keys ())
[документы] def ellipsoid_r_geocentric (эллипсоид, широта):
"" "Геоцентрический радиус опорного эллипсоида.
Дает расстояние от центра Земли и опорного эллипсоида.
как функция гео \ ** центрической ** широты.Примечание:
Чтобы получить радиусы для ** геодезической ** широты,
используйте: func: `ellipsoid_r_geodetic`.
Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геоцентрические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
г = нп.единицы (np.shape (lat)) * эллипсоид [0]
еще:
c = 1 - эллипсоид [1] ** 2
b = эллипсоид [0] * np.sqrt (c)
r = b / np.sqrt (c * cosd (лат) ** 2 + sind (лат) ** 2)
вернуть г
[документы] def ellipsoid_r_geodetic (эллипсоид, широта):
"" "Геодезический радиус опорного эллипсоида.
Дает расстояние от центра Земли и опорного эллипсоида.
как функция гео \ ** детической ** широты.
Примечание:
Чтобы получить радиусы для ** геоцентрической ** широты,
используйте: func: `ellipsoid_r_geocentric`.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геодезические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
r = np.ones (np.shape (lat)) * эллипсоид [0]
еще:
e2 = эллипсоид [1] ** 2
sin2 = синд (лат) ** 2
r = (эллипсоид [0] * np.sqrt ((1 - e2) ** 2 * sin2 +
cosd (лат) ** 2) / np.sqrt (1 - e2 * sin2))
вернуть г
[документы] def ellipsoid2d (эллипсоид, orbitinc):
"" "Приближенный эллипсоид для 2D расчетов.
Определяет приблизительный опорный эллипсоид, следующий по траектории орбиты.
Новый эллипсоид определяется просто, определяя радиус в точке
максимальная широта и по этому значению вычисляется новый эксцентриситет.
Орбита задается наклонением орбиты, т. Е.
обычно значение около 100 градусов для полярных солнечно-синхронных орбит.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
orbitinc (float): Наклон орбиты.
Возврат:
кортеж: измененный вектор эллипсоида.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
inrange (орбитинк, 0, 180,
exclude = 'оба',
text = 'Недействительный наклон орбиты.')
rp = ellipsoid_r_geocentric (эллипсоид, орбитинк)
вернуть эллипсоид [0], np.sqrt (1 - (rp / ellipsoid [0]) ** 2)
[документы] def ellipsoidcurvradius (эллипсоид, широта_гр, азимут):
"" "Устанавливает эллиспоид на локальный радиус кривизны
Вычисляет радиус кривизны для заданной широты и азимута.
угол, и использует это, чтобы установить сферический справочный эллипсоид
подходит для одномерных расчетов. Радиус кривизны лучше
локальное приближение, чем использование локального радиуса эллипсоида.
Для точного результата следует использовать * геодезическую * широту.Параметры:
lat_gd: Геодезическая широта.
азимут: Азимутальный угол (угол от плоскости NS).
Если возвращаются заданные радиусы кривизны, см. Выше.
Возврат:
кортеж: измененный эллипсоид.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
aterm = 1 - эллипсоид [1] ** 2 * sind (lat_gd) ** 2
rn = 1 / np.sqrt (aterm)
rm = (1 - эллипсоид [1] ** 2) * (rn / aterm)
e0 = (эллипсоид [0] / (cosd (азимут) ** 2.0 / погонный + синд (азимут) ** 2,0 / погонный))
e1 = 0
вернуть e0, e1
[docs] def cart2geocentric (x, y, z, lat0 = None, lon0 = None, za0 = None, aa0 = None):
"" "Преобразование декартовых координат в сферические координаты.
Геоцентрическая декартова система координат фиксирована относительно
Земля с центром в центре эллипсоида и ее координатами X-, Y-,
и оси Z, пересекающие поверхность в следующих точках:
* Ось X: экватор на нулевом меридиане (0 °, 0 °)
* Ось Y: экватор на 90 градусов восточной долготы (0 °, 90 °)
* Ось Z: Северный полюс (90 °, 0 °)
Распространенный синоним - "Центрированные на Земле", "Фиксированные на Земле координаты" или ECEF.Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
для случаев N-S. Необязательный ввод должен интерпретироваться как [x, y, z]
получается перемещением от [lat0, lon0] в направлении [za0, aa0].
Параметры:
x: координата в измерении x.
y: координата по оси y.
z: координата по оси z.
lat0: исходная широта.
lon0: Исходная долгота.
za0: исходный зенитный угол.aa0: Исходный азимутальный угол.
Возврат:
кортеж: Радиус, Широта, Долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
r = np.sqrt (x ** 2 + y ** 2 + z ** 2)
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
широта = np.rad2deg (np.arcsin (z / r))
lon = np.rad2deg (np.arctan2 (y, x))
если все (x не равно None для x в [lat0, lon0, za0, aa0]):
для i в диапазоне (np.size (r)):
если za0 [i] <1e-06 или za0 [i]> 180 - 1e-06:
lat [i] = lat0 [i]
lon [i] = lon0 [i]
if (abs (lat0 [i]) <90 - 1e-08 и
(abs (aa0 [i]) <1e-06 или abs (aa0 [i] - 180) <1e-06)):
если abs (lon [i] - lon0 [i]) <1:
lon [i] = lon0 [i]
еще:
если lon0 [i]> 0:
lon [i] = lon0 [i] - 180
еще:
lon [i] = lon0 [i] + 180
вернуть r, lat, lon
[документы] def geocentric2cart (r, lat, lon):
"" "Преобразование из сферической координаты в декартову позицию.См .: func: `cart2geocentric` для определения геоцентрического
система координат.
Параметры:
r: Радиус.
lat: Широта в градусах.
lon Долгота в градусах.
Возврат:
кортеж: координаты в измерениях x, y, z.
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
latrad = np.deg2rad (лат)
lonrad = np.deg2rad (долг)
х = г * нп.cos (латрад)
y = x * np.sin (лонрад)
х = х * np.cos (лонрад)
z = r * np.sin (латрад)
вернуть x, y, z
[docs] def cart2geodetic (x, y, z, ellipsoid = None):
"" "Преобразование декартовых координат в геодезические.
Геодезические координаты относятся к опорному эллипсоиду.
заданный входным эллипсоидом.
См. В документации модуля определение геоцентрической системы координат.
Параметры:
x: координаты в измерении x.
y: координаты в измерении y.
z: координаты в измерении z.эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: геодезическая высота, широта и долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
lon = np.rad2deg (np.arctan2 (y, x))
B0 = np.arctan2 (z, np.hypot (x, y))
B = np.ones (B0.shape)
e2 = эллипсоид [1] ** 2
если e2 == 0.0:
h, lat, lon = cart2geocentric (x, y, z)
h - = эллипсоид [0]
еще:
while (np.any (np.abs (B - B0)> 1e-10)):
N = эллипсоид [0] / np.sqrt (1 - e2 * np.sin (B0) ** 2)
h = np.hypot (x, y) / np.cos (B0) - N
B = B0.copy ()
B0 = np.arctan (z / np.hypot (x, y) * ((1-e2 * N / (N + h)) ** (- 1)))
широта = np.rad2deg (B)
вернуть ч, лат, долг
[docs] def geodetic2cart (h, lat, lon, ellipsoid = None):
"" "Преобразование из геодезических в геоцентрические декартовы координаты.Геодезические координаты относятся к опорному эллипсоиду.
заданный входным эллипсоидом.
См. В документации модуля определение геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.
lon: Геодезическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: координаты x, y, z... Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
а = эллипсоид [0]
e2 = эллипсоид [1] ** 2
N = a / np.sqrt (1 - e2 * sind (лат) ** 2)
x = (N + h) * (cosd (долг)) * (cosd (долг))
y = (N + h) * (cosd (lat)) * (sind (долг))
# np.ones (np.shape (lon)): Обеспечьте одинаковую форму x, y, z.z = (N * (1 - e2) + h) * (sind (лат)) * np.ones (np.shape (долг))
вернуть x, y, z
[docs] def geodetic2geocentric (h, lat, lon, ellipsoid = None, ** kwargs):
"" "Преобразование геодезических координат в геоцентрические.
Геодезические координаты относятся к опорному эллипсоиду.
заданный входным эллипсоидом.
См. В документации модуля определение геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.lon: Геодезическая долгота.
kwargs: Дополнительные аргументы ключевого слова для: func: `cart2geocentric`.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: радиус, геоцентрическая широта, геоцентрическая долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
cart = geodetic2cart (ч, широта, долгота, эллипсоид)
возврат cart2geocentric (* cart, ** kwargs)
[документы] def geocentric2geodetic (r, lat, lon, ellipsoid = None):
"" "Преобразование геоцентрических координат в геодезические.
Геодезические координаты относятся к опорному эллипсоиду.
заданный входным эллипсоидом.
См. В документации модуля определение геоцентрической системы координат.
Возврат:
кортеж: геодезическая высота, широта и долгота
Параметры:
r: Радиус:
lat: геоцентрическая широта.lon: геоцентрическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
тележка = geocentric2cart (r, lat, lon)
return cart2geodetic (* тележка, эллипсоид)
[документы] def great_circle_distance (lat1, lon1, lat2, lon2, r = None):
r "" "Рассчитать расстояние между двумя географическими положениями
Это расстояние между двумя точками по прямой, определяемое
их широта и долгота.2} \ справа)
Аргументы:
lat1: Широта позиции 1.
lon1: долгота позиции 1.
lat2: Широта позиции 2.
lon2: долгота позиции 2.
r (float): радиус (общий для обеих точек).
Возврат:
Если указан необязательный аргумент * r *, возвращается расстояние в метрах.
В противном случае возвращается угловое расстояние в градусах.
.. Взято с https://stackoverflow.com/a/29546836/90
"" "
lon1, lat1, lon2, lat2 = map (np.radians, [lon1, lat1, lon2, lat2])
dlon = lon2 - lon1
dlat = lat2 - lat1
а = нп.sin (dlat / 2.0) ** 2 + np.cos (lat1) * np.cos (lat2) * np.sin (
dlon / 2,0) ** 2
c = 2 * np.arcsin (np.sqrt (а))
если r равно None:
вернуть np.rad2deg (c)
еще:
вернуть r * c
[docs] def geographic_mean (lat, lon, h = 0, ellipsoid = None):
"" "Вычислить среднее положение для набора координат.
Параметры:
lat (float или ndarray): широта в градусах.
lon (float или ndarray): долгота в градусах.
h (float или ndarray): оптимальная высота для
каждая координата (по умолчанию).эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: средние значения широты и долготы в градусах.
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
x, y, z = geodetic2cart (
час,
лат,
лон
эллипсоид = эллипсоид)
mh, mlat, mlon = cart2geodetic (
np.mean (x),
np.mean (y),
np.mean (z),
эллипсоид = эллипсоид)
возврат млат, млон
[docs] def cartposlos2geocentric (x, y, z, dx, dy, dz, ppc = None,
lat0 = Нет, lon0 = Нет, za0 = Нет, aa0 = Нет):
"" "Преобразование декартовой точки POS / LOS в сферические координаты.Положение задается как (x, y, z), а линия прямой видимости задается как (dx, dy, dz).
Соответствующие величины в полярных координатах: (r, lat, lon)
и (za, aa) соответственно.
См. * Содержание * для определения систем координат.
Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
и азимутальный угол для случаев с севера на юг. Необязательный ввод должен интерпретироваться
поскольку [x, y, z] получается перемещением из [r0, lat0, lon0] в направлении
из [za0, aa0].Эта версия отличается от версии atmlab тем, что нормализует потери.
vector и требует все или ничего для работы необязательных аргументов.
Параметры:
x: координата в измерении x.
y: координата по оси y.
z: координата по оси z.
dx: компонент LOS в измерении x.
dy: компонент LOS в измерении y.
dz: компонент LOS в измерении z.
ppc: Константа пути распространения = r0 * sin (za0).
lat0: исходная широта.
lon0: Исходная долгота.za0: исходный зенитный угол.
aa0: Исходный азимутальный угол.
Возврат:
кортеж (ndarray): радиус, широта, долгота,
Зенитный угол, Азимутальный угол
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
# Вот драконы!
# Трансляция всех входных переменных в одну и ту же форму. По крайней мере (1)
if (ppc не равно None и za0 не равно None, а lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0 = _broadcast (
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0)
elif ppc не равно None:
x, y, z, dx, dy, dz, ppc = _broadcast (x, y, z, dx, dy, dz, ppc)
еще:
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
r, lat, lon = cart2geocentric (x, y, z, lat0, lon0, za0, aa0)
# Перенормировать длину переменных (не в atmlab)
norm_r = np.sqrt (dx ** 2 + dy ** 2 + dz ** 2)
dx = dx / norm_r
dy = dy / norm_r
dz = dz / norm_r
coslat = np.cos (np.deg2rad (широта))
sinlat = np.sin (np.deg2rad (лат))
coslon = np.cos (np.deg2rad (долг))
sinlon = np.sin (np.deg2rad (долг))
dr = np.clip (coslat * coslon * dx + sinlat * dz + coslat * sinlon * dy,
-1., 1.)
# Получить угол LOS
если ppc равно None:
za = np.rad2deg (np.arccos (dr))
еще:
za = np.rad2deg (np.arcsin (ppc / r))
aa = np.zeros (za.shape)
# Исправить зенит и азимутальный угол с дополнительным вводом, только когда все существует
if (za0 не равно None, а lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
# Определяем тип для зенита
noz = np.логическая_ор (za0 <1e-06, za0> 180 - 1e-06)
nan = np.isnan (za)
pre = np.logical_and (~ noz, nan)
# Либо установить, либо нет
za [noz] = za0 [noz]
za [pre] = 90.
# NB: удалена проверка на dr <0, поскольку установка dr == 1 более разумна
# Определить тип азимута
cir1 = abs (aa0) <1e-06
cir2 = np.logical_or (cir1, abs (aa0 - 180) <1e-06)
то же = np.equal (lon, lon0)
circ = np.logical_and (cir2, то же самое)
left = np.логическое_и (cir1, ~ то же)
right = np.logical_and (~ cir1, ~ то же)
# Это должно установить все случаи
aa [circ] = aa0 [circ]
аа [слева] = 180.
аа [справа] = 0.
еще:
# Определить тип выполняемых расчетов
noz = np.logical_or (za <1e-06, za> 180 - 1e-06)
pol = abs (широта)> 90 - 1e-08
pre = np.logical_and (~ noz, pol)
non = np.logical_and (~ noz, ~ pol)
аа [noz] = 0.
aa [pre] = np.rad2deg (np.arctan2 (dy [pre], dx [pre]))
dlat = (- sinlat [non] * coslon [non] / r [non] * dx [non] + coslat [non] /
r [non] * dz [non] - sinlat [non] * sinlon [non] / r [non] * dy [non]
)
dlon = (- sinlon [non] / coslat [non] / r [non] * dx [non] + coslon [non] /
coslat [non] / r [non] * dy [non])
aa [non] = (np.rad2deg (np.arccos (r [не] *
dlat / np.sin (np.deg2rad (za [non])))))
fix = np.logical_or (np.isnan (aa), ~ np.isreal (aa))
aa [np.logical_and (fix, dlat> = 0)] = 0
aa [np.logical_and (fix, dlat <0)] = 180
aa [np.logical_and (~ fix, dlon <0)] * = -1
вернуть r, lat, lon, za, aa
[документы] def geocentricposlos2cart (r, lat, lon, za, aa):
"" "
Преобразование из сферической POS / LOS в декартовую POS / LOS
См. Раздел Содержание для определения геоцентрической системы координат.Локальные углы прямой видимости определяются по системе ВОСТОК-СЕВЕР-ВВЕРХ:
за аа
90 0 указывает на север
90 90 очков на восток
0 аа баллов вверх
FORMAT [x, y, z, dx, dy, dz] = geocentricposlos2cart (r, lat, lon, za, az)
ВНЕ
Координата x в измерении x
Координата y в измерении y
Координата z по оси z
dx компонент LOS в измерении x
dy Компонент LOS в измерении y
dz LOS
В
r Радиус
широта Широта
долгота
зенитный угол
азимутальный угол
Портировано из атмлаба.Оригинальный автор: Бенгт Ридберг 2011-10-31
"" "
r, lat, lon, za, aa = _broadcast (r, lat, lon, za, aa)
если есть (r == 0):
Raise Exception ("Эта функция не обрабатывает случай r = 0")
если есть (lat <-90) или любые (lat> 90):
Raise RuntimeError ("Широта вне допустимого диапазона")
если есть (lon <-180) или любое (lon> 180):
Raise RuntimeError («Долгота вне допустимого диапазона»)
если есть (za <0) или любое (za> 180):
Raise RuntimeError («Зенитный угол вне допустимого диапазона»)
deg2rad = np.град2рад (1)
x = np.empty (r.shape)
y = np.empty (r.shape)
z = np. пусто (r.shape)
dx = np.empty (r.shape)
dy = np.empty (r.shape)
dz = np.empty (r.shape)
at_pole = abs (широта)> (90 - 1e-8)
если есть (at_pole):
s = np.sign (широта [at_pole])
х [at_pole] = 0.
y [at_pole] = 0.
z [at_pole] = s * r [at_pole]
dz [at_pole] = s * np.cos (deg2rad * (za [at_pole]))
dx [at_pole] = np.sin (deg2rad * (za))
dy [at_pole] = dx [at_pole] * np.sin (deg2rad * (aa))
dx [at_pole] * = np.cos (deg2rad * (aa))
not_pole = np.logical_not (at_pole)
если есть (not_pole):
latrad = deg2rad * lat [not_pole]
lonrad = deg2rad * lon [not_pole]
zarad = deg2rad * za [not_pole]
aarad = deg2rad * aa [not_pole]
coslat = np.cos (латрад)
sinlat = np.sin (латрад)
coslon = np.cos (лонрад)
sinlon = np.sin (лонрад)
cosza = np.cos (zarad)
sinza = np.sin (зарад)
cosaa = np.cos (aarad)
sinaa = np.sin (аарад)
x [not_pole] = r [not_pole] * coslat
y [not_pole] = x [not_pole] * sinlon
x [not_pole] * = кослон
z [not_pole] = r [not_pole] * sinlat
dr = cosza
dlat = sinza * cosaa
dlon = sinza * sinaa / coslat
dx [not_pole] = (coslat * coslon * dr - sinlat * coslon * dlat -
coslat * sinlon * dlon)
dz [not_pole] = sinlat * dr + coslat * dlat
dy [not_pole] = (coslat * sinlon * dr - sinlat * sinlon * dlat +
coslat * coslon * dlon)
вернуть x, y, z, dx, dy, dz
def get_ellipsoid_semiminor_axis (эллипсоид):
"" "Возвращает малую полуось эллипсоида.
"" "
вернуть эллипсоид [0] * np.sqrt (1.0 - эллипсоид [1] ** 2)
def line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, высота = 0,0):
"" "Находит точки пересечения прямой с эллипсоидом.
Решает относительно d:
$$ (X / a) ** 2 + (Y / a) ** 2 + (Z / b) ** 2 - 1 = 0 $$
$$ X = x + d * dx $$
$$ Y = y + d * dy $$
$$ Z = z + d * dz $$
где d - множитель sqrt (dx ** 2 + dy ** 2 + dz ** 2), a -
Большая полуось, b - малая полуось. X, Y, Z дает
точка пересечения.Если dx, dy, dz нормализованы, d - расстояние
в единицах размера эллипсоида. Если пересечения нет, код возвращает расстояние np.nan
Для действительного d точка на полпути между точками - это точка касания,
хотя он ниже эллипсоида + высота поверхности
Возврат:
d: массив параметров расстояния, последнее измерение дает 2 решения
Параметры:
x: геоцентрическая декартова координата x
y: геоцентрическая декартова координата y.
z: геоцентрическая декартова координата z.
dx: геоцентрическое декартово представление в формате dx
dy: геоцентрическое декартово отображение
dz: геоцентрический декартово вид dz
эллипозид: модель эллипсоида [a, e]
высота: высота над эллипсоидом до точки пересечения [по умолчанию ноль]
Делать:
Обратитесь к line_sphere_intersect, если эллипсоид является сферой
"" "
# большая полуось
a = эллипсоид [0] + высота
# малая полуось
b = get_ellipsoid_semiminor_axis (эллипсоид) + высота
# Если это скаляры, сделайте их массивами
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
# A * d ** 2 + B * d + C = 0, найти d
А = ((dx ** 2 + dy ** 2) / a ** 2 + dz ** 2 / b ** 2).сплющить ()
B = (2 * ((x * dx + y * dy) / a ** 2 + z * dz / b ** 2)). Flatten ()
C = ((y ** 2 + x ** 2) / a ** 2 + z ** 2 / b ** 2 - 1.0) .flatten ()
d = np.zeros ((len (A), 2))
для i в диапазоне (len (A)):
корни = np.roots ([A [i], B [i], C [i]])
если есть (np.isreal (корни)):
d [i, 0] = корни [0]
d [i, 1] = корни [1]
еще:
d [i, 0] = np.nan
d [i, 1] = np.nan
sh = []
для i в x.shape:
sh.append (i)
sh.append (2)
вернуть d.reshape (кортеж (sh))
def geometry_limb_zenith_angle (эллипсоид, r, широта, долгота,
аа = 0.0, alt = 0.0, za_acc = 1e-10):
"" "Численный метод вычисления геометрического зенитного угла лимба, зная
другие параметры спутника
Предполагает, что планета представляет собой эллипсоид, и вычисляет конечность численно
минимизация расстояния между соседними пересечениями эллипсоида.
Скорость сближения с прямым зенитным углом должна составлять 180/30 ** N,
хотя численные ошибки очень точной точности не защищены.
Параметры:
эллипсоид: эллипсоид [a, e]
r: геоцентрический радиус спутника
lat: геоцентрическая широта спутника
lon: геоцентрическая долгота спутника
aa: азимутальный угол спутника
alt: касательная высота
za_acc: точность зенитного угла.Предупреждение: бесконечный цикл, если он слишком мал
Возврат:
za: зенитный угол спутника для геометрии обзора конечностей. Форма как вход
"" "
если (za_acc == 0):
поднять RuntimeError ("Точность зенита не может быть 0")
r, lat, lon, aa, alt = _broadcast (r, lat, lon, aa, alt)
# Запомните форму, потому что мы сгладим эти массивы для упрощения цикла
sh = r.shape
r = r.flatten ()
lat = lat.flatten ()
lon = lon.flatten ()
aa = aa.flatten ()
alt = alt.flatten ()
za = np.empty_like (r)
для i в диапазоне (len (r)):
za_min = 0.0
za_max = 180,0
while True: # Пока не будет достигнута зенитная точность
# num = 31 означает 180/30 ** N - количество петель для достижения точности
zenith_angles = np.linspace (za_min, za_max, число = 31)
# Получение декартовых представлений для зенитной точности зондирования
x, y, z, dx, dy, dz = geocentricposlos2cart (r [i], lat [i], lon [i],
zenith_angles, aa [i])
# Получите пересечения с эллипсоидом на касательной высоте
d = line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, alt [i])
# Если мы каким-то образом разработали сценарий, который невозможен или плох
если нп.isnan (d) .all ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Все попытки упускают из виду эллипсоид».)
Элиф не np.isnan (d) .any ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Внутри эллипсоида или атмосферы»).
# Зенит конечностей за счет минимизации расстояния между перекрестками
D = d [:, 0] - d [:, 1]
# Вот достопримечательности
эти = np.nan_to_num (D)> 0
# Обновлен первый из зенитных углов, попадающих в атмосферу.
za_max = zenith_angles [эти] [0]
# Обновлен последний зенитный угол без атмосферы.
za_min = zenith_angles [np.logical_not (эти)] [- 1]
# Мы уже на месте?
если (za_max-za_min) >> x, y, z = geodetic2cart (30e3, 30., 30.)
>>> sat = сфера_плоскость_пересечение (np.массив ([x, y, z]), 6978e3)
"" "
assert r> 0.0, "Невозможно работать со сферой нулевого радиуса"
assert len (pos.shape) == 2, "Требуется (N, 3) как pos-shape"
d = np.linalg.norm (pos, axis = 1)
assert all (d> 0.0), «Невозможно работать с 0-вектором для позиции»
число_углов = лен (тета)
number_of_positions = pos.shape [0]
points = np.empty ((число_углов, число_позиций, 3))
если number_of_angles == 0:
точки возврата
# Если сфера находится под плоскостью или по касательной к плоскости
для ii в диапазоне (число_позиций):
если d [ii]> r:
для i в диапазоне (число_углов):
точки [i, ii,:] = np.массив ([np.nan, np.nan, np.nan])
Продолжать
elif d [ii] == r:
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:]
Продолжать
# (Нормализованный / единичный) вектор плоскости
n = pos [ii] / d [ii]
# Южный вектор
единицы, широта, долгота = cart2geocentric (n [0], n [1], n [2])
если (широта == 90,0):
v1 = np.array ([cosd (lon), sind (lon), 0.]) * sind (лат)
еще:
v1 = np.array ([cosd (долг) * синд (лат),
синд (долг) * синд (лат),
cosd (лат-180.0)])
# Восточный вектор
v2 = -np.cross (n, v1) # указывает на восток
# Радиус круга
rc = np.sqrt (r ** 2 - d [ii] ** 2)
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:] + rc * (cosd (theta [i]) * v1 +
синд (тета [я]) * v2)
точки возврата
def tunnel_distance (lat1, lon1, lat2, lon2):
"" "Рассчитайте туннельное расстояние между двумя точками на поверхности Земли.
Аргументы:
lat1: одиночное число или массив numpy с широтой в градусах.lon1: одиночное число или массив numpy с долготой в градусах.
lat2: одиночное число или массив numpy с широтой в градусах.
lon2: одиночное число или массив numpy с долготой в градусах.
Возврат:
Расстояние туннеля в метрах
"" "
points1 = np.column_stack (
geocentric2cart (constants.earth_radius, lat1, lon1)
)
points2 = np.column_stack (
geocentric2cart (constants.earth_radius, lat2, lon2)
)
return np.sqrt (np.sum ((points2 - points1) ** 2, axis = 1))
def _broadcast (* args):
"" "Аналогично broadcast_arrays в numpy, но с минимальным размером вывода (1,)
"" "
shape = np.трансляция (* аргументы) .shape
если не форма:
shape = (1,)
return [np.broadcast_to (array, shape) for array in args]
Перейти к основному содержанию
Поиск Поиск
- Где угодно
Поиск Поиск
Расширенный поиск- Войти | регистр
- Подписка / продление
- Учреждения
- Индивидуальные подписки
- Индивидуальное продление
- Библиотекари
- полные заказы Чикагский пакет
- Полный охват и охват содержимого
- Файлы KBART и RSS-каналы
- Разрешения и перепечатки
- Инициатива развивающихся стран Чикаго
- Даты отправки и претензии
- Часто задаваемые вопросы библиотекарей
- и платежи
- О нас
- Публикуйте у нас
- Новые журналы
- tners
- Подпишитесь на уведомления eTOC
- Пресс-релизы
- СМИ
- Издательство Чикагского университета
- Распределительный центр в Чикаго
- Чикагский университет
- Положения и условия
- Заявление об издательской этике
- Уведомление о конфиденциальности
- Доступность Chicago Journals
- Доступность вузов
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
- Свяжитесь с нами
- Запросы СМИ и рекламы
- Открытый доступ в Чикаго
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
Глоссарий
ГлоссарийГлоссарий
Об определении потока импульса гравитационной волны по радиозатменным данным GPS
Исследовательская статья 20 ноя 2013
Исследовательская статья | 20 ноя 2013
А.Фабер 1,2 , п. Ламедо 3 , т. Шмидт 1 , А. de la Torre 3 и J. Wickert 1 A. Faber et al. А. Фабер 1,2 , П. Ламедо 3 , т. Шмидт 1 , А. de la Torre 3 и J. Wickert 1- 1 Отдел 1, Геодезия и дистанционное зондирование, GFZ Немецкий исследовательский центр геонаук, Потсдам, Германия
- 2 Институт космических наук, Свободный университет Берлина, Берлин, Германия
- 3 Facultad de Ingeniería, Universidad Острал, Буэнос-Айрес, Аргентина
- 1 Отдел 1, геодезия и дистанционное зондирование, GFZ Немецкий исследовательский центр наук о Земле, Потсдам, Германия
- 2 Институт космических наук, Свободный университет Берлина, Берлин, Германия
- 3 Facultad de Ingeniería, Universidad Austral, Buenos Aires, Argentina
Глобальная система позиционирования (GPS), радиозатмение (RO) — это хорошо зарекомендовавший себя метод получения информации о глобальных гравитационных волнах (GW).RO использует сигналы GPS, полученные со спутников на низкой околоземной орбите, для зондирования границы атмосферы. Температурные профили получены с высоким вертикальным разрешением и обеспечивают глобальный охват при любых погодных условиях, предлагая возможность глобального мониторинга вертикальной структуры температуры и параметров атмосферных волн. Созвездие из шести спутников COSMIC / FORMOSAT-3 ежедневно обеспечивает около 2000 температурных профилей. В этом исследовании мы используем метод получения глобальных распределений длин горизонтальных гравитационных волн, который будет применяться при определении вертикального потока горизонтального импульса, переносимого гравитационными волнами.Здесь к данным COSMIC применяется метод определения реальной горизонтальной длины волны из трех вертикальных профилей. Рассчитываются горизонтальная и вертикальная длина волны, удельная потенциальная энергия ( E p ) и вертикальный поток горизонтального импульса (MF), и обсуждается их глобальное распределение.
Международная конференция по физической геодезии и геоматике ICPGG в июне 2021 года в Риге
Цели и задачи Международной научной конференции
Международная научно-исследовательская конференция — это федеративная организация, цель которой — объединить значительное количество разнообразных научных мероприятий для презентации. в рамках программы конференции.События будут проходить в течение определенного периода времени во время конференции в зависимости от количества и продолжительности презентаций. Благодаря своему высокому качеству, он представляет собой исключительную ценность для студентов, ученых и отраслевых исследователей.
ICPGG 2021: 15. Международная конференция по физической геодезии и геоматике стремится собрать вместе ведущих академических ученых, исследователей и ученых-исследователей для обмена и обмена своим опытом и результатами исследований по всем аспектам Физическая геодезия и геоматика.Он также предоставляет ведущую междисциплинарную платформу для исследователей, практиков и преподавателей, чтобы представить и обсудить самые последние инновации, тенденции и проблемы, а также встречающиеся практические проблемы и решения, принятые в области физической геодезии и геоматики
Призыв к взносам
Будущим авторам предлагается внести свой вклад и помочь в формировании конференции путем представления своих научных резюме, статей и электронных постеров.Кроме того, высококачественные исследовательские материалы, описывающие оригинальные и неопубликованные результаты концептуальных, конструктивных, эмпирических, экспериментальных или Сердечно приглашаем для выступления на конференции теоретические работы во всех областях физической геодезии и геоматики. Конференция приглашает участников в виде тезисов, докладов и электронных плакатов, посвященных темам и темам конференции, включая рисунки, таблицы и ссылки на новые исследовательские материалы.
Руководство для авторов
Пожалуйста, убедитесь, что ваша работа соответствует строгим правилам конференции по приему научных работ.Загружаемые версии контрольного списка для Полнотекстовые статьи и Реферативные статьи.
Пожалуйста, обратитесь к Правила подачи статей, Правила подачи тезисов и Информация об авторе перед подачей статьи.
Материалы конференции
Все представленные на конференцию доклады будут подвергнуты слепому рецензированию тремя компетентными рецензентами. Рецензируемые материалы конференций индексируются в Open Science Index, Google Scholar, Семантический ученый, Зенедо, OpenAIRE, БАЗА, WorldCAT, Шерпа / RoMEO, и другие индексные базы данных.Индикаторы импакт-фактора.
Специальные выпуски журнала
ICPGG 2021 объединилась с выпуском специального журнала на Физическая геодезия и геоматика. Ряд выбранных высокоэффективных полнотекстовых статей также будет рассмотрен для специальных выпусков журнала. Все представленные статьи будут рассмотрены в этом специальном выпуске журнала. Отбор докладов будет проводиться в процессе рецензирования, а также на этапе презентации на конференции.Представленные статьи не должны рассматриваться другими журналами или публикациями. Окончательное решение о выборе статьи будет принято на основании отчетов о коллегиальном обзоре, подготовленных приглашенными редакторами и главным редактором совместно. Избранные полнотекстовые статьи будут бесплатно опубликованы в Интернете.
Возможности для спонсоров и участников конференции
Конференция предлагает возможность стать спонсором конференции или экспонентом. Чтобы принять участие в качестве спонсора или экспонента, загрузите и заполните Форма заявки на спонсорство конференции.
Избранные статьи
- Гибридный алгоритм инверсии градиента силы тяжести — алгоритм оптимизации колонии муравьев для планирования движения мобильных роботов
Meng Wu - Оценка кинетических параметров с помощью термогравиметрии и калориметрии горения в микромасштабе
Рода Африие Менса, Линь Цзян, Соломон Асанте-Окьере, Сюй Цян, Кон Джин - Модель свободного терминала, скользящий режим с компенсацией силы тяжести: применение к системе экзоскелет-верхняя конечность
Сана Бембли, Нахла Крайеф Хаддад, Сафья Белгит - Анализ влияния конкурентов на розничного продавца с использованием ценности клиента и модели притяжения Хаффа
Йепенг Ченг, Ясухико Моримото - Размещение биосовместимой международной космической станции на геостационарной орбите
Тим Фальк, Крис Чатвин - Оценка толщины земной коры в бассейне Сокото на северо-западе Нигерии с использованием данных по гравитационной аномалии Буге
T.Т. Олугбенга, А. И. Оги - Гравитационное воздействие Солнца и Луны на отложения тяжелых минералов и частицы пыли в областях с низкой гравитацией Земли
Т. Б. Кару Джаясундара - Региональные аномалии низкой силы тяжести, влияющие на высокие концентрации тяжелых минералов на россыпных месторождениях
Т. Б. Кару Джаясундара - Оценка гравитационных аномалий на основе глобальных моделей по земным гравиметрическим данным
M.Йылмаз, И. Йылмаз, М. Уйсал - Оценка геопотенциальных моделей в Алжире с использованием стохастического метода, GPS / нивелирования и топографических данных
М. А. Меслем - Тройная диффузионная конвекция в вертикально колеблющейся жидкости Oldroyd-B
Самина Тараннум, С. Пранеш - Гравитационные частотные сдвиги для фотонов и частиц
Jing-Gang Xie - Моделирование искусственной нейронной сети и оптимизация на основе генетических алгоритмов гидравлического проектирования, связанного с просачиванием под бетонные гравитационные плотины на проницаемых почвах
Мукдад Аль-Джубури, Битин Датта - Влияние уменьшения наложенной статической нагрузки на боковые сейсмические деформации конструкций
H.Альнаджаджра, А. Тукан, М. Двайкат - Трехмерный высокоточный метод туннельной гравитационной разведки для скрытых высокоплотных рудных тел: исследование на примере месторождения Zn-Pb- (Ag-Ge), содержащего карбонат Zhaotong Maoping, на северо-востоке Юньнани, Китай
Han Run-Sheng, Li Wen -Яо, Ван Фэн, Лю Фэй, Цю Вэнь-Лун, Лэй Ли
состоит из электронного журнала, доступного только в режиме онлайн. и включает сообщения конференции (тезисы докладов и доклады).Зарегистрированные участники могут получить доступ к конференции, доступной в цифровом формате. судебных разбирательств (и сертификатов), посетив их страницы профиля.
Физико-геодезия
Геодинамика
Развитие физической геодезии
Методика измерения
Геопотенциальные единицы силы тяжести и геопотенциал
Нормальный потенциал
Возмущающий потенциал и геоид
Аномалии силы тяжести
Геофизика
Основы теории гравитации
Уравнение Лапласа и его решения
Нормальное гравитационное поле
Аномальные величины гравитационного поля
Геофизические редукции
Вертикальные системы отсчета
Уравнение Стокса и другие интегральные уравнения
Спектральные методы
Статистические методы
Приборы гравиметрические измерения
Геоид, средний уровень моря, рельеф поверхности моря
Приливы, атмосфера и движения земной коры
Исследование земного гравитационного поля
Гравиметрические методы
Статистические методы в физической геодезии
| Срок подачи тезисов / полнотекстовых статей | 29 апреля 2021 г. | |
| Уведомление о принятии / отказе | 13 мая 2021 г. | |
| Заключительный доклад (готовый к съемке) Срок подачи и ранней регистрации | 17 мая 2021 г. | |
| Даты конференций | 17-18 июня 2021 г. |
| Халед Эльбехиери | Университет ДеВри, США |
| Педро Льянос | Авиационный университет Эмбри-Риддла, США |
| Sepidehalsadat Hendi | Университет Британской Колумбии, Калифорния |
| Соломон Будник | utg, IL |
| Абдулрахаман Идрис Оги | Федеральный университет Бирнин Кебби, NG |
| Ричардсон М Абрахам-Адехумо | Университет Сан-Паулу, BR |
| Марина Чхитунидзе | М.Институт геофизики им. Нодиа, Тбилисский государственный университет им. Иване Джавахишвили, Тбилиси, Грузия, GE |
| Коллинз Молуа | Педагогический колледж, NG |
| Фреди Александр Фонсека Бенитес | Педагогический и технологический университет Колумбии, CO |
| Мария дель Кармен Фуэнте Фуэнтес | Педагогический и технологический университет Колумбии, CO |
| Мукдад аль-Джубури | Джеймс Кук, Австралия |
| Сатьендра Сингх | IIT (BHU) Варанаси, Индия |
| Петр Цыба | Евразийский национальный университет, Казахстан |
| Цзин-Ган Се | Varian Medical Systems, США |
| Hemantkumar Mehta | Национальный технологический институт имени Сардара Валлаббая, Сурат, Индия |
| Прадип Кумар Сингх Чаухан | Совет научно-промышленных исследований — Центральный научно-исследовательский институт строительства, Рурки, ИН |
| Хусейн Аль-Мусави | University Sains Malaysia, |
| Мохсен Фарахат | Центральный металлургический научно-исследовательский институт, |
| Муна Габуш Эль Дави | Университет Нилейн, SD |
| Джон Мукаби | Kensetsu Kaihatsu Consulting Engineers Ltd., KE |
| Рафиу Адегбола | Государственный университет Лагоса, NG |
| Первеиз Халид | Университет Пенджаба, PK |
| Джатау Шадрах Бенсон | Государственный университет Насарава, Кеффи, Нигерия, NG |
| Мохаммад Хоссейн Садеги | университет Зенджана, IR |
| Ифеани Чинвуко | Nnamdi Azikiwe Univeria Awka, NG |
| Ани Чинеду | Государственный университет Коги, Анигба, NG |
| Эммануэль Анаквуба | Университет Ннамди Азикиве, NG |
| Шазия Асим | Университет Куэйд-и-Азам, PK |
| Бенсон Шадрах Ятау | Государственный университет Насарава, NG |
| Хатам Куанбари | Исламский университет Азад, IR |
| Тип участия | Стоимость билетов за раннюю регистрацию | Стоимость регистрационного билета |
|---|---|---|
| Регистрация докладчика / постера для не учащихся | € 450 | € 500 |
| Студенческое выступление / регистрация докладчика | € 350 | € 400 |
| Регистрация слушателя | € 250 | € 300 |
| Дополнительная публикация | € 100 | |
Все материалы и услуги конференции будут доставлены участникам в цифровом виде с помощью онлайн-системы управления конференциями.Регистрация на конференцию включает следующие цифровые материалы и услуги:
- е-сертификаты [для авторов: свидетельство о посещении и представление; для слушателей: свидетельство о посещении; для кафедр: свидетельство о посещаемости и благодарность; для докладчиков: Сертификат на лучшую презентацию (в случае предоставления на основе оценки)]
- электронная программа
- электронная книга
- Значок электронного имени
- электронная квитанция
- электронная презентация
Типы презентаций:
- Физическая презентация — это устная конференц-презентация, сделанная с использованием цифровых технологий, включая встроенные цифровые элементы (тексты, таблицы, графики или видео) для совместного использования PowerPoint.
- Цифровая презентация — это презентация цифровой конференц-связи, которая создается с использованием цифровых технологий, включая встроенные цифровые элементы (тексты, таблицы, графики или видео) для совместного использования PowerPoint.
