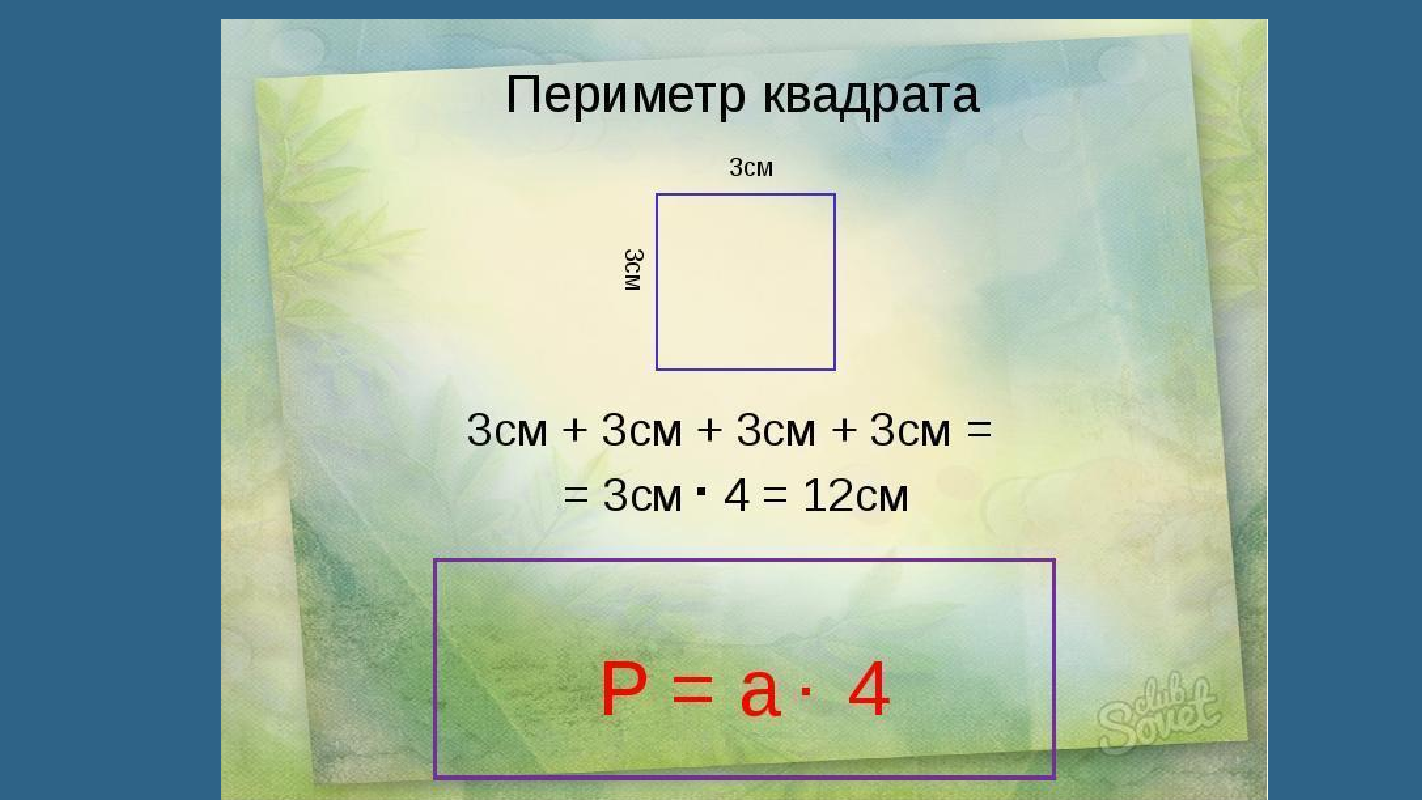
Площадь квадрата — формула, пример расчета
Квадрат – это правильный четырехугольник, в котором все углы и стороны равны между собой.
Довольно часто эту фигуру рассматривают, как частный случай ромба или прямоугольника. Диагонали квадрата равны между собой и используются в формуле площади квадрата через диагональ.
Для расчета площади рассмотрим формулу площади квадрата через диагонали:
То есть площадь квадрата равна квадрату длины диагонали поделенному на два. Учитывая, что стороны фигуры равны, можно рассчитать длину диагонали из формулы площади прямоугольного треугольника или по теореме Пифагора.
Рассмотрим пример расчета площади квадрата через диагональ. Пусть дан квадрат с диагональю d = 3 см. Необходимо вычислить его площадь:По этому примеру расчета площади квадрата через диагонали мы получили результат 4,5 .
Площадь квадрата через сторону
Найти площадь правильного четырехугольника можно и по его стороне. Формула площади квадрата очень проста:
Формула площади квадрата очень проста:
Подставим значение в выражение:
Длина стороны квадрата будет равна 2,1 cm.
Очень просто можно использовать формулу площади квадрата вписанного в окружность.
Диаметр описанной окружности будет равен диаметру квадрата. Так как квадрат считается правильным ромбом, можно использовать формулу расчета площади ромба. Она равна половине произведения его диагоналей. Диагонали квадрата равны, значит формула будет выглядеть так:
Рассмотрим пример расчета площади квадрата вписанного в окружность.
Площадь квадрата равна 18
Площадь квадрата через периметр
В некоторых задачах по условиям дается периметр квадрата и требуется расчет его площади. Формула площади квадрата через периметр выводится из значения периметра. Периметр – это сумма длин всех сторон фигуры. Т.к. в квадрате 4 равных стороны, то он будет равенОтсюда находим сторону фигуры Площадь квадрата по обычной формуле считается так: .
Формула площади квадрата через периметр выводится из значения периметра. Периметр – это сумма длин всех сторон фигуры. Т.к. в квадрате 4 равных стороны, то он будет равенОтсюда находим сторону фигуры Площадь квадрата по обычной формуле считается так: .
Рассмотрим пример расчета площади квадрата через периметр.
Находим сторону:
Теперь рассчитаем площадь:
Площадь данного квадрата равна 16 .
Онлайн калькулятор длины стороны вписанного в круг квадрата. Как узнать длину стороны вписанного в круг квадрата.
При помощи нашего калькулятора вы легко сможете узнать длину стороны вписанного в круг квадрата.
Для того что бы найти длину стороны вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
c2 = 2a2,
Таким образом
a = √c2/2
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
D = c
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=2√S/π
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=P/π
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=2R
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
c=D
мы можем узнать длину сторон квадрата используя теорему Пифагора
a = √c2/2
Как вычислить коэффициент уменьшения вписанного в квадрат квадрата под углом n градусов?
На форме расположен родительский контейнер-квадрат. В нем есть вписанный элемент — тоже квадрат, повернутый на произвольный n-угол при помощи CSS
transform:rotate(Ndeg) где N — угол от 0 до 360. При этом нужно, чтобы вписанный квадрат касался родительского контейнера и не выходил за его границы — для этого применяется transform:scale(func(N)) где func(N) — функция, возвращающая коэффициент трансформации для заданного угла.
Таблицы коэффициентов
const tbl={
0:1,
1:0.98,
2:0.96,
3:0.95,
4:0.93,
5:0.92,
6:0.91,
7:0.9,
8:0.89,
9:0.87,
10:0.86,
11:0.85,
12:0.84,
13:0.83,
14:0.82,
15:0.81,
16:0.8,
17:0.79,
18:0.79,
19:0.78,
20:0.77,
21:0.765,
22:0.76,
23:0.75,
24:0.755,
25:0.75,
26:0.745,
27:0.74,
28:0.735,
29:0.7325,
31:0.725,
32:0.72,
33:0.7175,
34:0.715,
35:0.7155,
36:0.716,
37:0.713,
38:0.71,
39:0.7075,
40:0.705,
41:0.705,
42:0.705,
43:0.705,
44:0.705,
45:0.7,
46:0.705,
47:0.705,
48:0.705,
49:0.705,
50:0.705,
51:0.7075,
52:0.71,
53:0.7125,
54:0.715,
55:0.7155,
56:0.716,
57:0.718,
58:0.72,
59:0.725,
60:0.
 73,
73,61:0.7325,
62:0.735,
63:0.74,
64:0.745,
65:0.7475,
66:0.75,
67:0.755,
68:0.76,
69:0.765,
70:0.77,
71:0.78,
72:0.79,
73:0.79,
75:0.81,
76:0.82,
77:0.83,
78:0.84,
79:0.85,
80:0.86,
81:0.87,
82:0.89,
83:0.9,
84:0.91,
85:0.92,
86:0.93,
87:0.95,
88:0.96,
89:0.98,
90:1,
}
НО, хранить массив вручную высчитанных коэффициентов (с точностью в 4 знака) как-то думается мне совсем не верный путь. Должна же быть какая-то формула для расчета коэффициента исходя из того что мы знаем угол поворота и все параметры родительского контейнера?
7 способов найти площадь прямоугольника
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.

5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
Критерий хи-квадрат Пирсона | Lit-review.
 ru (НМА Литобзор) обзоры, статистика для медицины
ru (НМА Литобзор) обзоры, статистика для медицины
Хи-квадрат Пирсона один из самых популярных статистических критериев для анализа качественных данных (номинальных, порядковых, ранговых), анализа частот. Однако, как и у каждого статистического критерия у хи-квадрата есть свои собственные правила применения метода, его интерпретации. Для того, чтобы Вы могли успешно овладеть этим ценнейшим статистическим инструментом сравнения статистических совокупностей по качественным данным предлагаем Вам ознакомиться с этой учебной статьей.
Правила использования хи-квадрата Пирсона
Условия применения хи-квадрата Пирсона
Как рассчитывать хи-квадрат Пирсона
Учет степеней свободы при применении хи-квадрата Пирсона
Пример корректной интерпретации хи-квадрата Пирсона
Как использовать хи-квадрат Пирсона?
Хи-квадрат используется прежде всего для анализа таблиц сопряженности (вид таблицы, которая учитывает совместное влияние фактора на исход, данные в таблице сопряженности должны быть представлены в виде частоты номинальных данных или интервалами, но не непрерывными количественными величинами).
Таблицы сопряженности могут принимать различные формы, простейшая таблица сопряженности выглядит следующим образом:
| Исход есть | Исхода нет | Всего | |
| Фактор риска есть | A | B | A+B |
| Фактора риска нет | C | D | C+D |
| Всего | A+C | B+D | A+B+C+D |
Как заполнить таблицу сопряженности? Обратимся к простому примеру:
Например, Вы хотите с помощью таблицы сопряженности и как следствия хи-квадрата Пирсона выяснить есть ли различия в частоте артериальной гипертонии в группах курящего и некурящего населения. Предполагается, что по остальным параметрам Ваши группы равномерны и превалирующим фактором риска развития артериальной гипертензии будет именно курение.
Для проведения исследования на основании ретроспективных данных (дизайн: случай-контроль) были отобраны две группы исследуемых — в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую группу вошли 80 некурящих такого же возраста, пола, и социального уровня (прочие систематически ошибки случайны).
В первой группе у 40 человек отмечалась артериальная гипертензия. Во второй — у 32 человек. Соответственно, референсное (нормальное) артериальное давление в группе «курильщиков» наблюдалось у 30 человек (70 — 40 = 30), а в группе «некурящих» нормальное АД наблюдалось у 48 (80 — 32 = 48).
Имея эти данные мы можем заполнить простейшую таблицу сопряженности:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
АД- артериальное давление
Как видно из таблицы: каждая строка соответствует группе пациентов, которая подвергается влиянию фактора, каждый столбец, в свою очередь, обозначает частоту исходов в группе (к примеру: произошло/ не произошло, как в нашем примере).
Таблицы сопряженности служат удобным средством визуализации комбинации частот «фактор- исход» и субстратом для расчета хи-квадрата Пирсона, который в нашем случае сможет дать статистически точный ответ о случайности или не случайности наших находок.
Условия применения статистического критерия хи-квадрата Пирсона
- Тип данных: параметры должны быть качественными цельночисленными частотами, измеренными в номинальной шкале (Например, тип диагноза)
бинарными (пол: мужской/женский, наличие или отсутствие заболевания)
порядковыми (степень артериальной гипертензии),
- Желательно, чтобы общее количество наблюдений было более 20,
- Ожидаемая частота, соответствующая нулевой гипотезе должна быть более 5, если ожидаемое явление принимает значение менее 5, то необходимо использовать точный Критерий Фишера.
- Для четырехпольных таблиц (2х2): Если ожидаемое значение принимает значение менее 10 (а именно 5<x<10), необходим расчет поправки Йетса таблиц сопряженности
- Сравниваемые частоты должны быть примерно одного размера
- Сопоставляемые группы должны быть независимыми (то есть единицы наблюдения в них разные, в отличие от связанных групп, анализирующих изменения «до-после» у одних и тех единиц наблюдений до и после вмешательства.
 Для таких ситуаций существует отдельный тест МакНемара (McNemar)
Для таких ситуаций существует отдельный тест МакНемара (McNemar)
Запрещается: использовать хи-квадрат для анализа непрерывных абсолютных данных, процентов и долей
Как рассчитать критерий хи-квадрат Пирсона?
Для оценки достоверности различий по методу хи-квадрата Пирсона (критерий соответствия, коэффициент согласия) анализируется различия между реальной существующими частотами в группах (Observed) и рассчитываемыми по формуле ожидаемыми «гипотетическими» частотами, которые соответствуют распределению хи-квадрат. При малом различии ожидаемых и наблюдаемых частот (хи-квадрат не достиг своего критического значения) мы принимаем нулевую гипотезу об отсутствии различий. Если же различия оказываются существенными (критическое значение хи-квадрата достигаются для заданного числа степеней свободы) мы отвергаем нулевую гипотезу и говорим о наличии статистически значимых различий.
Чем больше теоретические числа, рассчитанные на основе Но-гипотезы, будут отличаться от фактических, тем более «хи -квадрат» будет отличаться от 0, тем с большей вероятностью можно отклонить Но-гипотезу и говорить о статистической достоверности имеющихся различий в сравниваемых совокупностях.
Основная формула для расчета хи-квадрата Пирсона:
Зачем учитывать количество степеней свободы при расчете хи-квадрата?
Для того, чтобы не утомлять читателя пространными разъяснениями «о сумме квадратом нормально распределенных случайных величин» скажем лишь, что оценка критического значения хи-квадрата зависит от степени свободы изменения частот, что это значит на практике для пользователя хи-квадрата? То, что чем более многопольная таблица перед Вами, тем больше степеней свободы, чем она меньше, тем меньше. Формула расчета хи-квадрата следующая:
Degree of freedom (d.f.) = (c-1)(r-1)
Column (c) – количество столбцов частотами, r- количество строк с частотами.
Таким образом, количество степеней свободы для стандартной 2х2 таблицы сопряженности составит:
d.f. = (2-1)*(2-1)=1
и так далее.
Примеры расчета хи-квадрата Пирсона
Пример 1:
Необходимо определить наличие влияния предшествующей степени нарушения кровообращения на исход комиссуротомии (хирургическое разделение спаек при стенозе клапанного отверстия сердца). Пациенты поступали на комиссуротомию с различными исходными уровнями нарушения кровообращения. После комиссуротомии пациенты были выписаны с различными исходами операции.
Пациенты поступали на комиссуротомию с различными исходными уровнями нарушения кровообращения. После комиссуротомии пациенты были выписаны с различными исходами операции.
Фактор: Степень нарушения кровообращения
Исход: Результативность операции
Таблица: наблюдаемые (Observed) частоты распределения влияния степени нарушения кровообращения на результаты операции комиссуротомии
| Степень нарушения кровообращения | Всего больных | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 30 | 20 | 8 | 2 |
| III | 80 | 43 | 20 | 17 |
| IV | 60 | 10 | 40 | 10 |
| Всего | 170 | 73 | 68 | 29 |
| H0-гипотеза | 100% | 43% | 40% | 17% |
Первый этап
Расчет ожидаемых (Expected) величин (на основании групповых частот)
Второй этап
Сопоставление наблюдаемых и ожидаемых частот с нахождением их разницы (O-E)
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | +7 | -4 | -3 |
| III | +9 | -12 | +3 |
| IV | -16 | +16 | 0 |
| Всего | 0 | 0 | 0 |
Третий этап
Рассчитываем сумму отношений квадрата разности значений и делим ожидаемые данные (хи-квадрат) (O-E)2/E
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 49/13=3,77 | 16/12=1,33 | 9/5=1,80 |
| III | 81/34=2,38 | 144/32=4,50 | 9/14=0,64 |
| IV | 256/26=9,85 | 256/24=10,66 | 0/10*=0,10 |
| Всего | 16 | 16,49 | 2,54 |
как видно из данной таблицы одно из ожидаемых значений равно 0, в данном случае будет подставлена 1, корректнее применить точный критерий Фишера (см. Условия применения хи-квадрата Пирсона)
Условия применения хи-квадрата Пирсона)
Четвертый этап
Необходимо соотнести полученное значение хи-квадрата с критическим значением хи-квадрата.Возникает вопрос, откуда брать критическое значение? Критическое значение хи-квадрата, как и для большинства, статистических критериев зависит от степени свободы и уровня достоверности (alpha), который Вы выбираете.В нашем случае, наше количество степеней свободы равно (3-1)*(3-1)=4, уровень значимости, который мы хотим соблюсти равен 0,05Обратимся к таблице критических значение хи-квадрата:
- Xи-квадрат (для d.f.=4 p=0.05) = 9.488
- Xи-квадрат (для d.f.=4 p=0.01) = 13.27735,03 > 13,277;
- p<0,01
Пример корректной интерпретации: Предшествующая степень нарушения кровообращения влияет на исход комиссуротомии (однако! Мы не можем говорить о направленности связи, то есть: улучшает-ухудшает сказать не можем), оптимально указать степень свободы, точное значение хи-квадрата, если есть возможность рассчитать точное значение достоверности, то так же стоит указать и его или остановиться на критическом значении достоверности (p<0,05 или p<0,01 и так далее). В нашем случае:d.f.=4, x2=35,03, p< 0.01
В нашем случае:d.f.=4, x2=35,03, p< 0.01
Пример 2: Вернемся к нашему примеру с влиянием курения на развитие артериальной гипертензии:Исходная четырехпольная таблица:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
Для четырехпольных таблиц существует упрощенная формула расчета значения хи-квадрата:
| Исход + | Исход 0 | Всего | |
| Фактор + | a | b | a+b |
| Фактор 0 | c | d | c+d |
| Всего | a+c | b+d | N |
- x2= (40х48 – 32х30)х150 / (70)(80)(72)(78) = (1920 – 960)2х150/31449600 = 138240000/31449600 = 4,395
- Сравним полученное значение хи-квадрата с критическим значением (для степени свободы 1, и уровнем значимости 3,841)
Правильная интерпретация: Курение оказывает влияние на формирование повышенного артериального давления df=1, x2= 4,395, p<0,05
Заключение по хи-квадрату Пирсона
хи-квадрат Пирсона является удобным статистическим методом для анализа изменения частот, оформленными в таблицы сопряженности для несвязанных групп. Как и все статистически инструменты хи-квадрат Пирсона имеет свои правила, преимущества и ограничения применения. Будьте внимательны и хи-квадрат Пирсона Вас не разочарует.
Как и все статистически инструменты хи-квадрат Пирсона имеет свои правила, преимущества и ограничения применения. Будьте внимательны и хи-квадрат Пирсона Вас не разочарует.
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
влияние прививки на холерную инфекцию
В таблице ниже приведены сведения о числе людей, заболевших или не заболевших холерой, с указанием, была ли им сделана противохолерная прививка.
Фрагмент таблицы с исходными данными
Файл содержит данные по 2663 пациентам.
В первой переменной указано была ли сделана пациенту прививка, а во второй – был ли зафиксирован факт заболевания холерой после прививки.
Задача: Требуется выяснить, эффективна прививка или нет.
Мы критикуем прививку и выдвигаем гипотезу: связи между заболеваемостью и прививкой нет.
Наблюдаемые частоты: Для решения задачи построим таблицу сопряженности, т.е. сопряжем признаки:
Таблица с наблюдаемыми частотами
Четыре элемента таблицы, а именно 1022, 11, 1625, 5 — это частоты; мы имеем, таким образом, таблицу в виде квадрата вместо привычного ряда столбцов.
По ней строится критерий согласия хи-квадрат с некоторой выдвинутой гипотезой:
Нулевая гипотеза:
Переформулируем нашу задачу.
Значимо ли воздействие прививки на вероятность заболевания?
Попробуем принять в качестве нулевой гипотезы, что прививка не оказывает воздействия на заболевание и что видимый эффект от прививки есть результат случайных флуктуаций.
Мы должны, следовательно, сравнить элементы в таблице с соответствующими ожидаемыми элементами в предположении справедливости гипотезы.
Ожидаемые частоты.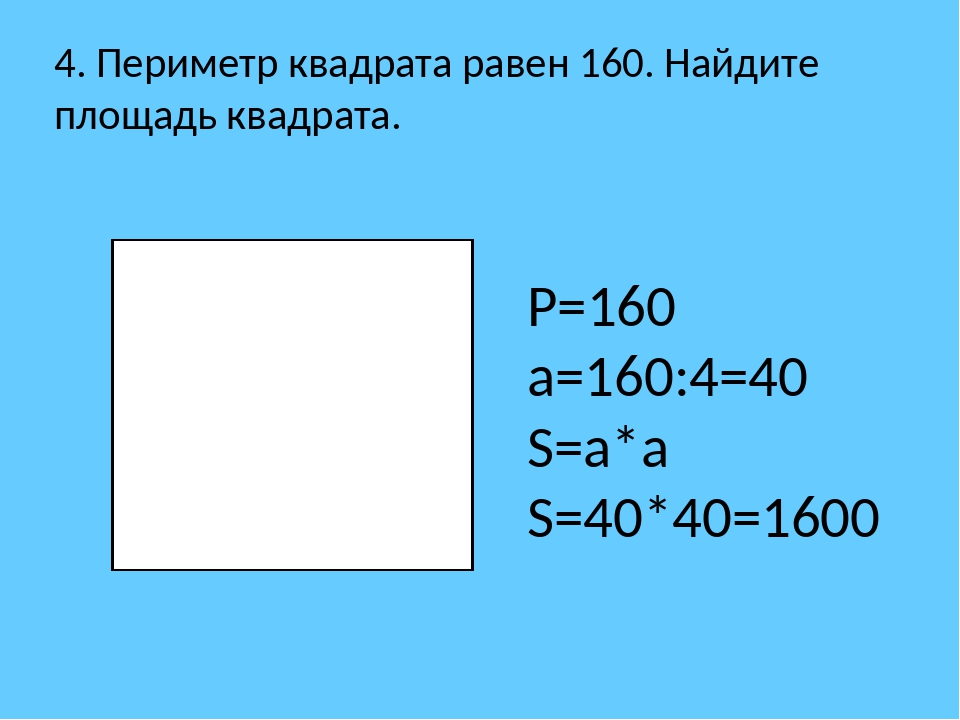 Из гипотезы следует, что для 2663 человек, находящихся в группе риска, ожидаемая доля заболевших после прививки будет той же, что и ожидаемая доля заболевших среди тех, кому прививку не делали; общее значение этих долей совпадает с долей заболевших во всей выборке, а именно p = 16/2663 (~0,006). Эти ожидаемые доли представлены в таблице ниже:
Из гипотезы следует, что для 2663 человек, находящихся в группе риска, ожидаемая доля заболевших после прививки будет той же, что и ожидаемая доля заболевших среди тех, кому прививку не делали; общее значение этих долей совпадает с долей заболевших во всей выборке, а именно p = 16/2663 (~0,006). Эти ожидаемые доли представлены в таблице ниже:
Подставляя, полученное значение p:
Таблица с ожидаемыми частотами
При нулевой гипотезе ожидаемая частота в любой ячейке может быть найдена умножением доли (p или 1-p) на маргинальное общее число соответствующей строки (1630 — для категории привитых, 1033 — для остальных).
В принципе, только один элемент следует вычислять умножением маргинально частоты на ожидаемую долю; остальные элементы находятся вычитанием.
Значение Xи-квадрат используется для оценки меры рассогласованности наблюдаемого и ожидаемого результата. Если, согласно нулевой гипотезе, ожидаемый результат будет сильно отличаться от наблюдаемых значений, значит стоит поставить под сомнение справедливость гипотезы.
Если, согласно нулевой гипотезе, ожидаемый результат будет сильно отличаться от наблюдаемых значений, значит стоит поставить под сомнение справедливость гипотезы.
Перед тем, рассчитывать значение хи-квадрат, рассмотрим некоторые особенности таблиц 2х2, которые заслуживают специального упоминания.
В некоторых случаях необходимо делать «поправку на непрерывность» (так называемая «поправка Йетса»). Такие расхождения могут возникать, когда в таблице встречаются малые частоты (меньше 10).
Математически, «поправка на непрерывность» уменьшает погрешность, возникающую при аппроксимации непрерывным распределением хи-квадрат точного выборочного распределения, которое является дискретным.
Вычислим значение хи-квадрат без поправки Йетса. Значение представляет собой сумму квадратов разностей наблюдаемой и ожидаемой частоты, деленную на соответствующую ожидаемую частоту:
(Смотрите значения в таблицах с наблюдаемыми и ожидаемыми частотами выше. )
)
Отметим, что в нашем случае, для более точного вычисления статистики хи-квадрат необходимо использовать поправку Йетса (пять пациентов заболели, несмотря на сделанную противохолерную прививку).
Поправка Йетса немного изменит таблицу наблюдаемых частот:
Модифицированная таблица с наблюдаемыми частотами
В модифицированной таблице частота «5» заменена на «5,5», а все остальные элементы изменены так, чтобы общие суммарные (маргинальные) частоты сохранились.
Отметим, что при такой модификации ожидаемые частоты остаются без изменения.
Теперь вычислим значение хи-квадрат с поправкой Йетса, пользуясь той же формулой, но в качестве наблюдаемых частот берем значения из модифицированной таблицы:
Чтобы оценить какова вероятность получить такое или большее значение хи-квадрат, при условии истинности нулевой гипотезы, необходимо вычислить уровень значимости (p-уровень).
Если он окажется маленьким (обычно берется меньше 0,05), то нулевую гипотезу следует отклонить.
Использование калькулятора таблиц сопряженности 2 на 2.Заполняем таблицу в интерактивном калькуляторе таблиц сопряженности 2х2
Согласно таблице наблюдаемых частот (номера групп и вариантов заменяем на удобные для нас обозначения).
- Устанавливаем галочку напротив поправки Йетса (поправка для случая малых частот).
- Нажимаем кнопку «Вычислить».
Полученные результаты (p-уровень значимости ~ 0.014 < 0.05) говорят о том, что нулевую гипотезу о независимости следует отвергнуть: прививка в действительности имеет некоторый предупредительный эффект.
В нашем случае, значение величины «Отношение шансов» говорит о том, что шанс заболеть у группы непривитых больше, чем у группы привитых. Этот факт подтверждается проведенным выше анализом.
Таким же образом могут быть проверены гипотезы о прививках против гриппа, эффективности диспансеризации и т.д.
В начало
Содержание портала
Расчитать индекс массы тела, калькулятор ИМТ
Индекс массы тела (ИМТ)
Индекс массы тела является показателем отношения веса и роста человека. Данный параметр помогает определить отклонения от нормальной массы тела в ту или иную сторону. Лишний вес опасен для человеческого здоровья, поскольку часто приводят к сердечным заболеваниям. Онлайн калькулятор индекса массы тела позволяет быстро и точно узнать, насколько ваш показатель веса соответствует норме. Чтобы рассчитать индекс массы тела необходимо выбрать в представленном сервисе свой рост и вес.
Индекс массы тела для женщин считается нормальным, если показатель входит в диапазон от 20 до 22. Для мужчин этот показатель должен быть от 23 до 25. Статистика показывает, что люди, у которых данный показатель остается в пределах 18-22, живут в среднем дольше, чем те, у кого есть проблемы с весом.
Если показатель ИМТ превышает 25, то это сигнал, что вам нужно менять свой образ жизни. Важно отметить, что используемая формула для расчета индекса массы тела может переоценить показатель ожирения для людей атлетического сложения, поскольку вычисления не учитывают мышечную массу.
Индекс массы тела стал особенно актуален в западных странах, где проблема с ожирением встала достаточно остро. В самом начале расчет имт разрабатывался для социологических исследования, поэтому ставить медицинский диагноз с помощью этих расчетов не совсем правильно.
Однако доступность и простота расчета сделала данный калькулятор очень популярным среди населения. Если индекс превышает число 30, то это с большой долей вероятности говорит об ожирении.
Нужно понимать, что индекс массы тела не годится для постановления диагноза, но он может помочь в качестве контроля в процессе опробования новой фитнес-программы или диеты.
Калькулятор ИМТ определит точку отсчета и позволит прослеживать изменения веса тела.
Формула расчета индекса массы тела (ИМТ)
Для того, чтобы узнать свой ИМТ необходимо лишь свой вес в килограммах разделить на квадрат роста в метрах.
ИМТ = ВЕС / РОСТ2
Формула не учитывает пол и возраст человека, несмотря на то что ИМТ мужчин выше чем ИМТ женщин, а также ИМТ выше у людей среднего возраста, а у детей и пожилых людей этот показатель ниже.
Сводная таблица значений
Интерпретация показателей ИМТ, в соответствии с ремомендациями Всемирной Организации Здравоохранения (ВОЗ)
| 16 и менее | Выраженный дефицит массы тела |
| 16—18,5 | Недостаточная (дефицит) масса тела |
| 18,5—25 | Норма |
| 25—30 | Избыточная масса тела (предожирение) |
| 30—35 | Ожирение первой степени |
| 35—40 | Ожирение второй степени |
| 40 и более | Ожирение третьей степени (морбидное) |
x²
Использование калькулятора
Найдите квадрат числа n.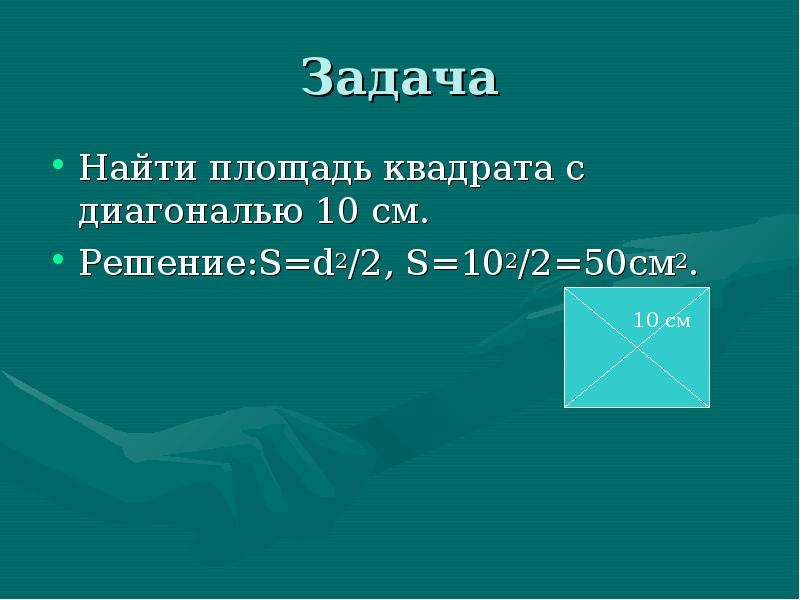 Введите положительные или отрицательные целые числа или десятичные числа или научную нотацию E.
Введите положительные или отрицательные целые числа или десятичные числа или научную нотацию E.
Возведение в квадрат отрицательных чисел
Если вы хотите возвести в квадрат отрицательные числа в этом калькуляторе, используйте круглые скобки при вводе.
- -5² означает -(5 × 5) = -25
- -(5)² означает -(5 × 5) = -25
- (-5)² означает (-5 × -5) = 25
Например, чтобы возвести -4 в квадрат, введите его в калькулятор как (-4) со скобками.Чтобы взять отрицательное число 4 в квадрате, введите его как -(4) или -4.
Когда выражение степени записывается с положительным значением, таким как 4², большинству легко понять, что это означает 4 × 4 = 16
Однако, когда оно записывается как отрицательное значение без круглых скобок, значение неоднозначно. Для разных людей это имеет разное значение.
Различные возможные интерпретации -4²:
1. минус (4 в квадрате) равен -4² = -(4)² = -(4 × 4) = -16
2.(минус 4) в квадрате равен (-4)² = (-4 × -4) = 16
Используйте круглые скобки, чтобы четко указать, какое вычисление вы действительно хотите выполнить.
В квадрате
Число n в квадрате записывается как n² и n² = n × n. Если n — целое число, то n² — полный квадрат.
Например, 3 в квадрате записывается как 3², а 3² = 3 × 3 = 9. Девять — это правильный квадрат.
Числа от 0 до 10 в квадрате
- 0 в квадрате равно 0² = 0 × 0 = 0
- 1 в квадрате равно 1² = 1 × 1 = 1
- 2 в квадрате равно 2² = 2 × 2 = 4
- 3 в квадрате равно 3² = 3 × 3 = 9
- 4 в квадрате равно 4² = 4 × 4 = 16
- 5 в квадрате равно 5² = 5 × 5 = 25
- 6 в квадрате равно 6² = 6 × 6 = 36
- 7 в квадрате равно 7² = 7 × 7 = 49
- 8 в квадрате равно 8² = 8 × 8 = 64
- 9 в квадрате равно 9² = 9 × 9 = 81
- 10 в квадрате равно 10² = 10 × 10 = 100
Ссылки/Дополнительная литература
Гудман, Лен и
Вайсштейн, Эрик В. «Квадратное число». От MathWorld — Веб-ресурс Wolfram.
Квадратный номер
«Квадратное число». От MathWorld — Веб-ресурс Wolfram.
Квадратный номер
Википедия «Квадратное число» на https://en.wikipedia.org/wiki/Квадратное_число
Калькулятор площади Пеннета| Science Primer
Квадрат Пеннета Multi-locus Punnett Squares can be hard to draw and are difficult to interpret. The large number of genotypes possible with multi-locus crosses makes it easier to avoid drawing the square. Instead, the probability of specific genotypes arising are calculated using equations. «> * показывает генотип * , который могут произвести две особи при скрещивании. Чтобы нарисовать квадрат, запишите все возможные комбинации аллелей Diploid organisms, such as humans, have two sets of chromosomes and therefore, two alleles for each gene. An organism’s genotype is a description of the alleles present at specific genetic loci.»> * , которые один из родителей может внести в свои гаметы, в верхней части прямоугольника и все возможные комбинации аллелей от другого родителя в левой части.Комбинации аллелей сверху и по бокам становятся метками для строк и столбцов внутри квадрата. Заполните генотипы в квадрате, заполнив его аллелями от каждого родителя. Поскольку вероятность возникновения всех комбинаций аллелей одинакова, квадрат Пеннета предсказывает вероятность скрещивания, дающего каждый генотип.
Один признак Punnett Square отслеживает два аллеля для каждого родителя. Квадрат имеет две строки и два столбца. Добавление дополнительных черт увеличивает размер площади Пеннета.3). Независимый набор обычно означает, что гены находятся на разных хромосомах The chromosome is considered the basic unit of DNA replication. Prokaryotic cells typically contain one (or a few) circular chromosomes. Eukaryotic cells with their much larger genomes have multiple linear chromosomes. The length and linear nature of Eukaryotic chromosomes increases the complexity involved in storing the genetic material and passing the proper amount to each daughter cell during cell replication.»> * s. Если гены двух признаков находятся в одной и той же хромосоме, аллели каждого признака всегда будут появляться в одних и тех же комбинациях (без учета рекомбинации).
С одной строкой или столбцом для каждой комбинации аллелей общее количество ячеек в квадрате Пеннета равно количеству строк, умноженному на количество столбцов. Квадраты Пеннета с несколькими признаками большие. В квадрате с тремя признаками 64 клетки. В квадрате с четырьмя признаками 256 клеток.
Генотип в каждой коробке с одинаковой вероятностью может быть получен в результате скрещивания.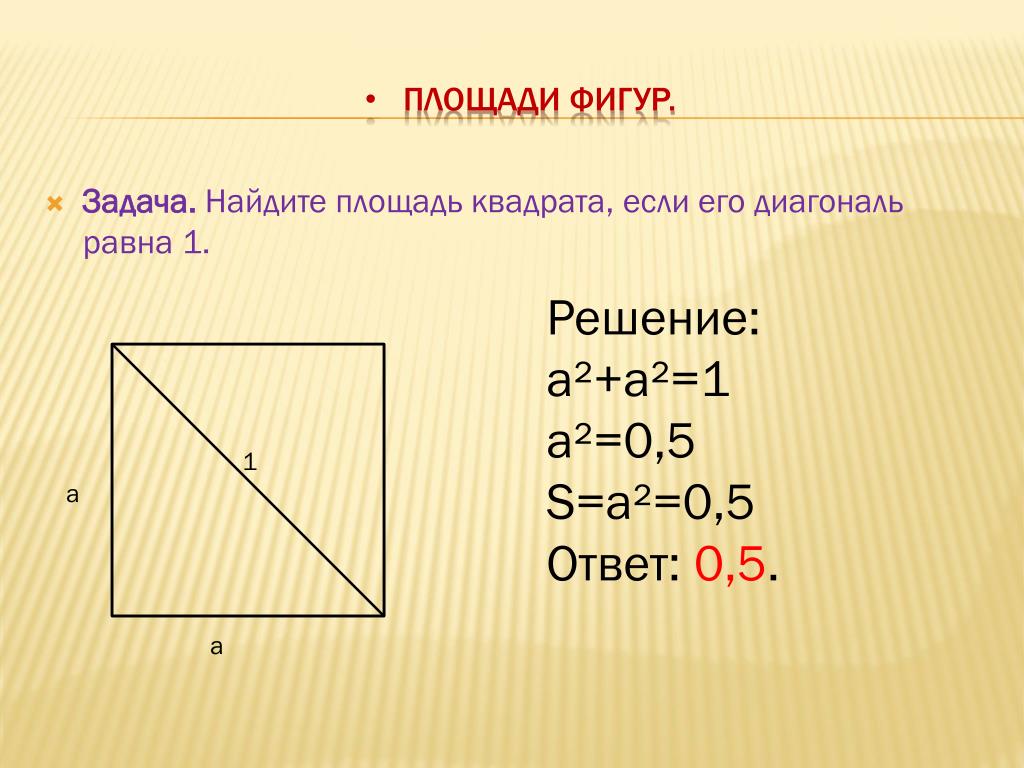 Квадрат Пеннета с двумя признаками имеет 16 ячеек. Вероятность скрещивания, дающего генотип в любой коробке, составляет 1 к 16. Если один и тот же генотип присутствует в двух коробках, вероятность его появления удваивается до 1/8 (1/16 + 1/16).
Квадрат Пеннета с двумя признаками имеет 16 ячеек. Вероятность скрещивания, дающего генотип в любой коробке, составляет 1 к 16. Если один и тот же генотип присутствует в двух коробках, вероятность его появления удваивается до 1/8 (1/16 + 1/16).
Если один из родителей является гомозиготным по одному или нескольким признакам, квадрат Пеннета по-прежнему содержит такое же количество клеток, но общее количество уникальных комбинаций аллелей равно 2, возведенному в степень числа признаков, по которым родитель является гетерозиготным. .
Обычно обсуждаемый квадрат Пеннета — это дигибридное скрещивание. Дигибридное скрещивание отслеживает два признака. Оба родителя гетерозиготны, и по одному аллелю каждого признака проявляет полное доминирование *. Это означает, что оба родителя имеют рецессивные аллели, но проявляют доминантный фенотип. Соотношение фенотипов, предсказанное для дигибридного скрещивания, составляет 9:3:3:1. Из шестнадцати возможных комбинаций аллелей:
Соотношение фенотипов, предсказанное для дигибридного скрещивания, составляет 9:3:3:1. Из шестнадцати возможных комбинаций аллелей:
- Девять комбинаций дают потомство с обоими доминирующими фенотипами.
- Каждая из трех комбинаций дает потомство с одним доминантным и одним рецессивным фенотипом.
- Одна комбинация дает двойное рецессивное потомство.
Более простая картина возникает, когда один из родителей гомозиготен по всем признакам. В этом случае аллели, внесенные гетерозиготным родителем, определяют всю изменчивость.Скрещивание двух признаков между гетерозиготным и гомозиготным индивидуумом дает четыре фенотипа, каждый из которых имеет одинаковую вероятность появления.
Можно рассмотреть более сложные узоры. В крайнем случае, когда для каждого признака существует более двух аллелей, а родители не обладают одинаковыми аллелями, общее количество генотипов равно количеству клеток в квадрате Пеннета.
В крайнем случае, когда для каждого признака существует более двух аллелей, а родители не обладают одинаковыми аллелями, общее количество генотипов равно количеству клеток в квадрате Пеннета.
Можно построить квадраты Пеннета для более чем двух признаков, но их сложно нарисовать и интерпретировать.Квадрат Пеннета для тетрагибридного скрещивания содержит 256 ячеек с 16 фенотипами и 81 генотипом. Третий аллель любого из признаков увеличивает число генотипов с 81 до 108.
Учитывая эту сложность, квадраты Пеннета — не лучший метод расчета соотношений генотипов и фенотипов для скрещиваний, включающих более одного признака.
Проверьте свое понимание с помощью набора задач калькулятора площади Пеннета.
Обзор видео
- Иллюстрации
- Наборы задач
Как вычислить квадрат в SQL
Проблема:
Вы хотите найти квадрат числа в SQL Server.
Пример:
Вы хотите вычислить квадрат каждого числа в столбце числа из таблицы данных .
Решение 1:
ВЫБРАТЬ номер, КВАДРАТ(число) КАК квадрат ИЗ данных;
Решение 2:
ВЫБРАТЬ номер, номер * номер КАК квадрат ИЗ данных;
Решение 3:
ВЫБРАТЬ номер, МОЩНОСТЬ(число, 2) КАК квадрат ИЗ данных;
Результат:
| номер | квадрат |
|---|---|
| 3 | 9 |
| 1 | 1 |
| 0.5 | 0,25 |
| 0 | 0 |
| -2 | 4 |
Обсуждение:
Одним из способов вычисления квадрата числа в SQL Server является использование функции SQUARE() . Он принимает число в качестве аргумента и возвращает число в квадрате.
Квадрат числа также можно вычислить как число * число , поэтому другой способ — просто использовать это выражение; никаких дополнительных функций не требуется.
Третий способ вычисления квадрата числа заключается в использовании функции POWER() . Эта функция принимает число и степень в качестве аргументов и возвращает усиленное число. Здесь вам нужно вычислить квадрат, поэтому степень равна 2. Итак, у вас есть POWER(number, 2) .
Точно так же вы можете вычислить любую степень числа, например. третья власть.
ВЫБРАТЬ POWER(число, 3) КАК третья_степень ИЗ данных;
Результат будет:
| номер | третья_степень |
|---|---|
| 3 | 27 |
| 1 | 1 |
| 0.5 | 0,125 |
| 0 | 0 |
| -2 | -8 |
Интерактивные тесты хи-квадрат
Интерактивный инструмент для расчета критерия хи-квадрат согласия и независимости.
© 2010-2022,
Кристофер Дж. Причер
Расчет теста хи-квадрат: интерактивный инструмент для расчета критерия согласия и независимости хи-квадрат
Кристофер Дж.Проповедник ( Университет Вандербильта )
Как цитировать эту страницу
Эту веб-утилиту можно цитировать в стиле APA следующим образом:
Проповедник, KJ (2001, апрель). Расчет теста хи-квадрат: интерактивный инструмент для расчета теста хи-квадрат на соответствие и независимость [Компьютерное программное обеспечение]. Доступно на http://quantpsy.org.
Цель этой страницы
Эта веб-страница предназначена для краткого ознакомления с тестами хи-квадрат независимости и согласия.Эти тесты используются для обнаружения групповых различий с использованием данных о частоте (количестве). Эта страница также предоставляет интерактивный инструмент, позволяющий исследователям проводить тесты хи-квадрат для своих собственных исследований. В любом вводном тексте по прикладной статистике должно быть хорошее описание этих тестов хи-квадрат, но ниже следует краткое введение.
О тесте независимости хи-квадрат
Часто исследователь хочет увидеть, варьируется ли частота случаев, обладающих некоторым качеством, между уровнями данного фактора или между комбинациями уровней двух или более факторов.В таких ситуациях подходящим тестом является критерий согласия хи-квадрат согласия или критерий хи-квадрат независимости для k групп .
Как это делается
Для проведения теста хи-квадрат исследователь вводит наблюдаемые частоты, соответствующие комбинациям уровней соответствующих факторов (здесь они называются «состояние» и «группа», но это обозначения для удобства). Затем вычисляются суммы элементов в строках и столбцах (назовем эти маргинальными Ns ).Критерий независимости хи-квадрат используется для проверки нулевой гипотезы о том, что частота внутри ячеек соответствует ожидаемой, учитывая эти предельные значения N. Критерий согласия хи-квадрат используется для проверки гипотезы о том, что общая выборка N равномерно распределена между всеми уровнями соответствующего фактора.
Ожидаемое значение в каждой ячейке, если истинно нулевое условие (т. е. если факторы не оказывают существенного влияния на наблюдаемые частоты в генеральной совокупности), представляет собой просто произведение суммы по строке и суммы по столбцу, деленное на общую выборку N для критерий независимости и N, деленное на количество уровней одного фактора для критерия согласия.Если O ij — это наблюдаемая частота, а E ij — ожидаемая частота для ячейки, соответствующей условию i th , а j th группа — это квадрат, :
Если есть только один интересующий фактор с уровнями ( k > 1), будет работать та же формула, где i или j установлены в 1. Представленный здесь тест можно использовать для проверки только 1- или двумерные массивы.Возможны массивы более высокой размерности, они основаны на том же принципе и даже используют ту же формулу, хотя они включают несколько вложенных сумм.
Как пользоваться этой страницей
Введите наблюдаемые частоты в белые ячейки. Я понимаю, что не так уж много дизайнов включают ровно 10 условий и 10 групп — если ваш дизайн меньше, то выберите некоторое подмножество строк и столбцов, в которое нужно ввести ваши данные. Например, если ваш дизайн (2 x 3), вы можете ввести свои данные в 6 ячеек в верхней левой части таблицы данных, определенных первыми двумя условиями и первыми тремя группами.Вы можете выбрать любое подмножество строк и столбцов для своих данных. Вы также можете оставить ячейки, соответствующие наблюдаемым частотам, нулевыми. Допускаются нецелочисленные наблюдаемые частоты, хотя трудно представить, как их можно получить в реальных исследованиях.
Если вы выполняете тест на соответствие, вы можете выбрать ввод данных в любом отдельном столбце или строке. Однако наблюдаемые нулевые частоты должны быть явно включены (т. е. вам нужно фактически ввести «0» в эти ячейки, в противном случае предполагается, что эти ячейки не являются частью вашего проекта). После того, как вы ввели свои данные, нажмите кнопку Calculate и ожидайте увидеть результат в бежевых ячейках (они должны быть белыми, если вы используете старые версии Netscape). Не паникуйте, если вы видите научное обозначение для вашего значения p — это просто означает, что p — это , на самом деле маленькое.
После того, как вы ввели свои данные, нажмите кнопку Calculate и ожидайте увидеть результат в бежевых ячейках (они должны быть белыми, если вы используете старые версии Netscape). Не паникуйте, если вы видите научное обозначение для вашего значения p — это просто означает, что p — это , на самом деле маленькое.
Этот инструмент также дает хи-квадрат, включающий поправку Йейтса для непрерывности . Эта коррекция часто используется для повышения точности выборочного распределения хи-квадрат при нулевых условиях.Вероятно, его следует использовать только для тестов 1-df (т. е. тестов на соответствие или тестов независимости с таблицами непредвиденных обстоятельств 2×2), поэтому используйте его на свой страх и риск для тестов с df>1.
Предупреждения
Использование тестов хи-квадрат является неуместным , если любая ожидаемая частота ниже 1 или если ожидаемая частота меньше 5 более чем в 20% ваших клеток. Ячейка состояния в нижней части таблицы сообщит вам, есть ли проблема. В случае 2 x 2 критерия независимости хи-квадрат ожидаемые частоты менее 5 обычно считаются приемлемыми, если используется поправка Йейтса.
В случае 2 x 2 критерия независимости хи-квадрат ожидаемые частоты менее 5 обычно считаются приемлемыми, если используется поправка Йейтса.
«Пользовательские» ожидаемые частоты
При использовании критерия согласия хи-квадрат иногда бывает полезно указать собственные ожидаемые частоты. Если для этого есть теоретическая причина, следующая таблица позволит вам ввести свои собственные E ij . Допускаются нецелые ожидаемые частоты. Используйте столько ячеек в этой таблице, сколько необходимо, убедившись, что (1) предельная сумма одинакова как для наблюдаемых, так и для ожидаемых частот, (2) нет ожидаемых частот меньше 1 и (3) не более 20% ожидаемых частот меньше 5.Если частота введена в ячейку Наблюдаемая, то частота также должна быть введена в соответствующую ячейку Ожидаемая (и наоборот).
Благодарности
Исходная версия опубликована в апреле 2001 г. Я благодарю Нэнси Бриггс и Ребекку Уайт за помощь в написании сценариев, а также Дерека Рукера, Джеффри Леонарделли и Тома Найгрена за тестирование ранних версий этой страницы. для вычисления площади.2)
х1 х2 х3
[1,] 1 4 4
[2,] 4 9 4
[3,] 9 16 4
для вычисления площади.2)
х1 х2 х3
[1,] 1 4 4
[2,] 4 9 4
[3,] 9 16 4
Все в порядке. Дайте мне знать, если вы используете какую-либо другую функцию для вычисления квадрата.
Подпишитесь на рассылку новостей и КОММЕНТАРИЙ ниже!
rbind в r-Объединить векторы, матрицы или кадры данных по строкам »
Пост «Вычислить площадь в R» впервые появился на finnstats.
РодственныеКак рассчитать площадь дома?
Существует стандарт для измерения площади в квадратных футах, где вам необходимо сделать максимально точные расчеты.Самый первый шаг — понять, насколько длинное и широкое ваше пространство.
Точное определение размеров комнаты по длине и ширине, включая каждый угол, поможет вам правильно измерить всю площадь.
Ниже приведено руководство по расчету квадратных футов вашего дома или комнаты. Сначала начнем с комнаты.
Для измерения площади и периметра стандартной квадратной или прямоугольной комнаты вам необходимо знать основную и простую формулу.
Площадь = Длина * Ширина (Д * Ш)
Периметр = (Длина) + (Ширина)
Площадь — это другое название квадратных метров. Таким образом, существует основной метод оценки квадратных футов комнаты.
Площадь в квадратных футах
–
Ориентировочная стоимость
–
Основной метод оценки площади в квадратных футах9000 можно продолжить расчеты.Найдя площадь квадратной или прямоугольной комнаты, вам нужно всего лишь перемножить длину и ширину, и вы получите квадратные метры площади вашей комнаты.
Квадратные метры = длина * ширина
Давайте возьмем один пример, предположим, что расстояние между первыми двумя стенами вашей комнаты составляет 13 футов, а расстояние между двумя другими стенами составляет 15 футов.
В этом случае ваша длина и ширина будут 15 футов и 13 футов. Вы умножаете оба, чтобы в результате получить площадь комнаты в квадратных футах.
15 футов * 13 футов = 195 квадратных футов
Помимо футов, вы также можете измерять в дюймах и конвертировать их в футы для расчета площади комнаты.Но не все комнаты могут быть прямоугольными и квадратными.
Они также могут быть неправильной формы. Также в некоторых номерах есть шкафы и столы с диванными гарнитурами. Таким образом, вы должны сделать детализацию в измерениях квадратных футов.
Оценка различных типов комнат Квадратные футыМы уже видели, как вычислить площадь квадратной или прямоугольной комнаты. Таким образом, чтобы узнать размеры различных типов комнат, ниже приведена хитрость —
Комнаты со шкафами и диванами Комнаты со шкафами и диванами обычно похожи на прямоугольные комнаты с небольшими прямоугольными надстройками.Таким образом, вычислите квадратные метры каждого прямоугольника и сложите их все вместе. Например,
Например,
Ваш шкаф имеет размеры 7 на 7 футов в длину и ширину соответственно. Размеры дивана 8 футов на 3 фута в длину и ширину. Итак, есть два одинаковых дивана в форме буквы L.
Размер и ширина вашей комнаты 12 футов на 12 футов. Итак, что вам нужно сделать, чтобы рассчитать площадь открытого пространства комнаты, то есть площадь ковра?
Квадратные метры будут суммой площади дивана и площади шкафа, которые затем будут вычтены из площади комнаты.
Площадь дивана = длина дивана * ширина дивана = 8 * 3 = 24 кв. фута
Площадь шкафа = длина шкафа * ширина шкафа = 7 * 7 = 49 кв. футов
Площадь комнаты = длина комнаты * Ширина комнаты = 12 * 12 = 144 кв. фута
Теперь
Сумма площади дивана и шкафа = площадь дивана + площадь шкафа = 24 + 49 = 73 кв. фута
Оставшаяся площадь = площадь площади комнаты – Площадь дивана и шкафа = 144 – 73 = 71 кв. фут
Комнаты неправильной формы Если у вас есть комнаты неправильной формы, вам нужен стандартный инструмент для измерения, применяемый к комнатам неправильной формы. Вам нужно разделить вашу комнату на отдельные комнатные секции, которые легко оценить самостоятельно, а затем просуммировать, чтобы получить результаты. Если в вашей комнате много углов, используйте формулу треугольника — это просто половина прямоугольника или квадрата.
Вам нужно разделить вашу комнату на отдельные комнатные секции, которые легко оценить самостоятельно, а затем просуммировать, чтобы получить результаты. Если в вашей комнате много углов, используйте формулу треугольника — это просто половина прямоугольника или квадрата.
Итак, для помещения неправильной формы формула выглядит так:
квадратных футов основной секции = длина * ширина
квадратных футов малой секции (1, 2, 3 и т. д.) = длина * ширина
квадратных метров площади помещения = Квадратные футы основной секции + Квадратные футы отдельных секций.
Возьмем пример,
Основная часть комнаты имеет размеры 12 на 12 футов, а другая дополнительная площадь имеет размеры 6 на 5 футов в длину и ширину. Чтобы найти общую площадь помещения неправильной формы, сначала посчитайте площади по отдельности и сложите их все вместе.
Площадь основной секции = 12 * 12 = 144 кв. фута
Площадь малой дополнительной секции = 6 * 5 = 30 кв. фута
Общая площадь помещения неправильной формы = 144 + 30 = 170 кв. Вот некоторые способы расчета площади комнаты.Вы можете рассчитать площадь всего дома, точно оценив разные комнаты одну за другой. Для измерения квадратных метров всего дома необходимо сложить площади разных комнат.
Вот некоторые способы расчета площади комнаты.Вы можете рассчитать площадь всего дома, точно оценив разные комнаты одну за другой. Для измерения квадратных метров всего дома необходимо сложить площади разных комнат.
- Гостиная
- Кухня
- Ванная комната
- Спальни
- Семейный номер
- Обеденная комната 9001
- Отопление и система охлаждения пространство
Они добавляют к домашним квадратный кадры, пока есть некоторые нет необходимости прибавлять к общей площади дома –
- Чердак
- Гараж
- Отдельное хранилище
- Домик у бассейна
Они не добавляют к общей площади дома.Вы можете упоминать их по-разному.
Подведение итогов Приведенное выше руководство поможет вам правильно рассчитать квадратные футы комнаты один за другим, чтобы оценить общую площадь дома. Это поможет вам выбрать и купить материал соответственно.
Как рассчитать квадратные футы для 7 фигур (с примерами)
- Развитие карьеры
- Как рассчитать квадратные футы для 7 фигур (с примерами)
28 октября 2021 г. то, сколько места может занимать объект, может быть важным навыком для новых домовладельцев, ландшафтных дизайнеров или профессионалов в области строительства.Один из способов подсчитать, сколько места использует проект, — найти его площадь в квадратных футах. Знание того, как рассчитать квадратные футы, может помочь вам решить, нужно ли вам уменьшить площадь перед переездом или добавить последние штрихи к вашему дому или двору. В этой статье мы обсудим, что такое квадратные метры, для чего люди его используют и как рассчитать квадратные метры нескольких форм, а также примеры расчетов.
Связанный: Базовые математические навыки: определения, примеры и способы их улучшения
Что описывает площадь в квадратных футах?
Квадратные метры — это термин, описывающий площадь фигуры, то есть пространство внутри границ или линий фигуры. Например, у квадрата четыре стороны одинаковой длины, а внутри этих линий находится площадь этого квадрата. То же самое верно для форм, таких как:
Например, у квадрата четыре стороны одинаковой длины, а внутри этих линий находится площадь этого квадрата. То же самое верно для форм, таких как:
01
треугольников
Trapezoids
- 2
- 2
Параллелограммы
Вы можете написать о измерениях на площади футы, используя аббревиатуру «ft.2». Вы также можете преобразовать другие измерения в квадратные футы, используя приведенные ниже преобразования:
Количество дюймов, деленное на 12, равно количеству квадратных футов
Количество ярдов, умноженное на три равно количеству квадратных футов
Количество сантиметров, умноженное на 0.03281 равно количеству квадратных футов
Количество метров, умноженное на 3,281, равно количеству квадратных футов
Как найти площадь различных фигур
Для чего используются квадратные метры?
Вы можете использовать квадратные метры в реальных контекстах, таких как:
Архитектура: Архитекторы используют квадратные метры для измерения пространства, которое может занимать здание или другие строительные объекты.

Картография: Картографы используют квадратные метры для определения площади, которую страны и другие ориентиры могут занимать на карте или глобусе.
Ландшафтный дизайн: Ландшафтные дизайнеры используют квадратные метры, чтобы определить, сколько места занимает двор или другой участок земли и что может поместиться в этом пространстве.
Недвижимость: Агенты по продаже недвижимости и подрядчики используют квадратные метры, чтобы описать, сколько площади имеет дом или другое рыночное здание, когда оно выставлено на продажу.
Вы также можете использовать квадратные метры в качестве первого шага к расчету кубических метров или объема площади. Например, вы можете использовать результат вычисления и умножить число на ширину фигуры.Если измерения в футах, то вы получите кубическое измерение. Это означает, что есть три стороны, которые вы измеряете, чтобы получить объем формы.
Связанный: Навыки, необходимые для ландшафтного дизайна
Методы расчета квадратных футов для различных форм
Различные формы имеют разные способы расчета квадратных метров. Для всех форм может быть полезно преобразовать измерение формы в квадратные футы, прежде чем выполнять расчет. Преобразование измерений может помочь вам сохранить форму в масштабе, особенно если стороны имеют разные измерения, такие как футы и дюймы или ярды и метры.Вы также можете выполнить расчет, а затем преобразовать окончательные измерения в квадратные футы, чтобы получить тот же результат.
Для всех форм может быть полезно преобразовать измерение формы в квадратные футы, прежде чем выполнять расчет. Преобразование измерений может помочь вам сохранить форму в масштабе, особенно если стороны имеют разные измерения, такие как футы и дюймы или ярды и метры.Вы также можете выполнить расчет, а затем преобразовать окончательные измерения в квадратные футы, чтобы получить тот же результат.
Используйте приведенные ниже методы, чтобы рассчитать квадратные футы для семи различных фигур:
Как рассчитать квадратные футы для квадратов и прямоугольников
Квадраты и прямоугольники используют одну и ту же формулу для расчета квадратных футов. Эта формула:
A = длина x ширина
В этом уравнении «A» — это общая площадь фигуры в квадратных футах.Длина — это измерение одной стороны формы в футах, а ширина — это измерение другой стороны формы в футах. Вы можете использовать приведенные ниже шаги, чтобы рассчитать площадь квадратов и прямоугольников по приведенной выше формуле:
При необходимости переведите измерения для каждой стороны фигуры в футы.

Умножьте длину и ширину фигуры, чтобы получить площадь квадрата или прямоугольника в квадратных футах.
Как рассчитать квадратные футы для треугольников
Формула квадратных метров для треугольников:
A = 1/2 основания x высота
В этом уравнении «A» — это площадь треугольника в квадратных футах, «1/2 основания» — это длина нижней стороны треугольника в футах, а высота — это расстояние по вертикали от нижней стороны треугольника до верхнего угла в футах.Вы можете использовать следующие шаги для вычисления площади треугольника:
Преобразуйте размеры основания и высоты в футы.
Разделите длину основания на два, чтобы получить половину основания.
Умножьте половину основания на высоту, чтобы найти площадь треугольника в квадратных футах.
Как вычислить квадратные футы для кругов
Чтобы вычислить площадь круга, необходимо использовать число пи, которое представлено символом π. Вы можете использовать десятичное число 3,14 для представления значения числа пи. Формула для расчета квадратных метров круга:
Вы можете использовать десятичное число 3,14 для представления значения числа пи. Формула для расчета квадратных метров круга:
A = π x радиус2
В этом уравнении «A» — это общая площадь в квадратных метрах, π равно 3,14, а радиус — это расстояние от точного центра круга. круг до внешнего края в футах. Чтобы вычислить площадь круга, выполните следующие действия:
Если значение еще не указано в футах, преобразуйте измерение радиуса в футы.
Умножьте длину радиуса на саму себя, чтобы получить футы в квадрате.
После того, как вы вычислили квадратные футы радиуса, умножьте результат на число пи, чтобы получить общую площадь круга в квадратных футах.
Как рассчитать площадь трапеции
Для расчета площади трапеции можно использовать формулу:
A = [(длина основания + длина верха) / 2] x высота
В этом уравнении , «А» — общая площадь фигуры в квадратных футах. Длина основания — это длина основания трапеции в футах, а длина вершины — это длина вершины трапеции в футах. Высота – это расстояние по вертикали от длины основания до длины вершины трапеции в футах. Вы можете использовать следующие шаги для вычисления площади трапеции:
Высота – это расстояние по вертикали от длины основания до длины вершины трапеции в футах. Вы можете использовать следующие шаги для вычисления площади трапеции:
При необходимости переведите измерения длины основания, длины вершины и высоты в футы.
Сложите длину основания и длину вершины вместе, чтобы вычислить площадь непрямоугольных сечений трапеции, образованных диагональными сторонами.
Разделите сумму длины основания и длины верха на два, чтобы учесть диагональные стороны в уравнении.
Умножьте результат на высоту, чтобы найти площадь трапеции в квадратных футах.
Связанный: Правила умножения: определение и примеры
Как вычислить квадратные футы для ромба
Чтобы вычислить квадратные метры ромба, вы можете использовать следующую формулу:
A = расстояние от одной пары противоположных углы x расстояние от другой пары противоположных углов
В этом уравнении «A» — это площадь ромба в квадратных футах, а расстояния от обеих пар противоположных углов — в футах. Вы можете вычислить площадь ромба, выполнив следующие действия:
Вы можете вычислить площадь ромба, выполнив следующие действия:
При необходимости преобразуйте измерения расстояний ромба в футы.
Умножьте внутренние длины, которые являются расстояниями от противоположных углов внутри ромба, чтобы найти площадь в квадратных футах. Внутренние длины пересекаются друг с другом в центре формы.
Как рассчитать площадь параллелограмма
Для расчета площади параллелограмма можно использовать следующую формулу:
A = основание x высота
В этом уравнении «A» — это площадь параллелограмм в квадратных футах, основание — это длина нижней стороны параллелограмма в футах, а высота — вертикальное расстояние от основания параллелограмма до верхней стороны в футах.Вы можете рассчитать площадь параллелограмма в квадратных футах, выполнив следующие шаги:
При необходимости переведите размеры основания и высоты в футы.
Умножьте основание на высоту параллелограмма, чтобы найти его площадь в квадратных футах.

Примеры расчета квадратных футов
Вот несколько примеров расчета квадратных футов для различных форм:
Пример ландшафтного дизайна
Ландшафтный дизайнер хочет рассчитать площадь заднего двора, чтобы определить, сколько удобрений ему нужно для него.Длина заднего двора 60 футов, а ширина 80 футов. Ландшафтный дизайнер использует формулу для расчета квадратных футов прямоугольника и выполняет следующие расчеты:
A = 60 футов x 80 футов = 4800 футов2
Ландшафтный дизайнер определяет, что им нужно купить достаточно удобрений, чтобы покрыть 4800 квадратных метров. футов земли.
Пример архитектуры
Архитектор хочет построить фонтан на круглом участке земли. Радиус земли составляет примерно 1,83 метра.Архитектор переводит это число из метров в футы и получает 6 футов. Затем они используют формулу для расчета площади круга в квадратных футах и выполняют следующие расчеты:
A = π x 62 = π x 36 = 113,10 фута2
Архитектор обнаруживает, что у них есть около 113,10 квадратных футов земли.

 Для таких ситуаций существует отдельный тест МакНемара (McNemar)
Для таких ситуаций существует отдельный тест МакНемара (McNemar)