Расчет коэффициента теплоотдачи на плоских и гофрированных поверхностях
Во многих инженерных задачах, связанных с теплопередачей, например, при проектировании теплообменных аппаратов и радиаторов охлаждения, важное значение имеет расчет коэффициента теплоотдачи. Коэффициент теплоотдачи, который чаще всего рассчитывается с помощью эмпирических формул, характеризует интенсивность теплообмена на поверхности твердого тела. В этой статье мы расскажем и покажем, как рассчитать коэффициент теплоотдачи на плоской поверхности с помощью среды численного моделирования COMSOL Multiphysics®.
Что такое коэффициент теплоотдачи?
Рассмотрим нагретую стенку или поверхность, находящуюся в контакте с потоком жидкости. Перенос теплоты в жидкости определяется преимущественно конвекцией. Аналогично, конвекцией определяется перенос теплоты через твердую стенку, омываемую с двух сторон двумя разными жидкостями, например, в теплообменных аппаратах. Интенсивность теплопередачи в обоих случаях пропорциональна разности температур, а коэффициент пропорциональности, собственно, и является  {\prime \prime}— плотность теплового потока, T_w— температура стенки, а T_\infty— характерная температура жидкости.
{\prime \prime}— плотность теплового потока, T_w— температура стенки, а T_\infty— характерная температура жидкости.
В качестве характерной температуры жидкости могут выступать температура жидкости вдали от стенки или среднемассовая температура в трубе.
Если объект находится в неограниченно большом объеме воздуха, можно предположить, что температура воздуха вдали от поверхности объекта является постоянной и известной величиной. Такие задачи теплообмена называются внешними.
Рассмотрим пристеночную область (пусть плоскость стенки расположена по нормали к оси
Математически этот процесс описывается уравнением [1]:
(2)
q ^{\prime \prime}=-k\bigg(\dfrac
{\partial T}{\partial y}\bigg)_{y=0}
Здесь k— коэффициент теплопроводности жидкости, а производная от T рассчитывается в области жидкости.
Из уравнений (1) и (2) следует, что коэффициент теплоотдачи можно определить следующим образом:
(3)
h=\dfrac{-k \bigg(\dfrac{\partial T} {\partial y}
\bigg)_{y=0}}{T_w {-} T_\infty}
Расчет коэффициента теплоотдачи в COMSOL Multiphysics®
На практике измерить градиент температуры на стенке довольно затруднительно. Кроме того, хотелось бы эффективно анализировать процессы теплообмена вблизи твердой поверхности без привлечения значительных вычислительных ресурсов. Поэтому для расчета коэффициента теплоотдачи, как правило, используются неаналитические методы.
Широко признанным методом расчета коэффициента теплоотдачи является использование уравнений подобия для безразмерного числа Нуссельта. Эти уравнения позволяют быстро рассчитать коэффициент теплоотдачи для разных условий теплообмена, в том числе при свободной и вынужденной конвекции в задачах внешнего обтекания и при течении в каналах. Однако этот подход можно использовать только для объектов правильной геометрической формы: для горизонтальных и вертикальных плоских поверхностей, цилиндров и сфер.
Если поверхность теплообмена в задаче имеет более сложную форму, коэффициент теплоотдачи можно рассчитать с помощью моделирования сопряженного теплообмена.
Рассмотрим эти два варианта решения задачи:
- Расчет коэффициента теплоотдачи на поверхностях простой геометрической формы (например, на плоской пластине):
- Моделирование сопряженного теплообмена
- Расчетные формулы; область течения не моделируется
- Вычисление коэффициента теплоотдачи на поверхностях сложной геометрической формы (например, на гофрированной пластине)
Отметим, что очень важно принимать во внимание режим течения жидкости, поскольку коэффициент теплоотдачи зависит от механизмов переноса теплоты в жидкости. В обоих случаях рассмотрим наиболее реалистичный вариант быстрого течения, например, в системе вентиляции или устройстве охлаждения электронной микросхемы. Таким образом, модель должна учитывать дополнительные механизмы переноса теплоты, обусловленные турбулентностью.
Пример 1. Теплообмен при вынужденном обтекании плоской горизонтальной пластины
Рассмотрим задачу об обтекании горизонтальной плоской пластины длиной 5 м, на которой задана постоянная плотность теплового потока 10 Вт/м2. Пластина обдувается воздухом со средней скоростью 0,5 м/с и температурой 283 K. На рисунке ниже представлена схема области течения и показаны профили скорости и температуры в пределах динамического (\delta ) и температурного (\delta {T}) пограничных слоев при ламинарном режиме обтекания.
Схематическое изображение ламинарного (сверху) и турбулентного (снизу) пограничных слоев на горизонтальной пластине.
Моделирование сопряженного теплообмена
В COMSOL Multiphysics поставленную задачу можно решить численно, если воспользоваться интерфейсом Conjugate Heat Transfer (Сопряженный теплообмен), который позволяет рассчитать поля течения и температуры в жидкости. Поля скорости и давления рассчитываются в области, занятой воздухом, а поле температуры ещё и в самой пластине.
На следующем рисунке показано распределение температуры в пределах расчетной области, включающей пластину и воздух. В области течения формируются температурный и динамический погранслои, которые занимают область над пластиной толщиной около 2 см.
Распределение температуры (график скалярного поля), изотерма на 11 °C (красная линия) и поле скорости (стрелки), показывающие температурный и динамический погранслои у поверхности пластины (масштабы осей не совпадают).
По результатам моделирования можно рассчитать плотность теплового потока, если обратиться к соответствующей встроенной переменной постобработки. Если разделить найденное значение на разность температур (T_w-T_\infty), получим коэффициент теплоотдачи (уравнение 3). На графике ниже показано, как изменяется рассчитанное значение коэффициента теплоотдачи вдоль пластины.
Расчет коэффициента теплоотдачи по формулам для числа Нуссельта
Уравнение для расчета числа Нуссельта при вынужденном обтекании плоской пластины можно найти в литературных источниках (например, в [1]).
Во втором варианте расчета мы решим ту же задачу, но без моделирования области течения; то есть мы воспользуемся формулами для расчета коэффициента теплоотдачи. В этом случае расчетная область включает в себя только твердое тело (пластину). Плотность теплового потока, передаваемая с поверхности нагретой пластины холодной жидкости, задается с помощью граничного условия
Настройки граничного условия Heat Flux (Тепловой поток).
С помощью этого условия можно рассчитать поле температуры в пластине. Зная коэффициент теплоотдачи на поверхности пластины, заданный в граничном условии Heat Flux (Тепловой поток), можно рассчитать плотность теплового потока: q=h\cdot(T_\infty-T).
Расчет коэффициента теплоотдачи
Рассчитать, как изменяется коэффициент теплоотдачи по длине пластины, можно с помощью любого из двух описанных выше методов. На рисунке ниже показано сравнение результатов расчета коэффициента теплоотдачи двумя методами.
Сравнение значений коэффициента теплоотдачи на плоской пластине, рассчитанных методом моделирования сопряженного теплообмена (синяя линия) и с помощью уравнений для числа Нуссельта (зеленая линия).
Как видно на графике, значения, полученные с помощью уравнений для числа Нуссельта, и значения, рассчитанные на основе численного моделирования сопряженного теплообмена, почти идентичны.
Интерес представляет интенсивность теплообмена на пластине, рассчитанная этими двумя методами:
- Формула для расчета числа Нуссельта: 50 Вт/м
- Сопряженный теплообмен: 49,884 Вт/м
В некоторых задачах эмпирические формулы для числа Нуссельта позволяют рассчитать плотность теплового потока с достаточно высокой точностью.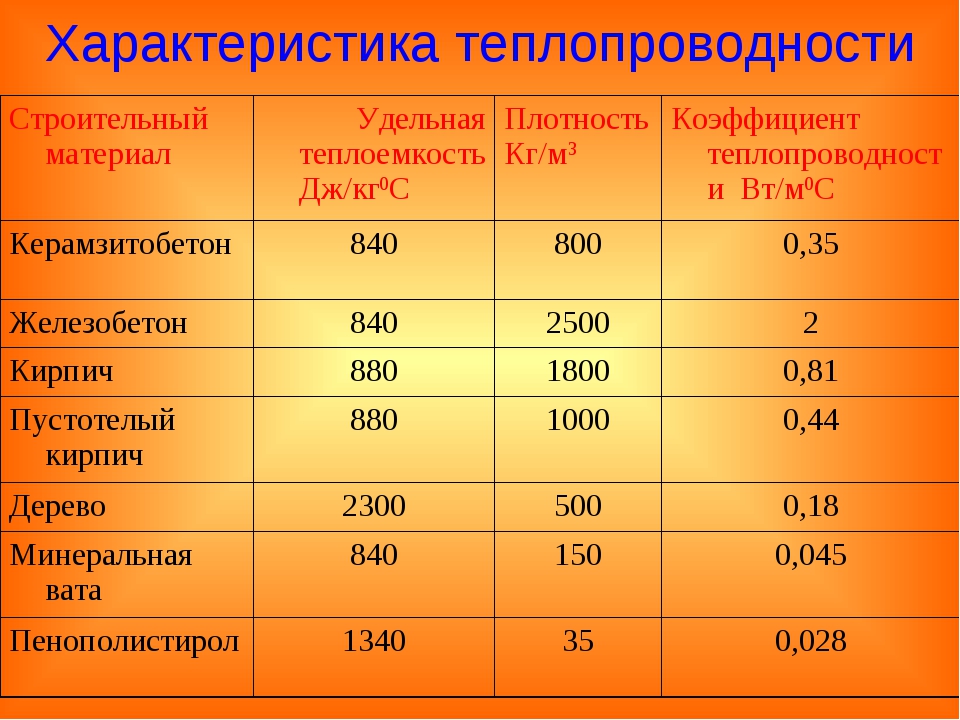 Теперь рассмотрим ситуацию, когда теплообмен происходит на поверхностии сложной формы, для которой нет формул расчета числа Нуссельта, и решить задачу можно только численно.
Теперь рассмотрим ситуацию, когда теплообмен происходит на поверхностии сложной формы, для которой нет формул расчета числа Нуссельта, и решить задачу можно только численно.
Пример 2. Течение у гофрированной поверхности горизонтальной пластины
Рассмотрим задачу с теми же исходными условиями, что и в первом случае, но только теперь верхняя поверхность пластины пусть будет гофрированной. На рисунке ниже представлена схема, иллюстрирующая постановку задачи. В этой модели одна из секций верхней поверхности пластины гофрирована. Остальные части пластины плоские.
Схема течения на горизонтальной пластине.
При такой форме поверхности стенки в пристеночной области появляются зоны рециркуляции, в результате чего интенсивность теплообмена повышается. На рисунке ниже представлено распределение температуры и линии тока.
Распределение температуры в градусах Цельсия (поверхность) и поле скорости (линии тока).
На графике слева показано изменение коэффициента теплоотдачи вдоль гофрированной пластины.
Изменение коэффициента теплоотдачи вдоль гофрированной пластины (слева) и вдоль плоской пластины (справа).
Для моделирования сопряженного теплообмена в моделях со сложной формой поверхностей могут потребоваться значительные вычислительные ресурсы, поэтому иногда предпочтение отдается альтернативным методам решения задачи. Хорошим вариантом решения является замена поверхности сложной формы на простую и подстановка значений коэффициента теплоотдачи, полученных на поверхности сложной формы с учетом геометрических параметров, поля скорости и разности температур. Следует отметить, что, даже если поверхность не является изотермической или если плотность теплового потока не постоянна, значение коэффициента теплоотдачи все равно представляет интерес для некоторых конфигураций, не слишком сильно отличающихся от исходной модели.
Для проверки рассмотрим простой вариант задачи о расчете коэффициента теплоотдачи на омываемой потоком гофрированной поверхности пластины. На основе полученных данных можно определить средний коэффициент теплоотдачи, который затем легко использовать в модели с плоской поверхностью пластины. Корректность такого приближенного подхода можно проверить, если проанализировать полный тепловой поток с поверхности или коэффициент теплоотдачи на основе моделирования сопряженного теплообмена.
Заключение
В этой статье мы рассказали о двух методах расчета коэффициента теплоотдачи. При моделировании сопряженного теплообмена можно использовать встроенные переменные COMSOL Multiphysics, содержащие значения плотности теплового потока. Применение граничного условия  / Рисунок 1-1.Теплопроводность через плоскую стенку в стационарном режиме. Что один процесс накладывает на другой.
/ Рисунок 1-1.Теплопроводность через плоскую стенку в стационарном режиме. Что один процесс накладывает на другой.
Во-первых, 1 газ (или жидкость) тепло должно подаваться к разделительной стенке. Далее тепло должно проходить через стенку, а в конце его воспринимают с противоположной поверхности стенки холодным газом (или холодной жидкостью).в этом разделе мы определим простейший случай, то есть постоянную область и тепловой поток плоской стенки, вместе с этим выведем основные законы теплопередачи. Поэтому сначала подумайте о плоской стенке толщиной B. Несмотря на различия, временная температура остается постоянной ’ / wi и / w₂ (рис. 1-1).Количество тепла, проходящего через стенку участка площади а в единицу времени при определенных перепадах температур, обозначается буквой Q*.
Отдельные процессы более подробно описаны в следующем разделе. Людмила Фирмаль
Согласно закону Фурье, это количество тепла определяется по формуле: «’Ф ^ О-я ^ 2)」 (Б6) Здесь 2 — это теплопроводность, которая характеризует свойства веществ, входящих в состав стен. Из Формулы (1-6) можно легко установить размерность теплопроводности. D-и 1 [ккал / м-ч-Град 1. л ВТТ-л »» gsg2> * Q отличается от термодинамики, что означает количество тепла независимо от времени. Количество тепла, проходящего через единицу площади поверхности в единицу времени, называется тепловым потоком. Тепловой поток, как следует из определения Если теплопроводность не зависит от температуры, как видно из рис.1, то температура внутри стенки уменьшается, а линейный закон падает от/ wi до Zw₂.Теплопроводность различных веществ описывается в appendix. As как видно из таблицы, среди твердых тел металлы обладают самой высокой теплопроводностью.
Из Формулы (1-6) можно легко установить размерность теплопроводности. D-и 1 [ккал / м-ч-Град 1. л ВТТ-л »» gsg2> * Q отличается от термодинамики, что означает количество тепла независимо от времени. Количество тепла, проходящего через единицу площади поверхности в единицу времени, называется тепловым потоком. Тепловой поток, как следует из определения Если теплопроводность не зависит от температуры, как видно из рис.1, то температура внутри стенки уменьшается, а линейный закон падает от/ wi до Zw₂.Теплопроводность различных веществ описывается в appendix. As как видно из таблицы, среди твердых тел металлы обладают самой высокой теплопроводностью.
Например, теплопроводность чугуна составляет около 45 ккал / м-ч * град, а меди-около 300 ккал! М-ч * град. Металлические сплавы обладают значительно меньшей теплопроводностью, чем чистые металлы. Например, теплопроводность нержавеющей стали составляет около 13.3 ккал! М-Ч’град. Теплопроводность неметаллических материалов составляет около 0,05-3 ккал! М’ч’град. 02), что соответствует разности потенциалов.
02), что соответствует разности потенциалов.
Отношение 6 / CL называется термическим сопротивлением и обозначается символом Rc. (1-дневный) (Это соответствует уравнению сопротивления R закона Ома).Обратная теплопроводность, или удельное тепловое сопротивление, соответствует удельному сопротивлению электротехники Предположим, что стена состоит из нескольких слоев различных материалов, например, 3 слоев, которые характеризуются коэффициентами теплопроводности X/, X₂, X3.Температуры соединения слоев могут быть скомпилированы по слоям tw2 и tW3 (рис. 1-2) C) : Если мы добавим эти равенства для каждого члена、 Эта формула позволяет определить количество тепла (подлежащего передаче).
Температура противоположной поверхности стенки и тепловое сопротивление многослойной стенки равны сумме теплового сопротивления каждого слоя, поэтому в рассматриваемом случае один и тот же закон может быть применен к сопротивлению, Соединенному последовательно в электротехнике. Инженерные (на самом деле, чаще всего встречаются стены, которые разделяют жидкости или gases. In в этом случае температура по обе стороны стены не известна. Только знать температуру жидкости по обе стороны стены. На рис. 1-3 показаны эти температуры Характер/]и Z₂.To определите температурное поле жидкости, » получите кривую, показанную на рисунке.
In в этом случае температура по обе стороны стены не известна. Только знать температуру жидкости по обе стороны стены. На рис. 1-3 показаны эти температуры Характер/]и Z₂.To определите температурное поле жидкости, » получите кривую, показанную на рисунке.
- Температурный градиент заметен только в относительно тонком слое вблизи самой стены, и в большинстве случаев даже на расстоянии от стены разница температур незначительна. Для простоты эта температурная кривая может быть заменена пунктирной линией на пунктирную линию. Это явление можно предположить, что тонкий пограничный слой (толщина d’) жидкости соединен со стенкой и находится вне этого слоя. Р2. Он проходит через многослойную стену в стационарном режиме. Плоская стена в режиме покоя. В результате хаотических движений в жидкости отсутствует температура difference.
As вы увидите позже, что это упрощенная картина гораздо более сложного процесса, но она объясняет основные явления и имеет преимущество всеобъемлющего clarity. In в пограничном слое, как и в твердых телах, тепло передается теплотой conduction. So, температурный градиент в слое выражается непосредственно, «теплопередача описывается формулой (1-6), при необходимости»заменяя величину теплопроводности жидкости или газа величиной K и толщиной D ’пограничного слоя. Итак, для количества тепла, подводимого к поверхности стены, получаем следующую формулу: (1-12) Количество передаваемого тепла Q можно определить, зная толщину пограничного слоя Y, но последний равен В значительной степени это зависит от характера движения жидкости. Например, это зависит от скорости движения жидкости вдоль стенок, формы самих стенок, поверхности стенок и прочего подобного factors. In на практике расчеты обычно выполняются с использованием значения отношения X / d’, без определения истинной толщины пограничного слоя b. это отношение называется коэффициентом теплопередачи и обозначается буквой A.
In в пограничном слое, как и в твердых телах, тепло передается теплотой conduction. So, температурный градиент в слое выражается непосредственно, «теплопередача описывается формулой (1-6), при необходимости»заменяя величину теплопроводности жидкости или газа величиной K и толщиной D ’пограничного слоя. Итак, для количества тепла, подводимого к поверхности стены, получаем следующую формулу: (1-12) Количество передаваемого тепла Q можно определить, зная толщину пограничного слоя Y, но последний равен В значительной степени это зависит от характера движения жидкости. Например, это зависит от скорости движения жидкости вдоль стенок, формы самих стенок, поверхности стенок и прочего подобного factors. In на практике расчеты обычно выполняются с использованием значения отношения X / d’, без определения истинной толщины пограничного слоя b. это отношение называется коэффициентом теплопередачи и обозначается буквой A.
Величина коэффициента теплопередачи, которая встречается в технической практике, приведена в таблице./ _ м, (1-13) Он был все еще открыт Исааком Ньютоном (1643-1727).Первоначально считалось, что коэффициент теплопередачи а характеризует свойства протекающих жидкостей или газов. Благодаря сравнительно недавним исследованиям в области теории теплопередачи, была установлена сложная природа этой величины elucidated. In в этой книге целая большая глава посвящена проблеме определения коэффициента теплоотдачи. 1-1.Дает представление об относительном размере этого параметра.
Поскольку коэффициент теплопередачи является коэффициентом теплопроводности, деленным на толщину пограничного слоя, ожидается, что газ с низкой теплопроводностью будет иметь более низкий коэффициент теплопередачи, чем жидкость. Вешалка. 1-1 подтверждает этот вывод. Таблица 1-1 Порядок величины коэффициента теплопередачи, ккал, 1м2град Перемещение воздуха. ………………………… 10-250. Движущаяся вода…………………………….. 500-5, 000 Кипяток……………………………….. 2 500-5 000 Конденсированный водяной пар………………… 500-25 000 Применив рисунок (1-13) к условиям, существующим на обеих стенках (Рисунок 1) 1-3, получим: В режиме покоя количество тепла, которое передается в обоих случаях, должно быть равным.
Эти 2 равны* Вы также мул закона Ома: Пишите в соответствующем формате (У4) Коэффициент передачи тепла R 1 / alₜ: Называемое тепловое сопротивление (1-15.
Терминальное сосуществование уравнений (1-8) и уравнений (1-14) позволяет установить зависимость между калорийностью и температурой и/или₂, передаваемой через стенку(рис.1-3). (1-16) Сумма частичного теплового сопротивления равна общему тепловому сопротивлению Rₒ теплопередачи. Поэтому в данном случае тот же закон применим и к электрическому сопротивлению, которое подключено в series. In в большинстве случаев в практических расчетах вместо термического сопротивления используются теплопроводность и коэффициент теплопередачи. После этого будет справедливо следующее уравнение, и вы легко получите его из уравнения (1-16). М = ка(/、-/、); (1-17) ка-АГ ’ (От 1 до 18) величина k называется коэффициентом теплопередачи, а размеры-ккал / м * -h-град.
Стена. Разный коэффициент теплопроводности L. и разная толщина b. если он состоит из нескольких слоев, то промежуточный член формулы (1-18) заменяется суммой.
(0.000222 + 0.000102) h•град / ккал. Это меньше половины предыдущего значения.
Смотрите также:
Коэффициент теплопроводности — Технарь
Множитель пропорциональности l в уравнениях (12.3) и (12.4) называется коэффициентом теплопроводности. Теплопроводность является физическим свойством вещества, характеризующим способность вещества проводить тепло. Из выражения (12.3) следует:
Коэффициент теплопроводности представляет собой количество тепла, проходящее в единицу времени через единицу поверхности при разности температур в один градус на пути в один метр.
Значения коэффициентов теплопроводности для различных веществ резко отличаются и зависят от структуры, плотности, влажности, давления и температуры материала. Поэтому в ответственных конструкциях, таких как изоляция подводных лодок или космических аппаратов, значения коэффициента теплопроводности конструкции определяется экспериментально для каждой конструкции. При обычных теплотехнических расчётах значения коэффициента теплопроводности принимаются из справочника.
Необходимо только, чтобы физические характеристики материала (влажность, плотность…), определяемые условиями эксплуатации, соответствовали табличным данным, приведенным в справочнике.
Зависимость теплопроводности от температуры имеет характер:
li = l0(1 + bti) (12.6)
где l0 — известный коэффициент теплопроводности при известной температуре t0;
b — константа, определяемая для данного материала экспериментально.
Наибольшие значение теплопроводности имеют металлы: у серебра l = 410 Вт/(м·град), у золота l = 300 Вт/(м·град), у чистой меди l = 395 Вт/(м·град), у алюминия l = 210 Вт/(м·град). Для большинства металлов повышение температуры приводит к уменьшению теплопроводности. К резкому снижению теплопроводности приводит наличие даже ничтожного количества примесей в металлах. Например, следы мышьяка в меди снижают коэффициент ее теплопроводности до l = 142 Вт/(м·град).
Железо с содержанием углерода 0,1% имеет l = 52 Вт/(м·град), при наличии углерода 1% — l = 40 Вт/(м·град).
Для чистых металлов теплопроводность и электропроводность пропорциональны друг другу.
Значения коэффициентов теплопроводности строительных и теплоизоляционных материалов лежат в пределах l = 0,02 — 3 Вт/(м·град). Рост температуры приводит к росту коэффициента теплопроводности в соответствии с зависимостью (12.6). Как правило, чем выше плотность материала, тем больше величина его теплопроводности. При выборе строительных и изоляционных материалов следует учесть высокую зависимость коэффициента теплопроводности от влажности материала. Причем нужно помнить, что теплопроводность влажного материала выше, чем теплопроводность отдельно сухого материала и теплопроводность воды. Например, сухой кирпич имеет коэффициент теплопроводности l = 0,3 Вт/(м·град), теплопроводность воды l = 0,6 Вт/(м·град), а теплопроводность влажного кирпича l = 0,9 Вт/(м·град).
В качестве теплоизоляционных обычно используют материалы с теплопроводностью менее l = 0,2 Вт/(м·град).
Теплопроводность капельных жидкостей, как и теплопроводность металлов, понижается при увеличении температуры.
Исключением является вода и глицерин. Значения коэффициентов теплопроводности капельных жидкостей находится в интервале l = 0,7 – 0,1 Вт/(м·град).
Величины коэффициентов теплопроводности газов на порядок меньше, чем капельных жидкостей l = 0,1 – 0,005 Вт/(м·град). В отличие от жидкостей и металлов, у газов повышение температуры приводит к росту теплопроводности, как и у строительных и изоляционных материалов.
От давления (кроме очень маленького и очень большого) теплопроводность практически не зависит.
Коэффициент теплопроводности
Строительные, отделочные материалы и утеплители
Если внутри тела имеется разность температур, то тепловая энергия переходит от более горячей его части к более холодной. Такой вид теплопередачи, обусловленный тепловыми движениями и столкновениями молекул, называется теплопроводностью. При достаточно высоких температурах в твердых телах его можно наблюдать визуально. Так, при нагревании стального стержня с одного конца в пламени газовой горелки тепловая энергия передается по стержню, и на некоторое расстояние от нагреваемого конца распространяется свечение (с удалением от места нагрева все менее интенсивное).
Интенсивность теплопередачи за счет теплопроводности зависит от градиента температуры, т.е. отношения dТ/dXразности температур на концах стержня к расстоянию между ними. Она зависит также от площади поперечного сечения стержня (в м2) и коэффициента теплопроводности материала [в соответствующих единицах Вт/(м К)]. Соотношение между этими величинами было выведено французским математиком Ж.Фурье и имеет следующий вид:
q=-kA*dT/dXгде q– тепловой поток, k– коэффициент теплопроводности, а A– площадь поперечного сечения. Это соотношение называется законом теплопроводности Фурье; знак «минус» в нем указывает на то, что теплота передается в направлении, обратном градиенту температуры.
Из закона Фурье следует, что тепловой поток можно понизить, уменьшив одну из величин – коэффициент теплопроводности, площадь или градиент температуры. Для здания в зимних условиях последние величины практически постоянны, а поэтому для поддержания в помещении нужной температуры остается уменьшать теплопроводность стен, т.
е. улучшать их теплоизоляцию.
В таблице представлены коэффициенты теплопроводности некоторых утеплителей и строительных материалов. Из таблицы видно, что одни материалы проводят тепло гораздо лучше других, но все они являются значительно худшими изоляторами, чем керамический теплоизолятор Астратек®.
Таблица коэффициентов теплопроводности некоторых материалов, Вт/м*КАлебастровые плиты 0,47
Алюминий 230
Асбест (шифер) 0,35
Асбест волокнистый 0,15
Асбестоцемент 1,76
Асбоцементные плиты 0,35
Астратек 0,0012
Асфальт 0,72
Асфальт в полах 0,8
Бакелит 0,23
Бетон на каменном щебне 1,3
Бетон на песке 0,7
Бетон пористый 1,4
Бетон сплошной 1,75
Бетон термоизоляционный 0,18
Битум 0,47
Бумага 0,14
Вата минеральная легкая 0,045
Вата минеральная тяжелая 0,055
Вата хлопковая 0,055
Вермикулитовые листы 0,1
Войлок шерстяной 0,045
Гипс строительный 0,35
Глинозем 2,33
Гравий (наполнитель) 0,93
Гранит, базальт 3,5
Грунт 10% воды 1,75
Грунт 20% воды 2,1
Грунт песчаный 1,16
Грунт сухой 0,4
Грунт утрамбованный 1,05
Гудрон 0,3
Древесина — доски 0,15
Древесина — фанера 0,15
Древесина твердых пород 0,2
Древесно-стружечная плита ДСП 0,2
Дюралюминий 160
Железобетон 1,7
Зола древесная 0,15
Известняк 1,7
Известь-песок раствор 0,87
Иней 0,47
Ипорка (вспененная смола) 0,038
Камень 1,4
Картон строительный многослойный 0,13
Картон теплоизолированный БТК-1 0,04
Каучук вспененный 0,03
Каучук натуральный 0,042
Каучук фторированный 0,055
Керамзитобетон 0,2
Кирпич кремнеземный 0,15
Кирпич пустотелый 0,44
Кирпич силикатный 0,81
Кирпич сплошной 0,67
Кирпич шлаковый 0,58
Кремнезистые плиты 0,07
Латунь 110
Лед 0°С 2,21
Лед -20°С 2,44
Лед -60°С 2,91
Липа, береза, клен, дуб (15% влажности) 0,15
Медь 380
Мипора 0,085
Опилки — засыпка 0,095
Опилки древесные сухие 0,065
ПВХ 0,19
Пенобетон 0,3
Пенопласт ПС-1 0,037
Пенопласт ПС-4 0,04
Пенопласт ПХВ-1 0,05
Пенопласт резопен ФРП 0,045
Пенополистирол ПС-Б 0,04
Пенополистирол ПС-БС 0,04
Пенополиуретановые листы 0,035
Пенополиуретановые панели 0,025
Пеностекло легкое 0,06
Пеностекло тяжелое 0,08
Пергамин 0,17
Перлит 0,05
Перлито-цементные плиты 0,08
Песок 0% влажности 0,33
Песок 10% влажности 0,97
Песок 20% влажности 1,33
Песчаник обожженный 1,5
Плитка облицовочная 1,05
Плитка термоизоляционная ПМТБ-2 0,036
Полистирол 0,082
Поролон 0,04
Портландцемент раствор 0,47
Пробковая плита 0,043
Пробковые листы легкие 0,035
Пробковые листы тяжелые 0,05
Резина 0,15
Рубероид 0,17
Сланец 2,1
Снег 1,5
Сосна обыкновенная, ель, пихта (450...550 кг/куб.м, 15% влажности) 0,15
Сосна смолистая (600…750 кг/куб.м, 15% влажности) 0,23
Сталь 52
Стекло 1,15
Стекловата 0,05
Стекловолокно 0,036
Стеклотекстолит 0,3
Стружки — набивка 0,12
Тефлон 0,25
Толь бумажный 0,23
Цементные плиты 1,92
Цемент-песок раствор 1,2
Чугун 56
Шлак гранулированный 0,15
Шлак котельный 0,29
Шлакобетон 0,6
Штукатурка сухая 0,21
Штукатурка цементная 0,9
Эбонит 0,16
Эбонит вспученный 0,03Из результатов приведенных коэффициентов теплопроводности следует, что Астратек на сегодняшний день обладает минимльным коэффициентом, а слой покрытия Астратек толщиной в 1 мм (в реальных условиях с учетом понижающих коэффициентов) обеспечивает те же изоляционные свойства, что и 50 мм рулонной изоляции или кирпичная кладка толщиной в 1-1,5 кирпича.
Поправки на теплопроводность горных пород по температуре и давлению: влияние на прогноз температуры подземных вод и определение теплового потока при геотермальной разведке | Геотермальная энергетика
Абдулагатов И.
М., Эмиров С.Н., Абдулагатова З.З., Аскеров С.Ю. Влияние давления и температуры на теплопроводность горных пород. Данные J Chem Eng. 2006; 51: 22–33.
Артикул Google Scholar
Ананд Дж., Сомертон В.Х., Гомаа Э.Прогнозирование теплопроводности пластов по другим известным свойствам. SPE J. 1973; 13: 267–72.
Google Scholar
Эти Л.Ф. Плотность, пористость и уплотнение осадочных пород. Бык AAPG. 1930; 14(1):194–200.
Google Scholar
Баллинг П., Майстренко Ю., Шек-Вендерот М. Глубокое термальное поле грабена Глюкштадт. Науки об окружающей среде Земли. 2013;70(3):3505–22.
Артикул Google Scholar
Бек А.Э. Тепловые свойства. В: Хенель Р., Рыбач Л., Стегена Л., редакторы. Справочник по определению плотности земного теплового потока. Дордрехт: Спрингер; 1988.
с. 87–165.
Глава Google Scholar
Бедар К., Комо Ф.А., Раймонд Дж., Мало М., Наср М. Геотермальная характеристика осадочного бассейна низменности Святого Лаврентия, Квебек, Канада.Нат Ресурс Рез. 2018;27(4):479–502. https://doi.org/10.1007/s11053-017-9363-2.
Артикул Google Scholar
Бекеши Э., Ленкей Л., Лимбергер Дж., Порколаб К., Балаш А., Бонте Д., Врейландт М., Хорват Ф., Клотинг С., ван Вис Д.Д. Модель подповерхностной температуры венгерской части Паннонского бассейна. Изменение планеты Глоб. 2018;171:48–64.
Артикул Google Scholar
Блэквелл Д.Д., Стил Дж.Л.Теплопроводность осадочных пород: измерение и значение. В: Naeser ND, McCulloh TH, редакторы. Термическая история осадочных бассейнов. Нью-Йорк: Спрингер; 1989. с. 13–36.
Глава Google Scholar
Блеш С.
Дж., Кулацки Ф.А., Кристенсен Р.Н. Применение интегральных методов для прогнозирования теплопередачи от хранилища ядерных отходов. Колумбус: отчет об открытом файле ONWI-495, Battelle Memorial Institute; 1983. с.12–7. https://doi.org/10.2172/5754517.
Книга Google Scholar
Деминг Д., Чепмен Д. Тепловой поток в надвиговом поясе Юта-Вайоминг на основе анализа данных о забойной температуре, измеренных в нефтяных и газовых скважинах. Дж Геофиз Рез. 1988; 93:13657–72.
Артикул Google Scholar
Дарем В.Б., Эбей А.Э., Триммер Д.А. Теплопроводность, диффузионная способность и расширение соли острова Эйвери при давлении и температуре.Ливермор, Калифорния. 1980. https://digital.library.unt.edu/ark:/67531/metadc1093573/. По состоянию на 8 октября 2019 г.
Элисон П., Нидерау Дж., Фогт С., Клаузер С. Количественная оценка неопределенности теплопроводности для моделирования бассейна.
Бык AAPG. 2019;103(8):1787–809.
Артикул Google Scholar
Эмиров С.Н., Бейбалаев В.Д., Гаджиев Г.Г., Рамазанова А.Е., Амирова А.А., Аливердиев А.А. К описанию температурно-барических зависимостей теплопроводности песчаника и керамики.J Phys Conf Ser. 2017;891:012335. https://doi.org/10.1088/1742-6596/891/1/012335.
Артикул Google Scholar
Фёрстер А., Фёрстер Х.Й. Состав земной коры и тепловой поток мантии: последствия поверхностного теплового потока и радиогенного производства тепла в Варисканских Рудных горах (Германия). Дж Геофиз Рез. 2000;105(B12):27917–38. https://doi.org/10.1029/2000JB
9.
Артикул Google Scholar
Фёрстер Х.Й., Фёрстер А., Оберхэнсли Р., Стромейер Д.Литосферный состав и термальная структура Аравийского щита в Иордании. Тектонофизика. 2010; 481(1–4):29–37.
Артикул Google Scholar
Фёрстер А.
, Фёрстер Х.Дж., Кренц О. Исследование потенциала усовершенствованной геотермальной системы (EGS) кристаллических пород для централизованного теплоснабжения (Эльбская зона, Саксония, Германия). Int J Earth Sci. 2018;104(1):89–101.
Артикул Google Scholar
Фреймарк Дж., Зиппель Дж., Шек-Вендерот М., Бэр К., Штиллер М., Фриче Дж. Г., Крахт М.Глубинное термальное поле грабена Верхнего Рейна. Тектонофизика. 2017; 694:114–29.
Артикул Google Scholar
Фукс С., Баллинг Н. Улучшение температурных прогнозов подземных тепловых моделей с использованием высококачественных входных данных. Часть 2: тематическое исследование датско-немецкого пограничного региона. Геотермия. 2016; 64:1–14.
Артикул Google Scholar
Фукс С., Фёрстер А.Прогноз теплопроводности осадочных толщ на основе каротажа: тематическое исследование Северо-Германского бассейна.
Геофиз J Междунар. 2014; 196: 291–311.
Артикул Google Scholar
Фукс С., Баллинг Н., Матисен А. Поле температуры и теплового потока глубоководных бассейнов в Дании — новые выводы из скважинного анализа и трехмерного геотермического моделирования. Геотермия. 2020. https://doi.org/10.1016/j.geothermics.2019.101722.
Артикул Google Scholar
Хастерок Д., Чепмен Д.С.Теплопродукция и геотермы континентальной литосферы. Научный бюллетень «Планета Земля». 2011; 307:59–70.
Артикул Google Scholar
Horai K, Susaki J. Влияние давления на теплопроводность силикатных пород до 12 кбар. Физ Планета Земля Интер. 1989; 55: 292–305.
Артикул Google Scholar
Hurtig E, Brugger H. Wärmeleitfähigkeitsmessungen unter einaxialem Druck.Тектонофизика.
1970; 10 (1–3): 67–77.
Артикул Google Scholar
Кукконен И.Т., Йокинен Дж., Сейпольд У. Зависимости свойств теплового переноса горных пород от температуры и давления: последствия для неопределенностей в тепловых моделях литосферы и новые лабораторные измерения пород с высоким содержанием золота в центральной части Фенноскандинавского щита. Сурв Геофиз. 1999; 20:33–59.
Артикул Google Scholar
Ли Ю., Деминг Д.Оценка температурных поправок на теплопроводность применительно к исследованиям земного теплового потока. Дж Геофиз Рез. 1998;103(B2):2447–54.
Артикул Google Scholar
Леменагер А., О’Нил С., Чжан С., Морган Э. Влияние теплопроводности, зависящей от температуры, на геотермальную структуру Сиднейского бассейна. Геотерм Энерджи. 2018. https://doi.org/10.1186/s40517-018-0092-5.
Артикул Google Scholar
Миранда М.
М., Матос Ч.Р., Родригес Н.В., Перейра АJSC, Коста Дж.Дж.Влияние температуры на теплопроводность гранита с высокой теплопродукцией из Центральной Португалии. Дж. Ибер Геол. 2019;45(1):147–61.
Артикул Google Scholar
Ноак В., Черубини Ю., Шек-Вендерот М., Леверенц Б., Хёдинг Т., Саймон А., Моек И. Оценка современного теплового поля (северо-восточная часть Немецкого бассейна) — выводы на основе трехмерного моделирования. Чем Эрде. 2010;70(S3):47–62.
Артикул Google Scholar
Ноак В., Шек-Вендерот М., Какаче М.Чувствительность трехмерных тепловых моделей к выбору граничных условий и тепловых свойств: тематическое исследование для района Бранденбург (северо-восток Немецкого бассейна). Науки об окружающей среде Земли. 2012;67(6):1695–711.
Артикул Google Scholar
Норден Б., Фёрстер А., Баллинг Н.
Тепловой поток и термический режим литосферы в Северо-Восточной Германской котловине. Тектонофизика. 2008; 460: 215–29.
Артикул Google Scholar
Норден Б., Фёрстер А., Берендс К., Краузе К., Штекен Л., Мейер Р.Геологическая трехмерная модель крупного района Зальцведель, Германия, для прогноза температуры и моделирования коллектора. Науки об окружающей среде Земли. 2012;67:511–26.
Артикул Google Scholar
Пауэлл В.Г., Чепмен Д.С., Боллинг Н., Бек А.Н. Континентальная плотность теплового потока. В: Хенель Р., Рыбач Л., Стегена Л., редакторы. Справочник по определению плотности земного теплового потока. Дордрехт: Kluwer Academics; 1988. с. 167–222.
Глава Google Scholar
Пшибыцин А.М., Шек-Вендерот М., Шнайдер М.Трехмерное кондуктивное тепловое поле Северо-Альпийского форландского бассейна: влияние глубинной структуры и прилегающих Европейских Альп.
Геотерм Энерджи. 2015;3(17):1–29.
Google Scholar
Рюхаак В., Рат В., Клаузер К. Обнаружение термальных аномалий в бассейне Моласса, южная Германия. Hydrogeol J. 2010;18(8):1897–915.
Артикул Google Scholar
Шац Дж. Ф., Симмонс Г.Теплопроводность земных материалов при высоких температурах. Дж Геофиз Рез. 1972; 77: 6966–83.
Артикул Google Scholar
Schintgen T, Förster A, Förster HJ, Norden B. Поверхностный тепловой поток и тепловая структура литосферы Реногерцинской зоны в районе Большого Люксембурга. Геотермия. 2015а; 56: 93–109.
Артикул Google Scholar
Schintgen T, Förster A, Förster HJ, Norden B.Исправление к «Поверхностному тепловому потоку и термической структуре литосферы Реногерцинской зоны в районе Большого Люксембурга».
Геотермия. 2015b;58:94.
Артикул Google Scholar
Шён Дж.Х. Физические свойства горных пород: основы и принципы петрофизики. В: Хельбиг К., Тейтель С., редакторы. Справочник по геофизической разведке: раздел 1, сейсморазведка. Оксфорд: Пергамон; 1996.
Google Scholar
Шён С.Дж.Глава 9 — Тепловые свойства. В: Schön JH, редактор. Справочник по разведке и добыче нефти. Амстердам: Эльзевир; 2011. с. 337–72.
Google Scholar
Schütz F, Förster HJ, Förster A. Термические условия центральной синайской микроплиты, полученные на основе новых значений поверхностного теплового потока и непрерывной регистрации температуры в скважине в центральном и южном Израиле. Дж Геодин. 2014;76:8–24.
Артикул Google Scholar
Зайпольд У.Глубинная зависимость теплотранспортных свойств типичных пород земной коры.
Физ Планета Земля Интер. 1992; 69: 299–303.
Артикул Google Scholar
Сейпольд Ю. Изменение свойств теплопереноса в земной коре. Дж Геодин. 1995; 20: 145–54.
Артикул Google Scholar
Сейпольд Ю. Температурная зависимость теплотранспортных свойств кристаллических пород — общий закон.Тектонофизика. 1998; 291:161–71.
Артикул Google Scholar
Seipold U. Der Wärmetransport in kristallinen Gesteinen unter den Bedingungen der kontinentalen Erdkruste. GeoForschungsZentrum Potsdam, научно-технический отдел, 2001 г. https://doi.org/10.2312/gfz.b103-010037.
Seipold U. Исследование теплотранспортных свойств амфиболитов: I. Зависимость от давления. Высокотемпературное высокое давление. 2002; 34: 299–306.
Артикул Google Scholar
Seipold U, Huenges E.
Термические свойства гнейсов и амфиболитов — исследования образцов горных пород KTB при высоких давлениях и температурах. Тектонофизика. 1998; 291:173–178.
Артикул Google Scholar
Секигучи К.А. Способ определения земного теплового потока в районах нефтяных бассейнов. Тектонофизика. 1984; 103: 67–79.
Артикул Google Scholar
Somerton WH. Термические свойства и температурно-зависимое поведение систем порода/флюид. Амстердам: Эльзевир; 1992.
Google Scholar
Сонибаре В.А., Сиппель Дж., ди Примио Р., Анка З., Шек-Вендерот М., Микеш Д. Современное тепловое поле и мезозойско-кайнозойская тепловая эволюция западной части бассейна Бредасдорп (Южная Африка): интегрированный трехмерный численный подход к прямому моделированию.Мар Петрол Геол. 2018;93:57–78.
Артикул Google Scholar
Велес М.
И., Блессент Д., Кордоба С., Лопес-Санчес Дж., Раймонд Дж., Парра-Паласио Э. Оценка геотермального потенциала вулкана Невадо-дель-Руис на основе измерений теплопроводности горных пород и численного моделирования теплопередачи. JS Am Earth Sci. 2018;81:153–64.
Артикул Google Scholar
Vosteen HD, Schellschmidt R.Влияние температуры на теплопроводность, теплоемкость и температуропроводность для различных типов горных пород. Физико-химическая Земля. 2003; 28: 499–509.
Артикул Google Scholar
Востин Х.Д., Рат В., Шмидт-Мумм А., Клаузер С. Термический режим Северо-Восточно-Германского бассейна по данным двухмерной инверсии. Тектонофизика. 2004; 386:81–95.
Артикул Google Scholar
Зот Г., Хенел Р.Теплопроводность. В: Хенель Р., Рыбач Л., Стегена Л., редакторы. Справочник по определению плотности земного теплового потока.
Дордрехт: Клювер; 1988. с. 449–66.
Глава Google Scholar
Corzan ХПВХ и теплопроводность: важные соображения
Теплопроводность является важным фактором при любом применении трубопровода как с точки зрения безопасности, так и ответственности. Материал трубопроводной системы с более низкой теплопроводностью будет поддерживать более низкую температуру поверхности при транспортировке горячих жидкостей.В определенных ситуациях это может снизить риск ожогов операторов, которые могут соприкоснуться с трубой.
Это особенно актуально для людей, работающих рядом с клапаном, насосом или впускным отверстием резервуара, где в непосредственной близости проходит несколько участков трубопровода. По данным Бюро статистики труда, в 2016 году случаи термических ожогов вызвали в среднем 6 дней отсутствия на работе.
Чтобы получить полное представление о свойствах теплопроводности ХПВХ, инженеры Corzan ® Industrial System рекомендуют начать со сравнения рейтингов теплопроводности.
Рейтинги теплопроводности
Стандартом для оценки теплопроводности материала является ASTM C177, «Стандартный метод испытаний для измерения стационарного теплового потока и свойств теплопередачи с помощью прибора с защищенной горячей пластиной ». Это контролируемый метод для измерения передачи тепла через материал.
ХПВХ маркиобладает исключительно низкой теплопроводностью — примерно в 1/300 меньше, чем у стали.Это связано с различиями в атомном расположении материалов.
График ниже помогает проиллюстрировать этот момент. Он показывает температуру поверхности трубы по отношению к внутренней температуре жидкости. Обратите внимание на:
- Температура поверхности трубопровода из углеродистой стали такая же, как и внутренняя температура жидкости, в то время как поверхность трубы из ХПВХ сохраняет гораздо более низкую температуру.
- Температура поверхности углеродистой стали практически такая же, как и температура жидкости, независимо от толщины ее стенки.
И наоборот, толщина стенки трубы из ХПВХ влияет на температуру ее поверхности, поскольку она обладает гораздо более высокой термостойкостью, чем сталь. Толщина стенки зависит от сортамента и размера трубы.
Расчетная температура поверхности трубы в зависимости от внутренней температуры жидкости
*Примечание. График предполагает температуру окружающей среды 68°F (20°C) и скорость потока воды 6,5 футов/сек. (2 м/с)
Независимо от материала, некоторые промышленные применения повышают температуру поверхности трубы до небезопасного уровня.В таких случаях следует подумать об изоляции.
Требования к изоляции трубопроводов
Преимущество низкой теплопроводности материала трубопровода заключается в том, что может потребоваться меньшая изоляция для поддержания постоянной температуры труб. Это верно независимо от того, является ли конечной целью защита от внешней температуры трубы или поддержание постоянной температуры внутри трубы.
Понимание максимальной температуры поверхности труб важно для безопасности рабочих.Как показано выше, температура поверхности трубы зависит от типа трубы, используемой для данного процесса. Независимо от материала трубопровода может потребоваться изоляция для защиты рабочих от опасности ожогов при работе с трубопроводной системой. Знание температуры поверхности трубы поможет определить, когда требуется изоляция для снижения опасности ожогов.
Кроме того, теплопроводный материал позволяет теплу отводиться быстрее, чем материалы, которые также не передают тепло.По этой причине теплопроводные трубы в средах с более низкой температурой, чем жидкость, которую они перекачивают, требуют дополнительной энергии для поддержания температуры жидкости. Количество дополнительной энергии зависит от требуемой температуры жидкости и температуры окружающей среды.
Независимо от причины изоляции, количество изоляции зависит от температуры жидкости, типа трубы и желаемого удержания тепла и может варьироваться от одного применения к другому.
Чтобы определить специфику вашей трубопроводной системы, обсудите ее с командой экспертов Corzan Industrial Systems.
Конденсат
Теплопроводность также играет роль в системах холодных трубопроводов.
При работе с холодными жидкостями, чем более теплопроводен материал трубопровода, тем ниже температура его поверхности. В подходящих условиях окружающей среды, когда температура поверхности трубы ниже точки росы окружающей среды, может образовываться конденсат, что представляет угрозу безопасности.
Рассмотрим жаркий и влажный завод, через который проходят холодные линии. Холодная поверхность трубы в сочетании с высокой температурой и насыщенным воздухом создает идеальные условия для образования конденсата на внешней стороне труб.Это может привести к:
- Пыль и грязь на трубах, смешиваясь с конденсатом и загрязняя стерильную среду.
- Лужи на полу, делая поверхности скользкими.
- Капание на инвентарь или другие хранящиеся предметы.
Материал трубопровода с меньшей теплопроводностью может помочь избежать таких ситуаций или, как минимум, уменьшить потребность в изоляции.
Любопытно, как трубы из ХПВХ сочетаются с металлом в других областях?
Уникальные характеристики ХПВХне ограничиваются теплопроводностью.Чтобы узнать больше, прочитайте статью «Металл по сравнению с системами трубопроводов из ХПВХ: какой материал для трубопроводов лучше подходит для промышленного применения?»
Теплопроводность теплоизоляционных материалов
Клеменс Дж. М. Ласанс Статьи, Керамика, Материалы, Соединения, Клеи, Подложки, Полупроводники, Технические данные испытаний и измерений, Теплопроводность, Тепловые изоляторы
В этом выпуске мы представляем обзор ряда материалы, которые часто используются в качестве теплоизоляторов.Мир был бы намного проще для инженеров-теплотехников, если бы только создатель предоставил нам выбор материалов, показывающих тот же диапазон значений теплопроводности, что и для электропроводности.
Увы, это не так. Таким образом, ни один из материалов, с которыми нам приходится жить, не может быть действительно квалифицирован термином «изолятор». Наиболее важная причина, по которой экспериментальная проверка кодов CFD (Computational Fluid Dynamics) является катастрофой (за исключением высоких скоростей), заключается в том, что всегда играет роль сопряженная теплопередача через опору.Рассмотрим, например, компонент на подложке в условиях естественной конвекции. Даже самый лучший изолятор не может предотвратить потери в 10% и более. Следовательно, адиабатические поверхности, так любимые численными аналитиками, не могут быть реализованы на практике.
В прилагаемой таблице также указана плотность, поскольку многие изоляторы частично состоят из воздуха. Следовательно, плотность сильно коррелирует с теплопроводностью. Опять же, все значения в таблице определены при комнатной температуре. Из-за присутствия воздуха температурная зависимость более сложная, чем для пластмасс и каучуков, у которых теплопроводность увеличивается на несколько процентов в диапазоне от 0-100 o С.
В этом диапазоне проводимость воздуха увеличивается примерно на 30%. Однако основной тепловой путь обычно по-прежнему покрыт пластиком; следовательно, преобладает температурная зависимость пластика. Обратите внимание на то, что некоторые материалы показывают значение ниже, чем у воздуха. Это может быть реализовано только в том случае, если размер пор, заполненных воздухом, меньше длины свободного пробега молекул воздуха.
Теплопроводность теплоизоляционных материалов @ 25 o C Материал Плотность
(кг/м 3 )Тепловая
проводимость
(Вт/мК)Воздух 1. 3
0,025 Алюминий 2 O 3 Пена 500 0,042 Балсовое дерево 130 0,05 Силикат кальция 240 0,051 Одеяло из керамического волокна 128 0,032 Пробка 150 0,043 Бумага для факсимильной связи 324 0.03 Пеностекло 144 0,035 Микротерм 240 0,021 Полистирол (воздух) 46 0,026 Полистирол (вакуум) 46 0,0081 Полистирол (пенопласт) 30 0,027 Полиуретан (жесткий) 40 0,032 Полиуретан (гибкий) 60 0. 042
Полиуретан (ПИР) 160 0,05 Вспененный каучук 100 0,042 SiO 2 пена 160 0,055 Вермикулит (вспученный) 300 0,069 Полезный инструмент для получения информации такого типа можно найти в Интернете по адресу www.tak2000.com/data2.htm#термо
Теплопроводность | Определение и пример
Теплопроводность большинства жидкостей и твердых тел зависит от температуры. Для паров это также зависит от давления. В общем:
Большинство материалов почти однородны, поэтому обычно мы можем написать k = k (T) . Аналогичные определения связаны с теплопроводностью в направлениях y и z (k y , k z ), но для изотропного материала теплопроводность не зависит от направления переноса, k x = k у = к г = к.
Обратите внимание, что закон Фурье применим ко всей материи, независимо от ее состояния (твердое, жидкое или газообразное), поэтому он также определен для жидкостей и газов.
Из приведенного выше уравнения следует, что поток тепла проводимости увеличивается с увеличением теплопроводности и увеличивается с увеличением разности температур. В общем, теплопроводность твердого тела больше, чем у жидкости, которая больше, чем у газа. Эта тенденция в значительной степени обусловлена различиями в межмолекулярных расстояниях для двух состояний вещества.В частности, алмаз обладает самой высокой твердостью и теплопроводностью среди всех сыпучих материалов.
Теплопроводность жидкостей (жидкостей и газов)
В физике жидкость — это вещество, которое постоянно деформируется (течет) под действием приложенного напряжения сдвига. Жидкости являются подмножеством фаз материи и включают жидкости , газы , плазму и, в некоторой степени, твердые пластмассы.
Поскольку межмолекулярное расстояние намного больше, а движение молекул более хаотично для жидкого состояния, чем для твердого состояния, перенос тепловой энергии менее эффективен.Следовательно, теплопроводность газов и жидкостей обычно меньше, чем у твердых тел. В жидкостях теплопроводность обусловлена атомной или молекулярной диффузией. В газах теплопроводность обусловлена диффузией молекул с более высокого энергетического уровня на более низкий уровень.
Теплопроводность газов
Влияние температуры, давления и химических соединений на теплопроводность газа можно объяснить с точки зрения кинетической теории газов .Воздух и другие газы обычно являются хорошими изоляторами при отсутствии конвекции. Таким образом, многие изоляционные материалы (например, полистирол) функционируют просто благодаря большому количеству заполненных газом карманов , которые предотвращают крупномасштабную конвекцию .
Чередование газового кармана и твердого материала приводит к тому, что тепло должно передаваться через множество поверхностей раздела, что приводит к быстрому снижению коэффициента теплопередачи.
Теплопроводность газов прямо пропорциональна плотности газа, средней молекулярной скорости и особенно длине свободного пробега молекулы.Длина свободного пробега также зависит от диаметра молекулы, при этом более крупные молекулы с большей вероятностью столкнутся, чем мелкие молекулы, что представляет собой среднее расстояние, пройденное энергоносителем (молекулой) до столкновения. Легкие газы, такие как водород и гелий обычно имеют высокую теплопроводность . Плотные газы, такие как ксенон и дихлордифторметан, обладают низкой теплопроводностью.
Как правило, теплопроводность газов увеличивается с повышением температуры.
Теплопроводность жидкостей
Как уже писалось, в жидкостях теплопроводность обусловлена атомной или молекулярной диффузией, но физические механизмы объяснения теплопроводности жидкостей изучены недостаточно.
Жидкости, как правило, обладают лучшей теплопроводностью, чем газы, а способность течь делает жидкость подходящей для отвода избыточного тепла от механических компонентов. Тепло можно отводить, пропуская жидкость через теплообменник.Теплоносители, используемые в ядерных реакторах, включают воду или жидкие металлы, такие как натрий или свинец.
Теплопроводность неметаллических жидкостей обычно уменьшается с повышением температуры.
Теплопроводность натрия
Жидкий натрий используется в качестве теплоносителя в некоторых типах ядерных реакторов , поскольку он имеет высокую теплопроводность и низкое сечение поглощения нейтронов, необходимое для достижения высокого нейтронного потока в реакторе.Высокие свойства теплопроводности эффективно создают резервуар теплоемкости, который обеспечивает тепловую инерцию против перегрева.Специальный справочник: Теплофизические свойства материалов для ядерной энергетики: Учебное пособие и сбор данных.
IAEA-THPH, МАГАТЭ, Вена, 2008 г. ISBN 978–92–0–106508–7.
Теплопроводность воды и пара
Вода и пар являются общей жидкостью, используемой для теплообмена в первом контуре (от поверхности твэлов к потоку теплоносителя) и во втором контуре.Благодаря наличию и высокой теплоемкости, используется как для охлаждения, так и для обогрева. Особенно эффективен перенос тепла посредством испарения и конденсации воды из-за ее очень большой скрытой теплоты парообразования .Недостатком является то, что реакторы с водяным замедлителем должны использовать первичный контур высокого давления для поддержания воды в жидком состоянии и для достижения достаточного термодинамического КПД.Вода и пар также реагируют с металлами, обычно используемыми в таких отраслях, как сталь и медь, которые быстрее окисляются необработанной водой и паром.
Практически на всех тепловых электростанциях (угольных, газовых, атомных) вода используется в качестве рабочего тела (используется в замкнутом контуре между котлом, паровой турбиной и конденсатором) и теплоносителя (используется для обмена отходящего тепла с водоемом). или унести путем выпаривания в градирне).
Теплопроводность воды
Теплопроводность пара
IAEA-THPH, МАГАТЭ, Вена, 2008 г. ISBN 978–92–0–106508–7.
Теплопроводность гелия
Гелий — это химический элемент с атомным номером 2 , что означает наличие 2 протонов и 2 электронов в атомной структуре. Химический символ для гелия — это He .Это бесцветный, без запаха, без вкуса, нетоксичный, инертный, одноатомный газ, первый в группе благородных газов в периодической таблице. Его температура кипения самая низкая среди всех элементов.
Из-за относительно низкой молярной (атомной) массы гелия его теплопроводность, удельная теплоемкость и скорость звука в газовой фазе выше, чем у любого другого газа, кроме водорода.
Из-за своей инертности и высокой теплопроводности, нейтронной прозрачности, а также из-за того, что он не образует радиоактивных изотопов в реакторных условиях, гелий используется в качестве теплоносителя в некоторых газоохлаждаемых ядерных реакторах (например, высокотемпературные газоохлаждаемые реакторы – ВТГР).
Специальный справочник: Теплофизические свойства материалов для ядерной энергетики: Учебное пособие и сбор данных.IAEA-THPH, МАГАТЭ, Вена, 2008 г. ISBN 978–92–0–106508–7.
Теплопроводность твердых тел
Перенос тепловой энергии в твердых телах обычно может быть обусловлен двумя эффектами:
9 теплопроводность, приводящая к теплопроводности в твердом теле, теплопроводность может быть выражена как:
- миграцией свободных электронов
- колебательными волнами решетки (фононами)
k = k e + k ph
Теплопроводность металлов
Металлы являются твердыми телами и как таковые обладают кристаллическая структура, в которой ионы (ядра с окружающими их оболочками остовных электронов) занимают трансляционно эквивалентные позиции в кристаллической решетке.
Металлы в целом имеют высокую электропроводность , высокую теплопроводность и высокую плотность. Соответственно перенос тепловой энергии может быть обусловлен двумя эффектами:
- миграцией свободных электронов
- колебательными волнами решетки (фононами).
Когда электроны и фононы переносят тепловую энергию, приводящую к теплопроводности в твердом теле, теплопроводность может быть выражена как: их структура связана с наличием носителей заряда, в частности электронов .Электрическая и теплопроводность металлов обусловлена тем, что их внешние электроны делокализованы . Их вклад в теплопроводность называется электронной теплопроводностью , k e . Фактически, в чистых металлах, таких как золото, серебро, медь и алюминий, тепловой ток, связанный с потоком электронов, намного превышает небольшой вклад, обусловленный потоком фононов.
Напротив, для сплавов вкладом k ph в k уже нельзя пренебречь.
Закон Видемана-Франца — число Лоренца
При заданной температуре тепло- и электропроводность металлов пропорциональны , но повышение температуры увеличивает теплопроводность при уменьшении электропроводности. Это поведение количественно выражено в законе Видемана-Франца . Этот закон гласит, что отношение электронного вклада теплопроводности ( k ) в электропроводность (σ) металла пропорционально температуре (T).Качественно эта взаимосвязь основана на том факте, что перенос тепла и электричества связан с участием свободных электронов в металле. Электропроводность уменьшается с увеличением скорости частиц, потому что столкновения отклоняют электроны от прямого переноса заряда. Однако теплопроводность увеличивается со средней скоростью частиц, поскольку это увеличивает прямой перенос энергии. Закон Видемана-Франца обычно хорошо соблюдается при высоких температурах.
Однако в области низких и промежуточных температур закон нарушается из-за неупругого рассеяния носителей заряда.
Следует отметить, что общая корреляция между электропроводностью и теплопроводностью не выполняется для других материалов из-за повышенной важности переносчиков фононов для теплоты в неметаллах.
Теплопроводность неметаллов
Для твердых неметаллических тел , k определяется в первую очередь k ph , которая увеличивается по мере уменьшения частоты взаимодействий между атомами и решеткой.Фактически, решеточная теплопроводность является доминирующим механизмом теплопроводности в неметаллах, если не единственным. В твердых телах атомы колеблются вокруг своих положений равновесия (кристаллическая решетка). Колебания атомов не независимы друг от друга, а довольно сильно связаны с соседними атомами. Регулярность расположения решетки оказывает важное влияние на k ph , при этом кристаллические (хорошо упорядоченные) материалы, такие как кварц , имеют более высокую теплопроводность, чем аморфные материалы, такие как стекло.
При достаточно высоких температурах k ph ∝ 1/T.
кванта колебательного поля кристалла называются « фононами ». Фонон — это коллективное возбуждение в периодическом упругом расположении атомов или молекул в конденсированных средах, таких как твердые тела и некоторые жидкости. Фононы играют важную роль во многих физических свойствах конденсированного вещества, таких как теплопроводность и электропроводность. Фактически, для кристаллических неметаллических твердых тел, таких как алмаз, k ph может быть довольно большим, превышая значения k, связанные с хорошими проводниками, такими как алюминий.В частности, алмаз обладает самой высокой твердостью и теплопроводностью (k = 1000 Вт/м·К) среди всех объемных материалов.
Теплопроводность диоксида урана
Большинство PWR используют урановое топливо , которое находится в форме диоксида урана . Диоксид урана представляет собой полупроводниковое твердое вещество черного цвета с очень низкой теплопроводностью .
.UO2 прессуется в гранулы , затем эти гранулы спекаются в твердое тело.С другой стороны, диоксид урана имеет очень высокую температуру плавления и хорошо известное поведение
Эти таблетки затем загружаются и герметизируются внутри топливного стержня (или топливной шашки), который изготовлен из сплавов циркония из-за его очень низкого поперечного сечения поглощения (в отличие от нержавеющей стали). Поверхность трубы, которая покрывает таблетки, называется оболочкой твэла . Топливные стержни являются базовым элементом ТВС.
Теплопроводность диоксида урана очень низкая по сравнению с металлическим ураном, нитридом урана, карбидом урана и циркониевым плакирующим материалом.Теплопроводность является одним из параметров, определяющих среднюю температуру топлива . Эта низкая теплопроводность может привести к локализованному перегреву в центральной линии топлива, поэтому этого перегрева следует избегать.
Перегрев топлива предотвращается за счет поддержания пиковой линейной скорости нагрева в установившемся режиме (LHR) или коэффициента теплового потока в горячем канале – F Q (z) ниже уровня, при котором происходит плавление центральной линии топлива. Расширение топливной таблетки при расплавлении центральной линии может привести к тому, что таблетка создаст нагрузку на оболочку вплоть до разрушения.
Теплопроводность твердого UO 2 с плотностью 95% оценивается по следующей зависимости [Клименко; Зорин]:
, где τ = T/1000. Неопределенность этой корреляции составляет +10% в диапазоне от 298,15 до 2000 К и +20% в диапазоне от 2000 до 3120 К. А.В. Клименко и В.М. Зорин. MEI Press, 2003.
Специальная ссылка: Теплофизические свойства материалов для ядерной энергетики: Учебное пособие и сбор данных.IAEA-THPH, МАГАТЭ, Вена, 2008 г. ISBN 978–92–0–106508–7.
Теплопроводность циркония
Цирконий представляет собой блестящий серо-белый прочный переходный металл, напоминающий гафний и, в меньшей степени, титан.
Цирконий в основном используется в качестве огнеупора и глушителя, хотя небольшие количества используются в качестве легирующего агента из-за его высокой коррозионной стойкости. Циркониевый сплав (например, Zr + 1% Nb) широко используется в качестве оболочки топлив ядерных реакторов.Желаемыми свойствами этих сплавов являются низкое сечение захвата нейтронов и коррозионная стойкость при нормальных условиях эксплуатации. Циркониевые сплавы имеют более низкую теплопроводность (около 18 Вт/м·К), чем чистый металлический цирконий (около 22 Вт/м·К).
Специальный справочник: Теплофизические свойства материалов для ядерной энергетики: Учебное пособие и сбор данных. IAEA-THPH, МАГАТЭ, Вена, 2008 г. ISBN 978–92–0–106508–7.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера для приема файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его.
Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Теплопроводность и коэффициент расширения
Теплопроводность свойство любого материала передавать тепло от одной точки к другой.Конечно, для того, чтобы тепло «текло», необходимо необходимая для существования разности температур в непрерывном сечении материала. Термальный проводимость аналогична электропроводности. Точно так же тепловое сопротивление является обратной величиной теплового сопротивления. проводимость, так как электрическое сопротивление является обратной величиной электропроводности.Коэффициент расширения скорость, с которой материал будет увеличиваться в длину при повышении температуры. Большинство материалов растут в довольно линейным образом, особенно в пределах определенного диапазона температур.Положительный коэффициент расширения указывает на то, что материал становится длиннее по мере увеличения его температуры.
Таковы большинство металлов. Лед — это известный пример отрицательного коэффициента расширения, так как он сжимается в длину с увеличением температуры (другими словами, лед расширяется по мере охлаждения).
Воздух (негазированный) 0,0003 Глинозем 0.276 Глинозем (85%) 0,118 Алюминий 2,165 0,23 2,7 0,81 Бериллия (99,5%) 1.969 Бериллия (97%) 1,575 Бериллия (95%) 1,161 Бериллий 1. 772
Бериллий-медь 1,063 Нитрид бора 0,394 Латунь (70/30) 1.220 Медь 3,937 0,17 8,9 0,45 Медь/Инв c /Медь 1,64 0,084 8,4 .020 Медь/Mo d /Медь 1.82 0,060 9,9 0,18 Медь/Mo d -Cu/Медь 2,45-2,80 0,60-0,10 9,4 0,26-0,30 Алмаз (комнатная температура) 6. 299
Эпоксидная смола 0.002 Эпоксидная смола (теплопроводящая) 0,008 ФР-4 (Г-10) 0,003 GaAs 0.591 Стекло 0,008 Золото 2,913 Компаунд радиатора 0.004 Гелий (жидкий) 0,000307 Инвар 0,11 0,013 8. 1
0,014 Железо 0.669 Ковар 0,17 0,59 8,3 0,020 Свинец 0,343 Магний 1.575 Слюда 0,007 Молибден 1,299 Монель 0,197 Майлар 0. 002
Никель 0,906 Азот (жидкий) 0,001411 Фенольный 0.002 Платина 0,734 Сапфир (ось А) 0,32 Сапфир (ось C) 0.35 Кремний (чистый) 1,457 Кремний (0,0025 Ом-см) 1,457 Карбид кремния 0. 90
Диоксид кремния (аморфный) 0,014 Диоксид кремния (кварц, ось а) 0,059 Диоксид кремния (кварц, ось с) 0.11 Силиконовая смазка 0,002 Силиконовый каучук 0,002 Нитрид кремния 0.16 — 0,33 Серебро 4. 173
Нержавеющая сталь (321) 0,146 Нержавеющая сталь (410) 0.240 Сталь (низкоуглеродистая) 0,669 Тефлон 0,002 Олово 0.630 Титан 0,219 0,086 4,4 0,016 Вольфрам 1,969 Вода 0. 0055
Цинк 1,024 a: приблизительные значения от 0 °C до 100 °C
b: Теплопроводность, деленная на удельный вес
(представлено доктором Карлом Цвебеном и К.А. Schmidt)
c: Инвар
d: Молибден
Теплопроводность сплавов платины при высоких температурах
Преимущество использования платины (Pt) в промышленности обусловлено ее уникальными свойствами, такими как ее каталитическая активность, высокая температура плавления (1), пластичность (2, 3) и химическая инертность в широком диапазоне температур (4, 5).Платина используется для производства биомедицинских компонентов, специальных химикатов, топливных элементов и катализаторов для борьбы с загрязнением окружающей среды, таких как автомобильные выхлопы, а также для ювелирных изделий, термопар и катодной защиты корпусов кораблей (3).
Одним из типичных применений платины являются электронные устройства, при этом толстопленочные проводники входят в число основных продуктов (6). Легирующие элементы, выбранные из металлов платиновой группы и благородных металлов, обычно используются для повышения прочности или защиты поверхности от неблагоприятных условий эксплуатации (3).Однако добавление легирующего элемента может ухудшить проводимость. До настоящего времени данные о проводимости платиновых сплавов были ограничены (7-12).
Настоящее исследование посвящено изучению параметров теплопроводности различных платиновых сплавов при высоких температурах. Во-первых, будет исследована зависимость теплопроводности от состава, и результаты будут упорядочены в соответствии с периодической таблицей; во-вторых, будет исследовано влияние наклепа; в-третьих, будет исследована температурная зависимость теплопроводности.
Зависимость теплопроводности от состава
Теплопроводность при 300 K для сплавов Pt в зависимости от концентрации растворенного вещества показана на рисунке 1 вместе с данными для чистой Pt (1, 13, 14).
Ванадий (V) и никель (Ni) были выбраны в качестве растворенных веществ. Никель принадлежит к той же колонке, что и Pt в периодической таблице (Pt-Ni — изоэлектронная система), а V расположен горизонтально далеко от Pt (Pt-V — неизоэлектронная система). Все сплавы, использованные в этом исследовании, имеют гранецентрированную кубическую форму (f.в.в) однофазный; тогда как в системе Pt-V превращение порядок-беспорядок происходит при стехиометрии 3 : 1. Данные для Pt 3 В с Г.К. неупорядоченная структура и упорядоченная структура D0 22 взяты из более ранней работы (15). Отметим, что термообработку при 1573 К в течение 1 ч проводили для достижения неупорядоченного состояния в Pt 3 V, а старение при 1020 К в течение 168 ч — для реакции упорядочения.
Рис. 1
Композиционная зависимость теплопроводности при 300 К в сплавах Pt-Ni и Pt-V.Данные для чистой Pt представлены сплошным квадратом на оси (1, 13, 14). Рекомендуемые значения для чистой Pt в этих источниках данных аналогичны.
Сплошной треугольник — данные для Pt 3 В с упорядоченной структурой D0 22 (15)
Теплопроводность чистой Pt, полученная в настоящем эксперименте, составила 77,8 Вт·м -1 К -1 , что несколько превышает литературные значения (1, 13, 14). Она монотонно уменьшалась с увеличением концентрации растворенного вещества для обоих сплавов.В используемых диапазонах составов графики зависимости проводимости от состава в каждом случае характеризуются резким максимумом при чистой Pt. Зависимость от состава более выражена в сплаве Pt-V, при этом добавление всего двух атомных процентов V снижает теплопроводность Pt наполовину. Скорость снижения теплопроводности становится меньше при более высоких концентрациях V, обычно превышающих десять атомных процентов.
Из рис. 1 видно, что теплопроводность увеличивается при образовании упорядоченной фазы D0 22 состава Pt 3 В.Это увеличение проводимости за счет упорядочения, по-видимому, является общей чертой, которая также проявляется в Pt 3 Cr со структурой L1 2 и в Ni 3 V(D0 22 ), Ni 3 Mn( L1 2 ) и Ni 3 Fe(L1 2 ) (15). Теплопроводность обычно ухудшается из-за рассеяния носителей в кристаллической решетке. Топологический и конфигурационный беспорядок, такой как примеси, вакансии и дефекты решетки, затрудняют течение теплоносителей.Следовательно, хорошо упорядоченные интерметаллиды должны иметь более высокую проводимость, чем их неупорядоченные сплавы, если предположить, что концентрации носителей в обеих фазах не меняются (16).
Главный вопрос, на который необходимо ответить, заключается в том, что отвечает за теплопроводность в сплавах Pt. Теплопроводность металлических материалов обычно состоит из электронной составляющей и фононной составляющей. Соотношение Видемана-Франца является критерием идентификации носителя теплопроводности.Закон Видемана-Франца гласит, что при высоких температурах отношение теплопроводности к электропроводности (обратное удельному сопротивлению) для всех металлов пропорционально абсолютной температуре. Когда электронный компонент вносит основной вклад в общую теплопроводность λ, соотношение Видемана-Франца должно выполняться (17-19), как в (уравнении i):
(i)
, где L число Лоренца, T — абсолютная температура, σ — электрическая проводимость.Константа универсальности λ/σ оказалась равной 7,5 × 10 -6 Ом K -1 при 300 К для чистых металлов (17).
Соотношение Видемана-Франца было исследовано для исследуемых сплавов Pt. На рис. 2 показана зависимость электропроводности (обратная величина удельного электрического сопротивления) от теплопроводности для сплавов Pt-Ni и Pt-V. Прямая линия показывает соотношение Видемана-Франца, определяемое (уравнением i) при 300 К. Все графики для сплавов Pt, включая чистую Pt, близки к этой линии.Это указывает на то, что сплавы Pt удовлетворяют соотношению Видемана-Франца при 300 К, даже высококонцентрированные сплавы.
Доминирующий носитель теплопроводности в сплавах Pt, таким образом, приписывается электрону, а не фонону: более конкретно, 6 s электронов считаются ответственными за теплопроводность.
Рис. 2
Зависимость Видемана-Франца для сплавов Pt-Ni и Pt-V при 300 К. Составы сплавов указаны в атомных процентах
Зависимость от составляющих
Рис. в сплавах Pt показывает резкое снижение теплопроводности при низких концентрациях растворенного вещества, до 2 атомных процентов, по сравнению со значением для чистой Pt.Хорошо известно, что Pt имеет широкий диапазон растворимости в твердом состоянии для большинства легирующих элементов (20). В этом разделе мы сосредоточимся на теплопроводности различных сплавов Pt-2 at.% X, чтобы определить влияние растворенного вещества X на теплопроводность Pt.
На рис. 3 приведены теплопроводности сплавов Pt-2 at.% X при 300 K. Раствор X расположен в порядке периодической таблицы. Можно ясно заметить, что добавление растворенного элемента снижает теплопроводность Pt. При принадлежности растворенного вещества X к В-подгруппе (Cu, Ga, Ge) в первый длительный период теплопроводность монотонно уменьшается по мере увеличения горизонтального расстояния X от растворителя Pt.Эта тенденция сохраняется и для растворенного вещества X во втором длительном периоде. Стоит отметить, что Al и Si, которые расположены выше Ga и Ge соответственно, также попадают на эту же линию.
Рис. 3
Теплопроводность при 300 К сплавов Pt-2 ат.% X в зависимости от атомного номера растворенного вещества X.
Сплошной черный квадрат показывает теплопроводность чистой Pt.
Данные для Pt-2 ат.% Al и Pt-2 ат.% Si представлены сплошными ромбовидными символами.
As, Pb и Bi не растворяются в Pt (20).
Данные по Tc отсутствуют, так как сплав нестабилен.
Нет данных для Zn, Cd, Hg и Tl, поскольку их более низкие температуры кипения препятствуют получению слитков сплава дуговой плавкой. Норбери изучал изменение удельного электрического сопротивления при добавлении растворенных веществ к Fe, Ni, Cu, Ag, Au и Mg, а также расплавленных состояний Na и K. Было обнаружено эмпирическое правило, согласно которому удельное электрическое сопротивление бинарных сплавов увеличивается с увеличением положения в них. Периодическая таблица растворенного элемента становится горизонтально удаленной от таблицы основного компонента.Текущие результаты подразумевают, что правило Норбери обычно выполняется для явлений переноса, управляемых электронами. Однако, в отличие от элементов подгруппы B, поведение более сложное, когда растворенное вещество принадлежит к остальным переходным элементам. В течение первого длительного периода теплопроводность монотонно уменьшается по мере удаления X от Pt. Это ломается в Mn. Разрушение происходит на элементах, удаленных от Pt, когда растворенное вещество X принадлежит к третьему длинному периоду. Примечательно, что Re наиболее существенно снижает теплопроводность Pt.Также следует отметить тот факт, что значения теплопроводности для растворенных веществ, принадлежащих к одной колонке, довольно близки друг к другу, что обычно демонстрируется в колонках IVA, VA и VIII (Fe, Ru, Os). Данные на рисунке 3 также свидетельствуют о том, что теплопроводность больше зависит от столбца растворенного вещества X и меньше зависит от периода.
Зависимость от деформационного упрочнения
Для изучения чувствительности к условиям изготовления теплопроводность была исследована как функция обжатия при холодной прокатке для некоторых платиновых сплавов.На рис. 4 показаны результаты для чистой Pt и для трех сплавов Pt. Небольшое снижение теплопроводности наблюдалось в чистой Pt, как правило, при степени обжатия холодной прокаткой выше 30%, в то время как для высококонцентрированных сплавов с более низкой проводимостью сохраняется довольно постоянное значение. Из полученных результатов следует, что теплопроводность этих сплавов в основном определяется исходным составом и вряд ли дефектной структурой, развившейся в процессе изготовления.
Рис. 4
Теплопроводность чистой Pt и сплавов Pt в зависимости от степени обжатия холодной прокаткой.Значения теплопроводности были измерены при 300 K
Зависимость от температуры
Зависимость теплопроводности сплавов Pt-Ni от температуры показана на рисунке 5 вместе со значениями для чистой Pt из источников данных, представленных пунктирной линией. (13, 14). Теплопроводность чистой Pt, измеренная в настоящей работе, монотонно возрастает с повышением температуры и достигает примерно 95 Вт·м -1 К -1 при 1100 К.Монотонный рост также подтверждается для справочных данных, хотя величина систематически ниже. Добавление Ni не меняет общей тенденции монотонного роста, а приводит лишь к смещению всех данных в сторону более низких значений. Кроме того, тщательное наблюдение показывает, что температурный коэффициент становится больше с увеличением концентрации никеля, и все данные сходятся при более высоких температурах.
Рис. 5
Зависимость теплопроводности от температуры для сплавов Pt-Ni.Данные для чистой Pt, рекомендуемые в источниках данных, показаны пунктирной линией (13, 14). Значения из источников данных аналогичны
Температурный коэффициент α в диапазоне температур от 300 до 1100 K был первоначально оценен из (Уравнение ii):
где λ 300 K и λ 1100 K – коэффициенты теплопроводности при указанных температурах. На рисунке 6 температурные коэффициенты, полученные для сплавов Pt, представлены в зависимости от теплопроводности при 300 K.
Рис. 6
Корреляция при 300 K между теплопроводностью и температурным коэффициентом для сплавов Pt-Ni и Pt-V. Каждое значение имеет состав сплава.
Десять значений для сплавов Pt-2 at.% X нанесены на график.
Элементы X второго длительного периода
Чистая Pt имела теплопроводность 77,8 Вт·м -1 К -1 при 300 К с положительным температурным коэффициентом 2,9 × 10 -4 К -1 .Теплопроводность монотонно уменьшается с ростом концентрации Ni, что сопровождается увеличением коэффициента. Такая обратная корреляция более четко видна на полулогарифмическом графике, см. рис. 6. Интересно, что большинство сплавов Pt-V имеют такую же корреляцию, за исключением сплава Pt-16V. Кроме того, различные выбранные элементы из второго длинного периода, показанного незакрашенными квадратами, также сохраняют ту же корреляцию, что означает, что корреляция может иметь универсальный характер. Обратная корреляция между α и λ 300 K может быть общей чертой для металлических материалов и хорошо задокументирована не только для бинарных твердых растворов, но и для многокомпонентных материалов, таких как стали и жаропрочные сплавы, а также для интерметаллических соединений (15, 22).
Выводы
Теплопроводность сплавов Pt была всесторонне исследована в зависимости от концентрации растворенного вещества, наклепа и температуры. Получены следующие результаты:
Теплопроводность сплавов Pt в основном определяется как составом сплава, так и температурой, и практически не зависит от деформационного упрочнения.
Легирование снижает теплопроводность Pt, а зависимость проводимости от состава характеризуется резким максимумом у чистой Pt.Соотношение Видемана-Франца для сплавов Pt указывает на то, что доминирующими носителями теплопроводности являются электроны.
Установлено, что теплопроводность монотонно уменьшается по мере того, как положение растворенного элемента в Периодической таблице удаляется по горизонтали от положения Pt (но только для элементов подгруппы B). Это аналог правила Норбери, первоначально предложенного для удельного электрического сопротивления.
Непрерывное увеличение теплопроводности с температурой наблюдается для сплавов Pt в диапазоне температур от 300 до 1100 К.

 / _ м, (1-13) Он был все еще открыт Исааком Ньютоном (1643-1727).Первоначально считалось, что коэффициент теплопередачи а характеризует свойства протекающих жидкостей или газов. Благодаря сравнительно недавним исследованиям в области теории теплопередачи, была установлена сложная природа этой величины elucidated. In в этой книге целая большая глава посвящена проблеме определения коэффициента теплоотдачи. 1-1.Дает представление об относительном размере этого параметра.
/ _ м, (1-13) Он был все еще открыт Исааком Ньютоном (1643-1727).Первоначально считалось, что коэффициент теплопередачи а характеризует свойства протекающих жидкостей или газов. Благодаря сравнительно недавним исследованиям в области теории теплопередачи, была установлена сложная природа этой величины elucidated. In в этой книге целая большая глава посвящена проблеме определения коэффициента теплоотдачи. 1-1.Дает представление об относительном размере этого параметра. Эти 2 равны* Вы также мул закона Ома: Пишите в соответствующем формате (У4) Коэффициент передачи тепла R 1 / alₜ: Называемое тепловое сопротивление (1-15.
Эти 2 равны* Вы также мул закона Ома: Пишите в соответствующем формате (У4) Коэффициент передачи тепла R 1 / alₜ: Называемое тепловое сопротивление (1-15. (0.000222 + 0.000102) h•град / ккал. Это меньше половины предыдущего значения.
(0.000222 + 0.000102) h•град / ккал. Это меньше половины предыдущего значения.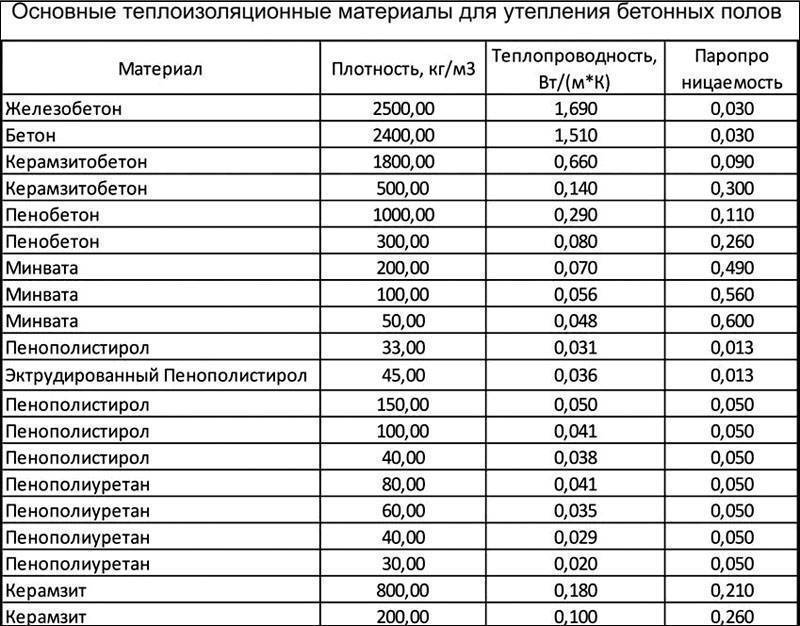 Необходимо только, чтобы физические характеристики материала (влажность, плотность…), определяемые условиями эксплуатации, соответствовали табличным данным, приведенным в справочнике.
Необходимо только, чтобы физические характеристики материала (влажность, плотность…), определяемые условиями эксплуатации, соответствовали табличным данным, приведенным в справочнике. Для чистых металлов теплопроводность и электропроводность пропорциональны друг другу.
Для чистых металлов теплопроводность и электропроводность пропорциональны друг другу.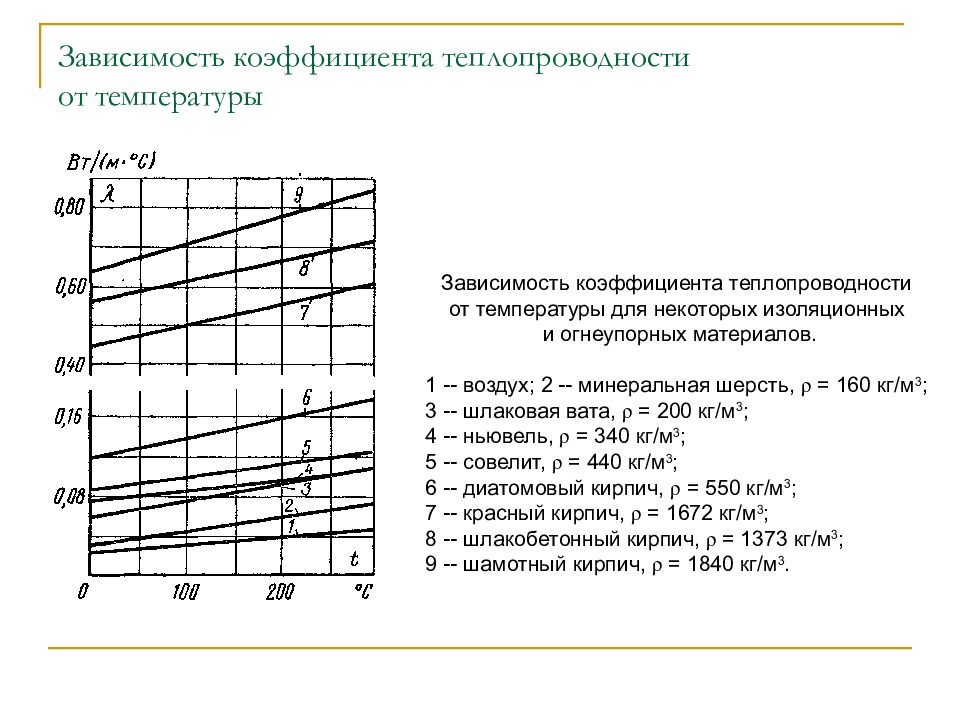 Исключением является вода и глицерин. Значения коэффициентов теплопроводности капельных жидкостей находится в интервале l = 0,7 – 0,1 Вт/(м·град).
Исключением является вода и глицерин. Значения коэффициентов теплопроводности капельных жидкостей находится в интервале l = 0,7 – 0,1 Вт/(м·град).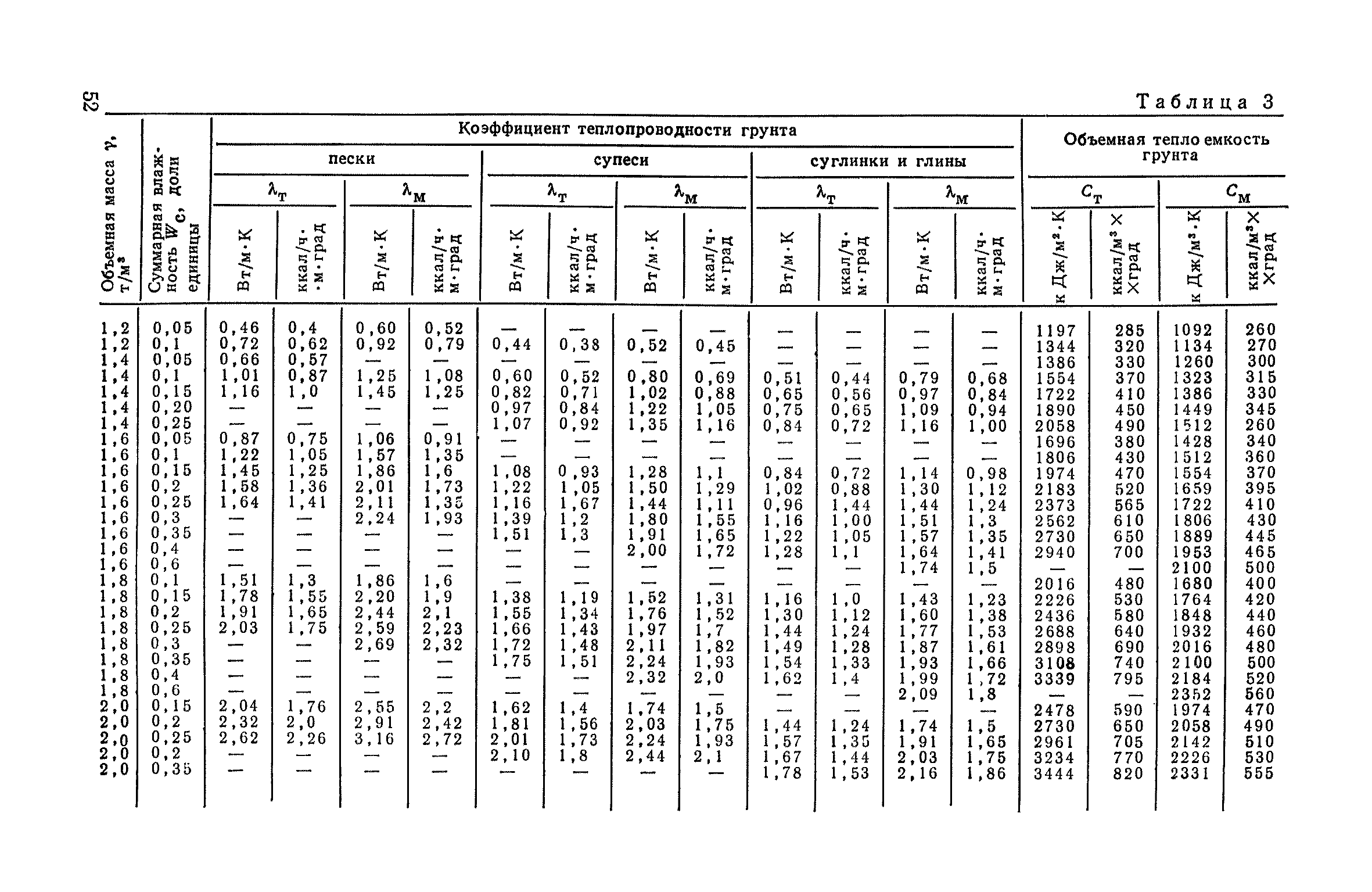
 е. улучшать их теплоизоляцию.
е. улучшать их теплоизоляцию.
 ..550 кг/куб.м, 15% влажности) 0,15
..550 кг/куб.м, 15% влажности) 0,15
 М., Эмиров С.Н., Абдулагатова З.З., Аскеров С.Ю. Влияние давления и температуры на теплопроводность горных пород. Данные J Chem Eng. 2006; 51: 22–33.
М., Эмиров С.Н., Абдулагатова З.З., Аскеров С.Ю. Влияние давления и температуры на теплопроводность горных пород. Данные J Chem Eng. 2006; 51: 22–33.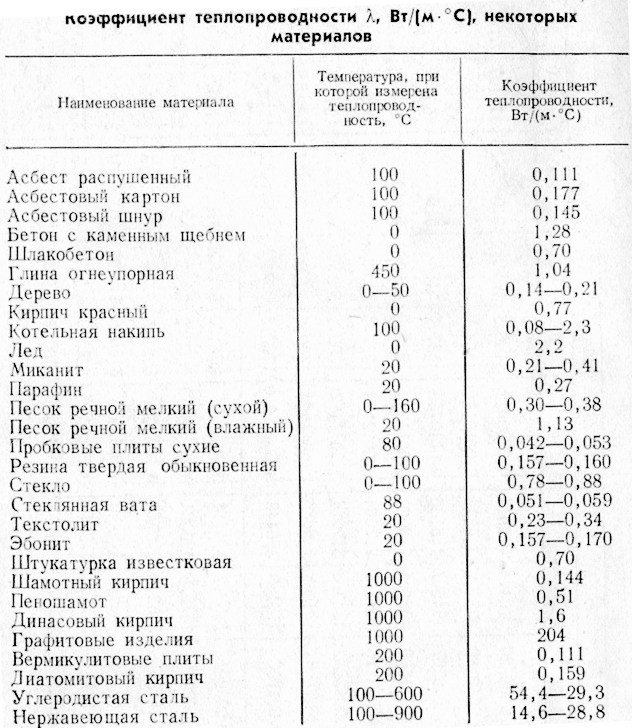 с. 87–165.
с. 87–165.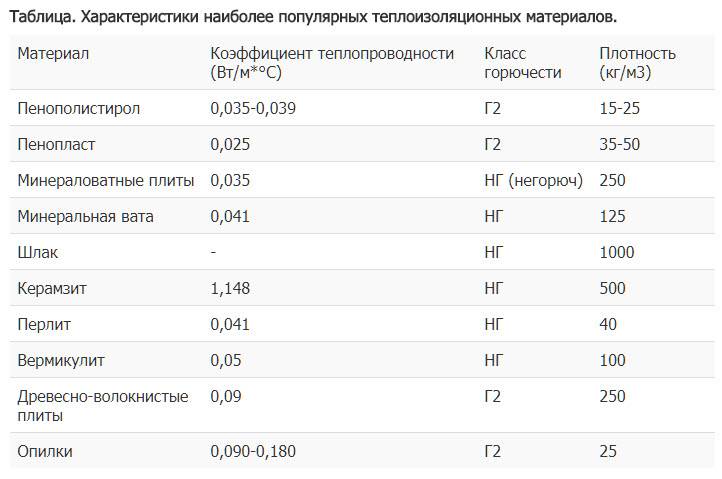 Дж., Кулацки Ф.А., Кристенсен Р.Н. Применение интегральных методов для прогнозирования теплопередачи от хранилища ядерных отходов. Колумбус: отчет об открытом файле ONWI-495, Battelle Memorial Institute; 1983. с.12–7. https://doi.org/10.2172/5754517.
Дж., Кулацки Ф.А., Кристенсен Р.Н. Применение интегральных методов для прогнозирования теплопередачи от хранилища ядерных отходов. Колумбус: отчет об открытом файле ONWI-495, Battelle Memorial Institute; 1983. с.12–7. https://doi.org/10.2172/5754517.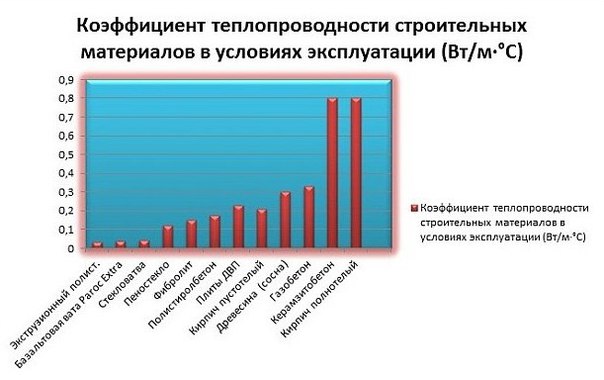 Бык AAPG. 2019;103(8):1787–809.
Бык AAPG. 2019;103(8):1787–809. Геофиз J Междунар. 2014; 196: 291–311.
Геофиз J Междунар. 2014; 196: 291–311. 1970; 10 (1–3): 67–77.
1970; 10 (1–3): 67–77. М., Матос Ч.Р., Родригес Н.В., Перейра АJSC, Коста Дж.Дж.Влияние температуры на теплопроводность гранита с высокой теплопродукцией из Центральной Португалии. Дж. Ибер Геол. 2019;45(1):147–61.
М., Матос Ч.Р., Родригес Н.В., Перейра АJSC, Коста Дж.Дж.Влияние температуры на теплопроводность гранита с высокой теплопродукцией из Центральной Португалии. Дж. Ибер Геол. 2019;45(1):147–61. Тепловой поток и термический режим литосферы в Северо-Восточной Германской котловине. Тектонофизика. 2008; 460: 215–29.
Тепловой поток и термический режим литосферы в Северо-Восточной Германской котловине. Тектонофизика. 2008; 460: 215–29. Геотерм Энерджи. 2015;3(17):1–29.
Геотерм Энерджи. 2015;3(17):1–29. Геотермия. 2015b;58:94.
Геотермия. 2015b;58:94.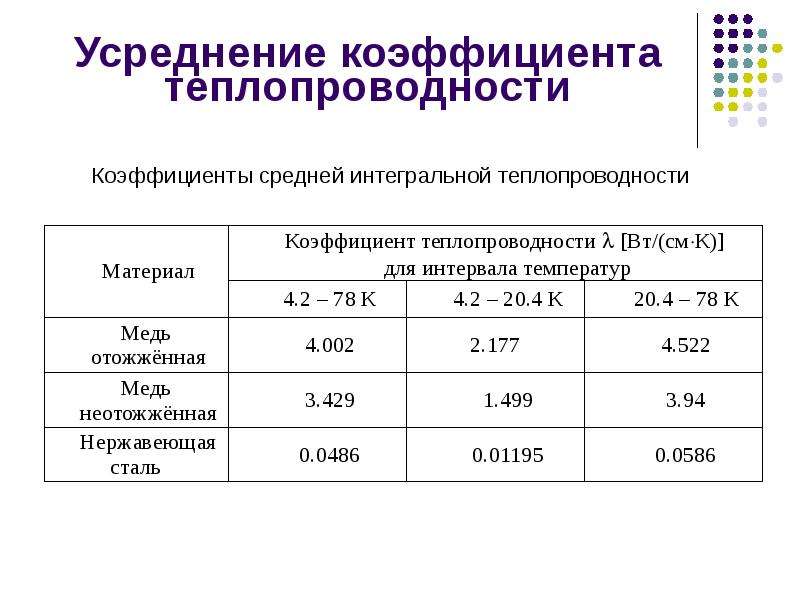 Физ Планета Земля Интер. 1992; 69: 299–303.
Физ Планета Земля Интер. 1992; 69: 299–303.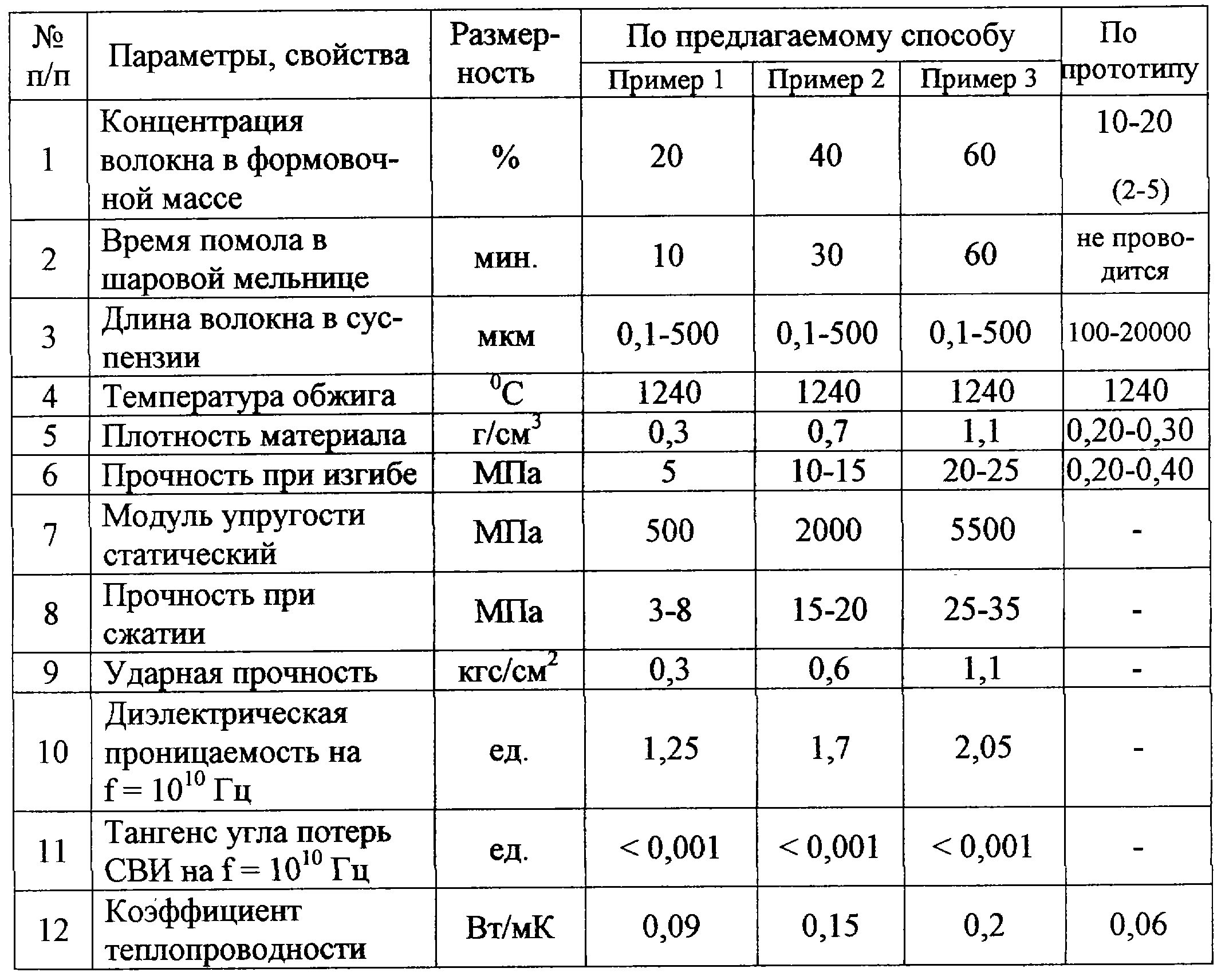 Термические свойства гнейсов и амфиболитов — исследования образцов горных пород KTB при высоких давлениях и температурах. Тектонофизика. 1998; 291:173–178.
Термические свойства гнейсов и амфиболитов — исследования образцов горных пород KTB при высоких давлениях и температурах. Тектонофизика. 1998; 291:173–178. И., Блессент Д., Кордоба С., Лопес-Санчес Дж., Раймонд Дж., Парра-Паласио Э. Оценка геотермального потенциала вулкана Невадо-дель-Руис на основе измерений теплопроводности горных пород и численного моделирования теплопередачи. JS Am Earth Sci. 2018;81:153–64.
И., Блессент Д., Кордоба С., Лопес-Санчес Дж., Раймонд Дж., Парра-Паласио Э. Оценка геотермального потенциала вулкана Невадо-дель-Руис на основе измерений теплопроводности горных пород и численного моделирования теплопередачи. JS Am Earth Sci. 2018;81:153–64. Дордрехт: Клювер; 1988. с. 449–66.
Дордрехт: Клювер; 1988. с. 449–66.
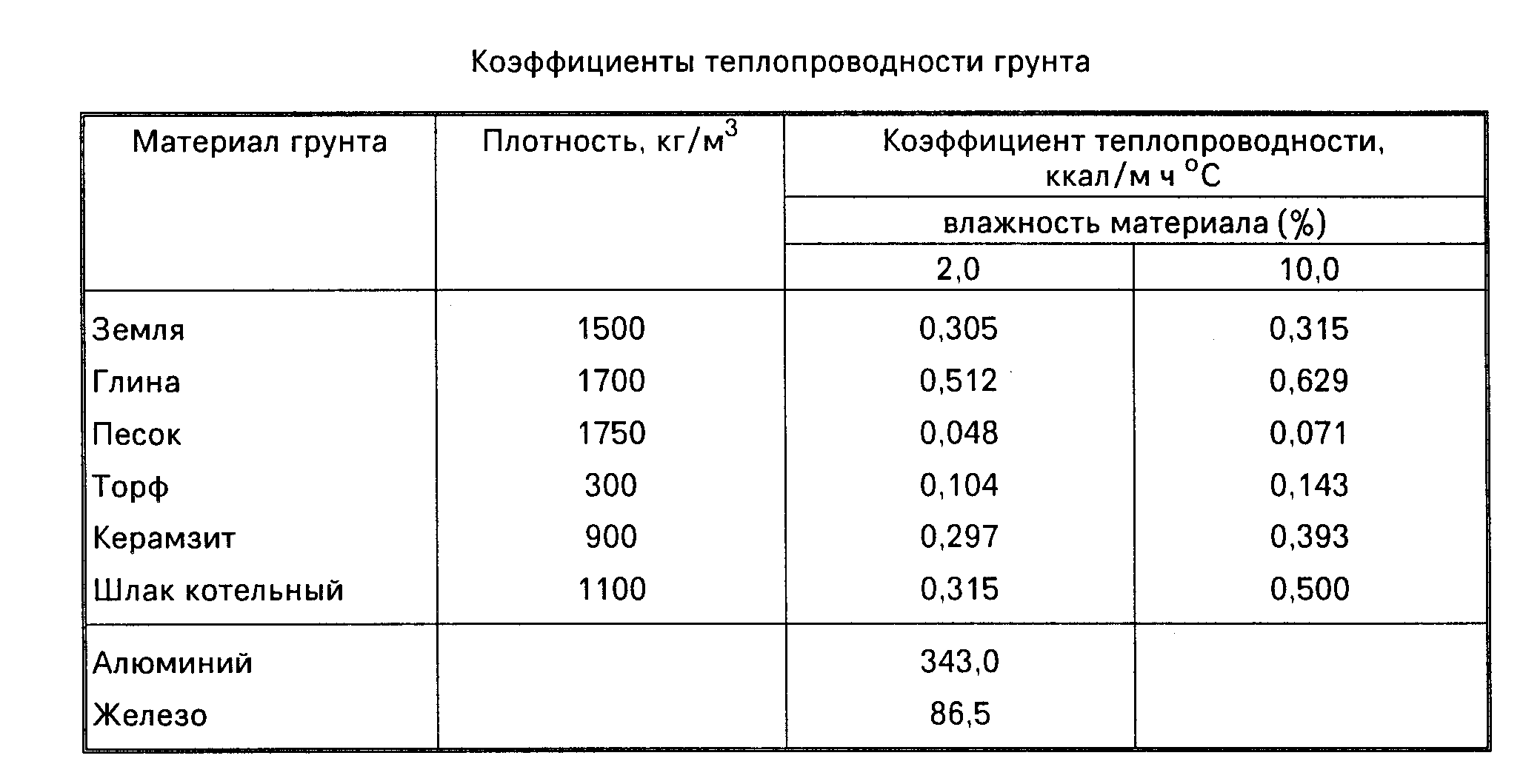 И наоборот, толщина стенки трубы из ХПВХ влияет на температуру ее поверхности, поскольку она обладает гораздо более высокой термостойкостью, чем сталь. Толщина стенки зависит от сортамента и размера трубы.
И наоборот, толщина стенки трубы из ХПВХ влияет на температуру ее поверхности, поскольку она обладает гораздо более высокой термостойкостью, чем сталь. Толщина стенки зависит от сортамента и размера трубы.
 Чтобы определить специфику вашей трубопроводной системы, обсудите ее с командой экспертов Corzan Industrial Systems.
Чтобы определить специфику вашей трубопроводной системы, обсудите ее с командой экспертов Corzan Industrial Systems.
 Увы, это не так. Таким образом, ни один из материалов, с которыми нам приходится жить, не может быть действительно квалифицирован термином «изолятор». Наиболее важная причина, по которой экспериментальная проверка кодов CFD (Computational Fluid Dynamics) является катастрофой (за исключением высоких скоростей), заключается в том, что всегда играет роль сопряженная теплопередача через опору.Рассмотрим, например, компонент на подложке в условиях естественной конвекции. Даже самый лучший изолятор не может предотвратить потери в 10% и более. Следовательно, адиабатические поверхности, так любимые численными аналитиками, не могут быть реализованы на практике.
Увы, это не так. Таким образом, ни один из материалов, с которыми нам приходится жить, не может быть действительно квалифицирован термином «изолятор». Наиболее важная причина, по которой экспериментальная проверка кодов CFD (Computational Fluid Dynamics) является катастрофой (за исключением высоких скоростей), заключается в том, что всегда играет роль сопряженная теплопередача через опору.Рассмотрим, например, компонент на подложке в условиях естественной конвекции. Даже самый лучший изолятор не может предотвратить потери в 10% и более. Следовательно, адиабатические поверхности, так любимые численными аналитиками, не могут быть реализованы на практике. В этом диапазоне проводимость воздуха увеличивается примерно на 30%. Однако основной тепловой путь обычно по-прежнему покрыт пластиком; следовательно, преобладает температурная зависимость пластика. Обратите внимание на то, что некоторые материалы показывают значение ниже, чем у воздуха. Это может быть реализовано только в том случае, если размер пор, заполненных воздухом, меньше длины свободного пробега молекул воздуха.
В этом диапазоне проводимость воздуха увеличивается примерно на 30%. Однако основной тепловой путь обычно по-прежнему покрыт пластиком; следовательно, преобладает температурная зависимость пластика. Обратите внимание на то, что некоторые материалы показывают значение ниже, чем у воздуха. Это может быть реализовано только в том случае, если размер пор, заполненных воздухом, меньше длины свободного пробега молекул воздуха. 042
042 Обратите внимание, что закон Фурье применим ко всей материи, независимо от ее состояния (твердое, жидкое или газообразное), поэтому он также определен для жидкостей и газов.
Обратите внимание, что закон Фурье применим ко всей материи, независимо от ее состояния (твердое, жидкое или газообразное), поэтому он также определен для жидкостей и газов. Поскольку межмолекулярное расстояние намного больше, а движение молекул более хаотично для жидкого состояния, чем для твердого состояния, перенос тепловой энергии менее эффективен.Следовательно, теплопроводность газов и жидкостей обычно меньше, чем у твердых тел. В жидкостях теплопроводность обусловлена атомной или молекулярной диффузией. В газах теплопроводность обусловлена диффузией молекул с более высокого энергетического уровня на более низкий уровень.
Поскольку межмолекулярное расстояние намного больше, а движение молекул более хаотично для жидкого состояния, чем для твердого состояния, перенос тепловой энергии менее эффективен.Следовательно, теплопроводность газов и жидкостей обычно меньше, чем у твердых тел. В жидкостях теплопроводность обусловлена атомной или молекулярной диффузией. В газах теплопроводность обусловлена диффузией молекул с более высокого энергетического уровня на более низкий уровень.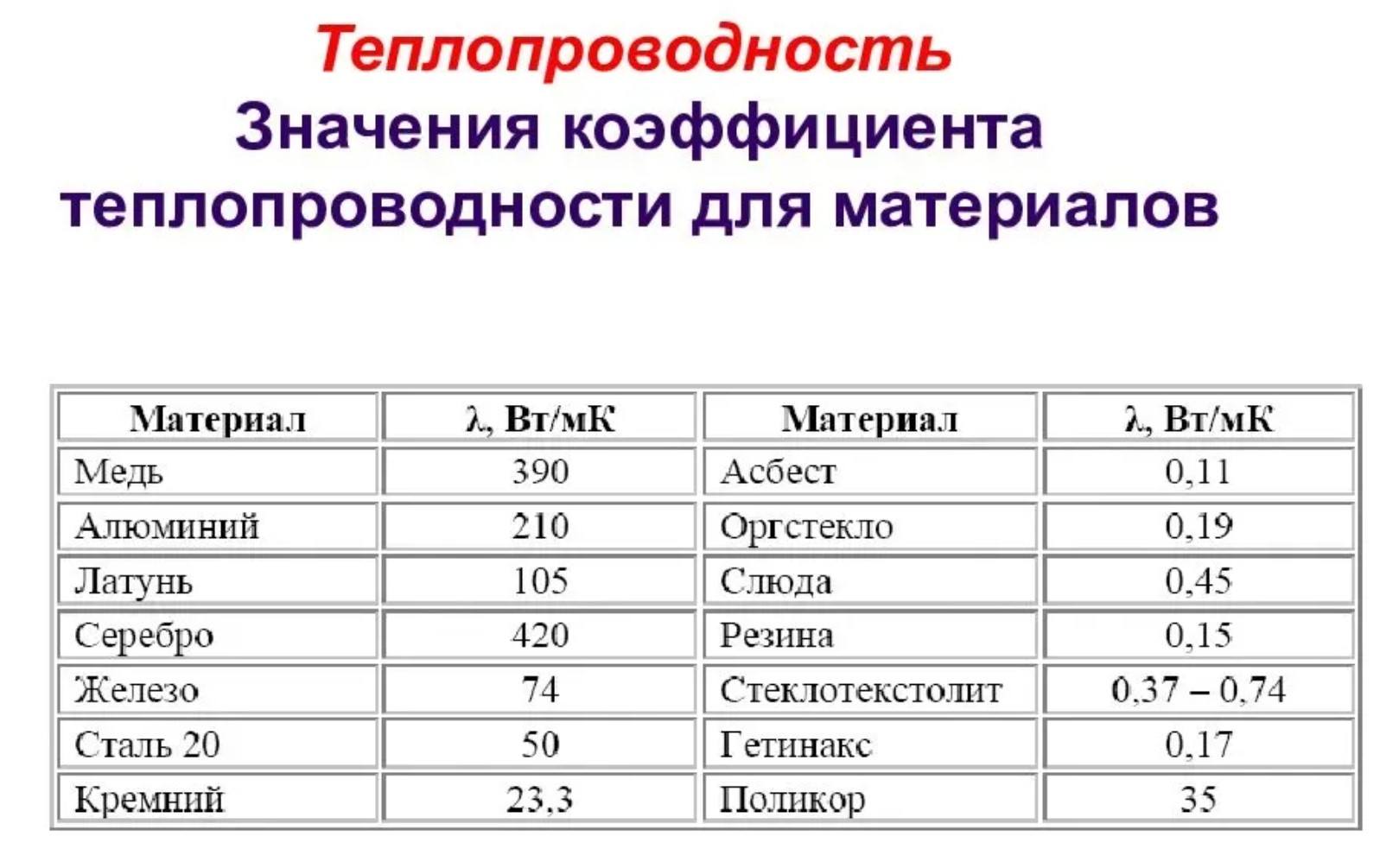 Чередование газового кармана и твердого материала приводит к тому, что тепло должно передаваться через множество поверхностей раздела, что приводит к быстрому снижению коэффициента теплопередачи.
Чередование газового кармана и твердого материала приводит к тому, что тепло должно передаваться через множество поверхностей раздела, что приводит к быстрому снижению коэффициента теплопередачи. Жидкости, как правило, обладают лучшей теплопроводностью, чем газы, а способность течь делает жидкость подходящей для отвода избыточного тепла от механических компонентов. Тепло можно отводить, пропуская жидкость через теплообменник.Теплоносители, используемые в ядерных реакторах, включают воду или жидкие металлы, такие как натрий или свинец.
Жидкости, как правило, обладают лучшей теплопроводностью, чем газы, а способность течь делает жидкость подходящей для отвода избыточного тепла от механических компонентов. Тепло можно отводить, пропуская жидкость через теплообменник.Теплоносители, используемые в ядерных реакторах, включают воду или жидкие металлы, такие как натрий или свинец. IAEA-THPH, МАГАТЭ, Вена, 2008 г. ISBN 978–92–0–106508–7.
IAEA-THPH, МАГАТЭ, Вена, 2008 г. ISBN 978–92–0–106508–7. Практически на всех тепловых электростанциях (угольных, газовых, атомных) вода используется в качестве рабочего тела (используется в замкнутом контуре между котлом, паровой турбиной и конденсатором) и теплоносителя (используется для обмена отходящего тепла с водоемом). или унести путем выпаривания в градирне).
Практически на всех тепловых электростанциях (угольных, газовых, атомных) вода используется в качестве рабочего тела (используется в замкнутом контуре между котлом, паровой турбиной и конденсатором) и теплоносителя (используется для обмена отходящего тепла с водоемом). или унести путем выпаривания в градирне). Из-за своей инертности и высокой теплопроводности, нейтронной прозрачности, а также из-за того, что он не образует радиоактивных изотопов в реакторных условиях, гелий используется в качестве теплоносителя в некоторых газоохлаждаемых ядерных реакторах (например, высокотемпературные газоохлаждаемые реакторы – ВТГР).
Из-за своей инертности и высокой теплопроводности, нейтронной прозрачности, а также из-за того, что он не образует радиоактивных изотопов в реакторных условиях, гелий используется в качестве теплоносителя в некоторых газоохлаждаемых ядерных реакторах (например, высокотемпературные газоохлаждаемые реакторы – ВТГР). Металлы в целом имеют высокую электропроводность , высокую теплопроводность и высокую плотность. Соответственно перенос тепловой энергии может быть обусловлен двумя эффектами:
Металлы в целом имеют высокую электропроводность , высокую теплопроводность и высокую плотность. Соответственно перенос тепловой энергии может быть обусловлен двумя эффектами: Напротив, для сплавов вкладом k ph в k уже нельзя пренебречь.
Напротив, для сплавов вкладом k ph в k уже нельзя пренебречь. Однако в области низких и промежуточных температур закон нарушается из-за неупругого рассеяния носителей заряда.
Однако в области низких и промежуточных температур закон нарушается из-за неупругого рассеяния носителей заряда. При достаточно высоких температурах k ph ∝ 1/T.
При достаточно высоких температурах k ph ∝ 1/T. С другой стороны, диоксид урана имеет очень высокую температуру плавления и хорошо известное поведение
С другой стороны, диоксид урана имеет очень высокую температуру плавления и хорошо известное поведение 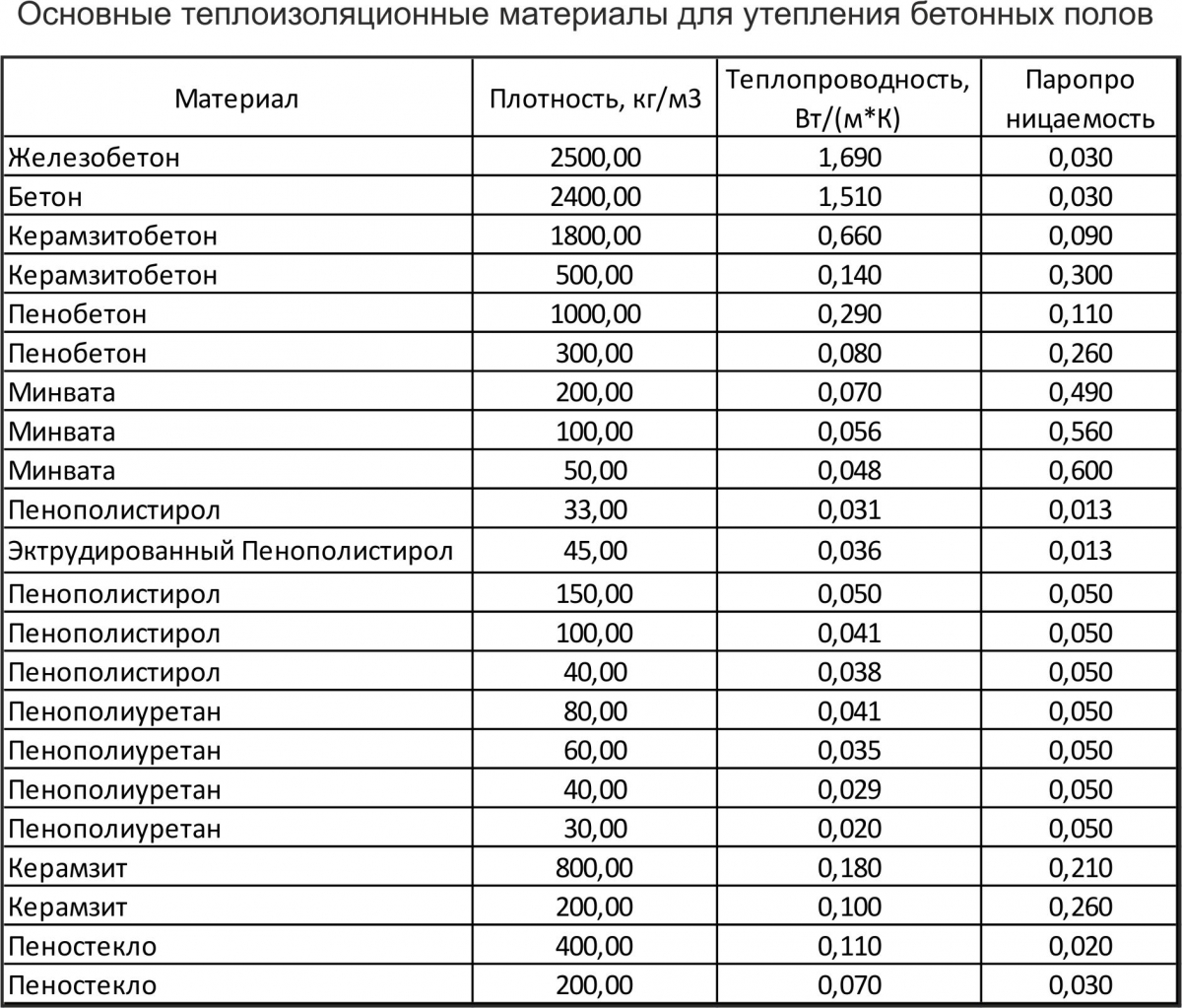 Перегрев топлива предотвращается за счет поддержания пиковой линейной скорости нагрева в установившемся режиме (LHR) или коэффициента теплового потока в горячем канале – F Q (z) ниже уровня, при котором происходит плавление центральной линии топлива. Расширение топливной таблетки при расплавлении центральной линии может привести к тому, что таблетка создаст нагрузку на оболочку вплоть до разрушения.
Перегрев топлива предотвращается за счет поддержания пиковой линейной скорости нагрева в установившемся режиме (LHR) или коэффициента теплового потока в горячем канале – F Q (z) ниже уровня, при котором происходит плавление центральной линии топлива. Расширение топливной таблетки при расплавлении центральной линии может привести к тому, что таблетка создаст нагрузку на оболочку вплоть до разрушения. Цирконий в основном используется в качестве огнеупора и глушителя, хотя небольшие количества используются в качестве легирующего агента из-за его высокой коррозионной стойкости. Циркониевый сплав (например, Zr + 1% Nb) широко используется в качестве оболочки топлив ядерных реакторов.Желаемыми свойствами этих сплавов являются низкое сечение захвата нейтронов и коррозионная стойкость при нормальных условиях эксплуатации. Циркониевые сплавы имеют более низкую теплопроводность (около 18 Вт/м·К), чем чистый металлический цирконий (около 22 Вт/м·К).
Цирконий в основном используется в качестве огнеупора и глушителя, хотя небольшие количества используются в качестве легирующего агента из-за его высокой коррозионной стойкости. Циркониевый сплав (например, Zr + 1% Nb) широко используется в качестве оболочки топлив ядерных реакторов.Желаемыми свойствами этих сплавов являются низкое сечение захвата нейтронов и коррозионная стойкость при нормальных условиях эксплуатации. Циркониевые сплавы имеют более низкую теплопроводность (около 18 Вт/м·К), чем чистый металлический цирконий (около 22 Вт/м·К).
 Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать. Таковы большинство металлов. Лед — это
известный пример отрицательного коэффициента расширения, так как он сжимается в длину с увеличением
температуры (другими словами, лед расширяется по мере охлаждения).
Таковы большинство металлов. Лед — это
известный пример отрицательного коэффициента расширения, так как он сжимается в длину с увеличением
температуры (другими словами, лед расширяется по мере охлаждения). 772
772 299
299 1
1 002
002 90
90 173
173 0055
0055
 Ванадий (V) и никель (Ni) были выбраны в качестве растворенных веществ. Никель принадлежит к той же колонке, что и Pt в периодической таблице (Pt-Ni — изоэлектронная система), а V расположен горизонтально далеко от Pt (Pt-V — неизоэлектронная система). Все сплавы, использованные в этом исследовании, имеют гранецентрированную кубическую форму (f.в.в) однофазный; тогда как в системе Pt-V превращение порядок-беспорядок происходит при стехиометрии 3 : 1. Данные для Pt 3 В с Г.К. неупорядоченная структура и упорядоченная структура D0 22 взяты из более ранней работы (15). Отметим, что термообработку при 1573 К в течение 1 ч проводили для достижения неупорядоченного состояния в Pt 3 V, а старение при 1020 К в течение 168 ч — для реакции упорядочения.
Ванадий (V) и никель (Ni) были выбраны в качестве растворенных веществ. Никель принадлежит к той же колонке, что и Pt в периодической таблице (Pt-Ni — изоэлектронная система), а V расположен горизонтально далеко от Pt (Pt-V — неизоэлектронная система). Все сплавы, использованные в этом исследовании, имеют гранецентрированную кубическую форму (f.в.в) однофазный; тогда как в системе Pt-V превращение порядок-беспорядок происходит при стехиометрии 3 : 1. Данные для Pt 3 В с Г.К. неупорядоченная структура и упорядоченная структура D0 22 взяты из более ранней работы (15). Отметим, что термообработку при 1573 К в течение 1 ч проводили для достижения неупорядоченного состояния в Pt 3 V, а старение при 1020 К в течение 168 ч — для реакции упорядочения. Сплошной треугольник — данные для Pt 3 В с упорядоченной структурой D0 22 (15)
Сплошной треугольник — данные для Pt 3 В с упорядоченной структурой D0 22 (15)