Как рассчитать квадратные метры стен комнаты, расчет площади стен
Приведу пример расчета пола и стен комнаты (кухни) в квадратных метрах.
Формула расчета простая, S = a*b, где S — площадь, а и b — соответственно, длина и ширина комнаты.
В нашем примере (рисунка с обмерами) вместо маленьких букв длина — А и ширина — Б., и противоположенных стен — Г и В.
Чтобы рассчитать площадь комнаты по полу:
— если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу
Чтобы рассчитать площадь комнаты по стенам:
Надо с начало сложить длины всех четырех сторон комнаты А + Б + Г + В и умножить на высоту потолка комнаты h, ( А + Б + Г + В)* h
— если у нас длина комнаты 5 метра, а ширина 3 метров, а высота потолка комнаты к примеру 2,5 метра, тогда надо ((5+3+5+3)*2,5= 40 кв.м.), в итоге получаем 40 кв.м. по стенам.
Но это еще не все, для того чтобы получить чистые квадратные метры стен комнаты для ремонта и отделки квартиры, надо из полученного вычесть двери и окно.
К примеру:
— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.
— а двери ширина 0,8 метров, а высота 2,05 метров.
Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,
Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,
Осталось вычесть от (40-2,4-1,64)= 35,96 кв.м.,
ИТОГО: Получили 35,96 кв.м. по стенам комнаты.
Если вы не хотите в ручную рассчитывать площадь стен или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором
Для расчёта необходимо измерить в метрах длину, ширину комнаты и высоту потолка и внести данные по порядку заполнив форму и вы автоматически получите расчет площади стен в квадратных метрах.
Калькулятор расчёта площади стен
Примечание:
Обращаем ваше внимание, что измерения необходимо проводить в метрах.
Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64.
Т.е. 2,6 — неправильно, 2.6 — правильно
Калькулятор рассчитывает только площадь стен, но без учета и вычета площади окон и дверей, для этого надо еще раз повторить расчеты на площадь окон и дверей описанные выше.
К примеру:
— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.
— а двери ширина 0,8 метров, а высота 2,05 метров.
Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,
Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,
Осталось вычесть от (от полученных расчетов автоматического калькулятора (площадь чистых стен) -2,4-1,64 (Окно и двери)= получим площадь стен с учетом вычета Окон и двери помещения (комнаты) в кв.
м.,
Чтобы рассчитать площадь комнаты по полу: воспользуйтесь нашим Калькулятором, чтобы расчитать площадь пола или потолка.
Калькулятор рассчитывает не только площадь пола или потолка, а также данный калькулятор можно использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т.д.,) к примеру таких как
Источник: remont-otdelka-m.ru
Как рассчитать площадь штукатурки? Формула расчета
При составлении сметы на ремонт и планировании затрат обязательно возникнет вопрос: какая площадь штукатурки? Какая получится квадратура штукатурки?
Эти данные нужны, чтобы подсчитать расход материалов, стоимость работы мастеров, определить время выполнения операций и т.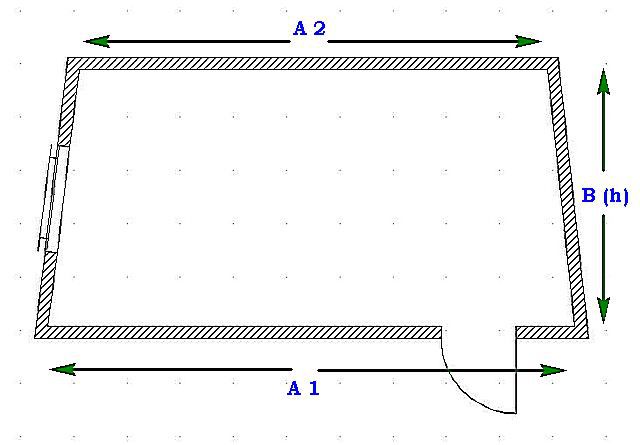
п. Несколько полезных советов помогут правильно выполнить замеры и сохранить их для дальнейшего использования
Как подсчитать размеры стен и потолка
Для этого придется просто вспомнить любимую школу и уроки геометрии. Известно, что площадь прямоугольника, это его длина, которую умножили на ширину. От полученного результата отнимают площадь оконных и дверных проемов, а также мест, где оштукатуривание не требуется.
Например, планируется ремонт комнаты шириной 3 метра, длиной 4 метра, пусть высота потолка будет 2,8 метра. В помещении есть окно размером полтора метра на метр и дверь с размерами два на один метр. Рассчитаем площадь (S) стен:
- S длинной стены 4 м Х 2,8 м = 11,2 м2
- S короткой стены 3 м Х 2,8 м = 8,4 м2
- Общая S всех четырех стен 11,2 м2 Х 2 + 8,4 м2 Х 2 = 39,2 м2
- S оконного проема 1,5 м Х 1 м = 1,5 м2
- S дверного проема 2 м Х 1 м = 2 м2
- Общая S проемов 1,5 м2 + 2 м2 = 3,5 м2
- S штукатурки стен 39,2 м2 — 3,5 м2 = 35,7 м2
- S потолка составит 3 м Х 4 м = 12 м2
При этом отдельно рассчитаем S потолка, которая составит 3 м Х 4 м = 12 м2 .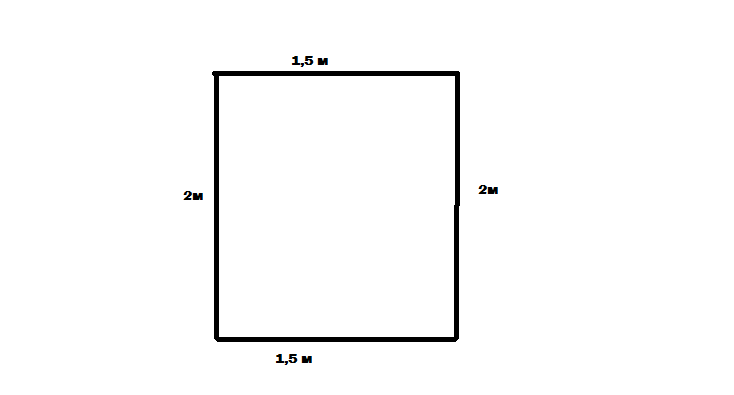
Почему площадь потолка считаем отдельно? Оштукатуривание потолка довольно специфичная и не такая популярная услуга, как оштукатуривание стен. Плюс работа по потолкам стоит дороже работы по стенам.
Если имеется помещение необычной формы, посчитать площадь будет немного сложнее. Возможно, понадобится вспомнить формулы площади треугольника, длины окружности и т.п. Чтобы упростить задачу, используют специальные программы — калькуляторы площади штукатурки. Такое приложение можно установить на телефон, планшет или компьютер.
Несколько полезных советов
Перед началом ремонта нужно точно измерить все помещения и проемы. Подойдет рулетка, обычная или лазерная. Нужно завести отдельную тетрадь для таких расчетов. Для каждой комнаты рекомендуется отвести несколько страниц. Записанные размеры не раз пригодятся во время ремонта. Они помогут быстро узнать нужное количество материалов, объем работ, оплату и т.п.
Чтобы быстро выполнить расчет, можно сначала сложить общую длину всех стен, а затем умножить результат на высоту потолка.
Остается отнять площадь проемов, полученная цифра покажет, какое количество квадратных метров нужно оштукатурить. Это верно для объектов, где высота потолка везде одинаковая. Если на разных этажах этот показатель различается, придется сделать поправку.
При штукатурке дверных и оконных откосов штукатурная площадь обычно считается в погонных метрах, без учета ширины (глубины) откоса. То есть, при оштукатуривании трех откосов стандартного окна с размерами 150см на 200см, штукатурная площадь составит 5 погонных метров. Некоторые штукатуры также считают погонными метрами участки стен шириной до 50-60 сантиметров.
На сайте штукатурим.рус вы найдете удобный онлайн калькулятор и привлекательные цены на механизированную штукатурку любых помещений. Мы предоставляем хорошую скидку при выполнении большого объема работ.
Как рассчитать площадь крыши дома
При начале строительства всегда возникает вопрос, как быстро и правильно выполнить расчет площади крыши? Данная операция, кажется, простой только на первый взгляд.
На практике же оказывается, что расчет бывает довольно сложным даже для опытных мастеров. Поскольку от его правильности напрямую зависит общее количество денег потраченных на строительство кровли. Учитывая дороговизну строительных материалов и стоимость монтажных работ, можно постараться уменьшить стоимость всего проекта. Попробуем разобраться, что необходимо для выполнения правильного подсчета квадратуры.Друзья, У-ра, свершилось и мы рады представить вам онлайн калькулятор для расчета площади крыши, теперь вам не нужно ничего прикидывать на листочке или в уме, все просто указал свои параметры и получил сразу ответ. Теперь вы будете точно знать сколько вам необходимо материала чтобы покрыть крышу. Вот ссылка на калькулятор -> Калькулятор площади кровли, расчет крыши онлайн. Кроме этого у нас появилось много других строительных калькуляторов посмотреть список всех вы можете на этой странице: Строительные калькуляторы
Основные этапы работ
Расчёт площади крыши всегда следует начинать с:
- ознакомления с будущим проектом кровли дома и запоминания наиболее ключевых параметров: длины конька, угла уклона, высоты, ширины и длины;
- определения типа кровельного материала, который будет использоваться.
Одной из самых важных характеристик является специальный расчетный коэффициент, присутствующий абсолютно во всех формулах. Его значение зависит от угла ската крыши и определяется следующими соотношениями
- при наклоне скатов 9°, коэффициент составит 1,01;
- для 14° – 1,03;
- для 18° – 1, 05;
- при 23° – 1,08;
- при 27° – 1,12;
- для 34° – 1,2.
Формулы и определения
Дома с подобного рода кровлями, обычно покрывают простыми материалами, а наиболее распространенная форма – прямоугольник. Чтобы посчитать площадь крыши нам понадобится знать длину ската и его ширину, которые следует перемножить между собой с заранее определенным расчетным коэффициентом.Для расчета площади двускатной крыши дома, необходимо учитывать значительно больше значений и факторов. Так, для ската длиной в 6 погонных метров и коньком 9,5 погонных метров, формула расчета примет следующий вид: длину конька следует умножить на длину ската и умножить на количество скатов (в нашем случае 2). Если понадобится рассчитать количество металочерепицы для этой крыши, тогда следует предварительно определиться с габаритами одного листа кровельного материала. Формула, которая позволит посчитать количество листов металочерепицы, имеет следующий вид: длину конька делят на ширину листа кровли и округляют к большему значению.Не следует забывать, что к площади односкатной крыши дома следует добавлять значение площади свеса ската, которое обязательно для крыш подобного типа.
Окончательные выводы
- первым делом необходимо поделить плоскость крыши дома на несколько геометрических фигур простой формы. Далее с помощью простых математических формул следует посчитать площадь каждой простой фигуры;
- длину скатов следует измерять от крайней точки карниза до самого конька;
- для расчета абсолютной площади кровли необходимо рассчитать площадь всех имеющихся элементов кровельной конструкции, после чего просуммировать их;
- каждый отдельный скат можно разбивать на различные по форме простые фигуры, посчитав площадь которых, вы сможете рассчитать квадратуру ската.
Следует знать, что при расчетах площади важно не забывать учитывать вентиляционные каналы, мансардные окна, дымоходы, парапеты, люки и другие элементы. В случае нарушения этого правила, существует большая вероятность возникновения дефицита строительных материалов при обустройстве кровли. Правильный и грамотный расчет площади, обеспечит все условия для оптимального расходования финансовых средств, связанных с покупкой и раскроем материала при возведении крыши дома.
сколько квадратов в листе, как посчитать и перевести, расчет площади
Это будет еще одна небольшая статья из серии «Все обо всем для юных строителей». Материал и правда не очень большой, не очень сложный, но крайне полезный. Сегодня мы поговорим о двух прекрасных вещах: фанере и математике.
Нас очень часто спрашивают «сколько весит фанера? а лист фанеры? а кубометр фанеры? а если квадратный метр фанеры?». Мы конечно же отвечаем на эти вопросы, ведь это наша работа. Но всем нам нужен отдых, хотя бы по ночам, хотя бы в выходные.
Итак, сегодня Ант-Снаб научит всех считать. Безусловно, мы не стремимся Теоретическая часть расчета довольна скучная и простая, поэтому пропустим ее Задача: Анатолий перфекционист и поэтому формат фанеры предпочитает 1525х1525 мм, толщина листа 9 мм. |
Решение:
1. Для начала Анатолию нужно определиться с количеством листов, которые вместе составят заветные 350 м2.
Для этого делим нужное нам количество квадратных метров на площадь листа (умножая длину листа на его ширину), округляем в бОльшую сторону:
350 / (1,525 х 1,525) = 350 / 2,3256… = 150,4988, округляем и получаем 151 лист
2. Далее Анатолию следует узнать количество листов в 1 кубе именно 151 / 47,777 = 3,1605… округляем и получаем 3,161 м3 3. Точный вес материалов из древесины очень сильно зависит от влажности, 3,161 х 700 = 2212,7 кг |
Именно столько будут весить 350 м2 березовой фанеры ФК с форматом листа 1525х1525 мм и толщиной 9 мм.
Мы бы посоветовали дачнику Анатолию заказать недорогую доставку и не тратить время в пробках. Но тут уж он сам решит.
Разделив общий вес на количество листов, можно узнать вес Подведем итог, 350 квадратных метров фанеры ФК 1525х1525х9 мм это: • 151 лист Хочется отдельно отметить, что вес листа фанеры 9 мм и, |
Как видите все довольно просто, даже если вы решите посчитать все самостоятельно. На этом сегодня все!
Расчёт гипсокартона. Как рассчитать расход гипсокартона?
Учимся считать, сколько гипсокартона необходимо для облицовки стен, устройства перегородок, подвесных потолков и сухой стяжки пола.
На фото: современные гипсокартонные системы от компании GYPROC (Гипрок).
Гипсокартон для пола и потолка
Одноуровневый гипсокартонный потолок. Чтобы посчитать расход гипсокартона, площадь помещения делим на площадь одного ГКЛ. Полученное число умножаем на коэффициент «запаса»: для помещений менее 10 кв.м – 1,3, для комнат 10-20 кв.м – 1,2, при площади более 20 кв. м – 1,1. Округляем до целого в большую сторону, получаем результат.
Пример расчета ГКЛ для потолка, стен и пола в комнате. Возьмем для примера комнату с длинной стеной 4 м и короткой 3,5 м (площадью 14 кв.м), с высотой потолков 2,75 м.
Считаем расход ГКЛ для одноуровневого потолка. Площадь потолка – 14 кв.м, делим на 3 кв. м (площадь листа гипсокартона стандартных параметров 1.200 х 2.500). Умножаем на коэффициент 1,2 («запас» для комнат площадью 10-20 кв.м) и получаем число 5.6, т.е. для потолка потребуется 6 листов гипсокартона. Для пола в этой же комнате расчеты совпадают.
Считаем расход гипсокартона для стен (обшивка в один слой). Предположим, в комнате имеется окно 2 х 1.5 м и дверной проем 0.8 х 2 м. Общая площадь стен (с проемами) – 38.5 кв.м (14х2.75 кв.м). За вычетом окна (3 кв.м) и двери (1.6 кв.м) имеем 33.9 квадратных метра. Делим на 3 кв.м (площадь ГКЛ), умножаем на коэффициент 1.2 и получаем расход 14 листов. Для обшивки в два слоя потребуется, соответственно, 28 листов гипсокартона.
Гипсокартон на потолок двух и более уровней. Расчет гипсокартона для двухуровневого и многоуровневого потолка будет сложнее. По сути, вам необходимо вычислить площадь каждого уровня и разделить ее на площадь одного ГКЛ.
- Первый уровень: его, как правило, делают «базовым», т.е. рассчитать его можно по формуле одноуровневого потолка.
- Второй и последующий уровни: если они представляют собой простые геометрические фигуры, рассчитать их площадь труда не составит. Для замысловатого рисунка: чем более нестандартными планируются потолки, чем больше изгибов и чем «мельче» рисунок уровня, тем больше будет отходов, и тем больший «запас» потребуется.
Схема монтажа – можно прорисовать схему монтажа листов ГКЛ по рисунку будущего потолка в уменьшенном масштабе, чтобы наглядно увидеть, как ляжет потолочный гипсокартон на каркас, и сколько листов нужно купить.
Гипсокартонный пол. Для выравнивания пола и придания ему теплоизоляционных свойств используют водостойкие ГКЛ. Расчеты необходимого количества листов производятся аналогично формуле одноуровневого потолка.
Расчет ГКЛ для стен и перегородок
Выравнивание стен. Количество листов гипсокартона для облицовки стен рассчитывается примерно так же, как и для подвесных потолков: считаем общую площадь стен (за вычетом площади окон и дверей) и делим на площадь одного ГКЛ. Не забываем про «запас», а также про дополнительный расход материала на отделку откосов, если планируется обшивать их гипсокартоном.
Пример расчета перегородки 4 х 2.75. Имеем 11 кв.м, без проемов. Выбираем гипсокартон стандартных размеров 1.200 х 2.500 (3 кв.м лист). Расход гипсокартона на 1 кв.м перегородки при обшивке в один слой – 2 кв.м, при обшивке в два слоя – 4 кв. м. Итого, для создания перегородки с однослойной обшивкой потребуется 22 кв.м гипсокартона. При площади листа 3 кв.м с коэффициентом погрешности 1.2 понадобится 9 листов гипсокартона. Для перегородок с обшивкой в два слоя расход ГКЛ составит 44 кв.м. Делим на 3 кв.м, умножаем на 1.2 – получаем 18 гипсокартонных листов.
Обшивка стен в два слоя. Это делают для придания дополнительной прочности или для увеличения тепло- и звукоизоляции. Соответственно, требуемое количество материала при расчетах удваивают.
Перегородки. В зависимости от выбранного типа, потребуется обшивка в 1 или 2 слоя. Не забываем, что перегородки обшиваются с обеих сторон, т.е. необходимо рассчитать удвоенный расход на каждый квадратный метр перегородки. Для расчета нужного количества ГКЛ, умножаем площадь перегородки на два – для обшивки в 1 слой, или же на 4 – для обшивки в 2 слоя. Делим на площадь одного листа гипсокартона, применяем коэффициент «запаса», округляем – и получаем нужное число листов.
Как рассчитать гипсокартон для фигруной перегородки. Если планируются фигурные ниши и проемы неправильной формы, не рекомендуется вычитать их площадь из площади перегородки. Наоборот, стоит учесть увеличение отходов при их устройстве – чем сложнее форма перегородки, тем выше делайте коэффициент запаса (1,3-1,4). При создании криволинейных перегородок: их периметр умножают на высоту и делают большой коэффициент запаса. Периметр можно посчитать, разбив кривую линию на небольшие прямолинейные отрезки. Учтите: гипсокартон гнут по длине листа, а не по ширине!
Как рассчитать площадь мансардного этажа? — Мансарды
Здравствуйте, хочу пристроить мансарду к дому, и встал вопрос, как рассчитать площадь мансардного этажа. Из школьного курса геометрии я, конечно, помню о нахождении площади прямоугольника, но мансардный этаж это все, же более сложная форма. Ломаная крыша, а еще двери и окна, которые так же должны быть учтены. Хотелось бы обшить готовую площадь вагонкой, и никак не могу понять, как и что перемножать? С уважением Владимир.
Ответ:
Здравствуйте, Владимир. Вы правы, расчет площади мансардного этажа несколько отличается от расчета площади, к примеру, обычной жилой комнаты, что обусловлено спецификой строения.
При определении площади мансарды учитываются многие величины, некоторые из которых уже давно приняты и указаны в СниПах. Именно оттуда берется высота жилого помещения, которая равна 2,5 метрам. Важно помнить, что весь расчетный процесс должен отображать измерение реальной площади по отношению к полезной. Для этого необходимо использовать соответствующие исходным нормам данные:
- уклон 300 – уровень узкой части наклона 1,5 метра;
- уклон 450 – 1,1 метр;
- свыше 600 – 0, 5 метра.
Если предусмотрены высоты поменьше, площадь умножается на понижающий коэффициент 0,7. Тогда вышеописанные значения несколько изменятся, и будут равняться для 300 – 1,2 метра, 450-600 – 0,8 метра, свыше 600 – нет границ.
Есть формула, которая поможет при расчете площади мансарды с кровлей в 450, выглядит она так:
Пп = A*L + 2В*0.7*L = L*(A + 1.4B), в которой Пп – площадь пола, А и В – ширина при высоте 1,1 и 0,8 метра соответственно, L – длина, 0,7 – понижающий коэффициент в случае меньшей высоты.
Зависимость площади мансарды от угла наклона кровлиСуществует также способ расчета мансардной крыши, при проведении которого нужно придерживаться некоторых правил, главным из которых является то, что зона полезной площади не принимается меньше 90 сантиметров от изгиба потолка до пола, так как меньшее значение принято считать глухой зоной.
Перед началом расчетов советуем набросать план крыши, разделив его схематически на простые геометрические фигуры. Определив площадь каждой из этих фигур, и сложив их, вы получите точную площадь мансардного этажа.
Чтобы определить площадь фигур, придется вспомнить школьный курс геометрии и формулы площади:
- квадрата – А2, где А означает длину каждой из сторон;
- прямоугольника – А х В, где А – длина, В – ширина;
- треугольника – Ah/2, где А – основание, h – высота фигуры;
- трапеции – h х (А + В)/2, где h – высота фигуры, А и В – верхнее и нижнее основания.
Вот таким нехитрым способом, сложив все полученные результаты, вы сможете получить максимально точное значение площади мансардного этажа.
Если вы затрудняетесь провести расчеты согласно вышеописанной формулы, то советуем воспользоваться компьютерными программами, которых существует огромное множество. Они не только позволяют значительно упростить процесс расчета площади, но и помогут избежать ошибок в расчетах. К примеру можно воспользоваться нашими калькуляторами для расчета площади мансарды, и расчета мансардной крыши!
| Q1) Подсчитайте количество квадратов на рисунке 1) 28 Решение: На рисунке можно пометить как показано. Q2) Подсчитайте количество квадратов на данном рисунке 1) 8 Решение: Рисунок могут быть помечены, как показано. Подробнее: Вопросы по подсчету числа треугольниковСкачать: Практические вопросы по подсчету геометрических фигурQ3) Подсчитайте количество квадратов на данном рисунке 1) 11 Решение: Цифра может быть помечены как показано. Q4) Подсчитайте количество квадратов на данном рисунке 1) 14 Решение: Рисунок могут быть помечены, как показано. Подробнее: Вопросы по подсчету числа прямоугольниковПодробнее: горячие клавиши для геометрических узоровQ5) Подсчитайте количество квадратов на рисунке 1) 18 Решение: На рисунке можно пометить как показано. Q6) Подсчитайте количество квадратов на данном рисунке 1) 6 Решение: Рисунок могут быть помечены, как показано. Подробнее: Вопросы по подсчету числа параллелограммовQ7) Подсчитайте количество квадратов на данном рисунке 1) 13 Решение: На рисунке можно пометить как показано. |
Сколько квадратов и прямоугольников на этом рисунке
В этой статье обсуждаются формулы для нахождения квадратов, и прямоугольников на заданном рисунке « n» количества строк и ‘m’ — количество столбцов
Подсчитать количество квадратов и прямоугольников в данной сетке N x M | Как считать квадрат в рассуждениях
Сколько квадратов на данной фигуре?
Сколько квадратов в фигуре с одинаковым количеством строк и столбцов
(т.e Количество квадратов в квадратной сетке)
Пример — 1:
Сколько квадратов в сетке 4 x 4
Решение : На рисунке выше 4 строки и 4 столбца. Итак, пусть n = 4
Здесь мы используем два типа формул для определения количества квадратов в сетке n x n следующим образом
Формула — 1
n 2 + (n -1) 2 + (n-2) 2 + — — — — — + (n — n) 2
Теперь подставьте n = 4 в приведенную выше формулу
= 4 2 + (4-1) 2 + (4-2) 2 + (4-3) 2 + (4-4) 2
= 16 + 9 + 4 + 1 + 0 = 30
Формула — 2
Примените формулу
Замените n = 4 в приведенной выше формуле
= 4 х 5 х 9/6 = 30
Итак, количество квадратов в сетке 4 x 4 равно 30
Пример -2
Сколько квадратов в сетке 5 x 5
Решение : На рисунке выше 5 строк и 5 столбцов.Следовательно, n = 5
Формула
n 2 + (n -1) 2 + (n-2) 2 + — — — — — + (n — n) 2
Таким образом, согласно вышеизложенному заменим n = 5
= 5 2 + (5-1) 2 + (5-2) 2 + (5-3) 2 + (5-4) 2 + (5-5) 2
= 25 + 16 + 9 + 4 + 1 + 0 = 55
Количество квадратов в сетке 5 x 5 — 55
Сколько квадратов в цифре: количество строк и m столбцов
(т.e Количество квадратов в прямоугольной сетке)
Пример — 3 Сколько квадратов в сетке 3 x 4
Решение : На рисунке выше 4 строки и 5 столбцов.
Пусть количество строк (n) = 4 и количество столбцов (m) = 5
Здесь мы используем простые формулы:
Формула-1
(n x m) + (n -1) (m — 1) + (n-2) (m- 2) + — — — — — + (n — n) или (m — m)
Теперь подставляем n = 5 и m = 4
= (4 x 5) + (4-1) (5-1) + (4-2) (5-2) + (4-3) (5-3) + (4-4) (5-4 )
= 20 + 12 + 6 + 2 +0 = 40
Формула-2
Здесь учитывается большое значение n
и.e n = 5 и m = 4, теперь подставьте эти значения в формулы выше
= [4 x 1 x 5/2] + [4 x 5 x 9/6]
= 10 + 30 = 40
Количество квадратов на рисунке = 40
Сколько прямоугольников на данной фигуре?
Подсчитать количество прямоугольников на рисунке с одинаковым количеством строк и столбцов сетки
(т.е. Подсчет прямоугольников в квадрате)
Пример — 4 Сколько прямоугольников в сетке 5 x 5
Решение : На рисунке выше 5 строк и 5 столбцов.
Пусть количество строк или столбцов (n) = 5
Здесь для поиска прямоугольников есть два метода
Формула — 1
[n + (n -1) + (n -2) + (n -3) + — — — — — + (n -n)] 2
Теперь подставьте значения « n » в приведенную выше формулу
= [5 + (5-1) + (5-2) + (5-3) + (5-4) + (5-5)] 2
= [5 + 4 + 3+ 2 + 1 +0] 2
= 15 х 15 = 225
Формула — 2
Для подсчета количества прямоугольников в квадрате по формуле
Теперь подставьте значения « n » в приведенную выше формулу
= [5 (5 + 1) / 2] 2 = [5 x 6/2] 2
= 15 2 = 225
Общее количество прямоугольников на рисунке = 225
Подсчитать количество прямоугольников на рисунке «n» строк и «m» столбцов
(т.e Подсчет прямоугольников внутри прямоугольника)
Пример — 5 Сколько прямоугольников в сетке 4 x 5
Решение: На рисунке выше 4 строки и 5 столбцов.
Пусть количество строк (n) = 4 и количество столбцов (m) = 5
Здесь для нахождения прямоугольников есть два метода
Формула — 1 (Формула для определения количества прямоугольников на рисунке с количеством строк «n» и «m» количеством столбцов)
[n + (n -1) + (n -2) + (n -3) + — — — — — + (n -n)] x [m + (m -1) + (m -2) + (м-3) + — — — — — + (м-м)]
Теперь подставьте значения « n » и « m » в приведенную выше формулу
.= [4 + (4-1) + (4-2) + (4-3) + (4-4)] x [5 + (5-1) + (5-2) + (5-3) + (5 — 4) + (5 — 5)]
= [4 +3 +2 +1 +0] x [5 + 4 + 3+ 2 + 1 +0]
= 10 х 15 = 150
Формула — 2
Теперь замените значения « n » и « m » в приведенной выше формуле
.= 4 х 5 х 5 х 6/4 = 150
Общее количество прямоугольников на рисунке = 150
Статьи по теме
Подсчитайте количество треугольников | Найдите количество треугольников в фигуре
.Проблемы с единичной цифрой и решения | Как найти единичную цифру числа
Система счисления | Как легко найти общее количество множителей для больших чисел
Основные понятия системы счисления в математике
Уловка для подсчета количества квадратов / треугольников в фигуре
Проблема подсчета количества квадратов на шахматной доске это классика.Эта деятельность начинаетсяс задачи встроенного квадрата и предлагает несколько расширений. По мере того, как учащиеся работают над этими проблемами, они должны понимать важность систематической организации свои данные.
Задайте ученикам следующую задачу:
Сколько квадратов на шахматной доске?Если учащиеся не знакомы с шахматной доской, это будет полезно иметь один под рукой. Некоторые студенты могут считать только отдельные маленькие квадратики на шахматной доске и используйте это число как их окончательный ответ.Другие узнают квадраты разного размера.
Пока студенты думают о проблеме, раздайте Рабочий лист «Шаблоны фигур» для учащихся, чтобы вырезать квадраты.
Шаблоны фигур Рабочие листы
Заметки для учителя
Следующие занятия могут охватывать несколько учебных часов. Учащиеся могут работать в группах для выполнения этих заданий.
Чтобы помочь учащимся, испытывающим трудности с визуализацией, разрешите им работать в группах. Таким образом, человек, не зависящий от поля, может направлять человек, зависящий от поля, чтобы увидеть вложенную фигуру, например, обводя рисунок на бумаге пальцем или карандашом.Также, учителя могут дать ученикам шаблоны для вырезания копий некоторых цифры. Эти копии затем можно перемещать и накладывать на оригинальный рисунок. Этот процесс позволяет студенту не только идентифицировать фигура как встроенная, но также для определения того, сколько позиций фигура занимает большую фигуру.
Подсчет квадратов
Нарисуйте на доске следующий рисунок или спроецируйте его на экран над головой:
- Скажите студентам: «Это квадрат 2 × 2.Задайте следующие вопросы:
Сколько маленьких квадратов вы видите? [4]
Сколько квадратов 2 × 2 вы видите? [1]
Сколько всего квадратов вы видите? [5]
- Ученики могут использовать свои вырезы, чтобы показать квадрат 3 × 3. Задайте следующие вопросы:
Сколько квадратов 1 × 1 вы видите? [9]
Сколько квадратов 2 × 2 вы видите? [4]
Сколько квадратов 3 × 3 вы видите? [1]
Сколько всего квадратов вы видите? [14]
- Студенты могут использовать свои вырезы, чтобы показать квадрат 4 и times4.Задайте следующие вопросы:
Сколько квадратов 1 × 1 вы видите? [16]
Сколько квадратов 2 × 2 вы видите? [9]
Сколько квадратов 3 × 3 вы видите? [4]
Сколько квадратов 4 × 4 вы видите? [1]
Сколько всего квадратов вы видите? [30]
- Попросите учащихся найти образец в вопросах 1-3. Делать предсказание общего количества квадратов в квадрате 5 × 5. Студенты должны проверить свои прогнозы, чтобы найти всего 55 квадратов (25 + 16 + 9 + 4 + 1).
- Вернитесь к вопросу, заданному в начале урока. «Как много квадратов на квадратной шахматной доске 8 × 8? Защитите свой ответ «.
Студенты могут использовать таблицу для организации своих данных. Например, студенты могут создать следующую таблицу:
| Размер квадрата | Количество квадратов |
| 1 × 1 | 64 |
| 2 × 2 | 49 |
| 3 × 3 | 36 |
Выполнив задание Подсчет квадратов , учащиеся могут приступить к следующей части урока.
Нарисуйте на доске фигуру, похожую на приведенную ниже, или спроецируйте наверху.
- Скажите студентам: «Эта цифра представляет собой столбец размером 2 строки × 3 столбца.
прямоугольник. Сколько прямоугольников каждого типа вы можете найти? Используйте ваш
вырезы, которые помогут вам ответить на эти вопросы «.
1 строка × 1 столбец [6]
1 строка × 2 столбца [4]
1 строка × 3 столбца [2]
2 ряд × 1 столбец [3]
2 ряд × 2 столбца [2]
2 ряд × 3 столбца [1]
Сколько всего прямоугольников встречается? [18] - Попросите учащихся нарисовать прямоугольник размером 3 строки × 4 столбца.Находить номер каждого типа прямоугольника. Организуйте данные в таблицу. Ищите шаблоны. Найдите общее количество прямоугольников. [Студенты Всего должно быть выделено 60 прямоугольников.]
- Попросите учащихся угадать количество прямоугольников в
Прямоугольник 6 рядов × 5 столбцов. Они должны использовать шаблон, найденный для
3 ряд ×: прямоугольник из 4 столбцов. Еще раз, они могут использовать таблицу, чтобы
организовать свои данные. [Студенты должны определить 315 прямоугольников.]
Таблицы для студентов могут выглядеть следующим образом:
- Попросите учащихся угадать количество прямоугольников в 4х4 кв.Учащиеся могут составить таблицу, аналогичную использованной ранее в этом уроке. [Студенты должны определить 100 прямоугольников.]
Подсчет равносторонних треугольников
Некоторые ученики могут закончить раньше, чем другие, поэтому они могут перейти к следующему занятию урока.
Нарисуйте на доске следующую фигуру или сделайте проекцию сверху.
- Спросите студентов: «Сколько треугольников в этой равносторонней стороне? измерения 2 единицы? «[Студенты должны назвать 4 маленьких, 1 большую или 5 общий.]
- Спросите студентов: «Сколько треугольников в этом равностороннем треугольнике со стороной размером 3 единицы?» Студенты могут захотеть использовать свои фигурки, чтобы помочь им. [Студенты должен определить 9 маленьких, 3 средних и 1 большой, всего 13 треугольники.]
- Студенты должны использовать свои ответы на вопросы 1 и 2, чтобы предсказать количество треугольников в равностороннем треугольнике со стороной измерения 4 шт.
- Чтобы проверить свои прогнозы, учащиеся должны посмотреть
для выкройки. Они могут посчитать, сколько треугольников каждого размера в
каждый из треугольников выше. Рассмотрим треугольники в обоих верхних положениях.
и нижнее положение, как показано ниже: Студенты могут создать таблицу для организации своих данных. Примерная таблица приведена ниже:
Положение Размер 1 Размер 2 Размер 3 Размер 4 Вверх 10 6 3 1 9 0 0 Всего 16 7 3 1 - Затем попросите учащихся создать равносторонний треугольник из размер 5.Студенты могут создать таблицу, подобную приведенной ниже, для организации свои данные.
- Студенты должны предсказать количество треугольников в равносторонний треугольник со стороной 6 ед. Они должны объяснить как они сделали свой прогноз. [Все числа треугольные. Для до треугольников цифры будет 21, 15, 10, 6, 3 и 1. нижних треугольников будут 15 размером 1, 6 размера 2 и 1 размера 3. Узор находится путем обратного отсчета каждого другое треугольное число, начинающееся с числа во втором столбце первый ряд.]
- Спросите студентов: «Какой самый большой треугольник вниз в равностороннем треугольнике со стороной размером 8 единиц?» [ Треугольники вниз никогда не могут быть больше, чем половина размера большого треугольник. Итак, самый большой вниз треугольник в треугольнике размером 8 единиц будет иметь размер 4.] «В равносторонний треугольник со стороной размером 11 единиц? »[В треугольнике размером 11 единиц он будет иметь размер 5.]
- В заключение попросите студентов объяснить, как они будут поступать. найти количество треугольников в равностороннем треугольнике со стороной мерка 10 шт.[Для треугольников от до найдите первые 10 треугольные числа. Перечисленные в обратном порядке, как они будут отображаться в таблице, это 55, 45, 36, 28, 21, 15, 10, 6, 3 и 1. нижних треугольников повторяют узор всех остальных. треугольное число, начинающееся с 45: 45, 28, 15, 6 и 1. Отметьте это результат, наблюдая, что ровно 1 нижних треугольников имеет размер 5. Это образованный соединением середин сторон большого треугольника размера 10.]
Считается ли гараж квадратными метрами?
Если вы готовитесь продать свой дом, то расчет площади в квадратных метрах необходим.Чтобы оценить точную стоимость дома, убедитесь, что вы включили в измерения все подходящие места в доме. Наиболее распространенным неизвестным в этом случае является то, учитывается ли гараж в общей площади в квадратных футах. Мы провели необходимое исследование, чтобы дать надежный ответ на этот вопрос.
При расчете общей площади дома в квадратных футах гараж не учитывается. Мы рассчитываем общую площадь в квадратных футах, складывая общую площадь всех жилых помещений в доме.Незаконченные гаражи по определению непригодны для проживания и не учитываются при измерении площади в квадратных футах. С другой стороны, если у вас есть правильно законченный гараж, включите его в общую площадь в квадратных метрах.
Это основная информация о том, как гараж вписывается в уравнение общей площади дома в квадратных футах. Потенциальные покупатели и агенты по недвижимости по-прежнему заинтересованы в размере гаража и его наличии в доме. Продолжайте читать, чтобы узнать больше о том, что считается жилой площадью и измерением общей площади в квадратных футах.
Учитываются ли гаражи в квадратных футах дома?
Риэлторы, домовладельцы и подрядчики рассчитывают квадратные метры по нескольким причинам. Людям, которые планируют продать дом, отремонтировать свой дом или установить новый пол, необходимы точные измерения площади в квадратных футах. При измерении общей площади дома необходимо исключить гараж, чердак и недостроенный подвал.
Мы всегда исключаем гараж, потому что он не соответствует определению жилой площади .Чтобы гараж засчитывался в общей площади вашего дома, вы должны закончить его и превратить в жилое пространство. Гараж должен обладать всеми остальными качествами дома, чтобы соответствовать определению жилой площади. Подробнее об этом мы расскажем ниже.
Что считается квадратным метром дома?
Стандартный квадратный метр включает все жилые или жилые помещения в доме. Жилая зона имеет чистые стены и пол, кондиционер или климат-контроль и имеет определенные требования к высоте.Это определение немного различается в зависимости от муниципального расположения дома.
Для требований по высоте обычно правило состоит в том, что потолок должен быть семи футов в высоту, чтобы комната считалась жилым пространством. Однако из этого правила есть исключения. Есть комнаты неправильной формы и сводчатые или соборные потолки. В таких случаях, по крайней мере, половина комнаты должна иметь потолок в семь футов.
Более конкретное измерение, называемое чистой жилой площадью , точно показывает, сколько места подходит для комфортного использования дома.Это измерение исключает небольшие участки дома, такие как оконные рамы. Если вы покупаете дом, не забудьте запросить это измерение, чтобы получить более точное представление о его стоимости.
В то время как жилые квадратные метры — это более конкретное измерение, площадь — более широкое измерение в коммерческой недвижимости. Измерение площади пола представляет собой все пространство, занимаемое зданием. Этот показатель полезен для понимания полного размера здания, связанного с размером собственности.
Считается ли готовый гараж жилым помещением?
Если они соответствуют остальным стандартам дома и считаются жилыми помещениями, готовые гаражи учитываются в общей площади в квадратных футах. Готовый гараж — это жилая площадь, если она соответствует требованиям отделки стен и пола, климат-контроля и доступности. В гаражах высота потолка никогда не бывает проблемой, поскольку в них хранятся автомобили и другое оборудование.
Отделка гаража может значительно повысить стоимость дома без значительных строительных вложений.Превращение недостроенного гаража в пригодное для жизни пространство требует соответствующих разрешений, как и для любого другого крупного проекта по благоустройству дома.
Считается ли пристроенный гараж площадью пола?
Измерение площади пола отличается от того, что мы до сих пор покрывали с помощью пригодных для жилья квадратных футов. Измерение площади пола включает больше элементов, чем измерение жилой площади в квадратных футах. В этом измерении нет различия между пригодным для жизни и нежилым пространством.Учитывается все, что является частью физического здания, но такие аксессуары, как навесы и бассейны, не учитываются.
Следовательно, пристроенные гаражи учитываются при измерении площади пола. Их легко преобразовать в жилые помещения, поскольку они прикреплены к основному зданию, уже подключены к электричеству и могут быть добавлены к системе климат-контроля. По этой причине заинтересованные стороны хотят, чтобы они были включены в это измерение.
Считается ли отдельно стоящий гараж площадью пола?
К сожалению, отдельно стоящие гаражи, готовые или недостроенные, не учитываются при измерении общей площади.В свою очередь, они также не учитываются при расчете общей жилой площади. Однако в качестве дополнительной функции к дому отдельно стоящие гаражи повышают общую стоимость недвижимости, как и пристроенный гараж.
Как рассчитывается квадратный метр?
Существует несколько методов и инструментов для измерения площади дома в квадратных футах. Самый простой способ — взять длину и ширину каждой комнаты и умножить эти два числа. Разделите большие комнаты на более мелкие сегменты, чтобы их было легче измерить.Наконец, сложите все умноженные измерения на общую площадь в квадратных футах.
Иногда единственный инструмент, который вам понадобится для измерения площади в квадратных футах, — это старомодная рулетка. Однако доступны и другие инструменты, если вы хотите упростить работу. Во-первых, измерительные колеса особенно полезны для измерения внешнего периметра дома.
Щелкните здесь, чтобы увидеть складное измерительное колесо Zozen на Amazon.
Во-вторых, лазерные измерительные приборы — это самый быстрый и точный метод измерения.Они могут стать палочкой-выручалочкой в помещениях с множеством углов и неровностей.
Нажмите здесь, чтобы увидеть лазерный измеритель Tacklife Classic на Amazon.
Подробнее о гаражах
Гаражи используются для хранения уличного оборудования или оборудования для отдыха, а также для защиты транспортных средств от непогоды. Они также функционируют как мастерские или игровые комнаты для взрослых и детей. Гараж делает недвижимость более привлекательной для большинства потенциальных покупателей, потому что у них много плюсов и очень мало минусов.В недостроенных гаражах нет даже инженерных сетей. В идеале гаражи должны быть достаточно большими, чтобы вместить самый большой из автомобилей. Но каковы обычные квадратные метры гаражей?
Сколько квадратных футов один гараж?
Обычно площадь одного гаража составляет около 308 квадратных футов. Этот размер варьируется в зависимости от гаража, но обычно диапазон составляет от 240 до 384 квадратных футов. Некоторые гаражи больше других и могут вместить дополнительное место для хранения вещей, стиральные машины, сушилки или второй открытый холодильник.
Какова площадь гаража на две машины?
Гараж на две машины примерно в два раза больше гаража на одну машину. Площадь этих больших гаражей составляет от 440 до 624 квадратных футов. Гаражи на две машины, как правило, немного больше, если в них есть две гаражные ворота на одну машину вместо одной большой гаражной двери.
При закрытии
Гаражи не являются жилыми помещениями, если они не закончены и не оборудованы климат-контролем. Если гаражи не закончены и не оборудованы климат-контролем, они не соответствуют определению жилых помещений .Хотя вы не сможете включить недостроенный или отдельно стоящий гараж в квадратные метры дома, потенциальные покупатели все же хотят знать о пространстве. Правильно отделанный гараж может стать отличным способом улучшить ваш дом и улучшить жилую площадь дома.
Пока вы здесь, пожалуйста, ознакомьтесь с некоторыми другими нашими публикациями по теме:
Считается ли прачечная квадратными метрами?
Считаются ли лестницы квадратными метрами?
Квадратный корень — Формула, примеры
Квадратный корень из числа — это операция, обратная возведению числа в квадрат.Квадрат числа — это значение степени 2 числа, а квадратный корень числа — это число, которое нам нужно умножить само на себя, чтобы получить исходное число. Если «a» является квадратным корнем из «b», это означает, что a × a = b. Квадрат любого числа всегда является положительным числом, поэтому каждое число имеет два квадратных корня, одно положительное значение и одно отрицательное значение. Например, и 2, и -2 являются квадратными корнями из 4. Но в большинстве случаев вы обнаружите, что только положительное значение записывается как квадратный корень.
Что такое квадратный корень?
Квадратный корень числа — это число, которое умножается на само себя, чтобы получить произведение. Мы узнали об экспонентах. Квадраты и квадратные корни являются специальными показателями. Рассмотрим число 9. Когда 3 умножается на само себя, получается 9 как произведение. Когда показатель степени равен 2, он называется квадратом. Когда показатель степени равен 1/2, он называется квадратным корнем. Например, √ (n × n) = √n 2 = n, где n — положительное целое число.
Определение квадратного корня
Квадратный корень числа — это значение степени 1/2 этого числа. Другими словами, это число, которое мы умножаем само на себя, чтобы получить исходное число. Он обозначен символом «√».
Методы нахождения квадратного корня чисел
Очень легко найти квадратный корень из числа, которое является полным квадратом. Полные квадраты — это те положительные числа, которые можно записать как произведение числа на само себя.другими словами, полные квадраты — это числа, представляющие собой значение степени 2 любого целого числа. Мы можем использовать четыре метода , чтобы найти квадратный корень из чисел , и эти методы следующие:
- Метод повторного вычитания квадратного корня
- Квадратный корень методом простого факторизации
- Квадратный корень методом оценки
- Квадратный корень методом длинного деления
Обратите внимание, что первые три метода можно удобно использовать для полных квадратов, а четвертый метод, т.е.Метод деления в столбик можно использовать для любого числа, независимо от того, является оно квадратом или нет.
Метод повторного вычитания квадратного корня
Это очень простой метод. Мы вычтем последовательные нечетные числа из числа, для которого мы находим квадратный корень, до тех пор, пока не достигнем 0. Количество раз, которое мы вычитаем, является квадратным корнем из данного числа. Этот метод работает только для полных квадратных чисел. Давайте найдем квадратный корень из 16, используя этот метод.
- 16 — 1 = 15
- 15–3 = 12
- 12-5 = 7
- 7-7 = 0
Вы можете заметить, что мы вычитали 4 раза.Таким образом, √16 = 4
Квадратный корень методом простого факторизации
Разложение любого числа на простые множители означает представление этого числа как произведения простых чисел. Чтобы найти квадратный корень из заданного числа с помощью метода разложения на простые множители, мы следуем шагам, приведенным ниже:
- Шаг 1: Разделите данное число на его простые множители.
- Шаг 2: Сформируйте пары одинаковых факторов так, чтобы оба фактора в каждой паре были равны.
- Шаг 3: Возьмите один множитель из пары.
- Шаг 4: Найдите произведение множителей, полученных путем взятия одного множителя из каждой пары.
- Шаг 5: Этот продукт является квадратным корнем из заданного числа.
Найдем этим методом квадратный корень из 144.
Этот метод работает, когда заданное число является точным квадратным числом.
Квадратный корень методом оценки
Оценка и приближение относятся к разумному предположению о фактическом значении, чтобы сделать вычисления более простыми и реалистичными.Этот метод помогает в оценке и приближении квадратного корня из заданного числа. Воспользуемся этим методом, чтобы найти √15. Найдите числа, ближайшие к точному квадрату 15. 9 и 16 — числа полного квадрата, ближайшие к 15. Мы знаем, что √16 = 4 и √9 = 3. Это означает, что √15 лежит между 3 и 4. Теперь нам нужно посмотрим, ближе ли √15 к 3 или 4. Рассмотрим 3,5 и 4. 3,5 2 = 12,25 и 4 2 = 16. Таким образом, √15 находится между 3,5 и 4 и ближе к 4.
Найдем квадраты 3.8 и 3.9. 3,8 2 = 14,44 и 3,9 2 = 15,21. Это означает, что √15 находится между 3,8 и 3,9. Мы можем повторить процесс и проверить между 3,85 и 3,9. Мы можем заметить, что √15 = 3,872.
Это очень долгий и трудоемкий процесс.
Квадратный корень методом длинного деления
Длинное деление — это метод деления больших чисел на шаги или части, разбивающий задачу деления на последовательность более простых шагов. Используя этот метод, мы можем найти точный квадратный корень из любого заданного числа.Давайте разберемся с процессом нахождения квадратного корня методом деления в длину на примере. Найдем квадратный корень из 180.
- Шаг 1: Поместите черту над каждой парой цифр номера, начиная с места единицы (крайняя правая сторона). У нас будет две пары, т.е. 1 и 80
- Шаг 2: Мы делим крайнее левое число на наибольшее число, квадрат которого меньше или равен числу в крайней левой паре.
Шаг 3: Введите число под следующей полосой справа от остатка.Добавьте последнюю цифру частного к делителю. Справа от полученной суммы найдите подходящее число, которое вместе с результатом суммы образует новый делитель для нового дивиденда, который переносится вниз.
Шаг 4: Новое число в частном будет иметь такое же число, как выбрано в делителе. Условие то же — меньше или равно дивиденду.
Шаг 5: Теперь продолжим этот процесс, используя десятичную точку и попарно добавляя нули к остатку.
Шаг 6: Полученное таким образом частное будет квадратным корнем из числа.
Таблица квадратного корня
Таблица квадратного корня содержит числа и их квадратные корни. Также полезно находить квадраты чисел. Вот список квадратных корней из полных квадратных чисел и некоторых неполных квадратных чисел от 1 до 10.
| Номер | Квадратный корень |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1,732 |
| 4 | 2 |
| 5 | 2,236 |
| 6 | 2.449 |
| 7 | 2,646 |
| 8 | 2,828 |
| 9 | 3 |
| 10 | 3.162 |
Квадратные корни из чисел, не являющихся полными квадратами, являются частью иррациональных чисел.
Формула квадратного корня
Квадратный корень — это не что иное, как показатель степени 1/2. Формула квадратного корня используется для нахождения квадратного корня числа. Мы знаем формулу экспоненты: \ (\ sqrt [\ text {n}] {x} \) = x 1 / n . Когда n = 2, мы называем это квадратным корнем. Мы можем использовать любой из вышеперечисленных методов для нахождения квадратного корня, например, разложение на простые множители, деление в столбик и так далее.9 1/2 = √9 = √ (3 × 3) = 3. Итак, формула для записи квадратного корня из числа: √x = x 1/2 .
Как упростить квадратный корень?
Чтобы упростить извлечение квадратного корня, нам нужно найти факторизацию данного числа на простые множители. Если фактор не может быть сгруппирован, оставьте их под символом квадратного корня. Правило упрощения квадратного корня: √xy = √ (x × y), где x и y — положительные целые числа. Например: √12 = \ (\ sqrt {2 \ times 2 \ times3} \) = 2√3
Для дробей действует аналогичное правило: √x / √y = √ (x / y).Например: √50 / √10 = √ (50/10) = √5
.Квадратный корень отрицательного числа
Квадратный корень отрицательного числа не может быть действительным числом, поскольку квадрат — это либо положительное число, либо ноль. Но у комплексных чисел есть решения для извлечения квадратного корня из отрицательного числа. Главный квадратный корень из -x: √ (-x) = i√x. Здесь i — квадратный корень из -1.
Например: возьмите точное квадратное число, такое как 16. Теперь давайте посмотрим на квадратный корень из -16.Настоящего квадратного корня из -16 не существует. √ (-16) = √16 × √ (-1) = 4i (as, √ (-1) = i), где i представлено как квадратный корень из -1. Итак, 4i — это квадратный корень из -16.
Квадрат числа
Любое число, возведенное в степень два (y 2 ), называется квадратом основания. Итак, 5 2 упоминается как квадрат 5, а 8 2 упоминается как квадрат 8. Мы можем легко найти квадрат числа, умножив основание на два раза.Например, 5 в квадрате — это 5 × 5 = 25, а 8 в квадрате — это 8 × 8 = 64. Когда мы находим квадрат целого числа, полученное число является одним из полных квадратов. Вот некоторые из идеальных квадратов, которые у нас есть: 4, 9, 16, 25, 36, 49, 64 и так далее. Квадрат числа, независимо от того, является ли оно положительным или отрицательным, всегда является положительным числом.
Как найти квадрат числа?
Квадрат числа можно найти, умножив число на само себя. Для однозначных чисел мы можем использовать таблицы умножения, чтобы найти квадрат, в то время как в случае двух или более двухзначных чисел мы выполняем умножение числа на само число, чтобы получить ответ.Например, 9 × 9 = 81, где 81 — это квадрат 9. Точно так же 3 × 3 = 9, где 9 — это квадрат 3.
Статьи по теме о квадратном корне:Ниже приводится список тем, которые тесно связаны с квадратными корнями.
Квадратный корень чисел
Часто задаваемые вопросы о Square Root
Что такое квадратный корень в математике?
Квадратный корень — это число, которое нам нужно умножить само на себя, чтобы получить исходное число.Например, 2 — это квадратный корень из 4, так как 2 × 2 = 4.
☛ Чек:
Как найти квадратный корень числа?
Квадратный корень из числа можно найти с помощью любого из четырех методов, приведенных ниже:
- Метод повторного вычитания
- Метод простой факторизации
- Метод оценки и приближения
- Метод длинного деления.
Как найти квадратный корень десятичного числа?
Квадратный корень десятичного числа можно найти с помощью метода оценки или метода деления в долгую.В случае десятичных чисел мы составляем пары частей целого числа и дробных частей отдельно. Затем мы выполняем процесс деления в столбик так же, как и любое другое целое число.
Может ли квадратный корень быть отрицательным?
Квадратный корень числа может быть отрицательным. Фактически, все идеальные квадраты, такие как 4, 9, 25, 36 и т. Д., Имеют два квадратных корня, одно положительное значение и одно отрицательное значение. Квадратные корни из 4 равны -2 и 2. Точно так же квадратные корни из 9 равны 3 и -3.
Как вы называете символ квадратного корня?
Символ, используемый для обозначения квадратного корня, называется радикальным знаком «√».Термин, записанный внутри радикального знака, называется подкоренным выражением.
Какова формула вычисления квадратного корня числа?
Квадратный корень любого числа можно выразить с помощью формулы: √y = y ½ .
Что такое квадрат и корень числа?
Квадрат и квадратный корень из числа являются обратной операцией друг для друга. Если возвести в квадрат число z, как (z × z) z 2 , тогда квадратный корень из z 2 i.е., √z равно числу z.
Какой метод используется для нахождения квадратного корня неидеальных квадратных чисел?
В математике несовершенное или несовершенное квадратное число считается числом в десятичной форме. Квадратный корень из неполного квадратного числа можно вычислить с помощью метода деления в длину.
Как упростить извлечение квадратного корня на калькуляторе?
Чтобы найти значение квадратного корня любого числа, нам просто нужно сначала вставить символ квадратного корня √x в калькулятор и ввести число x.
☛ Чек:
Как умножить два значения квадратного корня вместе?
Допустим, у нас есть два числа a и b. Сначала мы найдем квадратный корень из чисел a и b. Затем, найдя квадратный корень, мы умножим значение квадратного корня вместе. Давайте разберемся с этим на практической иллюстрации.
Квадратный корень из 4 равен 2, а квадратный корень из 16 равен 4. Теперь мы умножим значение квадратного корня из 4 и 16, т.е. 2 × 4 = 8.
Каковы применения формулы квадратного корня?
Существуют различные применения формулы квадратного корня
- Формула квадратного корня в основном используется в алгебре и геометрии.Это помогает найти корни квадратного уравнения.
- Мы можем легко вычислить площадь, объем и другие размеры, используя формулу квадратного корня.
- Широко используется инженерами.
Сколько квадратов на этой картинке?
Новые головоломки, которые, кажется, озадачивают всех в Интернете, появляются постоянно. Однако, несмотря на массовую неразбериху, по-прежнему легко думать: «Пшш, я не могу решить эту проблему». Верно. Мы почему-то думаем, что мы умнее подавляющего большинства интернет-пользователей.
Не говоря уже о мании величия, суть в том, что некоторые из этих головоломок сложны . А вот еще один. Это также удручающе сложно. Посмотреть на себя.
Именно эта головоломка заставила Интернет ломать голову, хотя сама идея проста: выяснить, сколько квадратов на картинке.
Легко, правда? Не так много. Эта фотография стала популярной в Facebook, и, согласно изображению, распространенному на сайте, 92 процента людей не могут правильно ответить на загадку.В Интернете есть масса ответов, и кажется, что люди просто не могут прийти к соглашению.
Однако есть один правильный ответ, и вы можете быть удивлены его результатом. Загвоздка здесь в том, что квадратов гораздо больше, чем кажется. Даже если вы посчитаете все угловые квадраты и большой окружающий квадрат, вы можете не получить их все. Давай, попробуй посчитать сам.
Все еще в тупике? Мы вам поможем. Правильный ответ на загадку — 40 квадратов.Правильно: это не 8, 16, 24, 28 или 30, и мы расскажем, почему. Изображение состоит из восьми крошечных квадратов, 18 отдельных квадратов, девяти квадратов 2 x 2, четырех квадратов 3 x 3 и одного квадрата 4 x 4.
Все еще не знаете, где найти эти предполагаемые квадраты? На изображении ниже это разбито, чтобы вы могли видеть каждый квадрат на изображении.
Playbuzz
Сколько квадратов вы пропустили? Те, что посередине, определенно сбили меня с толку. Это может быть математическое уравнение, чтобы выяснить это, но с хорошим глазом и некоторым простым счетом вы можете быть одним из немногих избранных, кто смог точно решить эту сложную головоломку.
Числа — квадратные корни — глубина
Многие математические операции имеют обратную или противоположную операцию. Вычитание противоположное сложения, деление — это обратное умножение и т. д. Квадрат, о котором мы узнали на предыдущем уроке (экспоненты), есть и обратное, называемое «нахождение квадратного корня». Помните, что квадрат числа — это число, умноженное на само число. Идеальные квадраты — это квадраты целых чисел: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100Квадратный корень числа n написано
это число, которое дает n при умножении на себя.Например,
потому что 10 х 10 = 100
Примеры
Вот квадратные корни из всех полных квадратов от 1 до 100.
В поисках квадрата корни чисел, которые не являются точными квадратами без калькулятора
1. Оценка — во-первых, подойдите как можно ближе, найдя два идеальных квадратных корня из ваших число находится между.
2.Делить — разделите ваше число на один из этих квадратных корней.
3. Среднее — возьмите среднее значение результата шага 2 и корень.
4. Используйте результат
шага 3, чтобы повторять шаги 2 и 3, пока вы не получите точное число
достаточно для вас.
Пример: Вычислите квадратный корень из 10 () до 2 знаков после запятой.
1. Найти
между двумя точными квадратными числами.
Решение:
3 2 = 9 и 4 2 = 16, поэтому
находится между 3 и 4.
2. Разделить 10 на 3. 10/3 = 3,33 (ответ можно округлить)
3. Среднее 3,33 и 3. (3,33 + 3) / 2 = 3,1667
Повторить шаг
2: 10 / 3,1667 = 3,1579
Повторите шаг 3: Среднее значение 3,1579 и 3,1667. (3,1579 + 3,1667) / 2 = 3,1623
Попробуй ответ -> Это 3.1623 в квадрате равно 10? 3,1623 x 3,1623 = 10,0001
Если это верно хватит тебе, можешь остановиться! В противном случае вы можете повторить шаги 2 и 3.