Как посчитать площадь комнаты, стены, пола, потолка
Инструменты для замеров
Для правильного подсчета общей квадратуры вам потребуется такой инструмент, как:
- строительная рулетка не менее 5 метров;
- ручка или карандаш;
- калькулятор;
- строительный уровень или аналогичное приспособление со шкалой;
- стремянка или табуретка;
- лист бумаги для записей.
Можно также воспользоваться специальными сервисами, доступными в интернете, однако, точность их не всегда бывает верной, а для максимальной точности лучше все сделать самостоятельно.
Перед тем как рассчитать площадь стен комнаты, необходимо обеспечить к ним свободный доступ и отодвинуть мебель для возможности беспрепятственного перемещения
Это очень важно, поскольку по исходным данным, полученным от замера, мы получаем общий объем помещения, а также квадратуру потолка и пола
Для максимальной точности рекомендуется перед замерами обозначить ровную линию немного выше уровня плинтусов при помощи строительного уровня или любой другой длинной и ровной рейки. Далее рулетку прикладывают горизонтально к поверхности над плинтусом и на бумаге записывают полученные данные. Следующим этапом замеряют расстояние от пола до потолка, опять прислонив рулетку к стене.
Далее рулетку прикладывают горизонтально к поверхности над плинтусом и на бумаге записывают полученные данные. Следующим этапом замеряют расстояние от пола до потолка, опять прислонив рулетку к стене.
Не забывайте записывать все полученные данные
Если помещение имеет форму прямоугольника, то для получения общей площади комнаты достаточно умножить полученную ширину на длину. Например, если стена по длине составляет 5 метров, а по ширине 3, то умножаем 5 на 3, получаем 15 квадратов.
Аналогичным образом замеряем каждую стену и складываем полученные значения в одну сумму. Например, в прямоугольной комнате 2 стены по 15 квадратных метров и 2 по 8, складываем эти значения 15х2=30, 8х2=16, 30+16=46. Итого общая сумма поверхности стен комнаты составила 46 квадратов.
Как высчитать квадратуру криволинейного помещения?
Порой в комнатах один из углов «срезан» или стена идёт под углом. Тогда действует тот же принцип деления сложных фигур на более простые, но часть из них будет треугольниками.
В сложных задачах, хороший чертёж – это половина успеха. Составьте план помещения, который поможет «делить» помещение на бумаге, а не в уме.
Скошенные углы в комнате
По сути, такая комната – это прямоугольник, от которого «отрезали» треугольник. Найдя площадь этого треугольника, и вычтя его из общей квадратуры, останется площадь комнаты.
Площадь треугольника находится по формуле:
S = ab:2
Где a и b – это катеты, или стороны перпендикулярные друг другу.
Скошенная же часть – это гипотенуза, которая не требуется для вычислений.
- Чтобы узнать «a», измеряется ширина той стены, где начинается срез, а затем противоположная стена и находится разница между ними (например, скошенная стена 1,7 м, а противоположная 3 м, значит, «a» = 1,3 м).
- Аналогично находится «b», только сравниваются длины комнаты (например, 5 м и 3,6 м. Вычисление: 5 – 3,6 = 1,4 м).
- Вычисляется площадь «срезанного» треугольника (1,3 х 1,4 : 2 = 1,82:2 = 0,91 м2).

- Согласно сделанным ранее замерам, если бы комнаты была прямоугольной, её габариты были бы 5 м на 3 м. А значит, квадратура 5 х 3 = 15 м2.
- Из общей квадратуры вычитаем площадь треугольника (15 – 0,91 = 14,09).
Прямоугольные помещения
Если комната имеет правильную (относительно) прямоугольную форму, без всевозможных выступов или ниш, то площадь ее вычисляется довольно просто. Для начала, нужно измерить длину и ширину комнаты, после чего результаты записать на бумажке, чтобы не забыть. Измерения можно производить как в метрах, так и в сантиметрах. Если замеры осуществляются в метрах, то после целых значений метров ставится запятая, а потом пишутся сантиметры. Например, 4 метра, 35 сантиметров следует записать: 4,35 м.
Измерив длину, например, 2,35 м и ширину 1,4 м, данные перемножаются. Например: 2,35 м х 1,4 м. В результате получается 3,290 м2 или 3,29 м2. Как правило, после запятой всегда оставляется две цифры. Если их больше, то значение округляется по правилам, которые излагались еще в начальных классах школы. При этом, можно округлять или до метров, или до сантиметров, в зависимости от требуемой точности. В основном, достаточно измерять с точностью до метров и лишь изредка требуется точность до сантиметров.
При этом, можно округлять или до метров, или до сантиметров, в зависимости от требуемой точности. В основном, достаточно измерять с точностью до метров и лишь изредка требуется точность до сантиметров.
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту
Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв.
 м. Округляем, получаем 5,1 кв. м.
м. Округляем, получаем 5,1 кв. м. - Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка
Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Полезные советы
- Идеальные параметры помещений редко когда найдешь. Потому, измерять нужную комнату положено в нескольких местах и выводить из этого среднее арифметическое значение.
 Кроме того, замеры производятся несколько раз, чтобы избежать ошибок и недочетов.
Кроме того, замеры производятся несколько раз, чтобы избежать ошибок и недочетов. - Периметр помещения с многочисленными неровностями и выступами проще измерить, если протянуть вдоль него шнур или веревку. Потом измерить его длину.
- Подсчеты лучше всего сразу отображать на листе бумаги в виде схемы – это поможет в дальнейшем ремонте и при выборе строительных и отделочных материалов. Если показать схему продавцу-консультанту – он грамотно подберет требуемое количество с учетом стыков и запаса, ориентируясь по метражу помещения.
Измерять комнату необходимо в нескольких местах и выводить из этого среднее арифметическое значение.
Строительство и ремонт – трудоемкий процесс, который требует не только физической и умственной работы, но и немалых материальных затрат. Качественно сделанные замеры помещений помогут вложить минимум усилий и денег.
Некачественные замеры растянут ремонт на длительный период, повлечет за собой проблемы и неудобства. Приведенные выше рекомендации и советы обучат, помогут и в чем-то облегчат жизнь участников этого непростого и интересного дела.
Считаем количество плитки
Зная площадь комнаты, рассчитать количество напольного покрытия будет несложно. Разберемся, как выяснить, сколько плитки понадобится для конкретной комнаты. Для этого нужно узнать, какова площадь одного элемента плиточного покрытия. Зная эти данные, легко произвести необходимые расчеты. Например:
- площадь комнаты – 15 м2;
- размер одной единицы плитки – 0,20х0,30 м.
Расчет количества плитки на пол
Таким образом, площадь одной плитки составит 0,2х0,3 = 0,06 м2. Далее общую площадь комнаты делим на площадь одной плитки и получаем: 15/0,06 = 250 единиц. Именно столько плиток потребуется, чтобы закрыть весь черновой пол в данном помещении. Точно таким же методом вычисляется и количество ламината или паркетной доски, а также других материалов.
Видео – Рассчитываем линолеум
Чтобы высчитать площадь пола в комнате, а затем – и расход материала, достаточно знать элементарные математические формулы и уметь пользоваться калькулятором. Имея последний под рукой (а сейчас калькулятор есть в каждом телефоне), произвести расчеты можно быстро. Главное – быть внимательными при снятии замеров.
Приступаем к расчетам
Прямоугольная комната
Это наиболее типичный и самый простой в расчете случай.
Площадь рассчитывается простым умножением длины на ширину комнаты. К примеру, комната размерами 2,4х3,8 метра будет иметь площадь 2,4*3,8=9,12 (квадратный метр).
Как рассчитать периметр потолка в этом случае? Тоже проще простого: он равен сумме удвоенной длины и удвоенной ширины. 2,4*2+3,8*2=12,4 метра.
Разумеется, при закупке профиля необходимо округлить суммарную его длину до значения, кратного размеру одной планки. То есть если в продаже есть только профиль UD длиной 2 метра, вам придется закупить 14 погонных метров, или 7 планок.
Задача для пятиклассника. Площадь равна произведению длины и ширины.
Комната с нишами и выступами
Как рассчитать площадь потолка в комнате, в которое есть стенные ниши, выступы или встроенные кладовки?
Задача будет ненамного сложнее предыдущей. Но все-таки сложнее.
- Рисуем эскиз комнаты. По возможности — с хотя бы примерным соблюдением пропорций.
- Измеряем и проставляем размеры всех прямых стен.
- А теперь, вооружившись угольником и линейкой, разбиваем эскиз на прямоугольники, одной стороной каждого из которых являются измеренные нами стены.
Задача сводится к несколько усложненному первому сценарию: вычисляем площадь каждого прямоугольника; затем суммируем все полученные площади.
Как посчитать периметр потолочного покрытия в этом случае? Это и вовсе простая задача после проведенных нами измерений: сложите длины всех стен.
И здесь расчет несложен. Достаточно мысленно разделить комнату на два прямоугольника.
Комната с косыми стенами
Ну, а если комната имеет форму сложного многогранника, у которого часть углов не является прямыми? Как рассчитать квадрат потолка тогда?
С периметром и здесь все просто: достаточно, вооружившись рулеткой, измерить протяженность всех стен.
Расчет площади же и здесь начнется с зарисовки эскиза и снятия всех размеров. Разница со сценарием номер два лишь в том, что после деления на простейшие элементы часть получившихся фигур будет не прямоугольниками, а треугольниками. Прямоугольными треугольниками.
Как вычислить площадь прямоугольного треугольника? Задача опять-таки для средней школы: площадь фигуры равна произведению катетов, разделенному на два. То есть если нам нужно рассчитать сегмент комнаты, у которого примыкающие к прямому углу стороны равны 1,2 и 0,95 метра — задача принимает вид S=1,2*0,95/2=0,57 м2.
Такая конфигурация помещения прекрасно делится на три прямоугольника и прямоугольный треугольник.
Комната с многоуровневым потолком
Как рассчитать квадрат потолка, идущего уступами? Такая картина весьма характерна для многоярусных гипсокартонных конструкций. При этом перепад высоты может иметь не только вид прямой или ломаной линии, но и представлять собой несколько дуг разного радиуса или и вовсе произвольную кривую.
Рассчитать площадь участка с криволинейной границей, безусловно, нелегко. Однако простая логика подсказывает, что сумма всех этих участков с горизонтальной поверхностью при условии, что стены вертикальны, равна… площади пола.
А раз так, то:
- Снимаем размеры со всех прямых участков стен.
- Вычисляем площадь пола по одной из приведенных выше методик.
- Замеряем обычной рулеткой высоту каждого вертикального участка потолка и его длину. На криволинейных участках вам придется измерять расстояния, суммируя небольшие фрагменты дуг, или попросить кого-то из домашних помочь вам с замерами.
- Умножаем для каждого вертикального участка потолка его высоту на протяженность. Прямой или криволинейный, он рассчитывается одним и тем же способом.
- Суммируем площадь пола и площади всех вертикальных уступов. Задача решена.
Расчет периметра потолка, думается, очевиден: и здесь он равен сумме всех отрезков, смежных со стенами.
И даже для такого потолка легко рассчитать площадь с приемлемой точностью. Разумеется, придется замерять длину всех криволинейных поверхностей
Площадь жилых помещений
Перед ремонтом начинается тщательное измерение всего, что есть – и ширина, и длина, и высота и даже диагонали
Дело в том, что при закупке стройматериалов, мы обращаем внимание, на какую площадь рассчитана та или иная упаковка, банка, или рулон обоев
Вычисляем площадь комнаты
Чтобы рассчитать, сколько надо обоев на одну комнату, необходимо произвести такие замеры:
- Высота потолка
- Ширина каждой стены
- Размеры окон и дверей
- Отдельно измерять ниши и выступы (если нестандартное помещение)
Высоту потолка можно измерять в одном месте. Это при условии, что пол ровный и расстояние от пола до потолка будет одинаково везде. Потом измеряем ширину каждой стены и умножаем на высоту. Это и есть площадь конкретной стенки.
Чтобы посчитать, сколько обоев нужно, надо суммировать площади всех стен. Но и это все. Ведь в комнате есть окна и двери, которые не надо оклеивать обоями. Поэтому, сначала вычисляем, сколько места они занимают, а потом уже вычитаем результат из полученной общей площади комнаты.
Вычислить квадратуру стен очень важно, ведь в результате этого мы не только правильно подберем обои, либо другие строительные материалы, но и сделаем правильною смету различных ремонтных работ. Ибо если нанимать работников для ремонта в жилом помещении, то их услуги тоже будут оцениваться от количества квадратных метров
Вычисление площади пола
Измеряем длину и ширину
Некоторые проблемы могут возникнуть с вычислением площади пола.
Обычная формула площади прямоугольника S=a×b может оказаться не совсем корректной в этом случае.
Бывает такое, когда стены в доме неровные, вследствие чего ширина пола в начале комнаты и в конце может быть разной.
Тогда измеряют ширину еще и посредине комнаты. Имея три различных результата, вычисляем среднее арифметическое этих данных — складываются все измерения и сумма делится на количество этих самых замеров. Результат будет хоть и не точный, но наиболее близок к этому.
Иногда в помещении может быть камин или же какая-то колонна, или просто ниша. В таком случае сосчитать необходимое количество паркета на пол становиться тяжелее.
Ведь он не нужен под камином, но им нужно застилать и выступ из комнаты. В подобных случаях нужно из общей площади вычитать ту, которая находится под камином или колонной. Или же наоборот, добавлять к общему еще и площадь ниши или эркера.
Как посчитать квадратные метры стены с окном
Сложнее будет иметь дело со стеной, на которой расположено окно.
В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.
- По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
- Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
- Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.
Зачем проводить расчет площади комнаты?
Мотивом для расчета площади комнаты могут послужить разнообразные факторы, но по большей части это связано с ремонтом в помещении. Наиболее частым предлогом для математического расчета, является:
- Планирование работы связанной с установкой подвесных потолков, когда существует потребность в знании количества материала для выполнения работ
- Устанавливая натяжные потолки, следует также, быть в курсе, площади в целях расчета материальных ресурсов на ремонт
- Окрашивание и шабровка потолка – не исключение и требует знания замеров, потому что все лакокрасочные работы и грунтовки анализируются на один м2
- Отделывая стены гипсокартонном также существует необходимость в знании площади стены в комнате
- При нанимание рабочих, например, для установления натяжного потолка, их объем работы, будет зависеть от каждого квадратного метра вашего потолка!
- Продавая дом или же, оформляя его, вам нужно обязательно знать, как измерить, площадь полка, стен, потолка.
Как посчитать площадь комнаты в квадратных метрах?
Во всех процессах, которые, так или иначе, связаны с недвижимостью, немаловажную роль играет величина площади, а именно квадратные метры. Для каких-либо операций могут понадобиться различные значения, будь то общая, жилая площадь комнаты или же прилегающая к частному дому территория.
Рассматриваемая характеристика является одной из самых важных, которая может повлиять на множество факторов: как стоимость услуг коммунального пользования, цену недвижимости, а также затраты на ремонт всего помещения или его части.
Несмотря на то, что многим кажется, что расчет квадратного метра площади комнаты достаточно прост, это является распространенным и грубым заблуждением. На самом деле, такого рода расчеты должны быть произведены точно, внимательно и аккуратно, потому как даже небольшая погрешность в таком деле, может обойтись дорогой ценой.
Это совсем не значит, что для расчета необходимо звать на помощь специалиста. Сегодня мы выясним, как посчитать площадь комнаты в м2, а также, что нужно учитывать, если она неправильной формы и т.д. Нужно понимать, что не все помещения имеют квадратную форму, так же стоит учитывать и различного рода неровности, выпуклости в комнате, такие как ниши, разная высота стен и т.д.
Расчет площади комнаты в квадратных метрах
Для того чтобы данный процесс был понятным и не сложным, необходимо понять саму суть изменений, а для этого необходимо составить пошаговую инструкцию измерения различных площадей, чем мы сейчас и займемся.
Какой бы ни была площадь комнаты, для ее расчета нужны всего три параметра – высота, ширина и длина, это знают все, кто учился в школе, но здесь есть перечень, причем, не маленький, различных тонкостей, деталей и нюансов, которые должны учитываться в процессе рассматриваемых расчетов.
Для начала нужно обзавестись инструментами, которые могут понадобится в процессе измерения, и только потом приступать к непосредственному делу, Итак: измерительная лента, ручка и лист, на котором измеряющий записывает все свои замеры и рассчитывает нужную ему величину.
Как посчитать площадь квадратуры пола и потолка
Рассмотрим для начала расчет квадратуры полового покрытия в комнате. Нам понадобиться для таких расчетов всего два параметра — ширина, и без сомнения, длина. Нужно сразу же отметить, что рассматриваемые замеры проводятся непосредственно у стеновых оснований, поэтому мебель и все лишние, мешающие замерам предметы, нужно будет либо сдвинуть, либо вынести из помещения.
Полученные замеры перемножают между собой, получая значение квадратные метры площади. Аналогичный процесс с вычислением квадратуры потолка. Конечно, можно посчитать площадь пола и обозначить квадратуру потолка аналогичным значением, но если нужны точные значения, придется измерить площадь и потолка, и пола, в отдельности, потому как не все помещения и комнаты правильной формы и идеально ровные.
Если комната квадратная, то проблем не возникнет, с комнатами неправильной формы все немного по-другому, но об этом чуть позже.
Как высчитать квадратный метр стены
Когда дело подходит к переклейке или же поклейке обоев, сразу становится вопрос измерения площади стен в комнате, здесь тоже своя система. Результат, который необходимо получить в данном случае — площадь стен м2.
Для проведения расчетов, необходимо знать два параметра ширину стен и их непосредственную высоту. Перемножим полученные замеры, мы получим нужный нам результат, причем, он будет измерен именно в метрах квадратных. Есть способ посчитать площадь комнаты в м2 без дополнительных усилий и траты времени, а именно при помощи рулетки лазерного типа.
Не стоит забывать, что площади дверных проемов, а также окон нужно вычислять отдельно, потому, как каждый из них имеет свое значение. Только узнав все эти данные, можно будет без проблем и лишних затрат приобрести обои для комнаты или помещения. Расчет общей площади стен в комнате будет следующим – от общей квадратуры стен нужно будет вычесть площадь окон и дверей, полученный результат и будет конечным.
Как посчитать комнаты неправильной формы в квадратных метрах
Если с квадратными и прямоугольными помещениями все предельно ясно, то с комнатами форму которых нельзя назвать правильной, все немного посложнее, без применения логики здесь не обойдется. Итак, способ, как рассчитать площадь комнаты в квадратных метрах, если она неправильной формы:
- Вычислять площадь квадрата и прямоугольника просто, поэтому, необходимо сделать так, чтобы расчеты такого типа нам пригодились и для неправильной формы комнаты.
- Визуально разбиваем ее на простые фигуры из геометрии (это может быть как квадрат, так и треугольник, все зависит от самой формы комнаты).
- Если визуальное воображение работает не очень хорошо, тогда можно прочертить линии на стенах, полу, потолке (где это понадобится).
- После разделения помещения на зоны из правильных геометрических фигур, приступаем к вычислению их площади в отдельности, чтобы потом просуммировать полученные результаты.
Как посчитать квадратные метры в комнате, в которых имеются ниши и выступы
В современных интерьерах сегодня нередко можно встретить различного рода дополнительные конструкции, которые делают дизайн современнее, а расчет площади – сложнее. Нишей можно назвать как углубление в стене, так и оконный проем, так что, в любом случае, необходимо будет учитывать и их размеры при расчете общей площади помещения.
Если необходимо рассчитать квадратные метры общей площади помещения, где есть различного рода выступ и углубления, понадобится измерить отдельно площадь квадратной или прямоугольной части помещения, и прибавить к ним площади ниш, выступов и всех неровностей.
В свою очередь, их площадь вычисляется по стандартному примеру вычисления – делим пространство на геометрические фигуры правильной формы и все.
Расчет криволинейных комнат в квадратных метрах
Случается так, что в некоторых помещениях (по различным причинам) некоторые углы срезаны или же стенка расположена не под 90 градусов, а площадь помещения вычислить надо. Здесь тоже применяется способ деления неправильных и сложных фигур на простые и правильные.
Стоит сразу же отметить, что в криволинейных комнатах даже деление на простые фигуры, не исключает получение треугольников. Чтобы не ошибиться в расчетах, лучше всего, начертить все фигуры, полученные при визуальном делении, на какой-нибудь бумаге, тогда процесс высчитывания квадратного метра площади будет проще и точнее.
Рекомендации для точного расчета площади комнат в квадратных метрах
Для того чтобы полученные результаты были точными, нужно в обязательном порядке измерять рулеткой стену в нескольких местах (инженеры не пользовались особой тщательностью измерений при строительстве многих зданий, поэтому ни стены, ни потолок не бывают идеальными).
После чего, нужно сложить все полученные результаты и разделить на количество точек измерения (получаем среднее арифметическое). Такое уточнение поможет избежать погрешностей и неточности измерений. Информация в статье поможет понять, как посчитать площадь комнаты в м2 и какие нюансы для этого необходимо знать.
Для измерения проема окна, в обязательном порядке меряются все части, независимо от того, кажется визуально, что они одинаковые или нет. Независимо от того, для каких целей вам понадобились замеры площади комнаты в квадратных метрах, проводить данные расчеты необходимо внимательно и тщательно.
Как правильно считать квадратуру — Рыболовный караван
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Часто требуется посчитать кубатуру комнаты, ее объем
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как посчитать площадь комнаты неправильной формы
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на план
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,75 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Формула расчета объема комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м 3 . Итак, объем помещения 44,8 куба.
Проверить работу строителей, определить объёмы работ и материалов легко, зная как посчитать квадратные метры пола или стен помещения с помощью простых геометрических формул, несложных вычислений и нехитрых приёмов.
В строительстве и отделочных работах почти все расценки на работы сведены к стоимости за квадратный метр. Квадратура поверхностей нужна и для подсчёта расхода материала (смотрите еще: советы для дома).
Метр квадратный это сколько?
Квадратным метром называется единица измерения площади, принятая в международной системе единиц, СИ. 1м² равен площади квадрата со стороной 1 м.
Знание простых правил и нескольких геометрических формул для подсчёта количества квадратных метров стен, полов, потолка позволит избежать ошибок в вычислениях и правильно определить нужные величины.
Инструменты для подсчёта
Для замера и расчёта понадобятся следующие предметы и инструменты:
- измерительная рулетка, необходимая длина рулетки 3-5 м;
- карандаш;
- лист бумаги для записей;
- калькулятор;
- строительный угольник.
Угольником размечают перпендикуляры – линии, пересекающиеся под прямым углом.
Площадь комнаты
Знание метража комнаты пригодится для определения стоимости полового покрытия, отделки потолка, количества и мощности осветительных приборов. Замеряя квадратуру помещения, проверяют соответствие площади, заявленной по проекту.
Измерения стен удобнее производить снизу, на уровне плинтуса. Сомнения в правильной форме помещения устраняют при помощи измерения диагоналей. Если диагонали комнаты равны, то углы – прямые, а помещение – прямоугольное.
Квадрат или прямоугольник
Самая распространенная форма комнаты в плане – квадратная или прямоугольная. Подсчёт квадратуры по полу при этом не составит особого труда:
- измеряют с помощью рулетки длину и ширину комнаты;
- перемножают цифры между собой, записывая результат на бумагу;
- выступы, колонны обмеряют, площадь элементов считают по тем же принципам, перемножая два размера;
- получившиеся цифры вычитают из площади комнаты.
При этом площадь потолка считают по тому же принципу, то есть умножают длину на ширину за вычетом технологических проемов, если таковые имеются.
Помещение неправильной формы
Эркеры, мансарды и комнаты домов со сложной архитектурой в плане часто имеют неправильную форму. Метраж нестандартной комнаты с полукругами, выступами, множеством углов подсчитать сложнее. Облегчают задачу, используя принцип деления сложных фигур на простые.
Пол, представляя как составную фигуру мысленно или отображая на бумаге, разделяют на стандартные геометрические элементы. Затем вычисляют площадь элементов по одному и складывают полученные величины.
Г-образные, Т-образные формы помещения в плане разбивают на прямоугольники и квадраты. Полукруглые поверхности принимают как часть круга.
Количество квадратных метров пола комнаты, в основе которой лежит трапеция, можно высчитать двумя способами:
- представив трапецию, как сочетание квадрата с двумя треугольниками. Получив значение фигур, цифры складывают;
- по формуле площади трапеции.
Для подсчёта по формуле измеряют две противоположные длинные стены, эти размеры дадут значения оснований. Значение высоты определяют путём замера перпендикуляра, проведённого от одного из углов меньшего основания к большему.
Формула площади трапеции S=1/2(А+В)*Н, где:
- S – искомая величина, площадь трапеции;
- А – основание трапеции;
- В – основание трапеции;
- Н – высота трапеции.
Площадь трапециевидной комнаты – половина суммы числовых значений оснований, умноженных на высоту.
Объем комнаты
Кубатура помещения, или объём в строительстве используется при подсчёте необходимой мощности отопления, вентиляции, кондиционирования комнаты.
Объём измеряется в кубических метрах. Единица записывается как 1 м³.
С точки зрения геометрии, помещение как фигура представляет собой шестигранник.
Измерив длину, ширину и высоту комнаты прямоугольной формы, перемножив полученные измерения, получают объём простого помещения.
Объём помещения сложной формы вычисляют следующим путём:
- пол комнаты разбивают на простые геометрические фигуры;
- вычисляют квадратуру каждой фигуры;
- полученные значения складывают и умножают на высоту до потолка.
Как посчитать квадратуру стен?
Размер стены в квадратных метрах нужен для подсчёта количества отделочных материалов, размещения полок, зеркал или навесных шкафов.
Сплошная стена
Квадратура стены рассчитывается аналогично площади пола – длина, высота стены после обмера перемножаются между собой. Учитывают все впадины и выступы, если такие есть. Стены мансардных помещений под крышей часто ломаной формы, сегменты находятся в разных плоскостях.
В этом случае участки стены измеряют по отдельности, переносят на бумагу. Подсчитывают площадь каждой отдельной геометрической фигуры и суммируют числа.
С окном
Определяя количество квадратных метров стены, оконные проёмы, как правило, исключают.
Торцевые грани стен возле окна называют откосами, их размеры также не входят в метраж стены и считаются отдельно, например при подсчёте штукатурных работ или шпаклёвки.
С дверью
Квадратуру дверного проёма из площади стены при расчёте вычитают. Откосы при необходимости измеряют отдельно.
Измеряем площадь неправильной фигуры
Высчитывая метраж декоративных арочных проёмов или стрельчатых окон, поступают по тому же принципу, разбивая сложную фигуру на несколько простых элементов.
С квадратами и прямоугольниками совмещают части круга и треугольники.
Окружность
Целый круг в интерьере встречается достаточно редко. Полностью круглым может быть окно, колонны, центральная часть многоуровневого потолка. В основном дело приходится иметь с частями круга: половиной или сегментами.
Рулеткой снимают размер между двумя противоположными точками круга. Этот отрезок будет называться диаметром. Радиус круга равен половине диаметра.
Подсчёт площади круга производят по формуле S = π*R², где:
- R – радиус;
- S – площадь круга;
- π – постоянная математическая величина, округлённая до значения 3,14.
Числовое значение площади полукруга получают делением полученного результата на 2.
Квадратура сектора круга равна произведению половины длины дуги сектора на радиус круга, вычисляется по формуле S = 1/2 L*R.
Треугольник
Формула площади треугольника S=1/2*Н*А, где:
- S – площадь треугольника;
- Н – высота;
- А – сторона треугольника.
Высоту треугольника получают, измеряя рулеткой перпендикуляр от угла, противоположного к стороне.
Посмотрите на видео ниже полезные советы для быстрого и правильного подсчета квадратуры стен и пола:
Статья полезна? Сохраните закладку или отметьте для друзей!
Начиная ремонт, первым делом нужно определить необходимое количество строительных материалов. Провести расчеты могут специалисты, которые будут выполнять работы. Но они часто делают вычисления с большой погрешностью в свою пользу. Рассмотрим, как самостоятельно посчитать площадь стен.
Инструменты для подсчета квадратных метров
Для расчетов понадобятся:
- уровень строительный;
- рулетка с ограничителем;
- длинная линейка и угольник;
- карандаш и бумага;
- калькулятор.
Для нанесения размеров нарисуем схему комнат. Обозначим двери, окна, ниши, выступы. Результаты замеров нанесем на чертеж.
Как рассчитать площадь прямоугольных стен
Измеряем высоту (h), длину (a), ширину (b).
Площадь: S = P × h
Периметр: P = (a + b) × 2
Вдоль плинтуса измеряем длину и ширину помещений.
Высоту — по вертикальному углу.
Р = (5 + 4) × 2 = 18 м;
Как правильно рассчитать площадь стен со сложной поверхностью
Не все помещения имеют строгую прямоугольную форму. В зданиях часто присутствуют замысловатые архитектурные элементы, усложняющие расчет.
Как посчитать квадратуру стен за вычетом проемов
При определении точного объема работ, вычтем размеры окон и дверей из общего количества квадратных метров стен комнаты. Для этого по краю рамы замеряем ширину и высоту окна, по краю коробки — габариты двери.
Перемножив длину и ширину проемов, получаем размер, который необходимо вычесть.
Аналогично действуем, если из подсчитываемой квадратуры комнаты нужно исключить печи, камины, радиаторы.
В помещении имеется окно 2,5 м × 1,5 м и дверь 0,9 м × 2,1 м.
S окна равна 2,5 × 1,5 = 3,75 м².
S двери равна 0,9 × 2,1 = 1,89 м².
S стен за вычетом проемов составляет 54 − 3,75 − 1,89 = 48,36 м².
Определение площади помещений неправильной формы
Для определения периметра зданий любых конфигураций сложим длины всех стен, включая выступы и ниши.
Проводить измерения помещений неправильной формы можно, разбив поверхность на несколько простых фигур.
Если у вас комната с прямоугольным выступом, вы имеете две фигуры, квадратуру которых легко вычислить, затем сложить.
Если элемент содержит в себе полукруг, для расчета нужно разбить его на полукруг и прямоугольник.
Как считать квадратные метры стен с круглыми элементами
Встречаются круглые и полукруглые жилые здания или строения с элементами окон или дверей в виде арки.
Их периметр можно определить, умножив диаметр на число π (Пи) = 3,14.
Квадратуру вертикальных поверхностей определяем, умножив полученное значение на высоту от пола до потолка.
S круга равна квадрату радиуса, умноженному на число π; полукруга — половине этой величины.
Если необходимо из квадратуры комнаты вычесть площадь круглых колонн или полукруглых выступающих элементов, при невозможности измерить диаметр или радиус, измеряем длину окружности (P) и применяем формулу: S = P² / 4π.
Как рассчитать квадратные метры конструкций в виде треугольника
В случае наличия комнаты с треугольными элементами, мы можем применить несколько формул, в зависимости от вида фигур:
Где a, b, c — длины сторон треугольника; p — периметр.
Объем помещения
Для определения объема необходимо высчитать площадь пола, и полученный показатель перемножить на высоту. V = S × h.
Расчет площади стен дома на калькуляторе
Существенно облегчат расчеты специальные программы, к которым относится строительный калькулятор в онлайн-версии.
Чтобы посмотреть, сколько квадратных метров составляют стены за вычетом проемов, достаточно выбрать геометрическую форму помещения и ввести показатели:
- ширину;
- длину;
- высоту;
- количество проемов;
- размеры окон и дверей.
Строительный калькулятор рассчитает количество отделочных материалов, необходимых для вашего ремонта.
Советы и рекомендации
Необходимо помнить, что геометрические параметры зданий редко могут быть идеальными. Поэтому для определения точных величин замеры лучше производить в нескольких местах, а затем выводить среднее арифметическое. Например, рассчитывая площадь комнаты по стенам, длину лучше измерять по потолку, плинтусу и в середине вертикальной плоскости. Высоту — в углах и середине стены по отвесу.
Чтобы вычислить периметр при наличии множества выступов и ниш разных форм, необходимо проложить вдоль всех элементов шнур, затем измерить его рулеткой.
Подсчитав точные параметры, можно идти в магазин за строительными материалами. Лучше показать схемы с нанесенными размерами продавцу-консультанту. Специалист поможет рассчитать расход материалов с учетом нахлеста, подбора рисунка обоев или потерь при резке плитки.
Как рассчитать площадь пола ( квадратуру комнаты )?
Наши покупатели часто просят рассчитать необходимое количество упаковок ламината или площадь помещения. Данная информация создана именно для таких случаев. Мы ни раз сталкивались с проблемой расчета напольного покрытия будь то ламинат или паркет… Кто-то однозначно понимает, как рассчитывается площадь в квадратных метрах, кто-то затрудняется с расчетом, НО так или иначе это полезно и тем и другим. И так, как же рассчитать площадь пола или комнаты для покупки напольного покрытия?
Вот пример нашей квартиры/дома:
И так, начните с создания эскиза помещений дома или квартиры. У вас должно получиться нечто подобное моей картинке. Далее начните измерять длину каждой стены от какого-то угла отмечая расстояния на вашем эскизе (как показано на рисунке). В итоге мы получаем схему расстояний каждого отдельного помещения. Теперь чтобы получить квадратуру каждого помещения мы должны перемножить расстояния исходящие от угла как показано на рисунке ниже:
Углы от которых мы множим расстояния до конечных точек обозначены красным цветом. Мы множим стену А на стену Б и получаем необходимую площадь в квадратных метрах. Естественно если вы сделали замеры в сантиметрах, то их нужно перевести в метры (по принципу — в каждом метре 100 сантиметров). Продолжая далее мы получаем квадратуру всех помещений. Сложив их воедино мы получим площадь нашей квартиры — 23,1+2,4+5,6 = 31,1 м2 Теперь мы можем вбивать в калькулятор расчета в интернет магазине BSpol.ru всю площадь или нужную нам комнату. Калькулятор автоматически рассчитает вам нужное количество упаковок и сумму заказа. ВНИМАНИЕ! Калькулятор округляет квадратуру кратно пачкам в большую сторону и не учитывает запас для сложных помещений. Запас покрытия для укладки «по прямой» должен составлять 3-5%, в случае укладки по диагонали 10-15%.
Почему при расчете нужного количества пачек ламината необходимо закладывать запас? В укладке напольного покрытия «по прямой» всегда есть вероятность ошибок при укладке. Такая ошибка может возникнуть в совершенно различных местах, например на запиле возле дверного проема или батареи. Так же частая ошибка при запиле в точках завершения покрытия. Различные сложные углы и выступы так же вызывают погрешности в укладке. При укладке «по диагонали» это особенно ощутимо, именно по этому есть четкое требование при такой укладке — брать запас не менее 15%. При укладке по диагонали точки окончания полосы (обрезки) не подходят для переноса на шаг следующей полосы, они идут в отброс.
С Уважением BSpol.ru
Узнаем как посчитать квадратуру комнаты: полезные советы мастера
Приступая к ремонтным работам, сначала оговаривают количество необходимых строительных материалов: клея, обоев, красок и лаков. Чтобы сделать такие вычисления и не приобрести слишком много или недостаточно расходных материалов, для начала определяют площадь помещения. Такое понятие потребуется не только при ремонте, но и при продаже недвижимости. Как посчитать квадратуру комнаты, получить и применить на практике собранные данные, постараемся понять.
Особенности вычисления
Если возникает вопрос, как правильно посчитать квадратуру комнаты, отталкивайтесь и от того, какие типы работ будут произведены.
Чтобы узнать необходимые данные, придется применить формулу. Подсчет проводится с учетом формы комнаты и наличия в ней дополнительных конструкций: лоджии, ниш, арок, перемычек, гардеробных.
Квадратура комнаты — это не только площадь пола. Потому при постановке вопроса, как посчитать квадратуру комнаты, нужно отталкиваться от предстоящих работ.
Так, при оштукатуривании вычисляют S стен и потолка, а для облицовки кухни плиткой потребуется расчет площади пола и поверхности стен на высоту 1,0-1,5 м. При проведении операции могут возникнуть трудности, если конструкция комнаты сложная: присутствуют балки, ниши или альковы, особенно если они располагаются вблизи оконных проемов.
Было бы ошибкой думать, что Sпола и Sпотолка равны. В мансарде, к примеру, скаты кровли нависают сверху над головой, образуя так называемый шатровый потолок. Сразу заметно, что квадратура напольного покрытия будет больше. Потому, приступая к ремонту в подкровельном помещении, площадь каждой поверхности рассчитывают по отдельности.
Расчет квадратуры прямоугольного помещения
В стандартной комнате пол всегда равен потолочному покрытию и высчитывается по формуле для прямоугольника S=AxB.
При обшивке гипсокартонными панелями, поклейке обоев, оштукатуривании, покраске стен и/или потолка, облицовке плиточными изделиями и других видах ремонтных работ, предусматривающих выравнивание и отделку настенного покрытия, требуется проводить расчет площади.
Все вычисления основаны на периметре и высоте комнаты. Измерив их при помощи рулетки, подставьте в формулу:
S=РхН, где Н – высота помещения, Р – периметр. Формула Р=2(А+В), где А и В – показатели длины сопредельных стен.
Не забудьте об оконных и дверных проемах, которые не подпадают под отделку. Их площадь необходимо отнять от общего числа.
Следовательно, перед тем как посчитать квадратуру комнаты для обоев, все оконные проемы измеряют, после чего вычисляют площадь каждого, суммируют и отнимают от Sкомнаты, получив в итоге квадратуру под отделку.
Важно! Запомните, что для дверных и арочных конструкций дополнительно используется формула для сегмента окружности или для полукруга.
Как получить результат измерений
Как посчитать квадратуру комнаты? Сначала обмеряйте стены. Для этого используйте обычную рулетку. Для помещения квадратной формы подойдет формула:
Sкомнаты = АхВ (А – длина; В – ширина).
*ширина умножается на высоту, после чего получается число, отражающее площадь комнаты в м2.
Применение формулы на практике
Проблемы не должны возникнуть, если вы знаете, как подсчитать квадратуру комнаты. Постарайтесь разобрать особенности вычисления площади помещения под поклейку обоев подробнее, согласно примеру.
Часто по завершении ремонтных работ остаются излишки материала. Или же под конец оклейки оказалось, что холста обоев не хватило. Планируя отделку, не забывайте о точном и правильном вычислении площади помещения. Так вы избавите себя от неудобных ситуаций в процессе оклейки обоев.
Как определить, сколько потребуется обойного полотна?
Здесь все зависит от периметра комнаты и ширины рулона. Имея эти данные в блокноте, подсчитать кубатуру не составит труда. В работе с таким материалом учитывайте его рисунок.
Проще всего оклеивать стену отрезками с простым изображением: полотна не придется подгонять. Если вы приобрели рулоны со сложными геометрическими узорами, приготовьтесь, что расход материала будет больше, ведь куски придется разрезать, чтобы элементы разных отрезов стыковались, образовав единое целое.
Важно! Независимо от текстуры и стиля полотна всегда добавляйте 2-3 сантиметра на припуск под плинтуса.
Подсчет обоев: как разобраться?
Рассмотрим на примере. При периметре в 12 м и стандартной ширине рулона 53 сантиметра для оклеивания стен понадобится 23 полосы обоев.
Важно! При поклейке внахлест не забывайте учесть припуски.
Если высота потолка в комнате 2,7 м, добавьте на припуск не менее 5 см. Так получается длина 1 полотна – 2,75 м. при стандартной длине материала в рулоне – 10,05 м из одной упаковки выходит 3 целых полосы. Для вычисления количества рулонов 23 делят на 3 и получают необходимое для отделки число упаковок – 7,54, то есть придется приобрести 8 рулонов обоев.
Облицовка ванной комнаты: сколько понадобится плитки
Расчет требуемого количества материала разберем на примере. Мастера пользуются проверенной методикой вычисления объемов расходного материала для отделки ванной комнаты.
Для этого замеряют стены и проводят расчет по формуле, чтобы посчитать квадратуру ванной комнаты. Здесь, как и при вычислении необходимого количества обоев из общей площади вычитают дверные и оконные проемы.
Рассмотрим на примере. Так, получив число в 21 квадратный метр, находят необходимое количество плиток. Сначала проводят расчет площади 1 керамического изделия, при размере 0,3 х 0,2 получаем 0,06 м2.
Sванной/Sизделия=n, где n – число плиток.
21/0,06=350 шт. Запас при укладке изделий составляет 10% от необходимого числа. Для примера, 35 штук. В итоге получается, что для облицовки ванной комнаты понадобится 385 целых плиточных квадратов.
Важно! Количество напольного покрытия определяют по той же схеме.
Теперь вам известно, как посчитать квадратуру ванной комнаты под плитку, для отделки обоями или для монтажа напольного покрытия.
Пользуясь простой формулой, можно самостоятельно определить, сколько отделочного материала, клеевой смеси, стяжки потребуется для проведения ремонтных в любом из помещений дома. Это удобно и просто, ведь нет необходимости нанимать специалистов для проведения такой простой работы.
Как рассчитать квадратные метры-Обучение гипсокартонным работам
Как считать площадь пола подробное руководство и калькулятор
Ремонт пола в квартире или доме требует точного расчета количества м2 в каждой комнате.
В связи с тем, что на сегодняшний день строительные материалы — товар достаточно дорогой, каждый, кто затеял ремонт, пытается как можно больше сэкономить на материалах.
Если вы не знаете, как правильно посчитать площадь неровного пола, который имеет нестандартные размеры — эта статья расскажет вам об этом.
Для чего могут пригодится расчеты?
Для чего нужно рассчитывать площадь пола:
- Чтобы купить необходимое количество материалов;
- Сэкономить на покупке напольного покрытия;
- Для того, чтобы определить количество жилой помощи в помещении;
- После строительства дома для определения соответствия с планом;
- При ремонте, для определения размеров будущей мебели и т. д;
Причин, по которым нужно вычислить площадь помещения — множество, решений же существует несколько.
Вычисление площади пола
Если комната стандартная (квадратная или прямоугольная), то вычислить площадь такого помещения сможет каждый. Для этого нужно узнать ширину и длину помещения, после чего просто перемножить эти показатели.
Если вы рассчитываете площадь помещения для потолка, то встроенные шкафы или камины никак не повлияют на замеры площади.
Проводить точные замеры помещений, в которых имеется встроенная мебель, необходимо, если вы планируете укладывать напольное покрытие. В случае, если камин или комод занимает не много места, его площадью можно пренебречь, если много — конструкцию на время можно разобрать или высчитать сколько места она занимает.
Как высчитать площадь пола с неправильными размерами?
Если комната имеет нестандартные размеры — вычисление площади пола будет происходить немного дольше и сложнее. Существует множество причин, по которым комната может иметь нестандартные формы, например, ниша в спальне или встроенный шкаф.
Стоит заметить, что способ найти площадь нестандартного пола все же можно. Для этого необходимо разбить помещение на небольшие геометрические фигуры, например, треугольники, квадраты, прямоугольники и т. д.
Конечно, есть множество других способов, как рассчитать площадь пола, но с помощью такого способа — это сделать намного проще.
Среди прочих способов, как можно высчитать площадь пола, достаточно посмотреть жилую и общую площадь в домовой книге, если домовой книги нет — в плане застройщика.
Как вычислить площадь помещения, в котором есть скошенные углы?
Вычислить площадь помещения, в котором есть скошенный угол — достаточно просто, для этого нужно:
- Вычислить стороны треугольника;
- Рассчитать площадь по формуле S = (a*b)/2. В этом случае a и b — катеты треугольника.
Если треугольник не прямой, то рассчитать его площадь можно с помощью формулы Герона.
Формула Герона.
Калькулятор расчета площади
Существует множество способов как найти площадь пола, одним из них является онлайн калькулятор, который позволит быстро и надежно рассчитать площадь любого помещения. От вас только требуется внести замеры в специальную таблицу.
Преимущества калькулятора расчета площади:
- Возможность высчитать площадь любой геометрической фигуры;
- Нет необходимости самостоятельно просчитывать;
- Скорость и точность расчетов.
Калькулятор расчета площади — это оптимальное решение вопроса, как быстро посчитать площадь пола комнаты.
Как посчитать необходимое количество плитки
Для того, чтобы узнать необходимое количество плитки, необходимой для укладки в той или иной комнате, необходимо узнать площадь помещения. Как быстро найти площадь пола любой комнаты — описано выше. После того, как площадь будет рассчитана, необходимо узнать площадь 1 плитки из выбранной коллекции. После этого нужно просчитать, сколько плиток необходимо для укладки её в комнате.
Пример:
- Площадь комнаты: 20 м2;
- Размеры плитки: 0,2 х 0,4 м;
- Площадь 1 плитки: 0,08 м2;
- Необходимое количество плиток: 250.
Таким способом можно узнать количество необходимой плитки. Таким же способом можно рассчитать необходимое количество паркетной доски или ламината. Стоит заметить, что в некоторых случаях количество необходимых материалов зависит от узора, который будет выполнен на напольной поверхности.
Советы
Для того, чтобы правильно рассчитать площадь пола — необходимо знать геометрические формулы или же уметь пользоваться онлайн калькулятором.
Данные по площади пола можно узнать из домовой книги. Комнаты, которые имеют сложную геометрическую форму проще всего рассчитывать с помощью деления их на небольшие геометрические объекты.
Узнать площадь полукруглой поверхности можно с помощью формулы: S = πR2/2 — радиус круга.
Считаем квадратуру помещения
Проще всего рассчитать квадратную площадь у прямоугольной поверхности, не важно — будь то потолок, пол, стена или что-либо другое. Для начала нужно узнать длину и ширину поверхности
Измерить эти показатели можно с помощью линейки или рулетки. Помещение очень редко (а по факту практически никогда) не бывает идеально правильным. Поэтому чтобы верно рассчитать квадратную площадь поверхности, нужно сделать не одно, а несколько замеров. Например, поскольку стены могут быть не ровными, лучше всего замерить пол сначала в одном конце комнаты, затем посередине, затем в конце. После этого вычисляют среднее арифметическое и получают, таким образом, более точную картину. Среднее арифметическое узнать очень просто. Для этого цифры всех трех замеров складывают и получившуюся сумму делят на три (по количеству замеров).
Так узнают ширину и длину помещения: пола, потолка или стены. После проведения этих замеров, можно узнать, количество квадратных метров. Формула крайне проста. Нужно ширину умножить на высоту. Если же помещение имеет нестандартную форму, например колонны, ниши, выступы и тому подобное, это помещение сначала следует разбить на более удобные для измерений формы. Например, все ниши измеряются отдельно, все выступы также отдельно, все колонны и прочие имеющиеся элементы интерьера также измеряются отдельно. Допустим, в помещении имеется две ниши. Чтобы узнать площадь пола в квадратных метрах, нужно замерить длину и ширину самого помещения, затем первой ниши, а затем второй ниши. Обе длины ниш складываются и записываются на бумаге. Затем складывается ширина этих ниш. Чтобы узнать количество квадратных метров, полученные две цифры перемножаются и добавляются к общим квадратным метрам основного помещения.
Как высчитать квадратуру криволинейного помещения
Если же в помещении имеются выступы, действовать следует иначе. В первую очередь измеряется длина и ширина помещения. После этого — выступов. Длины выступов суммируют, так же как и их ширину. Обе цифры перемножаются. В итоге получаются квадратные метры, которые вычитаются из общей площади помещения. Так же поступают с колоннами и другими элементами, которые занимают определенное место.
В случае совершенно нестандартной планировки, помещение разбивается на более удобные части. Это могут быть прямоугольники, треугольники и круги. Чтобы рассчитать квадратные метры каждой из этих фигур, следует воспользоваться соответствующими формулами. Например, для прямоугольных и квадратных — формулой, описанной выше. Для кругов — формулой расчета площади круга, а для треугольников — формулой расчета площади треугольника. Все эти формулы можно с легкостью найти в любом математическом справочнике или отыскать в интернете.
Рассчитать площадь пола, стены, потолка, а так же периметр комнате нашим калькулятором
Для начала нужно ввести следующие параметры.
Общие размеры помещения
С помощью нашего калькулятора Вы без труда сможете рассчитать:
- Периметр комнаты.
- Суммарная площадь стены.
- Площадь пола.
- Площадь потолка.
Перед тем как вводить данные, ознакомьтесь с инструкцией (находится ниже калькулятора). Данные расчеты можно использовать во время ремонта, чтобы знать например сколько линолеума или потолочной плитки может понадобиться для закрытия всех потребностей в материале. Рассчитать площадь стен будет полезно при оклейки стен обоями, чтобы определить сколько рулонов и клея нам необходимо приобрести – предлагаем воспользоваться калькулятором обоев.
Как рассчитать S стены в квадратных метрах
Рассчитать параметры помещения, как правило, необходимо в преддверии ремонта в комнате, квартире или доме. Целью производства таких действий является вычисление потребности в материалах и составления сметы и материальной ведомости. Как рассчитать площадь стен в квадратных метрах? Для этого понадобится произвести соответствующие измерения, понадобятся инструменты:
- рулетка с зацепом и фиксатором ленты;
- блокнот для составления эскизов помещения и записи результатов измерений;
- карандаш и маркер;
- калькулятор для расчета площади стен комнаты.
Замеры параметров стен и пола лучше производить вдвоем, непосредственно вдоль перегородки. Но если помещение заставлено тяжелой мебелью и нет доступа к объекту измерения, можно производить замер и посредине его, но нужно проследить, чтобы лента рулетки располагалась параллельно объекту, в противном случае результат может быть неверным. При производстве замеров нужно составить эскиз измеряемой перегородки, с указанием размеров оконных и дверных проемов и их расположения на стене. Эта информация может понадобиться при подсчете потребности в отделочных материалах. Кроме того, нужно произвести замер и толщины самой перемычки, поскольку торцевые поверхности в процессе ремонта обрабатываются лакокрасочным покрытием и рассчитать потребность в них также необходимо. Эти поверхности при замене столярки отделываются штукатуркой, шпатлевкой, потребность в которых рассчитывается предварительно.
Результаты замеров в каждом помещении квартиры или дома суммируются и составляется материальная ведомость, которая служит основанием для разработки сметы и расчета стоимости материалов. Измерение в квадратных метрах производится потому, что все нормативы расхода рассчитаны в единицах по отношению к этой единице. Но если помещение в плане представляет собой сложную фигуру, повозиться придется больше. Нужно на эскизе разбить план комнаты на элементарные многоугольники, представляющие собой прямоугольники, треугольники, секторы и сегменты. Затем рассчитывается поверхность каждой из них и суммируется. При производстве расчетов округление следует производить только на конечном результате до первого десятичного знака и в большую сторону.
Типовой онлайн калькулятор, широко представленный в интернете, позволяет бесплатно рассчитать величину перегородки в квадратных единицах по представленным данным. Он представляет собой табличку, в которую водятся первичные данные для расчета:
- длина помещения;
- ширина;
- высота.
Итоговый результат практически мгновенно появляется в последней колонке или строке таблички. Одновременно с перегородками калькулятор позволяет рассчитать также S потолка и пола.
Для примера представим расчет площади для комнаты.
Исходные данные для расчета: hазмеры помещения – длина 5.2, ширина, 3,2, высота 2,5 метра. В комнате устроена одна дверь размером 2,1х0,9 и одно окно 1,4х1,3 метра.
Расчет:
- Определяем размер периметра комнаты – 5,2*2 + 3,2*2 = 10,4 + 6,4 = 16,8 (метра).
- Рассчитываем S стен – 16,8*2,5 = 42 (м. кв.).
- Размер проема двери составит – 2,1*0,9 = 1,9 (м. кв.).
- Размер оконного проема – 1,4*1,3 = 1,8 (метра кв.).
- Общий размер проемов составит – 1,9 + 1,8 = 3,7 (м. кв.).
- Площадь перемычек – 42,0 – 3,7 = 38,3 (метра кв.).
Кроме полученных данных, используя замеры, можно сразу же рассчитать:
- S утепляемых участков, имеющих контакт с наружным пространством;
- количество гипсокартона для внутренней отделки;
- сколько рулонов обоев потребуется для финишной отделки.
- Как посчитать площадь поверхности трубы в м2
- Классификация металлических труб по диаметру
- Гофра жаростойкая, огнеупорная для дымохода — их виды
- Таблица пайки полипропиленовых труб и виды сварки
- Можно ли установить газовую колонку в ванной?
Как посчитать площадь потолка
При проведении ремонтных работ в жилом помещении особое внимание уделяют отделке поверхности потолка. Для того чтобы приобрести необходимое количество строительного материала для отделочных работ, важно изначально правильно произвести все замеры, после чего посчитать объемы стройматериалов. Как известно, если проводить все работы будут специалисты, то данную работу они возлагают на себя, в противном случае посчитать площадь потолка придется самостоятельно. Несмотря на то что формы могут отличаться, произвести предварительные расчеты не так сложно, как может показаться на первый взгляд. Чтобы не ошибиться, необходимо придерживаться всех рекомендаций, а в процессе подсчетов пользоваться соответствующими формулами.
Что необходимо для расчета площади потолка
Для того чтобы вычислить площадь, не требуется много времени и усилий. Все, что необходимо – вспомнить геометрические формулы по вычислению площади разных фигур и иметь под рукой необходимые инструменты.
Для проведения работ потребуются следующие предметы:
- рулетка – гораздо легче замерять лазерной рулеткой, но, если такой не имеется, то можно воспользоваться обычной;
- стремянка;
- строительный уровень;
- простой карандаш, маркер либо ручка;
- чистый лист бумаги;
- калькулятор.
После того как все подготовлено, можно приступать к определению формы и проведению подсчетов.
Совет! Необходимые формулы лучше найти заранее.
Как посчитать площадь потолка в квадратных метрах
На сегодняшний день можно встретить поверхности потолочной зоны любой геометрической формы. Для того чтобы высчитать площадь потолка в квадратных метрах, необходимо воспользоваться геометрическими формулами, благодаря которым можно произвести расчеты довольно легко и просто. Данная работа не отнимет много времени, если сразу учитывать все рекомендации и правильно измерять помещение.
Как посчитать квадратуру потолка прямоугольной комнаты
Как показывает практика, гораздо легче вычислять квадратуру потолка, имеющего правильную форму – квадрата либо прямоугольника, если при этом в помещении отсутствуют колонны, выступы и прочие декоративные элементы. Для того чтобы посчитать, сколько квадратных метров, необходимо произвести замеры длины и ширины.
Как показывает практика, многие отдают предпочтение лазерной рулетке. Для вычисления квадратных метров длину умножают на ширину. Например, размеры помещения составляют 2*1,5 м, соответственно площадь получится 3 кв. м.
Внимание! Допускается для удобства проводить измерения пола, так как в стандартных помещениях площадь пола и потолка одинаковые.
Как найти площадь потолка в помещении трапециевидной формы
Если рассматривать современные новостройки, то стоит отметить, что в таких квартирах поверхность зачастую бывает в форме трапеции. Не стоит пугаться в данном случае, так как произвести все необходимые работы можно довольно легко и без особых затруднений. Все что требуется, воспользоваться формулой и подставить в нее значение. Формула выглядит следующим образом:
S = ( a + b ) / 2 * h, где:
- b – параллельные стороны;
- h – расстояние между параллельными сторонами.
Допустим, что параллельные стороны имеют следующие размеры: 4 и 6 м, а перпендикулярное расстояние составляет 5 м. Остается подставить данные в формулу и получить результат:
( 4 + 6 ) / 2 * 5 = 10 / 2 * 5 = 5 * 5 = 23 кв. м.
Как высчитать площадь потолка треугольного помещения
В некоторых случаях можно встретить жилые помещения, которые имеют форму треугольника. В данном случае потребуется воспользоваться более сложной формулой, чем для простых форм. При необходимости можно визуально разделить помещение на прямоугольники и высчитать показатели каждой фигуры, в противном случае можно воспользоваться следующей формулой:
S = ½ * h * a, где:
- S – площадь;
- h – высота;
- a – сторона.
Первым делом рекомендуется вычислить показатель высоты треугольника, после при помощи рулетки выясняют показатель от угла до противоположной стороны, затем измеряют стороны фигуры.
Как вычислить площадь потолка округлой формы
Рассчитать, сколько квадратов потолок округлой формы, не так сложно, если придерживаться формулы. В данном деле важно убедиться, что поверхность действительно имеет форму правильного круга.
Самый простой и популярный способ – очертить в круге квадрат и брать его в качестве основы, но в таком случае потребуется приобретать для отделки помещения намного больше строительных материалов.
Второй вариант – провести несколько радиусов. Если они совпадают, то поверхность можно вычислить по обычной геометрической формуле. Для того чтобы вычислить площадь правильного круга, потребуется умножить радиус на число пи, которое равняется 3,14. Полученное произведение возводят в квадрат. Полученный показатель стоит разделить на 2 и получить конечный результат.
Как посчитать квадратные метры криволинейного потолка
Как показывает практика, намного сложнее дела обстоят с криволинейными формами, которые выполнены по более сложному конструктивному принципу. Как правило, такие конструкции фигурные, имеют несколько уровней – от 2 и более.
Необходимо придерживаться следующего алгоритма работ:
- Первым делом измеряют все прямые участки и отмечают их на схеме.
- Вычисляют площадь пола.
- При помощи рулетки выявляют высоту и длину всех вертикальных участков.
- Высоту умножают на длину.
В конечном итоге необходимо сложить все умноженные величины и получить результат в кв. м.
Внимание! В данном случае должны быть учтены все имеющиеся перепады.
Как рассчитать квадратуру потолка комнаты с косыми стенами
Если в помещении имеются косые стены, то необходимо измерить предварительно имеющийся скос и использовать его в качестве гипотенузы в прямоугольном треугольнике. После того как все замеры выполнены, можно подставлять полученные данные в формулу, которая выглядит следующим образом:
S = (катет * катет) / 2.
Стоит рассмотреть расчет на примере. Для вычисления катета потребуется взять известное значение, которое равно 1,75 м и отнять размер противоположной стены, равной 1,18 м. В итоге получается 0,57 м. Таким же образом необходимо вычислить второй катет. В результате площадь треугольной части составляет (0,57 * 0,57) / 2 = 0, 57 кв. м. После этого потребуется разделить помещение на две равные фигуры и получить их площадь.
Как узнать площадь потолка, если есть в помещении выступы и ниши
Зачастую в помещении можно наблюдать наличие разнообразных выступов, ниш и прочих декоративных элементов. В данном случае потребуется составить максимально точный чертеж с учетом всех пропорций. Поверхность условно разделяют на прямые фигуры, высчитывают их, после чего полученные значения складывают. При необходимости изначально можно найти общий показатель, после чего вычесть из него площадь, которую занимает каждая колонна либо ниша.
Как измерить площадь многоуровневого сложного потолка
Расчет многоуровневой сложной системы представляет большое количество затруднений, так как в данном случае потребуется измерять все имеющиеся перепады, прямые и ломаные линии.
Первым делом потребуется замерить и высчитать все имеющиеся вертикальные участки. Намного сложнее проводить работу с криволинейными участками, так как их потребуется разбить и определять площадь каждого отдельного фрагмента.
Важно! Точность полученных данных полностью зависит от точности расчета всех криволинейных фрагментов.
Заключение
Посчитать площадь потолка не так сложно, поэтому при проведении строительных работ данный момент не должен пугать. При отделке помещения важно заранее подготовить весь необходимый инструмент, правильно составить схему, указать на ней все требуемые размеры. После этого, воспользовавшись специальными формулами, стоит вычислить общую площадь поверхности в квадратных метрах. Только после этого можно приступать к приобретению строительных материалов. Важно учитывать, что несмотря на правильность произведения расчетов, рекомендуется приобретать строительный материал с небольшим запасом.
Отправить комментарий
Квадратурное правило Гаусса— обзор
5.1.3.3 Режимы песочных часов
Использование одноточечной квадратуры Гаусса значительно экономит вычислительные затраты, но может вызвать ложные режимы нулевой энергии , также называемые режимами песочных часов , которые ухудшают качество численное решение, и даже приводит к расходимости решения. Следовательно, необходимо принять специальные меры для подавления режима песочных часов.
Функция формы Ур. (5.29) 8-узлового элемента шестигранника также можно записать в матричной форме как
(5.49) N = 18 (+? T Λ1Tξ + Λ2Tη + Λ3Tζ + Γ1Tξη + Γ2Tηζ + Γ3Tξζ + Γ4Tξηζ)
с N = [N1N2N3N4N5N6N7N8]
и
Е = [11111111] T, Λ1 = [- 111- 1−111−1] T, Λ2 = [- 1−111−1−111] T, Λ3 = [- 1−1−1−11111] T, Γ1 = [1−11−11−11−1] T , Γ2 = [11−1−1−1−111] T, Γ3 = [1−1−11−111−1] T, Γ4 = [- 11−111−11−1] T.
Базовый вектор Σ представляет жесткое перемещение элемента, Λ1 представляет деформации растяжения и сжатия, а Λ2 и Λ3 представляют деформации сдвига. Базовые векторы Γ1, Γ2, Γ3 и Γ4 называются базовыми векторами песочных часов .В элементе шестигранника с 8 узлами существует 4 режима песочных часов в каждом направлении координат, что в сумме дает 12 режимов песочных часов. Рис. 5.2 иллюстрирует режимы песочных часов в направлении η .
Рисунок 5.2. Режимы песочных часов в элементе шестигранника с 8 узлами. Всего существует 12 режимов песочных часов.
Скорость точки внутри элемента определяется как
(5.50) vi (ξ, η, ζ) = NI (ξ, η, ζ) viI = Nvi
, где
vi = [vi1vi2vi3vi4vi5vi6vi7vi8] T
— вектор узловой скорости элемента, состоящий из компонентов скорости в направлении xi всех узлов в элементе.Уравнения. (5.50) и (5.49) показывают, что скорость vi (ξ, η, ζ) любой точки внутри элемента может быть выражена как линейная комбинация восьми основных векторов, а именно: Σ , Λ1 — Λ3, и с Γ1 через Γ4.
Для расчета напряжения и деформации требуются частные производные функции формы NI по xi, ∂NI / ∂xi, которые могут быть вычислены из ∂NI / ∂ξ, ∂NI / ∂η и ∂NI / ∂ ζ. Эти частные производные функции формы NI в центре тяжести (ξ = η = ζ = 0) элемента могут быть вычислены с помощью уравнения.(5.49) следующим образом:
(5.51) ∂N∂ξ = 18Λ1T, ∂N∂η = 18Λ2T, ∂N∂ζ = 18Λ3T
, в котором моды песочных часов с Γ1 по Γ4 исчезают. Следовательно, режимы песочных часов приводят к нулевой деформации и, следовательно, к нулевому напряжению в центре тяжести элемента, хотя они приводят к ненулевой деформации и ненулевому напряжению в другом месте. Поскольку используется одноточечная квадратура, узловая внутренняя сила Ур. (5.34) — это просто произведение объема и подынтегрального выражения, вычисленное в центре тяжести (ξ = η = ζ = 0) элемента, который равен нулю для режимов песочных часов из-за нулевого напряжения в центре тяжести.Другими словами, режимы песочных часов не будут генерировать узловую силу, то есть им не будет сопротивляться элемент, поэтому они приведут к паразитным колебаниям. Режимы песочных часов не вносят вклада в энергию деформации элемента. Вот почему они называются модами с нулевой энергией.
Например, в моделировании удара стержня Тейлора одноточечная квадратура Гаусса приводит к значительным паразитным колебаниям из-за режимов песочных часов, как показано на рис. 5.3 (a). Эти колебания могут быть эффективно устранены путем введения сил сопротивления песочным часам, как показано на рис.5.3 (б).
Рисунок 5.3. Колебания, вызванные режимами песочных часов (а) без управления песочными часами и (б) с контролем по песочным часам.
Режимы песочных часов можно эффективно подавить, используя схему управления вязкими песочными часами, то есть применяя силы сопротивления песочным часам. Можно проверить, что базовые векторы песочных часов ортогональны другим базовым векторам, т. Е. ΓkTΣ = 0 и ΓkTΛl = 0, где k = 1,2,3,4 и l = 1,2,3. Если базовый вектор песочных часов Γk не ортогонален вектору узловой скорости элемента vi, i.е.,
(5.52) hik = ΓkTvi ≠ 0,
моды песочных часов существуют в поле скорости элемента, так что силы вязкости должны применяться во всех узлах элемента, чтобы противостоять режимам песочных часов. Вязкие силы fikI, приложенные в узле I в направлении xi для сопротивления моде песочных часов Γk, должны быть пропорциональны hik и противоположны Γk, а именно:
(5.53) fikI = −αhhikΓkI, k = 1,2,3 , 4
где ΓkI — I -я компонента базового вектора песочных часов Γk.Коэффициент αh можно определить как
(5,54) αh = QhρVe2 / 3c4
, где Ve — объем элемента, c — скорость звука в материале, а Qh — определяемая пользователем константа, которая обычно берется из интервала от 0,05 до 0,15.
Силы сопротивления песочным часам Ур. (5.53) не ортогональны вращениям твердого тела, поэтому они плохо подходят для задач, связанных с большими поворотами жесткого тела. Фланаган и Беличко предложили силу сопротивления песочным часам, ортогональную вращениям твердого тела [121].Они определили поле скорости песочных часов как
(5.55) viIHG = vi − viILIN
с
(5.56) viILIN = v¯i + v¯i, j (xjI − x¯j),
(5.57) x ¯i = 18∑I = 18xiI, v¯i = 18∑I = 18viI.
Базовые векторы песочных часов затем определяются как
(5.58) γkI = ΓkI − NI, i∑J = 18xiJΓkJ.
Если вектор узловой скорости viI элемента не ортогонален базовому вектору песочных часов gik, то есть
(5.59) gik = ∑I = 18viIγkI ≠ 0,
, то моды песочных часов существуют в поле скорости элемента, так что необходимо применить силы сопротивления песочным часам fikI, которые пропорциональны gik и противоположны базовым векторам gik песочных часов, а именно:
(5.60) fikI = −αhgikγkI, k = 1,2,3,4.
Базовые векторы песочных часов ортогональны другим базовым векторам, так что работа, выполняемая силами сопротивления песочным часам, незначительна. Приведенная выше схема управления песочными часами проста и эффективна.
DLMF: 3,5 квадратурное
Обозначим через {pn} множество монических многочленов pn степени n. (коэффициент при xn равен 1), ортогональные относительно a положительная весовая функция w на конечном или бесконечном интервале (a, b); сравните § 18.2 (i). В квадратуре Гаусса (также известной как квадратура Гаусса – Кристоффеля ) используем (3.5.15) с узлы xk нули pn, а веса wk задаются
Неделя также известна как коэффициенты Кристоффеля или Номера Кристоффеля , и все они положительные. Остаток равен
где
и ξ — некоторая точка в (a, b). Как следствие, правило точное для любой многочлен f (x) степени ≤2n-1, то есть
В частности, при hm = ∫abpm (x) 2w (x) dx мы имеем конечную систему ортогональных многочлены pm (x) (m = 0,1,…, n-1) на {x1, x2,…, xn} относительно весов wk:
| 3.5.20_2 | ∑k = 1npℓ (xk) pm (xk) wk = hmδℓ, m, | ||
| для ℓ, m = 0,1,…, n-1. | |||
В практических приложениях весовая функция w (x) выбирается для моделирования асимптотика подынтегрального выражения при приближении к конечным точкам. Для Функции C∞ Квадратура Гаусса может быть очень эффективной. В адаптивном алгоритмы оценки узлов и весов могут вызвать трудности, если не известны точные значения.
Вывод квадратурных формул Гаусса см. Gautschi (2004, стр.22–32) , Gil et al. (2007a, §5.3) , и Дэвис и Рабиновиц (1984, §§2.7 и 3.6) . Stroud and Secrest (1966) включает вычислительные методы и обширные таблицы. Для дальнейших расширений, приложений, и вычисление ортогональных многочленов и формул типа Гаусса, см. Гаучи (1994, 1996, 2004) . Для эффективного проверка квадратурных правил Гаусса см. Gautschi (1983) .
Для классических ортогональных многочленов, связанных со следующими правилами Гаусса, см. § 18.б F (t) dt? \ label {1.15.2} \ tag {1.15.2} \]
Это вообще не проблема — вы просто меняете переменную. Итак, пусть
\ [x = \ frac {2t-ab} {ba}, \ quad t = \ frac {1} {2} [(ba) x + a + b], \ label {1. 5 c_ {5, i} \ f (x_ {5, i}), \ label {1.15.6} \ tag {1.15.6} \]
, где коэффициенты \ (c_ {l, i} \) (все положительные) перечислены вместе с корнями многочленов Лежандра из раздела 1.14.
Давай попробуем.
\ begin {array} {ccc}
x_ {5, i} & f (x_ {5, i}) & c_ {5, i} \\
\\
+0.906 \ 179 \ 845 \ 939 & 0.783 \ 266 \ 908 \ 39 & 0,236 \ 926 \ 885 \ 06 \\
+0,538 \ 469 \ 310 \ 106 и 0,734 \ 361 \ 739 \ 69 и 0,478 \ 628 \ 670 \ 50 \\
0,000 \ 000 \ 000 \ 000 & 0.555 \ 360 \ 367 \ 27 & 0,568 \ 888 \ 888 \ 89 \\
-0,538 \ 469 \ 310 \ 006 и 0,278 \ 501 \ 544 \ 60 & 0,478 \ 628 \ 670 \ 50 \\
-0,906 \ 179 \ 845 \ 939 & 0,057 \ 820 \ 630 \ 35 & 0,236 \ 926 \ 885 \ 06 \\
\ end {array}
, а выражение \ (\ ref {1.15.6} \) сводится к \ (1.000 \ 000 \ 000 \ 04 \), и предположительно могло бы приблизиться к 1, если бы мы дали \ (x_ {l, i} \ ) и \ (c_ {l, i} \) к более значащим цифрам.
Теперь вам нужно написать компьютерную программу для квадратуры Гаусса — вам, конечно же, придется хранить \ (x_ {l, i} \) и \ (c_ {l, i} \).2 x dx \\
\ end {array}
Все они могут быть интегрированы аналитически, поэтому я собираюсь предложить читателю оценить их сначала аналитически, а затем численно по правилу Симпсона и снова с помощью квадратуры Гаусса, и посмотреть, в скольких точках подынтегральное выражение должно оцениваться каждым метод достижения девяти или десятизначной точности. Я попробовал, и результаты следующие. Первый столбец — это ответ, второй столбец — количество точек, требуемых правилом Симпсона, а третий столбец — количество точек, требуемых квадратурой Гаусса.
\ begin {array} {ccccc}
(a) & 0,192 \ 259 \ 358 && 33 & 4 \\
(b) & 0,160 \ 602 \ 794 && 99 & 5 \\
(c) & −0,176 \ 820 \ 020 && 19 & 4 \\
(d) & 0,088 \ 755 \ 284 \ 4 && 111 & 5 \\
(e) & 2,588 \ 628 \ 633 && 453 & 7 \\
(f) & -0,733 \ 969 \ 175 && 143 & 8 \\
(г) & 0,636 \ 213 \ 346 && 31 & 5 \\
(ч) & 0,642 \ 699 \ 082 && 59 & 5 \\
\ end {array}
Давайте теперь посмотрим на четыре интеграла, которые мы встретили в разделе 1.2 dy} {\ sqrt {1-x}}, \), который, кажется, сразу подходит для гауссовой квадратурности. Прежде чем продолжить, напомним, что подынтегральное выражение становится бесконечным на верхнем пределе, и оно остается бесконечным после нашей замены переменной. Отметим, однако, что с квадратурой Гаусса, , мы не оцениваем подынтегральное выражение на верхнем пределе , так что это может показаться большим преимуществом метода перед методом Симпсона. Увы! — оказывается, что это не так. Если, например, мы используем квадратуру из 17 точек, наибольшее значение \ (x \), для которого мы вычисляем подынтегральное выражение, равно наибольшему решению \ (P_ {17} (x) = 0 \), которое равно \ (0.2 \ phi}}. \) Мне потребовалось 13 очков по правилу Симпсона, чтобы получить ответ на десять значащих цифр, \ (2.622 \ 057 \ 554 \). Чтобы сделать пределы \ (\ pm 1 \), подходящие для квадратуры Гаусса, мы можем сделать вторую замену (как в примере 2), \ (\ phi = \ frac {\ pi} {4} (x + 1 ) \). Если мы действительно хотим произвести впечатление на наших друзей, мы можем сделать две замены за один шаг, таким образом: Пусть \ (\ sin \ frac {\ pi} {4} (1 + x) = \ sqrt {2} \ sin \ frac {1} {2} \ theta \). 2 \ frac {\ pi} {4} (x + 1)}}, \), который теперь готов для гауссовой квадратуры.c -1} dx, \), где \ (c = \ cot \ frac {\ pi} {4} (x + 1) \). Используя 16-точечную квадратуру Гаусса, я получил 6,48. Таким образом, нам потребуется расширить нашу таблицу констант для метода Гаусса до гораздо более высокого порядка, чтобы использовать этот метод успешно. Несомненно, тогда метод Гаусса будет быстрее, чем метод Симпсона, но нам не нужен обширный (и трудно вычисляемый) набор констант для последнего. Еще один небольшой момент: вы могли заметить, что не сразу очевидно, что подынтегральное выражение равно нулю в конечных точках, и что требуется некоторая работа, чтобы доказать это.Но с помощью метода Гаусса вы не оцениваете подынтегральное выражение в конечных точках, так что беспокоиться об этом меньше!
Таким образом, мы обнаружили, что в большинстве случаев метод Гаусса намного быстрее, чем метод Симпсона. В некоторых случаях это ненамного быстрее. В других случаях это, вероятно, будет быстрее, чем правило Симпсона, но для его применения необходимы константы более высокого порядка. {th} $ — степени. Многочлен Лежандра $ P_n (\ xi) $.
Точность численного интегрирования существенно зависит от точности нулей $ \ xi_i $. Нет простого в использовании аналитического выражения для $ \ xi_i $, и обычно они вычисляются численно с помощью алгоритмов поиска корня.
Удивительно популярные математические справочники / программное обеспечение обеспечивают низкую точность $ \ xi_i, \, w_i $ (только 4-6 правильных цифр) за ограниченные $ n \ le 5 $. Очевидно, такая ситуация не отражает современных требований к вычислительным возможностям и точности многих приложений.Например, широко используемый тип с плавающей запятой double стандарта IEEE 754 способен хранить значения с точностью до 16 цифр (машинный эпсилон составляет около 1e-16 для 64 битов double ).
Эта страница предназначена для предоставления программных библиотек для вычисления высокоточных абсцисс $ \ xi_i $ и весов $ w_i $ для любого желаемого $ n $.
Квадратура Гаусса-Лежандра для C / C ++
Эта библиотека с открытым исходным кодом реализует численное интегрирование на основе квадратур Гаусса-Лежандра любого порядка.
Предварительно рассчитанные высокоточные абсциссы и веса с 25 правильными десятичными разрядами используются для определенных порядков n = 2,…, 20, 32, 64, 96, 100, 128, 256, 512, 1024. Хотя все значения могут быть найденные в исходном коде также доступны удобные для человека таблицы с абсциссами и весами. Узлы для всех остальных n генерируются «на лету» с точностью 1e-10 с помощью алгоритма быстрого поиска корня.
Библиотека также включает подпрограмму для численного интегрирования по двухмерному прямоугольнику с использованием произведения двух одномерных квадратур Гаусса.
Если вы ищете численное интегрирование по единичному диску (2D сфере), вас может заинтересовать эта страница Кубатурные формулы для единичного диска. Он содержит сведения о происхождении и исходный код на C / C ++.
Квадратура Гаусса-Лежандра для MATLAB
Существует несколько процедур для квадратур Гаусса, реализованных с использованием языка программирования Matlab. Все они имеют низкую производительность и даже некоторые из них дают результаты с низкой точностью.
Чтобы облегчить ситуацию, я разрабатываю квадратурный набор инструментов, который имеет интерфейс Matlab (m-файлы) и делегирует всю тяжелую работу высокопроизводительной библиотеке MEX, написанной на C / C ++ (см. Предыдущий раздел).Пока что он включает только правило Гаусса-Лежандра со многими другими:
Набор инструментов для квадратуры состоит из трех файлов:
GaussLegendre.m quadlab.mexw32 quadlab.mexw64
Toolbox был создан и протестирован с использованием Matlab R2010b как в 32-битной, так и в 64-битной версиях. Пример использования:
>> GaussLegendre (@ cos, -pi / 2, pi / 2,1024)
ans =
2.000000000000000
GaussLegendre () принимает функцию Matlab (встроенную или из m-файла), границы интегрирования $ [a, b] $, порядок квадратуры (например, 1024) и желаемую точность для узлов в качестве необязательного параметра.Также он возвращает векторы абсцисс и весов, если такие выходные данные указаны.
Сравнение производительности с самой быстрой подпрограммой на языке Matlab (порядок координат по x, время выполнения по оси y, набор инструментов для квадратуры зеленого, конкурент красный, чем ниже, тем лучше):
Помимо того, что скорость быстрее, библиотека обычно дает результаты с большей точностью благодаря к предварительно рассчитанным абсциссам и весам с высокой точностью.
Я расширяю набор квадратурных инструментов для Matlab другими правилами и адаптивными методами.Я был бы очень признателен за любые предложения по функциям и советы о том, какие методы включить в первую очередь.
Абсциссы и веса квадратур Гаусса-Лежандра
В таблице ниже перечислены квадратурные узлы Гаусса-Лежандра для n = 2,…, 20, 32, 64, 100 с точностью до 25 десятичных знаков. Данные для формул высшего порядка n = 128, 256, 512, 1024 можно найти в исходном коде библиотеки C / C ++.
| Абсциссы | Массы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | ± 0,57735026 | +1,0000000000000000000000000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 0 | 0,8888888888888888888888889 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,7745966692414833770358531 | 0,55555555555555555555556 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | ± 0,3399810435848562648026658 | 0.6521451548625461426269361 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,8611363115940525752239465 | 0,3478548451374538573730639 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 0 | +0,5688888888888888888888889 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,5384693101056830 | 3144+0,4786286704993664680412915 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0, | +0,23692688505618 | 142640 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | ± 0,23861 | 05017 | 0.46745726 | 3898703 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,6612093864662645136613996 | 0,3607615730481386075698335 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,9324695142031520278123016 | +0,17132449237 450402961 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 0 | 0,41795734693877551020 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,405845151377397166 | 640,3818300505051189449503698 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,7415311855993944398638648 | 0,2797053 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0.94 | +0,1294849661688696932706114 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | ± 0,1834346424956498049394761 | 0,3626837833783619829651504 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,525532409 | 89858177390+0,3137066458778872873379622 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,7966664774136267395 | 9 | 0,2223810344533744705443560 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,9602898564975362316835609 | +0,1012285362 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 0 | 0.3302393550012597631645251 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,32425342340380892 | +0,3123470770400028400686304 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,6133714327005 | +0,2606106964029354623187429 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,8360311073266357942994298 | +0,1806481606948574040584720 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,9681602395076260898355762 | +0,0812743883615744119718922 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | ± 0,1488743389816312108848260 | 0.2955242247147528701738930 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,4333953941292471 | 2659 | +0,2692667193099963550 | 9|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,67940956829062343274 | 0,21 | 625159820439955349 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,8650633666889845107320967 | +0,14945134 | 805931457763 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,973 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| +0,0666713443086881375935688 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 0 | 0,27292508677707144835 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0.2695431559523449723315320 | 0,2628045445102466621806889 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,51 | 2118159257257 | +0,2331937645919 | 37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,7301520055740493240934163 | 0,1862 9277342514260976 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,88706259976809529 | 578 | +0,125580369464 | 46346943|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,9782286581460569928039380 | +0,0556685671161736664827537 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | ± 0.125233408511468 | 24414 | 0,24 | 458134027850005624||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,3678314989981801937526915 | +0,2334925365383548087608499 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,5873179542866174472967024 | +0,203167426723065 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,76941943046870368938 | +0,1600783285433462263346525 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0, | 72563704748566784659 | +0,1069393259953184309602547 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,9815606342467192506 | 1 | 0.0471753363865118271946160 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | 0 | +0,232551553230873 | 45895 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,2304583159551347940655281 | 0,2262831802628972384120902 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,4484927510364468528779129 | +0,2078160475368885023125232 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,6423493394403402206439846 | +0,1781459807619457382800467 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,8015780 | 309 | 42065 | 0,1388735102197872384636018 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0. 83992229779652065478 | +0,0499837728447 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,9841830547185881494728294 | 0,0404840047653158795200216 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | ± +0,1080549487073436620662447 | +0,2152638534631577 8764 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,31 | 689278897604356718 | 0,2051984637212956039659241 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,5152486363581540 | 29070,1855383974779378137417166 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0.687292 | 16854701480198 | +0,1572031671581935345696019 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,8272013150697649931897947 | 0,12151857068746894148 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,9284348836635735173363911 | +0,0801580871597602098056333 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,9862838086968123388415973 | +0,0351194603317518630318329 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | 0 | 0,2025782419255612728806202 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,2011940939974345223006283 | 0.1984314853271115764561183 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,3941513470775633698972074 | 0,1861610000155622110268006 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,5709721726085388475372267 | +0,16626 | 169939335532009 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,7244177313601700474161861 | +0,1395706779261543144478048 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,8482065834104272162006483 | +0,1071592204671719350118695 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,937273392400705 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| +0,0703660474881081247092674 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0.9879925180204854284895657 | +0,0307532419961172683546284 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | ± 0,0950125098376374401853193 | +0,1894506104550684962853967 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,281603550779258 | +0,1826034150449235888667637 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,4580167776572273863424194 | +0,16 | 193950025381893121 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,6178762444026437484466718 | +0,1495959888165767320815017 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0.7554044083550030338951012 | +0,1246289712555338720524763 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,8656312023878317438804679 | 0,0951585116824927848099251 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,9445750230732325760779884 | 0,0622535239386478928628438 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,9894009349 | 9325961542 | 0,0271524594117540948517806 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | 0 | 0,1794464703562065254582656 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,1784841814958478558506775 | 0.1765627053669926463252710 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,3512317634538763152971855 | 0,1680041021564500445099707 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,5126 | 0,1540457610768102880814316 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,65767115 | 8503022 | 0,1351363684685254732863200 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,7815140038968014069252301 | 0,1118838471934039710947884 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,88023 | 0,08503614831717 | 835354 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0.9506755217687677612227170 | 0,0554595293739872011294402 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,9 | 4753144173356754340 | 0,0241483028685479319601100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | ± +0,0847750130417353012422619 | 0,16 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,2518862256 | 5095889729 | 0,1642764837458327229860538 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,4117511614628426460359318 | 0,1546846751262652449254180 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0.5597708310739475346078715 | +0,140642 | 06506512047313 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,60430603532078748911 | +0,1225552067114784601845191 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,8037049589725231156824175 | +0,1009420441062871655628140 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,89260246649755573606 | 0,07642573025488 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,9558239495713977551811959 | 0,0497145488949697964533349 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,9 | 1684209309467300160 | 0.0216160135264833103133427 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | 0 | 0,16105444984878369597 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,1603586456402253758680961 | +0,1589688433939543476499564 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,31656409996362983193 | 0,1527660420658596667788554 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,4645707413759609457172671 | 0,1426067021736066117757461 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0,6005453046616810234696382 | 0,1287539625393362276755158 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± 0.7209661773352293786170959 | +0,1115666455473339947160239 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ± +0,8227146565371428249789225 | 0,09146224499994644621 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
± 0,
Загрузка …% PDF-1.4 % 107 0 объект > endobj xref 107 87 0000000044 00000 н. 0000003101 00000 п. 0000003266 00000 н. 0000003899 00000 н. 0000005296 00000 н. 0000006292 00000 н. 0000007383 00000 п. 0000008383 00000 п. 0000009534 00000 п. 0000010149 00000 п. 0000011103 00000 п. 0000011945 00000 п. 0000012015 00000 п. 0000013088 00000 п. 0000013297 00000 п. 0000025221 00000 п. 0000026414 00000 п. 0000026731 00000 п. 0000026949 00000 п. 0000036634 00000 п. 0000037037 00000 п. 0000038231 00000 п. 0000038479 00000 п. 0000038690 00000 п. 0000043600 00000 п. 0000044016 00000 п. 0000045209 00000 п. 0000045599 00000 п. 0000045817 00000 п. 0000053903 00000 п. 0000054362 00000 п. 0000055554 00000 п. 0000055940 00000 п. 0000056138 00000 п. 0000059271 00000 п. 0000059678 00000 п. 0000060871 00000 п. 0000061330 00000 н. 0000062524 00000 п. 0000063143 00000 п. 0000063354 00000 п. 0000075930 00000 п. 0000076378 00000 п. 0000077409 00000 п. 0000077608 00000 п. 0000080521 00000 п. 0000081713 00000 п. 0000082053 00000 п. 0000082270 00000 п. 0000087974 00000 п. 0000088361 00000 п. 0000089553 00000 п. 0000089960 00000 н. 00000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
/ Размер 194 / Корень 108 0 R
>>
startxref
0
%% EOF
193 0 объект
>
ручей
xc«`b` ~ A @ K8-6htkU! tE ݉ KQ u1 | hʡzRVxJm + zy3 &; Zc] &] =: | REOreL
>.+ T’FO = sqvЋw / yƬ
j1T} yu3Na) dU3s_v6nWX ݚ -. # Y7, zF) 8 ~ lN. = 9EaӏxL5 cOnzzFɓ3 /) q {tZ ‘㫭} @Оценка и приоритезация рисковОпределение: Оценка воздействия риска — это процесс оценки вероятностей и последствий событий риска в случае их реализации. Затем результаты этой оценки используются для определения приоритетности рисков для определения степени важности от наиболее до наименее критической. Ранжирование рисков с точки зрения их критичности или важности дает руководству проекта представление о том, где могут потребоваться ресурсы для управления или смягчения реализации событий риска с высокой вероятностью / высокими последствиями. Ключевые слова: риск, оценка воздействия риска, управление рисками, приоритезация рисков MITER SE Роли и ожидания: MITRE системные инженеры (SE), работающие над государственными программами, должны анализировать риски в отношении воздействия, вероятности, зависимостей и сроков, а также определять приоритеты рисков, чтобы облегчить принятие решений спонсором или клиентами [1 ]. ФонОценка воздействия риска и приоритезация — это второй и третий этапы процесса, изображенного на Рисунке 1 [2]. Рисунок 1. Управление рисками: основные шагиОценка воздействия риска в программе системного проектированияНа этом этапе оценивается влияние каждого рискового события на проект. Обычно эта оценка рассматривает, как событие может повлиять на цели по стоимости, графику или техническим характеристикам. Однако воздействия не ограничиваются этими критериями; могут также потребоваться рассмотрение политических или экономических последствий. Также оценивается вероятность (шанс) возникновения каждого рискового события.Это часто включает использование методов оценки субъективной вероятности, особенно если обстоятельства препятствуют непосредственной оценке вероятности объективными методами (например, инженерный анализ, моделирование и симуляция). В главах 2 и 4 книги Гарви [2] обсуждается тема субъективных оценок вероятности, а также критерии оценки воздействия рискового события или его последствий для проекта. В рамках оценки рисков необходимо определить зависимости рисков, взаимозависимости и временные рамки потенциального воздействия (краткосрочного, среднесрочного или долгосрочного).Инструмент RiskNAV®, разработанный MITER, является примером инструмента, который может помочь выполнить эту оценку. Дополнительные сведения см. В статье «Инструменты управления рисками» в этом руководстве . При оценке риска важно сопоставить влияние оценки с рамками принятия решений. Для управления программой риски обычно оцениваются по стоимости, графику и целевым техническим характеристикам. Некоторые программы могут также включать надзор и соблюдение или политические воздействия. Гарви [2] предоставляет обширный набор рейтинговых шкал для проведения этих многокритериальных оценок, а также способы их объединения в общую меру воздействия или последствий.Эти шкалы обеспечивают последовательную основу для определения уровней воздействия риска по стоимости, графику, производительности и другим критериям, которые считаются важными для проекта. Кроме того, инструмент «Матрица рисков» может помочь оценить эти риски для конкретных программ (см. Статью «Инструменты управления рисками»). Выполнение оценок POET (политических, операционных, экономических, технических) и / или SWOT (сильных и слабых сторон, возможностей и угроз) может помочь определить движущие силы рисков. Дополнительные сведения об этих анализах см. В статье «Инструменты для обеспечения комплексной точки зрения» в разделе «Комплексная точка зрения» в разделе «Корпоративная инженерия». Для некоторых программ или проектов влияние риска на цели и задачи предприятия или организации более значимо для управляющей организации. Риски оцениваются с точки зрения потенциального негативного воздействия на цели предприятия. Использование инструментов управления рисками для предприятия и его компонентов может помочь в согласованности определения рисков. Эта согласованность аналогична приведенному ниже примеру шкалы, за исключением того, что оценка будет проводиться на уровне предприятия. В зависимости от важности компонента для успеха предприятия (например,g., риск использования коммерческой связи для поддержки военной операции и влияние предприятия на успех миссии по сравнению с риском использования коммерческой связи для транспортировки военной техники в мирное время), риски могут рассматриваться по-разному на уровне предприятия, даже если наборы решений одинаковые или похожие. Один из способов управления планами по проектированию предприятия — это создание портфелей возможностей технологических программ и инициатив, которые при синхронизации будут предоставлять поэтапные возможности, которые продвигают цели предприятия и результаты миссии.Портфель возможностей — это динамическая во времени организационная конструкция для предоставления возможностей в указанные эпохи; возможность может быть определена как способность достичь эффекта стандарта при определенных условиях с использованием нескольких комбинаций средств и способов выполнения набора задач [2]. С введением управления возможностями определение влияния риска на функциональные цели или задачи возможностей может дать ценную информацию о том, какие возможности подвергаются риску и какие риски потенциально могут существенно повлиять на способность реализовать возможности и / или повлиять на несколько областей возможностей. В управлении портфелем набор инвестиций администрируется на основе общей цели (целей), сроков, допуска к риску, взаимозависимостей затрат и цены, бюджета и изменений в соответствующей среде с течением времени. Эти факторы обычно применимы к среде государственных закупок (см. Статью «Управление портфелем» в разделе «Инженерия предприятия»). Для оценки риска портфеля, инвестиционного решения или анализа альтернативных задач использование категорий шкал областей риска может быть наиболее подходящим способом убедиться, что каждая альтернатива или вариант учитывает все области риска.Области риска могут включать в себя защиту, финансирование, ресурсы, график и уверенность в оценке затрат, техническую зрелость, способность соответствовать техническим характеристикам, возможность оперативного развертывания, интеграцию и совместимость, а также сложность. Шкалы определяются для каждой области риска, и каждая альтернатива оценивается по всем категориям. Оценка риска может также включать оперативное рассмотрение угрозы и уязвимости. Для анализа затрат и рисков определение границ неопределенности является оценкой риска. При определении подходящего подхода к оценке рисков важно учитывать потребность в информации. Ниже показаны примеры вероятности возникновения, шкалы оценки управления рисками программы и шкалы оценки инвестиционных рисков, которые используются в работе MITRE SE с государственными спонсорами или клиентами. RiskNav Пример вероятности возникновения
Таблица 2. Пример шкалы оценки инвестиционного риска
Приоритезация рисков в программе системного проектированияНа этапе приоритизации рисков общий набор идентифицированных рисковых событий, их оценки воздействия и их вероятности наступления «обрабатываются» для получения ранжирования идентифицированных рисков от наиболее к наименее критическому. Основная цель приоритезации рисков — сформировать основу для распределения ресурсов. Было разработано множество качественных и количественных методов для оценки воздействия рисков и определения приоритетов.Качественные методы включают анализ вероятности и воздействия, разработку матрицы вероятности и воздействия, категоризацию рисков, ранжирование частоты рисков (риски с множественными воздействиями) и оценку срочности рисков. Количественные методы включают взвешивание оценок кардинального риска последствий, вероятности и временных рамок; распределения вероятностей; Анализ чувствительности; анализ ожидаемой денежной стоимости; и моделирование и имитация. MITER разработал подходы минимального и максимального среднего (с использованием весовой шкалы, более серьезно взвешивающей максимальное или минимальное значение).Во всех этих методах используется экспертная оценка для выявления потенциальных воздействий, определения исходных данных и интерпретации данных [3]. Кроме того, MITER разработал инструмент RiskNAV®, который помогает руководителям оценивать и определять приоритеты программных рисков. RiskNav включает возможность взвешивать временные рамки в рейтинге рисков (например, сколько времени нужно реагировать / потенциально снижать). RiskNav используется рядом спонсоров и клиентов MITER. Подробную информацию о RiskNav см. В статье об инструментах управления рисками в этом руководстве. Передовой опыт и извлеченные урокиАдаптируйте критерии оценки к решению или проекту. При оценке рисков рекомендуйте методы и инструменты, подходящие для анализа. Например, если проект представляет собой проект управления предприятием или организационного надзора, то влияние риска лучше всего оценивать по целям, а не по техническим характеристикам, стоимости и графику. Если оценка направлена на определение риска инвестиционных вариантов, лучше всего подходит подход с использованием шкалы зон риска.Пример применения управления рисками можно найти в Руководстве по внедрению управления рисками [4] компании Cryptologic Systems Group. Задокументировать обоснование оценки воздействия и вероятности. Важно задокументировать обоснование или обоснование каждой оценки воздействия риска и рейтинга вероятности возникновения. Если условия или окружающая среда изменятся, оценку, возможно, придется пересмотреть. Обоснование помогает сообщить о значимости риска.При использовании подхода с использованием шкалы оценки инвестиций заявление о риске обычно включается в обоснование. Признать роль системной инженерии. Оценка и управление рисками — это роли системной инженерии, особенно по мере того, как проекты и программы становятся более сложными и взаимозависимыми. Принимаемые суждения требуют глубоких знаний о характеристиках системы и составляющих технологий, помимо знаний специалистов по проектированию. Кроме того, суждения о критичности риска делаются на системном и программном уровнях [5].Риск пересекает жизненный цикл системной инженерии, и компании MITER SE должны быть готовы реагировать на риски на всем протяжении — концепции и требований, рисков архитектурного уровня, рисков проектирования и разработки, рисков обучения, размещения на местах и рисков для окружающей среды. Компаниям MITRE SE рекомендуется выступать за участие SE в оценке и управлении рисками. Настройте подход к расстановке приоритетов для решения или проекта. Сопоставьте алгоритм, методы и инструменты приоритизации с потребностями оценки (например,g. потребности могут включать критичность по времени в качестве фактора приоритизации, способность видеть возможности под риском, необходимость единой оценки риска для портфеля, способность понимать риски с множественными воздействиями и многое другое). Каждая область риска — угроза, операционная, программная и т. Д. — будет иметь разные приоритеты. Как правило, приоритет отдается самим этим областям — риск серьезной угрозы может быть совершенно неприемлемым, и усилия могут быть прекращены. Если риски угрозы приемлемы, но операции не могут быть выполнены эффективно, то, опять же, усилия могут быть прекращены.Обязательно учитывайте эти различные решения и важность, чтобы помочь правительству оценить приоритеты снижения возникающих рисков. Рассмотрим инструмент MITRE RiskNAV®. RiskNav может быть подходящим для оценки и определения приоритетов рисков в вашей государственной программе. Компании MITER SE обнаружили, что наличие легкого доступа к этому проверенному инструменту и группе поддержки иногда побуждает группы правительственных программ принять более надежный процесс управления рисками, чем они могли бы в противном случае.Дополнительные сведения см. В статье «Инструменты управления рисками» настоящего Руководства по проектированию систем. Рассмотрим моделирование методом Монте-Карло. Моделирование Монте-Карло использует распределения вероятностей для оценки вероятности достижения определенных результатов, таких как стоимость или дата завершения [3]. Они эффективно использовались в ряде государственных программ MITRE, чтобы помочь проектным командам оценить риски, связанные с графиком. Ссылки и ресурсы
Дополнительные ссылки и ресурсы
|


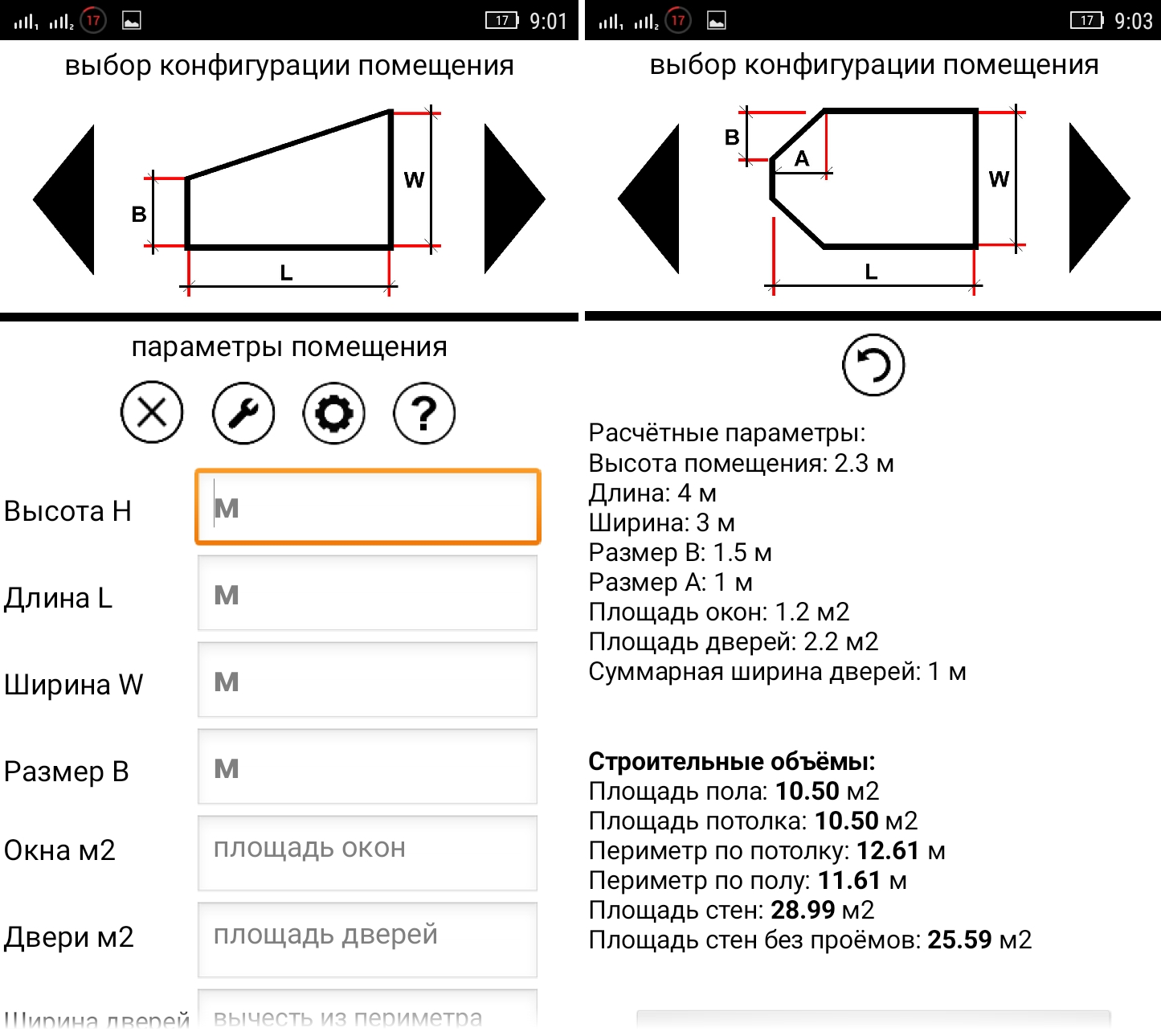 м. Округляем, получаем 5,1 кв. м.
м. Округляем, получаем 5,1 кв. м. Кроме того, замеры производятся несколько раз, чтобы избежать ошибок и недочетов.
Кроме того, замеры производятся несколько раз, чтобы избежать ошибок и недочетов.