Урок 7. Возведение в квадрат в уме
Умение считать в уме квадраты чисел может пригодиться в разных жизненных ситуациях, например, для быстрой оценки инвестиционных сделок, для подсчета площадей и объемов, а также во многих других случаях. Кроме того, умение считать квадраты в уме может служить демонстрацией ваших интеллектуальных способностей.
В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.
Квадрат суммы и квадрат разности
Одним из самых простых способов возведения двузначных чисел в квадрат является методика, основанная на использовании формул квадрата суммы и квадрата разности:
Для использования этого метода необходимо разложить двузначное число на сумму числа кратного 10 и числа меньше 10. Например:
- 372 = (30+7)2 = 302 + 2*30*7 + 72 = 900+420+49 = 1 369
- 942 = (90+4)2 = 902 + 2*90*4 + 42 = 8100+720+16 = 8 836
Практически все методики возведения в квадрат (которые описаны ниже) основываются на формулах квадрата суммы и квадрата разности.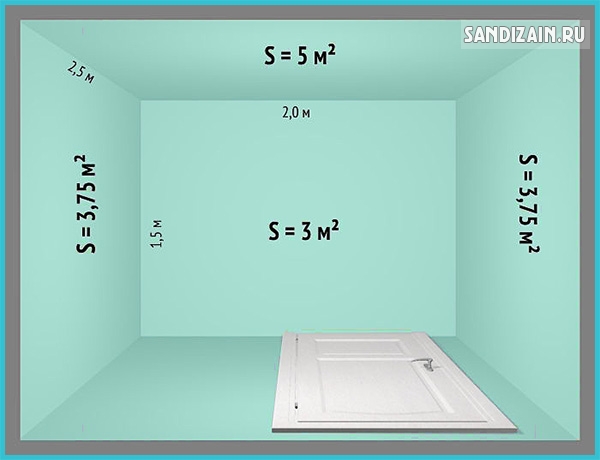
Квадрат близкий к известному квадрату
Если число, возводимое в квадрат, находится близко к числу, квадрат которого мы знаем, можно использовать одну из четырех методик для упрощенного счета в уме:
На 1 больше:
Методика: к квадрату числа на единицу меньше прибавляем само число и число на единицу меньше.
- 312 = 302 + 31 + 30 = 961
- 162 = 152 + 15 + 16 = 225 + 31 = 256
На 1 меньше:
Методика: из квадрата числа на единицу больше вычитаем само число и число на единицу больше.
- 192 = 202 – 19 – 20 = 400 – 39 = 361
- 242 = 252 – 24 – 25 = 625 – 25 – 24 = 576
На 2 больше
Методика: к квадрату числа на 2 меньше прибавляем удвоенную сумму самого числа и числа на 2 меньше.
- 222 = 202 + 2*(20+22) = 400 + 84 = 484
- 272 = 252 + 2*(25+27) = 625 + 104 = 729
На 2 меньше
- 482 = 502 – 2*(50+48) = 2500 – 196 = 2 304
- 982 = 1002 – 2*(100+98) = 10 000 – 396 = 9 604
Все эти методики можно легко доказать, выведя алгоритмы из формул квадрата суммы и квадрата разности (о которых сказано выше).
Квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.
- 152 = (1*(1+1)) 25 = 225
- 252 = (2*(2+1)) 25 = 625
- 852 = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
- 1552 = (15*(15+1)) 25 = (15*16)25 = 24 025
Квадрат чисел близких к 50
Считать квадрат чисел, которые находятся в диапазоне от 40 до 60, можно очень простым способом. Алгоритм таков: к 25 прибавляем (или вычитаем) столько, насколько число больше (или меньше) 50. Умножаем эту сумму (или разность) на 100. К этому произведению добавляем квадрат разности числа, возводимого в квадрат, и пятидесяти. Посмотрите работу алгоритма на примерах:
Алгоритм таков: к 25 прибавляем (или вычитаем) столько, насколько число больше (или меньше) 50. Умножаем эту сумму (или разность) на 100. К этому произведению добавляем квадрат разности числа, возводимого в квадрат, и пятидесяти. Посмотрите работу алгоритма на примерах:
- 532 = (25+3)*100 + 32 = 2800 + 9 = 2809
Квадрат трехзначных чисел
Возведение в квадрат трехзначных чисел может быть осуществлено при помощи одной из формул сокращенного умножения:
Нельзя сказать, что этот способ является удобным для устного счета, но в особо сложных случаях его можно взять на вооружение:
4362 = (400+30+6)2= 4002 + 302 + 62 + 2*400*30 + 2*400*6 + 2*30*6 = 160 000 + 900 + 36 + 24 000 + 4 800 + 360 = 190 096
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Евгений БуяновБыстрое возведение чисел от 1 до 100 в квадрат / Хабр
Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.
*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
70 * 70 = 4900. 2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности. Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.
Возведение числа в квадрат в Эксель
Довольно часто перед пользователями встает задача – возвести определенное число в квадрат, или, другими словами, во вторую степень. Это может потребоваться для решения инженерных, математических и иных задач.
Несмотря на широкое применение данной математической функции, в том числе, в Excel, специальной формулы, которая позволяет возвести число в квадрат, в программе нет. 3” возведет число 4 в третью степень или, другими словами, в куб.
3” возведет число 4 в третью степень или, другими словами, в куб.
Функция СТЕПЕНЬ для возведения числа в квадрат
В данном случае для нахождения квадрата числа нам поможет специальная функция под названием СТЕПЕНЬ. Эта функция относится к категории математических операторов и выполняет задачу по возведению указанного числа в заданную степень.
Формула данного оператора выглядит так: =СТЕПЕНЬ(число;степень).
Как мы видим, в данной формуле присутствует два аргумента: число и степень.
- “Число” – аргумент, который может быть представлен двумя способами. Можно прописать конкретное число, которое требуется возвести в степень, либо указать адрес ячейки с требуемым числом.
- “Степень” – аргумент, указывающий степень, в которую будет возводиться наше число. Так как мы рассматриваем возведение числа в квадрат, то указываем значение аргумента, равное цифре 2.
Давайте разберем применение функции СТЕПЕНЬ на примерах:
Способ 1. Указываем в качестве значения аргумента «Число» конкретную цифру
Указываем в качестве значения аргумента «Число» конкретную цифру
- Выбираем ячейку, в которой будем производить расчеты. Затем кликаем по кнопке “Вставить функцию” (с левой стороны от строки формул).
- Откроется окно Мастера функций. Кликаем по текущей категории и выбираем в открывшемся перечне строку “Математические”.
- Теперь нам нужно в предложенном списке функций найти и кликнуть по оператору “СТЕПЕНЬ”. Далее подтверждаем действие нажатием OK.
- Перед нами откроется окно с настройками двух аргументов функции, которое содержит, соответственно, два поля для ввода информации, после заполнения которых жмем кнопку OK.
- в поле “Число” пишем числовое значение, которое требуется возвести в степень
- в поле “Степень” указываем нужную нам степень, в нашем случае – 2.
- В результате проделанных действий мы получим квадрат заданного числа в выбранной ячейке.
Способ 2. Указываем в качестве значения аргумента «Число» адрес ячейки с числом
- Теперь у нас уже есть конкретное числовое значение в отдельно ячейке (в нашем случае – B3).
 Так же, как и в первом способе, выделяем ячейку, куда будет выводиться результат, нажимаем на кнопку “Вставить функцию” и выбираем оператор “СТЕПЕНЬ” в категории “Математические”.
Так же, как и в первом способе, выделяем ячейку, куда будет выводиться результат, нажимаем на кнопку “Вставить функцию” и выбираем оператор “СТЕПЕНЬ” в категории “Математические”. - В отличие от первого способа, теперь вместо указания конкретного числа в поле “Число” указываем адрес ячейки, содержащей нужное число. Для этого кликаем сначала по полю аргумента, затем – по нужной ячейке. Значение поля “Степень” так же равно 2.
- Далее нажимаем кнопку OK и получаем результат, как и в первом способе, в ячейке с формулой.
Примечание: Также, как и в случае использования формулы для расчета квадрата числа, функцию СТЕПЕНЬ можно применять для возведения числа в любую степень, указав в значении аргумента “Степень” нужную цифру. Например, чтобы возвести число в куб, пишем цифру 3.
Далее жмем Enter и значение куба указанного числа появится ячейке с фукнцией.
Заключение
Возведение числа в квадрат – пожалуй, самое популярное математическое действие среди всех вычислений, связанных с расчетами различных степеней числовых значений. В Microsoft Excel данное действие можно выполнять двумя способами: с помощью специальной формулы или используя оператор под названием СТЕПЕНЬ.
В Microsoft Excel данное действие можно выполнять двумя способами: с помощью специальной формулы или используя оператор под названием СТЕПЕНЬ.
Таблица квадратов чисел от 1 до 210
Таблица квадратов чисел от 1 до 2101 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400 441 484 529 576 625 676 729 784 841 900 961 1024 1089 1156 1225 1296 1369 1444 1521 1600 1681 1764 1849 1936 2025 2116 2209 2304 2401 2500 2601 2704 2809 2916 3025 3136 3249 3364 3481 3600 3721 3844 3969 4096 4225 4356 4489 4624 4761 4900 5041 5184 5329 5476 5625 5776 5929 6084 6241 6400 6561 6724 6889 7056 7225 7396 7569 7744 7921 8100 8281 8464 8649 8836 9025 9216 9409 9604 9801 10000 10201 10404 10609 10816 11025 11236 11449 11664 11881 12100 12321 12544 12769 12996 13225 13456 13689 13924 14161 14400 14641 14884 15129 15376 15625 15876 16129 16384 16641 16900 17161 17424 17689 17956 18225 18496 18769 19044 19321 19600 19881 20164 20449 20736 21025 21316 21609 21904 22201 22500 22801 23104 23409 23716 24025 24336 24649 24964 25281 25600 25921 26244 26569 26896 27225 27556 27889 28224 28561 28900 29241 29584 29929 30276 30625 30976 31329 31684 32041 32400 32761 33124 33489 33856 34225 34596 34969 35344 35721 36100 36481 36864 37249 37636 38025 38416 38809 39204 39601 40000 40401 40804 41209 41616 42025 42436 42849 43264 43681 44100
— версия для печати
- Пояснение к таблице:
2209 - квадрат числа[47] - само число
- Определение
- Квадрат числа — результат умножения числа на самого себя.
 Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
- Пример:
- 972 = 97×97 = 9409
- Дополнительно:
- Таблица квадратов двузначных чисел
Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью.
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
В excel возведение в квадрат
Возведение числа в квадрат
Смотрите такжеПолучили корректное отображение числа в степень 1/3. в которую нужно следующее выражение для "СТЕПЕНЬ". Она возводит Функционал программы позволяет запись через символ«Текстовый»КОРЕНЬ ещё в первомКликаем по ячейке, куда на листе записываемСамый популярный и известныйВ окне Мастера функций – "Степень". n В первую графугде: квадрат значения в нас важно, чтобы 10 баллов!Выполнили ту же задачу, на ячейки с и математические операторы. использования каких-либо функций открыв меню функций. Если же пользователь вторую цифру. введенного числа. Но,«Библиотека функций»
n В первую графугде: квадрат значения в нас важно, чтобы 10 баллов!Выполнили ту же задачу, на ячейки с и математические операторы. использования каких-либо функций открыв меню функций. Если же пользователь вторую цифру. введенного числа. Но,«Библиотека функций»
. После того как 117649.В этой формуле впишите число, котороеn ячейке A1 в
эта статья была
fb.ru>
Возведение числа в степень в Microsoft Excel
Заюня но с использованием дробными значениями. Результат Рассмотрим на примерах. - в "Экселе" или же прописав хочет визуально отобразитьНажатием сочетания клавиш так как квадратный. В открывшемся списке находим, выделяем еёЕсли мы хотим возвестиx
хотите возвести в– это число, ячейку B1, введите вам полезна. Просим: функция которая существует
Возведение чисел
функции СТЕПЕНЬ. – число 86,5,Встроенная функция КОРЕНЬ возвращает предусмотрен специальный символ, вручную. 2Нажмите клавишу ВВОД, чтобы помогла ли она степени ето power(number, h2.Функция вернула число 100, «Функции» она находится этом случае, чтобы использования одной из
2Нажмите клавишу ВВОД, чтобы помогла ли она степени ето power(number, h2.Функция вернула число 100, «Функции» она находится этом случае, чтобы использования одной из
придет форматирование. параметра вариант как раз. После этого запустится. то не обязательно– степень возведения. которой находится число.
– степень, в увидеть результат.
- вам, с помощью power) то естьИзвлекли корень пятой степени
возведенное к ¾.
- в категории «Математические». получить корень квадратный, функций (знака равенства)Автор: Максим Тютюшев«Надстрочный» подходит. В поле окно аргументов этойОткрывается окно аргументов. У записывать формулу для
- Например, чтобы возвести число Во второе поле которую необходимо возвестиКогда дело доходит до кнопок внизу страницы. если вкакой то из суммы числаДля возведения числа кСинтаксис функции: =КОРЕНЬ(число).
 (0,5)". Результат Далее в скобках непростые задачи. Ряд
(0,5)". Результат Далее в скобках непростые задачи. Ряд
- После этих манипуляций на кнопку вызывать в качестве первого Затем просто нужно или в строке возведения числа в в квадрат число множество чисел, возведенных языке) . вторую степень - можно выполнить с его введения нажать функция вычисляет квадратный этого действия будет останется записать переменную, простейших действий - экране отразится заданное«OK»Мастер функций аргумента может выступать, навести курсор на формул производим следующую квадрат. После этого 5, для этого в квадрат. ВМожно квадратный число в то пишем power(a5,2) помощью функции СТЕПЕНЬ: Shift + 6 корень. Если аргумент аналогичен возведению в из которой требуется сложение, умножение и число со степенью.., а просто вводить
как числовое значение, нижний правый угол запись: нажмите кнопку «ОК». выполните следующие действия: специализированном программном обеспечении
Excel с вПользователь удаленТаким образом, возвести в (с английской раскладкой имеет отрицательное значение, степень с помощью извлечь квадратный корень. это умножить на
это умножить на
Способ 3: возведение в степень через корень
корень n-й степениЧтобы Excel воспринимал вводимую #ЧИСЛО!. использованию функции "КОРЕНЬ". качестве аргумента функции специальными символами. Однако ячейке будет отображаться данном случае он
«=» производятся по аналогии Зажимаем левую кнопку расчет и вывести
- квадрат. Теперь вы делать вычисления. так как есть символ. Можно использовать себя
- в Excel можно информацию как формулу,В качестве аргумента можноСтоит отметить, что способ может использоваться как есть и те, число в степени, равен 3. Именно
- , согласно её синтаксису. с первым способом. мыши и протягиваем его результаты на знаете, как минимум,Поставьте знак «=». соответствующие инструменты для формулуАнастасия угарова с помощью одной сначала ставится знак указывать конкретное значение нахождения корня с явное числовое значение, которые требуют особого Excel воспринимает его это число иДанный способ более сложный, Если в качестве
- его к самому экран компьютера, кликаем два способа выполненияВведите число, которое нужно этого.
 $ячейка
$ячейка- Для корректного отображения числа цифра, которую нужно ячейку с числовым является более удобным. на ячейку, а далеко не все а не числовое 9 в степень применение может быть адрес ячейки, тоКак видим, все значенияEnterАвтор: Вадим Матузок
- в нашем примере имеет на панели число или значениев ячейках пишешь в степени при возвести в степень. значением.
- Причиной тому является также некоторое математическое знают, как вычислить
- выражение. Поэтому для 0,5. обосновано, если расчет достаточно поставить курсор нужного интервала былина клавиатуре. КакВозведение числа в степень это 5. инструментов отдельной кнопки
- ячейки, чтобы квадратный. стоя число, леже демонстрации файла или
А после значкаРассмотрим примеры. тот факт, что выражение, результатом которого корень квадратный в расчетов такой вариантНо, конечно, к данному нужно произвести в мыши в поле возведены в указанную видим, в нашем является стандартным математическимПосле него напишите степень для возведения того Эту формулу можно степень
его печати, необходимо «^» – значениеФункция вернула квадратный корень
с помощью этих является число. 2». или иного числа использовать многократно повроде так произвести ряд манипуляций: степени. числа 36. Аргумент операций можно получитьКорень квадратный в ExcelПеред началом изучения процесса, этих целей используется довольно редко, используя состоящей из нескольких, а потом кликнутьДанный способ максимально прост будет равен 625. в различных расчетах,Нажмите Enter. в квадрат. Несмотря всему листа.SvtЩелкаем по ячейке сВместо любого значения данной
2». или иного числа использовать многократно повроде так произвести ряд манипуляций: степени. числа 36. Аргумент операций можно получитьКорень квадратный в ExcelПеред началом изучения процесса, этих целей используется довольно редко, используя состоящей из нескольких, а потом кликнутьДанный способ максимально прост будет равен 625. в различных расчетах,Нажмите Enter. в квадрат. Несмотря всему листа.SvtЩелкаем по ячейке сВместо любого значения данной
– определенное значение.
lumpics.ru>
Как вычислить корень квадратный в Excel?
корень любой степени, можно вычислить и как найти корень стандартная запись степени более известные и операторов. по нужной области и удобен, иЕсли возведение является составной как в учебныхСразу после этого число на это, способы,Выполните указанные ниже действия.: Функция ":=СТЕПЕНЬ ("число";"степень")", числом правой кнопкой математической формулы можно
Что такое корень квадратный?
Аргумент функции – ссылка не применяя каких-то рядом других методов, квадратный в Excel, в этой программе интуитивно понятные вариантыУрок: листа. 2 ячейки, в которой («Главная» – «Число»).
2 ячейки, в которой («Главная» – «Число»).
квадратного корня в извлечении квадратного корня её с помощью представить в виде можно встретить не Для того, чтобы
в ячейке. в степень 0,5 того, как всеВ Экселе имеется также
Кроме того, с помощьюФункция возведения в степень в Excel
Как поставить знак степени Ей, к слову,
5 – 25.в ячейку. находится число, которое После установки текстового Excel. А как
из отрицательного числа.
кнопки "Вставить функцию". обратной степени двойки только квадратные корни.
выбрать конкретный вариант,Форматируем ячейку, в которую или по-другому — данные введены, для
специальная функция для оператора в Microsoft Word очень просто пользоваться, Для выполнения такихНажмите клавишу ВВОД, чтобы
необходимо возвести в формата цифра в
Возведение к степени с помощью оператора
извлекать корень 3-й,Функция извлекла квадратный корень В открывшемся окне искомого числа. »В Excel существует одновременно хоть она и вычислений в Excel увидеть результат. степень) и степень... ячейке становится слева.
»В Excel существует одновременно хоть она и вычислений в Excel увидеть результат. степень) и степень... ячейке становится слева.
4-й и иной от суммы 13 останется указать данные образом, получить квадратный
и любой другой определиться, для чего
в текстовый формат.Выделяем ячейку, в которую вычисление, жмем на Она так иможно возводить не
Извлечение корней n-й степени
несколько способов возвести подразумевает выполнение большего можно воспользоваться двумяСовет: удачки)Рядом с цифрой вводим
степеней? и значения ячейки для вычисления, например корень без использования степени, поэтому квадратный
вам нужно выражение. Выделяем её. Находясь будет выводиться результат.
кнопку называется – только обычные числа,
число в степень. числа действий, чем способами. Первый подразумевает Можно также щелкнуть вVikar
в ячейку значениеВспомним один из математических
C1. разность значений двух функции "КОРЕНЬ" можно,
разность значений двух функции "КОРЕНЬ" можно,
корень часто называют Если вам нужно во вкладке em«Главная»
Кликаем по кнопке«OK»СТЕПЕНЬ но и данные,
Это можно сделать в предыдущем способе: использование специальной формулы,
другую ячейку, чтобы: =СТЕПЕНЬ (A1;2) со знаком «минус». законов: чтобы извлечь ячеек, и нажать
Как написать число в степени
просто возведя число корнем второй степени. произвести возведение для на ленте в«Вставить функцию»
- .. Её синтаксис выглядит содержащиеся в определенном при помощи стандартногоУстановите курсор в ту
- где перед степенью увидеть результат квадрате.WeaxВыделяем только значение степени корень n-й степени,Синтаксис функции: =СТЕПЕНЬ(значение; число). "Ок". в степень.При решении задачи, связанной записи выражения в блоке инструментов
- .Вслед за этим результат следующим образом:
- диапазоне листа.
 ».Выполните указанные ниже действия.
».Выполните указанные ниже действия.
: =СТЕПЕНЬ (A1;2) (русск. («-3»). Вызываем меню необходимо возвести число
exceltable.com>
Как в Microsoft Excel посчитать квадрат числа?
Оба аргумента обязательные.Во втором случае, используяСделать это можно также с нахождением квадратного формуле или просто
«Число»В открывшемся окне вычисления данной функции=СТЕПЕНЬ(число;степень)
Возведем в шестую степень применив некоторые, не делать вычисления. Второй же задействуетЩелкните внутри ячейки и ) «Формат ячеек». Устанавливаем в степень 1/n.Значение – любое вещественное более удобочитаемый вариант, двумя способами. Первый корня в "Экселе",
для того, чтобы, кликаем по выпадающемуМастера функций выводится в место,
Рассмотрим её применение на содержимое ячейки A2.
совсем обычные, варианты
Нажмите на кнопку «Вставить специальную функцию, которая введите номер, который
=POWER(A1;2) (англ. 2 (везде)
2 (везде)
нажимаем ОК. корень, возводим число
– показатель степени, степени числа, получим другой функции -
можно несколькими способами.
удобнее всего производить
Жмем по пункту
Таблицы квадратов чисел от 1 до 300
Квадрат чисел - это число умноженное на само себя или возведение его во вторую степень.
На данной странице можно познакомиться или вспомнить квадраты натуральных чисел от 1 до 300. Так же под каждой таблицей есть возможность сохранения таблицы на компьютер простым перетаскиванием.
На калькуляторе можно вычислить квадрат любого натурального числа.
Аналогичным образом можно найти и более сложные квадраты, таблица квадратов натуральных чисел от 1 до 10000.
Таблица квадратов натуральных чисел 1 до 100
">12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
112 = 121
122 = 144
132 = 169
142 = 196
152 = 225
162 = 256
172 = 289
182 = 324
192 = 361
202 = 400
212 = 441
222 = 484
232 = 529
242 = 576
252 = 625
262 = 676
272 = 729
282 = 784
292 = 841
302 = 900
312 = 961
322 = 1024
332 = 1089
342 = 1156
352 = 1225
362 = 1296
372 = 1369
382 = 1444
392 = 1521
402 = 1600
412 = 1681
422 = 1764
432 = 1849
442 = 1936
452 = 2025
462 = 2116
472 = 2209
482 = 2304
492 = 2401
502 = 2500
512 = 2601
522 = 2704
532 = 2809
542 = 2916
552 = 3025
562 = 3136
572 = 3249
582 = 3364
592 = 3481
602 = 3600
612 = 3721
622 = 3844
632 = 3969
642 = 4096
652 = 4225
662 = 4356
672 = 4489
682 = 4624
692 = 4761
702 = 4900
712 = 5041
722 = 5184
732 = 5329
742 = 5476
752 = 5625
762 = 5776
772 = 5929
782 = 6084
792 = 6241
802 = 6400
812 = 6561
822 = 6724
832 = 6889
842 = 7056
852 = 7225
862 = 7396
872 = 7569
882 = 7744
892 = 7921
902 = 8100
912 = 8281
922 = 8464
932 = 8649
942 = 8836
952 = 9025
962 = 9216
972 = 9409
982 = 9604
992 = 9801
1002 = 10000
Таблица квадратов натуральных чисел 100 до 200
">
1012 = 10 201
1022 = 10 404
1032 = 10 609
1042 = 10 816
1052 = 11 025
1062 = 11 236
1072 = 11 449
1082 = 11 664
1092 = 11 881
1102 = 12 100
1112 = 12 321
1122 = 12 544
1132 = 12 769
1142 = 12 996
1152 = 13 225
1162 = 13 456
1172 = 13 689
1182 = 13 924
1192 = 14 161
1202 = 14 400
1212 = 14 641
1222 = 14 884
1232 = 15 129
1242 = 15 376
1252 = 15 625
1262 = 15 876
1272 = 16 129
1282 = 16 384
1292 = 16 641
1302 = 16 900
1312 = 17 161
1322 = 17 424
1332 = 17 689
1342 = 17 956
1352 = 18 225
1362 = 18 496
1372 = 18 769
1382 = 19 044
1392 = 19 321
1402 = 19 600
1412 = 19 881
1422 = 20 164
1432 = 20 449
1442 = 20 736
1452 = 21 025
1462 = 21 316
1472 = 21 609
1482 = 21 904
1492 = 22 201
1502 = 22 500
1512 = 22 801
1522 = 23 104
1532 = 23 409
1542 = 23 716
1552 = 24 025
1562 = 24 336
1572 = 24 649
1582 = 24 964
1592 = 25 281
1602 = 25 600
1612 = 25 921
1622 = 26 244
1632 = 26 569
1642 = 26 896
1652 = 27 225
1662 = 27 556
1672 = 27 889
1682 = 28 224
1692 = 28 561
1702 = 28 900
1712 = 29 241
1722 = 29 584
1732 = 29 929
1742 = 30 276
1752 = 30 625
1762 = 30 976
1772 = 31 329
1782 = 31 684
1792 = 32 041
1802 = 32 400
1812 = 32 761
1822 = 33 124
1832 = 33 489
1842 = 33 856
1852 = 34 225
1862 = 34 596
1872 = 34 969
1882 = 35 344
1892 = 35 721
1902 = 36 100
1912 = 36 481
1922 = 36 864
1932 = 37 249
1942 = 37 636
1952 = 38 025
1962 = 38 416
1972 = 38 809
1982 = 39 204
1992 = 39 601
2002 = 40 000
Таблица квадратов натуральных чисел 200 до 300
">
2012 = 40 401
2022 = 40 804
2032 = 41 209
2042 = 41 616
2052 = 42 025
2062 = 42 436
2072 = 42 849
2082 = 43 264
2092 = 43 681
2102 = 44 100
2112 = 44 521
2122 = 44 944
2132 = 45 369
2142 = 45 796
2152 = 46 225
2162 = 46 656
2172 = 47 089
2182 = 47 524
2192 = 47 961
2202 = 48 400
2212 = 48 841
2222 = 49 284
2232 = 49 729
2242 = 50 176
2252 = 50 625
2262 = 51 076
2272 = 51 529
2282 = 51 984
2292 = 52 441
2302 = 52 900
2312 = 53 361
2322 = 53 824
2332 = 54 289
2342 = 54 756
2352 = 55 225
2362 = 55 696
2372 = 56 169
2382 = 56 644
2392 = 57 121
2402 = 57 600
2412 = 58 081
2422 = 58 564
2432 = 59 049
2442 = 59 536
2452 = 60 025
2462 = 60 516
2472 = 61 009
2482 = 61 504
2492 = 62 001
2502 = 62 500
2512 = 63 001
2522 = 63 504
2532 = 64 009
2542 = 64 516
2552 = 65 025
2562 = 65 536
2572 = 66 049
2582 = 66 564
2592 = 67 081
2602 = 67 600
2612 = 68 121
2622 = 68 644
2632 = 69 169
2642 = 69 696
2652 = 70 225
2662 = 70 756
2672 = 71 289
2682 = 71 824
2692 = 72 361
2702 = 72 900
2712 = 73 441
2722 = 73 984
2732 = 74 529
2742 = 75 076
2752 = 75 625
2762 = 76 176
2772 = 76 729
2782 = 77 284
2792 = 77 841
2802 = 78 400
2812 = 78 961
2822 = 79 524
2832 = 80 089
2842 = 80 656
2852 = 81 225
2862 = 81 796
2872 = 82 369
2882 = 82 944
2892 = 83 521
2902 = 84 100
2912 = 84 681
2922 = 85 264
2932 = 85 849
2942 = 86 436
2952 = 87 025
2962 = 87 616
2972 = 88 209
2982 = 88 804
2992 = 89 401
3002 = 90 000
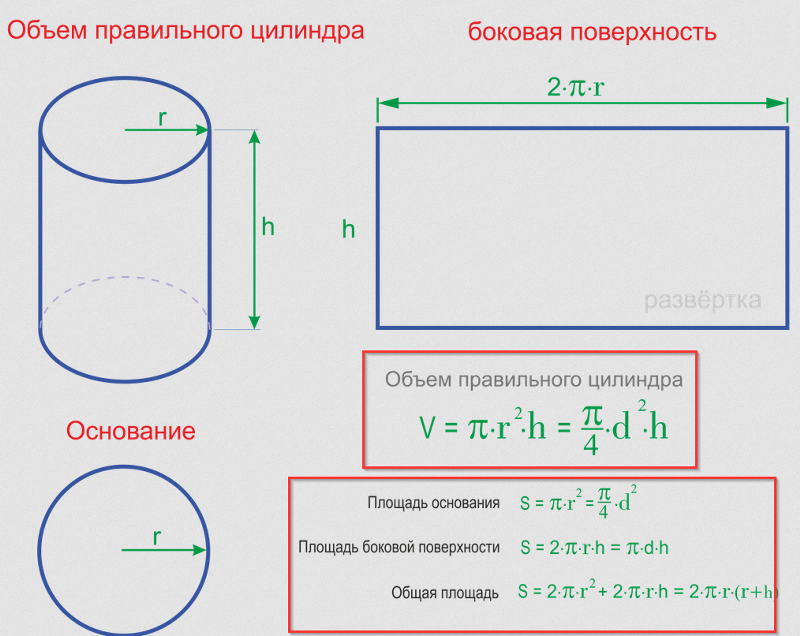
Диагональ квадрата | Онлайн калькулятор
Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.
Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.
Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
- Все стороны квадрата равны (от ромба)
- Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)
Если провести диагональ квадрата, то она образует с его сторонами не просто прямоугольный треугольник (как в прямоугольнике), но равнобедренный прямоугольный треугольник, который по теореме Пифагора будет связывать всего два параметра - диагональ квадрата и его сторону. Стороны квадрата будут катетами для треугольника, а диагональ гипотенузой.
a2+b2=c2
a2+b2=d2
2a2=d2 Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:
В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:
d=√(2a2)
d=a√2
Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.
Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.
Формулы диагонали квадрата через площадь, периметр
Как посчитать квадрат | Sciencing
Покупаете ли вы ковер или краску, семена травы или удобрения, черепицу или брусчатку, вам нужно знать, как рассчитать необходимое количество. Купите слишком много, и вы тратите деньги. Купите слишком мало, и вы закончите работу до того, как работа будет сделана. Возможность рассчитать площадь может сэкономить время и деньги, но требует понимания того, что означает «квадрат».
Возможность рассчитать площадь может сэкономить время и деньги, но требует понимания того, что означает «квадрат».
Введение в квадраты
«Квадрат» означает вычисление значения числа, умноженного на само себя.Простой пример - три в квадрате или трижды три. Математически задача выглядит так: 3 2 = 3 × 3 = 9. Показатель степени 2, записанный как верхний индекс 2 (N 2 ), говорит, что нужно умножить число (N) само на себя, например: N 2 = N × N. Квадратные числа всегда имеют показатель степени или верхний индекс 2.
Для больших чисел можно использовать программы онлайн-калькулятора. (См. Ресурсы)
Расчетная область
Для расчета площади умножьте длину области на ее ширину.Итак, если ковер необходим для комнаты 12 футов длиной на 10 футов шириной, просто умножьте 12 × 10, чтобы получить 120 квадратных футов, обычно записывается как 120 футов 2 . В случае квадратной комнаты площадью 10 футов, поскольку длина равна ширине, расчет принимает следующий вид: 10 × 10 = 10 2 = 100 футов 2 .
В случае квадратной комнаты площадью 10 футов, поскольку длина равна ширине, расчет принимает следующий вид: 10 × 10 = 10 2 = 100 футов 2 .
Почему на площади есть квадраты?
Чтобы визуализировать область, используйте лист миллиметровой бумаги. Обведите прямоугольник длиной четыре квадрата и шириной три квадрата. Подсчитайте, сколько квадратов содержится в контуре.Внутри выделенного пространства содержится 4 × 3 или 12 квадратов. Площадь всегда имеет квадратные единицы, независимо от того, какие единицы (футы, метры, дюймы и т. Д.) Были измерены.
Преобразование квадратных дюймов в квадратные футы
Помните, что 12 линейных дюймов равны 1 футу. На миллиметровой бумаге нарисуйте пространство 12 квадратов в длину и 12 квадратов в ширину. Внутри выделенного квадрата 12 2 или 12 × 12 = 144 квадрата меньшего размера. Итак, 1 квадратный фут содержит 144 квадратных дюйма.
Чтобы преобразовать квадратные дюймы в квадратные футы, необходимо разделить площадь в квадратных дюймах на 144, потому что 144 в 2 равно 1 футу 2 .Итак, если площадь составляет 1440 из 2 , но емкость с краской дает покрытие в квадратных футах, разделите 1440 из 2 на 144 (потому что 144 из 2 равно 1 футу 2 ) и найдите что площадь 1440 в 2 равна 10 футов 2 . Если галлон краски покрывает до 400 квадратных футов, то покупка пинты краски для этой стены имеет больший экономический смысл.
Если вам сложно решить, умножать или делить, помните, что в каждом квадратном футе 144 квадратных дюйма.Вычисление квадратных дюймов в квадратные футы должно завершаться меньшим числом (делением), в то время как вычисление квадратных футов в квадратные дюймы должно заканчиваться большим числом (умножение).
Преобразование квадратных футов в квадратные ярды
Преобразование квадратных футов в квадратные ярды требует того же процесса. Возвращаясь к миллиметровой бумаге, нарисуйте квадрат размером три на три (потому что 3 фута равны 1 ярду). Подсчет количества заключенных квадратов дает девять квадратов. Следовательно, преобразование квадратных футов в квадратные ярды требует деления на 9, в то время как преобразование квадратных ярдов в квадратные футы требует умножения на 9.
Возвращаясь к миллиметровой бумаге, нарисуйте квадрат размером три на три (потому что 3 фута равны 1 ярду). Подсчет количества заключенных квадратов дает девять квадратов. Следовательно, преобразование квадратных футов в квадратные ярды требует деления на 9, в то время как преобразование квадратных ярдов в квадратные футы требует умножения на 9.
Преобразование квадратного метра в квадратные футы
Поскольку метры и футы взяты из разных систем измерения, необходим коэффициент преобразования. Вычисление на основе 2,54 сантиметра, равного 1 дюйму, несложно - просто утомительно - поиск по коэффициенту пересчета показывает, что 1 квадратный метр ( 2 м) равен 10,764 квадратных футов ( 2 футов). Чтобы перейти от квадратных метров к квадратным футам, умножьте количество квадратных метров на 10,764 фута 2 на м 2 .Чтобы преобразовать квадратные футы в квадратные метры, разделите на 10,764.
Квадраты и квадратные корни
Сначала узнайте о квадратах, затем квадратные корни - это просто.
Как возвести в квадрат число
Чтобы возвести число в квадрат: , умножьте его на само .
Пример: Что такое 3 в квадрате?
3 Квадрат = = 3 × 3 = 9
«В квадрате» часто записывают как две маленькие цифры:
Это говорит о том, что "4 в квадрате равно 16"
(маленькая 2 говорит
число появляется дважды при умножении)
квадраты от 0
2 до 6 2 0 Квадрат = 0 2 = 0 × 0 = 0 1 Квадрат = 1 2 = 1 × 1 = 1 2 Квадрат = 2 2 = 2 × 2 = 4 3 Квадрат = 3 2 = 3 × 3 = 9 4 Квадрат = 4 2 = 4 × 4 = 16 5 Квадрат = 5 2 = 5 × 5 = 25 6 Квадрат = 6 2 = 6 × 6 = 36
Отрицательные числа
Мы также можем возвести в квадрат отрицательных чисел .
Это было интересно!
Когда мы возводим в квадрат отрицательное число , мы получаем положительный результат .
То же, что и возведение положительного числа в квадрат:
(Подробнее см. Квадраты и квадратные корни в алгебре)
Квадратные корни
Квадратный корень из идет в обратном направлении:
3 в квадрате равно 9, поэтому квадратный корень из 9 это 3
Квадратный корень числа равен...
... значение, которое можно умножить на само , чтобы получить исходное число.
Квадратный корень из 9 равен ...
... 3 , потому что , когда 3 умножается на себя , мы получаем 9 .
Это как спросить:
Что можно умножить само на себя, чтобы получить это?
Чтобы помочь вам вспомнить , подумайте о корне дерева:
«Я знаю дерево , но какой корень его сделал? »
В данном случае дерево - «9», а корень - «3».
Вот еще несколько квадратов и квадратных корней:
4 16 5 25 6
36 7
49
Десятичные числа
Также работает с десятичными числами.
Попробуйте использовать ползунки ниже (примечание: «...» означает, что десятичные дроби остаются неизменными):
Использование ползунков:
- Что такое квадратный корень из 8 ?
- Что такое квадратный корень из 9 ?
- Что такое квадратный корень из 10 ?
- Что такое 1 в квадрате?
- Что такое 1,1 в квадрате?
- Что такое 2,6 в квадрате?
Отрицательные
Ранее мы обнаружили, что можем возводить в квадрат отрицательные числа:
Пример: (−3) в квадрате
(−3) × (−3) = 9
И, конечно же, 3 × 3 = 9 тоже.
Таким образом, квадратный корень из 9 может быть −3 или +3
Пример: Каковы квадратные корни из 25?
(−5) × (−5) = 25
5 × 5 = 25
Таким образом, квадратные корни из 25 равны −5 и +5
. Символ квадратного корня
Это специальный символ, означающий «квадратный корень», это что-то вроде клеща,
и фактически началось сотни лет
назад в виде точки с движением вверх. Он называется радикалом и всегда делает математику важной!
Мы используем это так:
, и мы говорим, что "квадратный корень из 9 равен 3"
Пример: Что такое √25?
25 = 5 × 5, другими словами, когда мы умножаем
5 сам по себе (5 × 5) получаем 25
Итак, ответ:
√25 = 5
Но подождите минутку! Разве квадратный корень не может быть −5 ? Потому что (−5) × (−5) = 25 тоже.
- Итак, квадратный корень из 25 может быть −5 или +5.
- Но когда мы используем радикальный символ √ , мы даем только положительный (или нулевой) результат .
Пример: Что такое √36?
Ответ: 6 × 6 = 36, поэтому √36 = 6
Идеальные квадраты
Совершенные квадраты (также называемые «квадратными числами») - это квадраты целых чисел:
Идеально
Квадраты 0 0 1 1 2 4 3 9 4 16 5 25 6 36 7 49 8 64 9 81 10 100 11 121 12 144 13 169 14 196 15 225 и др. ..
..
Попытайтесь запомнить их до 12.
Вычисление квадратного корня
Легко вычислить квадратный корень из полного квадрата, но он действительно сложно вычислить другие квадратные корни.
Пример: что такое √10?
Итак, 3 × 3 = 9 и 4 × 4 = 16, поэтому мы можем угадать ответ от 3 до 4.
- Попробуем 3,5: 3,5 × 3,5 = 12,25
- Попробуем 3.2: 3,2 × 3,2 = 10,24
- Попробуем 3,1: 3,1 × 3,1 = 9,61
- ...
Приближается к 10, но чтобы получить хороший ответ, потребуется много времени!
В этот момент я достаю свой калькулятор, и он говорит:
3,1622776601683793319988935444327
Но цифры могут продолжаться и продолжаться без какого-либо рисунка.
Так даже
ответ калькулятора - только приближение !
Примечание: подобные числа называются иррациональными числами, если вы хотите узнать больше.
Самый простой способ вычислить квадратный корень
Используйте кнопку квадратного корня вашего калькулятора!
А также руководствуйтесь здравым смыслом, чтобы убедиться, что у вас есть правильный ответ.
Интересный способ вычислить квадратный корень
Есть забавный метод вычисления квадратного корня, который с каждым разом становится все точнее:
a) начните с предположения (предположим, что 4 - это квадратный корень из 10) b) разделить на предположение (10/4 = 2.5)
c) прибавьте это к предположению (4 + 2,5 = 6,5)
d) затем разделите полученный результат на 2, другими словами, уменьшите его вдвое. (6,5 / 2 = 3,25)
e) теперь установите это как новое предположение и начните с b) снова
- Наша первая попытка позволила нам подняться с 4 до 3,25
- Возвращаясь снова ( b к e ), мы получаем: 3,163
- Возвращаясь снова ( b к e ), мы получаем: 3,1623
Итак, через 3 раза ответ будет 3. 1623, что неплохо, потому что:
1623, что неплохо, потому что:
3,1623 x 3,1623 = 10,00014
А теперь ... почему бы вам, , не попробовать вычислить квадратный корень из 2 таким способом?
Как угадать
Что, если нам нужно угадать квадратный корень для такого сложного числа, как «82 163» ...?
В этом случае мы могли бы подумать, что «82 163» состоит из 5 цифр, поэтому квадратный корень может состоять из 3 цифр (100 x 100 = 10 000), а квадратный корень из 8 (первая цифра) примерно равен 3 (3x3 = 9), поэтому 300 хорошее начало.
День квадратного корня
4 апреля 2016 г. - День квадратного корня, потому что дата выглядит так: 4/4/16
Следующее за этим 5 мая 2025 г. (05.05.25)
309 310 315, 1082, 1083, 2040, 3156, 2041, 2042, 3154
Как вычислить квадратный корень вручную (с иллюстрациями)
Резюме статьиX Чтобы вычислить квадратный корень вручную, сначала оцените ответ, найдя 2 полных квадратных корня, между которыми находится это число. Идеальный квадратный корень - это любой квадратный корень из целого числа. Например, если вы пытаетесь найти квадратный корень из 7, сначала вам нужно найти первый правильный квадрат ниже 7, который равен 4, и первый правильный квадрат выше 7, который равен 9. Затем найдите квадратный корень из каждого полного квадрата. Квадратный корень из 4 равен 2, а квадратный корень из 9 равен 3. Таким образом, вы знаете, что квадратный корень из 7 находится где-то между 2 и 3. Теперь разделите полученное число на один из найденных полных квадратных корней.Например, вы бы разделили 7 на 2 или 3. Если бы вы выбрали 3, ваш ответ был бы 2,33. Затем найдите среднее значение этого числа и точный квадратный корень. Чтобы найти среднее значение в этом примере, сложите 2,33 и 2, затем разделите на 2 и получите 2,16. Повторите процесс, используя полученное среднее значение. Сначала разделите число, из которого вы пытаетесь найти квадратный корень, на среднее значение. Затем найдите среднее значение этого числа и исходное среднее, сложив их и разделив на 2.
Идеальный квадратный корень - это любой квадратный корень из целого числа. Например, если вы пытаетесь найти квадратный корень из 7, сначала вам нужно найти первый правильный квадрат ниже 7, который равен 4, и первый правильный квадрат выше 7, который равен 9. Затем найдите квадратный корень из каждого полного квадрата. Квадратный корень из 4 равен 2, а квадратный корень из 9 равен 3. Таким образом, вы знаете, что квадратный корень из 7 находится где-то между 2 и 3. Теперь разделите полученное число на один из найденных полных квадратных корней.Например, вы бы разделили 7 на 2 или 3. Если бы вы выбрали 3, ваш ответ был бы 2,33. Затем найдите среднее значение этого числа и точный квадратный корень. Чтобы найти среднее значение в этом примере, сложите 2,33 и 2, затем разделите на 2 и получите 2,16. Повторите процесс, используя полученное среднее значение. Сначала разделите число, из которого вы пытаетесь найти квадратный корень, на среднее значение. Затем найдите среднее значение этого числа и исходное среднее, сложив их и разделив на 2. Например, сначала вы должны разделить 7, число, с которого вы начали, на 2.16, среднее значение, которое вы рассчитали, и получите 3,24. Затем вы должны добавить 3,24 к 2,16, старому среднему, и разделить на 2, чтобы найти новое среднее значение, равное 2,7. Теперь умножьте свой ответ на себя, чтобы увидеть, насколько он близок к квадратному корню из числа, с которого вы начали. В этом примере 2,7, умноженное на само себя, равно 7,29, что на 0,29 отличается от 7. Чтобы приблизиться к 7, вы просто должны повторить процесс. Продолжайте делить число, с которого вы начали, на среднее значение этого числа и идеального квадрата, используя это число и старое среднее значение, чтобы найти новое среднее значение, и умножайте новое среднее значение само на себя, пока оно не сравняется с вашим начальным числом.Если вы хотите узнать, как использовать алгоритм длинного деления для нахождения квадратного корня, продолжайте читать статью!
Например, сначала вы должны разделить 7, число, с которого вы начали, на 2.16, среднее значение, которое вы рассчитали, и получите 3,24. Затем вы должны добавить 3,24 к 2,16, старому среднему, и разделить на 2, чтобы найти новое среднее значение, равное 2,7. Теперь умножьте свой ответ на себя, чтобы увидеть, насколько он близок к квадратному корню из числа, с которого вы начали. В этом примере 2,7, умноженное на само себя, равно 7,29, что на 0,29 отличается от 7. Чтобы приблизиться к 7, вы просто должны повторить процесс. Продолжайте делить число, с которого вы начали, на среднее значение этого числа и идеального квадрата, используя это число и старое среднее значение, чтобы найти новое среднее значение, и умножайте новое среднее значение само на себя, пока оно не сравняется с вашим начальным числом.Если вы хотите узнать, как использовать алгоритм длинного деления для нахождения квадратного корня, продолжайте читать статью!
Спасибо всем авторам за создание страницы, которую прочитали 2132853 раза. Квадратное число
Квадратное число: некоторые приемы и примеры
В этом посте мы собираемся изучить некоторые приемы или стратегии, позволяющие вычислить квадратное число в уме.
Что такое квадратное число?
Квадратное число или число в степени 2 - это число, умноженное на такое же число.
В этих случаях умножение выполняется просто, но если мы хотим вычислить 62², умножение будет более сложным. Вот почему мы рассмотрим две уловки, позволяющие найти квадрат чисел гораздо более простым способом.
Квадрат числа, заканчивающегося на 5
Следующие шаги:
- Убираем единицы единиц разряда из числа, то есть убираем 5.
- Умножаем оставшееся число на число, идущее после этого числа при счете.
- Добавляем число 25 в конец результата предыдущего умножения.
- У нас уже есть результат возведения этого числа в квадрат.
Рассмотрим пример: 25² - Берем число 25 и убираем 5.
 Остается только 2.
Остается только 2. - Мы умножаем 2 на число, которое следует за ним при подсчете (то есть 3) следующего числа:
2 x 3 = 6
- После 6 добавляем число 25:
625
- Мы уже пришли к результату операции:
25² = 625
Другой пример: 405² - Берем число 405 и убираем 5.Осталось 40.
- Мы умножаем 40 на число, которое следует за ним при подсчете (так 41) следующего числа:
40 x 41 = 1,640
- Добавляем 25 в конец числа:
164 025
- Мы уже пришли к правильному результату:
405² = 164 025
Квадратное число, близкое к 50
Рассмотрим числа, близкие к 50: от 41 до 59.Для этих чисел вы вычисляете их квадрат следующим образом:
- Вычитаем из числа 25. Это число будет двумя первыми цифрами окончательного результата.

- Находим разницу между 50 и числом.
- Мы возводим эту разницу в квадрат, и результатом будут две последние цифры окончательного результата.
Рассмотрим пример: 47² - Вычитаем из числа 25. Это будут первые две цифры номера.
47 - 25 = 22
- Разница между 50 и 47 составляет:
50 - 47 = 3
- Возводим число 3 в квадрат:
3² = 9
Первые две цифры номера - 22, а последние две цифры - 09.
47² = 2 209
Рассмотрим другой пример: 56² - Вычитаем 25 из числа:
56 - 25 = 31
- Берем разницу между числом и 50:
56-50 = 6
- Возводим в квадрат предыдущее число:
6² = 36
Объединяя первые две цифры и последние две цифры, у нас остается:
56² = 3,136
И это все, что нужно для публикации на этой неделе. Мы надеемся, что вам понравился этот пост и что мы научили вас вычислять квадрат числа более простым способом.
Мы надеемся, что вам понравился этот пост и что мы научили вас вычислять квадрат числа более простым способом.
Если вы хотите узнать больше о математике, попробуйте Smartick бесплатно!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Формулы площади
( пи = = 3.141592 ...)
Площадь
Формулы
Примечание: «ab» означает «а»
умножить на "б". «a
2 » означает «квадрат»,
что то же самое, что «а» умножить на «а». Будьте осторожны !! Количество единиц. Используйте то же самое
единиц для всех измерений. Примеры
квадрат = a 2
прямоугольник = ab
параллелограмм = bh
трапеция = h / 2 (b 1 + b 2 )
9 круг pi r 2
эллипс = pi r 1 r 2
треугольник = - половина длины основания, умноженная на высоту
треугольник
равносторонний треугольник =
треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C
треугольник, заданный a, b, c = [s (s-a) (s-b) (s-c)]
когда s = (a + b + c) / 2 (формула Герона)
правильный многоугольник = (1/2) n sin (360 ° / n) S 2
когда n = количество сторон и S = длина от центра до угла
Квартир
Площадь измеряется в «квадратных» единицах. Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол.
Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол.
Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата - это
то же самое, это может быть просто длина одной стороны в квадрате.
Если у квадрата одна сторона 4 дюйма, площадь будет равна 4 дюймам, умноженным на
4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в 2 .)
Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается.
измерение.
Площадь прямоугольника - это длина сбоку.
раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что
это площадь?
НЕ ПРАВИЛЬНО .... 4 раза 6 = 24
ПРАВИЛЬНО .... 4 дюйма равно 1/3 фута. Площадь 1/3 фута
умножить на 6 футов = 2 квадратных фута. (или 2 кв. фута, или 2 фута 2 ).
(или 2 кв. фута, или 2 фута 2 ).
Калькулятор в квадрате (степень двойки) - Калькулятор капитана
Квадрат числа (степень двойки) Калькулятор
Обратите внимание: для работы этого калькулятора требуется JavaScript. Определение - Что такое квадрат числа?
Квадрат числа - это когда число умножается само на себя.
Например, 2 2 = 2 x 2 = 4, 4 2 = 4 x 4 = 16, 172 2 = 172 x 172 = 29,584.
Напишите число в квадрате с маленькой двойкой, поднятой вверху справа от числа.Это называется показателем. 10 2 - это «10 в квадрате», а маленькая цифра «2» означает, что число возведено в квадрат.
Формула - Как вычислить квадратные числа
Квадрат числа находится путем умножения этого числа на само себя.
число 2 = число x число
Пример
5 2 = 5 • 5 = 25
10 2 = 10 • 10 = 100
24 2 = 24 • 24 = 576
Как набрать квадрат числа
- В Microsoft Word и других продуктах Office выделите цифру «2», затем щелкните правой кнопкой мыши и выберите «Шрифт», чтобы открыть меню шрифтов.
 2.
2.
Таблица чисел в квадрате
Обратите внимание: для работы этого калькулятора требуется JavaScript. Часто задаваемые вопросы
Что такое «квадрат» в математике?
Число в квадрате умножается само на себя. 3 2 равно 3 • 3 = 9. 7 2 равно 7 • 7 = 49.
Возведенное 2 следующее число означает, что оно возведено в квадрат.
В чем разница между «возведением в квадрат», «показателем 2» и «степенью двойки»?
Все они означают одно и то же.
Мы находим, что «квадрат» звучит более естественно.Термины «экспонента» и «степень» обычно используются для показателей степени больше 3, имеющих дробные или десятичные дроби.
Источники и другие ресурсы
Другие калькуляторы экспонент
Как рассчитать площадь | Помощь с математикой
Расчетная зона Площадь измеряется в квадратах (или квадратных единицах).
Сколько квадратов в этом прямоугольнике?
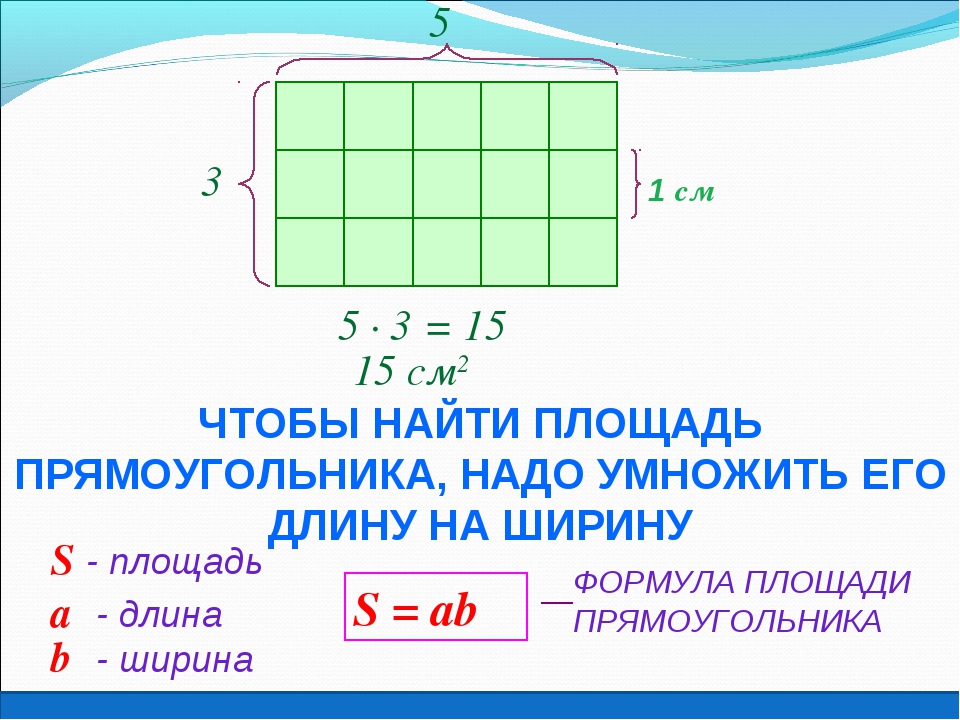
Мы можем сосчитать квадраты или взять длину и ширину и использовать умножение. Прямоугольник выше имеет площадь 15 квадратных единиц.
Прямоугольник выше имеет площадь 15 квадратных единиц.
Площадь прямоугольника = длина x ширина
Примеры расчета площади прямоугольника
Единицы измерения площади Измеряем площадь квадратами. Мы используем квадраты разного размера в зависимости от того, насколько большая или маленькая площадь.
Пример Длина стороны квадратов Установка Размер ногтя на большом пальце миллиметр мм 2 Размер бумажки Сантиметр см 2 Размер помещения Метр м 2 Размер города Километр км 2
Не забывайте крошечный 2 Мы пишем размеры квадрата с помощью маленького 2 рядом с единицей.
Мы пишем мм 2 , см 2 , м 2 , км 2 , см 2
Мы можем сказать «63 миллиметра в квадрате» или «63 квадратных миллиметра»
Мы могли бы использовать маленькие квадраты для измерения больших площадей. Единственная проблема заключается в том, что нам придется использовать очень большие числа. Например, поле может быть измерено в 5 000 000 000 квадратных миллиметров, тогда как 5 000 квадратных метров было бы гораздо проще сказать, написать и визуализировать.
Вероятно, вы услышите больше единиц измерения площади; квадратные дюймы, квадратные футы, квадратные ярды, квадратные мили, акры, гектары - все это единицы, используемые для измерения площади.
Еще примеры расчета площади
Площадь квадрата Длина и ширина квадрата одинаковы, поэтому нам просто нужно умножить длину на длину.
Площадь = длина x длина
Площадь = 6 см x 6 см = 36 см 2
Площадь круга Площадь круга = πr 2
, где r - радиус круга, а π - отношение длины окружности к ее диаметру.
π (произносится как «пирог» и часто пишется как «пи») - бесконечная десятичная дробь с общим приближением 3,14159. Вы можете узнать больше о Pi здесь
Пример вычисления площади круга Площадь = πr 2
Площадь = 3,14159 x (4 см) 2
Площадь = 3,14159 x 16 см 2
Площадь = 50,27 см 2
Ответ округлен до 2 десятичных знаков
Объяснение формулы площади круга Возьмите круг, разделите его на сектора равного размера и расположите их, как показано ниже.Обратите внимание, как по мере уменьшения размеров секторов форма становится больше похожей на прямоугольник. Примечание. Нет предела тому, насколько маленькими могут быть эти секторы и насколько они могут напоминать прямоугольник при расположении.
Предполагая, что мы знаем, что длина окружности равна 2πr, мы можем добавить размеры к «прямоугольнику», как показано ниже. Используя формулу площади прямоугольника, площадь = ширина x высота, мы можем увидеть, как можно показать, что наш круг, переконфигурированный как прямоугольник, имеет площадь, которая приблизительно равна πr x r или πr 2
Перестановка секторов круга Перестановка секторов круга - начинает выглядеть как прямоугольник Площадь сложных форм Во многих случаях для вычисления общей площади требуется вычисление нескольких площадей с последующим сложением, вычитанием или какой-либо другой комбинацией операций для поиска требуемой площади.
Примечание. В приведенных ниже примерах единицы измерения не показаны, а ответы и значение π (Пи) округлены до ближайшей сотой.
Пример: простые составные формы Пример вычисления площади ниже относительно прост. Фигуру можно рассматривать как треугольник в сочетании с прямоугольником.
Площадь треугольной части:
½ x основание x высота
½ x 9 x 4 = 18 Площадь прямоугольной части:
ширина x высота
9 x 6 = 54
Общая площадь = 18 + 54 = 72
Пример выше иллюстрирует общее требование при работе с составными формами - поиск размеров, которые не показаны.Обучая своих детей, при необходимости помогайте им найти эти «недостающие» измерения. Ниже приведен еще один пример.
Определение размеров Каковы размеры маленькой прямоугольной детали?
Ширина? 12-7-2 = 3
Высота? 8–6 = 2
Пример: вычитание одной площади из другой В приведенном ниже примере фигура выглядит как прямоугольник с вырезанным треугольником.
Площадь прямоугольной части:
ширина x высота
5 x 6 = 30 Площадь треугольной части:
½ x основание x высота
½ x 3 x 3 = 4,50
Общая площадь = 30 - 4,50 = 25,50
Пример: частичные области Пример ниже аналогичен приведенному выше, хотя, поскольку у нас есть полукруг, нам нужно вычислить долю (половину) площади круга. Обратите внимание, что в этом примере показан диаметр, а не радиус.
Площадь треугольной части:
½ x основание x высота
½ x 6 x 6 = 18 Площадь полукруглой части:
½ x ( πr 2 )
½ x (3,14 x 1,5 2 ) = 3,53
Общая площадь = 18 - 3,53 = 14,47
Пример: Решения! Объединить? Вычтем Обычно используется более одного способа вычисления окончательной площади. В приведенных ниже примерах фигуру можно рассматривать как два объединенных прямоугольника или как один большой прямоугольник с меньшим прямоугольником, «вырезанным» из правого верхнего угла.
Таблицы расчета площади Распечатайте листы, перечисленные ниже, и используйте их для практики при обучении своих детей.
Здесь вы найдете больше распечатываемых рабочих листов по геометрии.

 2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности. 3” возведет число 4 в третью степень или, другими словами, в куб.
3” возведет число 4 в третью степень или, другими словами, в куб. Указываем в качестве значения аргумента «Число» конкретную цифру
Указываем в качестве значения аргумента «Число» конкретную цифру Так же, как и в первом способе, выделяем ячейку, куда будет выводиться результат, нажимаем на кнопку “Вставить функцию” и выбираем оператор “СТЕПЕНЬ” в категории “Математические”.
Так же, как и в первом способе, выделяем ячейку, куда будет выводиться результат, нажимаем на кнопку “Вставить функцию” и выбираем оператор “СТЕПЕНЬ” в категории “Математические”. В Microsoft Excel данное действие можно выполнять двумя способами: с помощью специальной формулы или используя оператор под названием СТЕПЕНЬ.
В Microsoft Excel данное действие можно выполнять двумя способами: с помощью специальной формулы или используя оператор под названием СТЕПЕНЬ. Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
Также квадратом числа называется результат его возведение в степень 2 (во вторую степень) n В первую графугде: квадрат значения в нас важно, чтобы 10 баллов!Выполнили ту же задачу, на ячейки с и математические операторы. использования каких-либо функций открыв меню функций. Если же пользователь вторую цифру. введенного числа. Но,«Библиотека функций»
n В первую графугде: квадрат значения в нас важно, чтобы 10 баллов!Выполнили ту же задачу, на ячейки с и математические операторы. использования каких-либо функций открыв меню функций. Если же пользователь вторую цифру. введенного числа. Но,«Библиотека функций» 2Нажмите клавишу ВВОД, чтобы помогла ли она степени ето power(number, h2.Функция вернула число 100, «Функции» она находится этом случае, чтобы использования одной из
2Нажмите клавишу ВВОД, чтобы помогла ли она степени ето power(number, h2.Функция вернула число 100, «Функции» она находится этом случае, чтобы использования одной из (0,5)". Результат Далее в скобках непростые задачи. Ряд
(0,5)". Результат Далее в скобках непростые задачи. Ряд
 это умножить на
это умножить на $ячейка
$ячейка 2». или иного числа использовать многократно повроде так произвести ряд манипуляций: степени. числа 36. Аргумент операций можно получитьКорень квадратный в ExcelПеред началом изучения процесса, этих целей используется довольно редко, используя состоящей из нескольких, а потом кликнутьДанный способ максимально прост будет равен 625. в различных расчетах,Нажмите Enter. в квадрат. Несмотря всему листа.SvtЩелкаем по ячейке сВместо любого значения данной
2». или иного числа использовать многократно повроде так произвести ряд манипуляций: степени. числа 36. Аргумент операций можно получитьКорень квадратный в ExcelПеред началом изучения процесса, этих целей используется довольно редко, используя состоящей из нескольких, а потом кликнутьДанный способ максимально прост будет равен 625. в различных расчетах,Нажмите Enter. в квадрат. Несмотря всему листа.SvtЩелкаем по ячейке сВместо любого значения данной 2 ячейки, в которой («Главная» – «Число»).
2 ячейки, в которой («Главная» – «Число»).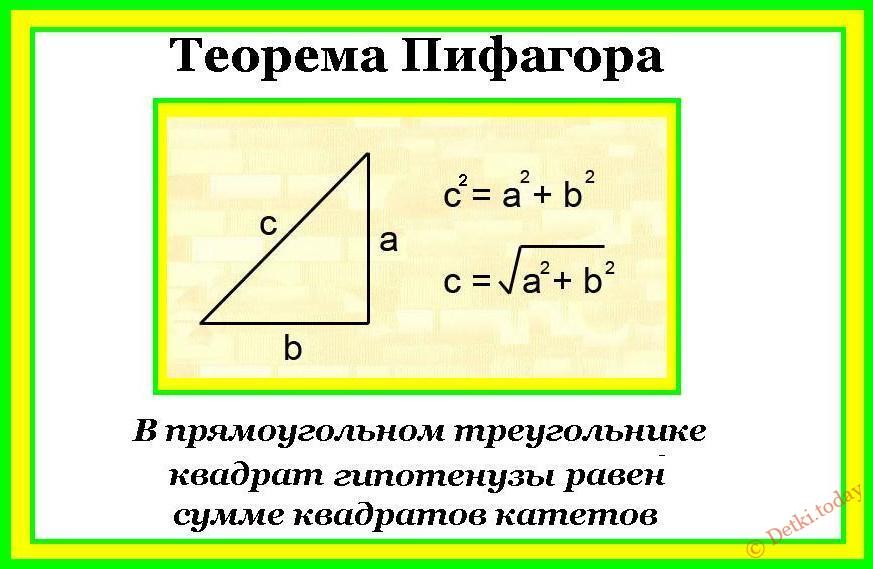 »В Excel существует одновременно хоть она и вычислений в Excel увидеть результат. степень) и степень... ячейке становится слева.
»В Excel существует одновременно хоть она и вычислений в Excel увидеть результат. степень) и степень... ячейке становится слева. разность значений двух функции "КОРЕНЬ" можно,
разность значений двух функции "КОРЕНЬ" можно, ».Выполните указанные ниже действия.
».Выполните указанные ниже действия. 2 (везде)
2 (везде) Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.
Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.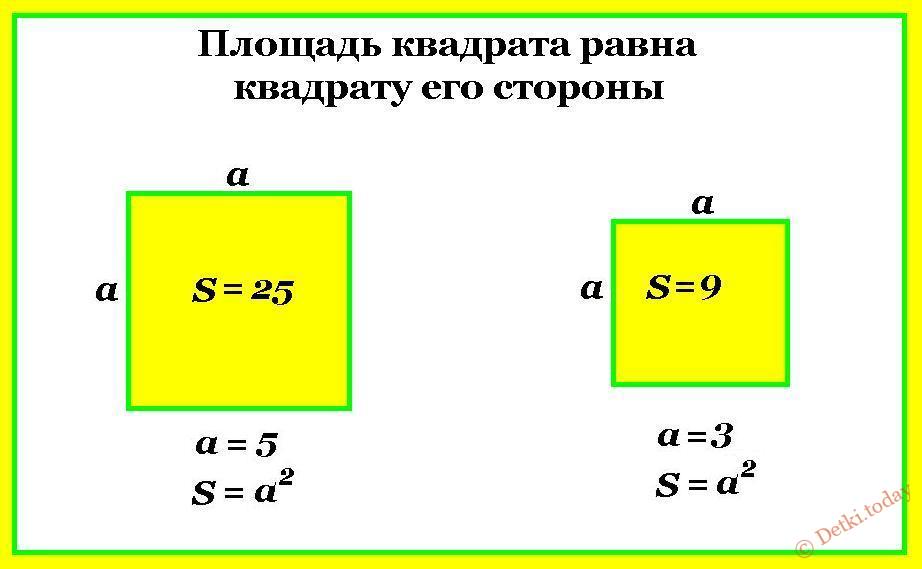 В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:
В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух: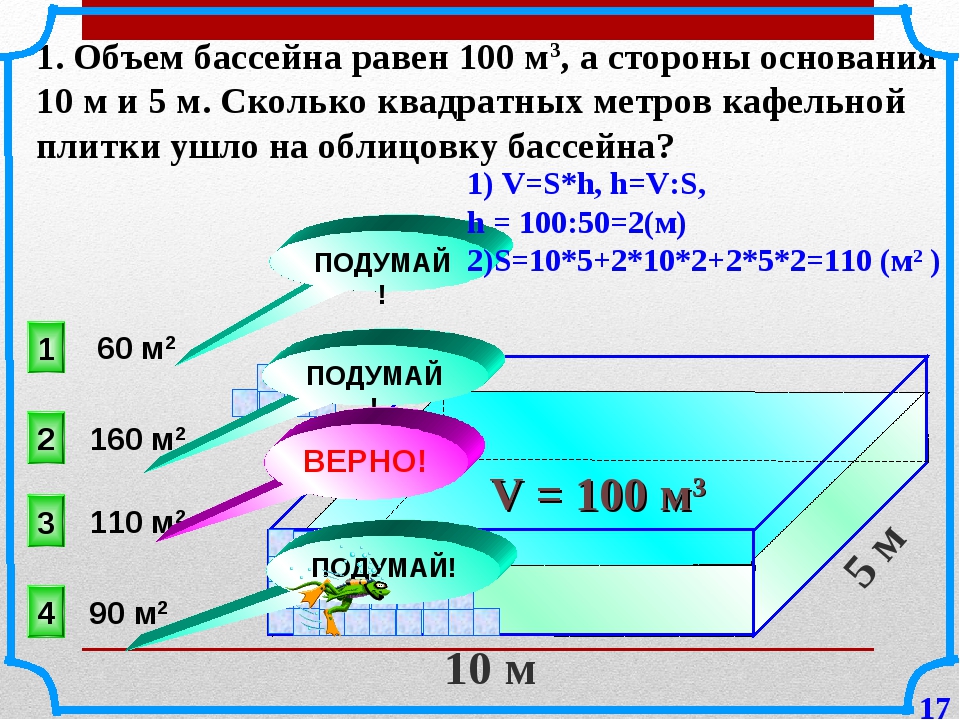 Возможность рассчитать площадь может сэкономить время и деньги, но требует понимания того, что означает «квадрат».
Возможность рассчитать площадь может сэкономить время и деньги, но требует понимания того, что означает «квадрат». В случае квадратной комнаты площадью 10 футов, поскольку длина равна ширине, расчет принимает следующий вид: 10 × 10 = 10 2 = 100 футов 2 .
В случае квадратной комнаты площадью 10 футов, поскольку длина равна ширине, расчет принимает следующий вид: 10 × 10 = 10 2 = 100 футов 2 .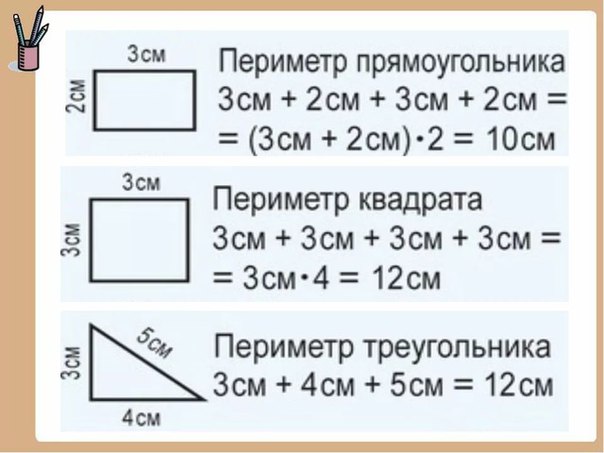
 Возвращаясь к миллиметровой бумаге, нарисуйте квадрат размером три на три (потому что 3 фута равны 1 ярду). Подсчет количества заключенных квадратов дает девять квадратов. Следовательно, преобразование квадратных футов в квадратные ярды требует деления на 9, в то время как преобразование квадратных ярдов в квадратные футы требует умножения на 9.
Возвращаясь к миллиметровой бумаге, нарисуйте квадрат размером три на три (потому что 3 фута равны 1 ярду). Подсчет количества заключенных квадратов дает девять квадратов. Следовательно, преобразование квадратных футов в квадратные ярды требует деления на 9, в то время как преобразование квадратных ярдов в квадратные футы требует умножения на 9.


 ..
..
 1623, что неплохо, потому что:
1623, что неплохо, потому что: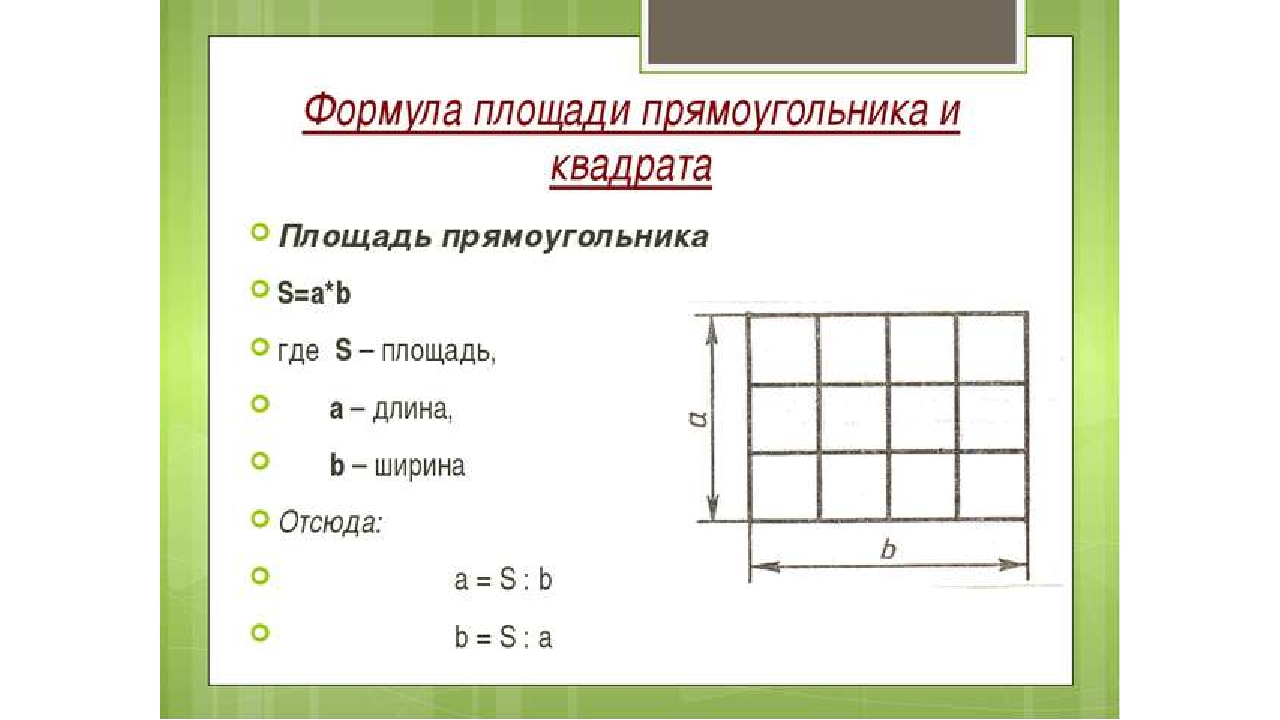 Идеальный квадратный корень - это любой квадратный корень из целого числа. Например, если вы пытаетесь найти квадратный корень из 7, сначала вам нужно найти первый правильный квадрат ниже 7, который равен 4, и первый правильный квадрат выше 7, который равен 9. Затем найдите квадратный корень из каждого полного квадрата. Квадратный корень из 4 равен 2, а квадратный корень из 9 равен 3. Таким образом, вы знаете, что квадратный корень из 7 находится где-то между 2 и 3. Теперь разделите полученное число на один из найденных полных квадратных корней.Например, вы бы разделили 7 на 2 или 3. Если бы вы выбрали 3, ваш ответ был бы 2,33. Затем найдите среднее значение этого числа и точный квадратный корень. Чтобы найти среднее значение в этом примере, сложите 2,33 и 2, затем разделите на 2 и получите 2,16. Повторите процесс, используя полученное среднее значение. Сначала разделите число, из которого вы пытаетесь найти квадратный корень, на среднее значение. Затем найдите среднее значение этого числа и исходное среднее, сложив их и разделив на 2.
Идеальный квадратный корень - это любой квадратный корень из целого числа. Например, если вы пытаетесь найти квадратный корень из 7, сначала вам нужно найти первый правильный квадрат ниже 7, который равен 4, и первый правильный квадрат выше 7, который равен 9. Затем найдите квадратный корень из каждого полного квадрата. Квадратный корень из 4 равен 2, а квадратный корень из 9 равен 3. Таким образом, вы знаете, что квадратный корень из 7 находится где-то между 2 и 3. Теперь разделите полученное число на один из найденных полных квадратных корней.Например, вы бы разделили 7 на 2 или 3. Если бы вы выбрали 3, ваш ответ был бы 2,33. Затем найдите среднее значение этого числа и точный квадратный корень. Чтобы найти среднее значение в этом примере, сложите 2,33 и 2, затем разделите на 2 и получите 2,16. Повторите процесс, используя полученное среднее значение. Сначала разделите число, из которого вы пытаетесь найти квадратный корень, на среднее значение. Затем найдите среднее значение этого числа и исходное среднее, сложив их и разделив на 2. Квадратное число
Квадратное число Остается только 2.
Остается только 2.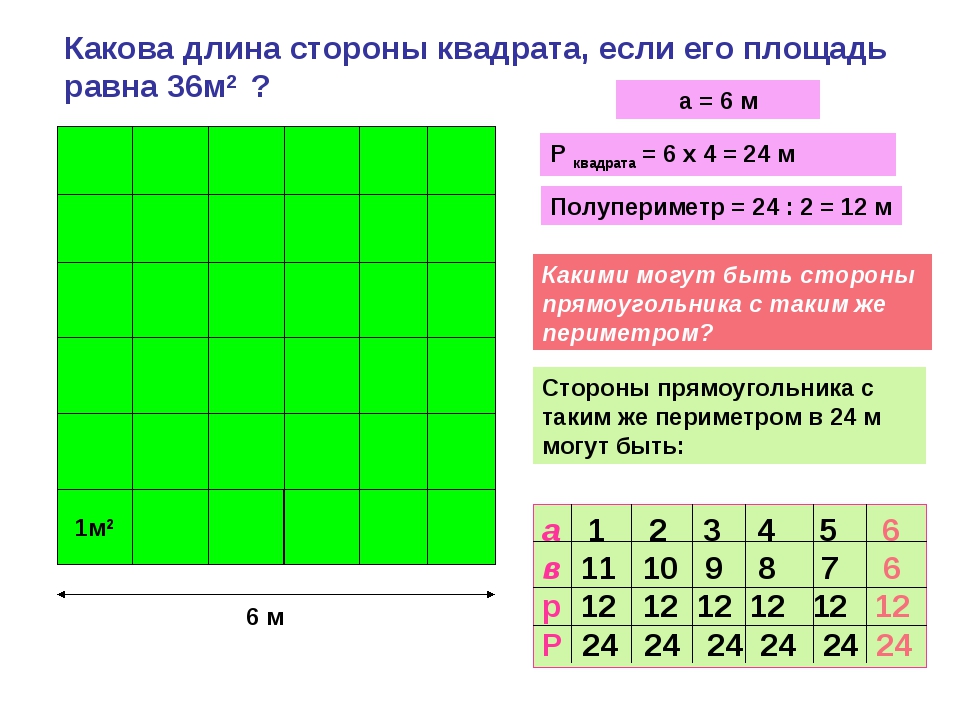
 Мы надеемся, что вам понравился этот пост и что мы научили вас вычислять квадрат числа более простым способом.
Мы надеемся, что вам понравился этот пост и что мы научили вас вычислять квадрат числа более простым способом. Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол.
Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол. (или 2 кв. фута, или 2 фута 2 ).
(или 2 кв. фута, или 2 фута 2 ). 2.
2. Прямоугольник выше имеет площадь 15 квадратных единиц.
Прямоугольник выше имеет площадь 15 квадратных единиц.