Калькулятор для расчета площади
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
Полезные калькуляторы Конвертер единиц площади | Конвертер единиц длины
Расчет площади прямоугольника
Результат:
S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля
Расчет площади треугольника
Способ нахождения площади треугольника: По трем сторонам По одной стороне и высоте, опущенной на эту сторону По двум сторонам и углу между ними
Результат:
S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля
Расчет площади круга
Рассчитать площадь круга, если известен:
ВычислитьРезультат:
S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля
Расчет площади параллелограмма
Способ нахождения площади параллелограмма:
По основанию и высоте параллелограмма
По двум сторонам и углу между ними
По двум диагоналям и углу между ними
Результат:
S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля
Расчет площади правильного многоугольника
Многоугольник с числом сторон n и длиной стороны а Многоугольник с числом сторон n, вписанный в окружность радиуса R Многоугольник с числом сторон n, описанный вокруг окружности радиуса r
ВычислитьРезультат:
S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля
Расчет площади эллипса
Результат:
S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля
Расчет площади сектора круга
Рассчитать площадь сектора круга, если известен:
r= мм см м км фут ярд дюйм миля |

|
|
θ= мм см м км фут ярд дюйм миля град. рад. |
Результат:
S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля
Расчет площади трапеции
Способ нахождения площади трапеции: По двум основаниям a,b и высоте h По двум основаниям a,b и боковым сторонам c,d
Результат:
S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
| Метрические единицы измерения площади: | |
| Квадратный метр, производная единица системы СИ 1 м2 = | 1 са (сантиар) |
| Квадратный километр — 1 км2 = | 1 000 000 м2 |
| Гектар — 1 га = | 10 000 м2 |
| Ар (сотка) — 1 а = | 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м) |
| 1 м2; | |
| Квадратный сантиметр, 10 000 см2 = | 1 м2; |
| Квадратный миллиметр, 1 000 000 мм2 = | 1 м2. |
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
Сегодня мы научимся быстро без калькулятора возводить большие выражения в квадрат. Под большими я подразумеваю числа в пределах от десяти до ста. Большие выражения крайне редко встречаются в настоящих задачах, а значения меньше десяти вы и так умеете считать, потому что это обычная таблица умножения. Материал сегодняшнего урока будет полезен достаточно опытным ученикам, потому что начинающие ученики просто не оценят скорость и эффективность этого приема.
Для начала давайте разберемся вообще, о чем идет речь. Предлагаю для примера сделать возведение произвольного числового выражения, как мы обычно это делаем. Скажем, 34. Возводим его, умножив само на себя столбиком:
\[{{34}^{2}}=\times \frac{34}{\frac{34}{+\frac{136}{\frac{102}{1156}}}}\]
1156 — это и есть квадрат 34.
Проблему данного способа можно описать двумя пунктами:
1) он требует письменного оформления;
2) в процессе вычисления очень легко допустить ошибку.
Сегодня мы научимся быстрому умножению без калькулятора, устно и практически без ошибок.
Итак, приступим. Для работы нам потребуется формула квадрата суммы и разности. Давайте запишем их:
\[{{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\]
\[{{(a-b)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\]
Что нам это дает? Дело в том, что любое значение в пределах от 10 до 100 представимо в виде числа $a$, которое делится на 10, и числа $b$, которое является остатком от деления на 10.
Например, 28 можно представить в следующем виде:
\[\begin{align}& {{28}^{2}} \\& 20+8 \\& 30-2 \\\end{align}\]
Аналогично представляем оставшиеся примеры:
\[\begin{align}& {{51}^{2}} \\& 50+1 \\& 60-9 \\\end{align}\]
\[\begin{align}& {{42}^{2}} \\& 40+2 \\& 50-8 \\\end{align}\]
\[\begin{align}& {{42}^{2}} \\& 40+2 \\& 50-8 \\\end{align}\]
\[\begin{align}& {{77}^{2}} \\& 70+7 \\& 80-3 \\\end{align}\]
\[\begin{align}& {{21}^{2}} \\& 20+1 \\& 30-9 \\\end{align}\]
\[\begin{align}& {{26}^{2}} \\& 20+6 \\& 30-4 \\\end{align}\]
\[\begin{align}& {{39}^{2}} \\& 30+9 \\& 40-1 \\\end{align}\]
\[\begin{align}& {{81}^{2}} \\& 80+1 \\& 90-9 \\\end{align}\]
Что дает нам такое представление? Дело в том, что при сумме или разности, мы можем применить вышеописанные выкладки. Разумеется, чтобы сократить вычисления, для каждого из элементов следует выбрать выражение с наименьшим вторым слагаемым. Например, из вариантов $20+8$ и $30-2$ следует выбрать вариант $30-2$.
Аналогично выбираем варианты и для остальных примеров:
\[\begin{align}& {{28}^{2}} \\& 30-2 \\\end{align}\]
\[\begin{align}& {{51}^{2}} \\& 50+1 \\\end{align}\]
\[\begin{align}& {{42}^{2}} \\& 40+2 \\\end{align}\]
\[\begin{align}& {{77}^{2}} \\& 80-3 \\\end{align}\]
\[\begin{align}& {{21}^{2}} \\& 20+1 \\\end{align}\]
\[\begin{align}& {{26}^{2}} \\& 30-4 \\\end{align}\]
\[\begin{align}& {{39}^{2}} \\& 40-1 \\\end{align}\]
\[\begin{align}& {{81}^{2}} \\& 80+1 \\\end{align}\]
Почему следует стремиться к уменьшению второго слагаемого при быстром умножении? Все дело в исходных выкладках квадрата суммы и разности. Дело в том, что слагаемое $2ab$ с плюсом или с минусом труднее всего считается при решении настоящих задач. И если множитель $a$, кратный 10, всегда перемножается легко, то вот с множителем $b$, который является числом в пределах от одного до десяти, у многих учеников регулярно возникают затруднения.
Можете самостоятельно попробовать рассчитать оба разложения, и вы убедитесь, что разложение с наименьшим вторым слагаемым считается проще. А мы перейдем к примерам, которые посчитаем без калькулятора:
\[{{28}^{2}}={{(30-2)}^{2}}=200-120+4=784\]
\[{{51}^{2}}={{(50+1)}^{2}}=2500+100+1=2601\]
\[{{42}^{2}}={{(40+2)}^{2}}=1600+160+4=1764\]
\[{{77}^{2}}={{(80-3)}^{2}}=6400-480+9=5929\]
\[{{21}^{2}}={{(20+1)}^{2}}=400+40+1=441\]
\[{{26}^{2}}={{(30-4)}^{2}}=900-240+16=676\]
\[{{39}^{2}}={{(40-1)}^{2}}=1600-80+1=1521\]
\[{{81}^{2}}={{(80+1)}^{2}}=6400+160+1=6561\]
Вот так за три минуты мы сделали умножение восьми примеров. Это меньше 25 секунд на каждое выражение. В реальности после небольшой тренировки вы будете считать еще быстрее. На подсчет любого двухзначного выражения у вас будет уходить не более пяти-шести секунд.
Но и это еще не все. Для тех, кому показанный прием кажется недостаточно быстрым и недостаточно крутым, предлагаю еще более быстрый способ умножения, который однако работает не для всех заданий, а лишь для тех, которые на единицу отличаются от кратных 10. В нашем уроке таких значений четыре: 51, 21, 81 и 39.
Казалось бы, куда уж быстрее, мы и так считаем их буквально в пару строчек. Но, на самом деле, ускориться можно, и делается это следующим образом. Записываем значение, кратное десяти, которое наиболее близкое нужному. Например, возьмем 51. Поэтому для начала возведем пятьдесят:
\[{{50}^{2}}=2500\]
Значения, кратные десяти, поддаются возведению в квадрат намного проще. А теперь к исходному выражению просто добавляем пятьдесят и 51. Ответ получится тот же самый:
\[{{51}^{2}}=2500+50+51=2601\]
И так со всеми числами, отличающимися на единицу.
Если значение, которое мы ищем, больше, чем то, которое мы считаем, то к полученному квадрату мы прибавляем числа. Если же искомое число меньше, как в случае с 39, то при выполнении действия, из квадрата нужно вычесть значение. Давайте потренируемся без использования калькулятора:
\[{{21}^{2}}=400+20+21=441\]
\[{{39}^{2}}=1600-40-39=1521\]
\[{{81}^{2}}=6400+80+81=6561\]
Как видите, во всех случаях ответы получаются одинаковыми. Более того, данный прием применим к любым смежным значениям. Например:
\[\begin{align}& {{26}^{2}}=625+25+26=676 \\& 26=25+1 \\\end{align}\]
При этом нам совсем не нужно вспоминать выкладки квадратов суммы и разности и использовать калькулятор. Скорость работы выше всяких похвал. Поэтому запоминайте, тренируйтесь и используйте на практике.
Ключевые моменты
С помощью этого приема вы сможете легко делать умножение любых натуральных чисел в пределах от 10 до 100. Причем все расчеты выполняются устно, без калькулятора и даже без бумаги!
Для начала запомните квадраты значений, кратных 10:
\[\begin{align}& {{10}^{2}}=100,{{20}^{2}}=400,{{30}^{2}}=900,…, \\& {{80}^{2}}=6400,{{90}^{2}}=8100. \\\end{align}\]
Далее — выкладки квадрата суммы или разности, в зависимости от того, к какому опорному значению ближе наше искомое выражение. Например:
\[\begin{align}& {{34}^{2}}={{(30+4)}^{2}}={{30}^{2}}+2\cdot 30\cdot 4+{{4}^{2}}= \\& =900+240+16=1156; \\\end{align}\]
\[\begin{align}& {{27}^{2}}={{(30-3)}^{2}}={{30}^{2}}-2\cdot 30\cdot 3+{{3}^{2}}= \\& =900-180+9=729. \\\end{align}\]
Как считать еще быстрее
Но это еще не все! С помощью данных выражений моментально можно сделать возведение в квадрат чисел, «смежных» с опорными. Например, мы знаем 152 (опорное значение), а надо найти 142 (смежное число, которое на единицу меньше опорного). Давайте запишем:
\[\begin{align}& {{14}^{2}}={{15}^{2}}-14-15= \\& =225-29=196. \\\end{align}\]
Обратите внимание: никакой мистики! Квадраты чисел, отличающиеся на 1, действительно получаются из умножения самих на себя опорных чисел, если вычесть или добавить два значения:
\[\begin{align}& {{31}^{2}}={{30}^{2}}+30+31= \\& =900+61=961. \\\end{align}\]
Почему так происходит? Давайте запишем формулу квадрата суммы (и разности). Пусть $n$ — наше опорное значение. Тогда они считаются так:
\[\begin{align}& {{(n-1)}^{2}}=(n-1)(n-1)= \\& =(n-1)\cdot n-(n-1)= \\& =={{n}^{2}}-n-(n-1) \\\end{align}\]
— это и есть формула.
\[\begin{align}& {{(n+1)}^{2}}=(n+1)(n+1)= \\& =(n+1)\cdot n+(n+1)= \\& ={{n}^{2}}+n+(n+1) \\\end{align}\]
— аналогичная формула для чисел, больших на 1.
Надеюсь, данный прием сэкономит вам время на всех ответственных контрольных и экзаменах по математике. А у меня на этом все. До встречи!
Смотрите также:
- Что такое числовая дробь

- Задача B1 — время, числа и проценты

- Пробный ЕГЭ 2012. Вариант 7 (без производных)

- Специфика работы с логарифмами в задаче B15

- Задача C1: тригонометрия и показательная функция — 1 вариант

При ремонте, покупке материалов нужно знать площадь помещений. Говорят еще «квадратура». Как посчитать площадь комнаты в квадратных метрах, что для этого нужно — будем рассматривать в статье.
Содержание статьи
Немного теории
Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.
 Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний
Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знанийЧто такое 1 см² и 1 м²
Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.
 Что такое один квадратный сантиметр
Что такое один квадратный сантиметрОдин квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м². В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².
Формулы
Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.
 При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата
При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадратаНадо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.
- Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
- Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
- Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².
В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.
Простейший калкулятор для расчета площади прямоугольной комнаты.
Перевод квадратных сантиметров в квадратные метры
Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:
- 80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
- 322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².
- 60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².
Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.
 Соотношение квадратных сантиметров и квадратных метров
Соотношение квадратных сантиметров и квадратных метровЕсли же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:
- 4000 см² / 10000 = 0,4 м²;
- 96000 см² / 10000 = 9,6 м²;
- 3600 см²/ 10000 = 0,36 м².
Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно. Нужно будет предварительно провести измерения, а потом заняться расчетами.
Как посчитать площадь комнаты в квадратных метрах
Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).
 Можно найти площадь комнаты зная длину и ширину
Можно найти площадь комнаты зная длину и ширинуИзмерения
Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.
 Схема комнаты с нанесенными измерениями
Схема комнаты с нанесенными измерениямиНа схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.
Как высчитать квадратуру комнаты
Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола. Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку. Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.
Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры. Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.
 Как найти площадь комнаты сложной формы
Как найти площадь комнаты сложной формы- Считаем большой прямоугольник: 5 м * 4,35 м = 21,75 м².
- Находим квадратуру маленького: 2,5 м * 2,65 м = 6,625 м².
- Площадь пола в этом помещении равна сумме 21,75 м² + 6,625 м² = 28,375 м².
При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.
Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.
 Получается, ищем площадь трех прямоугольников
Получается, ищем площадь трех прямоугольниковА недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.
Приведем пример расчета подставляя произвольные значения:
- Большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Для простоты округлим до 3,38 м².
- Средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м². Снова округлим до 0,67 м².
- Самый маленький прямоугольник (в нашем случае это будет квадрат): 0,57 м *0,57 м = 0,3249 м2, после округления имеем 0,33 м².
- Чтобы найти общую площадь складываем квадратуру двух прямоугольников и добавляем половину площади последнего, самого маленького участка. 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².
Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.
Площадь квартиры
Так как ремонт — это «бедствие», которое периодически нас посещает, лучше сделать план всей квартиры с подробными замерами. На этом же плане проставьте площади каждого помещения. После того, как рассчитаете квадратуру всех комнат, сложите цифры и получите метраж квартиры.
 Для плана лучше рассчитать метраж каждой комнаты
Для плана лучше рассчитать метраж каждой комнатыОдин вариант может быть как на рисунке выше — для того, чтобы знать именно площади каждого помещения. Это потребуется для закупки материалов. Но нужен будет еще план, на котором будут все длины. Простенки, ширина окон, дверей и т.д. Это потребуется, например, для разработки схем укладки ламината, напольной плитки или других покрытий. Нужен будет такой план и при планировании теплого пола.
Есть, кстати, приложение-калькулятор для телефона, при помощи которого все вычисления сделать очень просто.
При проведении ремонтных работ возникает вопрос: квадратный метр – это сколько необходимо материалов, чтобы его покрыть.
Чтобы не потратить лишние деньги, лучше для начала произвести расчет квадратных метров комнаты и только потом отправляться в магазин с конкретными требованиями.
На упаковках с красками, штукатуркой, грунтовкой обязательно обозначено, на какой размер помещения рассчитано данное количество смеси.
Главный вопрос – сколько необходимо упаковок или банок, чтобы хватило на площадь стен или пола.
Что такое квадратный метр
Для начала надо определиться, что из себя представляет квадратный метр. Люди, которые плохо учили в школе математику, все равно рано или поздно сталкиваются с проблемой подсчета количества строительных материалов. Поэтому квадратный метр – основная точка отсчета при определении площади помещения.
Если нарисовать квадрат (это геометрическая фигура с одинаковыми сторонами), и сторона будет равна 100 см, то при умножении на 100 получим число 10000 см. это означает, что размер данной фигуры 10000 см2. Можно проще. Посчитать в метрах: 100 см – это 1 м. Применяем формулу подсчета площади – перемножаем две стороны, то есть 1 умножаем на 1, получаем 1 м. Значит, размер квадрата 1 кв.м.
Инструменты для подсчета квадратных метров
Для вычислений необходимо подготовить калькулятор.
Если его нет, тогда таблицу умножения на обычной тетради для первоклассника.
Если стены имеют не 2, не 3 метра, а, например 2,5 метра, то лучше все-таки калькулятор. Это чересчур сложная нагрузка для мозга, который не привык работать с цифрами.
Желательно иметь под руками листок бумаги и ручку для записи.
Измерять необходимо рулеткой или сантиметром.
Формула подсчета квадратных метров
Чтобы рассчитать площадь, необходимо применить формулу квадратного метра А X B, где число А – это длина одной стороны, а число В – длина второй стороны. Они могут быть одинаковы, если форма пола или стены квадратная.
Чаще всего она не квадратная, а прямоугольная, то есть число А будет иметь одно значение, а число В – другое. Их необходимо будет перемножить в уме, или по таблице умножения, или на калькуляторе. И полученное число будет площадью, которую надо будет покрывать краской или еще чем-нибудь.
Это интересно! Иногда нужно знать как правильно высчитываются размеры. Сколько же дюймов в мм? Об этом можно прочесть в нашей статье.
Бывает, что форма пола не стандартная, а, например, трапециевидная. Тогда сложнее, особенно тем людям, кто не знает, что такое треугольник (такое тоже есть в природе). Чтобы рассчитать размер трапеции, необходимо посчитать сначала площадь прямоугольника в середине, потом величину каждого треугольника по бокам, потом эти три числа сложить. Не легче ли сразу позвать бригаду рабочих? Пускай они думают, как рассчитать квадратные метры комнаты.
Важно! Если на этом этапе возникло непонимание, то лучше сразу позвать учителя математики и попросить подсчитать, сколько кв. метров имеет комната.
Площадь пола или потолка
Потолка и пол в обычной квартире одинаковые. Как посчитать квадратные метры? Очень просто. Если помещение мансардное, тогда потолка там нет – есть только пол и стены.
Этап № 1. Измерить длину комнаты и записать полученное число на бумаге. Если число целое, тогда пишем просто цифру. Например, 5 (м). Если число больше 5, но меньше 6, тогда придется вспомнить десятичные дроби и написать, к примеру, 5,5 (м).
Этап № 2. Измерить ширину комнаты и записать аналогично. К примеру – 3м.
Этап № 3. Теперь необходимо перемножить эти два числа. Пример: 5 x 3 = 15м. Итак, площадь пола – 15 кв. м. Следовательно, размер потолка также будет равняться 15 кв. м. Записать это число отдельно и обвести ручкой.
Площадь сплошной стены
Как вычислить квадратуру сплошной стены? Так же, как мы измеряли пол или потолок. Алгоритм действий тот же, что и при подсчете размера пола:
- измерить длину стены и записать;
- измерить высоту;
- перемножить два числа – полученный результат и будет площадью в квадратных метрах.
Пример: высота 2,20 м, длина 7м. 7 x 2,2 = 15,4 м. Площадь стены – 15,4 кв. м.
Как посчитать квадратные метры стены с окном
Сложнее будет иметь дело со стеной, на которой расположено окно.
В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.
Алгоритм действий:
- По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
- Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
- Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.
Важно! Цифры, которые получаются при подсчетах, обязательно записывать и обводить ручкой, чтобы не потеряться в собственных расчетах.
Как посчитать квадратные метры стены с дверью
Похожие действия необходимо производить, когда требуется высчитать квадратные метры стены с дверью. Если дверь с математической точки зрения простой прямоугольник, то вычисляем ее площадь по обычной формуле А X В. То есть надо измерить высоту и длину, далее числа перемножить и получится размер двери.
Далее из площади стены вычитаем размер двери и получаем квадратуру, на которую необходимо будет покупать отделочные материалы. Если предыдущий хозяин квартиры сделал дверь с аркой, то здесь без вычисления размера круга никак не обойтись.
Измеряем площадь сложных фигур
Круг и треугольник – сложные фигуры для самостоятельного вычисления. Как измерить квадратные метры окружности, если нет математического или инженерного образования? Опять-таки по формуле.
Как измерить размер окружности
Существует формула вычисления площади круга. Есть такое постоянное число – отношение длины окружности к ее диаметру. Оно одинаково для всех размеров круга. Называется оно пи и равняется 3,14. Вот это число и используют при подсчетах.
Этап № 1. Замеряем диаметр (это линия, которая проходит через центр круга от одного края окружности к другому). Пускай диаметр будет равняться 3 м. Далее находим радиус – это половина длины диаметра. То есть 1,5 м. Записываем радиус на бумагу.
Этап № 2. Производим расчеты по формуле S = ПR2, где S – это площадь круга, П – постоянное число, а R – радиус окружности. Получается 3,14 x (1,5 x 1,5) = 7, 065. Площадь данного круга – 7,065 кв. м.
Но это площадь целого круга. Арка над дверью – это половина круга. Значит, еще нужно разделить данное число на два и далее прибавить к прямоугольной площади двери. 7,065 : 2 = 3,53 м2.
Как измерить площадь треугольника
Если предыдущий хозяин квартиры был математик, то он вполне мог сделать на потолке треугольные фигуры, которые приходится реставрировать и выделять другим цветом или штукатуркой. Придется считать, чтобы не переплачивать.
Расчет метра квадратного в треугольной фигуре начинается с внимательного осмотра этой фигуры.
Необходимо найти основание треугольника, то есть линию, на которую опираются две других (как крыша на доме). Далее провести линию из противоположной верхушки к основанию. Эти два числа записать.
- Этап № 1. Разделить основание треугольника на 2 и записать. Это число пригодится в недалеком будущем. Измерить высоту и тоже записать.
- Этап № 2. Произвести расчет м2 фигуры. Для этого необходимо использовать формулу: S = 0,5аh, где S – площадь треугольника, а – основание, а h – высота. Пример: основание 3 м, высота 2,5 м. Итого: 0,5 x 3 x 2,5 = 3,75. Размер треугольника – 3,75 м2. Записать, чтобы не забыть.
Советы и рекомендации
Таким образом можно высчитать площадь всей квартиры и расписать, что и каким цветом красить. Размеры всех стен и потолка сложить – получится число, на которое надо будет ориентироваться при покупке стройматериалов.
Совет! При расчетах лучше пригласить еще одного человека в помощь. Одна голова хорошо, а две надежнее.
Дело за малым – пойти в магазин и купить материалы. Здесь еще придется считать, так как не все упаковки предназначены для больших помещений. К примеру, размер потолка на кухне 3 x 3. Сколько квадратных метров штукатурки понадобится, если одной упаковкой можно покрыть 3 кв. м? Считаем: размер потолка 9 кв. м. Одна упаковка уходит на 3 кв. м. Следовательно, на весь потолок необходимо 3 пачки.
Если на упаковке написано, что расход на 12 квадратных метров, это означает, сколько материала надо, чтобы покрыть стену размером 3 x 4 м.
Или другой пример. Стена в квартире 6 на 4. Сколько квадратных метров необходимо закрасить? Умножаем 6 на 4, получаем 24 квадратных метра. Это сколько нужно банок краски по 3 л, если каждая банка расходуется на 6 кв. м? Считаем: 24 делим на 6. Получается 4. Значит, необходимо купить 4 трехлитровых банки краски для покрытия всей стены.
Для ремонтных работ всегда лучше взять немного больше материалов, чтобы потом не идти лишний раз в магазин. В будущем, если придется что-то подкрасить или подбелить, остатки материалов могут здорово выручить.
Видео по теме: квадратные метры в помещении
Главная » Разное » Как посчитать квадратуру комнаты, стен, потолка, пола
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.

Часто требуется посчитать кубатуру комнаты, ее объем
Площадь комнаты в квадратных метрах
Содержание статьи
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.

Как посчитать площадь комнаты неправильной формы
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Удобнее всего размеры наносить на план
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,75 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты

Формула расчета объема комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
Для чего в обыденной жизни могут пригодиться расчеты площади и объема помещений?
- Для планирования ремонта и покупки нужных материалов.
- В случае, когда для ремонтных и строительных работ нанимаются специалисты – они берут оплату по метражу, за каждый квадрат. В таких случаях велика вероятность обмана. Чтобы не пришлось платить им лишнее, а заодно и контролировать их работу и текущие расходы, нужно самому уметь вычислять площадь помещения и рассчитывать затраты, исходя из имеющихся величин.
- При покупке, продаже или аренде также важно уметь работать со схемами и чертежами, знать расчеты площадей и объемов, уметь их определять в документации.
- По поводу освещения – существуют определенные нормативы. Дабы им следовать в процессе установки осветительных приборов, нужно также уметь вычислять площадь.
- Когда есть замеры и вычислена площадь комнаты – проще выяснить и величину объема. Эти цифры нужны для установки оборудования сплит-систем, кондиционеров и так далее.
Чтобы правильно рассчитать объем и площадь помещения, нужно просто следовать формуле.
Как посчитать квадратные метры комнаты
В каких случаях требуется квадратура помещения:
- При установке на кухню модуля из шкафов.
- При оплате коммунальных услуг, где сумма рассчитывается исходя из метража.
- При оплате рабочим после ремонта. Их тарифы также привязаны к площадям и количеству метров.
- При определении нормативов освещения вычисляется площадь.
- При установке отопления, вентиляции и кондиционирования требуется знать объем (кубатуру) помещения. Он вычисляется с помощью величины площади.
- При расчете количества закупаемых материалов для планируемого ремонта.
Чтобы правильно высчитать необходимые величины нужно знать несколько формул и уметь с их помощью рассчитать квадратные метры стен, потолка и пола.

Квадратура помещения нужна при оплате коммунальных услуг, определении нормативов освещения, установке отопления и покупке материалов для ремонта.
Для этого потребуются простейшие инструменты:
- Рулетка. Механическая, размером от 3 до 5 метров. Ею измерять лучше вдвоем, чтобы избежать погрешностей. Минимальная единица измерения – миллиметр. Электронная, измеряет лазерным лучом. Получить измерительную величину можно просто направив луч в начальную точку. Единица измерения здесь – миллиметр или сантиметр.
Некоторые «умные» рулетки могут сразу высчитывать площадь помещения, не измеряя дополнительно что-то. С измерениями такой рулеткой можно справиться в одиночку, без дополнительной помощи. Плюс в быстроте измерений и расчетов. Минус в дороговизне и проблемах с измерением неправильных помещений.
- Калькулятор. Также для удобства в расчетах разработаны специальные компьютерные программы.
- Угольник строительный. Должен быть с длинными сторонами – в этом случае замеры получатся более точными.
- Блокнот или тетрадь для занесения всех схем, измерений, расчетов.
- Уровень. С его помощью можно рассчитать отклонения вертикали/горизонтали.

Прежде чем приступить к измерениям и расчетам, нужно подготовить все необходимые инструменты.
- Первое, что нужно сделать – это узнать, как рассчитывается квадратный метр. Здесь пригодится рулетка со шкалой в сантиметрах и метрах.
- Затем измеряется длина помещения и его ширина. Причем, ширина измеряется, прикладывая рулетку строго перпендикулярно длине.
- Измерения записываются вплоть до сантиметра. В сторону метров округлять не стоит.

Для измерения размеров помещения нужна обычная рулетка. Но существуют и “умные рулетки”. Они могут сразу высчитывать общую площадь.
Чтобы рассчитать квадраты на калькуляторе, нужно измеренную величину записать следующим образом: 1м=0.01 см. Если предположить, что длина комнаты – 3 метра 56 см, то на калькуляторе набрать 3,56. То же самое касается и ширины. В итоге, умножить длину комнаты на ее же ширину и получить величину квадратуры измеряемого помещения.

Для расчетов вам понадобится калькулятор и знание формул.
Для того, чтобы корректно измерить помещение, желательно освободить хотя бы две ее стороны от мебели и лишних предметов. В этом случае идеально измерять комнату на стадии ремонта.
Рулетка должна хорошо прилегать к измеряемой поверхности. Длину требуется измерить вдоль стены (или стен, если форма измеряемой фигуры не правильная). В начале измерений лучше проверить прямоугольность, измерив рулеткой диагонали помещения и сравнив цифры. Таким образом уточняется правильность формы.

Можно воспользоваться лазерной рулеткой. Такие дальномеры стали незаменимыми помощниками специалистов и умеют запоминать измерения и вычислять по ним площадь или кубатуру помещения.
А вот чтобы проверить прямые линии понадобится уровень. Реже большой строительный угольник или самодельный циркуль.

Уровень – инструмент для оценки соответствия поверхностей вертикальной и горизонтальной плоскости относительно земли.
Расчеты можно сразу переносить на схему. Обязательно измерять помещение несколько раз, во избежание ошибок. Во время замеров быть внимательным и собранным, следить абсолютно за всеми мелочами, которые могут повлиять на величины.
Площадь комнаты можно вычислить с помощью простой школьной формулы:
S=A*B.
- S – площадь;
- A – длина;
- B – ширина.
Подобным же образом можно вычислить и площадь каждой стены, пола и потолка.
В случае если помещение треугольной формы – нужно измерить длину и ширину, умножить друг на друга и разделить на 2.
Или по формуле:
S = (А*В)/2.

Площадь комнаты можно вычислить с помощью простой школьной формулы.
Как переводить квадратные метры и сантиметры
При замере помещений работать приходится с сотнями и тысячами сантиметров. Для удобства их переводят в метры. Например, расчет площади комнаты – 200 см * на 200 см = 40000 см.кв. Получается не маленькое число, которое следует разделить на 10000. Получается 4 м.кв.
Основные формулы расчета площадей разных фигур
- Прямоугольник – S=A*B.
- Квадрат – S=A2.
- Круг – S=nR2.
- Треугольник – S=(A*B)/2.

Помимо самостоятельных расчетов для вычисления площади и кубатуры можно воспользоваться специальными онлайн-калькуляторами.
Форма рассчитываемого помещения
Квадрат и прямоугольник
Это чуть ли не самые встречаемые в строительстве формами комнат. По вышеописанному принципу можно узнать их площади. В том случае, если есть выступы, колонны или другие архитектурные нюансы – нужно их обмерить и перемножить. В результате из общей площади вычитаются результаты замеров строительных элементов. Полученная цифра и является верной величиной.
Помимо часто встречаемых квадратных и прямоугольных комнат существуют еще и помещения «неправильной формы». К ним относятся следующие.

Чтобы рассчитать площадь квадратной комнаты, нужны школьные знания и минимальный набор инструментов.
Трапециевидные
Как считать площадь комнаты трапеции? Для этого нужно измерить две ее параллельные стены и высоту (Н), перпендикулярную им.
Высоту следует измерить в нескольких местах, чтобы убедиться в параллельности стен.
Формула, по которой затем вычисляется площадь трапеции:
S=1/2(A+B)*H

Вам понадобится рулетка, карандаш или ручка и лист бумаги.
С выступом
- Измерить длину и ширину комнаты без выступа.
- Измерить длину и ширину самого выступа.
- Вычислить обе площади и сложить.
В результате получается показатель общей площади.
С нишей
- Измерить длину и ширину общей площади.
- Измерить длину и ширину ниши.
- Рассчитать оба показателя и из общей площади вычесть площадь ниши.

Измерить площадь помещения не так уж и сложно. Главное, придерживаться всех правил.
Круглая
Для того, чтобы рассчитать площадь круга, нужно найти его радиус, высоту, длину хорды. Для расчета значения используется формула: S=n(R*R)/2, где S – площадь, n – число пи (3,14) и R – радиус.
Если у имеющейся квадратуры есть круглые элементы или колонны и их площадь нужно вычесть, при этом нельзя изменить радиус или диаметр, тогда измеряется длина окружности и применяется формула S=(P*P)/4n.

Чтобы рассчитать площадь круглого помещения, нужно найти радиус, высоту и длину хорды.
Полукруглая
Как высчитать квадратные метры комнаты, если она содержит в себе полукруг? Расчеты требуется производить после того, как этот элемент разбит на полукруг и прямоугольник. Посчитать обе площади и сложить сумму.
Части помещения с круглой и полукруглой формой можно измерить гибкой рулеткой или веревкой.
Такие формы жилищ встречаются с арками, эркерами, полукруглыми балконами и т.д.

Круглые или полукруглые формы можно измерить гибкой рулеткой или веревкой.
Как посчитать площадь стен
Такая информация требуется при покупке обоев, краски или отделочных материалов для стен.
Для этого нужно найти периметр комнаты. Из школьной программы известно, как его получить – сложить между собой сумму длин всех сторон. В данном случае следует измерить две длины смежных стен, сложить их и умножить вдвое.

Из школьной программы известно, что периметр можно найти, если сложить между собой сумму длин всех сторон.
Помимо длины и ширины стен, здесь необходима информация о высоте, длине и ширине имеющихся проемов дверей и окон.
Стену с окнами измеряют следующим образом: вычисляют общую площадь помещения, затем площадь окон и дверей и вычитают этот результат из общего. Если окно на стене не одно или с дверью – то складывают между собой площади всех проемов и вычитают их из общей.

Измерить стену с окнами не так уж и сложно. Из общей площади следует высчитать площадь окон и дверей.
Глухую стену измерить проще, и вычисляется она как площадь пола. Измеряется и длина, и высота стены, показатели умножают друг на друга. Стены мансарды или подобные – с неровностями и изломами разбиваются на правильные фигуры, и подсчитывается площадь каждой из них. После чего они складываются вместе.
После того, как подсчитаны площади всех стен – глухих, с окнами и дверьми, остается сложить их между собой – в результате получена общая площадь стен.

Если вам сложно разобраться в нюансах, можно пригласить специалистов, которые выполнят все расчеты быстро и точно.
Помещение с разноуровневым зонированием
При таком раскладе нужно действовать следующим образом:
- Все участки и элементы стен нужно померить.
- Измерить пол и вычислить его площадь.
- Измерить каждый вертикальный участок – нужны их высота и длина. Полученные величины перемножить.
- К полученному результату прибавить площадь пола.

Один из вариантов разноуровневого зонирования помещения.
Как посчитать площадь пола
Площадь пола принято считать без учета построек на нем в виде печи или камина. Для этого нужно вычислить, замерив всю площадь пола. Затем замерить площадь ненужного объекта. В конце вычесть из площади пола площадь объекта.

Для расчета площади пола важно знать его длину и ширину. Их можно измерить самостоятельно или подсмотреть в плане.
Площадь стен. Расчет на калькуляторе
Большое подспорье в расчетах дают специальные программы. Такие как онлайн-калькулятор. Он вычислит площадь, кубатуру и рассчитает сколько потребуется отделочных материалов для планируемого ремонта.
Например, чтобы посчитать площадь стены, вычтя проемы окна и двери, можно ввести ширину стены, длину, высоту, размеры окна и двери и их количество. Подобрать нужную формулу и готово.
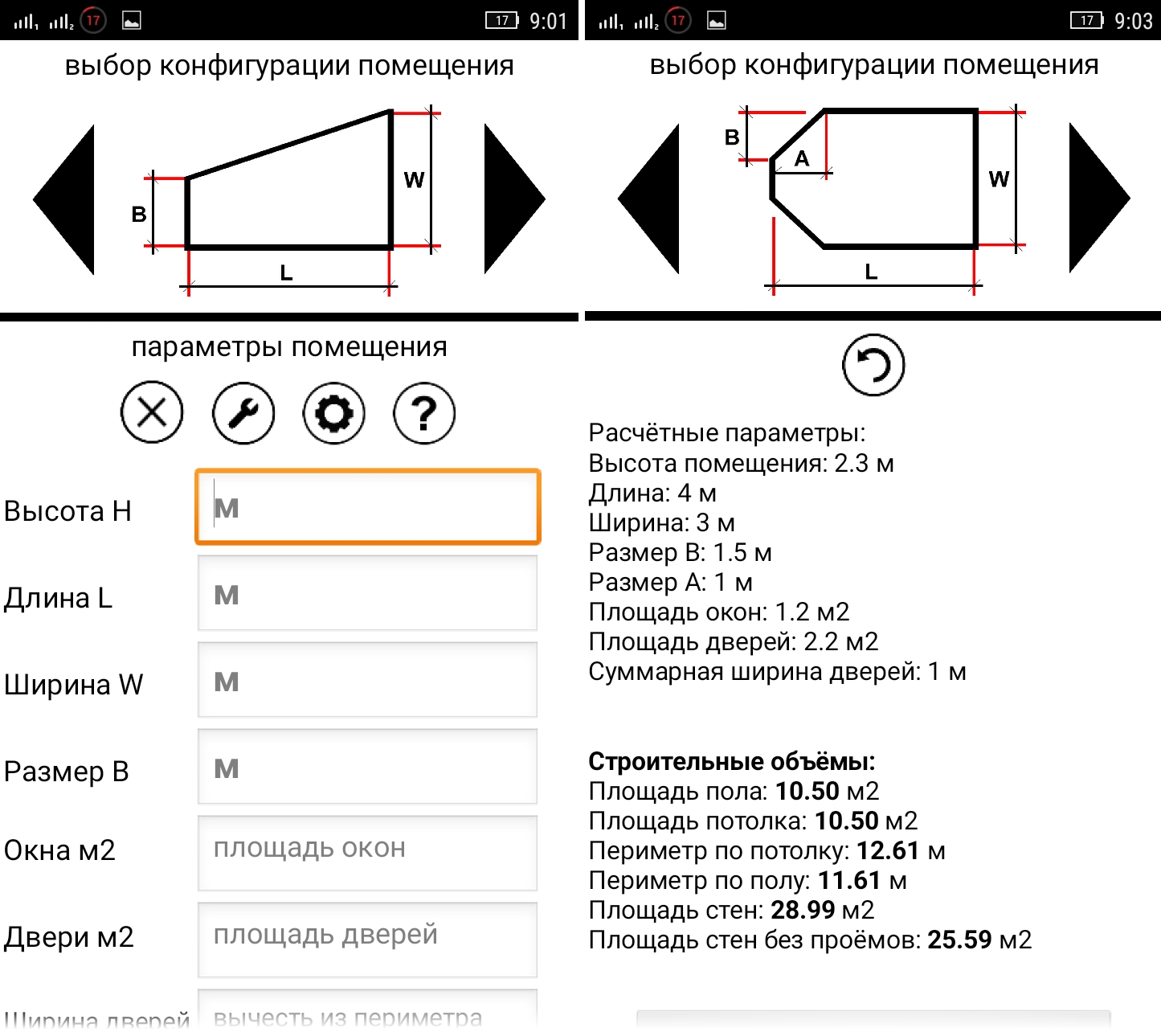
Благодаря онлайн-калькулятору вы легко и быстро сможете произвести расчет площади вашего помещения.
Нюансы расчета площади
В строящихся домах или новостройках замерами квартир занимается специалист. Все замеры производятся строго по правилам. Если произойдет какое-либо нарушение, то это повлечет за собой неправильные расчеты налога, а также в будущем возникнуть сложности при перепланировке.
Все замеры и схемы кадастровый инженер отображает в техпаспорте квартиры. Все происходит под наблюдением соответствующих органов. Также, информация о метраже отражается в договоре купли-продажи, в дарственной и при приватизации жилья.

В новостройках все замеры помещения производятся кадастровым инженером.
При перепланировке получают разрешение, где указывают точные величины замеров комнат в квартире.
Коммунальные платежи тоже рассчитываются исходя из метража квартиры, ее площади.
Существуют определения жилой и общей площади помещения:
- Жилая площадь – это сумма всех спален и гостиной в доме или квартире.
- Когда в документах прописывают общую площадь – это означает, что учтены замеры абсолютно всех помещений объекта. Но здесь важно знать – входит ли, например, в эту площадь балкон или лоджия, так как такие помещения (кухня, туалет, ванная и подсобки) обычно измеряются отдельно.
Все эти вычисления производятся в стандартных домах. Неотапливаемые помещения также учитываются в документации, и им присуждается пониженный коэффициент:
- Балконы и террасы – 0,3.
- Пристройки снаружи – 0,4.
- Балконы и лоджии – 0,5.
- Веранда – 0,8.
В старых домах и современных новостройках есть встроенные шкафы, которые при расчете жилой площади не учитываются, но включены в состав общей площади жилья. Этот нюанс важно помнить, когда потребуется верная величина площади квартиры.
Как определить кубатуру комнаты
Для того, чтобы высчитать объем комнаты нужно площадь ее умножить на высоту.
Есть еще один способ расчета. Для этого нужно:
- Измерить длину большей стены. Произвести это либо по самой стене, убрав лишние предметы, либо по полу.
- Измерить длину меньшей стены.
- Измерить высоту потолков. Для этого достаточно зацепить носик ленты рулетки за выступающую часть бордюра. Если таковой возможности нет – привлекается вся семья. Показатель записывается без округлений – до миллиметра.
- Полученные измерения перемножить между собой, получив требуемую величину.
Оба способа в результате дают один и тот же результат.

Существуют два способа определения кубатуры комнаты.
Но не нужно забывать, что комнаты не всегда имеют правильную прямоугольную или квадратную формы. Бывает, что нужно определить объем в комнате с многоуровневыми потолками, нишами, выступами и т.д.
Также как и при замере квадратуры – комнату придется разбить на несколько правильных фигур и каждую замерить. Вычислить объемы и сложить их между собой с помощью первого или второго способа расчетов.
Что делать если в объекте потолки разной высоты?
Измерить каждую комнату отдельно. Потом сложить все результаты, получив общий объем помещений.

Часто стены и потолок не имеют ровной квадратной формы. Для измерения площади комнаты со скошенным потолком потребуется отдельный способ вычислений.
Что делать если потолок в виде арки?
Здесь пригодится формула, с помощью которой рассчитывают объем цилиндра: V=n*R2*H.
- H – высота измеряемого цилиндра.
- R – радиус цилиндра в квадрате.
- n – число пи.
После вычисления объема цилиндра нужно вычесть из него лишнюю часть объема – пол.

Так выглядит потолок в виде арки. Расчеты здесь не сложные и основаны на использовании формул, которым учат в школе.
Комната неправильной формы
Если комната, например, с нишей, то в этом случае считаются отдельно параметры ниши и параметры комнаты. Потом из общего объема вычитается объем ниши.
Полезные советы
- Идеальные параметры помещений редко когда найдешь. Потому, измерять нужную комнату положено в нескольких местах и выводить из этого среднее арифметическое значение. Кроме того, замеры производятся несколько раз, чтобы избежать ошибок и недочетов.
- Периметр помещения с многочисленными неровностями и выступами проще измерить, если протянуть вдоль него шнур или веревку. Потом измерить его длину.
- Подсчеты лучше всего сразу отображать на листе бумаги в виде схемы – это поможет в дальнейшем ремонте и при выборе строительных и отделочных материалов. Если показать схему продавцу-консультанту – он грамотно подберет требуемое количество с учетом стыков и запаса, ориентируясь по метражу помещения.

Измерять комнату необходимо в нескольких местах и выводить из этого среднее арифметическое значение.
Строительство и ремонт – трудоемкий процесс, который требует не только физической и умственной работы, но и немалых материальных затрат. Качественно сделанные замеры помещений помогут вложить минимум усилий и денег.
Некачественные замеры растянут ремонт на длительный период, повлечет за собой проблемы и неудобства. Приведенные выше рекомендации и советы обучат, помогут и в чем-то облегчат жизнь участников этого непростого и интересного дела.
Видео: как посчитать площадь стен и рассчитать количество краски
Как узнать площадь комнаты в квадратных метрах
Можно поступить еще проще и просто все стороны помещения перемножить: потолок, пол, стены.
Перевод квадратных сантиметров в квадратные метры
Перед тем, как узнать сколько в комнате квадратных метров, очень важно разобраться в самих значениях, ведь когда идет расчет с сотнями сантиметров, их в любом случае необходимо переводить в метры. Делается это по следующей формуле, уже на известном примере: 160 см * 100 см – разница величин (в одном метре – 100 сантиметров), в итоге получается 16000 см2, которые нужно разделить на 10000 и получим = 1.60 м2.
Такими цифрами намного проще оперировать и запоминать. Тем более, что «квадратуру» помещения всегда измеряют именно в метрах. Для перевода необходимо подставлять следующие формулы:
- 8000 см² / 10000 = 0,8 м²;
- 34000 см² / 10000 = 3,4 м²;
- 2400 см²/ 10000 = 0,24 м².
Все достаточно просто и не составит труда составить такие несложные арифметические вычисления, даже школьнику. Очень важно перед тем, как узнать квадратуру комнаты, провести максимально точные измерения, после чего приступить к расчетам.
Как посчитать площадь комнаты в квадратных метрах
Необходимость в расчете площади возникает зачастую только во время ремонтных работ, строительства или при смене мебели. Практически все строительные материалы (например напольное покрытие) исчисляется в квадратных метрах. Для правильного расчета количества материала, важно знать площадь пола. Зная ширину и длину комнаты, найти площадь не вызовет никаких сложностей.
Измерения
Перед тем как измерить комнату в квадратных метрах, необходим минимальный набор предметов:
- калькулятор;
- рулетка;
- карандаш;
- лист бумаги.
На бумаге необходимо сделать подробный план помещения. Каждая стена должна быть измерена с использованием рулетки.
Внимание! Очень важно делать измерения на уровне пола, ведь бывают случаи (особенно в старых домах), когда стены немного завалены в одну из сторон. Так как происходит измерение пола, необходимо измерять с максимальным прилеганием к стенам.
Вторым этапом является проставление полученных измерений на плане. Лучше всего сразу делать это в метрах, но точность каждого замера должна быть до 1 сантиметра. Это необходимо для того, чтобы при выборе необходимого количества материалов, удалось максимально точно подобрать метраж требуемого материала. Рулонные напольные покрытия продаются в погонных метрах.


Округлять можно только в случае небольшого увеличения, чтобы в случае непредвиденных обстоятельство, было достаточное количество материала.
Как высчитать квадратуру комнаты
Чтобы понять, как узнать общую площадь комнаты, необходимо воспользоваться простой формулой и перемножить показания длины на ширину. Как показано на рисунке длинная стена имеет длину в 7 метров а противоположная только 4. Выходит площадь пола будет равна 28 м2. Именно таким образом и находят квадратуру. Обязательно требуется помнить о небольшом запасе, который потребуется для подгонки и подрезки, причем чем сложнее будет вариант укладки, тем больше потребуется брать запас.


Зачастую комнаты не имеют ровной квадратной или прямоугольной формы.Поэтому, перед тем как узнать площадь комнаты в квадратных метрах, необходимо просто разбить комнату на несколько простых фигур (квадраты и прямоугольники) и после считают общую квадратуру. Так например для комнаты у которой форма буквы Г, достаточно разбить ее на 2 прямоугольника, отдельно посчитать площадь, а потом сложить.
Выглядит это все следующим образом:
- вычисляем квадратуру большого прямоугольника: 5 умножаем на 4,35 и получаем 21,75 квадратных метров;
- теперь по тому же принципу второй: 2,5 на 2,65 и получаем 6,625 квадратов;
- далее суммируем общий результат 6,625 + 21,75 и получаем площадь комнаты в размере 28,375 квадратных метров.
Имея на руках полученный точный результат, можно немного округлить его в большую сторону и учитывать 28,4 квадратных метра.


В том случае, если комната имеет участок со срезанной стеной, как показано на картинке, тогда необходимо нарисовать прямоугольник таким образом, чтобы косая делила его на 2 треугольника. Тогда опять получается помещение по форме буквы Г. Далее можно вычислить площадь, по выше представленному методу.
Необходимо будет найти площадь трех прямоугольников. Недостающий участок – половина маленького прямоугольника. Достаточно будет просто найти его площадь и разделить на 2, после чего прибавить к остальным размерам.
Итак, для примера можно использовать следующие данные:
- большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Чтобы было проще, возьмем 3,38 м²;
- средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м². Опять произведем округление до 0,67 м²;
- самый маленький прямоугольник: 0,57 м *0,57 м = 0,3249 м2, доводим до 0,33 м²;
- теперь осталось только сложить получившиеся значения и прибавить ½ маленького прямоугольника: 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².
Это наиболее удобная методика, которой может воспользоваться любой желающий. Достаточно только разбивать сложную фигуру на несколько простых. Несмотря на то, что измерений будет больше, такой метод не требует больших усилий и временных потерь, а все вычисления можно сделать буквально на коленке.
Площадь квартиры
Многие утверждают, что ремонт – процесс, который практически невозможно закончить, его можно только приостановить. Несмотря на это, чтобы не превратить незначительный ремонт в глобальный, очень важно правильно рассчитать все необходимые цифры и провести нужные расчеты, одним из которых является измерение квадратуры.
Теперь вы знаете, как найти площадь комнаты зная длину и ширину и после всех выполненных манипуляций, достаточно просто сложить полученные данные по комнатам, тогда можно получить квадратуру всей квартиры.
Такой процесс требуется для закупки материалов. Последним этапом будет только проработка плана, где будут указаны все длины, ширина оконных и дверных рам и т.д. Это необходимо например для укладки напольной плитки или ламината. Такая схема потребуется при укладке теплого пола.
Существуют и современные приложения на смартфон или сервисы в интернете, которые упростят эти моменты и помогут найти площадь.
90000 Areas to Include When Calculating Square Footage 90001 90002 So you might think that you can just add all your measurements up, complete the calculations and be done, right? Not so fast — that’s how square footage can be confusing in the first place. It turns out there are several areas that should not be included in your calculations. 90003 90002 First off, there’s the matter of ceiling height. While you’re not measuring the three-dimensional area of a room (length x width x height) to get your overall square footage, in order for a room to be included in the total square footage of a house, the ceiling must be a certain height — so that crawl space does not count.To count in the square footage equation, a ceiling must be 7 feet (2.13 m) tall, or 6 feet 4 inches (1.9 m) with beams or any thing else that might hang down. If the ceiling is angled, it must be 7 feet or higher for at least half of the room’s floor area. If it is, then any part of the room with a ceiling of 5 feet (1.52 m) or higher should be included [source: Boddy]. If not, you should not include any of that space. 90003 90002 As for rooms in the house that are not finished, like basements or attics, they should not be included in the total square footage.In fact, any part of the house that is below ground level — even if it is only partially so — should not be included under any circumstances. Even if it a basement area is finished — which is to say that it is heated the same as the rest of the house and could be lived in year round — it does not count according to ANSI. In the past, many basements were counted as long as they had windows. However, ANSI needed a universal standard and as a result, basements were eliminated completely from their standards for calculating square footage [source: Williams].Porches may only be included if they are enclosed and heated using the same system as the rest of house. As for lofts and attics, the ceiling rules still apply, and you can only include them if you can reach them by stairs. Any part of a house that requires the use of a ladder to get to it does not count. 90003 90002 Outside, garages are not included, period. If the garage is attached to the house, the shared wall will serve as the outside wall of the house when determining square footage.The same goes for guesthouses, pool houses or any rooms that require you to leave the finished area of the main house to gain access. Whether they are finished or not, they can not be included in the square footage of the main residence [source: Boddy]. They should be reported as «bonus rooms.» However, if you have a finished area above an attached garage and you can get to it without leaving the house, go ahead and count it. 90003 90002 While these rules are widely accepted, you’ll always want to ask what standards were used to determine the square footage of a house.They may differ from realtor to realtor. If they used different standards, do not be afraid to ask for a detailed explanation of how the square footage was determined. 90003 90002 To learn more, visit the links on the following page. 90003 90014 Related HowStuffWorks Articles 90015 90014 Sources 90015 90018 90019 Atlas.org. «Istana Nurul Iman Palace.» (Accessed 03/19/09) http://www.atlas.org/location/istana-nurul-iman-palace 90020 90019 Boddy, Chet.»Measuring Houses and Counting Rooms.» Chet Boddy. (Accessed 03/10/2009) http://www.chetboddy.com/Pages/measuringhouses.html 90020 90019 Demesne. «Calculate Footage.» (Accessed 03/10/2009) http://www.demesne.info/Improve-Your-Home/calculate-feet.htm 90020 90019 MCWDN. «Area.» (Accessed 03/10/2009) http://www.mcwdn.org/Geometry/Area.html 90020 90019 North Carolina Real Estate Commission. «Residential Square Footage Guidelines.» (Accessed 03/17/2009) 90020 90019 PropEx. «Calculating Living Area.»(Accessed 03/10/2009) http://www.propex.com/C_SC_calcsf.htm 90020 90019 Sam Houston State University.» Fun Facts. «(Accessed 03/10/2009) http: //www.shsu. edu / ~ fye_www / facts.html 90020 90019 US Census Bureau. Median and Average Sales Prices of New Homes Sold in United States (accessed 03/19/2009) http://www.census.gov/const/uspriceann.pdf 90020 90019 US Census Bureau. Square Feet of Floor Area in New One-Family Houses Completed (accessed 03/19/2009) http://www.census.gov/const/C25Ann/sftotalsqft.pdf 90020 90019 Kass, Benny L. «How Big Is Your Condo? There Is No Right Answer.» Washington Post (accessed 03/20/09) http://www.washingtonpost.com/wp-dyn/content/article/2007/06/01/AR2007060100946_pf.html 90020 90019 Williams, John. «Square Footage — What do you mean it does not count?» Propex. (Accessed 03/17/2009) http://www.propex.com/C_G_calcsf2.htm 90020 90041 .90000 Square Footage Calculator 90001 90002 Calculate a 90003 Rectangle 90004 Area 90005 90006 90007 Calculator Use 90005 90009 Use this calculator to find the square footage, square yardage, square meters or acres for a building, home, garden or construction project. Calculate square footage, yardage, meters and acres for landscape, flooring, carpet, or tiling projects to estimate area and the amount of material you will need.Also calculate the cost of materials when you enter the price per square foot, price per square yard or price per square meter. 90010 90009 Price is entered in the fields, for example, as 90012 $ price: 3.00 per: 1 square unit: foot (ft²) 90012 meaning $ 3.00 per 1 square foot 90012 or 90012 $ price: 25.00 per 1000 square unit: foot (ft²) 90012 meaning $ 25.00 per тисячі square feet 90012 etc …. 90010 90009 If you want to calculate volume of bulk materials such as mulch or gravel you should use our calculator for cubic yards and cubic meters. 90010 90009 Enter measurements in US units or metric units. Calculate area from your measurements in inches (in), feet (ft), yards (yd), millimeters (mm), centimeters (cm), or meters (m). You can also enter decimal values.For example, if you have one measurement that is 7’3 «you can enter that as 7.25 feet (3» / 12 «= 0.25 ft). If you have a measurement of 245 cm you can also enter that as 2.45 m. 90010 90002 How to Calculate Square Footage 90005 90009 Square footage is area expressed in square feet. Likewise, square yardage is area expressed in square yards. Square meters is also a common measure of area. 90010 90009 Assume you have a rectangular area such as a room and, for example, you want to calculate the square footage area for flooring or carpet.90010 90009 The way to calculate a rectangular area is by measuring the length and width of your area then multiplying those two numbers together to get the area in feet squared (ft 90030 2 90031). If you have on oddly shaped area, such as an L-shape, split it into square or rectanglualar sections and treat them as two separate areas. Calculate the area of each section then add them together for your total. If your measurements are in different units, say feet and inches, you can first convert those values to feet, then multiply them together to get the square footage of the area.90010 90033 Measure 90034 90035 90036 Measure the sides of your area 90037 90038 90033 Convert all of your measurements to feet 90034 90035 90036 If you measured in feet skip to «Calculate the Area as Square Footage» 90037 90036 If you measured in feet & inches, divide inches by 12 and add that to your feet measure to get total feet 90037 90036 If you measured in another unit of measure, do the following to convert to feet 90012 — inches: divide by 12 and that is your measurement in feet 90012 — yards: multiply by 3 and that is your measurement in feet 90012 — centimeters: multiply by 0.03281 to convert to feet 90012 — meters: multiply by 3.281 to convert to feet 90037 90038 90033 Calculate the Area as Square Footage 90034 90035 90036 If you are measuring a square or rectangle area, multiply length times width; Length x Width = Area. 90037 90036 For other area shapes, see formulas below to calculate Area (ft 90030 2 90031) = Square Footage. 90037 90038 90002 Convert among square inch, square foot, square yard and square meter 90005 90009 You could, for example, perform all of your measurements in inches or centimeters, calculate area in square inches or square centimeters then convert your final answer to the unit you need such as square feet or square meters.90010 90009 To convert among square feet, yards and meters use the following conversion factors. For other units use our calculator for area conversions. 90010 90035 90036 Square Feet to Square Yards 90035 90036 multiply ft 90030 2 90031 by 0.11111 to get yd 90030 2 90031 90037 90038 90037 90036 Square Feet to Square Meters 90035 90036 multiply ft 90030 2 90031 by 0.092903 to get m 90030 2 90031 90037 90038 90037 90036 Square Yards to Square Feet 90035 90036 multiply yd 90030 2 90031 by 9 to get ft 90030 2 90031 90037 90038 90037 90036 Square Yards to Square Meters 90035 90036 multiply yd 90030 2 90031 by 0.836127 to get m 90030 2 90031 90037 90038 90037 90036 Square Meters to Square Feet 90035 90036 multiply m 90030 2 90031 by 10.7639 to get ft 90030 2 90031 90037 90038 90037 90036 Square Meters to Square Yards 90035 90036 multiply m 90030 2 90031 by 1.19599 to get yd 90030 2 90031 90037 90038 90037 90038 90002 Square Footage Formulas and Images for Different Areas 90005 90033 Square Area 90034 90135 90136 Calculate square footage for a square area 90137 90012 Using measurements in feet: 90009 Area (ft 90030 2 90031) = Side Length x Side Length 90010 90033 Rectangle Area 90034 .90000 How to Calculate the Heart Rate on an EKG Strip with the Six Second Rule 90001 90002 When you are interpreting an EKG, you must know how to count the heart rate. When you count the heart rate you are counting the ventricular and atrial rate. In this article, I am going to tell you how to count a heart rate using the six (6) second rule. 90003 90002 There are many ways you can count a heart rate on an EKG, but I find the six second rule to be the easiest and fastest way. In addition, the six second rule is great for counting heart rhythms that are not regular like, atrial fibrillation, atrial flutter, sinus arrhythmia, sinus rhythm with PVCs etc.90003 90002 Before you can understand how to count the heart rate using the 6 second rule, you must first be familiar with the squares found on the EKG paper. These squares are found on the background, behind the rhythm. These squares can be hard to see at time, so if you do not have the best vision, you may need a small magnifying glass. Each square and block represents a fraction of time. 90003 90008 Video on How to Count Heart Rate with 6 Second Rule 90009 90010 90011 90012 Here is a diagram to illustrate what I’m talking about: 90002 90014 90003 90002 90003 90002 Important things to note about the squares: 90003 90020 90021 Each large block contains 25 squares 90022 90021 Each small square represents 0.04 seconds of time 90022 90021 5 small squares equal 0.20 seconds of time 90022 90021 When you are trying to calculate the heart rate with the six second rule, you must count out enough LARGE squares to equal 6 seconds. Therefore, 90028 30 large squares would equal 6 seconds. 90029 90022 90031 90002 90028 Atrial Rate 90029 90003 90036 90021 Identify the p-waves 90022 90021 Beginning at the first p-wave start counting 30 large squares. 90022 90021 Then count how many p-waves are between the 30 large squares.90022 90021 Take that number and multiple it by 10 and this is your heart rate. 90022 90045 90002 90028 Ventricular Rate 90029 90003 90036 90021 Identify the r-waves 90022 90021 Beginning at the first r-wave start counting 30 large squares. 90022 90021 Then count how many r-waves are between the 30 large squares. 90022 90021 Take that number and multiple it by 10 and this is your heart rate. 90022 90045 90008 Quick Heart Rate Quiz 90009 90002 90063 90003 90002 Answer: 90028 Heart rate: 80 (normal sinus rhythm) 90029 90003 90002 90070 90003 90002 Answer: 90028 Heart Rate: 110s (sinus tachycardia) 90029 90003 90002 More EKG Tutorials 90003 .90000 Calculating Area | SkillsYouNeed 90001 90002 Area is a measure of how much space there is inside a shape. Calculating the area of a shape or surface can be useful in everyday life — for example you may need to know how much paint to buy to cover a wall or how much grass seed you need to sow a lawn. 90003 90002 This page covers the essentials you need to know in order to understand and calculate the areas of common shapes including squares and rectangles, triangles and circles.90003 90006 Calculating Area Using the Grid Method 90007 90002 When a shape is drawn on a scaled grid you can find the area by counting the number of grid squares inside the shape. 90003 90010 90002 In this example there are 10 grid squares inside the rectangle. 90003 90013 90002 In order to find an area value using the grid method, we need to know the size that a grid square represents. 90003 90002 This example uses centimetres, but the same method applies for any unit of length or distance.You could, for example be using inches, metres, miles, feet etc. 90003 90018 90002 In this example each grid square has a width of 1cm and a height of 1cm. In other words each grid square is one ‘square centimetre’. 90003 90002 Count the grid squares inside the large square to find its area .. 90003 90002 There are 16 small squares so the area of the large square is 16 square centimetres. 90003 90002 In mathematics we abbreviate ‘square centimetres’ to cm 90026 2 90027. The 90026 2 90027 means ‘squared’.90003 90002 Each grid square is 1cm 90026 2 90027. 90003 90002 The area of the large square is 16cm 90026 2 90027. 90003 90013 90002 90041 Counting squares on a grid to find the area works for all shapes — as long as the grid sizes are known. 90042 However, this method becomes more challenging when shapes do not fit the grid exactly or when you need to count fractions of grid squares. 90003 90044 90002 In this example the square does not fit exactly onto the grid. 90003 90002 We can still calculate the area by counting grid squares.90003 90049 90050 There are 25 full grid squares (shaded in blue). 90051 90050 10 half grid squares (shaded in yellow) — 10 half squares is the same as 5 full squares. 90051 90050 There is also 1 quarter square (shaded in green) — (¼ or 0.25 of a whole square). 90051 90050 Add the whole squares and fractions together: 25 + 5 + 0.25 = 30.25. 90051 90058 90002 The area of this square is therefore 30.25cm 90026 2 90027. 90003 90002 You can also write this as 30¼cm 90026 2 90027.90003 90013 90002 Although using a grid and counting squares within a shape is a very simple way of learning the concepts of area it is less useful for finding exact areas with more complex shapes, when there may be many fractions of grid squares to add together. 90003 90002 Area can be calculated using simple formulae, depending on the type of shape you are working with. 90003 90002 The remainder of this page explains and gives examples of how to calculate the area of a shape without using the grid system.90003 90013 90006 Areas of Simple Quadrilaterals: 90076 Squares and Rectangles and Parallelograms 90007 90002 The simplest (and most commonly used) area calculations are for squares and rectangles. 90003 90002 To find the area of a rectangle, multiply its height by its width. 90003 90002 For a square you only need to find the length of one of the sides (as each side is the same length) and then multiply this by itself to find the area. This is the same as saying length 90026 2 90027 or length squared.90003 90002 It is good practice to check that a shape is actually a square by measuring two sides. For example, the wall of a room may look like a square but when you measure it you find it is actually a rectangle. 90003 90088 90002 Often, in real life, shapes can be more complex. For example, imagine you want to find the area of a floor, so that you can order the right amount of carpet. 90003 90002 A typical floor-plan of a room may not consist of a simple rectangle or square: 90003 90093 90002 In this example, and other examples like it, the trick is to split the shape into several rectangles (or squares).It does not matter how you split the shape — any of the three solutions will result in the same answer. 90003 90002 Solution 1 and 2 require that you make two shapes and add their areas together to find the total area. 90003 90002 For solution 3 you make a larger shape (A) and subtract the smaller shape (B) from it to find the area. 90003 90013 90002 Another common problem is to the find the area of a border — a shape within another shape. 90003 90002 This example shows a path around a field — the path is 2m wide.90003 90002 Again, there are several ways to work out the area of the path in this example. 90003 90002 You could view the path as four separate rectangles, calculate their dimensions and then their area and finally add the areas together to give a total. 90003 90002 A faster way would be to work out the area of the whole shape and the area of the internal rectangle. Subtract the internal rectangle area from the whole leaving the area of the path. 90003 90111 90049 90050 The area of the whole shape is 16m × 10m = 160m 90026 2 90027.90051 90050 We can work out the dimensions of the middle section because we know the path around the edge is 2m wide. 90051 90050 The width of the whole shape is 16m and the width of the path across the whole shape is 4m (2m on the left of the shape and 2m on the right). 16m — 4m = 12m 90051 90050 We can do the same for the height: 10m — 2m — 2m = 6m 90051 90050 So we have calculated that the middle rectangle is 12m × 6m. 90051 90050 The area of the middle rectangle is therefore: 12m × 6m = 72m 90026 2 90027.90051 90050 Finally we take the area of the middle rectangle away from the area of the whole shape. 160 — 72 = 88m 90026 2 90027. 90051 90058 90002 The area of the path is 88m 90026 2 90027. 90003 90013 90002 A 90041 parallelogram 90042 is a four-sided shape with two pairs of sides with equal length — by definition a rectangle is a type of parallelogram. However, most people tend to think of parallelograms as four-sided shapes with angled lines, as illustrated here. 90003 90143 90002 The area of a parallelogram is calculated in the same way as for a rectangle (height × width) but it is important to understand that height does not mean the length of the vertical (or off vertical) sides but the distance between the sides.90003 90002 From the diagram you can see that the height is the distance between the top and bottom sides of the shape — not the length of the side. 90003 90002 Think of an imaginary line, at right angles, between the top and bottom sides. This is the height. 90003 90013 90006 Areas of Triangles 90007 90002 It can be useful to think of a triangle as half of a square or parallelogram. 90003 90155 90002 Assuming you know (or can measure) the dimensions of a triangle then you can quickly work out its area.90003 90002 The area of a triangle is (height × width) ÷ 2. 90003 90002 In other words you can work out the area of a triangle in the same way as the area for a square or parallelogram, then just divide your answer by 2. 90003 90002 The height of a triangle is measured as a right-angled line from the bottom line (base) to the ‘apex’ (top point) of the triangle. 90003 90002 90041 Here are some examples: 90042 90003 90168 90002 The area of the three triangles in the diagram above is the same.90003 90002 Each triangle has a width and height of 3cm. 90003 90002 The area is calculated: 90003 90002 (height × width) ÷ 2 90003 90002 3 × 3 = 9 90003 90002 9 ÷ 2 = 4.5 90003 90002 The area of each triangle is 4.5cm 90026 2 90027. 90003 90013 90002 In real-life situations you may be faced with a problem that requires you to find the area of a triangle, such as: 90003 90002 You want to paint the gable end of a barn. You only want to visit the decorating store once to get the right amount of paint.You know that a litre of paint will cover 10m 90026 2 90027 of wall. How much paint do you need to cover the gable end? 90003 90192 90002 90041 You need three measurements: 90042 90003 90002 A — The total height to the apex of the roof. 90003 90002 B — The height of the vertical walls. 90003 90002 C — The width of the building. 90003 90002 90041 In this example the measurements are: 90042 90003 90002 A — 12.4m 90003 90002 B — 6.6m 90003 90002 C — 11.6m 90003 90002 The next stage requires some additional calculations.Think about the building as two shapes, a rectangle and a triangle. From the measurements you have you can calculate the additional measurement needed to work out the area of the gable end. 90003 90215 90002 90041 Measurement D = 12.4 — 6.6 90042 90003 90002 90041 D = 5.8m 90042 90003 90002 You can now work out the area of the two parts of the wall: 90003 90002 Area of the rectangular part of the wall: 6.6 × 11.6 = 76.56m 90026 2 90027 90003 90002 Area of the triangular part of the wall: (5.8 × 11.6) ÷ 2 = 33.64m 90026 2 90027 90003 90002 Add these two areas together to find the total area: 90003 90002 90041 76.56 + 33.64 = 110.2m 90026 2 90027 90042 90003 90002 As you know that one litre of paint covers 10m 90026 2 90027 of wall so we can work out how many litres we need to buy: 90003 90002 110,2 ÷ 10 = 11.02 litres. 90003 90002 In reality you may find that paint is only sold in 5 litre or 1 litre cans, the result is just over 11 litres. You may be tempted to round down to 11 litres but, assuming we do not water down the paint, that will not be quite enough.So you will probably round up to the next whole litre and buy two 5 litre cans and two 1 litre cans making a total of 12 litres of paint. This will allow for any wastage and leave most of a litre left over for touching up at a later date. And do not forget, if you need to apply more than one coat of paint, you must multiply the quantity of paint for one coat by the number of coats required! 90003 90013 90006 Areas of Circles 90007 90002 In order to calculate the area of a circle you need to know its 90041 diameter 90042 or 90041 radius 90042.90003 90259 90002 The 90041 diameter 90042 of a circle is the length of a straight line from one side of the circle to the other that passes through the central point of the circle. The diameter is twice the length of the radius (diameter = radius × 2) 90003 90002 The 90041 radius 90042 of a circle is the length of a straight line from the central point of the circle to its edge. The radius is half of the diameter. (Radius = diameter ÷ 2) 90003 90002 You can measure the diameter or radius at any point around the circle — the important thing is to measure using a straight line that passes through (diameter) or ends at (radius) the centre of the circle.90003 90002 In practice, when measuring circles it is often easier to measure the diameter, then divide by 2 to find the radius. 90003 90002 You need the radius to work out the area of a circle, the formula is: 90003 90002 circle area = πR 90026 2 90027. 90003 90002 This means: 90003 90002 π = Pi is a constant that equals 3.142. 90003 90002 R = is the radius of the circle. 90003 90002 R 90026 2 90027 (radius squared) means radius × radius. 90003 90013 90002 Therefore a 90041 circle with a radius of 5cm 90042 has an area of: 90003 90002 3.142 × 5 × 5 = 78.55cm 90026 2 90027. 90003 90002 A 90041 circle with a diameter of 3m 90042 has an area: 90003 90002 First, we work out the radius (3m ÷ 2 = 1.5m) 90003 90002 Then apply the formula: 90003 90002 πR 90026 2 90027 90003 90002 3.142 × 1.5 × 1.5 = 7.0695. 90003 90002 The area of a circle with a diameter of 3m is 7.0695m 90026 2 90027. 90003 90013 90316 Final Example 90317 90002 This example pulls on much of the content of this page for solving simple area problems.90003 90320 90002 This is the Ruben M. Benjamin House in Bloomington Illinois, listed on The United States National Register of Historic Places (Record Number: 376599). 90003 90002 This example involves finding the area of the front of the house, the wooden slatted part — excluding the door and windows. The measurements you need are: 90003 90325 90326 90327 A — 9.7m 90328 90327 B — 7.6m 90328 90331 90326 90327 C — 8.8m 90328 90327 D — 4.5m 90328 90331 90326 90327 E — 2.3m 90328 90327 F — 2.7m 90328 90331 90326 90327 G — 1.2m 90328 90327 H — 1.0m 90328 90331 90350 90002 Notes: 90003 90049 90050 All measurements are approximate. 90051 90050 There is no need to worry about the border around the house — this has not been included in the measurements. 90051 90050 We assume all rectangular windows are the same size. 90051 90050 The round window measurement is the diameter of the window. 90051 90050 The measurement for the door includes the steps.90051 90058 90002 What is the area of the wooden slatted part of the house? 90003 90002 Workings and answers below: 90003 90013 90013 90002 Answers to above example 90003 90002 First, work out the area of the main shape of the house — that is the rectangle and triangle that make up the shape. 90003 90002 The main rectangle (B × C) 7.6 × 8.8 = 66.88m 90026 2 90027. 90003 90002 The height of the triangle is (A — B) 9.7 — 7.6 = 2.1. 90003 90002 The area of the triangle is therefore (2.1 × C) ÷ 2. 90076 2.1 × 8.8 = 18.48. 18.48 ÷ 2 = 9.24m 90026 2 90027. 90003 90002 The combined full area of the front of the house is the sum of the areas of the rectangle and triangle: 90003 90002 66.88 + 9.24 = 76.12m 90026 2 90027. 90003 90002 Next, work out the areas of the windows and doors, so they can be subtracted from the full area. 90003 90002 The area of the door and steps is (D × E) 4.5 × 2.3 = 10.35m 90026 2 90027. 90003 90002 The area of one rectangular window is (G × F) 1.2 × 2.7 = 3.24m 90026 2 90027. 90003 90002 There are five rectangular windows. Multiply the area of one window by 5. 90003 90002 3.24 × 5 = 16.2m2. (The total area of the rectangular windows). 90003 90002 The round window has a diameter of 1m its radius is therefore 0.5m. 90003 90002 Using πR 90026 2 90027, work out the area of the round window: 3.142 × 0.5 × 0.5 =. 0.7855m 90026 2 90027. 90003 90002 Next add up the areas of the door and windows. 90003 90002 (door area) 10.35 + (rectangle windows area) 16.2 + (round window area) 0.7855 = 27.3355 90003 90002 Finally, subtract the total area for the windows and doors from the full area. 90003 90002 76.12 — 27.3355 = 48.7845 90003 90002 The area of the wooden slatted front of the house, and the answer to the problem is: 48.7845m 90026 2 90027. 90003 90002 You may want to round the answer up to 48.8m 90026 2 90027 or 49m 90026 2 90027. 90003 90432 See our page on 90041 Estimation, Approximation and Rounding 90042. 90435 .

