Как посчитать площадь зная ширину и длину: Как рассчитать площадь комнаты? Как посчитать объем помещения? - Стройматериалы в Иркутске

Как найти площадь треугольника — Лайфхакер

Как найти площадь любого треугольника

Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.

Зная сторону и высоту

Умножьте сторону треугольника на высоту, проведённую к этой стороне.
Поделите результат на два.

S — искомая площадь треугольника.
a — сторона треугольника.
h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.

Зная две стороны и угол между ними

Посчитайте произведение двух известных сторон треугольника.
Найдите синус угла между выбранными сторонами.
Перемножьте полученные числа.
Поделите результат на два.

S — искомая площадь треугольника.
a и b — стороны треугольника.
α — угол между сторонами a и b.

Сейчас читают 🔥

Зная три стороны (формула Герона)

Посчитайте разности полупериметра треугольника и каждой из его сторон.
Найдите произведение полученных чисел.
Умножьте результат на полупериметр.
Найдите корень из полученного числа.

S — искомая площадь треугольника.
a, b, c — стороны треугольника.
p — полупериметр (равен половине от суммы всех сторон треугольника).

Зная три стороны и радиус описанной окружности

Найдите произведение всех сторон треугольника.
Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.

S — искомая площадь треугольника.
R — радиус описанной окружности.
a, b, c — стороны треугольника.

Зная радиус вписанной окружности и полупериметр

Умножьте радиус окружности, вписанной в треугольник, на полупериметр.

S — искомая площадь треугольника.
r — радиус вписанной окружности.
p — полупериметр треугольника (равен половине от суммы всех сторон).

Как найти площадь прямоугольного треугольника

Посчитайте произведение катетов треугольника.
Поделите результат на два.

S — искомая площадь треугольника.
a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.

Как найти площадь равнобедренного треугольника

Умножьте основание на высоту треугольника.
Поделите результат на два.

S — искомая площадь треугольника.
a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

Как найти площадь равностороннего треугольника

Умножьте квадрат стороны треугольника на корень из трёх.
Поделите результат на четыре.

S — искомая площадь треугольника.
a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

Читайте также 🧠👨🏻‍🎓✍🏻

Как посчитать площадь – формулы и примеры

С одной стороны нет ничего проще, как посчитать площадь любой поверхности (вертикальной, горизонтальной). Однако и здесь можно найти несколько нюансов и некоторые из них могут привести к трудностям. Разберём, что особенного может быть в вычислениях площади и рассмотрим несколько примеров. Прочтя этот материал, вы уже не будете плавать в этом вопросе. Заодно вспомните школьную программу с её формулами.

Казалось бы, что может быть прощеИсточник ar.aviarydecor.com

Почему не все так просто

Так вопрос, как рассчитать площадь любой поверхности может показаться смешным, ведь все мы учились в школе. Но не будем столь категоричными. Во-первых, со школьной скамьи многие из нас сошли со школьной скамьи очень давно. Во-вторых, не каждый раз в повседневной жизни приходится сталкиваться с необходимостью геометрических расчётов. И кое-что уже позабыто.

Ну и в третьих далеко не всегда поверхность имеет правильную форму. Тогда приходится изворачиваться, применяя более сложные приёмы расчёта. Это с квадратами и прямоугольниками все просто, но как быть в случае трапеции, треугольника и прочих сложных геометрических фигур?

Необходимость расчётов

Кто-то может задать и такой вопрос: «Собственно, а для чего потребуется рассчитать площадь?» Для этого есть определённые причины:

Полученные данные позволят подобрать нужное количество строительных материалов, дабы не переплачивать.
Рассчитав площадь, можно определить и объем помещения. А это уже главная характеристика, без которой не обойтись в случае выбора климатического оборудования, приборов отопления или системы вентиляции.

Некоторые коммунальные услуги как раз учитывают площадь помещения.
Выбор осветительных приборов, а точнее их количество, также зависит от этого рассчитываемого параметра.

Например, количество закупаемого ламината можно рассчитать, только зная площадь комнатыИсточник bazazakonov.

С чего начинать

Самое время вспомнить школьную математику – чтобы рассчитать площадь, необходимы три параметра:

Длина – обычно она бывает 4 либо 4,5 метра.
Ширина – стандартное значение для большинства домов это 3 или 3,5 метра.

Высота – в новостройках она обычно равна 2,5 метрам. А вот в постройках сталинской эпохи может составлять до 3 метров.

В решении задачи, как рассчитать площадь, не обойтись и без соответствующих инструментов:

рулетки;
строительного угольника;
карандаша;
калькулятора;
строительного уровня.

Если планируются много писать, то вместо листка бумаги лучше взять блокнот либо тетрадь. Листики имеют свойство теряться, причём, когда нужно не всегда найдёшь их потом. Рулетка обязательно должна быть с фиксатором, иначе возникнуть сложности и процедура расчётов превратится в настоящее мучение.

Алгоритм проведения расчётов

Если все подготовлено, то можно переходить к самим расчётам. Если нужно вычислить площадь поверхности правильной формы, то здесь нет ничего сложного – эти формулы уж точно никто не позабудет.

Без рулетки никакИсточник sv.decorexpro.com

Другое дело, когда стена, пол, потолок имеют сложные очертания. Здесь уже придётся сочетать различные приёмы. То есть поделить комнату на несколько блоков, после чего рассчитать площадь каждого из них. А далее от общей площади вычесть или прибавить их.

Вовсе не обязательно мерить длину стен строго вдоль плинтусов – замер можно проводить в любом удобном месте, если, скажем, мешает мебель. То есть выше, ниже, в середине, главное соблюсти при этом строгую параллель полу и потолку. Никаких диагоналей или наклонов! В противном случае расчёты будут неверными.

При возникновении трудностей можно всегда заручиться поддержкой кого-то из домашних.

Правильная геометрия

Каких-либо сложностей касательно того, как вычислить площадь, здесь нет. В случае простого прямоугольника достаточно замерить всего две стороны и высоту, ведь у такой фигуры противоположные стороны равны. Чтобы убедиться, что комната имеет правильные очертания, достаточно приложить к углам строительный угольник, правда не всегда удаётся получить чёткую картину.

Формула для расчёта прямоугольника известна каждому:

S=a⋅b, где:

S – рассчитываемая площадь;
a – длина;
b – ширина.

Кажется, что формулу площади прямоугольника забыть невозможно, хотя у некоторых получается и этоИсточник wezanu.ritobypus.ru.net

Такая формула актуальна для стен, потолка, пола, дверей, окон и прочих прямоугольных поверхностей. В случае запланированного ремонта важно получить чистые значения. Для этого следует от площади стены вычесть площадь дверей, окон.

Общую площадь всей комнаты можно рассчитать по такой формуле – h(a⋅2+b⋅2). Где h – высота помещения.

С квадратом все ещё проще – достаточно замерить одну сторону и возвести её значение в квадрат.

Помещения с неправильными очертаниями

Но как посчитать площадь комнаты, если она имеет неправильную форму поверхностей? Здесь есть некоторые нюансы:

Стены. В мансардной комнате стена может иметь форму трапеции или треугольника.
Потолок . В тех же мансардных помещениях данная плоскость может быть под определённым углом. Также есть варианты с ломаной поверхностью, когда несколько плоскостей пересекаются межу собой.

Но ничего страшного здесь нет и не нужно углубляться в тригонометрию. Достаточно любую сложную поверхность стен или потолка визуально разделить на несколько простых плоскостей. После этого остаётся рассчитать площадь каждой фигуры и сложить их вместе.

Случай чуть-чуть посложнее – но не намногоИсточник wezanu.

ritobypus.ru.net
Как посчитать квадратуру дома: несколько способов в зависимости от особенностей помещений

Для облегчения ниже приведём несколько формул площадей, которые могут пригодиться:

Круг:

S=π⋅R² – нужен только радиус.
Сектор круга определятся так – S=0,5pr.

Параллелограмм:

S=a⋅b⋅sin(α) – по двум сторонам и углу между ними.
S=a⋅h – по высоте и основанию.

Треугольник:

S=0,5⋅b⋅h – по основанию и высоте.
S=0,5⋅ab⋅sin(α) – по сторонам и углу.
S=√(p·(p-a)·(p-b)·(p-c)) – формула Герона по трем сторонам.

Трапеция

S=0,5⋅h⋅(a+b) – по высоте и основанию.
S=m⋅h – по средней линии и высоте.

Эллипс:

S = π⋅R1⋅R2 – по двум радиусам R1 и R2
S=π⋅a⋅b – через полуоси a и b.

Обозначения: π – 3,14159 (всем известное число пи), R – радиус, a, b, c – стороны фигуры, p – полупериметр (для формулы Герона), h – высота, m – средняя линия.

Простое решение вопроса

Как высчитать квадратный метр стен, потолка или пола, если нет свободного времени, в особенности, когда имеешь дело со сложными фигурами, но есть интернет? В этом случае задача существенно упрощается. В сети можно найти кучу онлайн-калькуляторов, которые проведут все расчёты за несколько секунд. Все что нужно – это задать нужные параметры.

С онлайн калькулятором расчёт площади существенно прощеИсточник doverie-mo.ru

Для удобства все измерения указываются в разных единицах измерения, исходя из конкретных нужд. С их помощью любого такого калькулятора легко рассчитать не только площадь помещений, но и земельных участков. Кроме того, полученный результат можно преобразовать в любую другую нужную единицу измерения.

Для наглядности ниже подробная инструкция расчёта площади с разными примерами:

Как делается расчёт радиаторов отопления по площади + калькулятор

Краткий итог

Проблем с расчётом площади нужных поверхностей возникнуть не должно, если следовать правилу – от сложного к простому. Именно в этом и кроется успех больших достижений человечества. Не нужно все усложнять, достаточно проявить волю и смекалку и тогда любая задача, какой бы она ни была, будет решена.

Площадь прямоугольника формула 4. Как посчитать площадь прямоугольника: практические советы

Площадь прямоугольника, как не будет дерзко звучать, но это важное понятие. В повседневной жизни мы постоянно сталкиваемся с ним. Узнать размер полей, огородов, рассчитать количество краски, необходимой для побелки потолка, сколько понадобится обоев для оклейки ко

мнаты и другое.

Геометрическая фигура

Для начала поговорим о прямоугольнике. Это фигура на плоскости, которая имеет четыре прямых угла, а ее противоположные стороны равны. Стороны его привыкли называть длиной и шириной. Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.

Площадь=длина*ширина

Но еще одна оговорка: длина и ширина должны быть выражены в одинаковых единицах измерения, то есть метр и метр, а не метр и сантиметр. Записывается площадь латинской буквой S. Для удобства обозначим длину латинской буквой b, а ширину латинской буквой a, как показано на рисунке. Отсюда мы делаем вывод, что единицей измерения площади является мм 2 , см 2 , м 2 и т. д.

Рассмотрим на конкретном примере, как найти площадь прямоугольника. Длина b=10 ед. Ширина a=6 ед. Решение: S=a*b, S=10 ед.*6 ед., S=60 ед 2 . Задача. Как узнать площадь прямоугольника, если длина в 2 раза больше ширины и составляет 18 м? Решение: если b=18 м, тогда а=b/2, a=9 м. Как найти площадь прямоугольника, если известны обе стороны? Правильно, подставить в формулу. S=a*b, S=18*9, S=162 м 2 . Ответ: 162 м 2 . Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.

Площади противоположных сторон равны. Вычислим площадь стены с размерами 5,5 м и 3 м. S стены 1 =5,5*3,

S стены 1 =16,5 м 2 . Следовательно, противоположная стена имеет площадь равную 16,5 м 2 . Найдем площади следующих двух стен. Стороны их, соответственно, равны 3,5 м и 3 м. S стены 2 =3,5*3, S стены 2 =10,5 м 2 . Значит, и противоположная сторона равна 10,5 м 2 . Сложим все результаты. 16,5+16,5+10,5+10,5=54 м 2 . Как вычислить площадь прямоугольника, если стороны выражены в разных единицах измерения. Ранее мы вычисляли площади в м 2 , то и в этом случае будем использовать метры. Тогда ширина рулона обоев будет равна 0,5 м. S рулона =10*0,5, S рулона =5 м 2 . Теперь узнаем, сколько рулонов необходимо для оклейки комнаты. 54:5=10,8 (рулонов). Так как они измеряются целыми числами, то нужно купить 11 рулонов обоев. Ответ: 11 рулонов обоев. Задача. Как вычислить площадь прямоугольника, если известно, что ширина на 3 см короче длины, а сумма сторон прямоугольника составляет 14 см? Решение: пусть длина х см, тогда ширина (х-3) см. х+(х-3)+х+(х-3)=14, 4х-6=14, 4х=20, х=5 см — длина прямоугольника, 5-3=2 см — ширина прямоугольника, S=5*2, S=10 см 2 Ответ: 10 см 2 .

Резюме

Рассмотрев примеры, надеюсь, стало понятно, как найти площадь прямоугольника. Напомню, что единицы измерения длины и ширины должны совпадать, иначе получится неправильный результат, чтобы не допустить ошибок, читайте задание внимательно. Иногда сторона может быть выражена через другую сторону, не стоит бояться. Обратитесь к нашим решенным задачам, вполне возможно, они могут помочь. Но хоть раз в жизни мы сталкиваемся с нахождением площади прямоугольника.

Инструкция

Например, вам , что длина одной из сторон (а) равна 7 см, а периметр прямоугольника (P) равен 20 см. Так как периметр любой фигуры равен сумме длин ее сторон, а у прямоугольника противоположные стороны равны, то его периметр а будет выглядеть следующим образом: P = 2 x (a + b), или P = 2a + 2b. Из этой формулы следует, что найти длину второй стороны (b) можно с помощью несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.

Теперь, зная длины обеих смежных сторон (a и b), вы сможете подставить их в формулу площади S = ab. В данном случае прямоугольника будет равна 7х3 = 21. Обратите на то, что единицами измерения будут уже не , а сантиметры квадратные, так как длин двух сторон единицы их измерения (сантиметры) вы тоже умножали друг на друга.

Источники:

как находится периметр прямоугольника

Плоская фигура, состоящая из четырех сторон и четырех прямых углов. Из всех фигур площадь прямоугольника приходится вычислять чаще других. Это и площадь квартиры, и площадь садового участка, и площадь поверхности стола или полки. Например, чтобы просто оклеить комнату обоями, вычисляют площадь ее прямоугольных стен.

Инструкция

Кстати, из прямоугольника можно легко вычислить площадь . Достаточно достроить прямоугольный до прямоугольника так, чтобы гипотенуза стала диагональю прямоугольника . Тогда будет очевидно, что площадь такого прямоугольника равна произведению катетов треугольника, а площадь самого треугольника, соответственно, равна половине произведения катетов.

Видео по теме

Частный случай параллелограмма — прямоугольник – известен только в геометрии Евклида. У прямоугольника равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.

Инструкция

Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями EFА. Согласно свойству прямоугольника его диагонали равны и пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.

Далее вычислите первую EF прямоугольника . Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.

Найдите вторую сторону прямоугольника FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.

Относится к простейшим плоским геометрическим фигурам и является одним из частных случаев параллелограмма. Отличительная черта такого параллелограмма — прямые углы во всех четырех вершинах. Ограниченную сторонами прямоугольника площадь можно вычислить несколькими способами, используя размеры его сторон, диагонали и углы между ними, радиус вписанной окружности и т.д.

Инструкция

Если известна величина угла (α), который составляет диагональ прямоугольника с одной из его сторон, а также длина (С) этой диагонали, то для вычисления площади можно задействовать определения тригонометрических в прямоугольном . Прямоугольный треугольник здесь образуют две стороны четырехугольника и его диагональ. Из определения косинуса вытекает, что длина одной из сторон будет равна произведению длины диагонали на угла, величина известна. Из определения синуса можно вывести формулу длины другой стороны — она равна произведению длины диагонали на синус все того же угла. Подставьте эти тождества в формулу из предыдущего шага, и получится, что для нахождения площади надо перемножить синус и косинус известного угла, а также длины диагонали прямоугольника : S=sin(α)*cos(α)*С².

Если кроме длины диагонали (С) прямоугольника известна величина угла (β), который образуют диагонали, то для вычисления площади фигуры можно тоже задействовать одну из тригонометрических функций — синус. Возведите в квадрат длину диагонали и умножьте полученный результат на половину синуса известного угла: S=С²*sin(β)/2.

Если известен (r) вписанной в прямоугольник окружности, то для вычисления площади возведите эту величину во вторую степень и увеличьте результат в четыре раза: S=4*r². Четырехугольник, в который можно , будет являться квадратом, а длина его стороны равна диаметру вписанной окружности, то есть удвоенному радиусу. Формула получена подстановкой длин сторон, выраженных через радиус в тождество из первого шага.

Если известны длины (P) и одной из сторон (A) прямоугольника , то для нахождения площади внутри этого периметра вычислите половину произведения длины стороны на разницу между длиной периметра и двумя длинами этой стороны: S=A*(P-2*A)/2.

Видео по теме

С задачей найти периметр или площадь многоугольника сталкиваются не только ученики на уроках геометрии. Порой ее случается решать и взрослому человеку. Приходилось ли вам рассчитывать необходимое количество обоев для комнаты? Или, может быть, вы измеряли протяженность дачного участка, чтобы огородить его забором? Так знания основ геометрии иногда незаменимы для осуществления важных проектов.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Формулы площади квадрата

Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.

Формула площади прямоугольника

Площадь прямоугольника

где S — Площадь прямоугольника,
— длины сторон прямоугольника.

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
a · b · sin α

Формулы площади ромба

Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.

Формулы площади трапеции

Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,

Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. 2$.

Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника. Средняя оценка: 4.4 . Всего получено оценок: 214.

Полезный калькулятор для школьников и взрослых позволяет быстро вычислить площадь прямоугольника по двум его сторонам. Подобный расчет мы часто производим не только в рамках школьного курса геометрии, но и в повседневной жизни. Например, если нужно посчитать площадь комнаты при ремонте квартиры, для расчета необходимого количества материалов.

Удобная навигация по статье:

Как рассчитать площадь прямоугольника

Прямоугольником принято называть геометрическую плоскую фигуру, которая имеет параллельно расположенные противоположные стороны при углах в 90 градусов. В качестве длины этой геометрической фигуры выступает величина, которая имеет большую сторону. При этом, за ширину принимается величина меньшей стороны. Для правильного вычисления площади прямоугольника Вам необходимо знать определённые параметры, которыми обладает данная фигура. В их числе:

диагональ;
ширина;
так называемый угол наклона к одной из сторон диагонали;
длина.

Таким образом, произвести расчёт площади прямоугольника можно различными способами. Всё зависит от количества информации о фигуре, а именно, какие величины нам точно известны.

Как вычислить площадь прямоугольника, имея линейные параметры его сторон?

Давайте в качестве обозначения длины прямоугольника будем использовать букву «а», для его ширины – букву «b», а площадь геометрической фигуры обозначим буквой «S». Согласно этому, наша формула будет выглядеть следующим образом: S = a x b.

Зная линейные параметры прямоугольника, можно легко определить его периметр последующей формуле: P = 2(a + b), где в качестве обозначения периметра мы используем букву «P».

Как можно вычислить площадь прямоугольника, зная величину одну из его сторон и диагональ?

Как нам известно, диагональ делит любой прямоугольник на два так называемых прямоугольных треугольника. Давайте присвоим диагонали индекс «с», а длину стороны обозначим буквой «а». Теперь необходимо произвести следующий порядок действий:

для начала необходимо найти длину неизвестной стороны. Для этого мы используем формулу Пифагора: b = V c2 – a2.
После этого, нам следует определить площадь нашей основной геометрической фигуры (прямоугольника) как площадь треугольника, умноженную на два: Sтр = ½ (а х в).
Согласно вышеописанной схеме расчёта площадь прямоугольника в данном случае будет равна: S = 2 x Sтр = а х в.

В том случае, если нам известны периметр прямоугольника, а также длина одной из его сторон, то площадь этой геометрической фигуры можно вычислить, определив длину второй стороны (b = (P – 2xa), по такой формуле: S = a x b.

Если же нам известны размер диагонали прямоугольника, а также угол между стороной и самой диагональю, то площадь можно вычислить при помощи следующих тригонометрических функций: Sтр = ½ х с2 х sinФ х cosФ.

При этом, общая площадь в данном случае будет составлять S = 2 x Sтр.

Площадь прямоугольника. Видео-урок.

Как рассчитать площадь комнаты

Простая комната прямоугольной или квадратной формы

Для того, чтобы узнать, как рассчитать площадь пола комнаты, вы должны определить его форму. В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах.

Формула по которой можно высчитать площадь:
S комнаты = А х B, где A – длина, B – ширина.

Для измерения можно взять обычную рулетку. Чтобы получить наиболее точный результат, рекомендуется измерить длину в начале стены и в конце и, если цифры будут отличаться, взять среднее арифметическое значение.

Комната, в которой имеются ниши или выступы

Если в комнате имеются ниши, выступы, сантехнические или вентиляционные конструкции, то необходимо измерить отдельно площадь каждого участка. Если это ниша в стене, то к площади комнаты нужно прибавить площадь углубления. Если это выступ, то соответственно, из площади помещения нужно будет вычесть его площадь.

Такому же принципу нужно следовать, если вы хотите узнать, как рассчитать площадь потолка комнаты. Ровный, прямоугольный потолок без каких-либо ниш и выступов означает, что его необходимо измерить по длине и ширине, а затем посчитать площадь простым умножением.

Если вы планируете утеплить пол с помощью нагревательных элементов, то из общей площади пола вам нужно будет вычесть площадь, которая занята тяжелой мебелью.

Комната сложной конфигурации

Нередко встречаются комнаты необычной формы. Если есть возможность, то нужно разделить помещение на несколько прямоугольников, посчитать площадь каждого и сложить.

Площадь комнаты в форме круга вычисляется по формуле:

S комнаты = πR², где R – радиус. Необходимо учитывать, сколько градусов в секторе.

Для расчета площади комнаты треугольной формы используют формулу Герона:

Sкомнаты = √ (P(P -A) х (Р — В) х (Р — С)), где Р – половина периметра треугольника, А, В, С – длины его сторон.

Полупериметр треугольника рассчитываем так: Р = (А + В + С) / 2

Комната со сложной конфигурацией стен.

Особенности расчета площади простых стен и стен, содержащих выступы и ниши

Теперь давайте рассмотрим такой важный момент, как расчет площади стен комнаты. Зная именно эту величину, вы сможете купить нужное количество обоев для ремонта. Конечно, вы можете обратиться к консультанту в строительном магазине, и он обязательно расскажет, как посчитать площадь стен. В этом нет ничего сложного: измерьте длину, ширину и высоту помещения. Далее площадь стен высчитываем по формуле:

Sстен = Р х С, где Р – периметр комнаты, С – высота стен.

Периметр комнаты считаем по формуле:

Р = (А + В) х 2, где A – длина, B – ширина.

Для получения более точных результатов, из общей площади стен необходимо вычесть площадь дверных и оконных проемов.

Площадь стен комнаты с выступами или углублениями будет отличаться от площади стен простой комнаты. Не забудьте к основному значению прибавить площадь стены выступающего или углубленного участка.

Будьте внимательны, производя измерения и расчеты. Если вы используете лазерную рулетку, то следите за тем, чтобы луч был направлен строго перпендикулярно стене, иначе вы получите большую погрешность в результатах.

Стены комнаты с выступами.

шаблоны для dle

Нахождение формул для площади – Элементарная математика

Формулы площади

Студенты, у которых есть неформальное представление о том, что площадь — это «количество двумерных «вещей»», содержащихся внутри области, могут изобрести для себя большинство формул, которые их часто просят просто запомнить. Каждая формула, которую они заново изобретают, помогает укрепить их понимание (и память) о других формулах, которые они знают. (См. также площадь поверхности.)

Площадь прямоугольников

Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников. Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, длина которого в 7 раз больше, будет иметь площадь 7 × 1.

Прямоугольник, который в два раза больше высоты, будет иметь вдвое большую площадь, поэтому площадь равна 2 × 7 единиц площади. Мы можем сосчитать два ряда по семь квадратов. Точно так же имеет 3 строки по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадрата, поэтому его площадь составляет 21 квадратную единицу.

Количество квадратов в одном ряду равно длине прямоугольника. Количество строк равно высоте прямоугольника.Итак, площадь равна длине × высоте.

Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как любая сторона, которую вы выберете.

Подходит для подсчета чисел. Это работает даже для дробей. Синий прямоугольник, показанный здесь, имеет высоту в половину единицы длины и ширину в пять с половиной единиц длины. Если мы выберем соответствующий квадрат в качестве нашей единицы площади, мы увидим, что синий прямоугольник содержит пять половинных единиц площади и одну четверть единицы площади, или всего две и три четверти единицы площади.(Розовые части показывают завершение каждой квадратной единицы площади.)

Чтобы включить все чисел, мы определяем площадь прямоугольника как те же единицы ).

Площадь параллелограмма

Получение идеи

Мы можем вычислить формулу площади параллелограмма, разрезав параллелограмм и переставив части так, чтобы получился прямоугольник.Поскольку параллелограмм и прямоугольник состоят из одних и тех же частей, они обязательно имеют одинаковую площадь. (См. определение области, чтобы узнать, почему эти области одинаковы.)

Мы видим, что они и имеют одинаковую длину основания (синий) и точно такую же высоту (зеленый). Потому что Base × Высота × Высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме для вычисления одинаковых площадок: База × Высота . (Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это сторона, которую вы выбрали первой. См. параллелограмм.)

На разрезе, показанном выше, легко увидеть, что базовая длина не изменилась. На самом деле перпендикулярный разрез можно сделать в любом месте вдоль основания.

Укрепление отверстий

Интуиция и доказательство

Это рассечение дает интуитивное понимание формулы площади параллелограмма, причины того, что он должен быть таким, какой он есть.Но мы не задавались вопросом, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидаем получить и результат наверняка выглядит именно так. Но внешность может быть обманчива. Что гарантирует нам, что при перемещении этого треугольника в результате получится прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результатом не всегда является идеальный прямоугольник, мы не можем использовать наши знания формулы площади прямоугольника для разработки формулы параллелограмма. В старших классах учащиеся смогут доказать, что две части параллелограмма, если их правильно собрать, образуют прямоугольник. В классах К-8 учащиеся по большей части должны опираться на визуальный эксперимент и получать интуитивное ощущение. Узнайте больше о том, почему эти рассечения работают.

Что, если мы выберем короткую сторону в качестве основания?

Мы вольны выбрать любую сторону в качестве базы; «высота» измеряется перпендикулярно стороне, которую мы выбрали в качестве основания. Если мы возьмем короткую сторону (синюю) за основу, показанное выше рассечение будет не таким убедительным.Резка по этой высоте и перестановка частей оставляет беспорядок:

В этом конкретном примере мы можем исправить беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?

Оказывается, любой параллелограмм, каким бы длинным и худым он ни был, можно разрезать таким образом, чтобы части — возможно, многие из них — можно было переставить в прямоугольник. Но требуется больше работы, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.

Несколько иная идея вскрытия значительно облегчает жизнь в этом случае. (Сами можете показать, что это работает и в исходном случае.)

Заключите параллелограмм в прямоугольник.
Две части прямоугольника, равные , а не внутри параллелограмма, являются конгруэнтными треугольниками.
Сдвиньте один из этих треугольников к другому, пока они не сойдутся в прямоугольник. Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше) и желтая область не изменилась (фигуры просто переместились), разница между ними — фиолетовыми областями — должна быть одинаковой.Как и прежде, мы также можем видеть, что размеры прямоугольной фиолетовой области — это основание и высота исходного параллелограмма.

Интуиция и доказательство, повторение: Опять же, рассечение дает существенное понимание, но требуется немного больше усилий, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят так, как если бы они совмещались, образуя прямоугольник, на самом деле подходят точно, а не только почти .

Почему так важно быть осторожным?

Когда мы будем строить другие формулы площади (см. ниже), мы захотим использовать наш способ нахождения площади параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило.Мы можем быть уверены, что перестановка частей не изменит площадь: в конце концов, именно так мы определяем площадь. Но мы также должны быть уверены, что детали подходят друг к другу так, как мы заявляем о , иначе мы не можем полагаться на сделанные нами измерения. И мы должны быть уверены, что правило основания × высоты не зависит от удачного выбора основания.

В большинстве учебных программ учащиеся не имеют достаточно систематической базы геометрических знаний до 8 класса, чтобы убедительно доказать, что эти рассечения работают.Но интуитивного понимания достаточно для объяснения и обоснования формул, а также хорошей основы для последующего изучения геометрии.

Площадь треугольника

Знание того, как найти площадь параллелограмма, поможет нам найти площадь треугольника.

Разрез треугольника

Мы можем разрезать треугольник на две части — одну из них на треугольник, а другую на трапецию — разрезав его параллельно основанию. Если мы разрежем высоту ровно пополам с помощью этого среза, две части соединятся вместе, чтобы получить параллелограмм с тем же основанием , но наполовину меньше высоты .

Итак, основание × половина высоты дает площадь треугольника. Аналогичный разрез показывает полубаза × высота . Любой из них сводится к bh .

Удвоение треугольника и последующее деление полученной площади пополам

Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием и той же высотой , что и треугольник.

Площадь параллелограмма равна основания × высоты , но это вдвое больше площади треугольника, поэтому площадь треугольника составляет из основания × высоты , как мы видели с методом рассечения.

(Как всегда, выберите «основание» и измерьте высоту перпендикулярно этому основанию, от основания до противоположной вершины.)

Площадь трапеции

Удвоение трапеции с последующим делением полученной площади пополам

Как и в случае с треугольником, две копии трапеции можно сложить вместе, чтобы получился параллелограмм.

Высота параллелограмма равна высоте трапеции, но его основание равно сумме двух оснований трапеции.Таким образом, площадь параллелограмма равна высоты × ( основание1 + основание2 ). Но эта площадь равна двум трапециям, поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.

Рассечение трапеции

Мы также можем разрезать трапецию так же, как мы разрезали треугольник, с одним срезом, сокращающим его высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого равно сумме двух оснований трапеции, а высота равна половине высоты трапеции.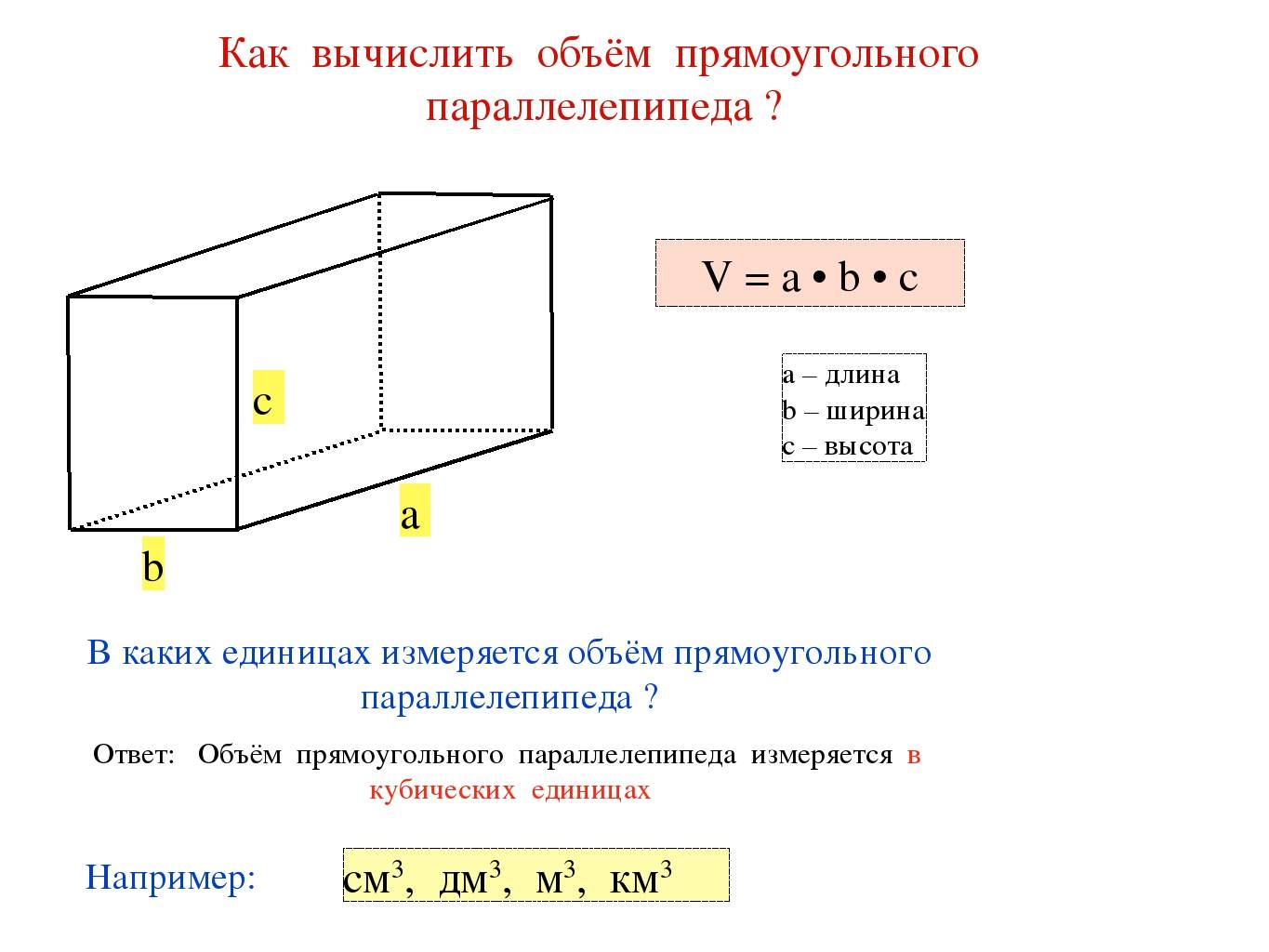

В случае трапеции основания нельзя выбирать произвольно. Две параллельных сторон являются основаниями, а высота, как всегда, является перпендикулярным расстоянием от одного основания до противоположного.

Площадь этого параллелограмма равна его высоте (половина высоты трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь равна полувысоты × ( основание1 + основание2 ). Поскольку параллелограмм состоит из того же «материала», что и трапеция, это тоже площадь трапеции.

В любом случае площадь трапеции равна × высоты × ( основание1 + основание2 ) .

Площадь других специальных четырехугольников

Площадь ромба

Площадь ромба можно найти, разрезав и переставив части так, чтобы получился параллелограмм. Это можно сделать несколькими способами:

Разрежьте более короткую диагональ (a), чтобы сформировать два конгруэнтных треугольника. Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы сформировать параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина большей диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
Другой подобный способ состоит в том, чтобы разрезать ромб на четыре конгруэнтных треугольника и перестроить их в прямоугольник с более короткой диагональю в качестве основания и половиной большей диагонали в качестве высоты.
Разрезав ромб на два конгруэнтных треугольника, мы можем вычислить площадь одного из треугольников, которая равна * основание (а) * высота (b) = ab.Затем умножьте на два, так как их два: 2 * ab = ab.

Зона воздушного змея

Площадь воздушного змея можно найти аналогично площади ромба. Если пересечь более длинную диагональ, получится два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с большей диагональю (b) в качестве основания и половиной меньшей диагонали (a) в качестве высоты. Таким образом, площадь становится b * a = ab. Более сложный подход включает в себя немного алгебры. Разрежьте воздушного змея по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (а) в качестве основания.Таким образом, площадь первого треугольника равна * волнистой линии, где волнистая линия — высота. Площадь второго треугольника равна a * (b — волнистая линия), где (b — волнистая линия) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится ( a * волнистой) + ( a * (b — волнистой)). Выделив a, мы имеем a (волнистый + b – волнистый) = ab.

Ну что ты знаешь. По сути, вам нужно знать только формулу площади параллелограмма, а затем вывести формулы для остальных.

Калькулятор прямоугольника

Прямоугольная форма

а = длина стороны а
b = длина стороны b
p = q = диагонали
P = периметр
А = площадь
√ = квадратный корень

Использование калькулятора

Используйте этот калькулятор, если вы знаете 2 значения для прямоугольника, включая 1 длину стороны, а также площадь, периметр или диагонали, и вы можете вычислить остальные 3 переменные прямоугольника. Квадратный калькулятор — это частный случай прямоугольника, в котором длины a и b равны.

Единицы: Обратите внимание, что единицы длины показаны для удобства. На расчеты они не влияют. Единицы используются для обозначения порядка вычисленных результатов, таких как футы, футы ² или футы ³ . Можно заменить любым другим базовым блоком.

Формулы прямоугольника

Площадь прямоугольника:
А = аб
Периметр прямоугольника:
Р = 2а + 2б
Диагонали многоугольника прямоугольника:
р = д = √(а ² + б ² )

Вычисления прямоугольников

Рассчитать A, P, p | Учитывая а, б
По заданным длинам сторон a и b вычислить площадь, периметр и диагонали
- А = аб
- Р = 2а + 2б
- р = д = √(а ² + б ² )
Рассчитать P, p, b | Учитывая А, а
Даны площадь и длина стороны a, вычислить периметр, диагонали и сторону b
- б = А/а
- Р = 2а + 2б
- р = д = √(а ² + б ² )
Рассчитать P, p, a | Дано А, б
По заданным площади и длине стороны b вычислить периметр, диагонали и сторону a
- а = А/б
- Р = 2а + 2б
- р = д = √(а ² + б ² )
Вычислить A, p, b | Учитывая П,
По заданным периметру и длине стороны a вычислить площадь, диагонали и сторону b
- б = (П — 2а) / 2
- А = аб
- р = д = √(а ² + б ² )
Вычислить A, p, a | Дано П, б
По периметру и длине стороны b вычислить площадь, диагонали и сторону a
- а = (П — 2б) / 2
- А = аб
- р = д = √(а ² + б ² )
Расчет A, P, b | Дан р, а
По диагоналям и длине стороны a вычислить площадь, периметр и сторону b
- б = √(р ² — а ² )
- А = аб
- Р = 2а + 2б
Расчет A, P, a | Дан р, б
По диагонали и длине стороны b вычислить площадь, периметр и сторону a
- а = √(р ² — б ² )
- А = аб
- Р = 2а + 2б

Узнайте все о коробке

Быстрый! Мне нужна помощь с: Выберите элемент справки по математике . ..Исчисление, Вычисление производных, Вычисление интеграции, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Расчет с комплексными числами, Умножение комплексных чисел, Полномочия комплексных чисел, Вычитание, преобразование площади, преобразование длины, преобразование массы, преобразование мощности, преобразование скорости, преобразование температуры, анализ объемных данных, поиск Анализ средних данных, Нахождение стандартного отклонения Анализ данных, ГистограммыДесятичные числа, Преобразование в дробьЭлектричество, Стоимость факторинга, Целочисленные коэффициенты, Наибольшие общие коэффициенты, Наименьшие общие дроби, Сложение дробей, Сравнение дробей, Преобразование дробей, Преобразование в десятичные дроби, Деление дробей, Умножение дробей, Сокращение дробей, Вычитание дробей, Что такое геометрия , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Any functionGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x,y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Уравнение из точки и наклонных линий, Уравнение из наклона и y-intLines, Уравнение из двух точек. Практика полиномовМатематика, Практика основ Метрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Разделение чисел, Умножение чисел, Сравнение чисел в ряду, Числовые числа в ряду, Размещение значений чисел, Произношение чисел, Округление чисел, Вычитание парабол, Графический полином, Сложение/вычитание многочленов. , Разложение на множители Разность квадратовПолиномы, Разложение на множители трехчленовПолиномы, Разложение на множители с GCFПолиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Что это такоеКвадратные уравнения, Квадратная формулаКвадратное уравнение ns, Решить с помощью FactoringRadicals, Other RootsRadicals, Square Roots Ratios, What they Repension, Saving forSale Price, Расчет научной нотации, Преобразование научной нотации, Разделение научной нотации, Умножение фигур, Прямоугольники, Упрощение, AnythingSimplifying, ExponentsSimplifying, LikeTermsSimplifying, ProductsTime, Think aboutTip, Figure aTrigonometry, Expressions Прямоугольные треугольникиWindchill, фигура

Как найти размеры прямоугольника | Домой Руководства

Автор Danielle Smyth Обновлено 15 декабря 2021 г.

Нахождение размеров прямоугольника — важный математический навык.Как и при нахождении размеров других геометрических фигур, вы должны следовать основным правилам и уравнениям для формул. Понимание этих принципов на первый взгляд может показаться неважным, но прилежный парень объясняет, что геометрия регулярно используется в повседневной жизни.

Основы прямоугольной геометрии

Разработчики видеоигр используют геометрические вычисления для проектирования своей графики, а архитекторы и дизайнеры используют геометрию для выполнения различных задач. Медицинские работники также часто используют его, особенно в медицинских приложениях, таких как МРТ, рентген, физиотерапия и ядерная визуализация.Вам также может понадобиться найти эти размеры, если вы работаете над проектом по благоустройству дома.

Чтобы найти размеры прямоугольника, вы начнете с нескольких измерений и выберите правильные уравнения для их подстановки. Двумя основными размерами прямоугольника являются длина (L) и ширина (W). Измерьте их в футах и дюймах с помощью рулетки или линейки. Оттуда вы можете вычислить площадь или периметр.

Вы можете упростить расчеты, преобразовав измерения в десятичные числа, чтобы избежать работы с дробями.Если вы используете дюймы, разделите на 12 следующим образом, используя в качестве примера 5 дюймов: 5 дюймов разделить на 12 = 0,42 фута.

Площадь и периметр: размеры прямоугольника

Важно различать площадь (A) и периметр (P) прямоугольников и квадратов. Согласно Куэмату, площадь — это количество пространства, занимаемое любой фигурой, например прямоугольником. Другими словами, общее количество квадратных единиц, которые могут поместиться в прямоугольник, определяет его фактическую площадь. Периметр — это измерение длины контура фигуры.В то время как площадь измеряется в квадратных единицах, периметр измеряется в футах, дюймах или сантиметрах.

Чтобы определить площадь, используйте это простое уравнение: Площадь = L, умноженная на W. Поскольку вы измеряете площадь в квадратных футах, ваше окончательное число должно отражать это. Если прямоугольник имеет длину 12 футов и ширину 6 футов, его площадь равна 72 квадратных фута. Когда некоторые измерения указаны в футах, а некоторые в дюймах, эти цифры должны быть преобразованы в футы, а затем в квадратные футы. Для этой операции разделите количество дюймов на 12.Например, 7 дюймов ÷ 12 = 0,583 фута.

Чтобы найти периметр, нужно сложить длины всех четырех сторон. Если у вас есть прямоугольник длиной 10 футов и шириной 8 футов, вы должны использовать уравнение 10 + 10 + 8 + 8 = 36. Это потому, что есть две стороны с длиной 10 футов и две стороны с 8-футовой длиной. ширина стопы.

2D-прямоугольники и 3D-прямоугольные призмы или кубоиды

В некоторых случаях может потребоваться вычислить размеры прямоугольника, который представляет собой просто два измерения.Это может быть полезно, если вы пытаетесь выяснить, какой размер ковра вам нужен для гостиной или если вы планируете прямоугольный огород. Приведенные выше формулы применимы к двумерным прямоугольникам.

В других случаях может потребоваться рассчитать размеры трехмерной фигуры, похожей на прямоугольник, например картонной коробки. Однако это не называется трехмерным прямоугольником; вместо этого его называют прямоугольной призмой или прямоугольным параллелепипедом. Вы можете рассчитать площадь поверхности такой формы.Это было бы полезно, если вам нужно выяснить, сколько оберточной бумаги вам понадобится, например, для упаковки пакета. Академия Хана объясняет, что для нахождения площади поверхности необходимо сложить площади всех шести граней или использовать формулу: площадь поверхности = 2lw + 2lh + 2hw.

Вы также можете рассчитать объем прямоугольного параллелепипеда. Это было бы полезно, если у вас есть прямоугольный аквариум и вам нужно знать, например, сколько воды потребуется для его заполнения. Формула для этого: объем = длина х ширина х высота.

Вещи вам понадобится

Paper

Область — область прямоугольников

Какая самая известная площадь в мире? Таймс Сквер? Площадь Тяньаньмэнь? Мэдисон парк? Квадратный корень? Губка Боб Квадратные Штаны?

Мы не хотим лопать ваши пузыри, но на самом деле ни один из них не является квадратом.

Квадраты — это четырехугольники, имеющие четыре прямых угла и четыре стороны одинаковой длины.Они также представляют собой особый тип прямоугольника. (Помните, что все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами.)

Но подождите. Если это прямоугольники, не можем ли мы просто использовать формулу площади для прямоугольников на квадратах? На самом деле мы можем, но мы сталкиваемся с небольшой проблемой. Какая сторона длина, а какая ширина?

Это своего рода вопрос с подвохом, потому что это не имеет значения. Так как все стороны квадрата одинаковы, длина и ширина точно такие же. Поскольку бессмысленно иметь две одинаковые стороны с разными именами, мы называем и длину, и ширину квадрата стороной .В конце концов, отдельные, но равные по своей сути неравны, и мы все за равенство.

Итак, когда мы применяем формулу A = lw к квадратам, мы можем сказать, что l = w = s , и в итоге получим A = 1

4 s 4 s Достаточно просто, не так ли?
Пример задачи
Найдите площадь квадрата.
Здесь у нас есть квадрат со стороной s = 4 единицы. Если бы мы не были уверены, что это квадрат, мы могли бы также сказать, что l = w = 4 единицы для прямоугольника.Однако, поскольку они равны, это, очевидно, квадрат. В любом случае мы можем воспользоваться формулой площади квадрата.

A = S = S = S = S 0 2
A = (4 единицы) ²
A = 16 единиц ²

Что касается площади квадратов, это действительно все, что есть сказать. Вероятно, вы столкнетесь с задачами, которые потребуют от вас найти l , w или s , прежде чем вы сможете вычислить A .Или, может быть, они попросят вас решить для одной из сторон, учитывая площадь. Есть много способов решить эти проблемы, но пока вы можете определить нужную формулу и переменную, которую ищете, проблем не должно возникнуть.

За исключением проблем с образцами, конечно.

Пример задачи

Найдите площадь квадрата с таким же периметром, как и прямоугольник ниже.

Периметр — это расстояние вокруг 2D-фигуры. В случае прямоугольника это просто сумма длин всех сторон.

P = 8 м + 10 м + 8 м + 10 м = 36 м

Итак, загадочный квадрат, площадь которого мы ищем, также имеет периметр 36 м.

Так как квадрат имеет стороны одинаковой длины, мы знаем, что его периметр будет равен сумме всех его сторон или 4-кратной длине любой стороны. Мы знаем, что периметр должен быть таким же, или 36 м, поэтому мы можем подставить его, чтобы найти на .

P = S = S + S + S + S + S
P = 4 S = 4 S
36 m = 4 S
S = 9 м

Теперь, когда мы знаем длину стороны квадрата, мы можем найти площадь.

A = S = S = S = S 0 2
A = (9 м) ² = 81 м ²

Область квадрата составляет 81 м ². Обратите внимание, что квадрат имеет тот же периметр, что и исходный прямоугольник, но площадь больше.

Площадь круга | Формула для радиуса, диаметра и длины окружности

Содержание

Какова площадь круга?
Как найти площадь круга

Как вычислить площадь круга
Площадь круга с использованием длины окружности

Какова площадь круга?

Круг не является квадратом, но площадь круга (количество внутреннего пространства, ограниченного кругом) измеряется в квадратных единицах.Найти площадь квадрата просто: длину умножить на ширину.

Круг, однако, имеет только диаметр , или расстояние в поперечнике. У него нет четко видимых длины и ширины, так как круг (по определению) — это множество всех точек, равноудалённых от данной точки в центре.

Тем не менее, имея только диаметр или половину диаметра ( радиус ), или даже только окружность (расстояние вокруг), можно вычислить площадь любого круга.

Как найти площадь круга

Напомним, что отношение длины окружности к ее диаметру всегда равно отношению 3.14159265, пи или π. Это число, π, умноженное на квадрат радиуса круга, дает площадь внутренней части круга в квадратных единицах.

Формула площади круга

Если вы знаете радиус r в любых единицах измерения (мм, см, м, дюймы, футы и т. д.), используйте формулу π r ² , чтобы найти площадь, A:

Ответом будут квадратные единицы линейных единиц, такие как мм2, см2, м2, квадратные дюймы, квадратные футы и так далее.

Вот круг радиусом 7 метров. Какова его площадь?

[вставить чертеж круга шириной 14 м, с радиусом 7 м]

А = π·r2

А = π × 72

А = π × 49

А = 153,9380 м2

Площадь круга с использованием диаметра

Если вы знаете диаметр d в любых единицах измерения, возьмите половину диаметра, чтобы получить радиус r в тех же единицах.

Вот жилой комплекс Сан-Сити, штат Аризона, круглый город диаметром 1.07 километров. Какова площадь Солнечного города?

Сначала найдите половину заданного диаметра, чтобы получить радиус:

1,072 = 0,535 км = 535 м

Подставьте радиус в нашу формулу:

А = π·r2

А = π × 5352

А = π × 286 225

А = 899 202,3572 м2

Чтобы перевести квадратные метры, м2, в квадратные километры, км2, разделите на 1 000 000:

А = 0,8992 км2

Самый западный круговой жилой комплекс Сан-Сити имеет площадь почти 1 квадратный километр!

Как вычислить площадь круга

Попробуйте эти вычисления площади для четырех разных кругов.Будь осторожен; некоторые дают радиус, r, и некоторые дают диаметр, d.

Не забудьте взять половину диаметра, чтобы найти радиус, прежде чем возвести радиус в квадрат и умножить на π.

Проблемы

Велосипедное колесо 406 мм
Колесо обозрения London Eye радиусом 60 метров
26-дюймовое велосипедное колесо
Самая большая в мире пицца имела радиус 61 фут 4 дюйма (736 дюймов)

Не подглядывайте в ответы, пока не сделаете расчеты!

ответы

Велосипедное колесо диаметром 406 мм имеет радиус r 203 мм:

А = πr2

А = π × 203 мм2

А = 637. 7433 мм2

Колесо обозрения London Eye Радиус 60 метров:

А = πr2

А = π × 60 м2

А = 188,4955 м2

26-дюймовое велосипедное колесо имеет радиус r 13 дюймов:

А = πr2

А = π × 13 дюйм2

A = 530,9291 дюйм2

Самая большая в мире пицца радиусом 736 дюймов:

А = πr2

А = π × 736 дюйм2

A = 1 701 788,17 дюйм2

Это 11 817.97 кв. футов пиццы! Ням! В любом случае, как вы справились с четырьмя задачами?

Площадь круга с использованием длины окружности

Если вы понятия не имеете, что такое радиус или диаметр, но знаете длину окружности С, вы можете еще найти площадь.

Формула площади и окружности

Окружность (расстояние по окружности) находится по этой формуле:

С = 2πr

Это означает, что мы можем взять формулу длины окружности и «решить для r», что дает нам:

г = C2π

Мы можем заменить r в нашей исходной формуле новым выражением:

А = π C2π2

Это выражение упрощается до следующего:

Эта формула работает всегда!

Как найти площадь с окружностью

Вот красивая пицца разумного размера , которую вы можете разделить с тремя друзьями. Вы случайно знаете, что длина окружности пиццы составляет 50,2655 дюйма, но не знаете ее общую площадь. Вы хотите знать, сколько квадратных дюймов пиццы придется каждому из вас.

[вставьте мультяшный рисунок типичной 16-дюймовой пиццы, но не указывайте диаметр]

Замените C на 50,2655 дюйма в формуле:

А = 50,265524π

А = 2526,62044π

A = 201,0620 дюйм2

Разделите общую площадь полноразмерной пиццы поровну между четырьмя друзьями, и каждый из вас получит 50.2655 дюймов2 пиццы! Это около трети квадратного фута на каждого из вас! Ням ням!

Следующий урок:

Площадь сектора круга

Вычисление периметра прямоугольников [Примеры вопросов]

Решение задач с прямоугольным периметром — навык, который имеет множество интересных практических применений. Например, мы можем использовать вычисления периметра для таких ситуаций, как требования к ограждению вокруг игрового поля, размеры рамы картины, расстояния вокруг пешеходной дорожки или размеры большого окна. Вычисление периметра прямоугольников — полезный навык, потому что он часто используется в нашей повседневной жизни.

Периметр прямоугольников Примеры вопросов

Давайте вспомним, что периметр относится к расстоянию вокруг внешней стороны двумерной формы. Может быть полезно визуализировать периметр в виде ограждения, окружающего парк или задний двор. Когда мы вычисляем периметр, мы, по сути, вычисляем общее расстояние вокруг этой двумерной формы.

Расчет задач периметра можно выполнять разными способами, но наиболее эффективная стратегия — просто использовать формулу периметра.

Чему равен периметр прямоугольника?

Формула периметра прямоугольника гласит, что P = (L + W) × 2, где P представляет периметр, L представляет длину, а W представляет ширину. Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр.Например, если прямоугольник ниже представляет собой сад, который нуждается в кирпичной рамке, мы можем использовать формулу периметра, чтобы определить, сколько футов кирпичной бордюры нам нужно всего.

Формула периметра прямоугольника

Формула утверждает, что P = (L + W) × 2, поэтому давайте подставим 14 футов для L и 6 футов для W. Теперь у нас есть P = (14 + 6) × 2, что упрощается до 40 или 40 футов.

Использование формулы периметра экономит нам немного времени, избегая альтернативной стратегии, которая заключалась бы в суммировании длин каждой стороны отдельно.14 + 6 + 14 + 6 даст правильный ответ, но эта стратегия обычно занимает больше времени, поэтому рекомендуется использовать формулу.

Однако не во всех задачах периметра можно получить длину и ширину таким простым способом. На самом деле, некоторые задачи о периметре дадут вам одно измерение, а также площадь прямоугольника. Чтобы решить такую проблему периметра, нам нужно пересмотреть наше понимание площади. Помните, чтобы вычислить площадь прямоугольника, мы просто умножаем длину на ширину.Прямоугольник размером 3,5 см на 4 см будет иметь площадь 14 см ², потому что 3,5 × 4 = 14. Давайте воспользуемся этим знанием площади и применим его к задаче периметра.

Например, предположим, что вам нужно обрамить большое прямоугольное окно площадью 35 квадратных футов и длиной 7 футов. Давайте используем то, что мы знаем о вычислении площади, чтобы найти периметр.

Мы знаем, что площадь поверхности находится путем умножения длины на ширину. Это означает, что семь умножить на что-то равно 35, 7 × ? = 35.Мы можем определить недостающую длину стороны, разделив 35 на 7, что равно 5. Теперь мы можем применить формулу периметра, потому что мы знаем, что длина равна 7 футам, а ширина — 5 футам.

P = (L + W) × 2 становится P = (7 + 5) × 2, что упрощается до 24 или 24 футов.

Теперь, когда мы рассмотрели формулу периметра и ее различные приложения, рассмотрим следующий вопрос. Есть ли у прямоугольника площадью 20 квадратных футов более одного возможного варианта периметра? Если вы сказали да, то вы правы.Прямоугольники с ограниченной площадью, например 20 квадратных футов, могут иметь различные периметры. Например, прямоугольник площадью 20 квадратных футов может иметь размеры 1 фут × 20 футов, 2 фута × 10 футов или 4 фута × 5 футов. Все эти варианты будут давать разные периметры, хотя все они имеют одинаковую площадь. . Давайте докажем эту концепцию, рассчитав периметр только что упомянутых трех возможных прямоугольников: 1 фут × 20 футов, 2 фута × 10 футов и 4 фута × 5 футов.

1 фут × 20 футов: P = (L + W) × 2 = (1 + 20) × 2 = 42 фута
2 фута × 10 футов = Д + Ш × 2 = (2 + 10) × 2 = 24 фута
4 фута × 5 футов = Д + Ш × 2 = 4 + 5 × 2 = 18 футов
*Также важно отметить, что формула P = (L + W) × 2 применима только к прямоугольникам.Эта формула будет работать только для четырехугольников, у которых два набора конгруэнтных сторон.

Примеры вопросов по периметру прямоугольника

Вот несколько примеров вопросов, касающихся площади прямоугольника.

Вопрос №1:

Какая формула используется для вычисления периметра прямоугольника?

$Периметр=4+(длина+ширина)$

$Периметр=\frac{(\text{длина}×\текст{ширина})}{2}$

$Периметр=( длина+ширина)×4 $

$Периметр=(длина+ширина)×2 $

Вопрос №3:

Определите периметр прямоугольника, если его площадь равна 64 м ² и его длина 16 м.

Ответ:

Чтобы определить периметр прямоугольника, нам сначала нужно определить ширину (w). Площадь прямоугольника вычисляется путем умножения $длина×ширина$, поэтому мы можем использовать следующее уравнение, чтобы найти недостающее значение (w).

Площадь = l × w
64 м ² =16 × w

Разделите обе стороны на 16, чтобы найти w.

w = 4 или 4 м

Теперь, когда мы знаем длину и ширину, мы можем использовать формулу $Периметр=(длина+ширина)×2$, чтобы найти периметр.Подставив 16 м в длину и 4 м в ширину, мы получим следующее: $Периметр=(16 м+4 м)×2$, что упрощается до 40 м. Периметр прямоугольника 40 метров.

Вопрос №5:

Глория проектирует сад для своего заднего двора. Она знает, что хочет иметь 24 квадратных фута в саду, но она гибка в отношении размеров. Она хочет поставить забор вокруг сада, но забор (за метр) может быть довольно дорогим, поэтому она хочет сравнить варианты.