Как посчитать длину стен, зная площадь комнаты
Статья будет полезна тем, кто столкнулся с необходимостью рассчитать планировку комнат в новостройке. Имеющийся на руках план всегда содержит информацию о площадях помещений квартиры, но не всегда в нем есть информация о длинах стен, перегородок, дверных и оконных проемов и т.д. Мы расскажем о том, как восполнить этот недостаток, воспользовавшись незатейливыми математическими расчетами, которые будут понятны даже семикласснику.
Предположим, у нас есть план квартиры, такой как показан на рисунке ниже. Этот план нам потребуется в электронном виде – в виде картинки, которую мы сможем открыть графическим редактором (например, в формате .jpeg или .png).
Если у Вас план только на бумаге, то можно его ровно без перекосов сфотографировать и сохранить в компьютер или загрузить с сайта застройщика, если такая возможность имеется.
В нем нам нужно выбрать любую комнату строго прямоугольной формы (или квадратной). В нашем примере выберем кухню, площадь которой нам известна, и составляет 15,13 квадратных метров.
Условно обозначим длину одной стороны прямоугольника буквой «a», длину другой «b», как принято в школьном курсе геометрии.
Площадь прямоугольника, как мы помним определяется произведением его сторон:
С помощью встроенного графического редактора Paint или другого, например, PickPick открываем наше изображение с планом квартиры. Затем с помощью инструмента «Выделение» вычисляем длину и ширину нашего прямоугольника в пикселях, как показано на рисунке ниже.
Полученные значения запишем, обозначив их, например, как «a» со штрихом и «b» со штрихом, для длины и ширины комнаты соответственно.
Более точной единицей измерения для полученных значений будет не «пиксель», а скорее сторона пикселя, поскольку пиксель представляет собой квадрат определенной площади и для измерения длин не очень подходит.
Подсчитаем площадь комнаты в пикселях:
Далее, введем коэффициент, который будет показывать насколько отличается длина стороны пикселя нашего изображения от длины квадратного метра. Обозначим этот коэффициент буквой «k».
Искомые значения длины и ширины комнаты, будут найдены по формуле:
Остается выяснить чему равен коэффициент. Для этого составим простое уравнение, из которого элементарно находим значение коэффициента, как корень из соотношения площадей в пикселях и в квадратных метрах.
Подставляем значение найденного коэффициента в формулы для нахождения длины и ширины комнаты и получаем искомые величины.
Зная коэффициент, мы можем получить длину в метрах для любого объекта в имеющемся плане. Нужно только узнать длину этого объекта в пикселях и умножить полученное значение на коэффициент.
Обращаю внимание, что значение вычисленного коэффициента подходит только для данного конкретного изображения, из которого этот коэффициент вычислялся. Если возьмете другое изображение, то коэффициент придется считать заново.
На этом все, если остались вопросы, оставляйте их в комментариях к статье.
Столкнулась с той же проблемой. Решила вопрос следующим образом.
1. Первое, что нам надо — распечатать план квартиры и найти на нём одну любую комнату правильной прямоугольной формы. Измеряем на распечатанном плане длину и ширину комнаты в см. В моём случае это было 2,5 см и 2,75 см.
2. Складываем 2,5 и 2,75 = 5,25. Соответственно, у нас есть сумма длин двух стен.
3. Вычисляем сколько в процентном соотношении от 5,25 занимает каждая стена. Составляем пропорцию.
5,25 — 100%
2,5 — х%
х = (2,5*100)/5,25 = 47,62% (округлила)
Соответственно вторая стена, которая 2,75 см на плане — 100% — 47,62% = 52,38%
3. Теперь берём известную нам по плану реальную площадь комнаты, в моём случае 2,51 метра квадратных. Находим корень из этого числа, для этого можно обратиться к Святому Гуглу, вбиваем в поисковик «корень квадратный из 2,51» и вуаля — 1,5842.
Что значит это число? Это значит, что если бы наша комната была идеально квадратной, то каждая стена была бы длиной 1,5842 м. Проверяем: 1,5842*1,5842 = 2,509.
4. Теперь мы можем найти реальную длину наших стен. Складываем длины двух стен 1,5842+1,5842 = 3,1684. — Сумма длин двух стен.
Благодаря процентному соотношению стен, которое мы нашли в первом пункте, мы можем узнать длину каждой из них.
Открываем калькулятор: 3,1684*47,62% = 1,5087м.
Вторую стену найти легко: 3,1684-1,50 = 1,6597м.
5. Чтобы не париться так с измерением следующих комнат, вычисляем масштаб!
Стена на плане длиной 2,5 см имеет реальную длину 150 см. Составляем пропорцию:
2,5 см — 150,87 см
1 см — х %
х = 60,34
Теперь мы знаем, что у нас масштаб плана 1: 60,3.
То есть 1 см на распечатанном плане соответствует 60,3 см в реальности. И теперь вы можете измерить всю квартиру по плану.
Скажу сразу, что масштаб данным способом получается примерный и может отличаться от настоящего на несколько сантиметров.
Инструкция для калькулятора расчета площади неправильного земельного участка

Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.
Важно! Важ участок должен приблизительно вписываться в окружность. Иначе расчеты будут не совсем точными.
Указываем все данные в метрах
A B, D A, C D, B C— Размер каждой стороны делянки.
Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.
Методика определения размеров участка ручным методом
Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков. Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.
Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².
После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.
В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах. Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.
Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.
Общие данные
Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.
Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).
На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.
Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.
И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.
Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.
Онлайн калькулятор: Сегмент круга
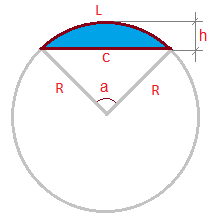
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:

Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисленияЗнаков после запятой: 2
save Сохранить extension Виджет
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Параметры сегмента по хорде и высоте
Точность вычисленияЗнаков после запятой: 2
Угол (градусы)
save Сохранить extension Виджет
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Площадь сегмента круга по радиусу и высоте
Точность вычисленияЗнаков после запятой: 2
Угол (градусы)
Найдите длину и ширину прямоугольника
Вопрос
Нарисуйте прямоугольник с периметром 18 см и площадью более 18 кв. Какие размеры?Ответ
ШАГ 1: Будет полезно, если вы сможете вспомнить основные свойства прямоугольника.Прямоугольник определяется размерами длины и ширины. Он имеет четыре стороны, а также противоположные стороны прямоугольника имеют одинаковую длину.Вам дан периметр прямоугольника. Как вы знаете, периметр — это общее расстояние вдоль внешней стороны прямоугольника. Формула, используемая для расчета периметра:
В формуле переменные × и × обозначают длину и ширину прямоугольника соответственно.ШАГ 2: Поскольку вы знаете значение периметра, вы можете произвести замену в формуле.
Делив обе стороны на 2, уравнение изменится на9 = л + ш или л + ш = 9.
ШАГ 3: Подумайте о возможных размерах, которые может иметь прямоугольник, если сумма длина и ширина равна 9 см. Но, учитывая, что площадь прямоугольника должна быть больше 18 кв. Это означает, что произведение длины и ширины должно быть больше 18.
Попробуйте разные значения l и w , чтобы сумма равнялась 9.Найдите соответствующие продукты, а затем составьте таблицу значений.
Если вы наблюдаете за таблицей, вы можете обнаружить, что площадь прямоугольника больше 18, только если размер прямоугольника равен либо 4 см на 5 см, либо 5 см на 4 см.ШАГ 4: Выберите любой из двух желаемых размеров. Затем, наконец, нарисуйте прямоугольник.
,Калькулятор длины, ширины и высоты к объему
Нажмите, чтобы обновить страницу с уникальным веб-адресом для закладки или обмена текущими настройками
✕ очистить настройки
К сожалению, рисунок не может быть отображен здесь, потому что ваш браузер не поддерживает HTML5 Canvas.Похожие инструменты
Руководство пользователя
Этот онлайн-инструмент рассчитывает объем прямоугольной коробки по размерам длины, ширины и высоты. Нет необходимости вводить значения в одних и тех же единицах измерения, просто выберите предпочтительные единицы для каждого измерения и рассчитанного объема.
После того, как измерения введены для длины, ширины и высоты, рассчитанный объем будет показан в поле для ответов. Также будет нарисован график формы и размеров тома, который будет обновляться при каждом изменении введенных значений.
Формула
Формула, используемая этим калькулятором для расчета объема прямоугольной коробки:
В = Д · Ш · В
символов
- V = Объем
- L = длина
- W = ширина
- H = высота
— длина, ширина и высота
Введите измерение длины, ширины и высоты для прямоугольной рамки.
Для преобразования единиц измерения, указанных для длины, ширины и высоты, используются следующие коэффициенты преобразования единиц СИ в метрах (м):
- нм (нм) — 0,000000001 м
- микрометров (мкм) — 0,000001 м
- мм (мм) — 0,001 м
- сантиметр (см) — 0,01 м
- дюйма (дюйма) — 0,0254 м
- футов (футов) — 0,3048 м
- ярдов — 0,9144 м
- метр (м) — 1 м
- км (км) — 1000 м
- мили (ми) — 1 609.344 м
- морская миля (нми) — 1852 м
Расчет объема
Это объем прямоугольной формы, который соответствует размерам, введенным для длины, ширины и высоты. Объем рассчитывается путем умножения каждого измерения и последующего преобразования его в выбранные объемные единицы.
Следующие коэффициенты пересчета в кубических метрах (м³) используются для преобразования рассчитанного объема в различные объемные единицы:
- кубических нанометра (куб. Нм) — 1 x 10 -27 м³
- кубических микрометров (куб. Мкм) — 1 x 10 -18 м³
- кубических миллиметра (куб. Мм) — 1 x 10 -9 м³
- кубических сантиметра (куб. См) — 1 x 10 -6 м³
- миллилитров (мл) — 1 x 10 -6 м³
- кубических дюйма (куб. Дюйм) — 1.6387064 x 10 -5 м³
- унции жидкости (жидких унций, имперский) — 2,84130625 x 10 -5 м³
- унции жидкости (жидкая унция, США) — 2.95735295625 x 10 -5 м³
- пинта (пт, жидкость США) — 4,73176473 x 10 -4 м³
- пинта (порт, имперский) — 5,6826125 x 10 -4 м³
- л (л) — 1 x 10 -3 м³
- галлона (галлон, жидкость США) — 3,785411784 x 10 -3 м³
- галлона (галлон, имперский) — 4.54609 x 10 -3 м³
- кубических футов (куб. Футов) — 0,028316846592 м³
- баррелей (баррель нефти) — 0,158987294928 м³
- куб. Ярда (куб. М) — 0,764554857984 м³
- кубометров (кубометров) — 1 м³
- кубических километра (куб. Км) — 1 x 10 +9 м³
- куб. Миля (куб. Миль) — 4168181825.440579584 м³
- кубическая морская миля (куб. Миль) — 6352182208 м³
приложений
Используйте этот калькулятор длины x ширины x высоты для определения объема в следующих приложениях:
- Объем посылки, подлежащей отправке, для добавления к отгрузочной документации
- Объем гравия, необходимый для заполнения дорожки, автостоянки или подъездной дороги.
- Емкость резервуара прямоугольного сечения.
- Объем грузового пространства легкового или грузового автомобиля или фургона.
- Объем загрузки автомобиля для перемещения хранилища.
- Максимальная вместимость, которую может вместить резервуар для воды.
- Сколько топлива требуется для заполнения бака.
- Размер пакета, необходимого для предотвращения утечек и разливов из контейнеров IBC.
- Количество мешков, необходимых для каждого материала для строительного проекта.
- Количество почвы, необходимое для заполнения сеялки.
- Количество воды, необходимое для заполнения аквариума / аквариума.
- Заполните емкость для пруда.
- Складское помещение вместимостью от габаритов. Объем емкости IBC
- .
- Объем заполнения бассейна.
- Место для багажа внутри чемодана.
- Цементная смесь, необходимая для заполнения фундаментов / фундаментов.
- Объем кузова пикапа.
- Громкость корпуса динамика.
- Емкость для кормления животных.
- Садовый сарай, солярий или теплица с цементным покрытием.
Помощь
25 x 10 x 12 дюймов бак в американских галлонах
Сколько американских галлонов будет вмещать резервуар шириной 10 дюймов, высотой 12 дюймов и длиной 25 дюймов?
Принимая во внимание внутренние размеры или отсутствие толщины стенки, объем резервуара составляет 12,987013 галлона США.
,Что такое круг?
«Локус — это кривая или другая фигура, образованная всеми точками, удовлетворяющими определенному уравнению».
Окружность — это односторонняя фигура, но она также может быть описана как местоположение точек, где каждая точка находится на одинаковом расстоянии (на одинаковом расстоянии) от центра.
Пожалуйста, добавьте этот сайт в свой рекламный блок!
Для написания этих статей требуются время и усилия, и авторам нужно зарабатывать.Пожалуйста, рассмотрите возможность включения этого сайта в свой блокатор рекламы, если считаете его полезным. Вы можете сделать это, щелкнув значок блокировщика на панели инструментов и отключив его. Блокатор все равно будет работать на других сайтах.
Спасибо!
Угол, образованный двумя лучами, исходящими из центра круга Углы колеблются от 0 до 360 градусов.
Мы часто «заимствуем» буквы из греческого алфавита, чтобы использовать их в математике.Таким образом, греческая буква «p», которая является π (pi) и произносится как «пирог», является отношением длины окружности к диаметру.
Мы также используем греческую букву θ (theta) и произносится «the — ta» для обозначения углов. части круга
Сектор — это часть круглого диска, окруженная двумя лучами и дугой.
Сегмент — это часть круглого диска, ограниченная дугой и хордой.
Полукруг — это особый случай сегмента, образованного, когда хорда равна длине диаметра.
Что такое Pi (π)?
Pi, представленный греческой буквой π — это отношение длины окружности к диаметру круга. Это нерациональное число, которое означает, что оно не может быть выражено в виде дроби в форме a / b, где a и b являются целыми числами.
Пи равно 3.1416 с округлением до 4 знаков после запятой.
Какова длина окружности круга?
Если диаметр круга равен D, а радиус равен R.
Тогда окружность C = πD
Но D = 2R
Так с точки зрения радиуса R
C = πD = 2πR
Какова площадь круга?
Площадь круга A = πR 2
Но D = R / 2
Таким образом, площадь с точки зрения радиуса R составляет
A = πR 2 = π (D / 2) 2 = πD 2 /4
Что такое градусы и радианы?
Углы измеряются в градусах, но иногда, чтобы сделать математику проще и элегантнее, лучше использовать радианы, что является еще одним способом обозначения угла.Радиан — это угол, образованный дугой длины, равной радиусу круга. («Субстанция» означает соединение двух линий от конца дуги до центра).
Длина дуги R, равная радиусу R, соответствует углу в 1 радиан.
Таким образом, если окружность окружности равна 2πR = 2π раз R, угол для полной окружности будет в 2π раз на один радиан = 2π
А 360 градусов = 2π радиан
Как преобразовать градусы в радианы
360 градусов = 2π радиан
Деление обеих сторон на 360 дает
1 градус = 2π / 360 радиан
Затем умножьте обе стороны на
θ градусов = (2π / 360) x θ = θ (π / 180) радиан
Чтобы преобразовать градусы в радианы, умножьте на π / 180
Как перевести из радианов в градусы
2π радиан = 360 градусов
Разделите обе стороны на 2π, давая
1 радиан = 360 / (2π) градусов
Умножим обе стороны на θ, поэтому для угла θ радианы
θ радиан = 360 / (2π) x θ = (180 / π) θ градусов
Итак, чтобы преобразовать радианы в градусы, умножьте на 180 / π
Как определить длину дуги
Вы можете определить длину дуги, рассчитав, какую долю составляет угол 360 градусов для полного круга.
Полный угол 360 градусов имеет связанную длину дуги, равную окружности C
Итак, 360 градусов соответствует длине дуги C = 2πR
Разделите на 360, чтобы найти длину дуги для одного градуса:
1 градус соответствует длине дуги 2πR / 360
Чтобы найти длину дуги для угла θ, умножьте приведенный выше результат на θ:
1 x θ соответствует длине дуги (2πR / 360) x θ
Таким образом, длина дуги s для угла θ равна:
с = (2πR / 360) x θ = πθR / 180
Для радианов вывод намного проще:
По определению 1 радиан соответствует длине дуги R
Итак, если угол равен θ радиан, умножение на θ дает:
Длина дуги s = R x θ = Rθ
Что такое синус и косинус?
Прямоугольный треугольник имеет один угол измерения 90 градусов.Сторона, противоположная этому углу, называется гипотенузой , , и это самая длинная сторона. Синус и косинус являются тригонометрическими функциями угла и являются отношениями длин двух других сторон к гипотенузе прямоугольного треугольника.
На диаграмме ниже один из углов представлен греческой буквой θ.
Сторона а известна как «противоположная» сторона, а сторона b является «смежной» стороной с углом θ.
синус θ = длина противоположной стороны / длина гипотенузы
косинус θ = длина соседней стороны / длина гипотенузы
Синус и косинус применяются к углу, не обязательно к углу в треугольнике, поэтому можно просто иметь две линии, встречающиеся в одной точке, и оценивать синус или cos для этого угла.Однако синус и cos получаются из сторон воображаемого прямоугольного треугольника, наложенного на линии. На второй диаграмме ниже вы можете представить прямоугольный треугольник, наложенный на фиолетовый треугольник, из которого можно определить противоположные и соседние стороны и гипотенузу.
В диапазоне от 0 до 90 градусов, синус находится в диапазоне от 0 до 1, и потому в диапазоне от 1 до 0
Помните, что синус и косинус зависят только от угла, а не от размера треугольника. Таким образом, если длина a изменяется на диаграмме ниже, когда треугольник изменяется в размере, гипотенуза c также изменяется в размере, но отношение a к c остается постоянным.
Синус и косинус иногда сокращаются до греха и cos
Как рассчитать площадь сектора круга
Общая площадь круга равна πR 2 , что соответствует углу 2π радиан для полного круга.
Если угол θ, то это θ / 2π — доля полного угла для круга.
Таким образом, площадь этого сектора умножается на общую площадь круга
.или
(θ / 2π) x (πR 2 ) = θR 2 /2
Как рассчитать длину хорды, создаваемой углом
Длину хорды можно рассчитать с помощью правила косинуса.
Для треугольника XYZ на диаграмме ниже сторона, противоположная углу θ, является хордой с длиной c.
Из правила косинуса:
c 2 = R 2 + R 2 -2RRCos θ
Упрощение:
c 2 = R 2 + R 2 -2R 2 Cos θ
или c 2 = 2R 2 (1 — Cos θ)
Но из формулы полуугольника (1-cos θ) / 2 = sin 2 (θ / 2) или (1-cos θ) = 2sin 2 (θ / 2)
Подставляя дает:
c 2 = 2R 2 (1 — Cos θ) = 2R 2 2sin 2 (θ / 2) = 4R 2 sin 2 (θ / 2)
Получение квадратных корней с обеих сторон дает:
c = 2 Rsin (θ / 2)
Более простой вывод, полученный путем разделения треугольника XYZ на 2 равных треугольника и использования отношения синуса между противоположностью и гипотенузой, показан в расчете площади сегмента ниже.
Как вычислить площадь отрезка круга
Чтобы вычислить площадь отрезка, ограниченного хордой и дугой, образованной углом θ, сначала определите площадь треугольника, а затем вычтите ее из площади сектор, дающий площадь сегмента. (см. диаграммы ниже)
Треугольник с углом θ можно разделить пополам, получив два прямоугольных треугольника с углами θ / 2.
Грех (θ / 2) = а / р
So a = RSin (θ / 2) (длина шнура c = 2a = 2RSin (θ / 2)
Cos (θ / 2) = b / R
So b = RCos (θ / 2)
Площадь треугольника XYZ равна половине основания по высоте перпендикуляра, поэтому, если основание — это хорда XY, половина основания — это a, а высота перпендикуляра — b.Таким образом, площадь:
ab
Подстановка для a и b дает:
RSin (θ / 2) RCos (θ / 2)
= R 2 Sin (θ / 2) Cos (θ / 2)
Но формула двойного угла утверждает, что Sin (2θ) = 2Sin (θ) Cos (θ)
Подставляя дает:
Площадь треугольника XYZ = R 2 Sin (θ / 2) Cos (θ / 2) = R 2 ((1/2) Sin θ) = (1/2) R 2 Sin θ
Также площадь сектора составляет:
R 2 (θ / 2)
А площадь сегмента — это разница между площадью сектора и треугольником, поэтому вычитание дает:
Площадь сегмента = R 2 (θ / 2) — (1/2) R 2 Грех θ
= (R 2 /2) (θ — Sin θ)
Уравнение круга в стандартной форме
Если центр круга расположен в начале координат, мы можем взять любую точку на окружности и наложить прямоугольный треугольник с гипотенузой, соединяющей эту точку с центром.
Тогда из теоремы Пифагора квадрат на гипотенузе равен сумме квадратов на двух других сторонах. Если радиус окружности равен r, то это гипотенуза прямоугольного треугольника, поэтому мы можем записать уравнение как:
x 2 + y 2 = r 2
Это уравнение круга в стандартной форме в декартовых координатах.
Если окружность центрирована в точке (a, b), уравнение окружности будет следующим:
(x — a) 2 + (y — b) 2 = r 2
Пример
Вот практический пример использования тригонометрии с дугами и хордами.Изогнутая стена построена перед зданием. Стена представляет собой часть круга. Необходимо определить расстояние от точек на кривой до стены здания (расстояние «B»), зная радиус кривизны R, длину хорды L, расстояние от хорды до стены S и расстояние от центральной линии до точки на Кривая А. Посмотрите, можете ли вы определить, как были получены уравнения. Подсказка: используйте теорему Пифагора.
,Треугольник Калькулятор
Пожалуйста, предоставьте 3 значения, включая как минимум одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Когда радианы выбраны в качестве единицы измерения угла, они могут принимать значения, такие как pi / 2, pi / 4 и т. Д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, где встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединяются тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами.Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются исходя из длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковую длину, это называется разносторонним, как показано ниже.
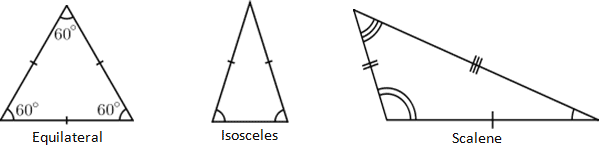
Отметки на краю треугольника представляют собой обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает равную длину.Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых различными числами концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины. Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет угловые метки, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто представление треугольника.Когда вводятся фактические значения, вывод калькулятора будет отражать, как должна выглядеть форма входного треугольника.
Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямые или наклонные. Прямой треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самый длинный край прямоугольного треугольника, то есть край, противоположный прямому углу, называется гипотенузой.Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупом треугольнике один из углов треугольника больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.
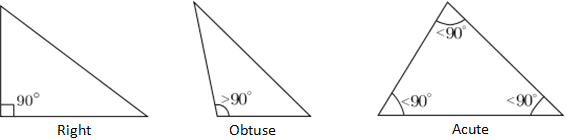
Факты о треугольнике, теоремы и законы
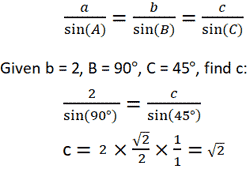
- Учитывая длины всех трех сторон любого треугольника, каждый угол может быть рассчитан с использованием следующего уравнения.Обратитесь к треугольнику выше, предполагая, что a, b и c являются известными значениями.
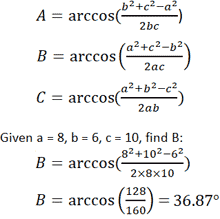
Площадь Треугольника
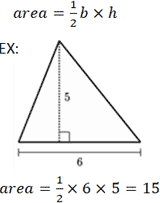
Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для расчета площади треугольника включает его основание b и высоту h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, до точки на основании, которая образует перпендикуляр.
Учитывая длину двух сторон и угол между ними, следующая формула может быть использована для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше. Дано a = 9, b = 7 и C = 30 °:
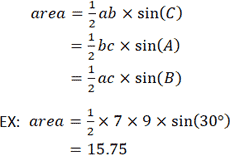
Другой метод расчета площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:
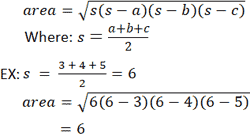
Медиана, инрадиус и оксирадиус
Медиана
Медиана треугольника определяется как длина отрезка, который простирается от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, все из которых будут пересекаться в центроиде (среднее арифметическое положение всех точек в треугольнике) треугольника.Обратитесь к рисунку, приведенному ниже, для пояснения.
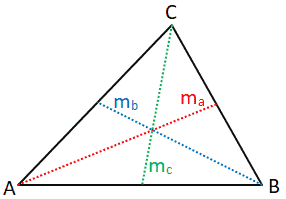
Медианы треугольника представлены отрезками линии m a , m b и m c . Длина каждой медианы может быть рассчитана следующим образом:
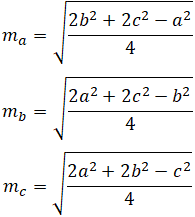
Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.
В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m и может быть рассчитана следующим образом:
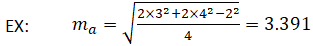
Inradius
Инрадиус — это радиус самого большого круга, который будет помещаться внутри данного многоугольника, в данном случае, треугольника.Inradius перпендикулярен каждой стороне многоугольника. В треугольнике значение радиуса можно определить, построив две угловые биссектрисы для определения стимулятора треугольника. Inradius — это перпендикулярное расстояние между стимулятором и одной из сторон треугольника. Любая сторона треугольника может использоваться до тех пор, пока определяется перпендикулярное расстояние между стороной и стимулятором, поскольку стимулятор, по определению, равноудален от каждой стороны треугольника.
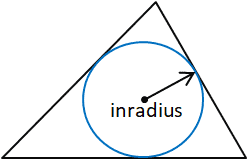
Для целей данного калькулятора, вычисление радиуса рассчитывается с использованием площади (площади) и полупериметра (ов) треугольника, а также следующих формул:
, где a, b и c — стороны треугольника
Circumradius
Циррадиус определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этого круга, где встречаются все перпендикулярные биссектрисы каждой стороны треугольника, является окружным центром треугольника и является точкой, из которой измеряется окружность. Окружный центр треугольника не обязательно должен быть внутри треугольника. Стоит отметить, что все треугольники имеют окружность (круг, проходящий через каждую вершину) и, следовательно, окружность.
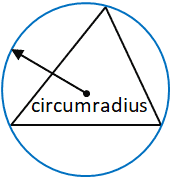
Для целей данного калькулятора круговой луч рассчитывается по следующей формуле:
Где a — сторона треугольника, а A — угол, противоположный стороне a
Хотя используются сторона А и угол А, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.
,