 Как рассчитать, посчитать объем помещения.
Как рассчитать, посчитать объем помещения.Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
ФормулаПример расчета объема помещения по формуле
Калькулятор площади стены или пола
Вставьте размеры помещения и получите результат.
Объем комнаты. Как рассчитать объем комнаты
В качестве вступления предлагаем разобраться с причинами, по которым нам может потребоваться рассчитать объем комнаты. Чаще всего сведения о количественном параметре пространства могут понадобиться:
а) при выборе и покупке домашнего кондиционера, так как эта техника подбирается исключительно на основании объема комнаты или помещения в целом;
б) при выборе и покупке домашнего отопительного радиатора, обогревающего конкретный объем комнаты;
в) при установке стационарного секционного радиатора, так как в этом случае объем комнаты будет влиять на количество необходимых секций.
При измерении объема помещения или комнаты, не помешает учитывать то, что объем измеряется кубометрами (кубическими метрами, метрами в кубе, м3), кубическими сантиметрами (сантиметр кубический, сантиметр в кубе, см3) или же литрами (в случае с жидкостями). Дополнительно можно сказать, что объем нередко ассоциируется с понятием вместимости, количеством внутреннего пространства.
Примечание: объем комнаты (м3) нередко путают с площадью комнаты (м2), что в корне неверно. Объем, в отличие от площади, величина трехмерная, учитывающая все 3 измерения:
- ширину
- высоту


Как рассчитать объем комнаты
Для выполнения необходимых вычислений нам нужно площадь комнаты помножить на высоту комнаты.
О том, как измерить площадь комнаты, мы уже говорили в статье сайта «Что Делать» под названием «Площадь комнаты. Как рассчитать площадь комнаты». Перейдя по ссылке, читатель может ознакомиться с материалом этой статьи. Тем не менее, чтобы не утруждать читателя, повторим еще раз, как рассчитывается площадь комнаты, и далее посчитаем объем комнаты:
СПОСОБ №1
1. Рассчитываем площадь:
- измеряем рулеткой длину большой стены (для простоты мерить можно по полу)
- измеряем рулеткой длину короткой стены
- умножаем первую цифру на вторую и получаем площадь (квадратуру, метры квадратные, м2)
2. Рассчитываем объем комнаты:
- измеряем высоту (расстояние от пола до потолка)
- умножаем высоту на площадь комнаты, которую мы вычислили на предыдущем этапе, получаем объем, измеряемый в кубометрах (метрах кубических, м3).
СПОСОБ №2
1. Рассчитываем объем как произведение 3-х измерений:
- измеряем по полу или стене (как будет удобней) длину большой стены
- измеряем рулеткой длину малой стены
- измеряем высоту потолков
- перемножаем 3 полученные величины и получаем тот же самый объем комнаты.
И первый, и второй способ вычисления объема комнаты дают идентичные (одинаковые) численные значения. Разница лишь в этапах выполнения расчетов.
Обязательно нужно подчеркнуть, что такие измерения годятся лишь в том случае, если комната имеет форму прямоугольного параллелепипеда. Выражаясь проще, если стены, пол и потолок комнаты представляют собою прямоугольники или же квадраты. В случае, когда нужно измерить объем комнаты, в которой есть выступы и перегородки, двухуровневый навесной потолок, альков и другие геометрические элементы, воспользуйтесь одним из советов, рассмотренных ниже.
Примечание: при выполнении измерений и расчетов, о которых будет сказано ниже, придется подключить свое воображение, мысленно разбив комнату на несколько геометрических фигур, измеряя их объемы по отдельности и суммируя полученные кубометры. Для простоты визуализации используйте распространенные формы вроде квадрата, параллелепипеда, цилиндра.
1. Измерить объем комнаты неправильной формы можно, если рассчитать площадь каждого ее элемента, сложить результаты и умножить общую площадь на высоту потолков. Аналогичная процедура описана в СПОСОБЕ №1.
2. При измерении объема помещения, в котором имеются потолки разной высоты, нужно:
- рассчитать по отдельности объем каждой из комнат
- сложить полученные расчетные данные, получив общий объем помещения.
3. Если потолок в комнате имеет арочную форму (альков), стоит воспользоваться формулой для расчета объема цилиндра: V= Pi * R2 * H. Где:
- Н – это высота цилиндра
- R – радиус цилиндра (R2 – радиус в квадрате)
- Pi – число «Пи», равное 3,14.
Определив объем всего цилиндра (коим, конечно, альков не является), остается отнять от него примерную часть лишнего (усеченного полом) объема.
4. Зная объемы всех отдельных элементов комнаты и помещения в целом, можно посчитать общий внутренний объем, сложив вместе все полученные кубометры.
Для многих, кто сталкивается с пиломатериалом, вопрос о том, как посчитать кубатуру необрезной и обрезной доски остаётся сложным заданием. В принципе, это довольно легко и просто. Ниже мы рассмотрим основные способы расчёта кубатуры доски.
На уроках геометрии довольно часто приходилось рассчитывать объём чего – либо. Ситуация точно также обстоит с обрезными пиломатериалами. Просто нужно перемножить ширину на высоту и на длину. Естественно, не нужно это делать на целой пачке бруса или доски. Достаточно будет, если вы посчитаете кубатуру одной доски (бруса), затем просто нужно пересчитать общее количество досок в пачке и кубатуру одной доски помножить на посчитанное количество досок. Ещё одно важно правило, при расчёте кубатуры одной доски, все размеры нужно привести к единому измерению, то есть или всё переводится в сантиметры, миллиметры или же в метры. А замеры мы проводим по следующим параметрам: толщина, ширина, длина.
При расчёте кубатуры необрезной доски, тоже измеряется ширина, длина и высота. Только в необрезных пиломатериалах невозможно рассчитать кубатуру одной доски, поэтому доску нужно уложить в пачку, обмерять и применить различные коэффициенты. Для более точного расчёта, лучше всего сложить доску в одну стопку, затем измерить посередине самую широкую и самую тонкую доски, далее сложить эти два показателя и разделить на два. В результате мы получим усреднённую ширину. А длину и высоту измеряем как обычно.
Далее нужно помножить толщину стопки на ширину и длину и применить понижающий коэффициент. По ГОСТу, для полубруса он составляет 0,5, а для необрезной доски 0,63. Но, очень часто, для упрощения расчётов, производители на пилорамах производят отгрузку пиломатериала, которые имеют коэффициент 0,7. Когда таким образом будет посчитана одна стопка, нужно переходить ко второй, третьей и так, до тех пор, пока не будет пересчитан весь пиломатериал.
Как посчитать кубатуру фундамента
- столбчатый
- ленточный
- плитный
При расчёте кубатуры фундамента столбчатого типа, сначала нужно рассчитать кубатуру одного бетонного столбика. Для этого умножается длина на ширину. Если же применяются столбики круглого сечения, то умножается радиус квадрата на коэффициент «Пи – 3,14» и получившийся результат умножаем на высоту столбика. Далее результат перемножается на общее количество столбиков, которые размещены по территории. Это и будет общая кубатура фундамента. В тех случаях, когда столбики соединены раствором, то нужно воспользоваться формулой параллелепипеда.
При расчёте кубатуры фундамента ленточного типа сначала определяется вид сечения. Когда оно одинаковое, то периметр территории умножается на толщину и длину. В том случае, когда оно разное, необходимо просто рассчитать объёмы каждого участка по отдельности и в итоге, сложить все полученные результаты.
Объём — количественная характеристика пространства. Объём помещения определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр.
Вам понадобится
- Для измерения объема помещения вам потребуется рулетка, лист бумаги, калькулятор, ручка.
Инструкция
Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед. Параллелепипед — это объемная фигура, у которой шесть граней (например комната: 4 стены, потолок, пол), и каждая из них является прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Объем прямоугольного параллелепипеда равен произведению трех его измерений. Кроме этой формулы можно измерить объем помещения умножив площадь пола на высоту.
Итак приступайте к вычислениям объема помещения. Измерьте длину одной стены (длинной стены),потом измерьте длину второй стены (короткой стены). Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно. Теперь измерьте высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Полученные данные запишите на листочек, чтобы не забыть. Теперь приступайте к вычислениям: умножите длину длинной стены на длину короткой стены, полученное произведение (число)умножите на высоту и вы получите требуемый результат. помещений вычисляют в различных случаях: 1) в случае покупки кондиционера воздуха, так как кондиционеры рассчитаны на определенный объем помещений- 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе напрямую зависит от объема помещения.
Если у вас комната неправильной формы, то есть состоит из как бы большого параллелепипеда и маленького. В данном случае необходимо измерить объем каждого из них отдельно, а потом сложить. Если в вашей комнате есть альков (ниша полукруглой формы), тогда его объем нужно высчитывать по формуле объема . Объем всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где? – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота. Представьте себе ваш альков как часть цилиндра, вычислите объем как бы всего цилиндра, потом посмотрите какую часть этого цилиндра занимает ваш альков,отнимите от общего объема лишнюю часть.
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
Инструкция
Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения . Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели и вы получите искомый объем.
Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения . Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания.
Полезный совет
При измерения радиуса алькова, пользуйтесь ниткой с иголкой, иголку воткните в воображаемый центр цилиндра и тяните нитку до стены, потом измерьте её длину.
Для многих, кто сталкивается с пиломатериалом, вопрос о том, как посчитать кубатуру необрезной и обрезной доски остаётся сложным заданием. В принципе, это довольно легко и просто. Ниже мы рассмотрим основные способы расчёта кубатуры доски.
На уроках геометрии довольно часто приходилось рассчитывать объём чего – либо. Ситуация точно также обстоит с обрезными пиломатериалами. Просто нужно перемножить ширину на высоту и на длину. Естественно, не нужно это делать на целой пачке бруса или доски. Достаточно будет, если вы посчитаете кубатуру одной доски (бруса), затем просто нужно пересчитать общее количество досок в пачке и кубатуру одной доски помножить на посчитанное количество досок. Ещё одно важно правило, при расчёте кубатуры одной доски, все размеры нужно привести к единому измерению, то есть или всё переводится в сантиметры, миллиметры или же в метры. А замеры мы проводим по следующим параметрам: толщина, ширина, длина.
При расчёте кубатуры необрезной доски, тоже измеряется ширина, длина и высота. Только в необрезных пиломатериалах невозможно рассчитать кубатуру одной доски, поэтому доску нужно уложить в пачку, обмерять и применить различные коэффициенты. Для более точного расчёта, лучше всего сложить доску в одну стопку, затем измерить посередине самую широкую и самую тонкую доски, далее сложить эти два показателя и разделить на два. В результате мы получим усреднённую ширину. А длину и высоту измеряем как обычно.
Далее нужно помножить толщину стопки на ширину и длину и применить понижающий коэффициент. По ГОСТу, для полубруса он составляет 0,5, а для необрезной доски 0,63. Но, очень часто, для упрощения расчётов, производители на пилорамах производят отгрузку пиломатериала, которые имеют коэффициент 0,7. Когда таким образом будет посчитана одна стопка, нужно переходить ко второй, третьей и так, до тех пор, пока не будет пересчитан весь пиломатериал.
Как посчитать кубатуру фундамента
- столбчатый
- ленточный
- плитный
При расчёте кубатуры фундамента столбчатого типа, сначала нужно рассчитать кубатуру одного бетонного столбика. Для этого умножается длина на ширину. Если же применяются столбики круглого сечения, то умножается радиус квадрата на коэффициент «Пи – 3,14» и получившийся результат умножаем на высоту столбика. Далее результат перемножается на общее количество столбиков, которые размещены по территории. Это и будет общая кубатура фундамента. В тех случаях, когда столбики соединены раствором, то нужно воспользоваться формулой параллелепипеда.
При расчёте кубатуры фундамента ленточного типа сначала определяется вид сечения. Когда оно одинаковое, то периметр территории умножается на толщину и длину. В том случае, когда оно разное, необходимо просто рассчитать объёмы каждого участка по отдельности и в итоге, сложить все полученные результаты.
Объём — количественная характеристика пространства. Объём помещения определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр.
Вам понадобится
- Для измерения объема помещения вам потребуется рулетка, лист бумаги, калькулятор, ручка.
Инструкция
Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед. Параллелепипед — это объемная фигура, у которой шесть граней (например комната: 4 стены, потолок, пол), и каждая из них является прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Объем прямоугольного параллелепипеда равен произведению трех его измерений. Кроме этой формулы можно измерить объем помещения умножив площадь пола на высоту.
Итак приступайте к вычислениям объема помещения. Измерьте длину одной стены (длинной стены),потом измерьте длину второй стены (короткой стены). Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно. Теперь измерьте высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Полученные данные запишите на листочек, чтобы не забыть. Теперь приступайте к вычислениям: умножите длину длинной стены на длину короткой стены, полученное произведение (число)умножите на высоту и вы получите требуемый результат. помещений вычисляют в различных случаях: 1) в случае покупки кондиционера воздуха, так как кондиционеры рассчитаны на определенный объем помещений- 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе напрямую зависит от объема помещения.
Если у вас комната неправильной формы, то есть состоит из как бы большого параллелепипеда и маленького. В данном случае необходимо измерить объем каждого из них отдельно, а потом сложить. Если в вашей комнате есть альков (ниша полукруглой формы), тогда его объем нужно высчитывать по формуле объема . Объем всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где? – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота. Представьте себе ваш альков как часть цилиндра, вычислите объем как бы всего цилиндра, потом посмотрите какую часть этого цилиндра занимает ваш альков,отнимите от общего объема лишнюю часть.
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
Инструкция
Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения . Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели и вы получите искомый объем.
Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения . Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешни
Как посчитать объем помещения
Объем – геометрический термин, позволяющий измерить количественные характеристики жилого и нежилого пространства.
Определить объемы помещения можно, обладая сведениями о его линейных размерах и характеристиками формы. Объем очень тесно переплетается с характеристиками вместимости. Наверняка каждому знакомы такие термины как внутренний объем сосуда или какой-либо тары.
Единица измерения объема классифицируется в соответствии с всемирными стандартами. Существует специальная система измерений – СИ, в соответствии с которой кубический метр, литр или сантиметр выступает метрической единицей объема.
Любое помещение, будь-то жилая комната или производственное помещение – имеет свои характеристики объема. Если рассматривать любое помещение с точки зрения геометрии, то комната сравнима с параллелепипедом. Это шестигранная фигура, в случае с комнатой грани ее – это стены, пол и потолок. Каждая из сторон комнаты – это прямоугольник. Как известно из геометрии, существует формула нахождения объема прямоугольного параллелепипеда. Объем данной фигуры вычисляется посредством умножения трех главных измерений параллелепипеда – длины, ширины и высоты граней. Также вычислить объем помещения можно по более простой формуле – площадь пола умножают на высоту комнаты.
Как узнать объём комнаты
Итак, каким же образом производят вычисления объема конкретной комнаты? Вначале измеряем длину стены, самой длинной в комнате. Затем определяем длину самой короткой стены в комнате. Все эти измерения проводятся на уровне пола, по линии пролегания плинтусов. При измерениях рулеточная лента должна располагаться ровно. Настал черед измерить и высоту потолка. Для этого необходимо провести рулетку от пола до потолка в одном из углов комнаты.
Все измерения необходимо записывать, с точностью до десятых частей. После этого можно приступить непосредственно к вычислению объемов комнаты. Берем длину самой большой стены, умножаем ее на длину самой маленькой стены, затем полученный результат умножаем на высоту комнаты. В итоге получаем необходимые цифры – объем комнаты.
Вычислить объем помещения бывает нужно в самых разных ситуациях. Так, объем комнаты нужно знать при установке секционного радиатора отопления. Количество секций в нем прямо зависит от объемов комнаты. Если устанавливается кондиционер, также нужно знать объемы помещения, поскольку отдельный кондиционер предназначен только для конкретного объема помещения.
Объём помещения сложной формы
В том случае, когда комната имеет неправильную форму, нужно исходить снова же, из фигуры параллелепипеда. В данном случае комната будет представлена большим и маленьким объемным телом. Так вот, объем нужно измерить отдельно у большого параллелепипеда, а затем – у маленького. После этого два объема складываются между собой. Бывает, что строение комнаты совершенно нестандартное, могут присутствовать арки и ниши полукруглой формации. В данном случае объемы нужно вычислять по другой формуле – объем цилиндра. Объем цилиндра всегда вычисляется по единой формуле – площадь его основания умножается на высоту цилиндрического тела. Полукруглые конструкции в комнате можно представить частью цилиндра, исходя из этого делаются расчеты полного объема цилиндра, а затем из них отнимается лишняя часть, в соответствии с размерами полукруглой ниши.
Как найти объем помещения
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения. Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
Как посчитать объем помещения
Объём — количественная черта места. Объём помещения определяется его формой и линейными размерами. С понятием объёма плотно сплетено понятие вместимость, другими словами объём внутреннего места сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр. Для вас понадобится Для измерения объема помещения для вас будет нужно рулетка, лист бумаги, калькулятор, ручка. 1 Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед.
Параллелепипед — это большая фигура, у которой 6 граней. и неважно какая из их есть прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Количество прямоугольного параллелепипеда равен произведению 3-х его измерений. Не считая этой формулы может быть измерить количество помещения умножив площадь пола на высоту.
2 Итак приступайте к вычислениям объема помещения. Определите длину одной стены ,позже определите длину 2-ой стены. Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно.
На данный момент определите высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Приобретенные данные запишите на листочек, чтоб не запамятовать.
Как посчитать объем в м3 бетона калькулятор
На данный момент приступайте к вычислениям: умножите длину длинноватой стены на длину недлинной стены, приобретенное произведение умножите на высоту и вы получите требуемый итог.
Объемы помещений вычисляют в различных случаях: 1) в случае приобретения кондюка воздуха, так как кондюки рассчитаны на определенный количество помещений; 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе находится в зависимости от объема помещения. 3 Если у вас комната неверной формы, другими словами складывается из вроде бы огромного параллелепипеда и малеханького. В данном случае необходимо измерить количество каждого из их раздельно, а позже сложить. Если в вашей комнате есть альков. тогда его количество нужно высчитывать по формуле объема цилиндра. Количество всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где. – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота.
Представьте для себя ваш альков как часть цилиндра, вычислите количество вроде бы всего цилиндра, позже поглядите какую часть этого цилиндра занимает ваш альков,отымите от общего объема лишнюю часть.
Как рассчитать площадь комнаты?
Если комната с четырьмя стенами и имеет стандартную геометрическую фигуру с прямыми углами, тогда необходимо измерить две стенки и умножив полученные две цифры друг на друга мы получим площадь помещения, а для объёма нужно умножить полученный результат на высоту. но это только при правильных геометрических фигурах.
Сложнее находить площадь и размеры, когда форма комнаты неправильного размера, например такого.
Тогда нужно применять все знания геометрии, а именно — разделить комнату на несколько правильных фигур и в соответствии с формулами этих фигур найти их площадь, а потом все результаты сложить вместе, тогда получится общая площадь помещения. Для нахождения высоты необходимо полученный результат общей площади умножить на высоту.
Ещё хуже обстоят дела с нестандартными помещениями с неправильными углами стен и крыши. Тогда придётся переносить все размеры помещения на бумагу, разделять его на правильные фигуры и исходя из каждой фигуры находить её площадь и объём, а потом полученные результаты суммировать.
В площадь помещения не входят выступы окон и прочего, что выше пола, но они входят в расчёт объёма помещения.
Как посчитать площадь помещения
В случае измерения комнаты неправильной формы для более точного подсчета площади рекомендуется разбить ее на прямоугольники. Подсчитав площадь каждого такого участка, можно узнать общую площадь комнаты путем простого суммирования всех полученных результатов.
Если же разбить комнату на прямоугольные участки не представляется возможным, то можно попробовать такие фигуры как треугольник либо сектор круга. Площадь треугольника считается по формуле Герона: S=v**).
Р — полупериметр треугольника, который можно рассчитать таким образом: р=/2
http://denisyakovlev.com
Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м². Площадь перехода — 15 м². Складываем три площади: 450 + 450 + 15, получается 915 м². Если высота здания составляет 3 м, то строительный объем будет 2745 м³.
Здания с чердачными перекрытиями
Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:
X = S¹ × h.
В этом случае под S¹ понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.
Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.
Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м². Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м³.
Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.
Дома без чердачного перекрытия
Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:
X = S² × L
S² — тоже площадь поперечного сечения, но не горизонтального, а вертикального. Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.
L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.
Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м², а строительный объем — 552 м³.
Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.
Если известна общая площадь
Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.
Если известна общая площадь, можно использовать формулу:
X = S × H × К
В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.
H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.
К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.
То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м², а высота в свету — 15 м. В этом случае показатель составит 24000 м³ с учетом поправочного коэффициента.
Если известна площадь застройки
Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:
X = S¹ × H¹ + S² × H²
S¹ в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. H¹ — высота дома, в которой можно не учитывать выступающие части крыши.
S² и H² — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.
Дома с мансардами
Мансарда — этаж в чердачном пространстве, фасад которого частично либо полностью образован поверхностями наклонной крыши. Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.
Чтобы найти строительный объем мансарды, нужно умножить площадь ее поперечного вертикального сечения на длину дома.
Ширину и высоту нужно измерять по внешнему обводу, вертикаль — до начала перекрытий. Все эти данные понадобятся для того, чтобы найти площадь вертикального сечения. Она равна половине произведения ширины, то есть основания, на высоту. Например, высота мансарды — 1,5 м, ширина, то есть основание — 6 м. Тогда площадь составит 9 м².
Полученное значение нужно умножить на длину дома. Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м².
Оставшуюся надземную часть нужно считать по предыдущим формулам, но высоту измерять до начала основания мансарды, то есть до верхнего перекрытия. Объемы мансарды, надземной и подземной частей нужно просто сложить.
Если здание имеет сложную форму
Расчет строительного объема для зданий сложной формы — например, с мезонинами, башенками и различными пристроями — намного сложнее. В этом случае нужно сначала найти строительный объем каждого конструктивного элемента, а потом сложить полученные значения.
Полная формула расчета строительного объема зависит от исходных данных — есть ли подвал, предусмотрены ли чердачные перекрытия, построена ли мансарда. Чтобы получить точное значение, нужно провести тщательные замеры и использовать сложные схемы подсчета. Если не хотите тратить время на это, обратитесь к профессионалам — они посчитают все быстрее и точнее.
формул объема
( pi = = 3.141592 …)Объемные формулы
Примечание: «ab» означает «а» умножается на «б». « 2 » означает «квадрат», который совпадает с «а» раз «а». «b 3 » означает «b cubed», то же самое как «б» раз «б» раз «Б».
Будь осторожен! Количество единиц. Используйте одинаковые единицы для всех измерений.Примеры
куб = 3
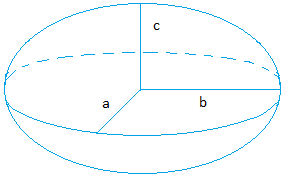
прямоугольная призма = a b c
нерегулярная призма = б ч
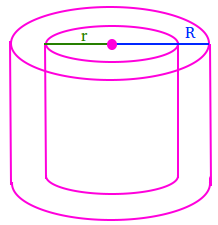
цилиндр = b ч = пи r 2 ч
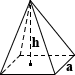
пирамида = (1/3) b ч
конус = (1/3) b ч = 1/3 пи r 2 ч
сфера = (4/3) пи р 3
эллипсоид = (4/3) pi r 1 r 2 r 3
Единицы
Объем измеряется в «кубических» единицах.Громкость числа — это количество кубиков, необходимое для его полного заполнения, например блоки в коробке.
Объем куба = сторона, сторона, сторона, время, сторона. поскольку каждая сторона квадрата одинакова, она может быть просто длиной сторона в кубе.
Если квадрат имеет одну сторону 4 дюйма, объем будет 4 дюйма, 4 дюйма, 4 дюйма или 64 кубических дюйма.(Cubic дюймы также могут быть записаны в 3 .)
Обязательно используйте одинаковые единицы для всех измерений. Вы не можете умножить футы на дюймы на ярды, это не делает идеально кубическое измерение.
Объем прямоугольной призмы — длина по сторона, умноженная на ширину, умноженная на высоту. Если ширина 4 дюйма, то длина 1 фут, а высота 3 фута, какой объем?
НЕ ПРАВИЛЬНО …. 4 раза 1 раз 3 = 12
ПРАВИЛЬНО …. 4 дюйма соответствует 1/3 фута. Объем составляет 1/3 фута на 1 фут на 3 фута = 1 кубический фут (или 1 куб. футов, или 1 фут 3 ).
Калькулятор объемаНиже приведен список калькуляторов объема для нескольких распространенных фигур. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».
Sphere Volume Calculator
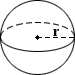 |
Калькулятор объема конуса
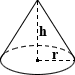 |
Cube Volume Calculator
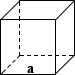 |
Калькулятор объема цилиндра
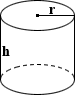 |
Прямоугольный калькулятор объема бака
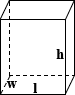 |
Калькулятор объема капсулы
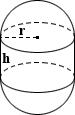 |
Калькулятор объема сферической крышки
Пожалуйста, укажите любые два значения ниже для расчета.
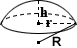 |
Конус Frustum Объем Калькулятор
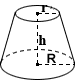 |
Ellipsoid Volume Calculator
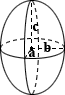 |
Калькулятор объема квадратной пирамиды
 |
Tube Volume Calculator
 |
Калькулятор площади поверхности | Калькулятор площади
Объем — это количественное определение трехмерного пространства, которое занимает вещество.Единицей СИ для объема является кубический метр или м 3 . По общему правилу объем контейнера, как правило, зависит от его вместимости и количества жидкости, которое он способен удерживать, а не от объема пространства, которое вытесняет реальный контейнер. Объемы многих форм могут быть рассчитаны с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на их более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, даже более сложных форм, можно рассчитать с помощью интегрального исчисления, если для границы формы существует формула.Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и является однородной, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере равно радиусу r .Скорее всего, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар состоит из пространства, ограниченного сферой. Независимо от этого различия шар и сфера имеют одинаковый радиус, центр и диаметр, и их объемы одинаковы. Как и в случае с кругом, самый длинный отрезок линии, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема сферы приведено ниже:
EX: Клэр хочет заполнить идеально сферический водяной шар радиусом 0.15 футов с уксусом, чтобы использовать его в борьбе с ее заклятым врагом Хильдой в эти выходные. Необходимый объем уксуса может быть рассчитан с использованием приведенного ниже уравнения:
объем = 4/3 × π × 0,15 3 = 0,141 фут 3
Конус
Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус формируется аналогично кругу с помощью набора отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, которая содержит окружность (или какое-либо другое основание).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. Д., Которые простираются бесконечно, не будут рассматриваться. Уравнение для расчета объема конуса выглядит следующим образом:
, где r — радиус, а h — высота конуса
EX: Беа намерена выйти из магазина мороженого, с трудом заработав 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что она предпочитает обычные сахарные шишки на 15% больше, чем вафельные, и должна определить, является ли потенциальный объем вафельного рожка на ≥ 15% больше, чем у сахарного рожка. Объем вафельного рожка с круглым основанием с радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать по приведенному ниже уравнению:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 в 3
Bea также вычисляет объем сахарного рожка и находит, что разница составляет <15%, и решает приобрести сахарный рожок.Теперь все, что ей нужно сделать, это использовать свое ангельское, детское обращение, чтобы манипулировать посохом, чтобы опустошать контейнеры с мороженым в ее конус.
куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых встречаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб является частным случаем многих классификаций форм в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:
Объем = 3
где a — длина ребра куба
EX: Боб, который родился в штате Вайоминг (и никогда не покидал штат), недавно посетил свою исконную родину в штате Небраска. Боб, пораженный великолепием штата Небраска и окружающей средой, непохожий на то, что он испытывал ранее, знал, что ему нужно взять с собой часть Небраски. У Боба кубический чемодан с длиной ребра 2 фута, и он рассчитывает объем почвы, который он может взять с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной оси прямой линии.Однако в общем использовании «цилиндр» относится к правому круглому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра приведено ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
EX: Келум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником переработки, он извлек три цилиндрических бочки с места незаконного сброса и очистил химические отходы от бочек, используя моющее средство для мытья посуды и воду. Каждый из бочек имеет радиус 3 фута и высоту 4 фута, и Caelum определяет объем песка, который может вместить каждый, используя уравнение ниже:
объем = π × 3 2 × 4 = 113,097 футов 3
Он успешно строит замок из песка в своем доме, и в качестве дополнительного бонуса ему удается экономить электроэнергию при ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.
Прямоугольный резервуар
Прямоугольный резервуар представляет собой обобщенную форму куба, где стороны могут иметь различную длину. Он ограничен шестью гранями, три из которых встречаются в его вершинах, и все они перпендикулярны их соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к пирогу.Она планирует отправиться в поход по тропе Калалау в Кауаи, и, хотя она очень подходит, Дарби беспокоится о своей способности завершить тропу из-за отсутствия пирога. Она решает упаковать только самое необходимое и хочет наполнить свою идеально прямоугольную пачку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно, тортиком. Точный объем торта, который она может поместить в свою пачку, рассчитывается ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы.Отсюда следует, что объем капсулы можно рассчитать путем объединения уравнений объема для сферы и правого круглого цилиндра:
| = 2 ч + | № 3 = № 2 ( | р + ч) |
, где r — радиус, а h — высота цилиндрической части
EX: Учитывая капсулу с радиусом 1,5 фута и высотой 3 фута, определите объем расплавленного молочного шоколада, который Джо может нести в капсуле времени, которую он хочет похоронить для будущих поколений, на своем пути самопознания через Гималаи:
объем = π × 1.5 2 × 3 + 4/3 × π × 1,5 3 = 35,343 фута 3
Сферическая крышка
Сферическая крышка — это часть сферы, которая отделена от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая крышка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера сегментирована с двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферического колпачка получено из уравнения сферического сегмента, где второй радиус равен 0.По отношению к сферической крышке, показанной в калькуляторе:
Учитывая два значения, калькулятор вычисляет третье значение и объем. Уравнения для преобразования высоты в радиусы приведены ниже:
Дано r и R : h = R ± √R 2 — r 2
где r — радиус основания, R — радиус сферы, а h — высота сферического колпачка
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы практиковать, решает саботировать мяч для гольфа Джеймса.Он отсекает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса, и ему необходимо рассчитать объем материала, необходимый для замены сферической крышки и исказить вес мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую Джек отрезал, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68–0,3) = 0,447 в 3
К сожалению для Джека, Джеймс случайно получил новую партию шаров за день до их игры, и все усилия Джека были напрасны.
Конический усеченный
Коническая усеченная часть — это часть твердого тела, которая остается при разрезании конуса двумя параллельными плоскостями. Этот калькулятор рассчитывает объем для правого круглого конуса специально. Типичные конические усеченные контуры, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы. Объем правого конического усеченного конуса рассчитывается по следующему уравнению:
| объем = | πh (r 2 + rR + R 2 ) |
, где r и R — радиусы оснований, h — высота усеченного конуса
EX: Bea успешно приобрела немного мороженого в сахарном конусе и только что съела его таким образом, чтобы мороженое было упаковано внутри конуса, а уровень поверхности мороженого был параллелен плоскости отверстия конуса.Она собирается съесть свой конус и оставшееся мороженое, когда ее брат схватил ее конус и откусил часть нижней части конуса, которая идеально параллельна ранее единственному отверстию. Теперь у Bea осталось мороженое с утечкой в правом конусе, и она должна рассчитать объем мороженого, которое она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма, с радиусами 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 в 3
Эллипсоид
Эллипсоид является трехмерным аналогом эллипса и является поверхностью, которая может быть описана как деформация сферы посредством масштабирования направленных элементов. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярных оси симметрии, а отрезки, ограничивающие эти оси симметрии, называются основными осями. Если все три имеют различную длину, эллипсоид обычно описывается как трехосный.Уравнение для расчета объема эллипсоида выглядит следующим образом:
, где a , b и c являются длинами осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он потребляет слишком много, и позволяет ему есть столько мяса, сколько он может вместить в булочку эллипсоидной формы. Таким образом, Xabat выдавливает булочку, чтобы максимизировать объем мяса, которое он может поместить в свой бутерброд. Учитывая, что его булочка имеет длину оси 1.5 дюймов, 2 дюйма и 5 дюймов, Xabat рассчитывает объем мяса, которое он может поместить в каждую выдолбленную булочку, следующим образом:
объем = 4/3 × π × 1,5 × 2 × 5 = 62,832 в 3
Квадратная пирамида
Геометрическая пирамида — это трехмерное тело, образованное путем соединения полигонального основания с точкой, называемой его вершиной, где многоугольник — это форма в плоскости, ограниченной конечным числом отрезков прямых линий. Существует много возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание — это квадрат.Другое различие, связанное с пирамидами, касается расположения вершины. Правая пирамида имеет вершину, которая находится прямо над центром тяжести своего основания. Независимо от того, где находится вершина пирамиды, пока ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды можно записать как:
Обобщенный объем пирамиды:
Объемные формулы
Здесь мы предоставим вам формулы объема для некоторых распространенных трехмерных фигур, а также для эллипсоида и полого цилиндра, которые не так часто встречаются.Куб:
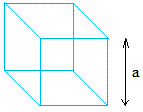 |
Цилиндр:
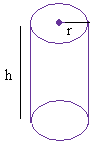 |
π = 3.14
ч — высота
р — радиус
Прямоугольное тело или кубовидная форма:
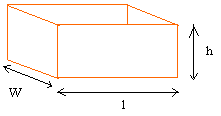 |
l — длина
w — ширина
h — высота
Сфера:
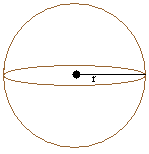 |
π = 3,14
r — радиус
Конус:
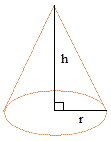 |
пи = 3.14
р — радиус
ч — высота
Пирамида:
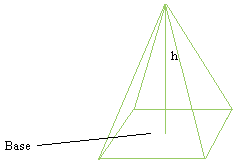 |
B — площадь основания
h — высота
Чуть менее распространенные формулы объема
Эллипсоид:
 Объем = (4 × π × a × b × c) / 3
Объем = (4 × π × a × b × c) / 3Использование π = 3,14
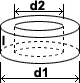
Полый цилиндр:
 Объем = π × R 2 × ч — π × r 2 × ч
Объем = π × R 2 × ч — π × r 2 × чОбъем = π × ч (R 2 — r 2 )
Используйте π = 3.14.
Как использовать формулы объема для расчета объема.
Куб
Длина стороны = a = 2 см
Объем = (2 см) = 2 см × 2 см × 2 см = 8 см 3
Цилиндр
Высота составляет 8 дюймов и радиус составляет 2 дюйма.
Объем = π × r 2 × h = 3,14 × (2 дюйма) 2 × 8 дюймов = 3,14 × 4 × 8 в 3
Объем = 3,14 × 32 в 3 = 100,48 в 3
Прямоугольный сплошной или кубовидный
Длина 6 см, ширина 3 см, высота 5 см.
Объем = l × w × h = 6 × 3 × 5 = 90 см 3
Сфера
Радиус = r = 20
Объем = (4 × π × r 3 ) / 3 = [4 × 3,14 × (20) 3 ] / 3 = 3,14 × (20) 3 × 4
Объем = 3,14 × 8000 × 4 = 3,14 × 32000 = 100480
Конус
Радиус равен равно 3, а высота равна 4.
Объем = (π × r 2 × ч) / 3 = [3,14 × (3) 2 × 4] / 3 = 3.14 × 9 × 4
Объем = 3,14 × 36 = 113,04
Пирамида
Пирамида имеет высоту 6 футов. Если основание пирамиды представляет собой квадрат длиной 2 фута, найдите объем.
Объем = (В × ч) / 3
B = Площадь основания = 2 фута × 2 фута = 4 фута 2
Объем = (4 × 6) / 3 фута 3 = 24/3 фута 3 = 8 футов 3
Эллипсоид
Радиусы эллипсоида 1 см, 2, см и 3 см.
Объем = (4 × π × a × b × c) / 3 = (4 × 3,14 × 1 × 2 × 3) / 3
Объем = (3,14 × 4 × 6) / 3 = (3,14 × 24) / 3 = 81,64 / 3 = 25,12 см. 3
Полый цилиндр
Внешний радиус 8, внутренний радиус 6 и высота 10.
Объем = π × ч (R 2 — r 2 ) = π × 10 (8 2 — 6 2 ) = π × 10 (64 — 36)
Объем = π × 10 (28) = π × 280 = 879,2
Новые уроки математики
Ваша электронная почта в безопасности с нами.Мы будем использовать его только для информирования вас о новых уроках математики.
,Как рассчитать молярный объем вещества и решаемые примеры
СМОТРЕТЬ БОЛЬШЕ
Проще говоря, молярный объем — это объем, занимаемый одним молем любого вещества при данной температуре и давлении.Обычно он применяется только к газам, где идентичность газа не влияет на объем. Наиболее распространенным примером для иллюстрации является молярный объем газа в STP (Стандартная температура и давление), который равен 22,4 л на 1 моль любого идеального газа при температуре, равной 273,15 К, и давлении, равном до 1,00 атм.
Чтобы вычислить молярный объем вещества, мы можем разделить молярную массу на его плотность. Математически выражая это как:
Vm = Mρ
где, V — объем газа
n — число молей газа, P — давление, T- температура
R — постоянная газа (значение зависит от единиц давления, объема и Температура)
Газовая постоянная R равна 8.314 Дж / моль . K
Пример: Проба чистого газообразного гелия занимает объем 6,8 л при 0 ° C и 100 кПа. Сколько молей газообразного гелия присутствует в образце?
Опции:
(а) 0,30 моль
(б) 0,15 моль
(в) 0,45 моль
(д) 0,60 моль
Ответ: (а)
Решение:
В (He (г) ) = объем газа гелия = 6,8 л. Условия
: STP (стандартная температура и давление, 0 ° C и 100 кПа)
So V м = молярный объем газа = 22.71 л моль -1
Пример: Какой объем занимают 3,70 моль газа N 2 на STP?
Опции:
(а) 84,0 л
(б) 50,0 л
(в) 72,5 л
(д) 22,4 л
Ответ: (а)
Решение: В (N 2 (г) ) = n (N 2 (г) ) × 22,71 (при STP)
= 3,70 × 22,71
= 84,0 л
