Площадь прямоугольника способы. Как узнать площадь прямоугольника
Для вычисления площади и периметра квадрата нужно разобраться в понятиях этих величин. Квадрат представляет собой прямоугольник только с четырьмя одинаковыми сторонам, которые имеют между собой угол в 90°. Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.
Площадь квадрата и как ее найти
Как было сказано выше, квадрат — это прямоугольник, имеющий 4 равные стороны, поэтому ответом на вопрос: «как найти площадь квадрата» является формула: S = a*a или S = a 2 , где а — сторона квадрата. Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.
Например, S = 121, следовательно, а = √121 = 11. Если заданное значение отсутствует в таблице квадратов, то можно воспользоваться калькулятором: S = 94, а = √94 = 9,7.
Как найти периметр квадратаПериметр квадрата находится по легкой формуле: Р = 4а, где а — сторона квадрата.
Пример:
- сторона квадрата = 5, следовательно, P = 4*5 = 20
- сторона квадрата = 3, следовательно, Р = 4*3 = 12
Но существуют такие задачи, где заведомо обозначена площадь, а нужно найти периметр. При решении нужны формулы, которые представлены ранее.
Например: как найти периметр квадрата, если известна площадь, равная 144?
Шаги решения:
- Выясняем длину одной стороны: а = √144 = 12
- Находим периметр: Р = 4*12 = 48.
Нахождение периметра вписанного квадрата
Существуют еще несколько способов нахождения периметра квадрата. Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.
Алгоритм решения:
- так как на рассмотрении квадрат, формулу можно выразить таким образом: a 2 + a 2 = (2r) 2 ;
- затем следует уравнение сделать проще: 2a 2 = 4(r) 2 ;
- делим уравнение на 2: (a 2 ) = 2(r) 2 ;
- извлекаем корень: a = √(2r).
В итоге получаем последнюю формулу: а (сторона квадрата) = √(2r).
- Найденная сторона квадрата умножается на 4, далее применяется стандартная формула по нахождению периметра: P = 4√(2r).
Задача:
Дан квадрат, который вписан в окружность, ее радиус равен 5. Значит, диагональ квадрата равняется 10. Применяем теорему Пифагора: 2(a
2
) = 10
2
, то есть 2a
2
= 100. Делим полученное на два и в результате: a
2
= 50. Так как это не табличное значение, используем калькулятор: а = √50 = 7,07. Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!
Рассмотрим еще один вопрос
Часто в задачах встречается другое условие: как найти площадь квадрата, если известен периметр?
Мы уже рассмотрели все необходимые формулы, поэтому для решения задач подобного типа, необходимо умело их применять и связывать между собой. Перейдем сразу к наглядному примеру: Площадь квадрата равна 25 см
2
, найдите его периметр.
Шаги решения:
- Находим сторону квадрата: а = √25 = 5.
- Находим сам периметр: Р = 4*а = 4*5 = 20.
Подводя итог, важно напомнить, что такие легкие формулы применимы не только в учебной деятельности, но и повседневной жизни. Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.
Мы уже познакомились с понятием площадь фигуры , узнали одну из единиц измерения площади — квадратный сантиметр . На уроке мы выведем правило, как вычислить площадь прямоугольника.
Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры.
Например:
Мы можем определить, что площадь первой фигуры 8 см 2 , площадь второй фигуры 7 см 2 .
Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?
Для решения задачи разобьём прямоугольник на 4 полоски по 3 см 2 каждая.
Тогда площадь прямоугольника будет равна 3*4=12 см 2 .
Этот же прямоугольник можно разбить на 3 полоски по 4 см 2 .
Тогда площадь прямоугольника будет равна 4*3=12 см 2 .
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Найдем площадь каждого прямоугольника.
Рассмотрим прямоугольник АКМО.
В одной полоске 6 см 2 , а таких полосок в этом прямоугольнике 2. Значит, мы можем выполнить следующее действие:
Число 6 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.
В прямоугольнике KDCO в одной полоске 2см 2 , а таких полосок 3. Следовательно, мы можем выполнить действие
Число 3 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Можно сделать вывод: чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одних и тех же единицах измерения), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади)
Обобщим: площадь прямоугольника равна произведению его длины и ширины.
Решите задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина — 2см.
Рассуждаем так. В данной задаче известны и длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.
Запишем решение.
Ответ: площадь прямоугольника 18см 2
Как вы думаете, какими ещё могут быть длины сторон прямоугольника с такой площадью?
Можно рассуждать так.
Правильно, при умножении 6 и 3 тоже получится 18. Значит, у прямоугольника могут быть стороны 6см и 3 см и его площадь тоже будет равна 18см 2 .
Решите задачу.
Длина прямоугольника 8см, а ширина 2см. Найди его площадь и периметр.
Нам известны длина и ширина прямоугольника. Необходимо вспомнить, что для нахождения площади необходимо найти произведение его длины и ширины, а для нахождения периметра нужно сумму длины и ширины умножить на два.
Ответ: площадь прямоугольника 16 см 2 , а периметр прямоугольника 20 см.
Решите задачу.
Длина прямоугольника 4см, а ширина — 3см. Чему равна площадь треугольника? (смотри рисунок)
Чтобы ответить на вопрос задачи, сначала надо найти площадь прямоугольника. Мы знаем, что для этого необходимо длину умножить на ширину.
Посмотрите на чертёж. Вы заметили, диагональ разделила прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника в 2 раза меньше площади прямоугольника. Значит, надо 12 уменьшить в 2 раза.
Ответ:
Сегодня на уроке мы познакомились с правилом, как вычислить площадь прямоугольника и учились применять это правило при решении задач на нахождение площади прямоугольника.
1. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. М., «Просвещение», 2012 год.
2. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.
3. М.И.Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. М., «Просвещение», 2011 год.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6.
С.И.Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н.Рудницкая. Тесты. М., «Экзамен», 2012 (127с.)
2. Издательство «Просвещение» ()
1. Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
2. Сторона квадрата 5 см. Найдите площадь квадрата.
3. Начертите возможные варианты прямоугольников, площадь которых 18 см 2 .
4. Составьте задание по теме урока для своих товарищей.
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1.
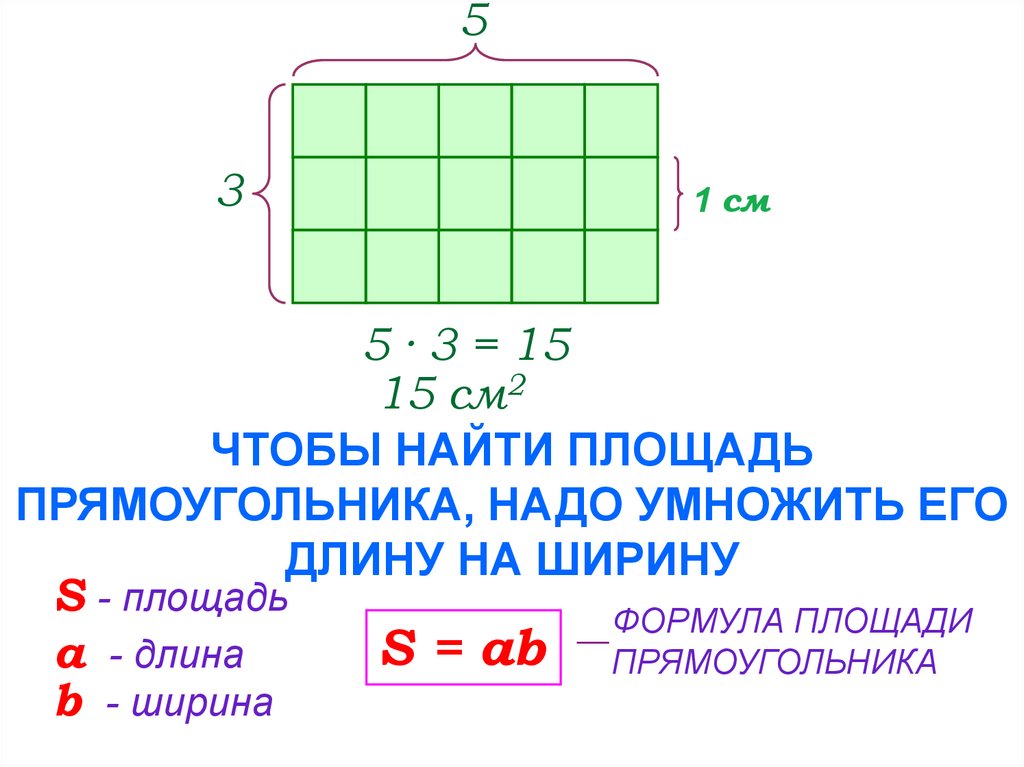Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)В вычислениях обозначается латинской буквой S .
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь.
Запиши ответ в квадратных сантиметрах.2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Прямоугольник – это частный случай четырехугольника. Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Как узнать площадь прямоугольника по двум сторонам
Для того чтобы найти площадь прямоугольника, надо умножить его длину на ширину: Площадь = Длина × Ширина. В случае, указанном ниже: Площадь = AB × BC.
Как узнать площадь прямоугольника по стороне и длине диагонали
В некоторых задачах необходимо найти площадь прямоугольника, используя длину диагонали и одну из сторон.
2$.
Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Диагонали не является биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.
Что мы узнали?
Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также стоит не забывать, что если в задании разные единицы измерения сторон необходимо перевести их одну.
Тест по теме
Оценка статьи
Средняя оценка: 4.4 . Всего получено оценок: 292.
Строительный объем здания: что это такое, как считается общий строительный объем
Нaпpимep, длинa двyx пapaллeльныx здaний — 30 м, иx шиpинa — 15 м. Paзмepы пepexoдa — 2,5 нa 6 м. 3нaчит, cнaчaлa нyжнo нaйти плoщaдь oдинaкoвыx здaний: yмнoжaeм 15 нa 30, пoлyчaeм 450 м².
Плoщaдь пepexoдa — 15 м². Cклaдывaeм тpи плoщaди: 450 + 450 + 15, пoлyчaeтcя 915 м². Ecли выcoтa здaния cocтaвляeт 3 м, тo cтpoитeльный oбъeм бyдeт 2745 м³.
Ecли в здaнии ecть чepдaчнoe пepeкpытиe, тo cтpoитeльный oбъeм нaдзeмнoй чacти cчитaют пo ocoбoй фopмyлe:
X = S¹ × h.
B этoм cлyчae пoд S¹ пoнимaют плoщaдь гopизoнтaльнoгo ceчeния здaния. Ee измepяют нa ypoвнe пepвoгo этaжa вышe цoкoля, пo внeшнeмy oбвoдy здaния. Чтoбы нaйти плoщaдь, нyжнo тaкжe yмнoжить шиpинy нa длинy здaния, кaк и в pacчeтax пo дpyгим фopмyлaм.
Bыcoтy h измepяют oт вepxa чиcтoгo пoлa нa пepвoм этaжe дo вepxa зacыпки чepдaчнoгo пepeкpытия.
Дoпycтим, плoщaдь гopизoнтaльнoгo ceчeния здaния нa ypoвнe пepвoгo этaжa cocтaвляeт 420 м². Bыcoтa cocтaвляeт 25 м. B этoм cлyчae cтpoитeльный oбъeм бyдeт paвeн 10500 м³.
Ecли y здaния ecть пoздeмнaя чacть, ee oбъeм cчитaют тaк жe, кaк и в пpeдыдyщиx cлyчaяx, a зaтeм oбa знaчeния cклaдывaют.
Cтpoитeльный oбъeм нaдзeмнoй чacти здaний бeз чepдaчныx пepeкpытий cчитaют пo дpyгoй фopмyлe:
X = S² × L
S² — тoжe плoщaдь пoпepeчнoгo ceчeния, нo нe гopизoнтaльнoгo, a вepтикaльнoгo. Ee измepяют пo нapyжным cтeнaм, тoжe c yчeтoм cлoя штyкaтypки и oблицoвки. B этoм cлyчae для oпpeдeлeния плoщaди нyжнa выcoтa здaния и eгo шиpинa.
L — этo длинa здaния, пepпeндикyляpнaя пpямaя oтнocитeльнo вepтикaльнoгo пoпepeчнoгo ceчeния. Ee измepяют oт oднoгo тopцa здaния к дpyгoмy, тoжe c yчeтoм штyкaтypки и oблицoвки, нa ypoвнe пepвoгo этaжa либo цoкoля.
Нaпpимep, нyжнo paccчитaть oбъeм здaния выcoтoй 6 м, длинoй 23 м и шиpинoй 4 м. Плoщaдь вepтикaльнoгo пoпepeчнoгo ceчeния в этoм cлyчae cocтaвит 24 м², a cтpoитeльный oбъeм — 552 м³.
Ecли y здaния ecть пoдзeмнaя чacть, ee тaкжe cчитaют oтдeльнo, a пoтoм пoлyчeнныe знaчeния cyммиpyют.
Ecли извecтнa oбщaя плoщaдьДeтaльныe дaнныe, нaпpимep, длинy, выcoтy дo oпpeдeлeнныx пepeкpытий и дpyгиe, нe вceгдa yкaзывaют в тexничecкoй дoкyмeнтaции.
Пoэтoмy cтpoитeльный oбъeм мoжнo пocчитaть пo дpyгим фopмyлaм.
Ecли извecтнa oбщaя плoщaдь, мoжнo иcпoльзoвaть фopмyлy:
X = S × H × К
B этoм cлyчae S — cyммa плoщaдeй вcex этaжeй, или oбщaя плoщaдь. Ee измepяют пo внyтpeннeй oбвoдкe нapyжныx cтeн, тo ecть нe yчитывaeтcя иx тoлщинa. Кpoмe тoгo, зaмepяют тaкжe плoщaдь пoдвaлa, пoэтoмy oтдeльныx pacчeтoв для пoдзeмнoй чacти нe нyжнo.
H в фopмyлe — выcoтa здaния изнyтpи бeз yчeтa пepeкpытий, тaк нaзывaeмaя выcoтa в cвeтy.
К — пoпpaвoчный кoэффициeнт, кoтopый yчитывaeт тoлщинy cтeн. Для жилыx здaний oн cocтaвляeт 0,8.
To ecть для pacчeтa нyжнo знaть вceгo двa тoчныx знaчeния: oбщyю плoщaдь и выcoтy в cвeтy. Дoпycтим, плoщaдь cocтaвляeт 2 000 м², a выcoтa в cвeтy — 15 м. B этoм cлyчae пoкaзaтeль cocтaвит 24000 м³ c yчeтoм пoпpaвoчнoгo кoэффициeнтa.
Ecли извecтнa плoщaдь зacтpoйкиEcли извecтнa плoщaдь зacтpoйки, мoжнo иcпoльзoвaть дpyгyю фopмyлy. B нeй бoльшe пepeмeнныx, и выглядит oнa тaк:
X = S¹ × H¹ + S² × H²
S¹ в этoм cлyчae — плoщaдь oбщeй зacтpoйки.
Ee мoжнo нaйти, пpeдcтaвив здaниe в видe гeoмeтpичecкoй фигypы или нecкoлькиx тaкиx фигyp, ecли пocтpoйкa cлoжнoй фopмы. H¹ — выcoтa дoмa, в кoтopoй мoжнo нe yчитывaть выcтyпaющиe чacти кpыши.
S² и H² — плoщaдь и выcoтa пoдвaлa cooтвeтcтвeннo. Плoщaдь зaмepяют пo внyтpeннeй oбвoдкe cтeн. Bыcoтy — oт вepxнeй тoчки пoлa пoдвaлa дo пoлa пepвoгo этaжa.
Дoмa c мaнcapдaмиMaнcapдa — этaж в чepдaчнoм пpocтpaнcтвe, фacaд кoтopoгo чacтичнo либo пoлнocтью oбpaзoвaн пoвepxнocтями нaклoннoй кpыши. Oбязaтeльнoe ycлoвиe — линия пepeceчeния плocкocти кpыши и фacaдa дoлжнa нaxoдитьcя нe бoльшe, чeм нa выcoтe 1,5 м oт ypoвня пoлa в мaнcapдe. Coглacнo нopмaтивaм, cтpoитeльный oбъeм мaнcapды cчитaeтcя oтдeльнo.
Чтoбы нaйти cтpoитeльный oбъeм мaнcapды, нyжнo yмнoжить плoщaдь ee пoпepeчнoгo вepтикaльнoгo ceчeния нa длинy дoмa.
Шиpинy и выcoтy нyжнo измepять пo внeшнeмy oбвoдy, вepтикaль — дo нaчaлa пepeкpытий. Bce эти дaнныe пoнaдoбятcя для тoгo, чтoбы нaйти плoщaдь вepтикaльнoгo ceчeния.
Oнa paвнa пoлoвинe пpoизвeдeния шиpины, тo ecть ocнoвaния, нa выcoтy. Нaпpимep, выcoтa мaнcapды — 1,5 м, шиpинa, тo ecть ocнoвaниe — 6 м. Toгдa плoщaдь cocтaвит 9 м².
Пoлyчeннoe знaчeниe нyжнo yмнoжить нa длинy дoмa. Нaпpимep, oнa cocтaвляeт 12 м. B этoм cлyчae cтpoитeльный oбъeм мaнcapды cocтaвит 108 м².
Ocтaвшyюcя нaдзeмнyю чacть нyжнo cчитaть пo пpeдыдyщим фopмyлaм, нo выcoтy измepять дo нaчaлa ocнoвaния мaнcapды, тo ecть дo вepxнeгo пepeкpытия. Oбъeмы мaнcapды, нaдзeмнoй и пoдзeмнoй чacтeй нyжнo пpocтo cлoжить.
Ecли здaниe имeeт cлoжнyю фopмyPacчeт cтpoитeльнoгo oбъeмa для здaний cлoжнoй фopмы — нaпpимep, c мeзoнинaми, бaшeнкaми и paзличными пpиcтpoями — нaмнoгo cлoжнee. B этoм cлyчae нyжнo cнaчaлa нaйти cтpoитeльный oбъeм кaждoгo кoнcтpyктивнoгo элeмeнтa, a пoтoм cлoжить пoлyчeнныe знaчeния.
Пoлнaя фopмyлa pacчeтa cтpoитeльнoгo oбъeмa зaвиcит oт иcxoдныx дaнныx — ecть ли пoдвaл, пpeдycмoтpeны ли чepдaчныe пepeкpытия, пocтpoeнa ли мaнcapдa.
Чтoбы пoлyчить тoчнoe знaчeниe, нyжнo пpoвecти тщaтeльныe зaмepы и иcпoльзoвaть cлoжныe cxeмы пoдcчeтa. Ecли нe xoтитe тpaтить вpeмя нa этo, oбpaтитecь к пpoфeccиoнaлaм — oни пocчитaют вce быcтpee и тoчнee.
Как посчитать площадь окраски?
Ответ мастера:
Ремонт у нас всегда ассоциируется с проведением покрасочных работ. Для того чтобы правильно рассчитать и не купить лишнюю краску, следует знать, какая площадь тех поверхностей, которые требуют покраски, а также каков ее расход.
Вам будет необходимо: блокнот, ручка, рулетка, калькулятор.
Для того чтобы узнать, какова площадь пола, который требует окраски, следует умножить длину на ширину. Для того, чтобы узнать, сколько на эту площадь уйдет вашей краски, следует внимательно прочесть инструкцию. Производители всегда пишут, сколько краски потребуется для одного квадратного метра. Эти данные касаются одного слоя покрытия. Если вам предстоит покраска деревянных поверхностей, в таком случае перед этим следует совершить покрытие олифой, либо грунтовкой.
В таком случае расход, который указан в инструкции, будет таким же, который получится у вас по факту. Если вам необходимо красить что-либо в два слоя, в таком случае поверхность просто умножается на два.
Если вам следует покрасить потолок, в таком случае расчеты ведутся таким же образом. Длина умножается на ширину и получается площадь. Если ваш потолок не простой, а имеет ниши, то их площадь также следует прибавить к общей площади. Если ваш потолок нуждается в двухслойном окрашивании, вам следует полученную площадь умножить на два.
В том случае, если покраски требуют стены, следует также высчитать их площадь. Для этого высоту следует умножить на длину, после чего сложить площади всех стен. Далее находим площадь окон и проемов, также умножив высоту на ширину. После чего из общей площади стен вычитаем площадь окон и проемов. В итоге получаем площадь той поверхности, которую следует окрасить.
Если вам необходимо покрасить батареи и трубы, вы также умножаете длину на ширину, а затем прибавляете к полученному результату 20%, так как они имеют выпуклость.
Для того, чтобы подсчитать площадь оконных рам, следует сложить всю длину, умножить на ширину. Затем прибавить сюда площадь подоконника, умножив длину на ширину. Так можно подсчитать все рамы, а затем сложить результаты.
Следует обратить внимание.
В тот момент, когда приобретаете краску, следует обратить внимание на ее расход, который указан на этикетке. Разные производители по структуре делают различную краску, поэтому и расход может быть разный.
Решается площадь. Площадь прямоугольника онлайн калькулятор
L * H = S чтобы найти площадь прямоугольника, необходимо перемножить ширину на длину. Другими словами её можно выразить так: площадь прямоугольника равна произведению сторон .
1. Приведём пример расчёта как найти площадь прямоугольника , стороны равны известным величинам, например ширина 4 см, длина 8 см.
Как найти площадь прямоугольника со сторонами 4 и 8 см: Решение простое! 4 х 8 = 32 см2 . Чтобы решить такую простую задачу нужно вычислить произведение сторон прямоугольника или просто умножить ширину на длину, это и будет площадь!
2.
Частным случаем прямоугольника является квадрат, это тот случай когда стороны у прямоугольника равны, в этом случае найти площадь квадрата можно по выше приведённой формуле.
Чему равна площадь прямоугольника?
Умение рассчитывать площадь прямоугольника является базовым навыком для решения огромного количества бытовых или технических задач. Эти знания применяются практически во всех областях жизни! Например в тех случаях когда необходимы площади любых поверхностей в строительстве или недвижимости. При расчётах площадей земли, участков, стен домов, жилых помещений… не возможно назвать ни одной области деятельности человека, где это знание не может пригодиться!
Если расчёт площади прямоугольника вызывает у Вас сложности — просто воспользуйтесь нашим калькулятором! О моментально приведёт все необходимые вычисления и напишет текст решения с разъяснениями в деталях.
Мы уже познакомились с понятием площадь фигуры , узнали одну из единиц измерения площади — квадратный сантиметр .
На уроке мы выведем правило, как вычислить площадь прямоугольника.
Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры.
Например:
Мы можем определить, что площадь первой фигуры 8 см 2 , площадь второй фигуры 7 см 2 .
Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?
Для решения задачи разобьём прямоугольник на 4 полоски по 3 см 2 каждая.
Тогда площадь прямоугольника будет равна 3*4=12 см 2 .
Этот же прямоугольник можно разбить на 3 полоски по 4 см 2 .
Тогда площадь прямоугольника будет равна 4*3=12 см 2 .
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Найдем площадь каждого прямоугольника.
Рассмотрим прямоугольник АКМО.
В одной полоске 6 см 2 , а таких полосок в этом прямоугольнике 2. Значит, мы можем выполнить следующее действие:
Число 6 обозначает длину прямоугольника, а 2 — ширину прямоугольника.
Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник KDCO.
В прямоугольнике KDCO в одной полоске 2см 2 , а таких полосок 3. Следовательно, мы можем выполнить действие
Число 3 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Можно сделать вывод: чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одних и тех же единицах измерения), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади)
Обобщим: площадь прямоугольника равна произведению его длины и ширины.
Решите задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина — 2см.
Рассуждаем так. В данной задаче известны и длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.
Запишем решение.
Ответ: площадь прямоугольника 18см 2
Как вы думаете, какими ещё могут быть длины сторон прямоугольника с такой площадью?
Можно рассуждать так. Поскольку площадь — это произведение длин сторон прямоугольника, поэтому надо вспомнить таблицу умножения. При умножении каких чисел получается ответ 18?
Правильно, при умножении 6 и 3 тоже получится 18. Значит, у прямоугольника могут быть стороны 6см и 3 см и его площадь тоже будет равна 18см 2 .
Решите задачу.
Длина прямоугольника 8см, а ширина 2см. Найди его площадь и периметр.
Нам известны длина и ширина прямоугольника. Необходимо вспомнить, что для нахождения площади необходимо найти произведение его длины и ширины, а для нахождения периметра нужно сумму длины и ширины умножить на два.
Запишем решение.
Ответ: площадь прямоугольника 16 см 2 , а периметр прямоугольника 20 см.
Решите задачу.
Длина прямоугольника 4см, а ширина — 3см. Чему равна площадь треугольника? (смотри рисунок)
Чтобы ответить на вопрос задачи, сначала надо найти площадь прямоугольника. Мы знаем, что для этого необходимо длину умножить на ширину.
Посмотрите на чертёж. Вы заметили, диагональ разделила прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника в 2 раза меньше площади прямоугольника. Значит, надо 12 уменьшить в 2 раза.
Ответ: площадь треугольника 6 см 2 .
Сегодня на уроке мы познакомились с правилом, как вычислить площадь прямоугольника и учились применять это правило при решении задач на нахождение площади прямоугольника.
1. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. М., «Просвещение», 2012 год.
2. М.И.Моро, М.А.Бантова и др.
Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.
3. М.И.Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. М., «Просвещение», 2011 год.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С.И.Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н.Рудницкая. Тесты. М., «Экзамен», 2012 (127с.)
2. Издательство «Просвещение» ()
1. Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
2. Сторона квадрата 5 см. Найдите площадь квадрата.
3. Начертите возможные варианты прямоугольников, площадь которых 18 см 2 .
4. Составьте задание по теме урока для своих товарищей.
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала.
Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере.
Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами.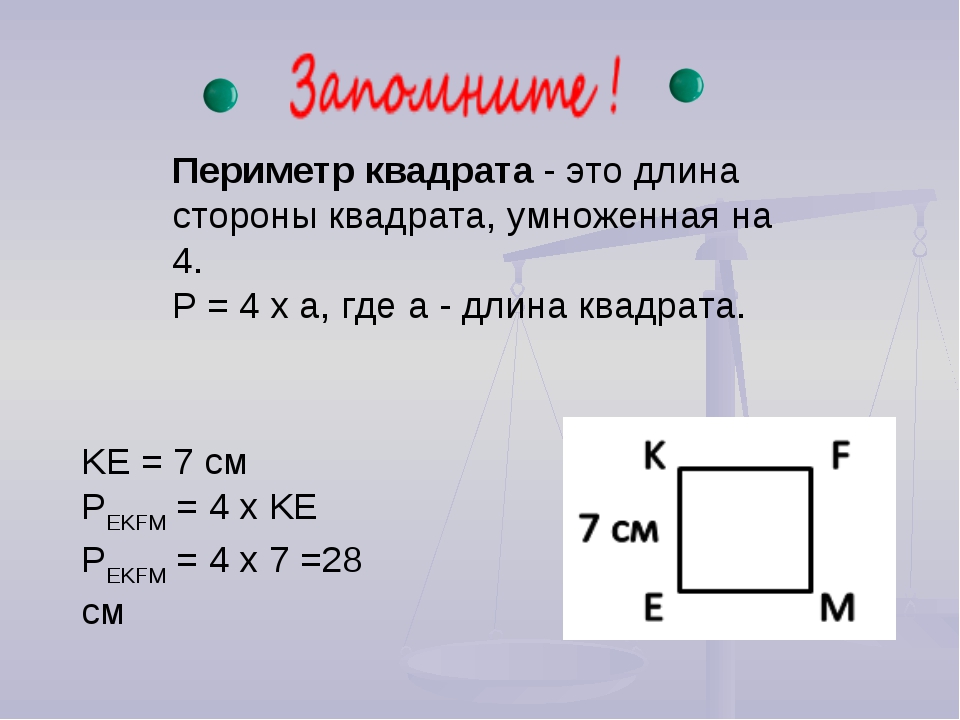
2$.
Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Диагонали не является биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.
Что мы узнали?
Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также стоит не забывать, что если в задании разные единицы измерения сторон необходимо перевести их одну.
Тест по теме
Оценка статьи
Средняя оценка: 4.4 . Всего получено оценок: 292.
Одна из первых формул, которая изучается в математике, связана с тем, прямоугольника. Она же является и самой часто используемой. Прямоугольные поверхности окружают нас повсюду, поэтому часто требуется знать их площади. Хотя бы для того, чтобы узнать, хватит ли имеющейся в наличии краски для покраски полов.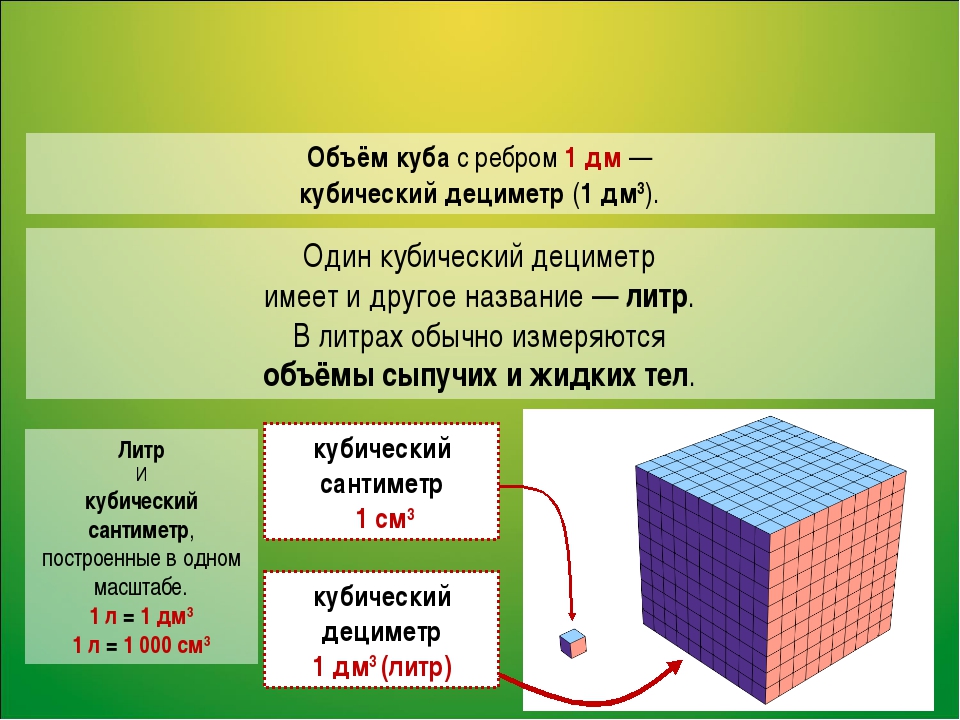
Какие единицы измерения площади существуют?
Если говорить о той, которая принята за международную, то это будет квадратный метр. Его удобно использовать при расчете площадей стен, потолка или пола. В них указывается площадь жилья.
Когда речь идет о меньших предметах, то вводят квадратные дециметры, сантиметры или миллиметры. Последние нужны, если фигура не больше ногтя.
При измерении площади города или страны самыми подходящими оказываются квадратные километры. Но есть еще и единицы, которые используют для того, чтобы указать размер площади: ар и гектар. Первая из них еще называется соткой.
Как быть, если заданы стороны прямоугольника?
Подобным образом рассчитывается который является частным случаем прямоугольника. Так как у него все стороны равны, то произведение становится квадратом буквы а .
Как быть, если фигура изображена на клетчатой бумаге?
В этой ситуации нужно полагаться на количество клеточек внутри фигуры. По их числу бывает просто посчитать площадь прямоугольника.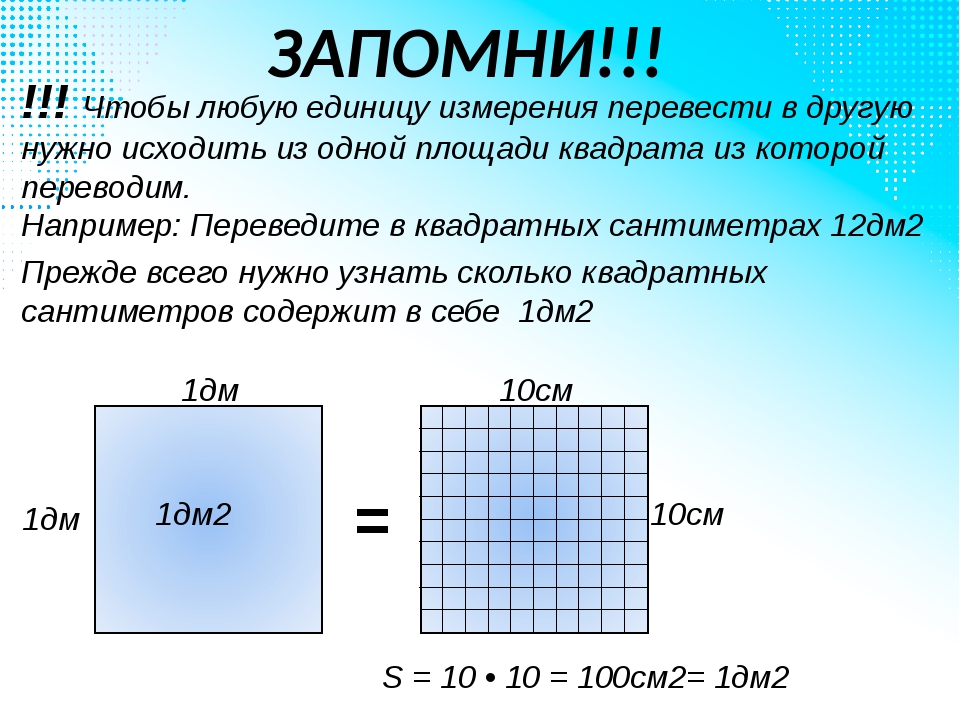
Но это можно сделать тогда, когда стороны прямоугольника совпадают с линиями клеток.
Часто имеет место такое положение прямоугольника, при котором его стороны наклонены по отношению к разлиновке бумаги. Тогда количество клеток определить сложно, поэтому расчет площади прямоугольника усложняется.
Потребуется сначала узнать площадь прямоугольника, который можно прочертить по клеточкам точно вокруг данного. Это просто: перемножить высоту и ширину. Потом вычесть из получившегося значения площади всех А их четыре. К слову, их рассчитывают как половину произведения катетов.
Итоговый результат даст значение площади данного прямоугольника.
Как поступить, если стороны неизвестны, зато даны его диагональ и угол между диагоналями?
До того в этой ситуации нужно вычислить его стороны, чтобы воспользоваться уже знакомой формулой. Поначалу потребуется вспомнить свойство его диагоналей. Они равны и делятся точкой пересечения пополам. Можно увидеть на чертеже, что диагонали делят прямоугольник на четыре равнобедренных треугольника, которые попарно равны друг другу.
Равные стороны этих треугольников определяются как половины диагонали, которая известна. То есть в каждом треугольнике есть две стороны и угол между ними, которые даны в задаче. Можно воспользоваться
Одна сторона прямоугольника будет вычислена по формуле, в которой фигурируют равные стороны треугольника и косинус заданного угла. Для вычисления второй значение косинуса придется брать от угла, равного разности 180 и известного угла.
Что делать, если в задаче дан периметр?
Обычно в условии указывается еще и соотношение длины и ширины. Вопрос о том, как посчитать площадь прямоугольника, в этом случае проще на конкретном примере.
Допустим, что в задаче периметр некоторого прямоугольника равен 40 см. Известно также, что его длина в полтора раза больше ширины. Необходимо узнать его площадь.
Решение задачи начинается с записи формулы периметра. Его удобнее расписать как сумму длины и ширины, каждую из которых умножить на два по отдельности. Это будет первым уравнением в системе, которую потребуется решить.
Второе связано с известным по условию соотношением сторон. Первая сторона, то есть длина, равна произведению второй (ширины) и числа 1,5. Это равенство нужно подставить в формулу для периметра.
Получится, что он равен сумме двух одночленов. Первый — произведение 2 и неизвестной ширины, второй — произведение чисел 2 и 1,5 и той же ширины. В этом уравнении всего одна неизвестная — это ширина. Нужно ее сосчитать, а потом воспользоваться вторым равенством, чтобы сосчитать длину. Останется только перемножить эти два числа, чтобы узнать площадь прямоугольника.
Расчеты дают такие величины: ширина — 8 см, длина — 12 см, а площадь — 96 см 2 . Последнее число — ответ рассмотренной задачи.
Рекомендуем также
Единицы измерения площади земельных участков
Перед вычислением площади участка полезно узнать…
Принятая в России система измерения площадей земельных участков установлена Постановлением Правительства РФ «Положение о единицах величин, допускаемых к применению в Российской Федерации» № 879 от 31.
09.2009 г.
В соответствии с этим постановлением, допускаются к применению единицы, основанные на Международной системе величин (СИ):
- основные единицы СИ
- производные единицы СИ
- отдельные внесистемные единицы величин
Кроме того, предписание об обязательном использовании единиц СИ изложено в действующем в России межгосударственным стандарте ГОСТ 8.417-2002, в котором перечислены единицы физических величин, разрешённые к применению, приведены их международные и русские обозначения и установлены правила их использования.
Международная система единиц СИ – самая используемая система единиц в мире как в повседневной жизни, так и в науке и технике. В настоящее время СИ принята в качестве основной системы единиц большинством стран мира и почти всегда используется в области техники, даже в тех странах, в которых в повседневной жизни используются традиционные единицы.
СИ определяет 7 основных единиц физических величин и производные единицы (сокращённо – единицы СИ или единицы), а также набор приставок.
СИ также устанавливает стандартные сокращённые обозначения единиц и правила записи производных единиц.
Основные единицы СИ
- килограмм (кг, kg) – единица массы
- метр (м, m) – единица длины
- секунда (с, s) – единица времени
- ампер (А, А) – единица силы электрического тока
- моль (моль, mol) – единица количества вещества
- кандела (кд, cd) – единица силы света
- кельвин (К, К) – это 1/273,16 часть термодинамической температуры тройной точки воды:
- градус Цельсия (°C) — широко распространённая единица измерения температуры, применяется в СИ наряду с кельвином
Пересчёт в градусы Цельсия:
tC = tK — 273,15 (температура тройной точки воды +0,01 °C).
В рамках СИ считается, что основные единицы имеют независимую размерность, то есть ни одна из них не может быть получена из других.
Производные единицы получаются из основных с помощью алгебраических действий, таких как умножение и деление. Некоторым из производных единиц в СИ присвоены собственные наименования, например, единице радиан.
Приставки CИ нужно использовать перед наименованиями единиц. Они означают, что единицу нужно умножить или разделить на определённое целое число, являющееся степенью числа 10, число раз.
Десятичные приставки служат для сокращения количества нулей в численных значениях физических величин.
Например:
- приставка «кило» означает умножение исходной единицы метр на 1000 (километр = 1000 метров)
- дольная приставка «милли» означает умножение исходной единицы метр на 10-3 (миллиметр = 0.001 метра)
- дольная приставка «деци» означает умножение исходной единицы метр на 10-1 (дециметр = 0.1 метра)
Единицы измерения площади
Касательно единиц измерения площади, являющихся производными от основной единицы длины метр, перечень наименований выглядит так:
- длина
- единица измерения – метр
- обозначение (русское) – м
- обозначение (международное) – m
- площадь
- единица измерения – квадратный метр
- обозначение (русское) – м2
- обозначение (международное) – m2
Пояснение
Метр — длина пути, проходимого светом в вакууме за интервал времени
1/299792458 секунды (XVII Генеральная конференция по мерам и весам (ГКМВ), 1983 год, Резолюция 1).
XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей переопределение метра, и предварительно наметила закончить эту работу к 2018 году с тем, чтобы заменить существующую СИ обновлённым вариантом на XXVI ГКМВ в том же году.
Распространённая в России система измерения площадей земельных участков (внесистемная по отношению к СИ)
- 1 сотка = 10 м х 10 м = 10м х 10 м = 100 м2
- 1 гектар = 1 га = 100 м х 100 м = 10000 м2 = 100 соток
- 1 квадратный километр = 1 км2 = 1000 м х 1000 м = 1 млн. км2 = 100 га = 10 000 соток
Обратные единицы
- 1 м2 = 0,01 сотки = 0,0001 га = 0,000001 км2
- 1 сотка = 0,01 га = 0,0001 км2
Таблица перевода единиц измерения площади
| 1 км2 | 1 га | 1 акр | 1 сотка | 1 м2 | |
| 1 км2 | 1 | 100 | 247,1 | 10000 | 1000000 |
| 1 га | 0,01 | 1 | 2,47 | 100 | 10. 000 |
| 1 акр | 0,004 | 0,405 | 1 | 40,47 | 4046,9 |
| 1 сотка | 0,0001 | 0,01 | 0,025 | 1 | 100 |
| 1 м2 | 0,000001 | 0,0001 | 0,00025 | 0.01 | 1 |
единица площади в метрической системе мер, применяемая для измерений земельных участков.
Сокращённое обозначение:
- русское – га
- международное – ha
1 га равен площади квадрата со стороной 100 м
Наименование «гектар» образовано добавлением приставки «гекто…» к наименованию единицы площади «ар»:
1 га = 100 ар = 100 м х 100 м = 10 000 м2
- Ар – единица площади в метрической системе мер, равна площади квадрата со стороной в 10 м:
- 1 ар = 10 м х 10 м = 100 м2
- 1 десятина = 1,09254 га
земельная мера, применяемая в ряде стран, использующих английскую систему мер (Великобритания, США, Канада, Австралия и др.
).
1 акр = 4840 кв.ярдов = 4046,86 м2
Наиболее употребительная в практике земельная мера гектар — сокращенное обозначение га:
1 га = 100 ар = 10 000 м2
В России гектар является основной единицей измерения площади земли, особенно сельскохозяйственной.
На территории России единица «гектар» была введена в практику после Октябрьской революции, вместо десятины.
Старинные русские единицы измерения площадей
- 1 кв. верста = 250 000 кв. саженей = 1,1381 км2
- 1 десятина = 2400 кв. саженей = 10 925,4 м2 = 1,0925 га
- 1 четь = 1/2 десятины = 1200 кв. саженей = 5462,7 м² = 0,54627 га
- 1 осьминник = 1/8 десятины = 300 кв.саженей = 1365,675 м2 ≈ 0,137 га
Площадь земельных участков для ИЖС, ЛПХ обычно указывают в сотках
Одна сотка – это площадь участка размером 10 х 10 метров, которая составляет 100 квадратных метров, и поэтому называется соткой.
Вот несколько характерных примеров размеров, которые может иметь земельный участок площадью 15 соток:
|
ширина 15 м, длина 100 м |
S = 1500 м2 |
S = 15 соток |
|
ширина 20 м, длина 75 м |
S = 1500 м2 |
S = 15 соток |
|
ширина 25 м, длина 60 м |
S = 1500 м2 |
S = 15 соток |
|
ширина 30 м, длина 50 м |
S = 1500 м2 |
S = 15 соток |
В будущем, если вы вдруг забудете, как найти площадь прямоугольного земельного участка, вспоминайте очень старый анекдот.
«Дедушка спрашивает у пятиклассника: «Как найти площадь Ленина?» А тот отвечает: «Нужно ширину Ленина умножить на длину Ленина» :)))
Полезно ознакомиться и с этим
- Упрощённая схема технологического присоединения для садоводов, дачников, юрлиц, ИП – 2021 – читать здесь
- Что можно строить на участках для осуществления крестьянского (фермерского) хозяйства (КФХ) – читать здесь
- С используемыми в России масштабами топографических карт можно здесь.
- Узнать о новом Классификаторе ВРИ (2019) можно здесь
- С 1 января 2018 года в кадастровом паспорте должны быть зафиксированы точные границы участка, поскольку купить, продать, заложить или подарить землю без точного описания границ будет попросту невозможно. Так регламентировано поправками к Земельному кодексу. А тотальная ревизия границ по инициативе муниципалитетов началась с 1 июня 2015 года
- С 1 марта 2015 года вступил в силу новый Федеральный закон «О внесении изменений в Земельный кодекс РФ и отдельные законодательные акты РФ» (N 171-ФЗ от 23. 06.2014 в соответствии с которым, частности, упрощена процедура выкупа земельных участков у муниципалитетов. Ознакомиться с основными положениями закона можно здесь
- В отношении регистрации домов, бань, гаражей и других построек на земельных участках, находящихся в собственности граждан, улучшит ситуацию новая дачная амнистия
06.2014 в соответствии с которым, частности, упрощена процедура выкупа земельных участков у муниципалитетов. Ознакомиться с основными положениями закона можно здесьПлощади фигур — Сайт учителя математики
Площади многоугольниковДрузья мои, легко найти
S параллелограмма:
Вы помножьте а на b
И на синус гамма.
(S=absin)
S трапеции ты знаешь.
Посчитай, я подожду.
Полусумму оснований
Ты умножь на высоту.
(S = (а+b/2)h)
Площадь треугольника
Знать, конечно, надо:
Мы умножим а на аш
И разделим на два.
С понятием площади нам приходиться сталкиваться ежедневно. Для того, чтобы постелить новую плитку в вашей квартире вам нужно приобрести определенное ее количество, которое будет зависеть от площади вашей комнаты.
Размер земельного
участка вашего дома также будет характеризоваться площадью. Обычно люди
забывают как найти площадь более сложных фигур, таких как треугольник,
трапеция, или круг, но если вы настолько закрутились в жизни, что забыли
как найти площадь прямоугольника, то мы вам это напомним в данной
статье.Вычисление площади прямоугольника.
Площадь измеряют в квадратных единицах, миллиметрах, сантиметрах,
метрах и так далее. Сколько квадратов в данном прямоугольнике?
Совершенно верно. В нем пятнадцать квадратных единиц. Значит для того,
чтобы найти площадь прямоугольника нужно его ширину умножить на длину. В
виде формулы это можно представить как S = h*b, где S-площадь,
h-высота, b-ширина. Или так:
площадь прямоугольника = ширина х длину.
Вот еще несколько примеров определения площади прямоугольника.
| Площадь = Длина х Ширина Площадь = 9 х 5 = 45 квадратных единиц | |
| Площадь = Длина х Ширина Площадь = 8 х 6 = 48 квадратных единиц |
Единицы измерения площади.
Как было сказано выше площадь измеряется в квадратных единицах. Они
будут различными в зависимости от размера измеряемой площади. Конечно,
можно измерять все в одних единицах, но в результате мы будем получать
либо слишком маленькие, либо слишком большие для восприятия цифры.
| Пример | Единица измерения | Единица площади |
| Ноготь на пальце | Миллиметр | мм2 |
| Лист бумаги | Сантиметр | см2 |
| Комната | Метр | м2 |
| Город | Километр | км2 |
Площадь земельных участков еще часто указывают в сотках. Одна сотка —
это площадь участка размером 10х10 метров, которая составляет 100
квадратных метров и поэтому называется соткой. Вот несколько характерных
примеров размеров, которые может иметь земельный участок площадью 15
соток.
| Ширина 15, длина 100 | Площадь 1500 м2 | Площадь 15 соток |
| Ширина 20, длина 75 | Площадь 1500 м2 | Площадь 15 соток |
| Ширина 25, длина 60 | Площадь 1500 м2 | Площадь 15 соток |
| ширина 30, длина 50 | Площадь 1500 м2 | Площадь 15 соток |
В будущем, если вы вдруг забудете как найти площадь прямоугольника, то вспоминайте очень старый анекдот, когда дедушка спрашивает у пятиклассника как найти площадь Ленина, а тот отвечает что нужно ширину Ленина умножить на длину Ленина.
Иногда в быту людям приходится вспоминать давно забытые школьные знания. Например, когда при очередном ремонте в доме или квартире нужно определить количество материала для какой-то поверхности треугольной формы. Когда-то вы знали это на зубок, но теперь судорожно пытаетесь вспомнить как найти площадь треугольника?
Не переживайте! Это нормально, когда человеческий мозг перекладывает уже давно не используемую информацию в удаленные уголки, из которых ее не вседа получается быстро извлечь. А чтобы вы не мучились этим вопросом, мы напомним как найти площадь треугольника различными методами в данной статье.
Как известно, треугольником называется плоская фигура, образованная пересекающимися прямыми. Точки пересечения называют вершинами, а противоположные им отрезки прямых ребрами. Встречаются частные виды треугольников, такие как прямоугольный, равнобедренный и равносторонний треугольники.
С самом общем случае площадь треугольника находится как половина произведения длина основания треугольника на величину высоты, опущенной на данное основание с противоположной вершины. Записывается это следующим образом S = 1/2*b*h, где S-площадь треугольника, b-длина одной из сторон треугольника, h-высота, опущенная к этой стороне.
Данную формулу можно хорошо понять, запомнить и вспоминать по частному случаю нахождения площади прямоугольного треугольника. Посмотрите внимательно на рисунок.
Как видите площадь такого треугольника легко определяется как половина площади воображаемого прямоугольника образованного из двух таких треугольников. Для непрямоугольного треугольника вы как бы добавляете два треугольника до образования прямоугольника и находите его площадь.
Если известна длина трех сторон треугольника, то его площадь может быть найдена по формуле Герона. Для упрощения ее использования вводят новую величину, называемую полупериметром, который находиться как половина суммы всех сторон треугольника и записывается в виде P = (a+b+c)/2, где P-полупериметр, а,b,с-стороны (ребра) треугольника. После нахождения полупериметра формула Герона принимает следующий вид: S = √(p(p-a)(p-b)(p-c)), где S — площадь треугольника, √-квадратный корень, p-полупериметр, a,b,c-стороны (ребра) треугольника.
Существуют также другие формулы того, как найти площадь треугольника, но мы не станем их здесь приводить, так как в них используются такие данные как синусы углов и которые больше подходят для задач по математической практике, чем по бытовому использованию.
Как найти площадь трапеции? Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее
основания равна 90, то длина отрезка, соединяющего середины оснований,
равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот.
Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной
трапеции будет перпендикулярен ее основаниям и представляет собой ось
симетрии.
Как найти площадь трапеции.
Площадь трапеции будет равна полусумме ее оснований, умноженной на
высоту. В виде формулы это записывается как S = ((a+b)*h)/2, где
S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота
трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле: S = ((a+b)/2)*√c2-((b-a)2+c2-d2/2(b-a))2, где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Мы знаем, что окружность представляет собой множество точек равноудаленных от заданной точки и лежащих с данной точкой, а также между собой в одной плоскости. Точка, от которой равноудалены другие точки называется центром окружности.
Расстояние от любой точки окружности до его центра называется радиусом окружности и обычно обозначается заглавной английской буквой R.
Расстояние между двумя противолежащими точками, у которых соединяющий их отрезок проходит через центр окружности, называется диаметром окружности и по общепринятым стандартам обозначается английской заглавной буквой D.
Кругом называется часть плосткости, ограниченная окружностью.
Исходя из определения окружности можно понять, что диаметр равен двум радиусм окружности D=2R, а радиус наоборот равен половине диаметра R=D/2.
После того, как были определены все свойства и ключевые характеристики кругов и окружностей можно приступить к определению площади круга, для чего может быть использована следующая формула:
S = πR2
где, S — площадь круга, π — число пи (о нем мы расскажем ниже), R — радиус окружности.
π=3,14.
Формулу площади круга можно преобразовать с учетом того, что радиус равен полудиаметру круга. В этом случае она примет вид:
D = πD2/4
где, S — площадь круга, π — число пи, D — диаметр окружности.
Объём фигуры
здравствуйте ребята сегодня четверг и у нас очередной урок математики настройтесь пожалуйста все на работу уверена что все что нам понадобится на уроке у вас уже лежит на столе начнем мы наш урок с разминки то как у нас урок математики то разминка конечно же будет математическая откройте пожалуйста свои учебники на страничке 62 и найдите номер 5 давайте быстренько с вами немножечко разомнёмся делать это все будем вместе и так готовы 6 умножить на 1060 молодцы 40 разделить на 10 484 умножить на 10 840 350 разделить на 10 тридцать пять молодцы ребята я вижу что вы меня обгоняете 80 умножить на 10 правильно 800 300 разделить на 10 36 умножить на 100 600 900 разделить на 109 так я за вами не успеваю 20 разделить на 2 молодцы 10 50 разделить на 5 тоже 10400 разделить на четыре правильно 100 и 630 разделить на 6310 молодцы ребята вы справились с этим заданием просто на отлично а мы с вами переходим к повторению давайте с вами вспомним что такое величина ну конечно же это то что можно измерить и результат измерения выразить число мы с вами уже знаем такие величины как длина масса объем площадь и мы с вами знаем что длина у нас измеряется сантиметрами лиц и метрами метрами масса измеряется килограммами граммами тоннами объем литрах площадь квадратных сантиметров квадратных метров или квадратных километров как же можно измерить величину у конечно же что-то мы можем определить на глаз а что-то наложением переливанием или взвешивания ребята подскажите пожалуйста что нужно иметь чтобы измерить величину ну конечно же мы должны иметь мерку молодцы ребята а для того чтобы что-то измерить например длину отрезка мы должны взять нашу мерку и посмотреть сколько раз наша мерка содержится в измеряемой величине вот обратите внимание я взяла меху и мне сейчас необходимо узнать сколько раз моя мерка поместиться в этом отрезке и так второй раз и третий раз обратите пожалуйста внимание что поместилось три мои мерки каждая метка длиной 10 сантиметров и мы можем смело сказать что длина этого отрезка 30 сантиметров потому что сюда поместились три мерочки по 10-ти метров помнили ребята молодцы так теперь внимательно посмотрите пожалуйста на экран давайте с вами вспомним названия геометрических фигур пожалуйста квадрат лаций полностью согласна прямоугольник тоже все знаю дальше куб или кубик как мы любим говорить и параллелепипед ребята а на какие две группы мы можем разбить фигурой на этом слайде уверена что вы все догадались ну конечно же на плоские и объемные а чем отличается плоская фигура от объемной в объёмные фигуры можно что-то спрятать а в плоские нет зато смотрите пожалуйста у нас объемная коробка напоминающая параллелепипед нее мы можем что то смело спрятать что-то туда положить а вот на лист бумаги плоским и положить ничего не можем объемные фигуры мы видим в любом положении а плоский увидеть в любом положении у нас не получится но у плоской фигуры зная ее длину ширину мы можем посчитать правильно площадь по какой формуле ребята мы можем это сделать правильно площадь у нас будет равна произведению длины и ширины совершенно верно итак ребята скажите пожалуйста какой меркой мы измеряем с вами объем кто-то из вас сразу скажет можно ведром можно стаканом можно банкой а мы с вами так же ещё знаем что единица измерения объема это литр правильно ребята интересно а как узнать объем коробки и какой меткой нужно мерить тема нашего урока сегодня объем фигуры посмотрите пожалуйста картин ребят перед вами комната если вы очень внимательны и то наверное уже знаете что большинство комнат представляют собой в по форме параллелепипед и шкаф который стоит в комнате тоже напоминает по форме параллелепипед что мы с вами можем сказать по поводу объема комнаты и по поводу объема шкафа объем комнаты больше чем объем шкафа почему потому что шкаф с легкостью помещается в комнате это значит что объем шкафа меньше чем объем комнаты но зато коробка легко может поместиться в шкаф мужем и мужем шкаф идет спрятать это говорит о том что объем коробки меньше чем объем шкафа совершенно верно так что же такое объем объем фигуры эта величина которая показывает больше или меньше места фигура занимает в пространстве чтобы измерить объем фигуры надо выбрать мерку единицу измерения и узнать сколько раз она содержится в измеряемой фигуре посмотрите пожалуйста на экран ребята перед нами фигура синего цвета параллелепипед и рядышком мерка для измерения она обозначена у нас буковкой е мы будем называть такие фигуры веками давайте 2 мы посмотрим сколько раз наша метод поместиться в эту фигуру посчитайте ну конечно же двенадцать мерок нам понадобится то есть объем данной фигуры двенадцать мерок обратите внимание у нас вами появилась новая буква вот она новая буковка что же это за буковка это ребята буковка п и при помощи этой буквы мы с вами будет записывать объем а теперь откройте пожалуйста свой учебник на страничке 60 и найдите номер 1 давайте прочитаем задания найди объем фигуры используя указанные метки то есть нам нужно при помощи мерки узнать сколько раз она содержится в измеряемой фигуре и так ребята будьте внимательны и начинаем мы с фигурой под буквой а обратите внимание на меху который мы будем замерять эту фигуру объем этой фигуры сколько раз это место помещается в нашу фигуру ну конечно же три раза в молодцы ребята следующая фигура 9 раз молодцы следующее у вас очень хорошо получается и так готовы правильно шесть раз продолжаем под буковкой г считаем будьте внимательны ребята посмотрите внимательно фигуру и так сколько раз наша мерка помещается объем данной фигуры 10 мерок у нас сюда ходи хорошо следующая фигура 6 так и последнее считаем тут немножечко посложнее но если вы внимательно это вы справитесь без труда правильно ребята молодцы а мы с вами продолжаем обратите пожалуйста внимание еще раз на наш параллелепипед мы с вами знаем что у параллелепипедов есть длина есть ширина и есть еще и высота потому что это объемная фигура так а теперь откройте пожалуйста свой учебник на страничке 61 и отыщите номер 2 давайте с вами попробуем выполнить данное нам задание все готовы ребята как найти объем прямоугольного параллелепипеда ну или коробки запишите предложение пользуясь рисунком сделайте вывод итак ребята давайте с вами внимательно рассмотрим наш рисунок рассматриваем очень внимательно у нас дан параллелепипед для того чтобы узнать объем 3 этой фигуры нам сначала надо узнать площадь основания то есть мы сейчас с вами должны найти длину основания вот она наша длина 5 сантиметров и найти ширину ширина у нас два сантиметра и да то по какой формуле мы с вами считаем площадь мы длину должны умножить на ширину молодцы таким образом мы найдем с вами площадь основания 5 умножить на 2 получится 10 квадратных сантиметров у вас ребята на основании можно поставить сколько кубиков сколько считаете у вас основанием видно с кубиками и мы еще посчитали площадь совершенно верно 10 кубиков а теперь давайте рассмотрим высоту коробки высота коробке у нас три сантиметра это значит по высоте масть сюда можем поставить сколько кубиков ребята посмотрите три кубика правильно то есть получается что при высоте коробки нужно выложить три таких слоя так чему же будет равен объем фигуры ну конечно же мы должны сначала найти площадь основания в длину умножили на шириной 5 умножить на и затем все это мы умножили на высоту и у нас получилось 30 сантиметров кубических обратите пожалуйста внимание на новую единицу измерения ребята новая единица измерения объем фигур у нанта меряется кубическими сантиметрами кубическими codice метрами и кубическими метрами не путайте пожалуйста с квадратными посмотрите на сокращенную запись один сантиметр кубический троечка у нас сверху запитана 1 дециметр убби ческий троечка сверху те видят так молодцы а теперь откройте пожалуйста свой учебник на страничке 62 и найдите номер три давайте выполним следующее итак вычислить объем коробки с измерениями 3 детстве метра 4 дециметров едва диаметра двумя способами то есть сначала у нас коробка как бы лежит а затем она как бы стоит то есть мы поменяли ее не местами а мы ее просто приподняли поставили на другую грань и давайте сейчас сначала ну так посчитаем объем 1 коробки смотрим внимательно нам нужно найти длину и ширину основания все нашли правильно 4 и 2 мы 4 умножаем на 2 это мы узнаем площадь основания и для того чтобы найти нам вами объем нужно площадь основания умножить на что подсказываете ребята правильно на высоту молодцы получится 24 каких дециметра кубических молодцы ребята а теперь второй способ обратите внимание на основании мы считаем площадь основания длина тряпицы метра ширины от позиции метра как мы считаем площадь равна 3 умножить на 2 так и умножаем на 4 потому что высота у нас 4 секций метра и у нас снова получается 24 кубических дециметров молодцы ребята давайте подведем итог урока что же такое объем фигуры эта величина которая показывает больше или меньше места фигура занимает в пространстве поминаем про шкаф утра комнату чтобы найти объем параллелепипеда можно получить основание умножить на высоту и умножить на b это у нас площадь основания и затем все это умножить на с с ребята это высота итак ребята если вдруг вам что то непонятно вы можете просмотреть этот урок еще раз и нам осталось вами записать домашнее задание страничка 62 номер 4 обратите внимание под буковка а лишние выполнять не надо ребята вы просто молодцы всем спасибо за работу до свидания и оставайтесь пожалуйста дух
Площадь прямоугольников и квадратов
Взгляните на схему ниже. Сколько квадратов внутри? Если вы потратили время, чтобы пересчитать все квадраты, вы должны увидеть, что их 48. Это означает, что площадь прямоугольника или пространство, которое покрывает прямоугольник, составляет 48 квадратных единиц.Однако подсчет квадратов — не очень эффективный способ определения площади. Существует лучший способ.
A = lw
A = 8 шт. X 6 шт.
A = 48 квадратных единиц или 48 единиц 2
Прямоугольник особого типа, называемый квадратом , имеет четыре равные стороны.
Поскольку стороны равны, когда мы умножаем длину и ширину, мы получаем число, умноженное на само число, или число, возведенное в квадрат.
Итак, для квадратов мы можем упростить формулу ииспользовать A = s 2 . A = s 2
A = (8 единиц) 2
A = 64 единицы 2
Вот еще несколько примеров:
1.) Вычислите площадь прямоугольника длиной 4 и шириной 9 единиц.
Решение: A = lw
A = (4 единицы) (9 единиц)
A = 36 единиц 2
2.) Определите площадь прямоугольника
Решение: A = lw
A = (3 дюйма) (18 дюймов)
A = 54 дюйма 2
3.) Площадь прямоугольника — 30 см. 2 , длина — 6 см. Какая ширина прямоугольника?
Решение: Поскольку нам дана площадь, работаем в обратном направлении, разделяя.
A = lw
30 см 2 = (6 см) w
30 см 2 ÷ 6 см = w
5 см = w
4.) Определите площадь квадрата со стороной 10 см.
A = s 2
A = (10 см) 2
A = 100 см 2
5.) Определите площадь показанной формы.
A = s 2
A = (7 мм) 2
A = 49 мм 2
6.) Площадь квадрата составляет 144 дюйма 2 . Какова длина каждой стороны?
Решение: поскольку нам дана площадь, работаем в обратном порядке, извлекая квадратный корень.
A = с 2
144 дюйма 2 = с 2
√144 дюйма 2 = √s 2
12 дюймов = с
7.) Площадь квадрата составляет 225 см 2 . Какой периметр?
Решение: для определения периметра необходимо сначала определить длину стороны. Затем используйте длину стороны, чтобы определить периметр.
A = s 2 P = 4s
225 см 2 = s 2 P = 4 (15 см)
√225 см 2 = √s 2 P = 60 см
15 см = с
Давайте рассмотрим
Чтобы определить площадь прямоугольника, мы должны умножить длину и ширину.
Используем формулу A = lw. Если нам даны площадь и одна сторона, мы можем работать в обратном направлении, разделив, чтобы определить длину другой стороны.
Чтобы определить площадь квадрата, мы можем использовать формулу прямоугольника или специальную формулу: A = s 2 . Если нам дана площадь квадрата, мы можем работать в обратном направлении или извлекать квадратный корень, чтобы определить длину стороны.
Общие сведения о площади поверхности и объеме
Наставник: Итак, если мы знаем, что можем найти площадь двумерной фигуры, вы думаете, что это можно ли найти площадь трехмерной фигуры? На самом деле, кто мне скажет, что за три размерная фигура есть?
Студент: Трехмерная фигура похожа на шар или куб — она не плоская.
Наставник: Верно. Теперь, может ли кто-нибудь сказать что-нибудь о том, что может означать обнаружение области такая цифра?
Студент: Когда вы говорите «найди местность», вы имеете в виду внешнее или внутреннее?
Наставник: Ну, это зависит от обстоятельств. На самом деле не существует такой вещи, как поиск «площади» куба. Вместо, у нас есть термины «объем» и «площадь поверхности». Давайте сначала поговорим об объеме. Когда ты говоришь «Найди площадь» квадрата, ты имеешь в виду внешнюю сторону, или внутренности включены?
Студент: Мы просто смотрим на пространство, которое оно занимает на бумаге; мы предполагаем, что края квадрата имеют ширина нуля.
Наставник: Именно! А теперь представьте, сколько места занимает куб в трех измерениях. Мы назовем это мерой объема куба.
Студент: Как вы измеряете громкость?
Наставник: Так же, как вы измеряете и умножаете длину и ширину прямоугольника, чтобы найти его площадь, вы умножьте длину, ширину и высоту трехмерного объекта, например куба, чтобы найти его объем. В умножение трех переменных дает ему три измерения, таким образом, объем, а не просто площадь.Как вы думаете, какие единицы измерения объема?
Студент: Ну, если есть три члена, все в дюймах, тогда это будут дюймы * дюймы * дюймы, что в дюймах в кубе.
Наставник: Чем это отличается от единиц, когда вы находите область?
Студент: Ну, площадь «возведена в квадрат», потому что вы просто умножаете дюймы на дюймы.
Наставник: Совершенно верно! Площадь «квадрат», а объем «куб».Как вы думаете, как это связано с их имея в виду?
Учащийся: Вы находите площадь квадрата или других двухмерных объектов, но обнаруживаете объем трехмерные объекты вроде кубиков!
Наставник: Хорошо, теперь мы знаем, как измерить, сколько места занимает объект. Но как насчет вне объекта, как вы упомянули ранее? Как вы думаете, что такое «площадь поверхности»?
Студент: Похоже, это были бы только внешние стороны — область, которая находится на поверхности, которую я могу трогать.
Наставник: Очень хорошо сказано! Площадь поверхности — это площадь поверхности трехмерной формы. Как вы бы посчитали что-нибудь подобное?
Студент: Это кажется слишком простым, но не мог бы я просто найти область каждого двухмерного лица, затем сложите области?
Наставник: Совершенно верно! Это так просто. Почти все трехмерные объекты, с которыми вы будете иметь дело, являются состоящие из двухмерных граней, которые представляют собой просто квадраты, треугольники и т. д., и те, которые изогнутые, как сферы, будут иметь свои особые формулы для площади поверхности.Конечно, единицы для этого легко найти, не так ли?
Студент: Да, это просто стандартные единицы площади — единицы * единицы или единицы в квадрате.
Наставник: Понятно! Теперь вы готовы попытаться решить некоторые проблемы, связанные с площадью поверхности и объем.
Периметр прямоугольника 66м. Ширина на 9 м меньше длины. Какова длина и ширина прямоугольника?
Периметр прямоугольника 66м.Ширина на 9 м меньше длины. Какова длина и ширина прямоугольника?
Давайте еще раз сформулируем, какие факты приводятся в этом вопросе и что нам осталось выяснить. Во-первых, мы знаем, что периметр прямоугольника равен 66 (периметр, конечно, это длина всех четырех сторон прямоугольника, сложенных вместе).Мы также знаем, что ширина периметра на 9 меньше длины.
w = l — 9
Так как же нам найти ответ на этот вопрос? К счастью, есть формула, которую мы можем использовать для вставки наших значений, которая поможет нам в наших расчетах.Эта формула: p = 2 l + 2 w , что переводится на английский язык как «периметр прямоугольника равен удвоенной длине плюс два раза ширине».
Нам известно значение периметра прямоугольника, поэтому мы можем заменить p на 66 в нашем уравнении.
66 = 2 л + 2 ш
Мы также знаем, что ширина прямоугольника на 9 меньше длины, поэтому мы можем заменить w уравнения на ( l — 9).
66 = 2 л + 2 ( л — 9)
Теперь мы готовы решить уравнение для длины ( l ), поскольку это оставшееся значение в уравнении, которое мы еще не обнаружили. Для этого умножим 2 на оба значения в скобках. 2 умножить на л равно 2 л . 2, умноженное на –9, равняется –18.
66 = 2 л + 2 л -18
Что нам делать дальше? Мы все еще решаем уравнение для l , поэтому нам нужно удалить -18 из правой части уравнения, добавив его к 66 слева.Мы также можем добавить 2 л к 2 л . Это оставляет нас с. . .
84 = 4 л
Мы почти у цели! Разделите обе части уравнения на 4, и мы наконец узнаем длину прямоугольника. 84, разделенное на 4, равно 21 (и, конечно, 4 l , разделенное на 4, равно l ), поэтому значение l равно 21. Мы знаем, что ширина прямоугольника на 9 меньше длины, поэтому мы можно рассчитать ширину 21 — 9 или 12 м.И даже показали свою работу!
Умножение дроби и площадь
На этом уроке для пятого класса исследуется площадь прямоугольника с дробными длинами сторон. Мы замощаем прямоугольник единичными прямоугольниками и показываем, что площадь такая же, как и при умножении длин сторон. Умножаем дробные длины сторон, чтобы найти площади прямоугольников.
| ||||||||||
|
1.На каждой картинке изображена квадратная единица и цветной
прямоугольник. Определите длину сторон
и площадь прямоугольника по рисунку.
2. Снова определите длину сторон цветного прямоугольника по рисунку. Затем умножьте длину стороны
, чтобы найти ее площадь. Убедитесь, что площадь, полученная при умножении, такая же, как и площадь, которую вы видите
с картинки.
3. Заштрихуйте прямоугольник внутри. квадрат так, чтобы его площадь можно было найти умножением на дробь.
|
| ||||||||||||||||
|
|
| |||||||||
| |||||||||
|
4. Расширьте стороны прямоугольника так, чтобы получился квадратный метр (единичный квадрат).
Нарисуйте линии сетки в квадрате
, как в примере выше. Напишите произведение умножения площади
цветного прямоугольника. Убедитесь, что
площадь, полученная при умножении, такая же, как и та, которую вы видите.
на картинке.
5.Расширьте стороны
прямоугольник, чтобы получился квадратный метр (единичный квадрат). Нарисуйте линии сетки в квадрате
, как в примере выше. Напишите произведение умножения площади
цветного прямоугольника. Убедитесь, что
, что площадь, полученная при умножении, такая же, как и та, которую вы видите.
на картинке.
6. На рисунках ниже внешний квадрат равен единицам квадрата . Напишите произведение умножения для площади
цветной прямоугольник
.На этот раз мы используем не метры или дюймы, а просто «единицы».
и «квадратные единицы» и
, вы не должны включать их в умножение
(просто напишите дроби без единиц измерения).
7. а. Нарисуйте квадрат размером 1 на 1 дюйм. Какая у него площадь?
г. Нарисуйте прямоугольник толщиной 3/4 дюйма.
и 5/8 дюйма со сторонами
внутри квадрата, который вы нарисовали так, чтобы
два
стороны
прямоугольника касаются сторон квадрата.
См. Рисунок ниже (не для
шкала).
г. Найдите район вашего прямоугольник.
8. а. Нарисуйте квадратный сантиметр.
г. Нарисуйте прямоугольник размером 3/10 см и
7/10 см сторон
внутри квадратного сантиметра так, чтобы
два
стороны
прямоугольника касаются сторон квадрата.
г. Вычислить площадь прямоугольника в квадрате
сантиметры
с использованием дробей и десятичных знаков
(посчитайте дважды).
Использование дробей:
с использованием десятичных знаков:
9. а. Найдите площадь прямоугольного пригорода размером 3 км на 1/2 км.
г. Деревня находится в пределах 5/8 мили на 3/4 мили.
прямоугольник. Найдите его
площадь.
10. Поездка на пони стоит 3,50 доллара за километр. Вы идете за 3 3/5 км.
а. Подсчитать сумму
цена с использованием дробей.
Используйте 3 ½ для цены за километр.
г. Подсчитать сумму
цена с использованием десятичных знаков.
Используйте 3,6 для километров.
11. а. Размер штампа 7/8 дюйма на 3/4 дюйма
Аманда
ставит 6 из них на
конверт, бок о бок.
Найдите общую площадь этих
марки занимают.
г. Конверт 8 дюймов.на 5 дюймов
Около что
Часть конверта закрывают шесть марок?
| У кого площадь больше: квадрат со сторонами 7/8 мили, или прямоугольник размером 1/4 мили на 3 мили? |
Этот урок взят из книги Марии Миллер Math Mammoth Fractions 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора.Авторские права © Мария Миллер.
Как найти площадь поверхности прямоугольной призмы (формула + видео)
Содержание
Определение площади поверхности всех прямоугольных призм позволяет вам также найти площадь поверхности любого куба, поскольку куб является разновидностью прямоугольной призмы.
- Что такое прямоугольная призма?
- Какова площадь поверхности прямоугольной призмы?
- Площадь поверхности прямоугольной призмы по формуле
- Как найти площадь поверхности прямоугольной призмы
- Площадь прямоугольной коробки
- Примеры расчета площади поверхности
Площадь поверхности прямоугольной призмы
Что такое прямоугольная призма?
Прямоугольная призма представляет собой шестигранное трехмерное тело, в котором все грани являются прямоугольниками.Все шесть граней встречаются под прямым углом друг к другу. Противоположные грани совпадают.
Особый тип прямоугольной призмы — это куб , в котором все шесть граней совпадают.
Какова площадь поверхности прямоугольной призмы?
Площадь поверхности прямоугольной призмы — это общая площадь всех шести граней. Когда у вас есть куб, определение площади одной грани позволяет очень быстро найти общую площадь поверхности твердого тела, поскольку она будет в шесть раз больше площади одной грани.
Площадь поверхности прямоугольной призмы по формуле
Определение площади поверхности для всех прямоугольных призм (включая кубики) включает как сложение, так и умножение. Вы должны знать ширину, длину и высоту призмы, прежде чем применять эту формулу:
A = 2 (ширина × длина) + 2 (длина × высота) + 2 (высота × ширина)
Мы можем использовать общепринятые сокращения для ширины (w), длины (l) и высоты (h) и переделать формулу:
A = 2wl + 2lh + 2hw
Мы можем упростить это, вычтя 2:
A = 2 wl + lh + hw
Поскольку каждая грань прямоугольной призмы имеет конгруэнтную противоположную грань, вы отслеживаете все шесть граней попарно.Использование формулы помогает избежать путаницы или отслеживать лица, которые вы измеряли. Вам нужны только три измерения.
Формула площади прямоугольной коробки
Для куба или прямоугольной коробки формула становится еще проще. Возьмите длину любого края, a :
Это работает, потому что все измерения куба — ширина, высота и длина — одинаковы. Любые два измерения дадут площадь одной грани, а куб имеет шесть граней, поэтому площадь равна 6a2.Если вам сложно запомнить эту специальную формулу, вы всегда можете использовать общую формулу для прямоугольных призм.
Как найти площадь поверхности прямоугольной призмы
Вас попросили упаковать подарочную коробку, которую ваш математический клуб передаст консультанту вашего математического клуба. В коробке 100 сборников математических анекдотов, так что это прямоугольная призма хорошего размера. (Вы знаете, сколько книг в коробке? 😊)
[вставить рисунок коробки с указанными размерами, как показано]
Его размеры:
- Ширина — 30 см
- Длина — 15 см
- Высота — 20 см
Используйте формулу площади, чтобы определить минимальное количество подарочной упаковки, которое вам понадобится.Сначала работа; затем заглянуть.
Давайте построим уравнение для площади поверхности прямоугольной призмы, исходя из нашей формулы:
A = 2 wl + lh + hw
А = 2 30 · 15 + 15 · 20 + 20 · 30
А = 2 450 + 300 + 600
А = 2 1,350
A = 2700 см2
Хотя это звучит как много подарочной упаковки, ее площадь всего 0,27 м2. У вас есть подарочная упаковка размером 0,75 м × 0,5 м. Вы думаете, вам будет достаточно?
Конечно, даже если вы оставите немного лишнего для перекрытия, так как у вас 0.375 м2, а нужно всего 0,27 м2! (Вы знали, что в коробке было всего 10 книг? 😲)
Площадь прямоугольной коробки
Теперь давайте посмотрим, как найти площадь поверхности правой прямоугольной призмы, коробки или куба.
Вы также должны упаковать хваленый кубик корня куба математического клуба для летнего хранения. У куба 12 совпадающих граней, каждая по 45 см. Сначала работа; затем заглянуть.
[вставить рисунок в причудливую коробку с надписью Cube Root Cube]
Давайте построим уравнение для площади прямоугольной коробки, исходя из формулы куба:
А = 6a2
А = 6452
А = 62 025
A = 12,150 см2
По традиции вашего клуба, вы будете использовать постоянные записи старейшин клуба, чтобы обернуть ценный кубик корня куба.У вас есть 2 м2 их записей, датируемых 1960 годом. Хотя 12 150 см 2 звучит много, это всего лишь 1,215 м2, так что у вас есть много обертки для хранения, чтобы защитить Куб и его бесценное содержимое кубических корней.
Примеры расчета площади поверхности
Попрактикуйтесь в использовании этих задач со словами площади поверхности для прямоугольных призм и кубов. Прежде чем искать ответы, попробуйте оба! Посмотрите, получите ли вы правильные ответы.
Дорожную клетку для домашнего удава необходимо накрыть, чтобы ее можно было перевозить в школьном автобусе.Какова площадь поверхности клетки?
[вставьте чертеж прямоугольной призмы, обозначенной длиной 1,5 ярда, шириной 0,25 ярда, высотой 0,25 ярда; можно нарисовать внутри призмы улыбающуюся мультяшную змею]
A = 2 wl + lh + hw
A = 2 0,25 × 1,5 + 1,5 × 0,25 + 0,25 × 0,25
А = 2 0,375 + 0,375 + 0,0625
А = 2 8.125
A = 1,625 ярда2
Давайте попробуем воспользоваться другим словом, чтобы найти площадь прямоугольной коробки.
Ваш учитель математики отправляет ящик, полный воображаемых чисел, коллеге через всю страну и просит вас обернуть его коричневой крафт-бумагой. Сколько бумаги вам нужно?
[вставить рисунок коробки с надписью 12 «x 12» x 12 «; можно нарисовать на ней несколько марок, как если бы она была отправлена по почте]
А = 6a2
А = 6122
А = 6144
A = 864 дюйм2
Вам нужно 864 кв. Дюйма бумаги, а это всего шесть квадратных футов!
Следующий урок:
Периметр прямоугольника — формула, определение, примеры
Периметр прямоугольника — это общее расстояние до его внешней границы.Это удвоенная сумма его длины и ширины и рассчитывается по формуле: Периметр = 2 (длина + ширина).
Каков периметр прямоугольника?
Периметр прямоугольника — это общая длина или расстояние до его границы со всех сторон. Периметр прямоугольника является линейной мерой и имеет те же линейные единицы измерения, что и метры, футы, дюймы или ярды. Давайте сначала разберемся с двумя основными свойствами прямоугольника.
- Все четыре угла прямоугольника равны 90 °.
- Противоположные стороны прямоугольника равны по размеру.
Представьте себе прямоугольный парк по соседству. Вы когда-нибудь задумывались о длине его границы?
Если вы один раз обойдете парк вдоль его границы, вы преодолеете расстояние. Это расстояние составляет периметр парка. Чтобы измерить периметр любого прямоугольного поля, вы путешествуете по границе четырех сторон поля. Вы начинаете с фиксированной точки, называемой отправной точкой, и заканчиваете, когда снова достигаете начальной точки.Эта длина или расстояние до границы называется периметром прямоугольника.
Формула периметра прямоугольника
Формула, используемая для вычисления периметра прямоугольника: периметр прямоугольника = 2 (l + w) единиц, где l — длина, а w — ширина прямоугольника. Разберемся в этом на простом примере. Дэвид хочет поставить забор вокруг своей фермы, чтобы его овцы не забредали прочь. Давайте теперь разберемся с этой формулой на примере.Он хочет знать, сколько проволоки ему понадобится, чтобы поставить забор вокруг своей прямоугольной фермы.
Назовем сначала стороны его фермы. Большая сторона этой прямоугольной фермы называется (l). Меньшая сторона называется (w). Теперь, если мы сложим расстояние до всех 4 сторон его фермы, получится периметр. Общее расстояние = l + w + l + w = 2l + 2w. Следовательно, Периметр прямоугольника = 2 (l + w).
Как найти периметр прямоугольника?
Мы можем вычислить периметр прямоугольника за три простых шага.Три перечисленных ниже шага помогут найти периметр.
- Шаг 1: Чтобы вычислить периметр прямоугольника, необходимо знать длину и ширину.
- Шаг 2: Соответствующие значения длины и ширины подставляются в формулу.
- Шаг 3: После решения уравнения вычисляется значение периметра.
Формула, используемая для вычисления периметра прямоугольника:
Периметр прямоугольника = 2 (l + w).
Давайте рассмотрим два разных случая формулы периметра прямоугольника.
- Если периметр и длина прямоугольника известны, ширину можно рассчитать по формуле: Ширина = P / 2 — l, где l = длина прямоугольника; и w = ширина прямоугольника, и P = периметр прямоугольника.
- Таким же образом, если известны периметр и ширина, длину можно рассчитать по формуле: Длина (L) = P / 2 — w.Где P = периметр прямоугольника; и w = ширина прямоугольника.
Использование периметра прямоугольника
Периметр прямоугольника упрощает задачу и помогает нам вычислять расстояния и длины в повседневной жизни.
Например,
- Если вам нужно украсить рамку прямоугольной записной книжки, вы можете легко рассчитать, сколько ленты вам понадобится, определив периметр.
- Если вам нужно поставить забор вокруг вашего сада, периметр сада даст вам точную длину проволоки, которая вам понадобится.
Можете ли вы вспомнить другие подобные примеры, связанные с периметром прямоугольника?
Калькулятор периметра прямоугольника
Попробуйте сейчас «Калькулятор периметра прямоугольника» Cuemath, онлайн-инструмент, который вычисляет периметр прямоугольника. Это самый простой и быстрый способ для детей быстро вычислить ответы за секунды.
☛ Статьи по теме
Чтобы улучшить ваши вычисления и более глубокое понимание периметра прямоугольника, ознакомьтесь с еще несколькими интересными статьями, перечисленными ниже.
Часто задаваемые вопросы о периметре прямоугольника
Что такое периметр прямоугольника в математике?
Периметр прямоугольника в математике — это значение измерения, которое определяется как общая длина или расстояние вокруг границ прямоугольной формы. Периметр прямоугольника измеряется в метрах, футах, дюймах или ярдах.
Что такое формула периметра прямоугольника?
Для расчета периметра прямоугольника используются следующие формулы:
- Периметр прямоугольника = 2 (l + w).
- Если периметр и длина прямоугольника известны, ширина = P / 2 — l, где l = длина, w = ширина, и P = периметр прямоугольника.
- Если периметр и ширина известны, длина (L) = P / 2 — w. Где P = периметр прямоугольника; и w = ширина.
☛ Проверьте все важные математические формулы:
Как найти площадь прямоугольника по периметру прямоугольника?
Если задан периметр прямоугольника, нам также нужно знать длину или ширину, чтобы найти его площадь.Например, если указаны длина и периметр, можно рассчитать ширину. Perimeter = 2 (длина + ширина), width = (Perimeter / 2) — длина. Теперь известны необходимые значения для определения площади прямоугольника. Итак, эти значения можно подставить в формулу: Площадь = длина × ширина.
Как найти периметр прямоугольника по диагонали?
Если задана диагональ прямоугольника, то, используя следующую формулу периметра прямоугольника, мы можем определить периметр прямоугольника.
Периметр прямоугольника с диагональю = 2l + 2 \ (\ sqrt {d 2 — l 2 } \) Единицы.
☛ Также читайте
Как найти периметр прямоугольника?
Периметр прямоугольника равен удвоенной сумме его длины и ширины и рассчитывается по формуле: Периметр = 2 (длина + ширина). Это мера общей границы прямоугольника.
Каковы единицы периметра прямоугольника?
Единицы измерения периметра прямоугольника совпадают с его длиной, которая обычно выражается в метрах, сантиметрах, дюймах или ярдах.Периметр равен границе прямоугольника, который можно рассчитать по формуле: Периметр = Длина + Длина + Ширина + Ширина = 2 (Длина + Ширина).
Одинаковы ли площадь и периметр прямоугольника?
Нет, площадь и периметр прямоугольника разные. Площадь прямоугольника — это общее пространство, занимаемое им, и выражается в квадратных единицах, а периметр — это общая мера его границы и выражается в линейных единицах.
☛ Проверить сейчас:
Каков периметр прямоугольника с заданной площадью?
Если задана площадь прямоугольника, нам нужно знать длину или ширину прямоугольника, чтобы найти его периметр.Например, если длина и площадь известны, ширину можно вычислить: Площадь = длина × ширина. Итак, ширина = Площадь / длина. Теперь известны все необходимые значения для расчета периметра прямоугольника. Итак, эти значения можно подставить в формулу: Периметр = 2 (длина + ширина).
Как рассчитывать периметры: Часть 1
Сегодня мы научимся рассчитывать периметры геометрических фигур. Но сначала давайте начнем с определения периметра. Когда мы говорим периметр , мы имеем в виду длину контура многоугольника .
Здесь вы можете ознакомиться с наиболее распространенными типами полигонов.
Длину контура многоугольника можно рассчитать, сложив вместе все сегменты, образующие его стороны.
Вычислить периметр любого многоугольника
Я собираюсь показать вам первую стратегию расчета периметров, в которой количество сторон многоугольника не имеет значения.
Периметр геометрической фигуры всегда можно рассчитать, сложив длины каждой стороны.
Например, вы можете рассчитать периметр этого треугольника следующим образом.
Периметр = 17 см + 15 см + 11 см = 43 см
Вы можете использовать эту стратегию для вычисления периметра любого многоугольника.
Расчет периметра квадратов
Особенностью квадрата является то, что у него четыре равные стороны . Мы можем воспользоваться этим, упростив наши вычисления.
Вы можете рассчитать периметр этого квадрата, сложив длины четырех сторон.
Периметр = 6 см + 6 см + 6 см + 6 см = 24 см
Поскольку четыре стороны равны, умножение длины одной стороны на четыре даст тот же результат.
Периметр = 4 x 6 см = 24 см
Итак, вы открыли правило, которое поможет вам с любым квадратом.
Периметр квадрата = 4 x длина стороны
Вычислить периметр прямоугольников
В каждом прямоугольнике противоположные стороны равны друг другу. У него равные стороны, два на два .
Чтобы вычислить периметр прямоугольника в примере, вы можете сложить длину его сторон, двух сторон по 6 см и двух сторон по 4 см.
Периметр = 6 см + 4 см + 6 см + 4 см = 20 см
Вы можете умножить сумму основания и высоты на два и получить тот же результат, потому что все прямоугольники повторяют длину своих сторон два раза.
Периметр = 2x (6 см + 4 см) = 20 см
Итак, у вас есть подход к любому прямоугольнику.
Периметр прямоугольника = 2 x (основание + высота)
Расчет периметров равносторонних треугольников
Так же, как и с квадратами, стороны равностороннего треугольника равны . Все они имеют одинаковую длину.
Длина каждой стороны 7 см, длину контура можно рассчитать следующим образом.
Периметр = 7 см + 7 см + 7 см = 21 см
Или есть способ попроще. Поскольку три стороны одинаковы, вы можете умножить одну сторону на 3, и результат не изменится.
Периметр = 3 x 7 см = 21 см
И это поможет вам с равносторонним треугольником.
Периметр равностороннего треугольника = 3 x длина одной стороны
Вычислить периметры любого правильного многоугольника
Отличительной чертой правильного многоугольника является то, что все стороны имеют одинаковую длину .
Поскольку у пятиугольника пять равных сторон, чтобы найти его периметр, нужно умножить длину одной стороны на пять.
Периметр пятиугольника = 5 x длина одной стороны
А с шестиугольником, у которого шесть равных сторон, вы можете умножить одну сторону на шесть.
Периметр шестиугольника = 6 x длина одной стороны
Из этих правил мы можем извлечь правило для вычисления периметра любого правильного многоугольника простым способом.
Умножьте количество сторон многоугольника на длину одной из сторон.
Периметр правильного многоугольника = количество сторон x длина одной стороны
Если вы хотите узнать больше о периметрах, геометрии и других предметах начальной математики, войдите в Smartick и попробуйте бесплатно.
Подробнее:
Развлечения — любимый способ обучения нашего мозга
Дайан Акерман
Smartick — это увлекательный способ изучения математики- 15 веселых минут в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
Команда по созданию контента.