Давление насыщенного пара формула – Давление насыщенного пара.

Давление насыщенного пара.

И что будет происходить с насыщенным паром, если уменьшить занимаемый им объем? Например, если сжимать пар, находящийся в равновесии с жидкостью в цилиндре под поршнем, поддерживая температуру содержи­мого цилиндра постоянной.

При сжатии пара равновесие нач­нет нарушаться. Плотность пара в первый момент немного увеличится, и из газа в жидкость начнет переходить большее число молекул, чем из жидкости в газ. Ведь число молекул, покидающих жидкость в единицу времени, зависит только от температуры, и сжатие пара это число не меняет. Процесс продолжа­ется до тех пор, пока вновь не установится динамическое равно­весие и плотность пара, а значит, и концентрация его молекул не примут прежнее значение. Следова­тельно, концентрация молекул на­сыщенного пара при постоянной температуре не зависит от его объема.

Так как давление п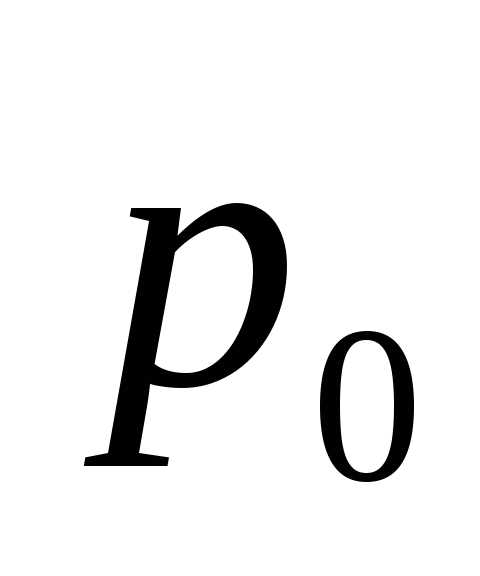ропорциональ­но концентрации молекул (p = nkT), то из этого определения следует, что давление насыщенного пара не зависит oт занимаемого им объема.

Давление пара , при котором жидкость находится в равновесии со своим паром, называют давлением насыщенного пара.

• Ненасыщенный пар.

Мы много раз употребляли слова газ и пар. Никакой принципиальной разницы между газом и паром нет. Но если при неизменной температуре газ простым сжатием можно превратить в жидкость, то мы называем его паром, точнее, ненасыщенным паром.

• Зависимость давления насыщен­ного пара от температуры.

Состояние насыщенного пара, как говорит опыт, приближенно описывается уравне­нием состояния идеального газа, а его давление определяется формулой

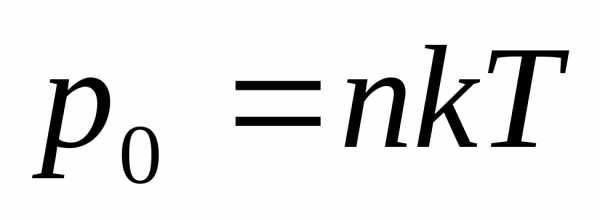
С ростом температуры давление растет. Так как д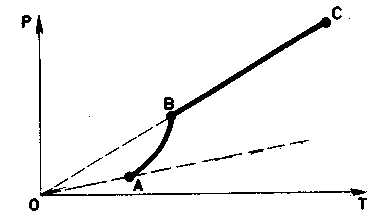авление насыщен­ного пара не зависит от объема, оно зависит только от температуры.

Однако эта зависимость ро(Т), найденная экспериментально, не яв­ляется прямо пропорциональной, как у идеального газа при постоян­ном объеме. С увеличением темпера­туры давление насыщенного пара растет быстрее, чем давление идеаль­ного газа (рис. 30, участок кривой

АВ). Это становится особенно оче­видным, если провести изохору через точку А (пунктирная прямая) Почему это происходит?

Однако эта зависимость р(Т), найденная экспериментально, не яв­ляется прямо пропорциональной, как у идеального газа при постоян­ном объеме. С увеличением темпера­туры давление насыщенного парабыстрее, чем давление идеаль­ного газа (рис. 30).Почему это происходит?

При нагревании жидкости в за­крытом сосуде часть жидкости превращается в пар. В результате согласно формуле

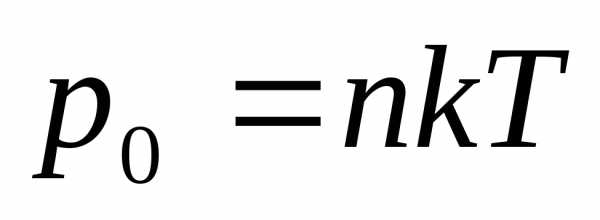давление насыщенного пара растет не только вследствие повышения температуры жидкости, но и вследствие увеличе­ния концентрации молекул (плот­ности) пара. В основном увеличение давления при повышении температуры определяется именно увели­чением концентрации. Главное раз­личие в поведении идеального газа и насыщенного пара состоит в том, что при изменении температуры пара в закрытом сосуде (или при изменении объема при постоянной температуре) меняется масса пара. Жидкость частично превращается в пар или, напротив, пар частично конденсируется. Когда вся жидкость испарится, пар при дальнейшем нагревании перестанет быть насыщенным и его давление при постоянном объеме будет возрастать прямо пропорцио­нально абсолютной температуре (см. рис. 30, участок ВС).

studfiles.net

Давление насыщенного пара — Класс!ная физика

Давление насыщенного пара

«Физика — 10 класс»

Как вы думаете, что будет происходить с насыщенным паром, если уменьшить занимаемый им объём: например, если сжимать пар, находящийся в равновесии с жидкостью в цилиндре под поршнем, поддерживая температуру содержимого цилиндра постоянной?

При сжатии пара равновесие начнёт нарушаться. Плотность пара в первый момент немного увеличится, и из газа в жидкость начнёт переходить большее число молекул, чем из жидкости в газ. Ведь число молекул, покидающих жидкость в единицу времени, зависит только от температуры, и сжатие пара это число не меняет. Процесс продолжается до тех пор, пока вновь не установится динамическое равновесие и плотность пара, а значит, и концентрация его молекул не примут прежних своих значений. Следовательно,

концентрация молекул насыщенного пара при постоянной температуре не зависит от его объёма.

Так как давление пропорционально концентрации молекул (р = nkT), то из этого определения следует, что давление насыщенного пара не зависит от занимаемого им объёма.

Давление р_{н. п} пара, при котором жидкость находится в равновесии со своим паром, называют давлением насыщенного пара.

При сжатии насыщенного пара всё большая часть его переходит в жидкое состояние. Жидкость данной массы занимает меньший объём, чем пар той же массы. В результате объём пара при неизменной его плотности уменьшается.

Газовые законы для насыщенного пара несправедливы (при любом объёме при постоянной температуре давление насыщенного пара одинаково). В то же время состояние насыщенного пара достаточно точно описывается уравнением Менделеева-Клапейрона.

Ненасыщенный пар

>Если пар постепенно сжимают при постоянной температуре, а превращение его в жидкость не происходит, то такой пар называют

ненасыщенным.

При уменьшении объёма (рис. 11.1) давление ненасыщенного пара увеличивается (участок 1—2) подобно тому, как изменяется давление при уменьшении объёма идеального газа. При определённом объёме пар становится насыщенным, и при дальнейшем его сжатии происходит превращение его в жидкость (участок 2—3). В этом случае над жидкостью уже будет находиться насыщенный пар.

Как только весь пар превратится в жидкость, дальнейшее уменьшение объёма вызовет резкое увеличение давления (жидкость малосжимаема).

Однако пар превращается в жидкость не при любой температуре. Если температура выше некоторого значения, то, как бы мы ни сжимали газ, он никогда не превратится в жидкость.

>Максимальная температура, при которой пар ещё может превратиться в жидкость, называется критической температурой.

Каждому веществу соответствует своя критическая температура, у гелия T_кр = 4 К, у азота T_кр = 126 К.

Состояние вещества при температуре выше критической называется газом; при температуре ниже критической, когда у пара есть возможность превратиться в жидкость, — паром.

Свойства насыщенного и ненасыщенного пара различны.

Зависимость давления насыщенного пара от температуры.

Состояние насыщенного пара, как показывает опыт, приближённо описывается уравнением состояния идеального газа (10.4), а его давление определяется формулой

р_{н. п} = nkT.         (11.1)

С ростом температуры давление растёт.

Так как давление насыщенного пара не зависит от объёма, то, следова тельно, оно зависит только от температуры.

Однако зависимость давления р_{н. п} от температуры Т, найденная экспериментально, не является прямо пропорциональной, как у идеального газа при постоянном объёме. С увеличением температуры давление реального насыщенного пара растёт быстрее, чем давление идеального газа (рис. 11.2, участок кривой АВ). Это становится очевидным, если провести изохоры идеального газа через точки А и В (штриховые прямые). Почему это происходит?

При нагревании жидкости в закрытом сосуде часть жидкости превращается в пар. В результате согласно формуле (11.1) давление насыщенного пара растёт не только вследствие повышения температуры жидкости, но и вследствие увеличения концентрации молекул (плотности) пара.

В основном увеличение давления при повышении температуры определяется именно увеличением концентрации. Главное различие в поведении идеального газа и насыщенного пара состоит в том, что при изменении температуры пара в закрытом сосуде (или при изменении объёма при постоянной температуре) изменяется масса пара.

Почему составляются таблицы зависимости давления насыщенного пара от температуры и нет таблиц зависимости давления газа от температуры?

Жидкость частично превращается в пар, или, напротив, пар частично конденсируется. С идеальным газом ничего подобного не происходит.

Когда вся жидкость испарится, пар при дальнейшем нагревании перестанет быть насыщенным и его давление при постоянном объёме будет возрастать прямо пропорционально абсолютной температуре (см. рис. 11.2, участок кривой ВС).

Кипение.

По мере увеличения температуры жидкости интенсивность испарения увеличивается. Наконец, жидкость начинает кипеть. При кипении по всему объёму жидкости образуются быстро растущие пузырьки пара, которые всплывают на поверхность.

Кипение — это процесс парообразования, происходящий по всему объёму жидкости при температуре кипения.

При каких условиях начинается кипение?

На что расходуется при кипении подводимое к жидкости тепло с точки зрения молекулярно-кинетической теории?

Температура кипения жидкости остаётся постоянной. Это происходит потому, что вся подводимая к жидкости энергия расходуется на превращение её в пар.

В жидкости всегда присутствуют растворённые газы, выделяющиеся на дне и стенках сосуда, а также на взвешенных в жидкости пылинках, которые являются центрами парообразования. Пары жидкости, находящиеся внутри пузырьков, являются насыщенными. С увеличением температуры давление насыщенных паров возрастает и пузырьки увеличиваются в размерах. Под действием выталкивающей силы они всплывают вверх. Если верхние слои жидкости имеют более низкую температуру, то в этих слоях происходит конденсация пара в пузырьках. Давление стремительно падает, и пузырьки захлопываются. Захлопывание происходит настолько быстро, что стенки пузырька, сталкиваясь, производят нечто вроде взрыва. Множество таких микровзрывов создаёт характерный шум. Когда жидкость достаточно прогреется, пузырьки перестанут захлопываться и всплывут на поверхность. Жидкость закипит.

Зависимость давления насыщенного пара от температуры объясняет, почему температура кипения жидкости зависит от давления на её поверхность. Пузырёк пара может расти, когда давление насыщенного пара внутри его немного превосходит давление в жидкости, которое складывается из давления воздуха на поверхность жидкости (внешнее давление) и гидростатического давления столба жидкости.

Обратим внимание на то, что испарение жидкости происходит и при температурах, меньших температуры кипения, но только с поверхности жидкости, при кипении же образование пара происходит по всему объёму жидкости.

Кипение начинается при температуре, при которой давление насыщенного пара в пузырьках сравнивается и становится чуть больше давления в жидкости.

Чем больше внешнее давление, тем выше температура кипения.

Так, в паровом котле при давлении, достигающем 1,6 • 10⁶ Па, вода не кипит и при температуре 200 °С. В медицинских учреждениях в герметически закрытых сосудах — автоклавах (рис. 11.3) кипение воды также происходит при повышенном давлении. Поэтому температура кипения жидкости значительно выше 100 °С. Автоклавы применяют, например, для стерилизации хирургических инструментов, ускорения приготовления пищи (скороварка), консервации пищи, проведения химических реакций.

И наоборот, уменьшая внешнее давление, мы тем самым понижаем температуру кипения.

Откачивая насосом воздух и пары воды из колбы, можно заставить воду кипеть при комнатной температуре. При подъёме в горы атмосферное давление уменьшается, поэтому уменьшается температура кипения. На высоте 7134 м (пик Ленина на Памире) давление приближённо равно 4 • 10⁴ Па (300 мм рт. ст.). Вода кипит там примерно при 70 °С. Сварить мясо в этих условиях невозможно.

У каждой жидкости своя температура кипения, которая зависит от свойств жидкости. При одной и той же температуре давление насыщенного пара разных жидкостей различно.

Например, при температуре 100 °С давление насыщенных паров воды равно 101 325 Па (760 мм рт. ст.), а паров ртути — всего лишь 117 Па (0,88 мм рт. ст.). Так как кипение происходит при той же температуре, при которой давление насыщенного пара равно внешнему давлению, то вода при 100 °С закипает, а ртуть нет. Кипит ртуть при температуре 357 °С при нормальном давлении.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Основы термодинамики. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика

Насыщенный пар — Давление насыщенного пара — Влажность воздуха — Примеры решения задач по теме «Насыщенный пар. Влажность воздуха» — Кристаллические тела — Аморфные тела — Внутренняя энергия — Работа в термодинамике — Примеры решения задач по теме «Внутренняя энергия. Работа» — Количество теплоты. Уравнение теплового баланса — Примеры решения задач по теме: «Количество теплоты. Уравнение теплового баланса» — Первый закон термодинамики — Применение первого закона термодинамики к различным процессам — Примеры решения задач по теме: «Первый закон термодинамики» — Второй закон термодинамики — Статистический характер второго закона термодинамики — Принцип действия тепловых двигателей. Коэффициент полезного действия (КПД) тепловых двигателей — Примеры решения задач по теме: «КПД тепловых двигателей»

class-fizika.ru

Давление насыщенного пара над раствором. Закон рауля.

1. Растворы нелетучих веществ в летучих растворителях.

р_A⁰– давление насыщенного пара над чистым растворителем.

р_A–давление насыщенного пара над раствором.

Давление насыщенного пара р_A⁰ над растворителем или жидкостью определяется межмолекулярным взаимодействием внутри жидкости. Чем больше сила взаимодействия f_A—A между молекулами, тем меньше пара над жидкостью, и соответственно, тем меньше давление этого парар_A⁰ <<<.

Давление насыщенного пора над раствором р_Aпри нелетучем растворенном веществе В отличается от давления насыщенного пара над чистым растворителемр_A⁰. Для нахождения этого отличия в зависимости от состава идеального раствора рассмотрим условия равновесияi-го компонента в растворе и в парообразном состоянии. Это равновесие определяется равенством химических потенциалов:

, где

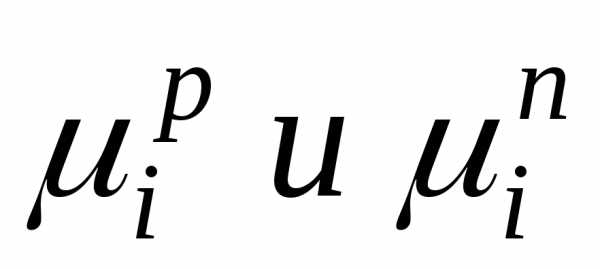– химические потенциалыi-го компонента в растворе и в парообразном состоянии.

Химический потенциал можно выразить через парциальное давление:

Если i-й компонент подчиняется законом идеальных газов, то дифференцируя это уравнение, получим:

(*)

Теперь из уравнений и (*) выразим изменения мольной доли растворенного вещества следующим образом:

Проведем интегрирование этого уравнения от р_A⁰дор_Aи отN_A=1 доN_A, изменяющегося в пределах 0<N_A<1, гдеN_A– мольная доля растворителя в растворе; для чистого растворителяN_A=1,

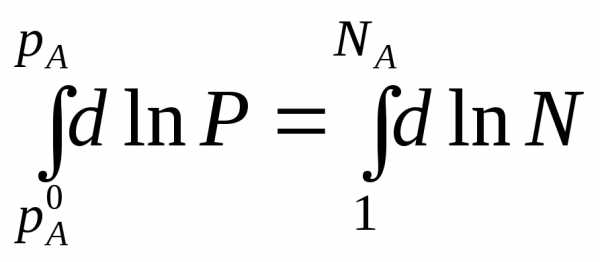
После интегрирования получаем:

(1) (*)

Давление насыщенного пара над растворомр_Aравно произведению его давления над чистым растворителем р_A⁰ на его мольную долюN_A.

Если раствор состоит из двух компонентов А(р-ль) и В(в-во), то мольная доля растворенного вещества равна N_B=1-N_A. Тогда уравнение (*) трансформируется:

Если N_В – мольная доля растворенного вещества, то

(2) (**)

Формулы (*) и (**) отражают различные способы выражениязакона Рауля.

Разность (р_A⁰— р_A) характеризует понижение давления насыщенного пара над раствором, а отношение (р_A⁰— р_A)/ р_A⁰ – относительное понижение давления насыщенного пара.

Тогда закон Рауля формулируется следующим образом:относительное понижение давления пара над раствором равно мольной доле растворенного вещества в растворе.

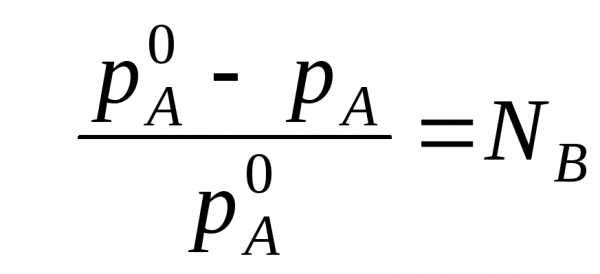
Закон Рауля применим к идеальным и сильно разбавленным растворам.

Максимальноедавление пара, создаваемое жидкостью – давление её насыщенного пара при данной температуре.

ДНП растет с температурой.

Когда ДНП становится равным внешнему давлению, жидкость закипает.

Пример.Вычислим давление пара при 373 К (100⁰С) над водным раствором сахарозы, мольная доля которой составляетN_B=1,01∙10^-3, для воды р_A⁰=1,013∙10⁵ Па.

Согласно уравнению (**)

Как следует из полученных данных, над раствором сахарозы происходит весьма незначительное снижение давления насыщенного пара воды по сравнению с чистой водой.

2. Идеальные растворы из двух летучих компонентов.

А

В

А+В

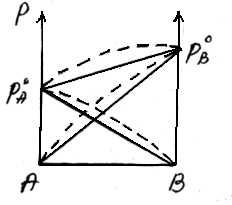
р_A⁰ р_В⁰ р_A+ р_В

Общее давление пара над раствором рбудет равно сумме парциальных давлений его компонентов; для раствора, содержащего компоненты А и В, общее давление р=р_А+р_В.

На основании уравнения (*), как для компонента А, так и для компонента В, можно считать, аN_А=1-N_В.

Общее давление будет равно:

(3) (***)

Это уравнение характеризует линейную зависимость давления от мольной доли компонента В, что можно отобразить графически.

На рисунке по оси ординат слева отложены парциальные давления компонента А, которые изменяются от 0 до р_A⁰, а справа – изменения парциального давления компонента В. Общее давлениеризменяется отр_A⁰ дор_В⁰.Линейная зависимостьобщего и парциальных давлений от состава растворахарактерна для идеальных и разбавленных растворов(ΔV=0; ΔH=0; ΔS=ΔS_и.г).

Практически, идеальными свойствами обладает раствор бензола в толуоле, что объясняется незначительностью сия межмолекулярного взаимодействия между молекулами всех компонентов раствора. Поэтому общее давление над раствором бензола в толуоле равно сумме парциальных давлений каждого из компонентов.

В случае предельно разбавленных растворов, концентрация растворенного вещества в которых бесконечно мала, давление пара (газа) растворителя выражается в соответствии сзаконом Рауля:

Давление паров растворенного вещества, которого в предельно разбавленном растворе ничтожно мало, не подчиняется закону Рауля. В этом случае давление пара над раствором описывается законом Генри, который формулируется так:при постоянной температуре парциальное давление растворенного вещества р_Г пропорционально его мольной доле:

,

где К_Г – коэффициент пропорциональности, называемыйконстантой Генри(справочная величина), которая зависит от температуры и природы компонентов раствора, но не зависит от давления.

Для неидеальных растворов линейная зависимость общего давления от состава раствора нарушается: наблюдается положительное и отрицательное отклонения. Причем, как правило, эти отклонения одного знака как для общего давления р, так и для парциальных давленийр_Aир_Вкомпонентов раствора.

Положительное отклонение от закона Рауля наблюдается в том случае, когда в растворе идет диссоциация молекул компонентов в растворе. Такие растворы образуются с поглощением теплоты (ΔH>0), т.е. процесс растворения будет эндотермическим.

ΔH>0, f_A-A > f_A-В

Отрицательное отклонение от закона Рауля наблюдается в случае ассоциации (укрупнения) частиц, формирующих раствор, и образования более прочных связей. При этом растворение идет с выделением теплоты (ΔH<0), т.е. процесс экзотермический.

ΔH<0, f_A-A < f_A-В

studfiles.net

Молекулярная физика.

Глава 4. Взаимные превращения жидкостей и газов. Лекция 27. Насыщенный пар. Критическая температура. Влажность воздуха.

• Испарение и конденсация.

Хоро­шо закрытый флакон с духами может стоять очень долго, и коли­чество духов в нем не изменится. Если же флакон оставить открытым, то, взглянув на него через доста­точно продолжительное время, вы увидите, что жидкости в нем нет. Жидкость, в которой растворены ароматические вещества, испари­лась.

Но как можно объяснить это явление.

Молекулы жидкости движутся беспорядочно. Чем выше температу­ра жидкости, тем больше кинетиче­ская энергия молекул. Среднее же значение кинетической энергии мо­лекул при заданной температуре имеет определенную величину. У каждой молекулы кинетическая энер­гия в данный момент может ока­заться как меньше, так и больше средней. В какой-то момент кине­тическая энергия отдельных молекул может стать настолько большой, что они окажутся способными вы­лететь из жидкости, преодолев силы притяжения остальных молекул. В этом и состоит процесс испарения.

Вылетевшая молекула принимает участие в беспорядочном тепловом движении газа. Беспорядочно дви­гаясь, она может навсегда удалить­ся от поверхности жидкости, нахо­дящейся в открытом сосуде, но может и вернуться снова в жидкость. Такой процесс называют конденса­цией.

Если поток воздуха над сосудом уносит с собой образовавшиеся пары жидкости, то жидкость испаряется быстрее, так как у молекулы пара уменьшается возможность вновь вер­нуться в жидкость. Чем выше темпе­ратура жидкости, тем большее число молекул имеет достаточную для вылета из жидкости кинетическую энергию, тем быстрее идет испарение.

При испарении жидкость поки­дают более быстрые молекулы, поэтому средняя кинетическая энер­гия молекул жидкости уменьшается. Это означает, что происходит пони­жение температуры жидкости. Смо­чив руку какой-нибудь быстро испа­ряющейся жидкостью (бензином или ацетоном), вы тут же почувствуете сильное охлаждение смоченного мес­та. Охлаждение усилится, если на руку подуть.

Если лишить жидкость возмож­ности испаряться, то охлаждение ее будет происходить гораздо мед­леннее. Вспомните, как долго осты­вает жирный суп. Слой жира на его поверхности мешает выходу быстрых молекул воды.

• Насыщенный пар.

Если сосуд с жидкостью плотно закрыть, то убыль ее вскоре прекратится. При неизменной температуре система жидкость — пар придет в состояние теплового равновесия, и будет нахо­диться в нем сколь угодно долго. Одновременно с процессом испаре­ния происходит и конденсация, оба процесса в среднем компенси­руют друг друга.

В первый момент, после того как жидкость нальют в сосуд и закроют его, жидкость будет испаряться, и плотность пара над ней будет увеличиваться. Однако одновремен­но с этим будет расти и число молекул, возвращающихся в жид­кость. Чем больше плотность пара, тем большее число его молекул возвращается в жидкость. В резуль­тате в закрытом сосуде при по­стоянной температуре установится динамическое (подвижное) равно­весие между жидкостью и паром, т. е. число молекул, покидающих поверхность жидкости, равно в сред­нем числу молекул пара, возвратив­шихся за то же время в жидкость

Пар, находящийся в динамиче­ском равновесии со своей жидкостью, называют насыщенным паром.

studfiles.net

6. Давление насыщенных паров

Давление насыщенных паров — это давление, производимое паровой фазой, которая находится в равновесии с жидкостью при определенной температуре. Давление насыщенных паров индивидуального чистого вещества зависит только от температуры. Для смесей и таких продуктов, как нефть и нефтепродукты, давление насыщенных паров зависит не только от температуры, но и от состава паровой и жидкой фаз и их соотношения. Поэтому определение давления насыщенных паров нефтепродуктов представляет большие трудности. Однако для узких нефтяных фракций, выкипающих в узком интервале температур без заметного изменения состава фаз, можно с известной степенью приближения считать однозначной зависимость давления насыщенных паров от температуры. Единица давления в системе единиц СИ — паскаль (Па). Кратные единицы кПа, МПа. Паскаль — давление, вызываемое силой 1 ньютон (Н), равномерно распределенной по поверхности площадью 1м² и нормально к ней направленной.

При изучении фракционного состава нефтей и проведении технологических расчетов аппаратуры приходится пересчитывать давление насыщенных паров нефтепродуктов при одной температуре на давление при другой, а также температуру кипения нефтяных фракций от одного давления к другому. Для осуществления таких пересчетов предложены формулы и номограммы (Приложения 7 и 8).

Пример 11. Узкая нефтяная фракция при атмосферном давлении имеет среднюю температуру кипения 149°С. Какова температура кипения этой фракции при 266,6 кПа?

Решение. По графику (Приложение 7) на оси координат находят точку, соответствующую температуре 149°С, и из этой точки проводят прямую, параллельную оси абсцисс, до пересечения с вертикальной линией, отвечающей давлению 101,3 кПа. Получают точку А, которая легла на искомый луч. Затем от точки, соответствующей давлению 266,6 кПа, проводят вертикаль до пересечения с найденным лучом в точке В. Из точки В проводят горизонтальную линию, параллельную оси абсцисс, до пересечения со шкалой температур в точке С. Эта точка дает значение искомой температуры кипения, равной 190°С.

Пример 12. При разгонке мазута из колбы Кляйзена температура паров в момент замера была равна 150°С, а остаточное давление 0,266 кПа. Какова температура паров при атмосферном давлении?

Решение. Используют номограмму (Приложение 8). На левой шкале номограммы отмечают температуру 150°С, на правой шкале — давление 0,266 кПа. Эти точки соединяют прямой, и в точке пересечения со шкалой «температура кипения при нормальном давлении» находят значение искомой температуры, равной 330°С.

Для подсчета давления насыщенных паров узких нефтяных фракций при низких давлениях пользуются формулой Ашворта

(25)

где Р — давление насыщенных паров, Па; Т — соответствующая температура, К; Т_о — температура кипения фракции при атмосферном давлении, К; f(T) — функция температуры Т, выражаемая уравнением

(26)

Функцию f(T₀) определяют аналогично. Значения функции для различных температур (Т и Т₀) приведены в Приложении 9.

Пример 13.Узкая нефтяная фракция при атмосферном давлении имеет среднюю температуру кипения 170°С. Определить давление насыщенных паров этой фракции при 260°С.

Решение. Для решения задачи используем формулу Ашворта (25).

По Приложению 9 найдем значения f(T₀) для температуры 170°С и f(T) для температуры 260°С

f(T₀) = 4,124 f(T) = 2,924

Подставим эти величины в формулу (25)

По таблицам антилогарифмов находим значение этого числа и получим

Р — 3158 = 590 900

Р = 590 900 + 3158 = 594 058 Па

Давление насыщенных паров данной фракции при 260°С

Р = 594 058 Па

На давление насыщенных паров оказывает влияние фракционный состав, отношения объемов паров и жидкости в рабочем баллоне, температура. При низких температурах и температурах, близких к начальной температуре кипения фракции, формула Ашворта дает несколько заниженные значения давления насыщенных паров.

Для определения давления насыщенных паров светлых нефтепродуктов и их узких фракций предложена формула

, кПа (27)

где

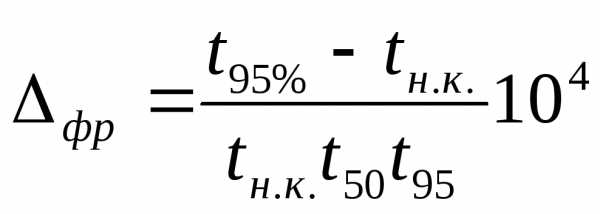
Для товарных бензинов 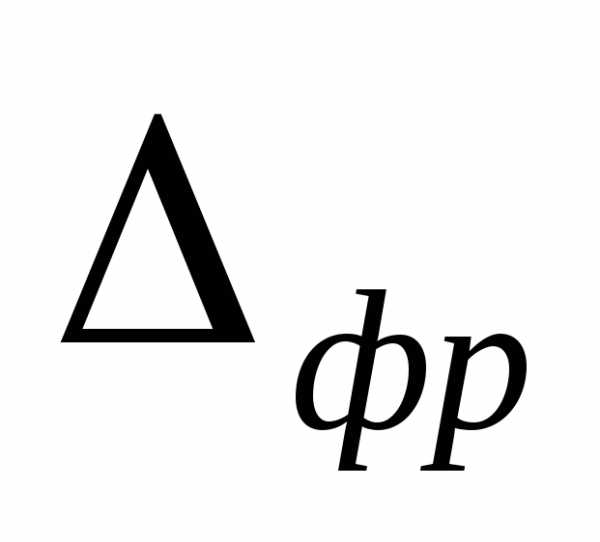= 1,5 — 2,5.

Эта формула дает возможность определить давление насыщенных паров светлых нефтепродуктов, используя характерные температуры кипения.

Задача 18. Узкая нефтяная фракция при давлении Р₀ имеет среднюю температуру кипения t₀⁰С. Какова температура кипения этой фракции при Р₁ кПа?

параметры	вариант
	1	2	3	4	5	6	7	8	9	10
t00С	38	71	232	27	127	45	399	138	218	427
Р0 кПа	103	103	103	104	104	105	105	106	106	107
Р1 кПа	104	5×103	5×103	105	106	106	106	105	105	105

Задача 19. При разгонке нефтепродукта температура паров в момент замера была равна t₀⁰С, а остаточное давление Р₀ кПа. Какова температура паров при атмосферном давлении?

параметры	вариант
	1	2	3	4	5	6	7	8	9	10
t00С	150	100	110	120	130	140	150	160	200	250
Р0 кПа	35	30	40	4	0,2	0,01	0,6	2	60	100

Задача 20. Узкая нефтяная фракция при атмосферном давлении имеет среднюю температуру кипения t₀⁰С. Определить давление насыщенных паров этой фракции при t₁⁰С.

параметры	вариант
	1	2	3	4	5	6	7	8	9	10
t00С	20	30	60	80	240	260	280	300	320	340
t10С	160	170	200	220	380	400	420	440	460	480

studfiles.net

5.3. Давление паров и диаграммы состояний Зависимость давления насыщенного пара от температуры. Тройная точка. Влияние давления на температуру фазового перехода. Формула Клаузиуса – Клапейрона.

Используя (5.3), запишем условие равновесия конденсированная фаза – пар, считая пар идеальным газом:



Отсюда равновесное давление пара, т.е. давление насыщенного пара над конденсированной (жидкой или твердой) фазой при произвольной температуре описывается формулой:

.

Аналогично условиям равновесия двух фаз, равновесие трех фаз одного и того же вещества определяется равенствами

Т_I=Т_II=Т_III,р_I=р_II=р_III,_I=_II=_III.

Если обозначить снова общие значения давления и температуры трех фаз посредством риТ, то мы получим условия

_I(р,Т) =_II(р,Т) =_III(р,Т).

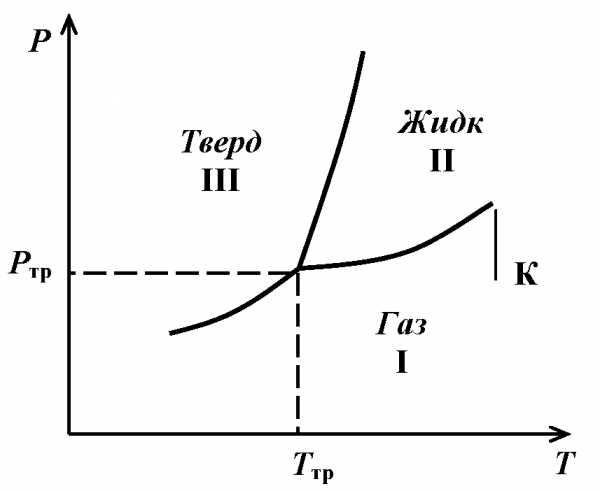
Это – два уравнения с двумя неизвестными риТ.Они имеют в качестве решенияединственную пару значенийриТ, графическим изображением которой в координатахр-Т будет точка. Состояния, в которых одновременно существуют в равновесии три фазы – это так называемыетрой­ные точки.

Трой­ная точка на диаграмме в координатах р-Тизобразится (см. рис. 5.3) изолированными точками, являющимися точками пересечения кривых равновесия каждых двух из трех фаз. ОбластиI, II, III здесь – области существования трех разных однородных индивидуальных фаз. Равновесие более чем трех фаз одного и того же вещества, очевидно, невозможно. Формально математически это следует из того, что тогда уравнений связи между неизвестными становится больше числа неизвестных.

Рис. 5.3. Тройная точка в координатах температура – давление. К – критическая точка

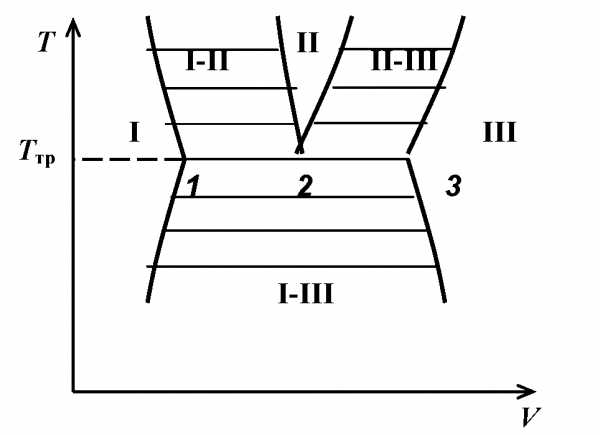
На диаграмме в координатах Т-Vокрестность тройной точки имеет вид, изо­браженный на рис. 5.4, где заштрихованные области – области попар­ного равновесия фаз; удельные объемы трех фаз, находящихся в равновесии в тройной точке, определяются абсциссами точек1, 2, 3.

Рис. 5.4. Тройная точка в координатах давление – температура

Как отмечалось выше, энтальпия и энтропия конденсированных веществ слабо зависит от давления. Поэтому для таких тел при давлениях, не слишком сильно отличающихся от стан­дартных, можно приближенно принять:

G(T,р)_cond = H_T – T·S_T – Т· = 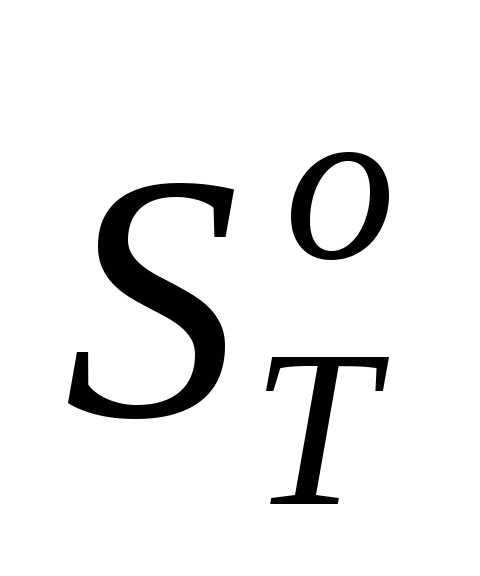

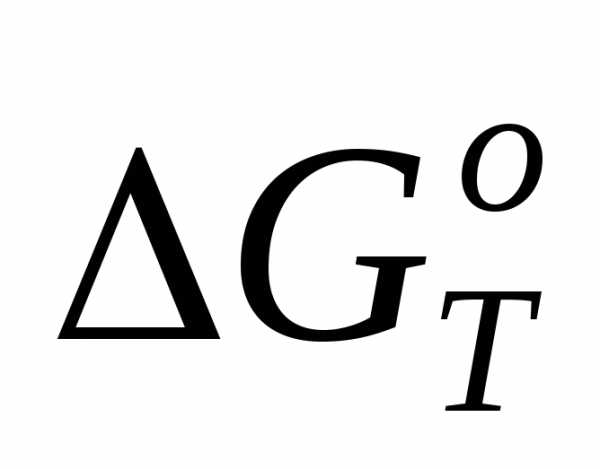
что означает слабую зависимость от давления температур плав­ления и полиморфных превращений в твердых телах. Но такая зависимость все же существует, и связана она, как и для газов, с изменением объема конденсированного тела во время фазового перехода. Это изменение объема приводит к совершению некоторой работы, что и следует учесть при точном расчете фазового равновесия.

Продифференцируем по температуре обе стороны условия равновесия двух фаз, записанного в виде

G_I(р,T) =G_II(р,Т) ,

где G – потенциал Гиббса, приходящийся на один моль. При этом учтем, что давлениерне независимая переменная, а функция температуры, опреде­ляемая этим самым уравнением. Поэтому:

и, поскольку из (3.10) следует, что :

,

где SиV – молярные энтропия и объем, получаем:

.

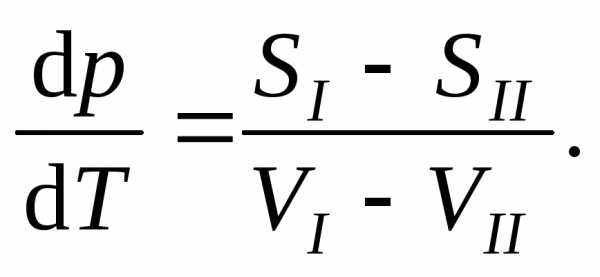В этой формуле разность S_I – S_II можно выразить через реально измеряемую величину – теплоту перехода из одной фазы в другую. ПодставляяH_ф.п. =Т·(S_II – S_I), на­ходим так называемуюформулу Клапейрона – Клаузиуса

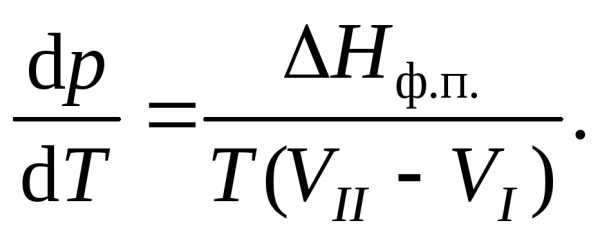
Она определяет изменение давления находящихся в равновесии фаз при изменении температуры, или, другими словами, изменение давления с температурой вдоль кривой равновесия фаз. Та же формула, написанная в виде

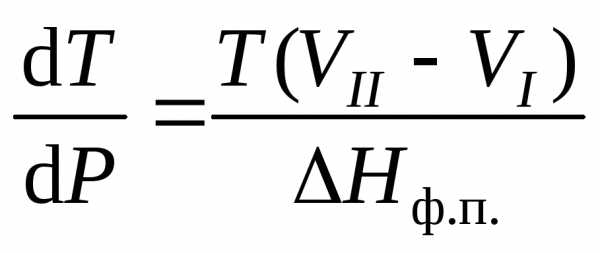
определяет изменение температуры перехода между двумя фазами (напри­мер, точки плавления или кипения) при изменении давления. Так как молекулярный объем газа всегда много больше объема жидкости, а при переходе жидкости в пар тепло поглощается, то, следователь­но, температура кипения при увеличении давления всегда повышается (dT/dр > 0). Точка же плавления при увеличении давления повы­шается или понижается, смотря по тому, увеличивается или умень­шается объем при плавлении. Именно из-за изменения объема при фазовом переходе температура тройной точки не совпадает с температурой фазового перехода при нормальном давлении в 1 ата, которая обычно приводится в справочниках.

studfiles.net

Зависимость давления и плотности насыщенного пара от температуры

Знакомство с изотермами реального газа при различных температурах (см. рис. 6.4) позволяет сделать вывод о том, что давление насыщенного пара возрастает с увеличением температуры. Так как давление насыщенного пара не зависит от объема, то, следовательно, оно зависит только от температуры. Однако зависимость р(Т), найденная экспериментально, не является пропорциональной, как у идеального газа при постоянном объеме (закон Шарля). С увеличением температуры давление насыщенного пара растет быстрее, чем давление идеального газа (рис. 6.5, участок кривой АВ). Это становится особенно очевидным, если провести изохору через точку А (пунктирная прямая). Почему это происходит?

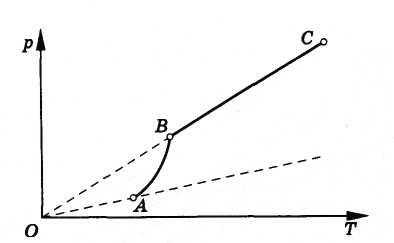
Рис. 6.5

При нагревании жидкости с паром в закрытом сосуде часть жидкости превращается в пар. С ростом температуры увеличивается скорость испарения и равновесие между жидкостью и паром нарушается. Концентрация молекул, а следовательно, и плотность пара возрастают. Так продолжается до тех пор, пока плотность пара не увеличится настолько, что процесс конденсации уравновесит процесс испарения. В результате согласно формуле р = nkT давление насыщенного пара растет не только вследствие повышения температуры, но и вследствие увеличения концентрации молекул (плотности) пара. При этом главную роль в увеличении давления насыщенного пара играет рост концентрации молекул пара, а не повышение его температуры.

Основное различие в поведении идеального газа и насыщенного пара состоит в том, что при изменении температуры пара в закрытом сосуде (или при изменении объема пара при постоянной температуре) меняется масса пара. Жидкость частично превращается в пар или, напротив, пар частично конденсируется. С идеальным газом ничего подобного не происходит.

Когда вся жидкость испарится, пар при дальнейшем нагревании перестанет быть насыщенным и его давление при постоянном объеме будет возрастать прямо пропорционально абсолютной температуре в соответствии с законом Шарля (см. рис. 6.5, участок ВС).

Изотермы реального газа, полученные экспериментально, описывают состояние газа, равновесие между газом и жидкостью и жидкое состояние. С их помощью можно проследить за зависимостью давления насыщенного пара от температуры.

§ 6.4. Критическая температура. Критическое состояние

Вещество может находиться в жидком состоянии не при любой температуре. Есть предел.

Критическая температура

При достаточно высоких температурах горизонтальный участок изотермы реального газа (см. рис. 6.4) становится совсем коротким и при некоторой температуре обращается в точку (на рис. 6.4 — точка К). Эту температуру называют критической. Критической называется температура, при которой исчезают различия в физических свойствах между жидкостью и паром, находящимся с ней в динамическом равновесии. Каждое вещество имеет свою критическую температуру. Например, критическая температура для углекислоты СО₂ равна t_к = 31 °С, а для воды — t_к = 374 °С.

Критическое состояние

Состояние, соответствующее точке К, в которую обращается горизонтальный участок изотермы при температуре Т = Т_к, называют критическим состоянием (критическая точка). Давление и объем в этом состоянии называют критическими. Критическое давление для углекислого газа равно 7,4 · 10⁶ Па (73 атм), а для воды 2,2 · 10⁷ Па (218 атм). В критическом состоянии жидкость имеет максимальный объем, а насыщенный пар — максимальное давление.

studfiles.net