ось бруса — это… Что такое ось бруса?
ОСЬ НЕЙТРАЛЬНАЯ — в сопротивлении материалов, линия в поперечном сечении изгибаемой балки (см. ИЗГИБ БРУСА), в точках к рой норм. напряжения равны нулю. О. н. делит сечение на две части, в одной из к рых норм. напряжения явл. растягивающими, а в другой сжимающими … Физическая энциклопедия
Ось нейтральная — При изгибе бруса волокна его между двумя поперечными сечениями частью удлиняются, частью укорачиваются. В случае простого изгиба, согласно принятой теории (см. Изгиб), в месте перехода от вытянутых волокон к сжатым расположен бесконечно тонкий… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Нейтральная ось — Изогнутая балка. Нейтральный слой показан пунктиром. Его пересечение с поперечным сечением балки даёт нейтральную ось. Нейтральная ось (в сопротивлении материалов) линия в поперечном сечении изгибаемой ба … Википедия
ИЗГИБ — бруса, деформированное состояние, возникающее в брусе под действием сил и моментов, перпендикулярных его оси, и сопровождающееся её искривлением (об И. пластинки и оболочки (см. ПЛАСТИНКИ, ОБОЛОЧКА)). Возникающие при И. в поперечном сечении бруса … Физическая энциклопедия
Изгиб — способ деформации твердого тела, под влиянием действующих на него внешних сил, при котором изменяется кривизна какой либо его геометрической оси. Теоретически разработан преимущественно И. брусьев и стержней, т. е. таких геометрических тел,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Изгиб — в сопротивлении материалов, вид деформации, характеризующийся искривлением (изменением кривизны) оси или срединной поверхности деформируемого объекта (бруса, балки, плиты, оболочки и др.) под действием внешних сил или температуры.… … Большая советская энциклопедия
Изгиб — [bend] 1. Вид деформации, характеризующейся искривлением (изменением кривизны) оси или срединной поверхности деформируемого тела (бруса, балки, плиты, оболочки и др.) под действием внешних сил или температуры. Применительно к прямому брусу… … Энциклопедический словарь по металлургии
Мельницы мукомольные — Этим словом обозначают и большое здание с установленными в нем машинами для получения муки, и нередко очень небольшую, ручную машинку, размалывающую зерна. В отдаленное от нас время размельчение зерен, весьма несовершенное, производилось в ступах … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Повозки военные* — придаются полевым войскам для перевозки боевых припасов, запасных вещей и инструментов, необходимых для содержания в исправности материальной части на походе и в бою, провианта, фуража, канцелярских дел, денежной казны, больных, раненых. В… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Повозки военные — придаются полевым войскам для перевозки боевых припасов, запасных вещей и инструментов, необходимых для содержания в исправности материальной части на походе и в бою, провианта, фуража, канцелярских дел, денежной казны, больных, раненых. В… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Ось бруса — Энциклопедия по машиностроению XXL
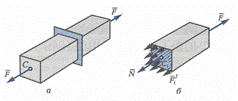
Брусья — элементы конструкций, у которых один размер (длина)значительно больше других (рис, 90, а). Основными геометрическими характеристиками бруса являются его ось и поперечное сечение. Ось бруса — линия, соединяющая центры тяжести всех его поперечных сечений. В зависимости от формы оси брусья могут быть либо прямолинейными (рис. 90, а), либо криволинейными (рис. 90, б). Брус с прямолинейной осью часто называют стержнем. [c.127]Сложный изгиб с растяжением (сжатием) прямого бруса. Если па балку действуют и продольные и поперечные нагрузки, пересекающие ось бруса, то в общем случае (рис. 325, а) в поперечных сечениях возникают изгибающие моменты и в двух плоскостях, поперечные силы и Qy, а также продольная сила М (рис. 325, б). Таким образом, в этом случае будет сложный изгиб с
Ось бруса — это линия, соединяющая центры тяжести его поперечных сечений. [c.6]
Образцы нормальные для испытаний 27 Опоры балки 133 Ось бруса 8 [c.358]
Разрежем брус по некоторому сечению 1—1 на участке АВ. Отбросив верхнюю часть (рис. 2.12, б), определим в сечении 1—I нормальную силу, обозначив ее IV] . На оставленную часть бруса действует только одна сила В, направленная отсечения 1—1. Согласно принятому правилу знаков, ее проекцию на ось бруса считаем положительной. Поэтому
Моменты инерции сечения относительно главных центральных осей называются главными центральными моментами инерции. Плоскости, проведенные через ось бруса и главные оси инерции его поперечного сечения, называются главными плоскостями. [c.196]
При изгибе, как установлено в предыдущих параграфах, под действием поперечных нагрузок продольная ось бруса (балки) искривляется. Если изгиб протекает в пределах упругих свойств материала, т. е. в пределах действия закона Гука, то после снятия нагрузок ось бруса снова выпрямляется. Поэтому изогнутую ось бруса называют упругой линией. По форме, которую при нагружении бруса принимает его упругая линия, можно судить об угловых и линейных перемещениях при изгибе.
Представим себе, что стальной брус круглого поперечного сечения нагружен двумя парами сил таким образом (рис. 2.104, а), что плоскость действия первой перпендикулярна оси бруса, а плоскость действия второй проходит через ось бруса. Тогда момент Aii первой пары скручивает брус, а момент М второй пары его изгибает. При таком нагружении бруса в его поперечных сечениях возникают два внутренних силовых фактора — крутящий и изгибающий А4 моменты, причем по всей длине бруса М =М , [c.240]
Если на брус постоянного сечения с прямолинейной центральной осью действуют внешние силы и пары сил, расположенные в плоскости, проходящей через центральную ось, то ось бруса будет деформироваться. В поперечных сечениях бруса возникают изгибающие моменты, т. е. внутренние моменты, действующие в плоскости, перпендикулярной плоскости поперечного сечения. Такой вид нагружения называют изгибом. Брус, закрепленный на опорах и работающий в основном на изгиб, называется балкой.
Рассмотрим чистый изгиб бруса постоянного поперечного сечения под действием. моментов УИ зр, приложенных на торцах бруса (рис. 11.8). В любом сечении бруса изгибающий момент один и тот же, и изменение кривизны для всех участков будет одинаковым. Поэтому при чистом изгибе ось бруса принимает форму дуги окружности. Верхние волокна бруса удлиняются, а нижние укорачиваются. В средней части бруса находится слой волокон п—п, который не изменяет своей длины. Плоскость, содержащая эти волокна, называется нейтральной плоскостью.
В продольных сечениях, проходящих через ось бруса, действуют также касательные напряжения, которые на основании закона парности касательных напряжений равны напряжениям по поперечному сечению в соответствующих точках. [c.199]
С геометрической точки зрения изгиб бруса сопровождается изменением кривизны оси бруса. Первоначально прямолинейная ось бруса становится криволинейной при его изгибе.
Обозначим радиус кривизны изогнутой оси бруса через р. Удлинение волокна АА будет равно разности длин дуг и 00 , но длина дуги ЛЛх = (р + у)й(б, а дуги ООх = рйв- Мы предположили, что нейтральный слой, а, следовательно, и ось бруса при [c.252]
Если ось бруса вертикальна, то собственный вес вызывает деформацию растяжения или сжатия. Рассмотрим брус постоянного сечения весом С, длиной /, закрепленный верхним концом и нагруженный только собственным весом О (рис. 19.9). [c.200]
Примем ось бруса за oxz, а главные центральные оси инерции поперечного сечения за оси ох-[ и 0x2, при этом ось oxi направим в сторону растянутых волокон (рис. 15).
Ось бруса до деформации a i = a 2=0, как показывают формулы [c.98]
N — продольная сила (проекция главного вектора внутренних сил на ось бруса) [c.5]
При чистом изгибе ось бруса искривляется, а сечения, оставаясь нормальными к изогнутой оси, поворачиваются как абсолютно жесткие диски (рис. 11, б). При этом волокна испытывают растяжение либо- сжатие. Закон распределения деформаций волокон имеет вид [c.11]
Ось бруса искривляется, так как сечения поворачиваются относительно главной центральной оси сечения г. При чистом изгибе имеют место два перемещения поступательное — г/(х) (прогиб балки) и угловое — Фг (х) (угол поворота сечения).
Настоятельно рекомендуем обозначать продольную ось бруса буквой 2, как это принято теперь во всех утвержденных учебниках. Сделано это потому, что по ГОСТам на профили проката буквами X и 1/ обозначены главные центральные оси поперечного сечения. Обозначать, как это иногда делают, продольную ось буквой X, а потом вводить для одной из главных центральных осей букву г, по мнению кафедр сопротивления материалов ряда ведущих вузов, нецелесообразно. [c.56]
Особо следует рассмотреть случай пространственного изгиба бруса круглого поперечного сечения (мы не можем подобрать подходящего специального наименования для этого случая). Очевидно, упругая линия бруса — пространственная кривая, но в то же время в каждом поперечном сечении силовая и нулевая линии взаимно перпендикулярны, что характерно для прямого изгиба. Расчет на прочность ведется (как при обычном прямом изгибе) по результирующему (суммарному) изгибающему моменту. Конечно, сказанное о брусе круглого (сплошного или кольцевого) поперечного сечения справедливо и для бруса с сечением в форме квадрата или любого правильного многоугольника, т. е. для бруса с сечениями, у которых все центральные оси главные. Об этом, естест венно, надо сказать, но расчеты удобнее вести по формулам косого, а не прямого изгиба. [c.141]
Продольная сила в этом сечении N P, эту силу находим, проектируя на ось бруса z внешние и внутренние силы, действующие на оставленную часть. Легко видеть, что то же значение продольной силы сохраняется для любого сечения участка II, т. е. n J=N[=P (для произвольного сечения Ь—Ь, проведенного на II участке, продольная сила определяется на основе рис. 2-1,б). [c.17]
Продольной силой называется сумма проекций на ось Ог (продольную ось бруса) всех внутренних сил, возникающих в поперечном сечении. [c.92]
Продольная ось бруса после деформации остается прямой линией. [c.120]
Кривой брус может быть пространственным и плоским. Если ось бруса представляет собой пространственную кривую, то это пространственный кривой брус. Если же ось бруса плоская кривая, то и брус называется плоским кривым брусом. На практике чаще встречаются плоские кривые брусья с постоянной или переменной кривизной. Примерами плоских кривых брусьев могут служить арки, станины машин, звенья цепей, рым-болты и т. п. (рис. 16.1.1). [c.281]
Если на некотором участке бруса интенсивность = 0 (Q = onst), то ось бруса будет изогнута по кривой третьего порядка. [c.142]
Представим себе заделанный в стену прямой брус (рис. 1.42), Если к концу бруса приложить силу р так, чтобы линия ее действия пересекала ось бруса (рис. 1.42, а), то, как показывает опыт, брус можно только изогнуть. Если же к брусу приложить силу Р, как на рис. 1.42, б, то брус можно не только изогнуть, но и скрутить, так как в последнем случае сила р эквивалентна силе и паре сил с моментом М=Р(с112) (рис, [c.35]
Пример 2.1. Защемленный в сечешш О брус нагружен в сечениях А, В л С осевыми силами, как показано на рис. 2.12, а. Пренебрегая силой тяжести бруса, [c.160]
Плоскость, проходящая через ось бруса и главную ценгра.аьную ось поперечного сечения. — главная плоскость. [c.207]
В обще.м случае продольная сила в произвольном сечении бруса численно равна алгебраической сумма п-роекций на ось бруса всех внешних сил, действующих на тело по одну сторону от сечения. В приведенных примерах все силы действуют по оси бруса, а потому справедливо упрощенное определение, приведенное выше, [c.188]
Введем некоторые понятия. Плоскость, проходящая через одну из главных центральных осей сечения и геометрическую ось бруса, называется главной плоскостью. Плоскость, в которой действуют внешние нагрузки, вызывающие изгиб балки, называется аыовой плоскостью. Линия пересечения силовой плоскости с плоскостью поперечного сечения бруса носит название силовой линии. [c.251]
При прямом изгибе изогнутая ось бруса лежпт в силовой плоскости, при косом — изогнутая ось бруса находится в плоскости, отличной от силовой, [c.251]
Как бы пи проходила силовая плоскость, брус круглого сплошного или трубчатого сечения испытывать косого изгиба не может, так как любая плоскость, проходящая через ось бруса, будет гдав-ной и, следовательно, действующие в ней силы вызовут прямой изгиб. [c.307]
Мир — к1рутящий момент (проекция вектора момента внутренних сил на ось бруса). [c.5]
Прямой изгиб — деформация, вызванная системой сил, перпендикулярных оси бруса, и пар сил, лежащих в одной из главных плоскостей (зруса. Главная плоскость — плоскость, проходящ 1Я через ось бруса и одну из лаи-ных центральных осей инерции сечения. Плоскость хОу (рис. 1.28) — плоскость действия нагрузок — главная плоскоспъ, т. е. она проходит через ось бруса с и главную центральную ось у. [c.24]
Хотя курс сопротивления материалов, изучаемый в техникумах, содержит только р1зсчеты прямого бруса (лнщь в качестве дополнительного вопроса в некоторых техникумах рассматривают расчет тонкостенных сосудов), но учащимся необходимо дать понятие не только о брусе, но и о пластинке, оболочке и массивном теле. Совершенно недостаточно характеризовать брус как тело, одно измерение которого (длина) существенно больще двух других. Надо раскрыть понятие о брусе так, чтобы учащиеся получили четкое представление о поперечном сечении и оси бруса, а далее о типах брусьев (прямые, кривые, ступенчато и непрерывно переменного сечения). [c.53]
Изгибом (в общем смысле) будем называть нагружение бруса, при котором в его поперечных сечениях возникают изги-баюи ий момент и поперечная сила. Можно добавить, что с геометрической точки зрения изгиб характеризуется тем, что первоначально прямолинейная ось бруса обращается в криволинейную (а у кривого бруса изменяется кривизна его оси). [c.118]
Терминология и определения. В большинстве случаев в учебной литературе под термином косой изгиб понимается изгиб бруса нагрузками, расположенными в одной из плоскостей, проходящих через ось бруса, но не совпадающих ни с одной из его главных плоскостей (иногда говорят главных плоскостей инерции). При этом предполагается, что для всего бруса существует единая силовая плоскость. По предлагаемой терминологии этот случай должен быть назван плоским косым изгибом. Наименование плоский обосновано тем, что упругая линия бруса — плоская кривая, а косым изгиб назван потому, что брус гнется не туда, куда его гнут (куда направлена нагрузка), т. е. плоскость изгиба не совпадает с силовой плоскостью. Из сказанного должно быть ясно, что называть простой изгиб бруса плоским крайне неудачно — термин плоский указывает на вид упругой линии (расположение ее в одной плоскости), а это возможно и при косом изгибе. Кроме того, даже просто стилистически неверно противопоставлять плоский изгиб косому, ясно, что логичнее называть простой изгиб прямым, тогда противопоставление оправдано в одном случае изгиб прямой (брус изгибается в направлении действия сил, т. е. в той же плоскости), в другом — косой (брус изгибается косо , т. е. не в плоскости действия нагрузки). [c.140]
В атучаях, когда ось бруса прямолинейна и жесткость поперечного сечения в пределах отдельных участков постоянна, интеграл Мора целесообразно вычислять графоаналитическим методом, применяя правило Верещагина. [c.138]
Ось бруса центральная — Энциклопедия по машиностроению XXL
Моменты инерции сечения относительно главных центральных осей называются главными центральными моментами инерции. Плоскости, проведенные через ось бруса и главные оси инерции его поперечного сечения, называются главными плоскостями. [c.196]Если на брус постоянного сечения с прямолинейной центральной осью действуют внешние силы и пары сил, расположенные в плоскости, проходящей через центральную ось, то ось бруса будет деформироваться. В поперечных сечениях бруса возникают изгибающие моменты, т. е. внутренние моменты, действующие в плоскости, перпендикулярной плоскости поперечного сечения. Такой вид нагружения называют изгибом. Брус, закрепленный на опорах и работающий в основном на изгиб, называется балкой. [c.134]
Примем ось бруса за oxz, а главные центральные оси инерции поперечного сечения за оси ох-[ и 0x2, при этом ось oxi направим в сторону растянутых волокон (рис. 15). [c.96]
Ось бруса искривляется, так как сечения поворачиваются относительно главной центральной оси сечения г. При чистом изгибе имеют место два перемещения поступательное — г/(х) (прогиб балки) и угловое — Фг (х) (угол поворота сечения). [c.14]
Настоятельно рекомендуем обозначать продольную ось бруса буквой 2, как это принято теперь во всех утвержденных учебниках. Сделано это потому, что по ГОСТам на профили проката буквами X и 1/ обозначены главные центральные оси поперечного сечения. Обозначать, как это иногда делают, продольную ось буквой X, а потом вводить для одной из главных центральных осей букву г, по мнению кафедр сопротивления материалов ряда ведущих вузов, нецелесообразно. [c.56]
Особо следует рассмотреть случай пространственного изгиба бруса круглого поперечного сечения (мы не можем подобрать подходящего специального наименования для этого случая). Очевидно, упругая линия бруса — пространственная кривая, но в то же время в каждом поперечном сечении силовая и нулевая линии взаимно перпендикулярны, что характерно для прямого изгиба. Расчет на прочность ведется (как при обычном прямом изгибе) по результирующему (суммарному) изгибающему моменту. Конечно, сказанное о брусе круглого (сплошного или кольцевого) поперечного сечения справедливо и для бруса с сечением в форме квадрата или любого правильного многоугольника, т. е. для бруса с сечениями, у которых все центральные оси главные. Об этом, естест венно, надо сказать, но расчеты удобнее вести по формулам косого, а не прямого изгиба. [c.141]
Плоский изгиб. Рассмотрим брус цилиндрической или призматической формы с прямолинейной центральной осью. Любая плоскость, содержащая центральную ось бруса, называется центральной. [c.143]
Так как за оси х и у нами приняты главные центральные оси инерции площади поперечного сечения бруса, центробежный момент инерции равен нулю, вследствие чего нулю равен и изгибающий момент Му. Поскольку ось х —центральная, статический момент 5 относительно этой оси равен нулю отсюда нулю равна и продольная сила N. [c.117]
Плоскость, проходящая через ось бруса и главную центральную ось поперечного сечения, называется главной плоскостью. [c.312]
Если прямой изгиб является частным случаем поперечного, то косой изгиб — комбинация прямых изгибов в плоскостях Оху и Oxz и есть общий вариант поперечного изгиба. Название этого вида деформации связано с тем, что в общем случае деформированная ось бруса является пространственной кривой. Вариант равенства Jy = Jz в определении исключается, так как в этом случае любая центральная система координат является главной (см. утверждение 3.8). И, следовательно, одну из осей всегда можно совместить с вектором изгибающего момента Мц = = —Му + М к. В результате придем к прямому поперечному изгибу (см. гл. 5). [c.187]
Пример. Рассмотрим изгиб бруса прямоугольного сечения в плоскости [xz)[Ox — центральная ось бруса длиной /, Ь — ширина, h — толщина). Из гипотезы плоских сечений в главе II получена формула [c.246]
Из данного выше определения центрального растяжения сжатия и из уравнений равновесия вида (2.1.6) отсеченной части бруса, образованной поперечным сечением, следуют определенные требования к внешним нагрузкам. Ясно, что центральное растяжение-сжатие бруса возникает только при таких нагрузках на него, при которых отлична от нуля только сумма проекций на ось бруса х всех действующих на отсеченную часть нагрузок. А суммы их проекций на лежащие в плоскости попе- [c.64]
Итак, при центральном растяжении-сжатии прямая до деформации ось бруса остается прямой и при деформации. [c.69]
При центральном растяжении-сжатии ось бруса остается прямолинейной, а плоские до деформации поперечные сечения остаются плоскими и нормальными к оси бруса после деформации. [c.70]
Потенциальную энергию от изгибающих моментов М , т.е. первое слагаемое в формуле (8.7.3), можно получить так же, как получена потенциальная энергия бруса при центральном растяжении сжатии в п. 4.7.1. Для этого рассмотрим элемент балки длиной dx. При его деформации под действием изгибающих моментов Mz ось бруса получит кривизну 1/р = Mz/EJz (см. формулу (8.3.1)), и поэтому правое сечение повернется относительно левого на угол da = dx/р (рис. 8.63). Если условно считать левое сечение неподвижным (т.е. вести рассуждения в системе координат, связанной с левым сечением), то при деформации элемента момент [c.231]
Если ось бруса вертикальна, то его собственный вес вызывает центральное растяжение или сжатие. Если вертикальный брус закреплен верхним концом, то собственного веса он растягивается, а при закреплении нижнего конца — сжимается. Собственный вес вертикального бруса можно рассматривать как продольную (осевую) внешнюю нагрузку, распределенную вдоль оси бруса. [c.45]
Ограничимся рассмотрением брусьев, поперечные сечения которых имеют по меньшей мере одну ось симметрии. Как известно, ось симметрии и перпендикулярная ей центральная ось являются главными центральными осями сечения. Плоскость, проходящая через продольную ось бруса и одну из главных центральных осей его поперечного сечения, называется главной плоскостью бруса (иногда ее называют главной плоскостью инерции). [c.221]
Р] — допускаемое значение силы р — полное напряжение, давление Qx, Яу, С — поперечная сила, действующая соответственно вдоль главной оси X или у, или суммарная д — интенсивность распределенной нагрузки [9] — допускаемое значение интенсивности распределенной нагрузки и — потенциальная энергия деформации и — удельная потенциальная энергия деформации — осевой момент сопротивления сечения, соответственно относительно оси к или у Й7р — полярный момент сопротивления X, у, г — координаты рассматриваемой точки (обозначения осей координат г—продольная ось бруса, х и у — главные центральные оси его поперечного сечения) [c.7]
Плоскость, проходящая через ось бруСа и одну из главных центральных осей инерции его поперечного сечения, называется главной плоскостью инерции. [c.168]
Напомним, что главной плоскостью бруса называется плоскость, проходящая через продольную ось бруса и одну из главных центральных осей инерции его сечения. [c.191]
Рассмотрим сначала случай чистого изгиба бруса, сечение которого обладает двумя осями симметрии, причём изгиб происходит в одной из этих плоскостей. Пусть оси х, у будут осями симметрии поперечного сечения, ось г—центральная продольная ось бруса и (у, г) — плоскость изгиба. Обозначим через х — кривизну центральной оси бруса в результате изгиба, Ь(у) — ширину и Л — высоту сечения (рис. 44). Удовлетворяя условиям совместности дефор-. [c.126]
В данном разделе рассматривается нагружение бруса поперечными силами и парами сил, лежащими в одной, проходящей через ось бруса, плоскости, называемой силовой. Линия пересечения силовой плоскости с плоскостью поперечного сечения называется силовой линией. Если силовая линия совпадает с главной центральной осью, изогнутая ось бруса (его упругая. пиния) располагается в силовой плоскости и такой вид изгиба называется плоским поперечным, в противном случае — косым. Существуют более сложные формы изгиба, которые будут рассмотрены позже. [c.119]
Таким образом, прочность бруса достаточна наибольшее по абсолютному значению напряжение в опасном сечении не превышает [о, =160 МПа. Эпюра суммарных напряжений построена на рис. 2.99, в. Заметим, что нейтральная линия в сечении бруса параллельна центральной оси инерции. [c.235]
Будем рассматривать брусья, поперечные сечения которых имеют хотя бы одну ось симметрии. Как известно, ось симметрии и перпендикулярная ей центральная ось являются главными центральными осями сечения. Если силовая плос- [c.256]
Если силовая плоскость проходит через главную центральную ось у поперечного сечения, то брус (балка) испытывает прямой изгиб в вертикальной плоскости. [c.258]
Как уже было отмечено, поперечный изгиб бруса молглавная центральная ось поперечного сечения, с которой совпадает линия действия изгибающей силы Р, не является осью симметрий сечения . Возникающее в этом случае кручение можно устранить путем приложения изгибающей силы Р по линии, параллельной главной центральной оси и проходящей через определенную точку в плоскости поперечного сечения, называемую центром изгиба. [c.206]
Если брус изгибается только силой Р, параллельной главной центральной оси Хг, то Qjt, = О, Q, = Р и равенство (8.18) принимает вид [c.207]
Система координат выбирается следующим образом начало в центре тяжести поперечного сечения, ось г — по внешней нормали к сечению (т. е. вдоль оси бруса), оси х и у совпадают с так называемыми главными центральными осями сечения (см. гл. V). Если сечение имеет хотя бы одну ось симметрии, то она является главной центральной осью и, следовательно, одной из координатных осей х или у). [c.6]
Плоский косой изгиб бруса возникает под действием нагрузок, плоскость действия которых (силовая плоскость) не совпадает ни с одной из главных плоскостей инерции (рис. 8-2). При этом виде изгиба упругая линия бруса — плоская кривая, н е л е ж а щ а я в силовой плоскости. Если поперечое сечение бруса таково, что любая его центральная ось является главной (некоторые примеры таких сечений представлены на рис. 8-3), то независимо от положения силовой плоскости изгиб будет прямым. [c.180]
При построении эпюр для пространственного бруса применяется скользящая система координат (рис. 9-5). Ось г всегда направлена вдоль оси бруса (для бруса с одним жестко защемленным и другим свободным концом ось 2 направляют в сторону свободного конца). Оси хну совпадают с главными центральными осями инерции рассматриваемого сечения. Оси координат образуют правовинтовую систему. Рекомендуется вначале изобразить систему координат на одном из гори.зонтальных участков, например на участке II (см. рис. 9-5). Ось у направляем вверх, а ось х—вправо (если смотреть с конца оси г). Переход на следующий участок производится путем поворота системы координат вокруг той оси, которая перпендикулярна к плоскости двух данных участков переход от участка II к участку III совершается путем поворота вокруг оси г/а, а от участка II к участку / — вокруг оси Х2- [c.216]
Для бруса, подвергающегося одновременному действию поперечной и осевой нагрузок (а также для бруса с начальной кривизной) говорить о потере устойчивости прямолинейной формы равновесия (в плоскости действия поперечных нагрузок) лишено смысла. Поэтому эйлерова сила должна рассматриваться лишь как некоторое обозначение, введенное по аналогии с формулой Эйлера для критической силы центрально сжимаемого прямолинейного стержня. Формальное различие в вычислении эйлеровой силы и критической силы (по формуле Эйлера) следует из приведенных в тексте указаний о моменте инерции и гибкости. [c.262]
Полученное выражение позволяет вычисли1ь величину касательных напряжений, возникающих в продольных сечениях бруса. Напряжения в поперечных сечениях равны им, как парные. Зависимое ь т от в сечении определяется через статический момент 5. При подходе к верхней кромке сечения площадь заштрихованной части сечения (рис. 146, б) уменьшаечея до нуля. Здесь, следовательно, 5 = 0. При подходе к нижней кромке заштрихованная часть охватывает все сечение. Так как ось х — центральная, то и здесь = 0. Поэтому [c.136]
Введем некоторые понятия. Плоскость, проходящая через одну из главных центральных осей сечения и геометрическую ось бруса, называется главной плоскостью. Плоскость, в которой действуют внешние нагрузки, вызывающие изгиб балки, называется аыовой плоскостью. Линия пересечения силовой плоскости с плоскостью поперечного сечения бруса носит название силовой линии. [c.251]
Прямой изгиб — деформация, вызванная системой сил, перпендикулярных оси бруса, и пар сил, лежащих в одной из главных плоскостей (зруса. Главная плоскость — плоскость, проходящ 1Я через ось бруса и одну из лаи-ных центральных осей инерции сечения. Плоскость хОу (рис. 1.28) — плоскость действия нагрузок — главная плоскоспъ, т. е. она проходит через ось бруса с и главную центральную ось у. [c.24]
В настоящей главе рассмотрен прямой изгиб, возникающий в том случае, когда изгибающрш момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. Прямой изгиб возникает, например, тогда, когда на прямой брус действует нагрузка в виде системы сосредоточенных сил, расположенных в одной плоскости, проходящей через одну из главных центральных осей инерции каждого поперечного сечения бруса в этой же плоскости располагается изогнутая ось бруса. [c.208]
Главной плоскостью бруса называется плоскость, проходящая через ось бруса и одну из главньк центральных осей инерции каждого его поперечного сечения. [c.240]
Гла-вным достижением Бресса в инженерной науке была его теория кривого бруса с ее применениями в проектировании арок ). В первой части этой книги он рассматривает внецентренное сжатие призматического бруса. Частный случай бруса прямоугольного сечения, нагруженного в плоскости симметрии, был уже исследован Томасом Юнгом (см. стр. 117). Бресс ставит задачу в общем виде и показывает, что если построить для поперечного сечения бруса центральный эллипс инерции (рис. 74), то направление нейтральной оси можно легко установить для любого положения нагрузки. Если точку О приложения нагрузки перемещать по прямой m, то нейтральная ось будет оставаться параллельной каса- [c.178]
Изгибом бруса нюывается такая его деформация, которая сопровождается изменением кривизны его осевой линии. Введем понятие продольного волокна как совокупности материальных точек бруса, расположенных непрерывно вдоль линии, параллельной оси бруса. Малый отрезок этой материальной линии назовем малым продольным волокном. Брусья с прямолинейной осью называются балками, если они испытывают преимущественно деформацию изгиба. Рассмотрим изгиб балок постоянного по длине поперечного сечения. При этом ось Ог направим вдоль оси балки, а оси Ох и Оу совместим с главными центральными осями инерции поперечного сечения. Плоскости Охг и Оуг в этом случае называются главными центральными плоскостями инерции балки. Различают балки сплошного и тонкостенного поперечных сечений (см. 1.2). [c.227]
ось бруса — это… Что такое ось бруса?
ось бруса — Линия, соединяющая центры тяжести поперечных сечений бруса. [http://www.isopromat.ru/sopromat/terms] Тематики строительная механика, сопротивление материалов EN axis of beam … Справочник технического переводчика
ОСЬ НЕЙТРАЛЬНАЯ — в сопротивлении материалов, линия в поперечном сечении изгибаемой балки (см. ИЗГИБ БРУСА), в точках к рой норм. напряжения равны нулю. О. н. делит сечение на две части, в одной из к рых норм. напряжения явл. растягивающими, а в другой сжимающими … Физическая энциклопедия
Ось нейтральная — При изгибе бруса волокна его между двумя поперечными сечениями частью удлиняются, частью укорачиваются. В случае простого изгиба, согласно принятой теории (см. Изгиб), в месте перехода от вытянутых волокон к сжатым расположен бесконечно тонкий… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Нейтральная ось — Изогнутая балка. Нейтральный слой показан пунктиром. Его пересечение с поперечным сечением балки даёт нейтральную ось. Нейтральная ось (в сопротивлении материалов) линия в поперечном сечении изгибаемой ба … Википедия
ИЗГИБ — бруса, деформированное состояние, возникающее в брусе под действием сил и моментов, перпендикулярных его оси, и сопровождающееся её искривлением (об И. пластинки и оболочки (см. ПЛАСТИНКИ, ОБОЛОЧКА)). Возникающие при И. в поперечном сечении бруса … Физическая энциклопедия
Изгиб — способ деформации твердого тела, под влиянием действующих на него внешних сил, при котором изменяется кривизна какой либо его геометрической оси. Теоретически разработан преимущественно И. брусьев и стержней, т. е. таких геометрических тел,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Изгиб — в сопротивлении материалов, вид деформации, характеризующийся искривлением (изменением кривизны) оси или срединной поверхности деформируемого объекта (бруса, балки, плиты, оболочки и др.) под действием внешних сил или температуры.… … Большая советская энциклопедия
Изгиб — [bend] 1. Вид деформации, характеризующейся искривлением (изменением кривизны) оси или срединной поверхности деформируемого тела (бруса, балки, плиты, оболочки и др.) под действием внешних сил или температуры. Применительно к прямому брусу… … Энциклопедический словарь по металлургии
Мельницы мукомольные — Этим словом обозначают и большое здание с установленными в нем машинами для получения муки, и нередко очень небольшую, ручную машинку, размалывающую зерна. В отдаленное от нас время размельчение зерен, весьма несовершенное, производилось в ступах … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Повозки военные* — придаются полевым войскам для перевозки боевых припасов, запасных вещей и инструментов, необходимых для содержания в исправности материальной части на походе и в бою, провианта, фуража, канцелярских дел, денежной казны, больных, раненых. В… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Повозки военные — придаются полевым войскам для перевозки боевых припасов, запасных вещей и инструментов, необходимых для содержания в исправности материальной части на походе и в бою, провианта, фуража, канцелярских дел, денежной казны, больных, раненых. В… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Ось — брус — Большая Энциклопедия Нефти и Газа, статья, страница 1
Ось — брус
Cтраница 1
Ось бруса лежит в нейтральном слое, а значит, при изгибе ее длина не изменяется. Следовательно, горизонтальные перемещения отдельных точек оси ( центров тяжести поперечных сечений балки) получаются за счет ее искривления. При малых деформациях упругая линия представляет собой весьма пологую кривую, поэтому горизонтальные перемещения по сравнению с вертикальными ничтожно малы и ими пренебрегают. [1]
Ось бруса считаем заданной в осях OXyZ. [2]
Ось бруса имеет форму окружности. [3]
Ось бруса ОС после деформации остается прямой линией. [4]
Осью бруса называется линия, соединяющая центры тяжести его поперечных сечений. [5]
Осью бруса называют линию, проходящую через центры тяжести всех поперечных сечений. [6]
Если ось бруса вертикальна, то его собственный вес вызывает центральное растяжение или сжатие. Если вертикальный брус закреплен верхним концом, то от собственного веса он растягивается, а при закреплении нижнего конца — сжимается. [7]
Если ось бруса вертикальна, то его собственный вес вызывает центральное растяжение или сжатие. Если вертикальный брус закреплен верхним концом, то от собственного веса он растягивается, а при закреплении нижнего конца-сжимается. [8]
Если ось бруса вертикальна, то собственный вес вызывает деформацию растяжения или сжатия. [9]
Если ось бруса вертикальна, то собственный вес вызывает деформацию растяжения или сжатия. [10]
При изгибе ось бруса искривляется. [11]
Что называется осью бруса. [12]
При центральном растяжении-сжатии ось бруса остается прямолинейной, а плоские до деформации поперечные сечения остаются плоскими и нормальными к оси бруса после деформации. [13]
Для этого параллельно оси бруса проводим тонкую начальную или базовую линию, перпендикулярно которой в определенном масштабе вправо откладываем отрезки, изображающие положительные значения продольной силы, а влево — отрицательные. Получившаяся ступенчатая фигура, ограниченная основной линией и заштрихованная перпендикулярно базовой линии, и есть искомая эпюра нормальных сил по длине бруса. СВ), а далее постоянное отрицательное значение нормальной силы сохраняется во всех поперечных сечениях бруса вплоть до сечения В; при переходе через сечение В эпюра снова испытывает скачок от значения — F до — — F, характеризующий переход от сжатого участка СВ к растянутому В А. Абсолютное значение скачка равно силе 2F, приложенной к брусу в этом сечении. В заключение заметим, что скачки на эпюрах всегда по абсолютному значению равны модулям внешних сил, приложенных в этом месте к брусу. [14]
Расстояния ( вдоль оси бруса) между поперечными сечениями не изменяются. [15]
Страницы: 1 2 3 4
Термины
ТерминыРасчетная схема, модели и гипотезы сопромата
Как и любая наука, сопромат использует моделирование (упрощение с сохранением существенного) своих задач. Модель задачи называется РАСЧЕТНОЙ СХЕМОЙ. Сопромат использует также следующие термины:ДЕФОРМАЦИЯ (в широком смысле слова) — изменение формы и/или размеров тела, вызванное изменением взаимного положения частиц (атомов, молекул) этого тела — под влиянием внешней нагрузки или изменения температуры. Для БРУСА (см ниже) различают деформации (бруса в целом): РАСТЯЖЕНИЕ-СЖАТИЕ (увеличение-уменьшение продольного размера), ИЗГИБ (изменение кривизны продольной оси), КРУЧЕНИЕ (взаимный поворот поперечных сечений относительно продольной оси). Рассматривая элементарный объём тела dV = dx*dy*dz различают 3 ЛИНЕЙНЫЕ деформации (соответственно вдоль осей X,Y,Z) и 3 УГЛОВЫЕ деформации (изменение первоначально прямых углов между координатными осями X,Y,Z). Линейные деформации — АБСОЮТНЫЕ — есть приращение длины отрезка (представьте себе цепочку атомов) при нагружении (=> деформировании) тела. Линейные деформации — ОТНОСИТЕЛЬНЫЕ — есть отношение абсолютных деформаций (приращений длины) к первоначальной величине деформированного отрезка. При уменьшении длины деформируемого отрезка (стремится к нулю) относительная деформация имеет предел, обозначаемый — соответственно вдоль X,Y,Z.
Угловые деформации обозначются, соответственно:- Схематизация формы элементов конструкций.
- БРУС (СТЕРЖЕНЬ) — деформируемое тело один размер которого (длина) во много раз больше двух других (ширина (толщина), высота).
- БАЛКА — брус, расположенный горизонтально. Преобладающей деформацией является ИЗГИБ.
- ОБОЛОЧКА— деформируемое тело один размер которого (толщина) во много раз меньше двух других.
- ПРОДОЛЬНАЯ ОСЬ бруса — линия, проходящая через центры тяжести (центры площади) поперечных сечений бруса.
- ПОПЕРЕЧНОЕ СЕЧЕНИЕ бруса — сечение бруса плоскостью, перпендикулярной продольной оси бруса.
- ЦЕНТРАЛЬНЫЕ ОСИ сечения (плоской фигуры) — оси, проходящие через ЦЕНТР тяжести (центр площади ).
- ГЛАВНЫЕ ОСИ сечения — оси, относительно которых (среди всевозможных осей сечения, проходящих через данную точку) осевые моменты инерции экстремальны (как функция угла наклона оси) (а центробежный момент равен нулю).
- ГЛАВНЫЕ ЦЕНТРАЛЬНЫЕ ОСИ сечения — оси сечения, являющиеся одновременно и главными и центральными.
- ВОЛОКНО — это понятие вводится для повышения наглядности. Под волокном понимают цепочку частиц деформируемого тела. Продольные волокна параллельны продольной оси Z бруса. Реальные волокна существуют в волокнистых материалах, например, дереве. Воображаемые волокна помогают представить картину деформирования.
- Схематизация (внешних) нагрузок (сил).
- По типу контакта.
- СОСРЕДОТОЧЕННЫЕ силы: приложены к части внешней поверхности тела, размеры которой малы в сравнении с размерами тела. На схеме изображается как вектор (стрелка). Будем обозначать: F1, F2, F3 и т д.
- РАСПРЕДЕЛЕННАЯ нагрузка (РН): приложена к части поверхности тела или ко всей поверхности. Для ПОСТОЯННОЙ РН (ПРН) задается её ИНТЕНСИВНОСТЬ. Интенсивность ПРН, распределенной по поверхности тела задается, например, в кН/м2, Па, МПа т е в единицах давления. Интенсивность ПРН, распределенной по длине бруса задается, например, в кН/м. Для непостоянных РН задается закон изменения. Будем обозначать: q1, q2 и т д.
- По закону изменения во времени:
- СТАТИЧЕСКАЯ (постоянная) нагрузка. Во времени не изменяется или изменяется настолько медленно, что возникающими при нагружении деформируемого тела ускорениями и соответствующими силами инерции можно пренебречь. Если не оговорено особо, нагрузка предполагается статической.
- Нагрузка с заданным законом изменения во времени.
- Удар.
- По типу контакта.
- Схематизация материала. Если не оговорено особо, то:
- Материал предполагается ОДНОРОДНЫМ, т е свойства материала в любой точке тела одинаковы (не зависят от координат точки).
- Материал предполагается ИЗОТРОПНЫМ, т е свойства материала не зависят от направления измерения.
- Материал предполагается идеално ЛИНЕЙНО-УПРУГИМ, т е деформация пропорциональна нагрузке (выполняется ЗАКОН ГУКА).
- (Расчетная) схема (задача) называется ПЛОСКОЙ, если продольная ось бруса и внешняя нагрузка расположены в одной плоскости (плоскости рисунка — схемы).
- ВНУТРЕННИЕ СИЛЫ — силы взаимодействия между частицами тела, возникающие в результате деформации.
- МЕТОД СЕЧЕНИЙ (см рис 1) - мысленное разделение тела на две части каким либо сечением. При этом ВНУТРЕННИЕ СИЛЫ взаимодействия между частицами, расположенными вблизи друг от друга, но разделенными сечением, можно рассматривать как ВНЕШНИЕ — для каждой из частей тела. Так как обычно в сопротивлении материалов рассматриваются покоющиеся элементы конструкций, то система внеших сил (включая силы, приложенные со стороны другой части тела), приложенных к каждой из частей тела является УРАВНОВЕШЕННОЙ. Это позволяет составить уравнения равновесия, в которые войдет заданная внешняя нагрузка, приложенная к отсеченной части и неизвестные усилия, приложенные со стороны другой (мысленно отбрасываемой) части тела. Так как число независимых уравнений равновесия для пространственной системы сил равно 6, а для плоской — 3, то мы можем найти не более 6 величин, характеризующих неизвестную систему внутренних сил взаимодействия между частями тела, на которые мы его мысленно разделили сечением. В сопротивлении материалов метод сечений применяется к поперечным сечениям БРУСА (стержня) и позволяет найти 6 характеристик внутренних сил. Эти характеристики называются ВНУТРЕННИМИ СИЛОВЫМИ ФАКТОРАМИ.
- ГРУЗОВОЙ УЧАСТОК — часть бруса, для которой эпюра есть непрерывная линия, выражаемая единой формулой.
Практически сначала определяются ГРАНИЦЫ грузовых участков, а грузовой участок — часть бруса между границами.
Границей грузового участка является сечение:
- — являющееся началом/концом бруса или местом излома продольной оси.
- — в котором приложена сосредоточенная нагрузка или пара сил или начинается/заканчивается распределенная нагрузка.
- — в котором имеется опора (но это — частный случай предыдущего пункта, т к опора создает реакцию — сосредоточенную силу).
Основные понятия и определения. Сопротивление материалов — Студопедия
Сопротивление материалов
ВВЕДЕНИЕ
Курс лекций
Учебная дисциплина «Детали машин и основы конструирования» в базовой части использует методы расчётов на прочность, излагаемые в курсе сопротивления материалов. Краткое изложение этих методов приведено ниже в качестве вводной части к лекционному курсу деталей машин.
Сопротивление материалов (СМ) — раздел механики деформируемого тела, который рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость.
Прочностью называется способность материала конструкции сопротивляться разрушению под действием внутренних напряжений, обусловленных воздействием внешних сил.
Жесткостью называется способность конструкции деформироваться при внешнем воздействии без существенного изменения геометрических размеров.
Устойчивостью называется способность конструкции сопротивляться усилиям, стремящимся вывести ее из состояния равновесия (например, изгибу при действии осевой нагрузки на стержень).
На практике встречаются конструкции сложной формы, которые могут быть представлены состоящими из простых элементов: брусьев, оболочек (пластин) и массивов. Материал тел при этом считается сплошным, однородным и изотропным, т.е. имеющим одинаковые свойства во всех точках по всем направлениям.
Брус, основной расчетный элемент в СМ, — тело, поперечные размеры которого (b x h) малы по сравнению с его длиной l.
Оболочка– тело, толщина которого значительно меньше его размеров в плане. Плоская оболочка называется пластина.
Массив – тело, у которого все его размеры имеют один порядок.
В настоящем учебном курсе рассматриваются только брусья.
Брусья бывают прямолинейными и криволинейными, постоянного и переменного сечения. Брус (горизонтальный или наклонный), работающий в основном на изгиб, называется балка. Брус, работающий в основном на растяжение-сжатие, называется стержень.
Геометрическое место точек, являющихся центрами тяжести поперечных сечений бруса называется его осью (осью балки, стержня).
Плоское сечение, перпендикулярное оси бруса называется поперечным сечением, а параллельное оси – продольным сечением.
При эксплуатации машин и сооружений их элементы подвергаются воздействию различных внешних нагрузок, которые классифицируются по следующим признакам:
Нагрузки активные и реактивные. Активные нагрузки являются первопричиной возникающий деформаций и они обычно известны. Реакции связей возникают в местах закрепления конструктивных элементов (т.е. на опорах) и они определяются из уравнений статического равновесия.
Нагрузки распределенные и сосредоточенные. Все поверхностные нагрузки являются распределенными по поверхности (размерность Н/м2), а в случае бруса – по его оси (размерность Н/м). Объемные нагрузки, такие как вес, считаются распределенными по поверхности, либо сосредоточенными в центре масс элемента. При малой площади распределения нагрузка считается сосредоточенной в точке приложения. Для бруса сосредоточенными считаются силы и моменты, их размерность соответственно Н и Нм.
Нагрузки статические и динамические. Статические нагрузки имеют постоянную величину и место приложения, динамические нагрузки характеризуются переменностью величины, направления или места приложения.
Под действием внешних нагрузок брус деформируется и возникающие при этом внутренние силы упругости уравновешивают внешние силы. Деформации могут быть упругими (линейными и нелинейными), когда после снятия внешней нагрузки тело полностью восстанавливает свои размеры и форму. Если после снятия нагрузки форма и размеры не восстанавливаются полностью, то возникающие деформации называются остаточными (пластическими).
В зависимости от характера и места приложения нагрузки брус деформируется по-разному. Для определения его напряженного состояния применяют метод сечений – брус рассекают плоскостью, перпендикулярной его оси на две части и рассматривают равновесие одной из них.
На рис.2.1 показан прямолинейный брус (стержень), нагруженный продольной силой F. Уравнение равновесия правой части бруса имеет вид:
 SF = 0 или F – N = 0,
SF = 0 или F – N = 0,
откуда найдем F = N.
|
Тогда величина нормального напряжения s, характеризующего интенсивность внутренних сил упругости в точках поперечного сечения (при равномерном распределении сил упругости по сечению) составит
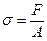 , (2.1)
, (2.1)
где А – площадь поперечного сечения бруса.
Напряжением называется интенсивность внутренних сил в точках поперечного сечения. Напряжение измеряется в паскалях (1 Па = 1 Н/м2) или чаще в мегапаскалях (1 МПа = 1 Н/мм2).
В примере рис.2.1 внутренние силы направлены по нормали к плоскости поперечного сечения и поэтому называются нормальными напряжениями, обозначаемыми буквой s. Внутренние силы в плоскости сечения характеризуются касательными напряжениями, обозначаются буквой t.
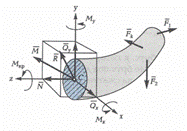 В общем случае нагружения (рис.2.2) все внутренние силы деформированного бруса можно привести к главному вектору
В общем случае нагружения (рис.2.2) все внутренние силы деформированного бруса можно привести к главному вектору  и главному моменту
и главному моменту 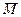 . Располагаем оси декартовых координат так, что начало координат лежит в центре тяжести сечения (на оси бруса), оси x и y — в плоскости сечения, ось z – перпендикулярно сечению.
. Располагаем оси декартовых координат так, что начало координат лежит в центре тяжести сечения (на оси бруса), оси x и y — в плоскости сечения, ось z – перпендикулярно сечению.
|
Разлагаем силовые факторы 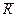 и
и 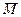 на 6 компонент: три силы N, Qx, Qy и три момента Mx, My и Mкр – они называются внутренними силовыми факторами или силовыми факторами в поперечном сечении.
на 6 компонент: три силы N, Qx, Qy и три момента Mx, My и Mкр – они называются внутренними силовыми факторами или силовыми факторами в поперечном сечении.
Каждая из компонент имеет характерное название и соответствует определенной деформации с соответствующим видом напряжения (см. таблицу 2.1).
Таблица 2.1.
Внутренние силовые факторы и соответствующие напряжения
| Внутренний силовой фактор | Вид деформации | Напряжение в поперечном сечении | ||
| Обозначение | Наименование | Обозначение | Наименование | |
| N | Продольная сила | Растяжение-сжатие | s | Нормальное |
| Qx | Поперечная сила | Сдвиг | t | Касательное |
| Qy | Поперечная сила | Сдвиг | t | Касательное |
| Mx | Изгибающий момент относительно оси х | Изгиб | s | Нормальное |
| My | Изгибающий момент относительно оси y | Изгиб | s | Нормальное |
| Mкр | Крутящий момент вокруг оси z | Кручение | t | Касательное |
Построение гистограмм-NCES Kids ‘Zone
Построение гистограмм
Гистограммы можно использовать, чтобы показать, как что-то меняется со временем, или для сравнения разных времен. Гистограммы хороши для построения данных, охватывающих многие годы (или дни, недели …), имеющих действительно большие изменения от года к году (или день ото дня …), или их можно использовать для сравнения различных элементов в таблице. связанная категория (например: сравнение чего-либо между разными состояниями). На следующих страницах описаны различные части гистограммы.
Название
Название предлагает краткое объяснение того, что находится на вашем графике. Это помогает читателю понять, на что он собирается смотреть. Он может быть креативным или простым, если он сообщает, что изображено на графике. Название этого графика говорит читателю, что график содержит информацию об уровне безработицы среди лиц в возрасте 25 лет и старше за 2004 год с разбивкой по высшему уровню образования.
Источник
Источник объясняет, где вы нашли информацию на вашем графике.Важно отдать должное тем, кто собирал ваши данные! На этом графике источник сообщает нам, что мы нашли информацию из Общего ядра данных NCES.
Ось X
Гистограммы имеют ось x и ось y. В большинстве гистограмм, подобных приведенной выше, ось X проходит горизонтально (плоско). Иногда гистограммы делают так, что столбцы располагаются сбоку, как на графике ниже. Затем на оси абсцисс есть числа, представляющие разные периоды времени или названия сравниваемых вещей.На этих графиках по оси абсцисс обозначены названия состояний.
Ось Y
На большинстве гистограмм, подобных приведенной выше, ось Y проходит вертикально (нас и вниз). Иногда гистограммы делают так, что столбцы располагаются боком, как на графике слева. Тогда ось Y горизонтальна (плоская). Обычно на оси ординат есть числа, обозначающие количество измеряемого материала. Ось Y обычно начинает отсчет с 0 и может быть разделена на любое количество равных частей.На этих гистограммах ось Y измеряет количество школ.
Данные
Самая важная часть вашего графика — это информация или данные, которые он содержит. Гистограммы могут представлять данные разными способами и могут одновременно отображать более одной группы данных. Первый график — это обычная гистограмма с одной группой данных. На втором графике две группы данных, которые сложены. Последний график — это еще один график с двумя группами данных, но они представлены рядом, а не сложены.
Легенда
Легенда сообщает нам, что представляет собой каждая полоса. Как и на карте, легенда помогает читателю понять, на что он смотрит. Примеры легенды можно найти на втором и третьем графиках выше.
Закрыть окно
.r — как установить ось x штрихового графика
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Общественные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним возможности технической карьеры
- Талант Нанять технических талантов
, как удалить пробел между полосами и осью x в ggplot2 в редакции r
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Общественные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним возможности технической карьеры
- Талант Нанять технических талантов
