Что такое ось бруса: Ось бруса — Энциклопедия по машиностроению XXL

Ось бруса — Энциклопедия по машиностроению XXL

Брусья — элементы конструкций, у которых один размер (длина)значительно больше других (рис, 90, а). Основными геометрическими характеристиками бруса являются его ось и поперечное сечение. Ось бруса — линия, соединяющая центры тяжести всех его поперечных сечений. В зависимости от формы оси брусья могут быть либо прямолинейными (рис. 90, а), либо криволинейными (рис. 90, б). Брус с прямолинейной осью часто называют стержнем.  [c.127]
Изложенные выше методы расчетов на прочность для различных видов деформаций предполагают определенную схематизацию элементов конструкций и внешней нагрузки. Так, внешняя нагрузка переносится на ось бруса и прикладывается к ней в виде сил и пар. Полученная таким образом нагрузка на ось может, очевидно, соответствовать действительным способам приложения внешних сил к поверхности бруса. Однако распределение напряжений внутри бруса в том и другом случаях будет не везде одинаковым.  [c.214]

Сложный изгиб с растяжением (сжатием) прямого бруса. Если па балку действуют и продольные и поперечные нагрузки, пересекающие ось бруса, то в общем случае (рис. 325, а) в поперечных сечениях возникают изгибающие моменты и в двух плоскостях, поперечные силы и Qy, а также продольная сила М (рис. 325, б). Таким образом, в этом случае будет сложный изгиб с  [c.338]

Ось бруса — это линия, соединяющая центры тяжести его поперечных сечений.  [c.6]

Образцы нормальные для испытаний 27 Опоры балки 133 Ось бруса 8  

[c.358]

Разрежем брус по некоторому сечению 1—1 на участке АВ. Отбросив верхнюю часть (рис. 2.12, б), определим в сечении 1—I нормальную силу, обозначив ее IV] . На оставленную часть бруса действует только одна сила В, направленная отсечения 1—1. Согласно принятому правилу знаков, ее проекцию на ось бруса считаем положительной. Поэтому  [c.160]

Моменты инерции сечения относительно главных центральных осей называются главными центральными моментами инерции. Плоскости, проведенные через ось бруса и главные оси инерции его поперечного сечения, называются главными плоскостями.  

[c.196]

При изгибе, как установлено в предыдущих параграфах, под действием поперечных нагрузок продольная ось бруса (балки) искривляется. Если изгиб протекает в пределах упругих свойств материала, т. е. в пределах действия закона Гука, то после снятия нагрузок ось бруса снова выпрямляется. Поэтому изогнутую ось бруса называют упругой линией. По форме, которую при нагружении бруса принимает его упругая линия, можно судить об угловых и линейных перемещениях при изгибе.  [c.221]

Представим себе, что стальной брус круглого поперечного сечения нагружен двумя парами сил таким образом (рис. 2.104, а), что плоскость действия первой перпендикулярна оси бруса, а плоскость действия второй проходит через ось бруса.

Тогда момент Aii первой пары скручивает брус, а момент М второй пары его изгибает. При таком нагружении бруса в его поперечных сечениях возникают два внутренних силовых фактора — крутящий и изгибающий А4 моменты, причем по всей длине бруса М =М ,  [c.240]

Если на брус постоянного сечения с прямолинейной центральной осью действуют внешние силы и пары сил, расположенные в плоскости, проходящей через центральную ось, то ось бруса будет деформироваться. В поперечных сечениях бруса возникают изгибающие моменты, т. е. внутренние моменты, действующие в плоскости, перпендикулярной плоскости поперечного сечения. Такой вид нагружения называют изгибом. Брус, закрепленный на опорах и работающий в основном на изгиб, называется балкой.   [c.134]

Рассмотрим чистый изгиб бруса постоянного поперечного сечения под действием. моментов УИ зр, приложенных на торцах бруса (рис. 11.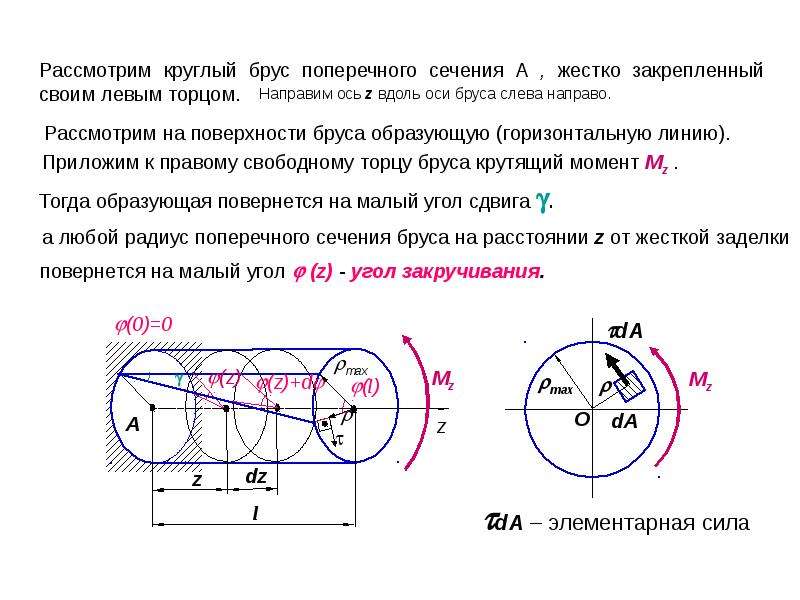 8). В любом сечении бруса изгибающий момент один и тот же, и изменение кривизны для всех участков будет одинаковым. Поэтому при чистом изгибе ось бруса принимает форму дуги окружности. Верхние волокна бруса удлиняются, а нижние укорачиваются. В средней части бруса находится слой волокон п—п, который не изменяет своей длины. Плоскость, содержащая эти волокна, называется нейтральной плоскостью.  

[c.138]

В продольных сечениях, проходящих через ось бруса, действуют также касательные напряжения, которые на основании закона парности касательных напряжений равны напряжениям по поперечному сечению в соответствующих точках.  [c.199]

С геометрической точки зрения изгиб бруса сопровождается изменением кривизны оси бруса. Первоначально прямолинейная ось бруса становится криволинейной при его изгибе.  

[c.251]

Обозначим радиус кривизны изогнутой оси бруса через р. Удлинение волокна АА будет равно разности длин дуг и 00 , но длина дуги ЛЛх = (р + у)й(б, а дуги ООх = рйв- Мы предположили, что нейтральный слой, а, следовательно, и ось бруса при  [c. 252]

Если ось бруса вертикальна, то собственный вес вызывает деформацию растяжения или сжатия. Рассмотрим брус постоянного сечения весом С, длиной /, закрепленный верхним концом и нагруженный только собственным весом О (рис. 19.9).  [c.200]

Примем ось бруса за oxz, а главные центральные оси инерции поперечного сечения за оси ох-[ и 0x2, при этом ось oxi направим в сторону растянутых волокон (рис. 15).  

[c.96]

Ось бруса до деформации a i = a 2=0, как показывают формулы  [c.98]

N — продольная сила (проекция главного вектора внутренних сил на ось бруса)  [c.5]

При чистом изгибе ось бруса искривляется, а сечения, оставаясь нормальными к изогнутой оси, поворачиваются как абсолютно жесткие диски (рис. 11, б). При этом волокна испытывают растяжение либо- сжатие. Закон распределения деформаций волокон имеет вид  [c.11]

Ось бруса искривляется, так как сечения поворачиваются относительно главной центральной оси сечения г.

При чистом изгибе имеют место два перемещения поступательное — г/(х) (прогиб балки) и угловое — Фг (х) (угол поворота сечения).  [c.14]

Настоятельно рекомендуем обозначать продольную ось бруса буквой 2, как это принято теперь во всех утвержденных учебниках. Сделано это потому, что по ГОСТам на профили проката буквами X и 1/ обозначены главные центральные оси поперечного сечения. Обозначать, как это иногда делают, продольную ось буквой X, а потом вводить для одной из главных центральных осей букву г, по мнению кафедр сопротивления материалов ряда ведущих вузов, нецелесообразно.  

[c.56]

Особо следует рассмотреть случай пространственного изгиба бруса круглого поперечного сечения (мы не можем подобрать подходящего специального наименования для этого случая). Очевидно, упругая линия бруса — пространственная кривая, но в то же время в каждом поперечном сечении силовая и нулевая линии взаимно перпендикулярны, что характерно для прямого изгиба. Расчет на прочность ведется (как при обычном прямом изгибе) по результирующему (суммарному) изгибающему моменту. Конечно, сказанное о брусе круглого (сплошного или кольцевого) поперечного сечения справедливо и для бруса с сечением в форме квадрата или любого правильного многоугольника, т. е. для бруса с сечениями, у которых все центральные оси главные. Об этом, естест венно, надо сказать, но расчеты удобнее вести по формулам косого, а не прямого изгиба.  

[c.141]

Продольная сила в этом сечении N P, эту силу находим, проектируя на ось бруса z внешние и внутренние силы, действующие на оставленную часть. Легко видеть, что то же значение продольной силы сохраняется для любого сечения участка II, т. е. n J=N[=P (для произвольного сечения Ь—Ь, проведенного на II участке, продольная сила определяется на основе рис. 2-1,б).  [c.17]

Продольной силой называется сумма проекций на ось Ог (продольную ось бруса) всех внутренних сил, возникающих в поперечном сечении.

 [c.92]

Продольная ось бруса после деформации остается прямой линией.  [c.120]

Кривой брус может быть пространственным и плоским. Если ось бруса представляет собой пространственную кривую, то это пространственный кривой брус. Если же ось бруса плоская кривая, то и брус называется плоским кривым брусом. На практике чаще встречаются плоские кривые брусья с постоянной или переменной кривизной. Примерами плоских кривых брусьев могут служить арки, станины машин, звенья цепей, рым-болты и т. п. (рис. 16.1.1).  

[c.281]

Если на некотором участке бруса интенсивность = 0 (Q = onst), то ось бруса будет изогнута по кривой третьего порядка.  [c.142]

Представим себе заделанный в стену прямой брус (рис. 1.42), Если к концу бруса приложить силу р так, чтобы линия ее действия пересекала ось бруса (рис. 1.42, а), то, как показывает опыт, брус можно только изогнуть. Если же к брусу приложить силу Р, как на рис. 1.42, б, то брус можно не только изогнуть, но и скрутить, так как в последнем случае сила р эквивалентна силе и паре сил с моментом М=Р(с112) (рис,  [c.35]

Пример 2.1. Защемленный в сечешш О брус нагружен в сечениях А, В л С осевыми силами, как показано на рис. 2.12, а. Пренебрегая силой тяжести бруса,  [c.160]

Плоскость, проходящая через ось бруса и главную ценгра.аьную ось поперечного сечения. — главная плоскость.  [c.207]

В обще.м случае продольная сила в произвольном сечении бруса численно равна алгебраической сумма п-роекций на ось бруса всех внешних сил, действующих на тело по одну сторону от сечения. В приведенных примерах все силы действуют по оси бруса, а потому справедливо упрощенное определение, приведенное выше,  [c.188]

Введем некоторые понятия. Плоскость, проходящая через одну из главных центральных осей сечения и геометрическую ось бруса, называется главной плоскостью. Плоскость, в которой действуют внешние нагрузки, вызывающие изгиб балки, называется аыовой плоскостью. Линия пересечения силовой плоскости с плоскостью поперечного сечения бруса носит название силовой линии.  [c.251]

При прямом изгибе изогнутая ось бруса лежпт в силовой плоскости, при косом — изогнутая ось бруса находится в плоскости, отличной от силовой,  [c.251]

Как бы пи проходила силовая плоскость, брус круглого сплошного или трубчатого сечения испытывать косого изгиба не может, так как любая плоскость, проходящая через ось бруса, будет гдав-ной и, следовательно, действующие в ней силы вызовут прямой изгиб.  [c.307]

Мир — к1рутящий момент (проекция вектора момента внутренних сил на ось бруса).  [c.5]

Прямой изгиб — деформация, вызванная системой сил, перпендикулярных оси бруса, и пар сил, лежащих в одной из главных плоскостей (зруса. Главная плоскость — плоскость, проходящ 1Я через ось бруса и одну из лаи-ных центральных осей инерции сечения. Плоскость хОу (рис. 1.28) — плоскость действия нагрузок — главная плоскоспъ, т. е. она проходит через ось бруса с и главную центральную ось у.  [c.24]

Хотя курс сопротивления материалов, изучаемый в техникумах, содержит только р1зсчеты прямого бруса (лнщь в качестве дополнительного вопроса в некоторых техникумах рассматривают расчет тонкостенных сосудов), но учащимся необходимо дать понятие не только о брусе, но и о пластинке, оболочке и массивном теле. Совершенно недостаточно характеризовать брус как тело, одно измерение которого (длина) существенно больще двух других. Надо раскрыть понятие о брусе так, чтобы учащиеся получили четкое представление о поперечном сечении и оси бруса, а далее о типах брусьев (прямые, кривые, ступенчато и непрерывно переменного сечения).  [c.53]

Изгибом (в общем смысле) будем называть нагружение бруса, при котором в его поперечных сечениях возникают изги-баюи ий момент и поперечная сила. Можно добавить, что с геометрической точки зрения изгиб характеризуется тем, что первоначально прямолинейная ось бруса обращается в криволинейную (а у кривого бруса изменяется кривизна его оси).  [c.118]

Терминология и определения. В большинстве случаев в учебной литературе под термином косой изгиб понимается изгиб бруса нагрузками, расположенными в одной из плоскостей, проходящих через ось бруса, но не совпадающих ни с одной из его главных плоскостей (иногда говорят главных плоскостей инерции). При этом предполагается, что для всего бруса существует единая силовая плоскость. По предлагаемой терминологии этот случай должен быть назван плоским косым изгибом. Наименование плоский обосновано тем, что упругая линия бруса — плоская кривая, а косым изгиб назван потому, что брус гнется не туда, куда его гнут (куда направлена нагрузка), т. е. плоскость изгиба не совпадает с силовой плоскостью. Из сказанного должно быть ясно, что называть простой изгиб бруса плоским крайне неудачно — термин плоский указывает на вид упругой линии (расположение ее в одной плоскости), а это возможно и при косом изгибе. Кроме того, даже просто стилистически неверно противопоставлять плоский изгиб косому, ясно, что логичнее называть простой изгиб прямым, тогда противопоставление оправдано в одном случае изгиб прямой (брус изгибается в направлении действия сил, т. е. в той же плоскости), в другом — косой (брус изгибается косо , т. е. не в плоскости действия нагрузки).  [c.140]

В атучаях, когда ось бруса прямолинейна и жесткость поперечного сечения в пределах отдельных участков постоянна, интеграл Мора целесообразно вычислять графоаналитическим методом, применяя правило Верещагина.  [c.138]

---

Ось бруса центральная — Энциклопедия по машиностроению XXL

Моменты инерции сечения относительно главных центральных осей называются главными центральными моментами инерции. Плоскости, проведенные через ось бруса и главные оси инерции его поперечного сечения, называются главными плоскостями.  [c.196]

Если на брус постоянного сечения с прямолинейной центральной осью действуют внешние силы и пары сил, расположенные в плоскости, проходящей через центральную ось, то ось бруса будет деформироваться. В поперечных сечениях бруса возникают изгибающие моменты, т. е. внутренние моменты, действующие в плоскости, перпендикулярной плоскости поперечного сечения. Такой вид нагружения называют изгибом. Брус, закрепленный на опорах и работающий в основном на изгиб, называется балкой.  [c.134]

Примем ось бруса за oxz, а главные центральные оси инерции поперечного сечения за оси ох-[ и 0x2, при этом ось oxi направим в сторону растянутых волокон (рис. 15).  [c.96]

Ось бруса искривляется, так как сечения поворачиваются относительно главной центральной оси сечения г. При чистом изгибе имеют место два перемещения поступательное — г/(х) (прогиб балки) и угловое — Фг (х) (угол поворота сечения).  [c.14]

Настоятельно рекомендуем обозначать продольную ось бруса буквой 2, как это принято теперь во всех утвержденных учебниках. Сделано это потому, что по ГОСТам на профили проката буквами X и 1/ обозначены главные центральные оси поперечного сечения. Обозначать, как это иногда делают, продольную ось буквой X, а потом вводить для одной из главных центральных осей букву г, по мнению кафедр сопротивления материалов ряда ведущих вузов, нецелесообразно.  [c.56]

Особо следует рассмотреть случай пространственного изгиба бруса круглого поперечного сечения (мы не можем подобрать подходящего специального наименования для этого случая). Очевидно, упругая линия бруса — пространственная кривая, но в то же время в каждом поперечном сечении силовая и нулевая линии взаимно перпендикулярны, что характерно для прямого изгиба. Расчет на прочность ведется (как при обычном прямом изгибе) по результирующему (суммарному) изгибающему моменту. Конечно, сказанное о брусе круглого (сплошного или кольцевого) поперечного сечения справедливо и для бруса с сечением в форме квадрата или любого правильного многоугольника, т. е. для бруса с сечениями, у которых все центральные оси главные. Об этом, естест венно, надо сказать, но расчеты удобнее вести по формулам косого, а не прямого изгиба.  [c.141]

Плоский изгиб. Рассмотрим брус цилиндрической или призматической формы с прямолинейной центральной осью. Любая плоскость, содержащая центральную ось бруса, называется центральной.  [c.143]

Так как за оси х и у нами приняты главные центральные оси инерции площади поперечного сечения бруса, центробежный момент инерции равен нулю, вследствие чего нулю равен и изгибающий момент Му. Поскольку ось х —центральная, статический момент 5 относительно этой оси равен нулю отсюда нулю равна и продольная сила N.  [c.117]

Плоскость, проходящая через ось бруса и главную центральную ось поперечного сечения, называется главной плоскостью.  [c.312]

Если прямой изгиб является частным случаем поперечного, то косой изгиб — комбинация прямых изгибов в плоскостях Оху и Oxz и есть общий вариант поперечного изгиба. Название этого вида деформации связано с тем, что в общем случае деформированная ось бруса является пространственной кривой. Вариант равенства Jy = Jz в определении исключается, так как в этом случае любая центральная система координат является главной (см. утверждение 3.8). И, следовательно, одну из осей всегда можно совместить с вектором изгибающего момента Мц = = —Му + М к. В результате придем к прямому поперечному изгибу (см. гл. 5).  [c.187]

Пример. Рассмотрим изгиб бруса прямоугольного сечения в плоскости [xz)[Ox — центральная ось бруса длиной /, Ь — ширина, h — толщина). Из гипотезы плоских сечений в главе II получена формула  [c.246]

Из данного выше определения центрального растяжения сжатия и из уравнений равновесия вида (2.1.6) отсеченной части бруса, образованной поперечным сечением, следуют определенные требования к внешним нагрузкам. Ясно, что центральное растяжение-сжатие бруса возникает только при таких нагрузках на него, при которых отлична от нуля только сумма проекций на ось бруса х всех действующих на отсеченную часть нагрузок. А суммы их проекций на лежащие в плоскости попе-  [c. 64]

Итак, при центральном растяжении-сжатии прямая до деформации ось бруса остается прямой и при деформации.  [c.69]

При центральном растяжении-сжатии ось бруса остается прямолинейной, а плоские до деформации поперечные сечения остаются плоскими и нормальными к оси бруса после деформации.  [c.70]

Потенциальную энергию от изгибающих моментов М , т.е. первое слагаемое в формуле (8.7.3), можно получить так же, как получена потенциальная энергия бруса при центральном растяжении сжатии в п. 4.7.1. Для этого рассмотрим элемент балки длиной dx. При его деформации под действием изгибающих моментов Mz ось бруса получит кривизну 1/р = Mz/EJz (см. формулу (8.3.1)), и поэтому правое сечение повернется относительно левого на угол da = dx/р (рис. 8.63). Если условно считать левое сечение неподвижным (т.е. вести рассуждения в системе координат, связанной с левым сечением), то при деформации элемента момент  [c.231]

Если ось бруса вертикальна, то его собственный вес вызывает центральное растяжение или сжатие. Если вертикальный брус закреплен верхним концом, то собственного веса он растягивается, а при закреплении нижнего конца — сжимается. Собственный вес вертикального бруса можно рассматривать как продольную (осевую) внешнюю нагрузку, распределенную вдоль оси бруса.  [c.45]

Ограничимся рассмотрением брусьев, поперечные сечения которых имеют по меньшей мере одну ось симметрии. Как известно, ось симметрии и перпендикулярная ей центральная ось являются главными центральными осями сечения. Плоскость, проходящая через продольную ось бруса и одну из главных центральных осей его поперечного сечения, называется главной плоскостью бруса (иногда ее называют главной плоскостью инерции).  [c.221]

Р] — допускаемое значение силы р — полное напряжение, давление Qx, Яу, С — поперечная сила, действующая соответственно вдоль главной оси X или у, или суммарная д — интенсивность распределенной нагрузки [9] — допускаемое значение интенсивности распределенной нагрузки и — потенциальная энергия деформации и — удельная потенциальная энергия деформации — осевой момент сопротивления сечения, соответственно относительно оси к или у Й7р — полярный момент сопротивления X, у, г — координаты рассматриваемой точки (обозначения осей координат г—продольная ось бруса, х и у — главные центральные оси его поперечного сечения)  [c. 7]

Плоскость, проходящая через ось бруСа и одну из главных центральных осей инерции его поперечного сечения, называется главной плоскостью инерции.  [c.168]

Напомним, что главной плоскостью бруса называется плоскость, проходящая через продольную ось бруса и одну из главных центральных осей инерции его сечения.  [c.191]

Рассмотрим сначала случай чистого изгиба бруса, сечение которого обладает двумя осями симметрии, причём изгиб происходит в одной из этих плоскостей. Пусть оси х, у будут осями симметрии поперечного сечения, ось г—центральная продольная ось бруса и (у, г) — плоскость изгиба. Обозначим через х — кривизну центральной оси бруса в результате изгиба, Ь(у) — ширину и Л — высоту сечения (рис. 44). Удовлетворяя условиям совместности дефор-.  [c.126]

В данном разделе рассматривается нагружение бруса поперечными силами и парами сил, лежащими в одной, проходящей через ось бруса, плоскости, называемой силовой. Линия пересечения силовой плоскости с плоскостью поперечного сечения называется силовой линией. Если силовая линия совпадает с главной центральной осью, изогнутая ось бруса (его упругая. пиния) располагается в силовой плоскости и такой вид изгиба называется плоским поперечным, в противном случае — косым. Существуют более сложные формы изгиба, которые будут рассмотрены позже.  [c.119]

Таким образом, прочность бруса достаточна наибольшее по абсолютному значению напряжение в опасном сечении не превышает [о, =160 МПа. Эпюра суммарных напряжений построена на рис. 2.99, в. Заметим, что нейтральная линия в сечении бруса параллельна центральной оси инерции.  [c.235]

Будем рассматривать брусья, поперечные сечения которых имеют хотя бы одну ось симметрии. Как известно, ось симметрии и перпендикулярная ей центральная ось являются главными центральными осями сечения. Если силовая плос-  [c.256]

Если силовая плоскость проходит через главную центральную ось у поперечного сечения, то брус (балка) испытывает прямой изгиб в вертикальной плоскости.  [c.258]

Как уже было отмечено, поперечный изгиб бруса молглавная центральная ось поперечного сечения, с которой совпадает линия действия изгибающей силы Р, не является осью симметрий сечения . Возникающее в этом случае кручение можно устранить путем приложения изгибающей силы Р по линии, параллельной главной центральной оси и проходящей через определенную точку в плоскости поперечного сечения, называемую центром изгиба.  [c.206]

Если брус изгибается только силой Р, параллельной главной центральной оси Хг, то Qjt, = О, Q, = Р и равенство (8.18) принимает вид  [c.207]

Система координат выбирается следующим образом начало в центре тяжести поперечного сечения, ось г — по внешней нормали к сечению (т. е. вдоль оси бруса), оси х и у совпадают с так называемыми главными центральными осями сечения (см. гл. V). Если сечение имеет хотя бы одну ось симметрии, то она является главной центральной осью и, следовательно, одной из координатных осей х или у).  [c.6]

Плоский косой изгиб бруса возникает под действием нагрузок, плоскость действия которых (силовая плоскость) не совпадает ни с одной из главных плоскостей инерции (рис. 8-2). При этом виде изгиба упругая линия бруса — плоская кривая, н е л е ж а щ а я в силовой плоскости. Если поперечое сечение бруса таково, что любая его центральная ось является главной (некоторые примеры таких сечений представлены на рис. 8-3), то независимо от положения силовой плоскости изгиб будет прямым.  [c.180]

При построении эпюр для пространственного бруса применяется скользящая система координат (рис. 9-5). Ось г всегда направлена вдоль оси бруса (для бруса с одним жестко защемленным и другим свободным концом ось 2 направляют в сторону свободного конца). Оси хну совпадают с главными центральными осями инерции рассматриваемого сечения. Оси координат образуют правовинтовую систему. Рекомендуется вначале изобразить систему координат на одном из гори.зонтальных участков, например на участке II (см. рис. 9-5). Ось у направляем вверх, а ось х—вправо (если смотреть с конца оси г). Переход на следующий участок производится путем поворота системы координат вокруг той оси, которая перпендикулярна к плоскости двух данных участков переход от участка II к участку III совершается путем поворота вокруг оси г/а, а от участка II к участку / — вокруг оси Х2-  [c.216]

Для бруса, подвергающегося одновременному действию поперечной и осевой нагрузок (а также для бруса с начальной кривизной) говорить о потере устойчивости прямолинейной формы равновесия (в плоскости действия поперечных нагрузок) лишено смысла. Поэтому эйлерова сила должна рассматриваться лишь как некоторое обозначение, введенное по аналогии с формулой Эйлера для критической силы центрально сжимаемого прямолинейного стержня. Формальное различие в вычислении эйлеровой силы и критической силы (по формуле Эйлера) следует из приведенных в тексте указаний о моменте инерции и гибкости.  [c.262]

Полученное выражение позволяет вычисли1ь величину касательных напряжений, возникающих в продольных сечениях бруса.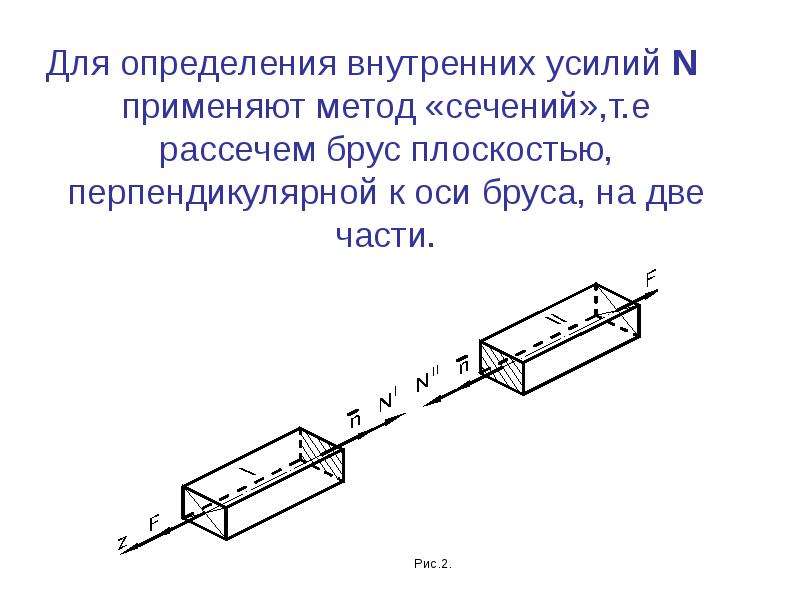 Напряжения в поперечных сечениях равны им, как парные. Зависимое ь т от в сечении определяется через статический момент 5. При подходе к верхней кромке сечения площадь заштрихованной части сечения (рис. 146, б) уменьшаечея до нуля. Здесь, следовательно, 5 = 0. При подходе к нижней кромке заштрихованная часть охватывает все сечение. Так как ось х — центральная, то и здесь = 0. Поэтому  [c.136]

Введем некоторые понятия. Плоскость, проходящая через одну из главных центральных осей сечения и геометрическую ось бруса, называется главной плоскостью. Плоскость, в которой действуют внешние нагрузки, вызывающие изгиб балки, называется аыовой плоскостью. Линия пересечения силовой плоскости с плоскостью поперечного сечения бруса носит название силовой линии.  [c.251]

Прямой изгиб — деформация, вызванная системой сил, перпендикулярных оси бруса, и пар сил, лежащих в одной из главных плоскостей (зруса. Главная плоскость — плоскость, проходящ 1Я через ось бруса и одну из лаи-ных центральных осей инерции сечения. Плоскость хОу (рис. 1.28) — плоскость действия нагрузок — главная плоскоспъ, т. е. она проходит через ось бруса с и главную центральную ось у.  [c.24]

В настоящей главе рассмотрен прямой изгиб, возникающий в том случае, когда изгибающрш момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. Прямой изгиб возникает, например, тогда, когда на прямой брус действует нагрузка в виде системы сосредоточенных сил, расположенных в одной плоскости, проходящей через одну из главных центральных осей инерции каждого поперечного сечения бруса в этой же плоскости располагается изогнутая ось бруса.  [c.208]

Главной плоскостью бруса называется плоскость, проходящая через ось бруса и одну из главньк центральных осей инерции каждого его поперечного сечения.  [c.240]

Гла-вным достижением Бресса в инженерной науке была его теория кривого бруса с ее применениями в проектировании арок ). В первой части этой книги он рассматривает внецентренное сжатие призматического бруса. Частный случай бруса прямоугольного сечения, нагруженного в плоскости симметрии, был уже исследован Томасом Юнгом (см. стр. 117). Бресс ставит задачу в общем виде и показывает, что если построить для поперечного сечения бруса центральный эллипс инерции (рис. 74), то направление нейтральной оси можно легко установить для любого положения нагрузки. Если точку О приложения нагрузки перемещать по прямой m, то нейтральная ось будет оставаться параллельной каса-  [c.178]

Изгибом бруса нюывается такая его деформация, которая сопровождается изменением кривизны его осевой линии. Введем понятие продольного волокна как совокупности материальных точек бруса, расположенных непрерывно вдоль линии, параллельной оси бруса. Малый отрезок этой материальной линии назовем малым продольным волокном. Брусья с прямолинейной осью называются балками, если они испытывают преимущественно деформацию изгиба.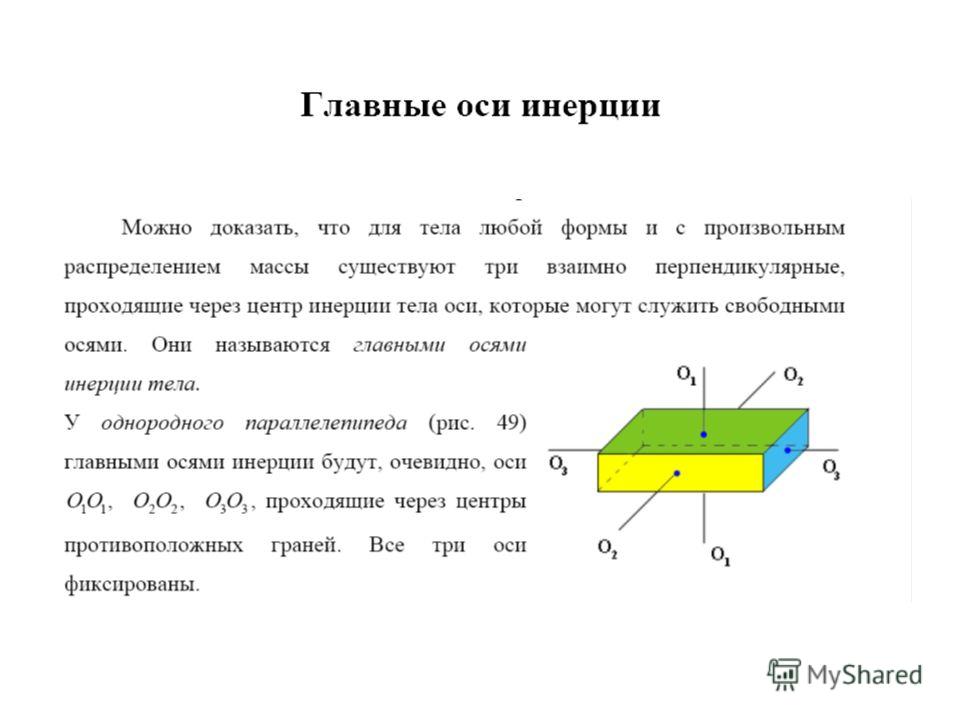 Рассмотрим изгиб балок постоянного по длине поперечного сечения. При этом ось Ог направим вдоль оси балки, а оси Ох и Оу совместим с главными центральными осями инерции поперечного сечения. Плоскости Охг и Оуг в этом случае называются главными центральными плоскостями инерции балки. Различают балки сплошного и тонкостенного поперечных сечений (см. 1.2).  [c.227]

---

Ось — брус — Большая Энциклопедия Нефти и Газа, статья, страница 1

Ось — брус

Cтраница 1

Ось бруса лежит в нейтральном слое, а значит, при изгибе ее длина не изменяется. Следовательно, горизонтальные перемещения отдельных точек оси ( центров тяжести поперечных сечений балки) получаются за счет ее искривления. При малых деформациях упругая линия представляет собой весьма пологую кривую, поэтому горизонтальные перемещения по сравнению с вертикальными ничтожно малы и ими пренебрегают.  [1]

Ось бруса считаем заданной в осях OXyZ.  [2]

Ось бруса имеет форму окружности.  [3]

Ось бруса ОС после деформации остается прямой линией.  [4]

Осью бруса называется линия, соединяющая центры тяжести его поперечных сечений.  [5]

Осью бруса называют линию, проходящую через центры тяжести всех поперечных сечений.  [6]

Если ось бруса вертикальна, то его собственный вес вызывает центральное растяжение или сжатие. Если вертикальный брус закреплен верхним концом, то от собственного веса он растягивается, а при закреплении нижнего конца — сжимается.  [7]

Если ось бруса вертикальна, то его собственный вес вызывает центральное растяжение или сжатие. Если вертикальный брус закреплен верхним концом, то от собственного веса он растягивается, а при закреплении нижнего конца-сжимается.  [8]

Если ось бруса вертикальна, то собственный вес вызывает деформацию растяжения или сжатия.  [9]

Если ось бруса вертикальна, то собственный вес вызывает деформацию растяжения или сжатия.  [10]

При изгибе ось бруса искривляется.  [11]

Что называется осью бруса.  [12]

При центральном растяжении-сжатии ось бруса остается прямолинейной, а плоские до деформации поперечные сечения остаются плоскими и нормальными к оси бруса после деформации.  [13]

Для этого параллельно оси бруса проводим тонкую начальную или базовую линию, перпендикулярно которой в определенном масштабе вправо откладываем отрезки, изображающие положительные значения продольной силы, а влево — отрицательные. Получившаяся ступенчатая фигура, ограниченная основной линией и заштрихованная перпендикулярно базовой линии, и есть искомая эпюра нормальных сил по длине бруса. СВ), а далее постоянное отрицательное значение нормальной силы сохраняется во всех поперечных сечениях бруса вплоть до сечения В; при переходе через сечение В эпюра снова испытывает скачок от значения — F до — — F, характеризующий переход от сжатого участка СВ к растянутому В А. Абсолютное значение скачка равно силе 2F, приложенной к брусу в этом сечении. В заключение заметим, что скачки на эпюрах всегда по абсолютному значению равны модулям внешних сил, приложенных в этом месте к брусу.  [14]

Расстояния ( вдоль оси бруса) между поперечными сечениями не изменяются.  [15]

Страницы:      1    2    3    4

Сопротивление материалов.

Изгиб.

Сопротивление материалов

Изгиб



Основные понятия об изгибе

Деформация изгиба характеризуется потерей прямолинейности или первоначальной формы линией балки (ее осью) при приложении внешней нагрузки. При этом, в отличие от деформации сдвига, линия балки изменяет свою форму плавно.
Легко убедиться, что на сопротивляемость изгибу влияет не только площадь поперечного сечения балки (бруса, стержня и т. д.), но и геометрическая форма этого сечения.

Поскольку изгиб тела (балки, бруса и т. п.) осуществляется относительно какой-либо оси, на сопротивляемость изгибу влияет величина осевого момента инерции сечения тела относительно этой оси.
Для сравнения — при деформации кручения сечение тела подвергается закручиванию относительно полюса (точки), поэтому на сопротивление кручению оказывает влияние полярный момент инерции этого сечения.

На изгиб могут работать многие элементы конструкций – оси, валы, балки, зубья зубчатых колес, рычаги, тяги и т. д.

В сопротивлении материалов рассматривают несколько типов изгибов:
— в зависимости от характера внешней нагрузки, приложенной к брусу, различают чистый изгиб и поперечный изгиб;
— в зависимости от расположения плоскости действия изгибающей нагрузки относительно оси бруса — прямой изгиб и косой изгиб.

***

Чистый и поперечный изгиб балки

Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент (рис. 2).
Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил. Тогда в каждом сечении бруса будут действовать только изгибающие моменты.

Если же изгиб имеет место в результате приложения к брусу поперечной силы (рис. 3), то такой изгиб называется поперечным. В этом случае в каждом сечении бруса действует и поперечная сила, и изгибающий момент (кроме сечения, к которому приложена внешняя нагрузка).

Если брус имеет хоть одну ось симметрии, и плоскость действия нагрузок совпадает с ней, то имеет место прямой изгиб, если же это условие не выполняется, то имеет место косой изгиб.

При изучении деформации изгиба будем мысленно представлять себе, что балка (брус) состоит из бесчисленного количества продольных, параллельных оси волокон.
Чтобы наглядно представить деформацию прямого изгиба, проведем опыт с резиновым брусом, на котором нанесена сетка продольных и поперечных линий.
Подвергнув такой брус прямому изгибу, можно заметить, что (рис. 1):

— поперечные линии останутся при деформации прямыми, но повернутся под углом друг другу;
— сечения бруса расширятся в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне;
— продольные прямые линии искривятся.

Из этого опыта можно сделать вывод, что:

— при чистом изгибе справедлива гипотеза плоских сечений;
— волокна, лежащие на выпуклой стороне растягиваются, на вогнутой стороне – сжимаются, а на границе между ними лежит нейтральный слой волокон, которые только искривляются, не изменяя своей длины.

Полагая справедливой гипотезу о не надавливании волокон, можно утверждать, что при чистом изгибе в поперечном сечении бруса возникают только нормальные напряжения растяжения и сжатия, неравномерно распределенные по сечению.
Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью. Очевидно, что на нейтральной оси нормальные напряжения равны нулю.

***

Изгибающий момент и поперечная сила

Как известно из теоретической механики, опорные реакции балок определяют, составляя и решая уравнения равновесия статики для всей балки. При решении задач сопротивления материалов, и определении внутренних силовых факторов в брусьях, мы учитывали реакции связей наравне с внешними нагрузками, действующими на брусья.
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией – осью, к которой приложены активные и реактивные силы (нагрузки и реакции связей).

Рассмотрим два случая:

1. К балке приложены две равные и противоположные по знаку пары сил.
Рассматривая равновесие части балки, расположенной слева или справа от сечения 1-1 (рис. 2), видим, что во всех поперечных сечениях возникает только изгибающий момент М_и, равный внешнему моменту. Таким образом, это случай чистого изгиба.

Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки.

Обратим внимание на то, что изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента.

2. К балке приложены активные и реактивные силы (нагрузки и реакции связей), перпендикулярные оси (рис. 3). Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибающий момент М_и и поперечная сила Q.
Из этого следует, что в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающему моменту, но и касательные, соответствующие поперечной силе.

Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки.

Обратим внимание на то, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы.

Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным.



У балки, находящейся в равновесии вод действием плоской системы сил, алгебраическая сумма моментов всех активных и реактивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сечения, численно равна сумме моментов всех внешних сил, действующих на балку правее сечения.
Таким образом, изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести сечения всех внешних сил, действующих на балку справа или слева от сечения.

У балки, находящейся в равновесии под действием плоской системы сил, перпендикулярных оси (т. е. системы параллельных сил), алгебраическая сумма всех внешних сил равна нулю; следовательно сумма внешних сил, действующих на балку левее сечения, численно равна алгебраической сумме сил, действующих на балку правее сечения.
Таким образом, поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения.

Так как правила знаков статики неприемлемы для установления знаков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно: Если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот, если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент в сечении считается отрицательным (рис 4,a).

Если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, если равнодействующая направлена вниз, то поперечная сила в сечении считается отрицательной; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 4,b). Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемлённым, а связи отброшенными и замененными реакциями.

Еще раз отметим, что для определения реакций связей пользуются правилами знаков статики, а для определения знаков изгибающего момента и поперечной силы – правилами знаков сопротивления материалов.
Правило знаков для изгибающих моментов иногда называют «правилом дождя», имея в виду, что в случае выпуклости вниз образуется воронка, в которой задерживается дождевая вода (знак положительный), и наоборот – если под действием нагрузок балка выгибается дугой вверх, вода на ней не задерживается (знак изгибающих моментов отрицательный).

***

Материалы раздела «Изгиб»:

Деформация кручения



Главная страница

Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

№ вопроса	1	2	3	4	5	6	7	8	9	10
Правильный вариант ответа	3	1	3	2	3	2	2	1	2	3

7. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ

Изгиб – вид деформации, при котором происходит искривление оси прямого бруса или изменение кривизны кривого бруса. Изгиб плоский (прямой изгиб) – случай изгиба, при котором внешние силы лежат в главной плоскости инерции и являются перпендикулярными к геометрическим осям. Если сечение имеет ось симметрии, то внешние силы располагаются в плоскости симметрии. Главная плоскость инерции – плоскость, проходящая через геометрическую ось бруса и главную ось инерции. Изгиб чистый – вид деформации, при котором из шести внутренних усилий не равно нулю одно – изгибающий момент Mz или My. Изгиб поперечный – случай изгиба, при котором в сечениях бруса наряду с изгибающим моментом М действует и поперечная сила Q. В нагруженном состоянии балка прогибается так, что часть волокон укорачивается, другая часть волокон удлиняется. Нейтральный слой – слой волокон, в котором нормальные напряжения отсутствуют. Нейтральная ось – след пересечения нейтрального слоя с плоскостью поперечного сечения. Балка – конструктивный элемент, с прямолинейной геометрической осью, обычно в виде бруса, работающий главным образом на изгиб. Балка простая – однопролетная балка без консолей, лежащая на двух опорах: шарнирно-подвижной и шарнирно-неподвижной. Расстояние между опорами называют пролетом. Консоль – балка с одним защемленным концом или часть балки, свешивающаяся за опору. Рис. 7.1. Схема взаимного расположения силовой плоскости и плоскостей инерции Силовая плоскость Главные плоскости инерции Опоры и опорные реакции Схемы реальных опорных устройств можно свести к трем типам. Шарнирно-подвижная опора допускает поворот опорного сечения и перемещение его в одном направлении. Опорная реакция перпендикулярно к плоскости опирания катков. Шарнирно-неподвижная опора допускает только поворот опорного сечения балки. Реакция имеет две составляющие: горизонтальную и вертикальную. Жесткая заделка (защемление) не допускает поворота опорного сечения и любых его перемещений. Имеет три реакции: горизонтальную и вертикальную составляющие, а также опорный момент.

Изгиб прямого бруса — Студопедия

Ранее было показано, что деформация изгиба характеризуется возникновением в поперечных сечениях бруса изгибающих моментов и часто – поперечных сил.

При возникновении в сечении бруса только изгибающих моментов, изгиб называют чистым. Если кроме изгибающих моментов возникают поперечные силы, то изгиб называют поперечным.

Деформация изгиба имеет место в результате действия внешних сил, приложенных перпендикулярно к оси бруса. Другим условием возникновения деформации изгиба является действие на брус пары сил действующих в плоскости проходящей через ось бруса. Третьим условием возникновения является одновременное действие двух названных условий.

Внешние силы обычно представляют собой результат действия отдельных частей конструкции, опирающихся на данный брус. Их можно свести к сосредоточенным силам, равномерно или неравномерно распределенным по длине руса нагрузкам и парам сил.

В общем задача изучения плоского изгиба сводится к следующему:

Изучению внутренних сил, возникающих в сечении балки;

Установлению закона распределения внутренних сил (напряжений) по сечению;

Выводу формул для определения напряжений и для подбора сечений балок;

Изучению линейных и угловых перемещений – прогибов и углов поворота поперечных сечений балок.

Рассмотрим брус свободно лежащий на двух опорах, который находится под действием двух сил F₁ и F₂, расположенных в плоскости ее симметрии. Отбросим опоры и заменим их силами реакции F_р1 и F_р2. Определим возникающие при этом внутренние силы при помощи метода сечений.

Сечением 1-1 на расстоянии z от левой опоры рассечем брус на две части, отбросив правую рассмотрим условие равновесия оставшейся части. Очевидно, что действие внутренних сил будет эквивалентно действию отброшенной части бруса на оставшуюся. Заменим действие отброшенной части на оставшуюся внутренними силами, равнодействующая которых рассоложена в плоскости действия внешних сил F_р1 и F₁. Рассмотрев уравнения равновесия, можно показать, что внутренние силы в рассматриваемом сечении приводятся к силе Q_y и паре сил с моментом М_х.

Q_y=F_p1-F₁; M_x=F_p1z-F₁(z-a)

Проекция равнодействующей внутренних сил в сечении на ось, перпендикулярную к оси бруса, называется поперечной силой в рассматриваемом сечении и обозначается Q_y или Q.

Момент равнодействующей внутренних сл относительно центра тяжести рассматриваемого сечения называется изгибающим моментом.

Исходя из условия равновесия можно сделать вывод: поперечная сила в рассматриваемом сечении бруса численно равна алгебраической сумме проекций всех сил, действующих по одну сторону сечения, на ось, перпендикулярную к оси бруса.

Изгибающий момент в рассматриваемом сечении бруса численно равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону сечения, относительно его центра тяжести.

Для выяснения какие напряжения в сечениях бруса будут соответствовать указанным силовым факторам (поперечной силе и крутящему моменту) рассмотрим простейший опыт. Возьмем резиновый брусок прямоугольного сечения, нанеся предварительно на нем продольную линию, и ряд поперечных параллельных между собой линий. Приложим к концам бруса две равные, расположенные в одной плоскости, но противоположные по направлению пары сил с моментом М. В результате опыта оказывается, сто поперечные параллельные линии остались прямыми и нормальными к оси бруса; расстояния между концами на выпуклой стороне увеличились, а на вогнутой уменьшились; расстояния между ними посредине оси балки остались прежними; ширина поперечного сечения сжатой зоны балки увеличилась, а растянутой уменьшилась.

На основе этих опытных данных можно сделать заключение о том, что на выпуклой стороне руса имеет место растяжение, а на вогнутой сжатие. Следовательно, в поперечных сечениях бруса возникают нормальные напряжения. Слой волокон расположенный в середине высоты бруса, не меняет своей длины, а только искривляется. Такой слой называется нейтральным слоем. Нейтральный слой в брусе, испытывающем чистый изгиб, расположен в плоскости, проходящей через центр тяжести сечения.

Опытным путем установлено, что волокна бруса при изгибе испытывают только растяжение и сжатие. Следовательно, для определения нормального напряжения можно воспользоваться законом Гука.

Произведя ряд математических преобразований на основе теории сопротивления материалов, можно получить формулу:

1/ρ – кривизна изогнутой оси бруса;

EJ_x – жесткость сечения бруса;

Данное равенство читается следующим образом: кривизна изогнутой оси бруса прямо пропорциональна изгибающему моменту и обратно пропорциональна жесткости сечения бруса.

И далее формулу для определения нормальных напряжений в симметричных сечениях бруса:

Величина W_x называется осевым моментом сопротивления сечения и является геометрической характеристикой поперечного сечения бруса, определяющей его прочность при изгибе. Данная величина рассчитана для часто применяемых сечений и приводится в справочниках.

Величина осевого момента сопротивления входит в формулу для нормальных напряжений в знаменатель, следовательно, чем больше его значение, тем прочнее брус. С точки зрения экономии материала наиболее рациональными будут сечения, у которых при меньшей площади будут большие моменты сопротивления. Так например более выгодным будет прямоугольное сечение, у которого высота больше ширины, чем квадратное той же площади.

Как было показано напряжения вблизи нейтральной оси незначительны, поэтому целесообразно сосредоточить материал вдали от нее. С этой целью применяют балки в форме швеллера или двутавра. Распространено применение кольцевого сечения.

Для некоторых сечений повышения момента сопротивления можно добиться не увеличением высоты сечения, а наоборот путем ее уменьшения. Например, для круглого сечения момент сопротивления может увеличится если срезать сегменты на высоту 0,11d.

Кроме нормальных напряжений при изгибе имеют место также и касательные напряжения. Действуют они по площадкам параллельным нейтральному слою. Величину касательных напряжений определяют по формуле:

Q – поперечная сила в рассматриваемом сечении;

J_x – момент инерции относительно нейтральной оси всего поперечного сечения бруса;

S_x – статический момент относительно нейтральной оси той части поперечного сечения, которая лежит выше или ниже рассматриваемой площадки;

b – ширина сечения на уровне площадки, по которой определяются касательные напряжения.

НАПРЯЖЕНИЕ ПРИ ИЗГИБЕ И РАСЧЕТ БРУСЬЕВ НА…

Во всех точках поперечного сечения бруса при поперечном изгибе возникают нормальные и касательные напряжения (на рис. 5.1,6 эти напряжения показаны в точках, отстоящих на расстоянии Y от оси X):

Рис. 5.1

Условные обозначения.

Mx, Q — внутренние усилия: изгибающий момент и поперечная сила, они изменяются вдоль бруса и определяются с помощью построения эпюр;

у — координата точек поперечного сечения, в которых определяются напряжения;

b — ширина сечения в месте определения касательных напряжений;

Jx — главный центральный момент инерции -момент инерции относительно центральной оси х,

сx* — статический момент относительно нейтральной оси ж той части площади поперечного сечения, которая расположена выше (или ниже) продольного сечения — выше или ниже уровня у, в точках которого определяются касательные напряжения.

Эти формулы выведены в главных центральных осях поперечного сечения бруса. На рис. 5.1 это оси X, У. При этом ось Y совпадает с осью симметрии сечения, а ось X, перпендикулярная плоскости изгиба, проходит через центр тяжести сечения и является нейтральной осью: нормальные напряжения в точках этой оси равны нулю. Ось Z — ось бруса.

Таким образом, на уровне у напряжения, определяемые вышеприведенными формулами, постоянны, не зависят от координаты X.

С увеличением координаты у нормальные напряжения увеличиваются и в наиболее удаленных от нейтральной оси точках достигают наибольшего значения:

Для расчетов используется специальная геометрическая характеристика — момент сопротивления сечения при изгибе:

Касательные напряжения, наоборот, уменьшаются и в наиболее удаленных от нейтральной оси точках обращаются в нуль, а а области нейтральной оси достигают наибольших значений (рис . Об этом говорит сайт https://intellect.icu . 5.1,г). Кроме того, наибольшие значения касательных напряжений значительно меньше максимальных значений нормальных напряжений: так для консольного стержня прямоугольного поперечного сечения, нагруженного сосредоточенной силой на свободном конце, отношение максимальных значений этих напряжений

где l, h — длина бруса и высота его поперечного сечения.

Поэтому, при l >> h, что имеет место в большинстве случаев, касательные напряжения по сравнению с нормальными пренебрежимо малы и при расчетах на прочность не учитываются.

Условие прочности имеет следующий вид:

— допускаемое напряжение .

Процесс расчета бруса на прочность следует вести в определенной последовательности. При этом необходимо:

Определить весь комплекс внешних сил, в том числе и реакций опор. Прежде всего, необходимо определить все реакции опор, так как реакции входят в число внешних сил. Если при этом число реакций равно числу линейно независимых уравнений статики, то все реакции находятся из статических уравнений. Построить эпюры внутренних усилий , по которым определить опасные сечения. Построение эпюр внутренних усилий выполняется с использованием метода сечений и начинается с деления бруса на участки. Границами участков служат места приложения сосредоточенных сил или моментов, места начала и конца действия распределенных нагрузок.

Далее на каждом участке выбирается произвольное сечение, для которого составляются выражения для определения внутренних усилий, по которым строятся эпюры (графики) этих усилий.

По эпюрам внутренних усилий определяются опасные сечения, в которых эти усилия достигают наибольших значений.

В большинстве случаев основным внутренним усилием при расчетах бруса на прочность является изгибающий момент и связанные с ним нормальные напряжения.

3. В опасных сечениях определить максимальные нормальные напряжения и для наибольшего из этих напряжений проверить выполнение условия прочности.

После определения положения опасных сечений с наибольшими значениями изгибающих моментов, в этих сечениях вычисляют наибольшие нормальные напряжения:

а) Для брусьев из пластичного материала, при равенстве по величине пределов текучести при растяжении и сжатии, наибольшие расчетные напряжения возникают в «опасных» точках, которые наиболее удалены от нейтральной оси.

Эти напряжения сравниваются с допускаемым напряжением :

после чего делается заключение о прочности бруса.

б) Если же брус изготовлен из хрупкого материала: , то в опасных сечениях наибольшие нормальные напряжения определяются и в растянутых, и в сжатых зонах поперечного сечения и путем сравнения их с соответствующими допускаемыми напряжениями при растяжении и сжатии :

решается вопрос о прочности бруса.

Определение столбчатой ​​диаграммы

Что такое гистограмма?

Гистограмма — это диаграмма, на которой данные отображаются с использованием прямоугольных столбцов или столбцов (называемых ячейками), которые представляют общее количество наблюдений в данных для этой категории. Гистограммы могут отображаться с вертикальными столбцами, горизонтальными полосами, сравнительными столбцами (несколько столбцов для отображения сравнения значений) или составными столбцами (столбцы, содержащие несколько типов информации).

Гистограммы обычно используются в финансовом анализе для отображения данных.Диаграмма объема запасов — это обычно используемый тип вертикальной гистограммы. Гистограмма — это пример гистограммы, используемой в статистическом анализе, который отображает распределение вероятностей в некоторых данных или выборке.

Ключевые выводы

• Гистограммы могут быть созданы для отображения данных несколькими наглядными способами.
Гистограммы
• имеют оси X и Y и могут использоваться для демонстрации одной, двух или многих категорий данных.
• Данные представлены в вертикальных или горизонтальных столбцах.
• Столбцы могут содержать несколько помеченных переменных (или только одну), или они могут быть сгруппированы вместе (или нет) для целей сравнения.

Что такое гистограмма

Назначение гистограммы — быстро передать относительную информацию, поскольку столбцы отображают количество для определенной категории. Вертикальная ось гистограммы называется осью y, а нижняя часть гистограммы называется осью x.

При интерпретации гистограммы длина столбцов / столбцов определяет значение, как описано на оси Y.

Ось x может быть любой переменной, например, временем, или категорией, которая измеряется, например, прибылью на акцию (EPS), выручкой и / или денежным потоком. В торговле гистограммы часто используются для отображения объема торгов и отображаются на панели под графиком цен ценной бумаги.

Изображение Сабрины Цзян © Investopedia 2021

Функции гистограммы

Типичная гистограмма имеет метку или заголовок, ось x, ось y, шкалы или приращения для оси и столбцы.Некоторые графики могут также иметь легенду, которая указывает, что представляют различные цвета, например, в столбчатой ​​диаграмме с накоплением.

Гистограммы идеально подходят для сравнения двух или более значений или значений с течением времени. Данные отображаются либо по горизонтали, либо по вертикали. Отдельные гистограммы используются для отображения дискретных значений элемента в категории. Например, гистограмма может отображать количество мужчин с определенной чертой для определенного возраста. Дискретное значение или количество случаев, когда у человека есть определенная черта, отображается путем изменения длины полосы.Больше экземпляров означает более длинную полосу, а меньшее количество экземпляров означает более короткую полосу. В этом примере для каждой возрастной или возрастной группы установлена ​​своя планка.

В техническом анализе график объема показывает, какой объем был в каждый конкретный день. Ось X показывает дни, а полоса, идущая вверх с этого дня, показывает, какой объем был по оси Y.

Если на графике есть четко определенная нулевая точка, а набор данных имеет как положительные, так и отрицательные значения по отношению к этой точке, столбцы все еще могут отображаться.Полосы над нулевой линией обычно представляют положительные значения (проверьте шкалу), а столбцы под нулевой линией обычно показывают отрицательные значения.

Данные могут отображаться горизонтально или вертикально. Для переключения ориентации переключаются оси x и y.

Типы гистограмм

Сгруппированные гистограммы

Сгруппированные гистограммы, также называемые сгруппированными гистограммами, представляют дискретные значения для нескольких элементов, относящихся к одной и той же категории.

Гистограмма может отображать количество людей, мужчин и женщин, с определенной чертой для определенного возраста.Совокупное количество экземпляров можно объединить в одну панель. В качестве альтернативы, экземпляры могут оставаться разделенными по полу; одна полоса для всех мужских экземпляров и одна полоса для всех женских экземпляров будут помещены рядом для каждой возрастной или возрастной группы.

Гистограммы с накоплением

Сложенные гистограммы или составные гистограммы делят совокупную сумму на части. Эти части обычно обозначаются разными цветами для каждой секции. В приведенном выше примере совокупность экземпляров как для мужчин, так и для женщин может быть объединена в одну полосу, но панель может быть разделена на несколько секций, представленных разными цветами.

Сложенные столбцы требуют легенды или специальной маркировки, чтобы определить, что показывают различные части полосы.

Гистограммы в техническом анализе

В некоторых формах технического анализа используются гистограммы. Например, трейдеры могут использовать гистограмму расхождения конвергенции скользящих средних (MACD), которая является популярным техническим индикатором, показывающим разницу между линией MACD и сигнальной линией.

Следующий дневной график Apple Inc.акций показывает три типа гистограмм.

Изображение Сабрины Цзян © Investopedia 2021

Справа находится цена по объему, тип горизонтальной гистограммы, которая показывает разброс объемов в зависимости от цены.

Внизу диаграммы объем — это тип вертикальной гистограммы, на которой показаны столбцы, представляющие количество акций, торгуемых за день.

Наконец, гистограмма MACD показывает разделение между MACD и сигнальной линией. Когда гистограмма пересекает нулевую линию, это означает, что MACD и сигнальная линия пересеклись, что некоторые трейдеры используют в качестве торгового сигнала.

Столбиковая диаграмма против гистограммы

Гистограмма отображает данные в столбцах, а гистограмма — это термин технического анализа, описывающий отображение цен открытия, максимума, минимума, закрытия (иногда открытие не указывается) для конкретной ценной бумаги в течение определенного периода времени с использованием вертикальной полосы. . Маленькие горизонтальные линии проходят слева и справа от вертикальной полосы, показывая цены открытия и закрытия.

В отличие от гистограммы, полоса цен охватывает только релевантные цены и не простирается полностью вверх от оси абсцисс.

Ограничения гистограммы

Гистограмма — это способ отображения информации. Выбор данных для отображения может повлиять на их интерпретацию. Например, если выбран слишком большой масштаб, данные могут показаться незначительными, хотя на самом деле они могут быть очень значительными, но масштаб не позволяет провести соответствующее сравнение.

Гистограммы также могут сделать данные привлекательными, хотя на самом деле им может не хватать содержания. Как и в случае со всеми данными, проверьте источник, из которого они поступают, и убедитесь, что это достаточно большой пул или образец.

Например, просмотр данных об объеме акций всего за несколько дней не дает много релевантной информации. Тем не менее, если посмотреть, как недавний объем сравнивается с объемом за последний год, технический трейдер получит больше информации для анализа объема.

Построение гистограмм-NCES Kids ‘Zone

Построение гистограмм

Гистограммы можно использовать, чтобы показать, как что-то меняется с течением времени, или для сравнения разных периодов времени. Гистограммы хороши для отображения данных за многие годы (дни, недели.. .), имеет действительно большие изменения из года в год (или изо дня в день …), или их можно использовать для сравнения различных элементов в связанной категории (например, для сравнения чего-либо между разными состояниями). На следующих страницах описаны различные части гистограммы.

Название

Название предлагает краткое объяснение того, что находится на вашем графике. Это помогает читателю понять, на что он собирается смотреть. Он может быть творческим или простым, если он говорит о том, что изображено на графике.Название этого графика говорит читателю, что график содержит информацию об уровне безработицы среди лиц в возрасте 25 лет и старше за 2004 год с разбивкой по высшему уровню образования.

Источник

Источник объясняет, где вы нашли информацию на своем графике. Важно отдать должное тем, кто собирал ваши данные! На этом графике источник сообщает нам, что мы нашли информацию из Общего ядра данных NCES.

Ось X

Гистограммы имеют ось x и ось y. В большинстве гистограмм, подобных приведенной выше, ось X проходит горизонтально (плоско). Иногда столбиковые диаграммы строятся так, что столбцы располагаются сбоку, как на графике ниже. Затем на оси абсцисс есть числа, представляющие разные периоды времени или названия сравниваемых вещей. На этих графиках по оси абсцисс обозначены названия состояний.

Ось Y

На большинстве гистограмм, подобных приведенной выше, ось Y проходит вертикально (нас и вниз).Иногда столбиковые диаграммы делают так, что столбцы располагаются боком, как на графике слева. Тогда ось Y горизонтальна (плоская). Обычно на оси ординат есть числа, обозначающие количество измеряемого материала. Ось Y обычно начинает отсчет с 0 и может быть разделена на любое количество равных частей. На этих гистограммах ось Y измеряет количество школ.

Данные

Самая важная часть вашего графика — это информация или данные, которые он содержит.Гистограммы могут представлять данные разными способами и могут представлять более одной группы данных одновременно. Первый график — это обычная гистограмма с одной группой данных. Второй график содержит две группы данных, которые сложены друг с другом. Последний график — это еще один график с двумя группами данных, но они представлены рядом, а не сложены.

Легенда

Легенда сообщает нам, что представляет собой каждая полоса.Как и на карте, легенда помогает читателю понять, на что он смотрит. Примеры легенды можно найти на втором и третьем графиках выше.

Close Window

Bar Graph — Узнайте о столбчатых диаграммах и столбчатых диаграммах

Что такое гистограмма, используемая для

Гистограмма (также известная как гистограмма или гистограмма) — это визуальный инструмент, который использует столбцы для сравнения данных между категориями. Гистограмма может располагаться горизонтально или вертикально.Важно знать, что чем длиннее полоса, тем больше ее значение.

Гистограммы состоят из двух осей. На вертикальной гистограмме, как показано выше, горизонтальная ось (или ось x) показывает категории данных. В этом примере это годы. Вертикальная ось (или ось Y) — это масштаб. Цветные полосы — это ряд данных.

Гистограммы имеют три ключевых атрибута:

• Столбиковая диаграмма упрощает быстрое сравнение наборов данных между различными группами.
• График представляет категории на одной оси и дискретное значение на другой. Цель состоит в том, чтобы показать взаимосвязь между двумя осями.
Гистограммы
• также могут отображать большие изменения данных с течением времени.

Столбиковая диаграмма против линейной диаграммы

Гистограммы отображают данные аналогично линейным графикам. Линейные графики полезны для отображения небольших изменений тенденции во времени. Гистограммы лучше подходят для сравнения больших изменений или различий в данных между группами.

Когда использовать гистограмму

Гистограммы — это эффективный способ сравнения элементов между разными группами. Эта гистограмма показывает сравнение чисел на квартальной основе за четырехлетний период времени. Пользователи этой диаграммы могут сравнивать данные по кварталам в годовом тренде, а также видеть, как годовые продажи распределяются в течение каждого года.

Гистограммы — чрезвычайно эффективный визуальный элемент для использования в презентациях и отчетах. Они популярны, потому что позволяют читателю распознавать закономерности или тенденции гораздо легче, чем смотреть на таблицу числовых данных.

Типы гистограмм

При визуальном представлении данных следует учитывать несколько различных стилей гистограмм.

Вертикальная гистограмма

Самый распространенный тип гистограммы — это вертикальная гистограмма. Это очень полезно при представлении ряда данных с течением времени.

Одним из недостатков вертикальных гистограмм является то, что они не оставляют много места в нижней части диаграммы, если требуются длинные метки.

Горизонтальная гистограмма

Преобразование вертикальных данных в горизонтальную гистограмму решает эту проблему.По вертикальной оси достаточно места для длинной метки, как показано ниже.

Гистограмма с накоплением

Гистограмма с накоплением — это визуальный элемент, который может передавать много информации.

Убедитесь, что вы выбрали тип графика, который наилучшим образом представляет данные, которые вы хотите выделить.

Как создать гистограмму

Шаг первый — убедиться, что данные отформатированы правильно для гистограммы.

На вкладке «Вставить » в SmartDraw щелкните Graph и выберите тип Bar Graph..

Выберите файл данных для импорта, и SmartDraw автоматически сгенерирует гистограмму.

После импорта вы можете легко изменить заголовок, размещение легенды и даже быстро изменить тип графика с помощью опций Edit Graph или просто дважды щелкнув импортированную диаграмму.

Как изменить вертикальную ось на гистограмме Excel

i Jupiterimages / Comstock / Getty Images

Microsoft Excel 2007 — это программа для работы с электронными таблицами, которая помогает сортировать и классифицировать большие объемы данных.Он также может помочь вам в создании профессионально выглядящих графиков, в том числе гистограмм. Гистограмма — это диаграмма, на которой есть столбцы для представления данных. Вкладка «Инструменты диаграммы» в Excel, расположенная на ленте (верхняя панель инструментов), дает вам сотни вариантов настройки гистограмм, включая размещение, цвет, заливку и ориентацию. После того, как вы создали гистограмму в Excel, вы можете изменить параметры вертикальной оси на гистограмме с помощью инструментов диаграммы.

Шаг 1

Щелкните вертикальную ось гистограммы.

Step 2

Щелкните вкладку «Макет» в разделе «Инструменты диаграммы».

Шаг 3

Щелкните «Выбор формата». Первая вкладка во всплывающем окне, «Параметры оси», позволяет вам изменять общие параметры, такие как интервал между делениями и размещение меток осей. Например, если вы хотите, чтобы метки вертикальной оси отображались перед полосами (а не посередине), щелкните переключатель «Между отметками» в разделе «Ось положения».

Step 4

Выберите размещение вертикальной оси на вкладке «Параметры оси».Для вертикальной оси под гистограммой выберите «низкий» в раскрывающемся меню рядом с «Метки осей». Для оси над полосами выберите «Высокий» в раскрывающемся меню.

Step 5

Щелкните вкладку «Заливка» во всплывающем окне «Выбор формата», чтобы дать вашим числам фон или заливку. Щелкните переключатель «Градиентная заливка» для градиентной заливки или щелкните «Сплошная заливка» для получения сплошного фона с числами.

Шаг 6

Измените выравнивание текста с горизонтального (чтение по горизонтали) на вертикальное (чтение сверху вниз), щелкнув вкладку «выравнивание» и выбрав «Повернуть весь текст на 90 градусов» в раскрывающемся меню. поле рядом с надписью «Направление текста.»Вы также можете выбрать пользовательские углы и поля на этой вкладке.

Свойства столбчатой ​​диаграммы — Ось категории

Опция	Описание
Колонны	Задает столбец или иерархия, которые будут отображаться на оси категорий.
Настройки …	Открывает Передовой Диалог настроек, в котором вы можете изменить режим масштабирования из категоричный на непрерывный и наоборот, а также изменяющийся режим категории, чтобы определить, какие комбинации показывать.
Диапазон
Мин.	Определяет нижнее значение диапазона оси. Оставьте поле пустым, чтобы автоматически отрегулируйте диапазон до самого низкого на данный момент значения в отфильтрованном данные.
Макс	Определяет верхнее значение диапазона оси.Оставьте поле пустым, чтобы автоматически отрегулируйте диапазон до самого высокого на данный момент значения в отфильтрованном данные.
Набор к текущему диапазону	Позволяет установить ось диапазон до текущих отфильтрованных значений.
Включить происхождение	Доступно только для непрерывных осей.Всегда включает координаты (0, 0) в визуализацию, независимо от фильтрации.
Показать ползунок масштабирования	Показывает ползунок масштабирования, который можно вручную манипулировать, чтобы просматривать только интересные столбцы на гистограмме.
Показать линии сетки	Указывает, должны ли линии сетки быть видимым. Комментарий: это относится к вертикальным линиям сетки. на вертикальной гистограмме и горизонтальные линии сетки на горизонтальной гистограмма.
Масштаб этикетки
Показать этикетки	Задает должны ли быть видны метки шкалы.
Горизонтально	Показывает масштаб надписи по горизонтали.
Вертикально	Показывает масштаб этикетки вертикально.
Макс. количество этикеток	Выбрать установите флажок, чтобы указать максимальное количество меток шкалы, которые будут показано. Ограничение количества этикеток может улучшить читаемость на оси масштабируются с множеством значений.
Этикетка Рендеринг…	[Доступно только когда только выбранный столбец может быть категориальным. Например, если выбранный столбец является строковым или двоичным столбцом.] Открывает этикетку Диалог рендеринга, в котором вы можете изменить метод рендеринга подписей осей от текста к изображениям в соответствующих случаях.
Масштаб
Журнал шкала	В наличии только для непрерывных осей.Изменяет масштаб с линейного масштаба в десятичной логарифмической шкале [log10 (x)].
Реверс шкала	Реверс текущий порядок сортировки, чтобы отображалось наименьшее значение вверху шкалы.

Где начать и закончить шкалу оси Y

Дебаты по оси Y — одни из самых горячо обсуждаемых среди крутых компьютерных ботаников, таких как я и мои друзья.Идти со мной выпить — либо утомительно, либо утомительно, в зависимости от твоего уровня ботаника. Итак, позвольте мне прояснить параметры дискуссии, в том числе о том, где ботаники в основном согласны, а где нет, и что я советую. Этот пост является обновлением того, что я написал много лет назад, и с тех пор мое мышление изменилось.

Специалисты по компьютерной визуализации согласны с тем, что столбиковые диаграммы должны начинаться с нуля.

Общая идея заключается в том, что зритель должен иметь возможность использовать линейку для измерения частей вашей визуализации и обнаруживать, что измерения пропорциональны данным, которые они представляют.

В случае гистограммы это означает, что ось y всегда должна начинаться с нуля.

Полосы на гистограмме кодируют данные по их длине, поэтому, если мы усечем длину, начав ось с какого-то другого значения, кроме нуля, мы плохо искажаем визуальное представление. Мой друг Крис Лизи называет это «Осью кабельных новостей», потому что это очень распространено в программах новостей на телевидении.

Любители данных не всегда согласны с тем, что графики других типов должны начинаться с нуля.

За пределами столбчатых диаграмм вопрос о том, должна ли ось y начинаться с нуля, все еще остается предметом споров. Бывают случаи, когда в этом нет никакого смысла.

Если ноль не входит в область возможных точек данных, возможно, его не нужно включать в ось и

Визуализация активности фондового рынка — отличный пример. Если бы ось y начиналась с нуля, визуальный элемент выглядел бы как плоская линия. Мы не увидим никаких вариаций, и изображение станет для нас бессмысленным.Но (скрещенные пальцы) ноль не является возможной точкой данных в наборе данных по фондовому рынку, поэтому нет никакого реального оправдания начинать ось с нуля.

Кроме столбчатых диаграмм, я рекомендую ось и , основанную на чем-то разумном для ваших данных. Может быть, минимум оси — это ваша исторически самая низкая точка. Может быть, этот минимум должен быть той точкой, когда вам нужно будет предупредить начальство. Может быть, минимум — это момент, когда ваша команда решила, что нужен другой образ действий.Что бы вы ни выбрали, просто выберите. Сделайте это осмысленным и преднамеренным. Это не то, что программа автоматически решает за вас (хотя это место для начала вашего мыслительного процесса).

Любители данных не всегда соглашаются, где должна заканчиваться шкала.

Некоторые считают, что, например, части целых данных всегда должны выполняться в масштабе, который достигает 100%.

Я думаю, что это сжимает данные и создает неудобный график, на котором мы не можем полностью увидеть, что происходит.Подобно моему руководству относительно того, где должен заканчиваться график, маловероятно, что какой-либо из этих столбцов когда-либо достигнет 100%, поэтому, в моих последних размышлениях о масштабах осей, он не должен доходить до 100%.

Мы действительно сможем увидеть данные более четко, если выберем ось, которая находится ближе к тому, где заканчиваются наши реальные данные.

Несмотря на то, что это дает нашим данным полное представление, оно может упустить части истории. Эти варианты ответов на опрос (а не данные, которые я полностью собрал) взяты из Human Rights Campaign.Скажем, в качестве гипотетического случая они были заинтересованы в вербовке некоторых людей, которые говорили «нет», в тех, кто сказал «нет», но я идентифицирую себя как союзник. Предположим, они знают, что не изменят мнения всех в группе «Нет», но они поставили цель увеличить процент, сообщающих о союзниках, до 75%. Это должно стать новым максимумом для этой шкалы.

и, желательно, обозначим цель как таковую, чтобы наши рассуждения были очевидны. Дело в том, что вы должны выбрать максимум для своего масштаба, который имеет смысл.Может быть, максимум — это ваша цель или ваша самая успешная кампания. Таким образом, сама ось становится частью истории, которую вам нужно рассказать о ваших данных.

Этот и другие советы являются частью второго издания документа «Эффективное представление данных», вышедшего в июне 2017 г. и уже доступного для предварительного заказа.

Создание синхронизированной гистограммы осей

В столбчатой ​​диаграмме масштаб (нормальный vs.log) и диапазон (от минимума до максимума) оси Y критически важны для понимания бизнес-метрик, таких как доходы и расходы. В двухосных гистограммах, где две метрики отображаются рядом, общая шкала оси Y сразу суммирует различия между этими двумя метриками.

Например, при быстром взгляде на эту диаграмму слева кажется, что доход и прибыль почти одинаковы, что вводит в заблуждение конечных пользователей. Как видно на диаграмме справа, линейчатая диаграмма с синхронизированными осями позволяет пользователям быстро визуально понять истинную взаимосвязь.Пользователи могут включить это на существующих двойных гистограммах, щелкнув ось правой кнопкой мыши или изменив тип визуализации на «Синхронизированная гистограмма осей».

1. Открыть досье.
2. На верхней панели инструментов щелкните Вставить визуализацию .
3. Выберите Bar > Синхронизированная линейчатая диаграмма осей .
4. Дважды щелкните, чтобы добавить как минимум два показателя и один атрибут.

5. Чтобы отменить синхронизацию, щелкните правой кнопкой мыши по оси и снимите флажок Синхронизировать масштаб оси .